Abstract
This paper is devoted to the numerical treatment of two-dimensional Fredholm integral equations, defined on general curvilinear domains of the plane. A Nyström method, based on a suitable Gauss-like cubature formula, recently proposed in the literature is proposed. The convergence, stability and good conditioning of the method are proved in suitable subspaces of continuous functions of Sobolev type. The cubature formula, on which the Nyström method is constructed, has an error that behaves like the best polynomial approximation of the integrand function. Consequently, it is also shown how the Nyström method inherits this property and, hence, the proposed numerical strategy is fast when the involved known functions are smooth. Some numerical examples illustrate the efficiency of the method, also in comparison with other methods known in the literature.
MSC:
65R20; 65D10; 65D32; 41A10
1. Introduction
This paper deals with the numerical approximation of the solution of Fredholm integral equations (FIEs) of the second kind
where is a curvilinear compact domain of the plane, the boundary of which is a Jordan curve, , k and g are given continuous functions defined on and , respectively, while f is the unknown function.
Fredholm integral equations are a classical topic in functional analysis, and arise in different areas, as computer graphics [1,2], physics of plasma, fluid mechanics, electrochemical reaction (see for instance [3] and the references therein). In these fields, some problems can be modeled directly by means of a FIE or, in other cases, can lead to these kind of equations but starting for instance from boundary value problems (see, for instance, [4]).
In recent years, several different numerical approaches for solving FIEs appeared. Essentially, the proposed strategy depends on the geometry of the domain on which the integral equation is defined.
If the domain is a polygon, several approaches are known. The traditional one is to take a suitable triangularization of the domain and then to construct piecewise interpolation or cubature, leading to the corresponding collocation or Nyström methods (see, for instance, [4], Chapter 5). More recently, in the case of rectangular domains, some global approximation methods (i.e., essentially based on the polynomial approximation) were proposed in [5,6,7], and in the case of the triangular domain in [8]. These methods, for their nature, lead to a fast convergence, when the known functions of the equation are smooth.
To our knowledge, very little is known when the planar domain has a general boundary. In [3,9], some collocation methods based on radial basis functions were proposed for the case of general domains of the plane.
Moreover, some results can be obtained in the particular cases in which the curvilinear domain can be reduced, by transformation, to a rectangle. Nevertheless, such kinds of transformations, even if they exist, can produce a deterioration in the smoothness of the known functions and, consequently, they can lead to a slow convergence, even if the original known functions are very smooth. For instance, if the original known functions of the equation have derivative of every high degree, the transformed ones can be just Lipischitz or with a fixed low continuous derivative (see [7], Example 5).
Therefore, the aim of this paper is to construct a Nyström method based on a Gauss-like cubature formula, which was proposed in [10]. The idea of the authors in [10] was constructing a formula for a domain, the boundary of which is a piecewise polynomial curve. Then, under suitable assumptions of regularity, the boundary of the general domain is approximated by a suitable piecewise polynomial curve and, hence, in order to approximate the integral defined on the original domain, the cubature formula, defined for the curvilinear polygons, is used.
The final cubature formula behaves essentially as the best polynomial approximation of the integrating function, and this means that the smoother the function is, the faster the convergence is. This property allows us to construct a stable, convergent, and well conditioned Nyström method based on the named cubature formula. The rate of convergence of the method is once again the same of the best polynomial approximation of the known functions of the equation, and consequently of the solution of the equation itself.
Moreover, the Nyström interpolant has a closed form that can be evaluated in any point of the domain , i.e., no additional approximation strategy is necessary in order to evaluate the approximating solution in .
Several numerical tests show the goodness of the proposed method, also in the case when the boundary of the domain has singular points or cusps (like in the case of cardioid or deltoid), providing that the cubature nodes fall inside .
The organization of the paper is as follows. Section 2 is devoted to the collection of some definitions, approximation tools, and the description of the cubature formula. In Section 3, the Nyström method is described and the main results are stated. Section 4 collects some numerical tests confirming the theoretical expectations. Finally, Section 5 contains the proofs, while Section 6 is devoted to the conclusions.
2. Notations and Preliminary Results
In this section, we recall some definitions and preliminary results.
First of all, from now on, we will denote by a generic positive constant, having different values in different estimates. Moreover, if depends on some quantities say then we will write . On the contrary, for saying that is independent of , we will use .
2.1. Approximation Tools
Now, let be a rectangle and denote the space of the continuous functions on R. As usual, can be equipped with the uniform norm . From now on, the notations and will denote the function as depending on the only variable z or s, respectively. For smoother functions, we introduce the following Sobolev-type space
where the superscript denotes the derivative of the one-dimensional function or , and . We equip with the norm
Now, let be the space of bivariate algebraic polynomials of total degree n and be the space of bivariate polynomials of degree n in each variable. Obviously, . We denote by and the errors of best polynomial approximation on R for bivariate continuous functions by means of polynomials in and , respectively, i.e.,
From the definitions, it follows that
In [7], the following Favard-type inequality was proved when :
and therefore, due to the linearity, the same inequality holds true for any general rectangle R.
Moreover, by (2), the same estimate can be stated also for , i.e.,
2.2. An Algebraic Cubature Formula on Curvilinear Polygons
In order to describe the cubature formula, which is the base of the proposed Nyström method, we recall some definitions and properties of a planar parametric curve (see [11]).
We consider simple closed curves, i.e., curves parametrized on
for which is continuous and injective on and , with . Moreover, we assume that is piecewise , i.e., there is at most a finite number of breakpoints , where ( is considered a breakpoint if ).
The space of piecewise parametric curves on the partition of , generated by a fixed set of “parameter breakpoints” , is endowed with the norm
where , for is piecewise continuous.
Let a singular point be a point such that or , and we define a cusp as a breakpoint , such that , for some (which means, in particular, that the left and right tangents at the point have opposite directions). We say that a curve in is generalized regular if it has no singular points and no cusps.
Now, let be a compact domain (the closure of a bounded and simply connected open set), whose boundary is a Jordan piecewise polynomial parametric curve , , given counter-clockwise by a sequence of polynomial parametric curves , with , defined in the interval , and “breakpoints”
with (i.e., ). Furthermore, let be the minimal rectangle containing H, , , , and are the nodes and weights of the Gauss–Legendre rule in . The cubature formula proposed in [10] for the integral of the bivariate function f on the domain H, i.e., , is defined as follows:
with
where
In [10], it was proved that this formula is exact for , and stable, since it results in
We underline that, as discussed in [10], in general, the nodes of this cubature formula are not contained in the domain H, but only in the minimal rectangle with sides parallel to the axes.
However, the nodes are inside the cubature domain when there exists a straight line l such that the following property holds:
- is connected;
- Every segment q orthogonal to l is such that is connected.
When property holds, a change in coordinates so that l becomes parallel to the new y-axis implies that all the cubature nodes are in H, and that all the weights are nonnegative, taking as (which defines the nodes of the cubature formula) the intersection point of l with the new x-axis. For a detailed discussion on this, the interested reader can consult [10] and the references therein.
Go back now to a general domain , and assume that it is a compact domain whose boundary is a Jordan (simple and closed) curve, defined parametrically by two piecewise smooth functions that are not polynomials
In [10], it was suggested to use the Chebfun package [12] in order to provide two piecewise polynomials (interpolating at Chebychev–Lobatto nodes), such that
where is the machine precision and denotes the ordinary maximum norm on . Denoting by the domain whose boundary is defined as
in [10], it was proposed to approximate
with , and then approximate with .
Obviously, in order to construct the cubature for , it is necessary that is still a Jordan curve; that is, essentially a simple curve. There exist sufficient conditions (see, for instance, [11,13]) such that is reasonable to assume that Chebfun constructs a Jordan curve if the original boundary of is piecewise and a generalized regular curve, in the sense that it has no singular points and no cusps.
Concerning the convergence of the cubature rule, the following results were proven in [10]. For any subset of , we denote by the error of best polynomial approximation of the function f by means of bivariate polynomials of total degree m, with respect to the uniform norm on . Moreover, let denote the minimal rectangle containing .
Theorem 1
([10], Theorem 3). Let Ω be a compact domain in , whose boundary (9) is a Jordan curve, and let be the domain with the boundary, as in (11). Assume that , are at least piecewise Hölder continuous and satisfy (10). The following cubature error estimate holds for Formula (7) with
where , and , in the general case, while when Ω satisfies Property , and denotes the closed disk centered at the origin with radius .
In the case when the approximated boundary is not guaranteed to be simple, as for example if the original curve has some singular points, the following error estimate holds true.
Theorem 2
([10], Theorem 5). Let Ω be as in (9), and , be the piecewise polynomial approximating curve (10). Assume that the integrand f is Hölder-continuous with constant C and exponent on the minimal rectangle containing , where . Then, the following estimate holds for the error of the cubature formula (7) with :
where .
3. Numerical Methods for FIE
Using standard arguments, it is possible to prove that if is continuous, then K is compact, as a map of into itself, and consequently the Fredholm Alternative holds true for (14) in (see, for instance, [4]).
From now on, we will denote (respectively ) for meaning that the function k of four variables is considered as a function of only (respectively of ).
Hence, if for some , it is where is the minimal rectangle containing , then it immediately follows that , for any (see, for instance, [7], Proposition 3.1).
Therefore, if then, by (14), we deduce that .
A Nyström Method
The Nyström method consists in approximating
by means of the finite dimensional operator, obtained by means of the cubature Formula (7)
Therefore, we consider the finite dimensional equation
whose unknown is . Collocating the equation on the same set of knots of cardinality , we obtain the following linear system
, which can be rewritten as
, where is the Kronecker delta, and
are the unknowns of the system.
Setting
and
the linear system can be rewritten in compact form as
Linear System (16) and finite-dimensional Equation (15) are equivalent. Indeed, the numerical approximant of f, called the Nyström interpolant, can be constructed using the value of since, for any , it is
while, obviously, if is known, then satisfy the linear system, as the linear system is constructed.
Now, let , where denotes here the maximum absolute row sum norm. The next theorem states the convergence, stability, and well conditioning of the proposed Nyström method.
Theorem 3.
Under the hypothesis of Theorem 1 for the domain Ω and with the definition given for , let , and assume k to be continuous on . Then, the method is stable, i.e., are uniformly bounded, the equivalent linear system has a unique solution, and is well conditioned, since
Moreover, if , the Nyström interpolant converges to the unique solution , and there holds
where .
Remark 1.
We underline that convergence estimate (18) holds true for both expressions of . Nevertheless, it is almost clear that, if the Property cannot apply, then the assumptions on the known functions necessarily have to be fulfilled on , which really seems to be a stronger request. On the contrary, for domains for which the weights are positive and the nodes are all inside Ω, practically all the assumptions on the known functions (and consequently on the solution) are made on the original domain Ω.
The following corollary states the order of convergence of the method in the general case, and with the stronger assumptions on the known functions.
Corollary 1.
Under the hypothesis of Theorem 3, assume that for some
then , and
Remark 2.
We finally remark that in the case where the boundary of Ω is not regular, from Theorem 2, we can obtain a convergent Nyström method once again. Nevertheless, we are not able to deduce a precise order of convergence. But, as the numerical test shows, there is a numerical evidence that the order of convergence is always the same. In other words, the leading terms seem to be always given by the rate of the best polynomial approximation of the known functions.
4. Numerical Tests
In this section, we test the method just described on some numerical examples. For the computations, we used the Matlab package ChebfunGauss in [14]. In the following tables, we have shown the error of the method and the conditioning of the linear systems for increasing values of n and, consequently, of the degree of exactness of the cubature formula, denoted by . The error was computed as the relative discrete error on a grid of equidistant nodes in
where , , . When was not known, was used instead, for a large enough .
In the tables, , with as in (8), denotes the dimension of the linear systems.
First of all, we propose three tests on different domains.
Example 1.
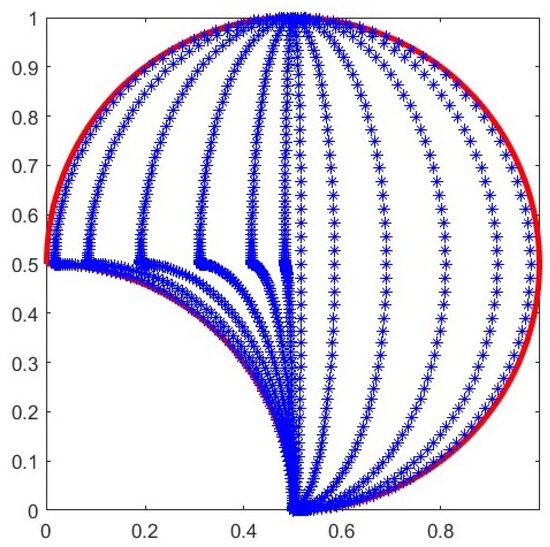

Consider the following equation
where the domain Ω is a lune defined as the difference of two disks with radius centered in and , respectively. Therefore, the boundary can be represented by the curve
The solution of this equation is not known.
We chose as base-line , and, in this way, Property is satisfied and all the nodes lie inside the domain. The boundary is approximated around machine precision by Chebfun with on the first arc and also on the second arc. The kernel, the known functions and the parameter μ, are defined as
As , , and the boundary of the domain is generalized and regular (since the breakpoints and are not cusps), according to the theoretical estimates (see Corollary 1), we expect an error behaving as . The conditioning of the linear system is of the order of tens, and the numerical results are better than the theoretical estimates. See Figure 1 and Table 1.

Figure 1.
Cubature points on the lune for with base-line : the blue stars are the cubature points and the red line describes the boundary of the domain.

Table 1.
Numerical results for Example 1.
Example 2.
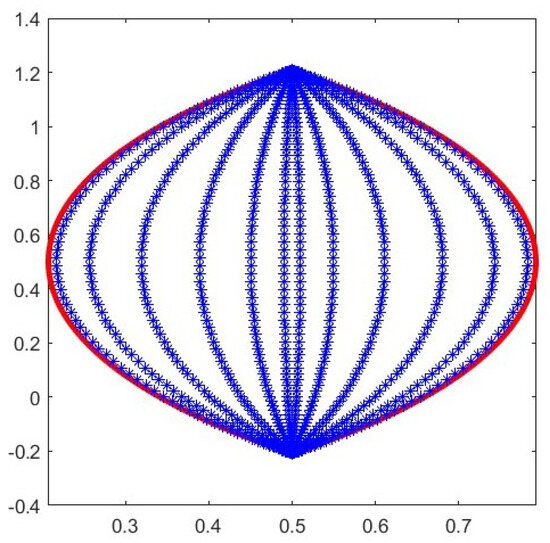

Consider the equation
where Ω is the intersection of two disks with radius 1 centered in and and, consequently, its boundary can be represented by the curve
Also, in this case, the exact solution is not known.
We chose , as the base-line joining the breakpoints , which gives the property to the domain. The boundary is approximated around machine precision by Chebfun, with , on the first arc and , on the second arc. The kernel, the known functions and the parameter μ are defined as
As and , and the curve is generalized regular, according to Corollary 1, we expect an error of the order . We underline that we have better numerical results than theoretical expectation. See Figure 2 and Table 2.

Figure 2.
Cubaturepoints on the intersection of two disks for with base-line : the blue stars are the cubature points and the red line describes the boundary of the domain.

Table 2.
Numerical results for Example 2.
Example 3.
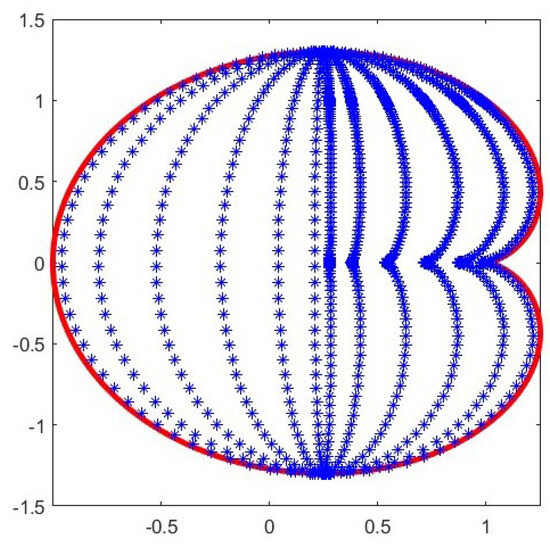

We consider the following equation
where the domain Ω is a cardioid with the following parametric equations
As in the previous examples, we do not know the exact solution. The boundary is approximated around machine precision by Chebfun, with and . To guarantee Property in the domain, we chose as the base-line. The kernel, the known functions, and the parameter μ are
In this case, we cannot apply Corollary 1, but we observe that, since , then the order of the best polynomial approximation for these functions is and the numerical evidence agrees with this rate. See Figure 3 and Table 3.

Figure 3.
Cubature points on the cardioid for with base-line : the blue stars are the cubature points and the red line describes the boundary of the domain.

Table 3.
Numerical results for Example 3.
Example 4.
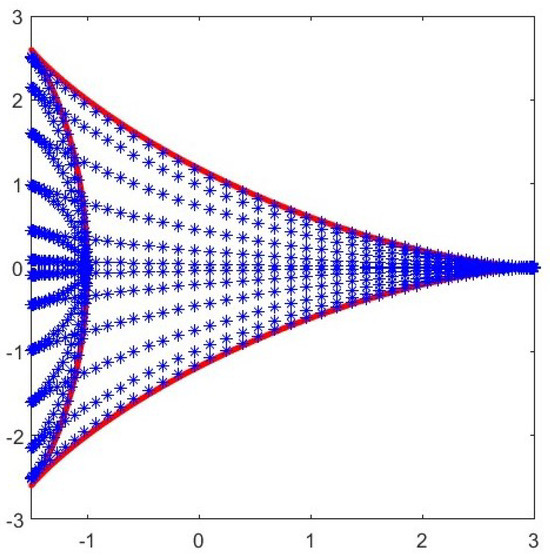

Consider the following equation
In this case, we also do not know the exact solution. The domain Ω is a deltoid, whose boundary is a tricuspoid (also known as Steiner’s hypocicloid) with parametric equations
where we set (see [15] for the properties of such a curve). Due to the shape of the boundary, there is no way to satisfy Property N, so we have chosen the straight line as the base-line (which is a symmetry axis of the domain); the boundary is approximated around machine precision by Chebfun, with and on each of the three regular arcs. The kernel, the known function, and the parameter μ are
Also, in this case, we cannot apply Corollary 1, but we observe that since , then the order of the best polynomial approximation for these functions is and the numerical evidence agrees with this rate. See Figure 4 and Table 4.

Figure 4.
Cubature points on the deltoid for with base-line : the blue stars are the cubature points and the red line describes the boundary of the domain.

Table 4.
Numerical results for Example 4.
Comparison with Other Methods
In this subsection, we compare our Nyström method with other methods found in the literature.
Example 5.

Consider the following equation
with taken by [9], where the authors propose a collocation method based on radial basis functions. The exact solution is . The domain Ω is an ellipse with center , whose boundary is described by parametric equations
Due to the shape of the boundary, to satisfy Property N, we chose the straight line as the base-line; the boundary is approximated around machine precision by Chebfun, with and . The kernel, the known function, and the parameter μ are
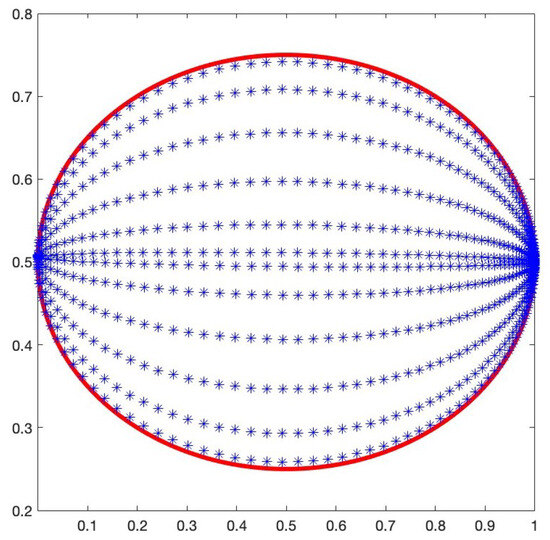
As , and the curve is generalized regular, according to Corollary 1, we expect an error of the order , and the numerical evidence agrees with this rate. We underline that the best error in [9] is , while our method reaches the machine precision. See Figure 5 and Table 5.

Figure 5.
Cubature points on the ellipse for with base-line : the blue stars are the cubature points and the red line describes the boundary of the domain.

Table 5.
Numerical results for Example 5.
Now, we compare the Nyström method just described with the one proposed in [7]. It is a Nyström method based on a cubature formula obtained as the tensor product of two univariate Gaussian rules. From a Gaussian formula
where and denotes the Legendre Christoffel numbers and zeros, respectively, the corresponding Nyström interpolant is defined as
In [7], the convergence and stability of the method were proved. Denote simply by the Sobolev space defined on the square .
Theorem 4
([7], Theorem 3.1). Assume that in . Denote by the unique solution of (14) in for a given . If, in addition, for some ,
then there holds
We remark that the two Nyström methods have exactly the same rate of convergence, as we can see comparing (18) and (21).
We want to show that if the domain can be transformed in a square, and the known functions preserve the original smoothness, then the Nyström method based on the tensorial Gaussian cubature is preferable, since it requires a lower order of the linear system and so a lower computational cost, as we can see in the following two examples.
Example 6.


In this example we consider the equation
whose exact solution is .
Ω is the unit disk, with boundary parametrized as
We chose as the base-line. The boundary is approximated around machine precision by Chebfun, with and . The kernel, the known functions, and the parameter μ are
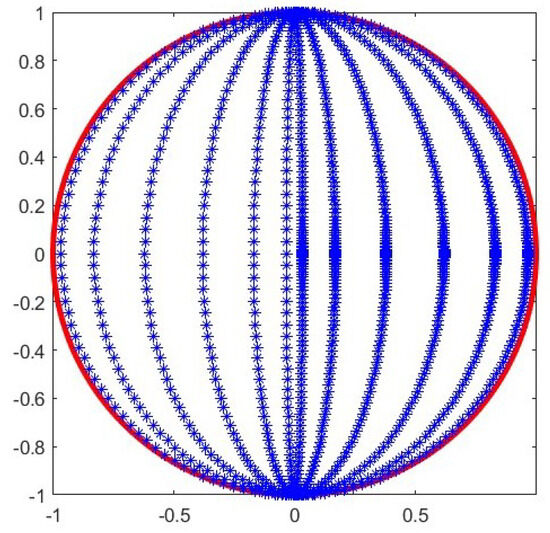
As , according to the theoretical estimates, we expect an error behaving as . See Figure 6 and Table 6 and Table 7.

Figure 6.
Cubature points on the unit disk for with base-line . The blue stars are the cubature points and the red line describes the boundary of the domain.

Table 6.
Numerical results for Example 6: Nyström method based on a curvilinear cubature formula.

Table 7.
Numerical results for Example 6: Nyström method based on a tensorial product of two univariate Gaussian formulas.
Example 7.
whose exact solution is .


Ω is a convex set defined parametrically as
We chose as the base-line. The boundary is approximated around machine precision by Chebfun, with and on the first and also on the second arc (the boundary is already described as a polynomial curve). The kernel, the known functions, and the parameter μ are
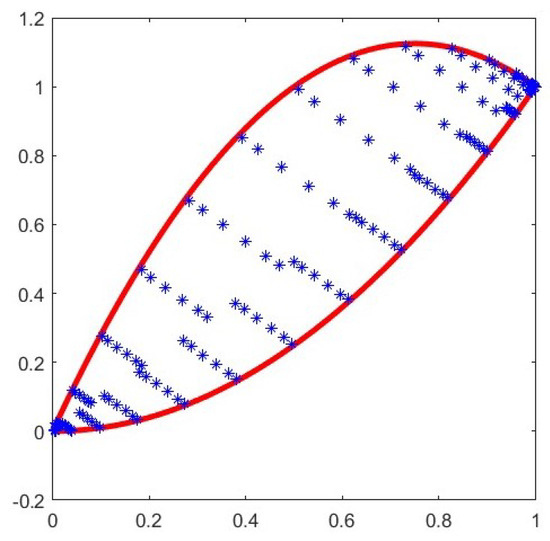
As , according to the theoretical estimates, we expect an error behaving as . See Figure 7 and Table 8 and Table 9.

Figure 7.
Cubature points on the convex set for with base-line . The blue stars are the cubature points and the red line describes the boundary of the domain.

Table 8.
Numerical results for Example 7: Nyström method based on a curvilinear cubature formula.

Table 9.
Numerical results for Example 7: Nyström method based on a tensorial product of two univariate Gaussian formulas.
5. The Proofs
In this section, we prove the convergence, stability, and well conditioning of the proposed numerical method.
Proof of Theorem 3.
We want to show that the Nyström method is convergent and stable in .
To prove the stability, we have to show that
In fact, if (22) holds, then
and so the Nyström interpolant is bounded.
Using standard arguments (see [4]), (22) follows if
- The sequence is collectively compact;
- .
We can prove sentence 2 immediately, thanks to the principle of uniform boundedness, if we show that
Condition 1, that is, the collectively compactness of the sequence , can be proved in a classical way, if we can show that
(see, for instance, [4,7]). To prove (26), take an arbitrary polynomial , such that is of total degree m, and consider the polynomial
which is still of total degree m, for any f. Then, for any
and, therefore,
Thus, since the cubature formula is stable, and is arbitrarily chosen, we can conclude that
and (26) follows.
About the convergence, from the definition of and it follows, in a standard way, that
and so, by (25), (18) follows.
Finally, the good conditioning of the linear system, i.e., (17), follows by standard arguments (see once again [4,7]), essentially due to the convergence of the cubature formula for any continuous function on . □
6. Conclusions
In this study, we developed a Nyström method to solve the two-dimensional linear Fredholm integral equations of the second kind on a general curvilinear domain. The method is based on the use of a cubature formula previously introduced in [10]. The proposed scheme can be used to various kinds of regions, without transforming the known functions of the equation and providing an approximant of the solution that can be evaluated in any point of the domain. The convergence, stability, and well conditioning of the method are proven. The method has a rate of convergence comparable with that of the best polynomial approximation of the solution.
Author Contributions
Conceptualization, M.G.R. and A.L.L.; methodology, M.G.R. and A.L.L.; software and validation, A.L.L.; formal analysis, M.G.R.; investigation, M.G.R. and A.L.L.; writing—original draft preparation, A.L.L.; writing—review and editing, M.G.R.; funding acquisition, M.G.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Gruppo Nazionale per il Calcolo Scientifico–INdAM, 2023 project “Approssimazione ed integrazione multivariata con applicazioni ad equazioni integrali”.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are deeply grateful to the anonymous reviewers for their valuable comments, remarks and suggestions, which have improved the quality of the paper. Moreover they want to thank Sommariva and Vianello from the University of Padua, for the interesting discussions on the topics of the paper. The research has been accomplished within RITA (Research ITalian network on Approximation) and the research group TAA-UMI (Teoria dell’Approssimazione e Applicazioni-Unione Matematica Italiana).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Keller, A. Instant Radiosity. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH’97), Los Angeles, CA, USA, 3–8 August 1997; ACM Press, Addison-Wesley Publishing Co.: New York, NY, USA, 1997; pp. 49–56. [Google Scholar] [CrossRef]
- Kajiya, J.T. The Rendering Equation. SIGGRAPH Comput. Graph. 1986, 20, 143–150. [Google Scholar] [CrossRef]
- Assari, P.; Adibi, H.; Dehghan, M. A numerical method for solving linear integral equations of the second kind on the non-rectangular domains based on the meshless method. Appl. Math. Model. 2013, 37, 9269–9294. [Google Scholar] [CrossRef]
- Atkinson, K.E. The Numerical Solution of Integral Equation of the Second Kind; Cambridge Monographs on Applied and Computational Mathematics: Cambridge, UK, 1997. [Google Scholar]
- Laguardia, A.L.; Russo, M.G. Numerical methods for Fredholm integral equations based on Padua points. Dolomites Res. Notes Approx. 2022, 15, 65–77. [Google Scholar]
- Occorsio, D.; Russo, M.G. Bivariate generalized Bernstein operators and their application to Fredholm integral equations. Publ. Inst. Math. 2016, 100, 141–162. [Google Scholar] [CrossRef]
- Occorsio, D.; Russo, M.G. Numerical methods for Fredholm integral equations on the square. Appl. Math. Comput. 2011, 218, 2318–2333. [Google Scholar] [CrossRef]
- Mastroianni, G.; Milovanovic, G.; Occorsio, D. Nyström Method for Fredholm Integral Equations of the Second Kind in Two Variables on a Triangle. Appl. Math. Comput. 2013, 219, 7653–7662. [Google Scholar] [CrossRef]
- Fatahi, H.; Saber-Nadjafi, J.; Shivanian, E. A new spectral meshless radial point interpolation (SMRPI) method for the two-dimensional Fredholm integral equations on general domains with error analysis. J. Comput. Appl. Math. 2016, 294, 196–209. [Google Scholar] [CrossRef]
- Santin, G.; Sommariva, A.; Vianello, M. An algebraic cubature formula on curvilinear polygons. Appl. Math. Comput. 2011, 217, 10003–10015. [Google Scholar] [CrossRef][Green Version]
- Bos, L.; Vianello, M. On simple approximation to simple curves. Dolomites Res. Notes Approx. 2010, 23, 1–6. [Google Scholar]
- Trefethen, L.N. Chebfun Version 4.0.; The Chebfun Development Team: Oxford, UK, 2011. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quaternoni, A.; Zang, T.A. Spectral Methods; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sommariva, A.; Vianello, M. ChebfunGauss: A Matlab Code for Gauss-Green Cubature by the Chebfun Package. Available online: https://www.math.unipd.it/~alvise/software.html (accessed on 30 October 2023).
- Lockwood, E.H. A Book of Curves; Paperback—Re-Issue of the 1963 Edition; Cambridge University Press: Cambridge, UK, 1961. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).