Analyzing Russia–Ukraine War Patterns Based on Lanchester Model Using SINDy Algorithm
Abstract
1. Introduction
2. Lanchester Model
3. Russia–Ukraine Data
4. SINDy Algorithm
5. Proposed Method
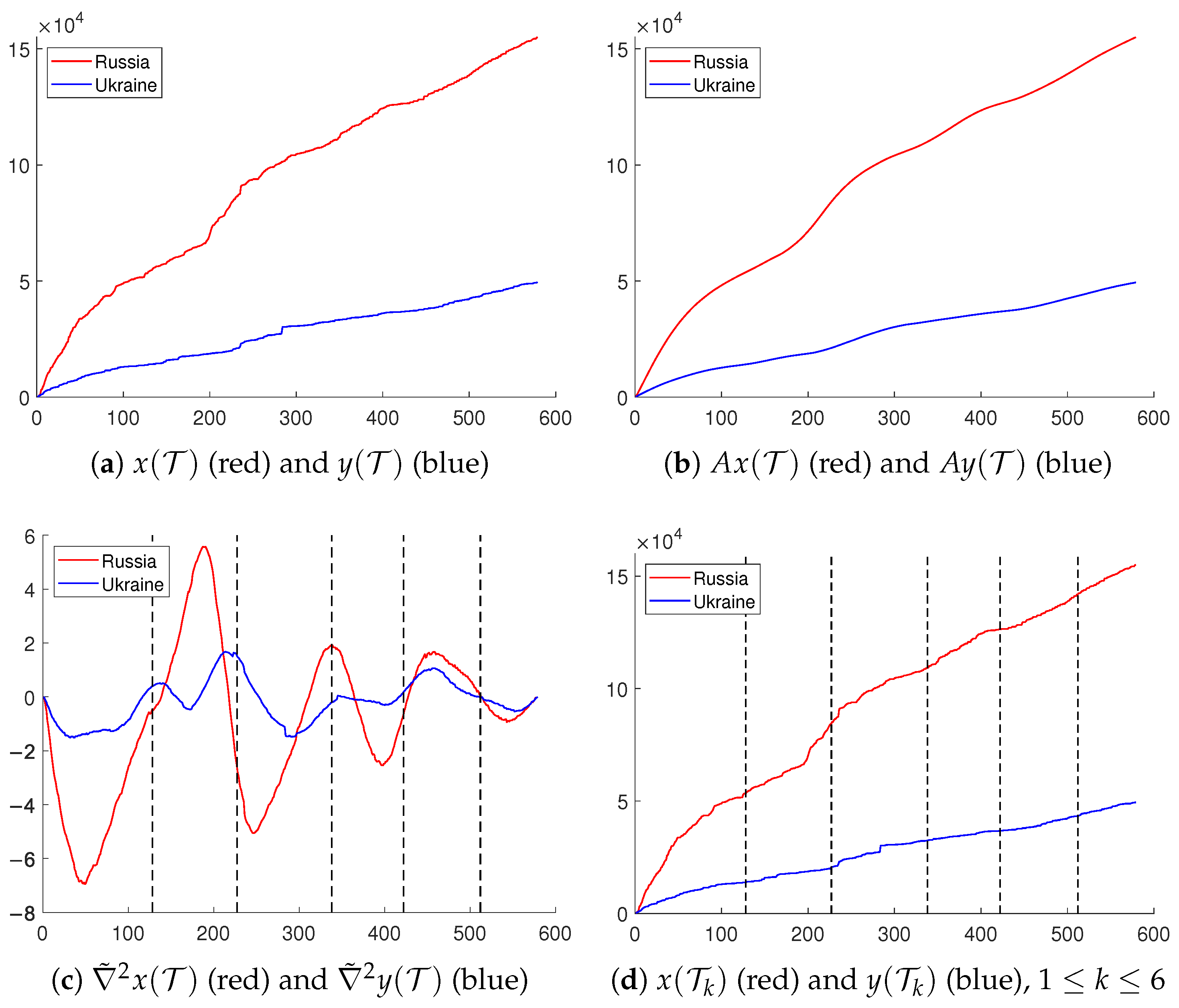
5.1. Partition of Data
5.2. Identification of System
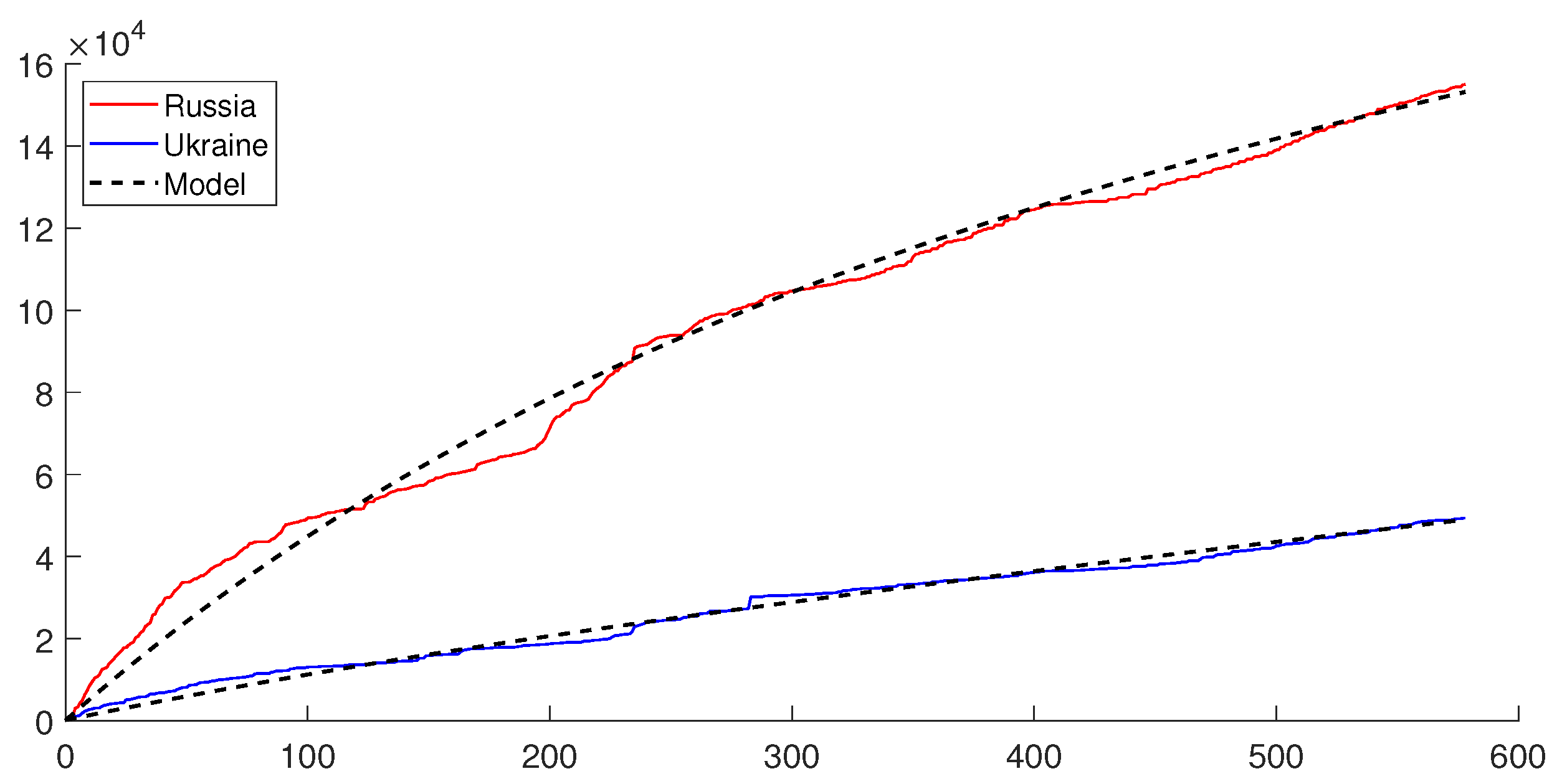
6. Simulations
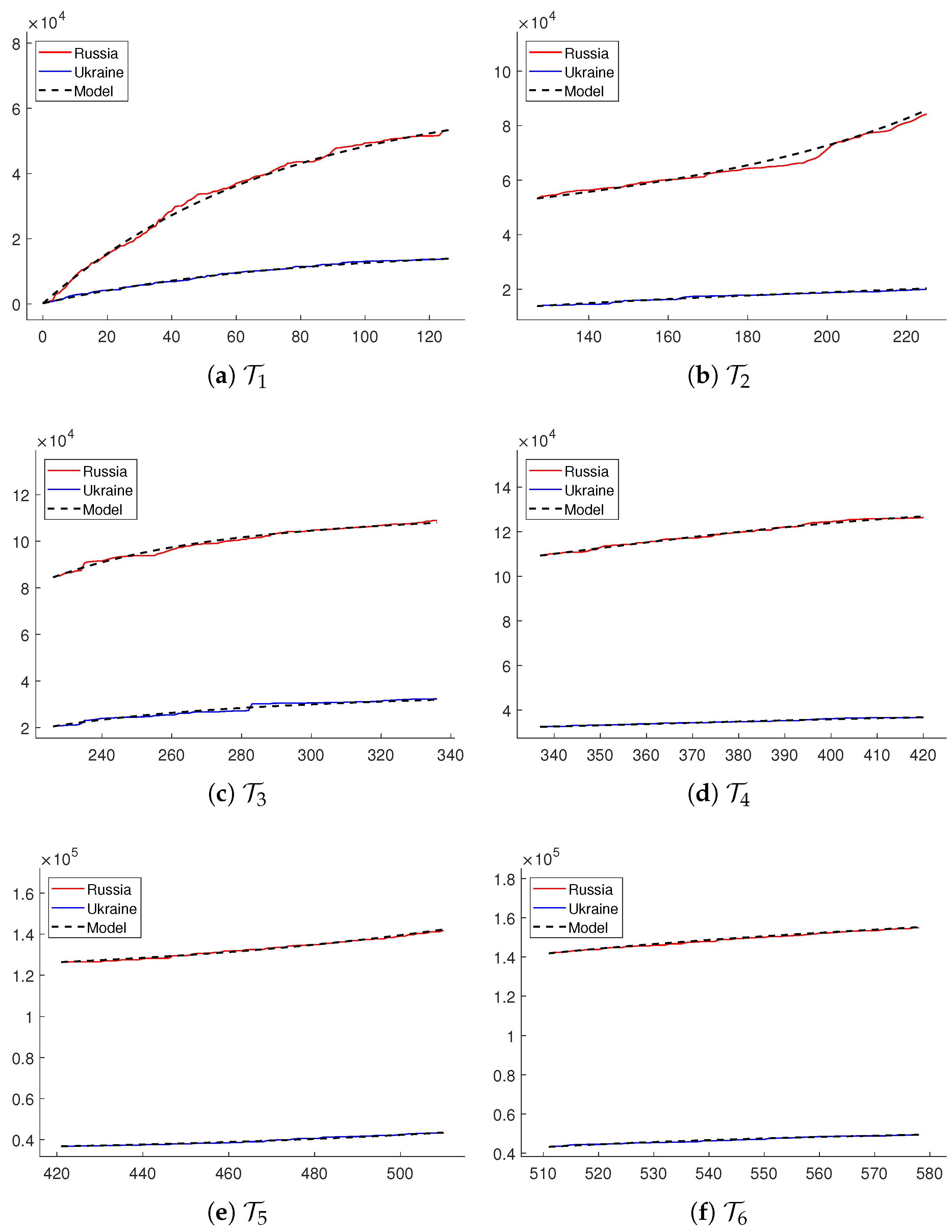
6.1. Partitioned Times
6.2. Identified Systems
- System over . From the data and with the initial values and , we obtained the coefficients of the system (11) as
- System over . For the measurements and with the initial values 53,307 and 13,835, the coefficients were determined as
- System over . The losses and with the initial observations 84,524 and 20,525 were fitted by the system (11) with the coefficients
- System over . The cumulative losses over with the initial measurements 109,293 and 32,461 were modeled by the system with coefficients
- System over . With the initial measurements 126,402 and 36,758, the estimation of the system over resulted in the coefficient
- System over . We modeled the dynamics of losses over with 141,866 and 43,289 in terms of coefficients
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lanchester, F.W. Aircraft in Warfare: The Dawn of the Fourth Arm, 1st ed.; Constable and Co.: London, UK, 1916. [Google Scholar]
- Morse, P.M.; Kimball, G.E. Methods of Operations Research, 1st ed.; John Wiley: New York, NY, USA, 1951. [Google Scholar]
- Weiss, H.K. Combat Models and Historical Data: The U.S. Civil War. Oper. Res. 1966, 14, 759–790. [Google Scholar] [CrossRef]
- Peterson, R. On the Logarithmic Law of Combat and Its Application to Tank Combat. Oper. Res. 1967, 15, 557–558. [Google Scholar] [CrossRef]
- Dietchman, S.J. A Lanchester Model of Guerrilla Warfare. Oper. Res. 1962, 10, 818–827. [Google Scholar] [CrossRef]
- Schaffer, M.B. Lanchester Models of Guerrilla Engagements. Oper. Res. 1968, 16, 457–488. [Google Scholar] [CrossRef]
- Hartley, D.S.; Helmbold, R.S. Validating Lanchester’s square law and other attrition models. Nav. Res. Log. 1995, 42, 609–633. [Google Scholar] [CrossRef]
- Kress, M. Lanchester Models for Irregular Warfare. Mathematics 2020, 8, 737. [Google Scholar] [CrossRef]
- Cangiotti, N.; Capolli, M.; Sensi, M. A generalization of unaimed fire Lanchester’s model in multi-battle warfare. Oper. Res. Int. J. 2023, 23, 38. [Google Scholar] [CrossRef]
- Keane, T. Combat modelling with partial differential equations. Appl. Math. Model. 2011, 35, 2723–2735. [Google Scholar] [CrossRef]
- Coulson, S.G. Lanchester modelling of intelligence in combat. IMA J. Manag. Math. 2019, 30, 149–164. [Google Scholar] [CrossRef]
- Spradlin, C.; Spradlin, G. Lanchester’s equations in three dimensions. Comput. Math. Appl. 2007, 35, 999–1011. [Google Scholar] [CrossRef]
- Clifton, E. A brief review on the application of Lanchester’s models of combat in nonhuman animals. Ecol. Psychol. 2020, 32, 181–191. [Google Scholar] [CrossRef]
- Johnson, D.D.P.; MacKay, N.J. Fight the Power: Lanchester’s laws of combat in human evolution. Evol. Hum. Behav. 2013, 36, 152–163. [Google Scholar] [CrossRef]
- Jørgensen, S.; Sigué, S. A Lanchester-Type Dynamic Game of Advertising and Pricing. In Games in Management Science; Sigue, P.-O., Taboubi, S., Pineau, S., Eds.; Springer: New York, NY, USA, 2020; pp. 1–14. [Google Scholar]
- Stanescu, M.; Barriga, N.; Buro, M. Using Lanchester Attrition Laws for Combat Prediction in StarCraft. In Proceedings of the Eleventh AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE-15), Santa Cruz, CA, USA, 14–18 November 2015; pp. 86–92. [Google Scholar]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Natl. Acad. Sci. USA 2020, 113, 3932–3937. [Google Scholar] [CrossRef]
- Jiang, Y.-X.; Xiong, X.; Zhang, S.; Wang, J.-X.; Li, J.-C.; Du, L. Modeling and prediction of the transmission dynamics of COVID-19 based on the SINDy-LM method. Nonlinear Dyn. 2021, 105, 2775–2794. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Sthapit, S.; Maple, C. Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation. Sustainability 2022, 14, 2051. [Google Scholar] [CrossRef]
- Ren, Y.; Adams, C.; Melz, T. Uncertainty Analysis and Experimental Validation of Identifying the Governing Equation of an Oscillator Using Sparse Regression. Appl. Sci. 2022, 12, 747. [Google Scholar] [CrossRef]
- Wei, B. Sparse dynamical system identification with simultaneous structural parameters and initial condition estimation. Chaos, Solitons Fractals 2022, 165, 112866. [Google Scholar] [CrossRef]
- Ayankoso, S.; Olejnik, P. Time-Series Machine Learning Techniques for Modeling and Identification of Mechatronic Systems with Friction: A Review and Real Application. Electronics 2023, 12, 3669. [Google Scholar] [CrossRef]
- Dong, X.; Bai, Y.-L.; Lu, Y.; Fan, M. An improved sparse identification of nonlinear dynamics with Akaike information criterion and group sparsity. Nonlinear Dyn. 2023, 111, 1485–1510. [Google Scholar] [CrossRef]
- Champion, K.P.; Brunton, S.L.; Kutz, J.N. Discovery of Nonlinear Multiscale Systems: Sampling Strategies and Embeddings. SIAM J. Appl. Dyn. Syst. 2019, 18, 312–333. [Google Scholar] [CrossRef]
- Oryx’ Site. Available online: https://www.oryxspioenkop.com/2022/02/attack-on-europe-documenting-equipment.html (accessed on 1 August 2023).
- Turkes, T. Fitting Lanchester and Other Equations to the Battle of Kursk Data. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, March 2000. [Google Scholar]
- Zhang, L.; Schaeffer, H. On the convergence of the SINDy algorithm. Multiscale Model. Simul. 2019, 17, 948–972. [Google Scholar] [CrossRef]
- Levin, D. The approximation power of moving least-squares. Math. Comput. 1998, 67, 1517–1531. [Google Scholar] [CrossRef]
- Allen, L. An Introduction to Mathematical Biology; Pearson: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Duffey, R.B. Dynamic theory of losses in wars and conflicts. Eur. J. Oper. Res. 2017, 261, 1013–1027. [Google Scholar] [CrossRef]


| Equipment Types | Weights | Equipments |
|---|---|---|
| Tanks | 40 | Tanks |
| Self-Propelled Tank Missile Systems | ||
| Artillery | 20 | Artillery |
| Self-Propelled Artillery | ||
| Towed Artillery | ||
| Multiple Rocket Launchers | ||
| Artillery Support Vehicles Furthermore, Equipment | ||
| Armored Vehicles | 5 | Armoured Fighting Vehicles |
| Armoured Personnel Carriers | ||
| Infantry Fighting Vehicles | ||
| Infantry Mobility Vehicles | ||
| Mine-Resistant Ambush Protected | ||
| Support Equipments | 5 | Command Posts |
| Communications Stations | ||
| Communications Vehicles | ||
| Engineering Vehicles Furthermore, Equipment | ||
| Anti-tank Personal Firearms and Mortars | 3 | Anti-Tank Guided Missiles |
| Mortars | ||
| Other Combat Vehicles | 3 | Trucks |
| Vehicles and Jeeps |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, D.; Jeong, B. Analyzing Russia–Ukraine War Patterns Based on Lanchester Model Using SINDy Algorithm. Mathematics 2024, 12, 851. https://doi.org/10.3390/math12060851
Chung D, Jeong B. Analyzing Russia–Ukraine War Patterns Based on Lanchester Model Using SINDy Algorithm. Mathematics. 2024; 12(6):851. https://doi.org/10.3390/math12060851
Chicago/Turabian StyleChung, Daewon, and Byeongseon Jeong. 2024. "Analyzing Russia–Ukraine War Patterns Based on Lanchester Model Using SINDy Algorithm" Mathematics 12, no. 6: 851. https://doi.org/10.3390/math12060851
APA StyleChung, D., & Jeong, B. (2024). Analyzing Russia–Ukraine War Patterns Based on Lanchester Model Using SINDy Algorithm. Mathematics, 12(6), 851. https://doi.org/10.3390/math12060851







