Abstract
The particles of micron and submicron sizes (PM 2.5 and less) in gas environments pose a significant danger to humanity due to the emergence of specific and very dangerous diseases of the cardiovascular, respiratory, and immune systems of the human body. Such particles are the most difficult to detect; therefore, their effects on human health have only been discovered in recent decades. Classical ultrasonic coagulation by sinusoidal action turns out to be ineffective for PM 2.5 due to the peculiarities of the physical mechanisms of hydrodynamic and orthokinetic interaction realized in gaseous media. This article presents a theoretical justification for choosing ways to increase the efficiency of ultrasonic coagulation of PM 2.5 by creating special conditions under which nonlinear disturbances of the velocity and pressure of the gas phase in the ultrasonic field occur. The authors performed simulations of ultrasonic coagulation under nonlinear disturbances of the velocity (vortex) and the pressure (shock waves), which has numerical difficulties due to the instability of existing methods. As a result of the numerical analysis, the possibility of increasing the coagulation rate of particles in the submicron size range up to limit values (13 times due to nonlinear pressure disturbances, and an additional increase of at least 2 times due to aerosol compaction in the vortex field of gas velocity) was shown.
Keywords:
ultrasonic; simulation; aerosol; shock wave; vortex; nonlinear disturbances; pressure; velocity MSC:
76T15
1. Introduction
The particles of micron and submicron sizes (PM 2.5 and less) in gas environments pose a significant danger to humanity due to the emergence of specific and very dangerous diseases of the cardiovascular, respiratory, and immune systems of the human body [1,2,3,4]. Such particles are the most difficult to detect; therefore, their effects on human health have only been discovered in recent decades. The most promising solution to this problem today may be the implementation of various physical mechanisms that can ensure the combination of such particles into larger agglomerates, which can be subsequently removed by existing gas cleaning methods. Therefore, special attention is being paid to the development of one of the most effective physical principles for the preliminary coalescence of particles into agglomerates: ultrasonic coagulation [5,6,7,8,9,10,11,12,13,14]. However, known approaches to ultrasonic coagulation by sinusoidal action turn out to be ineffective for PM2.5 due to the peculiarities of the physical mechanisms of hydrodynamic [9,10] and orthokinetic [11] interaction realized in gaseous media.
The orthokinetic mechanism has a weak effect due to the lower inertia of small particles and the fact that the probability of collision due to orthokinetic interaction is linearly proportional to the amplitude of the oscillatory velocity, and the hydrodynamic interaction is linearly proportional to the second power of the amplitude of the oscillatory velocity. The probability of hydrodynamic interaction is limited by the small cross-sectional area of particle collision and the small ratio of the Bjerknes force due to convective transport (second-order effect) [9,10], which is proportional to the square of the particle size, and to the viscous drag force, which depends linearly on the size.
Therefore, there is a need to search for new mechanisms that can solve this problem, i.e., in studying the possibilities of increasing the efficiency of coagulation due to nonlinear disturbances of oscillations and establishing the limit of such possibilities. Since the basic physical parameters characterizing the acoustic field in the gas phase are speed and pressure, the most obvious directions for increasing efficiency are as follows:
- -
- Creation of nonlinear gas pressure disturbances, which under certain conditions lead to the periodic formation of shock waves [15];
- -
- Creation of nonlinear disturbances in gas velocity, which are stationary vortex flows [16].
Nonlinear gas pressure distortions are associated with convective transfer of the gas phase. As a consequence, there is a partial increase in the local speed of sound in the gas phase at the moment when the maximum absolute value of speed is reached. Meanwhile, at the moments when the vibrational velocity of the gas reaches zero, the speed of sound remains the same. As a result, due to the difference in the speed of sound, a sharp jump in gas pressure occurs, which causes the formation of a shock wave. The physical feasibility of periodic shock waves has been justified theoretically and confirmed experimentally in works published previously, particularly in the Journal of Acoustics [15,17,18].
One of the possible mechanisms for increasing the efficiency of coagulation due to periodic shock waves is an increase in the collision cross-sectional area (due to Brownian motion) and an increase in the rate of convergence of particles due to nonlinear and non-equilibrium processes in the gas phase [19,20,21].
Experimental results on stationary vortex flows obtained by various authors [22,23,24], including the authors of this article, indicate that the speed of acoustic flows initiated by an ultrasonic field (with a sound pressure level more than 160 dB), without the forced supply of an external gas flow, can reach several centimeters per second with normal acceleration, which has a value in the order of 1 m/s2. Thus, the sound pressure level increases the contribution of vortex acoustic flows to coagulation efficiency (due to increasing the power of the emitter, creating conditions for focusing vibrations, thereby creating resonant conditions).
Thus, creating conditions for the distortion of the main physical quantities (pressure and velocity) characterizing the parameters of the gas phase can ensure an increase in the ultrasonic coagulation efficiency. At the same time, it is obvious that creating conditions for the maximal manifestation of such effects will allow one to approach the maximum capabilities of coagulation. What is meant here is creating resonant conditions and/or using counter-directed emitters [17,18,25,26] for nonlinear pressure disturbances in the form of periodic shock waves, creating resonant conditions and simultaneous bending vibrations of the radiating surface for the emergence of vortex acoustic flows [24]. Bending vibrations of the emitter make it possible to reduce the average radius of curvature of the vortices and thereby increase the speed of inertial transfer of particles between streamlines, as well as creating many such vortices.
To evaluate the possibilities of increasing the rate of ultrasonic coagulation using each of the listed effects, and to understand the mechanisms of increasing the rate of coagulation, we carried out comprehensive studies of the process of PM2.5’s interactions when various physical parameters of the gas are distorted.
Existing mathematical models of ultrasonic coagulation mainly consider the classical sinusoidal effect (starting with the work of W. Konig, carried out in the late 19th–early 20th centuries, and ending with modern studies of ultrasonic coagulation in a uniform acoustic field of a traveling wave [9] and in standing waves [27,28]).
However, such approaches do not take into account the features associated with the interaction of particles in a nonlinearly distorted pressure field, for the following reasons:
- -
- The influence of the Knudsen number on the main driving force of the hydrodynamic interaction of particles is not taken into account (only the influence of this number on the force of viscous resistance, which balances the force of hydrodynamic interaction and determines the final approach speed of the particles, is considered);
- -
- They do not take into account the change in the effective cross-sectional area of the collision caused by Brownian motion when the pressure of the gas phase changes.
The feasibility of studying the influence of these factors on the speed (including the maximum speed) of coagulation today is supported by the presence of a huge number of fundamental studies on the mechanics of dispersed systems (starting with the works of N.A. Protodyakonov, carried out in the 20th century, and ending with modern publications devoted to the mechanics of flow of rarefied gas, taking into account the mutual diffusion of gas molecules and the partial non-equilibrium of the process [29]). In addition, the mechanism of the occurrence of Brownian motion of submicron particles has been widely studied [29,30,31,32], and mathematical theories of random processes [31,32] have been created that make it possible to predict the characteristics of such motion.
Regarding taking into account the influence of gas flow on a spatially inhomogeneous change in the concentration of particles interacting with one another under the influence of an arbitrary external physical field [33,34,35,36], the previously proposed models were built either with the assumption that the movement speeds of particles of different sizes are identical, regardless of the sequence of association of small particles into agglomerates (integro-differential models, when the macroscopic evolution of concentrations of particles of different sizes is considered, representing continuous functions that satisfy the integro-differential equation) [33,34], or as numerical models that require individual tracking of the behavior of local groups of particles throughout the entire period of oscillations (discrete phase model) [35,36]. The latest models are distinguished not only by their enormous computational complexity, but also by their instability to small disturbances in the form of numerical approximation errors, and they also produce multiple errors in calculations when trying to take into account the collision of particles from different groups due to the force of hydrodynamic interaction, and not the difference in the translational motion velocities of groups of particles.
Integro-differential models, if they are also acceptable for describing coagulation in vortex acoustic flows (when a vortex in the gas phase rotates many times faster than coagulation occurs, the previously mentioned assumption of equal velocities is valid), then in the presence of nonlinear terms—e.g., the collision integral, or even a discrete sum in the form of a quadratic form of concentrations—the problem of their numerical implementation arises.
Thus, to increase the efficiency of ultrasonic coagulation achieved through nonlinear effects, the goal of this work is a theoretically justification of increasing of efficiency due to nonlinear disturbances of pressure and velocity.
For this goal, the following tasks must be solved:
- -
- Improving the model of interaction of individual particles, specifically taking into account mutual diffusion and free-molecular effects when determining the strength of hydrodynamic interaction, along with the influence of pressure disturbances on the change in the effective cross-sectional area of the collision;
- -
- Construction of an initial boundary value problem of spatially inhomogeneous evolution of the concentration of an ensemble of particles at nonlinear disturbances of velocity (acoustic vortices);
- -
- Development of a numerical algorithm for the initial boundary value problem;
- -
- Calculation of the coagulation rate limit at different particle sizes and ultrasonic influence parameters.
Therefore, it is necessary to develop two numerical models of the interaction of individual particles and the evolution of the aerosol ensemble, taking into account the listed factors, to search for modes and conditions that ensure that we approach the limiting capabilities of ultrasonic coagulation.
The developed models are presented in the following sections.
2. Statement of the Research Objectives
The numerical models being developed should be aimed at determining the rate of particle enlargement depending on the modes of formation of nonlinear disturbances. The rate of particle enlargement is determined according to the following expression:
where D30 is the volumetric average particle diameter (m), ni is the countable concentration of particles of size Di (m–3), and the sign < > means averaging the function along the length of the ultrasonic disturbance.
Since the ultimate goal of this study is to determine the limiting capabilities of ultrasonic coagulation, it is necessary to determine the maximum coagulation speed during the entire time of the process, according to Expression (2):
Based on the definition of the average volume diameter, the rate of enlargement in accordance with Expression (1) depends on the concentrations of aerosol particles of various sizes.
In turn, according to the most well-known and experimentally confirmed probabilistic approach of Smoluchowski, the evolution of concentrations of aerosol particles is described by the following generalized equation:
where ni is the concentration of particles of standard size i1/3d0 (d0—nominal diameter of the smallest particle), βi,j is the probability of collision of particles of sizes i1/3d0 and j1/3d0 under the influence of an ultrasonic field in the gas phase, and Ui is the transfer speed of particles of standard size i1/3d0.
Thus, the development of a numerical model of the interaction of individual pairs of particles should be aimed at determining the probability of particle collisions. When analyzing the influence of nonlinear pressure distortions on the efficiency of coagulation of individual particles, the coagulation speed can be determined as a value proportional to the probability of particle collision and their concentration (the change in concentration is considered to be spatially uniform). Since the particle concentration decreases over time, the maximum coagulation rate is achieved at the beginning of the process (t = 0).
In turn, the development of a numerical model that describes the spatially inhomogeneous evolution of concentration in vortex acoustic flows should be aimed at reducing the dimensionality of Equation (3). In this case, the coagulation rate will not necessarily reach a maximum at the initial moment in time, since over time the aerosol becomes denser due to inertial transport in vortices.
According to Equation (3), the numerical calculations should have three stages:
- Calculation of the collision cross-section square due to Brownian motion.
- Calculation of the probability of particle collision by nonlinear pressure disturbances.
- Calculation of the maximum coagulation rate (2) by solving the generalized Equation (3) for concentrations.
The numerical models developed according to these stages, along with the results of calculating the influence of nonlinear disturbances of gas velocity and pressure on the coagulation rate, are described in the following sections.
3. Theoretical Analysis of Physical Mechanisms and Construction of a Model of the Influence of Nonlinear Pressure Disturbances on the Efficiency of PM2.5 Coagulation
As already mentioned, the analysis of the influence of nonlinear pressure disturbances on the coagulation rate is carried out for individual particles. Accordingly, theoretical analysis of the influence of nonlinear pressure disturbances aims to develop a model to determine the particle collision probability. The basis for determining the particle collision probability is the general Expression (4) [9]:
where is the hydrodynamic interaction component (m3/s) and is the orthokinetic interaction component (m3/s).
The collision probability components are determined according to the following expressions:
where is the particle interaction force (N), is the collision cross-sectional area (m2), n is a unit vector indicating the direction of the line of particle centers relative to the wave vector of the ultrasonic field, is the dispersion (squared uncertainty) of the spatial position of the particle (m), l is the distance between particles (m), and c is the speed of propagation of ultrasonic vibrations in the carrier gas phase (m/s).
From a comparison of the two components, it follows that , i.e., hydrodynamic interaction, as stated in the introduction, is decisive. The probability of hydrodynamic interaction linearly depends on the cross-sectional area of the collision.
3.1. Cross-Sectional Area Due to Brownian Motion
According to the available data [19,20], Brownian motion affects the cross-sectional area of the collision. This influence was not previously considered, while when Brownian motion is taken into account the collision cross-sectional area is determined by the dispersion of the spatial position of the particle in accordance with Expression (8), first obtained as follows:
It is obvious that collisions of moving molecules of the gas phase with particles (Figure 1) lead to a change in the cross-sectional area of the collision according to Expression (8). The cross-sectional area is increased due to the increasing amplitude of local oscillations caused by Brownian motion [37].
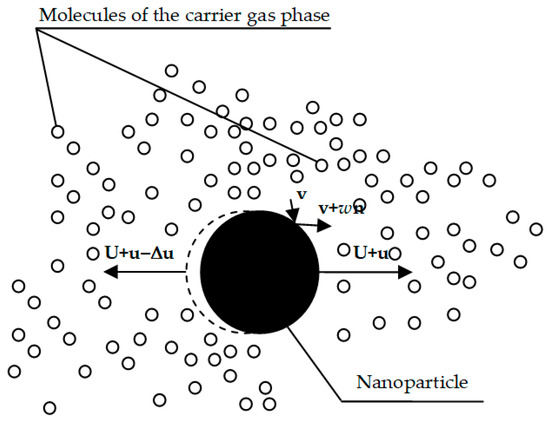
Figure 1.
Schematic representation of the process of collision of gas-phase molecules with a submicron particle and the change in particle speed as a result of an elementary act of collision; v—random speed of movement of gas-phase molecules; u—random component of the velocity of a particle, caused by the thermal collision of gas-phase molecules with the particle; U—deterministic component of the speed of movement caused by the entrainment of a particle in the oscillatory motion of the gas flow.
The calculation of the cross-sectional area takes into account the following assumptions:
- -
- The speed of a particle after the collision of a molecule with it is determined by the momentum conservation law;
- -
- All collisions are absolutely elastic;
- -
- Collisions are equally probable in all possible directions with similar probability.
The spatial position of a particle as a result of a sequence of elementary acts of collision between the particle and molecules of the gas phase is determined by the following expression:
where ti is the time of occurrence of the i-th elementary act of collision between a molecule and a particle (s), ui is the particle speed as a result of the i-th elementary act of collision (m/s), and ri is the particle coordinate vector at the moment of occurrence of the i-th elementary collision event (m).
The speed of a particle as a result of the i-th elementary act of collision is determined according to the law of conservation of momentum (following expressions):
: momentum conservation law for the “particle-colliding molecule” system (see Figure 1);
and : general expressions for the consequent changes in particle and molecule velocity (see Figure 1).
The parameter w is determined from the law of conservation of energy:
where M is the particle mass (kg) and m is mass of the gas-phase molecule (kg).
The velocities of molecules are randomly generated by the Monte Carlo method according to Maxwell’s law:
The distribution function of particles velocity remains similar after the action of previous collisions:
This makes it possible to consider the pressure constant when determining the instantaneous effective cross-section for particle collisions over time, which is much less than the period of ultrasonic oscillations:
- In an undistorted ultrasonic field, which represents classical sinusoidal pressure oscillations:
- In a distorted ultrasonic pressure field, which represents a periodic shock-wave change in pressure in accordance with the following expression:
If , then the ultrasonic field consists of compression pulses; if , then the ultrasonic field consists of rarefaction pulses, where T is the period of nonlinear ultrasonic field oscillations (s); pA is the amplitude of the ultrasonic disturbances (Pa), and τ is the characteristic pulse duration (s).
The presented expression for the distorted pressure of a shock wave is an approximation of pressure oscillograms formed in acoustic beams (pulses) and/or standing waves, previously obtained experimentally [15] and theoretically [17].
For an undistorted continuous sinusoidal stimulus, the effective collision cross-section changes little (less than 10 percent increase). For a distorted ultrasonic field , during the formation of the compression phase of the wave , the increase in the collision area, even for the smallest particles (0.1…0.2 microns or 100…200 nm), does not exceed 1.3–1.4-fold, and only with the formation of a rarefaction phase under ultrasonic influence () does the collision square increase up to 2-fold at the powers provided by modern ultrasonic radiators [24,25,26].
Furthermore, the collision probability can be calculated with using the model for the change in cross-section area due to Brownian motion and the influence of acoustic pressure disturbances on it. The model for collision probability is described in the next subsection.
3.2. Collision Probability Due to Nonlinear Pressure Disturbances and Free-Molecular Effects
To calculate the probability of coagulation, the following assumptions were made:
- That all particles and agglomerates are spherical.
- The particles and agglomerates are stable and are not broken.
- At each particle collision, a new agglomerate is formed.
- The volume of the new agglomerate is direct sum of the volumes of the sub-particles.
The obtained data on the square of the collision cross-section allowed us to proceed to the study of the process of particles’ hydrodynamic interaction, which, according to [9], can be determined by the radiation pressure of the ultrasonic influence reflected from a neighboring particle:
where f21 is the interaction force between particles (N), p is the gas pressure disturbance near a particle initiated by a neighboring particle (Pa), u is the disturbance of the gas velocity near a particle initiated by a neighboring particle (m), and n is the normal vector to the surface of the particle.
Since the particles under consideration are submicron (up to 0.1 μm), and the distance between them is comparable to the gas-phase molecules’ free path (0.07 μm in air at normal conditions [38], and this value increases with the rarefaction of pressure), to calculate the reflected ultrasonic fields, quasi-gas-dynamic equations were used, taking into account free-molecular effects (i.e., the mutual diffusion of the gas phase and the non-equilibrium of the process of changing pressure in the gas phase) [39]:
where u is the movement speed of the gas-phase molecules (m/s), is the gas-phase density (kg/m3), τ is the relaxation time required to transition to an equilibrium state (s), and Π is the stress tensor in the gas phase (Pa).
The solution of the presented system of equations made it possible to determine the disturbance fields of pressure and gas velocity around an individual particle under a given ultrasonic influence (sinusoidal, or with predominant phases of compression or rarefaction). The solution allowed us to calculate the force of radiation pressure on a neighboring particle from the observed disturbance fields, as well as the probability of hydrodynamic interaction.
Since the process of propagation of ultrasonic influence is adiabatic, the system of Equations (11)–(13) is transformed as follows:
Next, the system is supplemented with the surface boundary condition of the particle (17) from which reflection occurs, and with Conditions (18) and (19) at a distance exceeding the distance between neighboring particles (at infinity):
where is the static pressure in gas without ultrasonic disturbances (Pa), PA is the pressure of ultrasonic influence (Pa), and k is the wave vector of the ultrasonic field (m−1).
The distribution of pressure disturbances near a spherical particle is determined by Expression (20) and consists of three components:
where prefl is the pressure component in ultrasonic influences reflected from a particle (Pa).
In real gas-dispersed systems, the distance between particles exceeds the gas molecules’ mean free path (70 nm), and the determination of the velocity and pressure disturbances is based on the asymptotic expansion in powers of the gas relaxation time (the time required for the transition to an equilibrium state and the adoption of microscopic parameters of an ensemble of molecules corresponding to the parameters of the gas) and the external ultrasonic influence amplitude:
Based on the presented asymptotic expansions, the system of mass and momentum conservation equations is decomposed into several equations in orders of relaxation time (coefficients at different powers):
at n > 0:
or
where Fn, Gn, Hn, Kn, Jn are functions of , …, , , …, , and their derivatives; satisfies zero boundary conditions (17)–(19).
Thus, the solutions of Equations (14)–(19) can be reduced to solve the nonlinear (21) and (22) and linear problems with non-zero right parts (25) and (26).
The finite element method for linear problems is well known and verified (weak formulations of linear problems and examples of solutions by the finite element method were generalized using FreeFEM++ software by version 4.13 [40]).
Nonlinear problems for (, , ) were solved by the iterative method for Navier–Stokes equations [14]. For solving by this method, the authors used the following transformation of Equations (21) and (22) to (27) and (28), respectively:
where .
The iterative method was verified in work [14].
Substitution of the observed particle interaction force f21 into the expression for the collision probability allowed us to calculate the maximum speed of particle coagulation depending on the acoustic disturbance parameters:
The determined coagulation rate dependences are presented in the next section.
4. Results of Calculations of the Influence of Nonlinear Pressure Disturbances on the Coagulation Efficiency of PM2.5
The results of calculating the coagulation rate are presented in Figure 2a–c and Figure 3a–e. Here and below, the maximum achievable coagulation rate is given throughout the entire duration of the process. A monodisperse aerosol with a given fixed particle size was taken as the initial aerosol. As follows from the dependences presented in Figure 3, ultrasonic exposure in the form of pulses (both with a predominant compression phase (pA > 0) and a predominant rarefaction phase (pA < 0)) accelerates the coagulation process compared to sinusoidal ultrasonic exposure. At the same time, the coagulation rate increases with decreasing duration of the rarefaction or compression phases, even when the root-mean-square value of the sound pressure is maintained (total input energy).
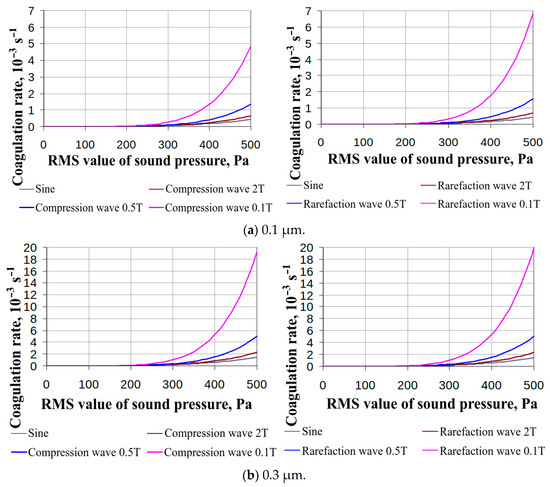
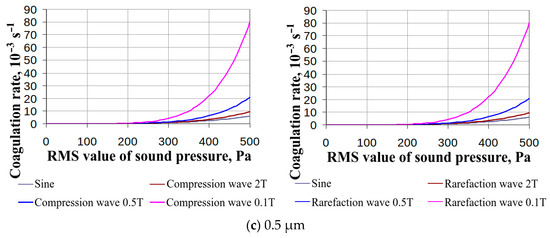
Figure 2.
Dependence of the maximum coagulation rate on the root-mean-square value of pressure at various particle sizes and exposure conditions (compression and rarefaction waves, diameter range from 0.1 to 0.5 μm).
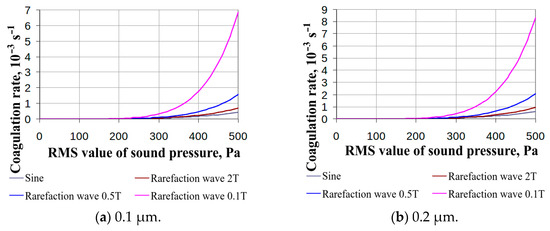
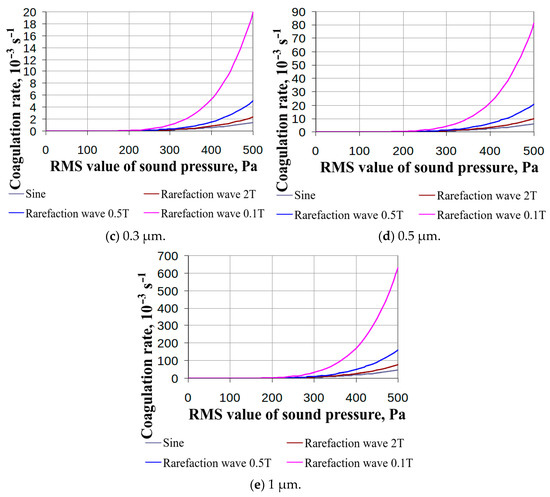
Figure 3.
Dependence of the maximum coagulation rate on the root-mean-square value of pressure at various particle sizes and exposure conditions (rarefaction waves only, diameter range from 0.1 to 1 μm).
This is due to nonlinear effects that occur with a sharp increase in the instantaneous sound pressure value.
In these and subsequent dependences, the value T (the period of acoustic disturbances) is equal to 1/22,000 s. Here and below (unless specifically stated), the dependences were obtained at a constant particle count concentration of 1 × 1013 m−3, which corresponds to a mass concentration of less than 0.01 g/m3 even for particles 1 micron in size.
The presented dependences (Figure 2) indicate that nonlinearly distorted pressure fluctuations contribute to increasing the efficiency of coagulation over the entire range of particle sizes. The data obtained show an increase in the efficiency of coagulation using pulsed ultrasound while maintaining the amount of input energy. At the same time, the coagulation rate increases by 13 times due to the disturbance of the ultrasonic pressure field during the implementation of a shock-wave (pulse) effect with a predominant rarefaction phase. The shock wave with a predominant compression phase gives a smaller effect (in the range of 1.2–1.3 times from 0.1-micron particles) due to the smaller collision cross-section.
From 0.3 microns, the compression and rarefaction shock waves give almost identical effects, because the gaseous phase is almost continuous. For 0.1-micron particles, the Brownian motion has a significant effect.
Therefore, below are the dependences of coagulation efficiency on the root-mean-square value of sound pressure with a predominant rarefaction phase for different particle sizes (Figure 3a–e):
In this case, shock waves with a predominant rarefaction phase retain an increased effect compared to waves with a predominant compression phase up to particles 0.5 μm in size.
However, since the coagulation rate is linearly proportional to the concentration of particles, when it comes to fine purification of gases from the most dangerous fractions, as the concentration decreases, the effectiveness of coagulation, even in nonlinearly disturbed pressure fields, is reduced to nothing. Meanwhile, particles can cause negative effects on human health even at a concentration of less than 1011 m−3, which is 100 times less than the concentration accepted in the above calculations.
Therefore, there is a need to create conditions for compaction of the aerosol mass to increase the coagulation rate due to a local increase in concentration, i.e., studies of the influence of nonlinear velocity disturbances arising during the formation of vortex acoustic flows.
The mathematical formulation of the problem of calculating the coagulation rate, taking into account the formation of vortex acoustic flows, is given in the next section.
5. Theoretical Analysis of Physical Mechanisms and Construction of a Model of the Influence of Nonlinear Velocity Disturbances on the Efficiency of PM2.5 Coagulation
The construction of a model of the influence of nonlinear velocity disturbances is aimed at reducing the dimensionality of the generalized Smoluchowski equation, in accordance with the formulation of the problem presented in Section 2.
Therefore, it is necessary to develop a system of assumptions to find ways to reduce the dimensionality of the initial boundary value problem. When theoretically analyzing the influence of nonlinear gas velocity disturbances on the efficiency of coagulation, the following assumptions are made:
- Vortex acoustic flows (nonlinear velocity distortions) are stationary. This assumption is determined by the fact that an increase in the speed of acoustic flows arising due to the absorption of the energy of ultrasonic vibrations leads to a proportional increase in the force of viscous friction, which impedes the flow.
At the same time, the absorbed energy of ultrasonic vibrations includes a kinetic component (energy that turns into kinetic energy of the liquid) and a thermal component (energy that turns into heat due to fluctuations in the force of viscous friction).
As the speed of acoustic flows increases, the kinetic component of the absorbed energy of ultrasonic vibrations is balanced by the work against the forces of viscous friction in the flows.
- 2.
- In a stationary flow of the gas phase, particles drift at a constant speed , where τp is the particle relaxation time (s) and u is the particle movement speed (m/s).
This assumption is justified by expanding the velocity of the particle in a small parameter (29) and substituting it into the equation of motion (30), which, according to the proposed formulation of the problem, describes the involvement of the particle in stationary vortex gas flows:
where t is the time (s), up is the particle speed (m/s), is the particle relaxation time (s), T is the period of ultrasonic vibrations (s), rp is the particle coordinate vector (m), and u is the velocity of the stationary gas-phase flow at a point with coordinate t.
With a particle size of no more than 2.5 microns, the ratio .
Thus, it is sufficient to limit ourselves to the term of the expansion in the first power of the relaxation time:
- 3.
- The characteristic time of particle coagulation exceeds the time of complete rotation of the particle around the streamline. This assumption is due to the low efficiency of classical ultrasonic coagulation of particles when it comes to fine gas purification from small particles.
- 4.
- The characteristic transition time of particles between streamlines of a vortex flow is much greater than the time of a complete revolution around the streamline.
- 5.
- As a consequence of Assumptions 3 and 4, the concentration of particles within one streamline can be considered to be the same, and the contributions of inertial transport of particles and coagulation among them are additive.
To simulate the conditions for the simulation of vortex acoustic flows, the equation of dynamics of an incompressible gas under the action of an equivalent external force caused by the absorption of acoustic vibrations was used. The equivalent volumetric external force was determined according to the expression given in the works [13,14].
Next, we propose an approach that is intended to reduce the dimensionality of the problem in order to consider not spatially inhomogeneous coagulation over all coordinates, but only to track the evolution of the number of particles on each streamline, determined by one parameter—the stream function, which can be introduced for stationary flows.
5.1. Reducing the Dimensionality of the Initial Boundary Value Problem of Ultrasonic Aerosol Coagulation with Nonlinear Velocity Disturbances
As noted earlier, reducing the dimensionality of the problem is possible based on the assumption that the concentrations are equal along the streamline. The method of reducing the dimensionality of the problem is based on representing the gas flow velocity in the form of partial derivatives of the stream function.
According to the accepted assumption of the same concentrations along the streamline, the concentration of a separate fraction of the aerosol cloud included in the generalized Smoluchowski equation (Equation (4); see Section 1) can be determined as a function of the stream function ψ (hereinafter, the index is omitted).
To formulate the initial boundary value problem, in terms of the dependence of the concentrations of particles of each standard size on the stream function (in order to ultimately determine the limiting coagulation rate as the maximum rate of particle enlargement, depending on the concentrations, according to Expression (2)—averaging of the enlargement rate over the wavelength uses ultrasonic vibrations, within which a vortex is formed [13,14]), the equation for the evolution of particle concentrations is derived in the following sequence:
- 1.
- Using the Gauss–Ostrogradsky formula, the properties of continuity of functions nk(r, t), and taking into account the arbitrariness of the volume V, the general integral equation for the balance of the number of particles in volume V and flows through the boundary of volume V is represented in differential form:
- 2.
- Next, Equation (24) is integrated along the streamlines. Within each streamline, particles move rapidly, the speed of which is many times greater than the speed of transition between streamlines. As a result of integration along streamlines, the equation for the evolution of an aerosol cloud (24) is transformed to the following form (32):where the averaging sign < > means
This equation is non-stationary and can be solved in the space–time domain:
The following subsection describes the new algorithm developed by authors for the numerical solution of the posed initial boundary value problem.
5.2. Algorithm for the Numerical Solution of the Initial Boundary Value Problem of Calculating Ultrasonic Coagulation of Aerosols in Vortex Acoustic Flows
The algorithm for the numerical solution of a three-dimensional initial boundary value problem consists of the following steps:
- Calculation of the acoustic field of vibrational velocities of the gas phase in the sounded volume.
- Calculation of the field of laminar vortex acoustic flows based on the numerical solution of the Navier–Stokes equations using the iterative method [14].
- Calculation of the field of amplitudes of turbulent velocity disturbances.
- Calculation of averages included in Equation (32) at various discrete values of the current functions.
- Polynomial approximation of the averages from Step 4 as functions of ψ.
- Iterative solution of the concentration evolution equation using a discrete phase model. As mentioned early, DPMs in 2D and 3D problems have large numerical instability. In the proposed algorithm, the instability was significantly reduced due to the reduction in the problem’s dimensionality. In fact, the 1D problem was solved instead of the 2D problem. In modified DPMs, each group contains particles characterized by a stream function defining the group position instead of coordinates.
For verification of the new numerical model, the test calculation was performed for the simplest stream function:
where UF is the velocity of the fluid at a distance which equals to from the vortex center (m/s), while is the length of the ultrasonic wave (m).
The ultrasonic field in the test case is fixed as spatially uniform.
At the stream function, at the averaging by expression (33) Equation (32) can be simplified to (34)
where Ci,j are constants with the same dimensionality as the particle collision probability.
If at i > 1 or j > 1 Ci,j = 0, Equation (34) has an exact solution:
For the verification of the algorithm, the test solutions were calculated and compared with exact solutions for the smallest particles (concentration: n1(t), which is uniform in volume in the test case under the test vortex stream function).
The results of the test calculations at different counts of particle groups in the DPM are presented in Figure 4.
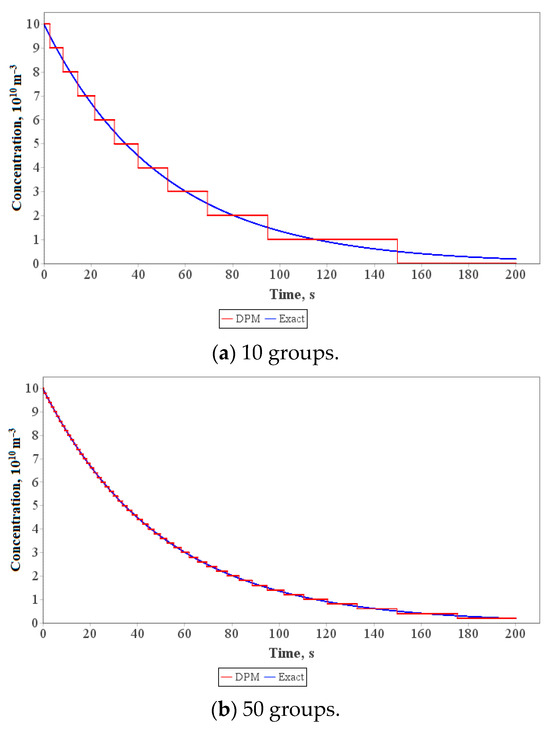
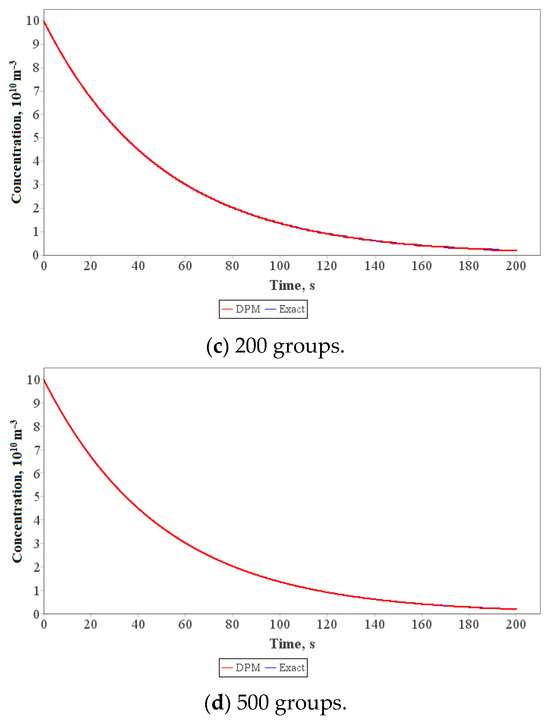
Figure 4.
Dependence of the smallest particle concentration on time at different group counts in the DPM.
According to the dependences, after 200 groups the numerical solution is almost equal to the exact solution. Thus, the proposed numerical algorithm is verified.
The following section describes the results of calculations of the influence of nonlinear velocity disturbances on the maximum efficiency (speed) of coagulation, obtained using the developed algorithm.
6. Results of Calculations of the Influence of Nonlinear Disturbances in Gas Velocity on the Efficiency of Coagulation
Since the ongoing research is aimed at searching for the maximum capabilities of ultrasonic coagulation, the condition for the occurrence of the most intense nonlinear velocity disturbances was initially identified—the optimal size of the air gap at which the speed of vortex acoustic flows is maximal was established, based on the calculation of the acoustic field. The speed of the vortex acoustic flows was calculated based on the solution of the Navier–Stokes equations with an equivalent volumetric force causing the acoustic drift of the gas. The volumetric force was determined according to the expression given in [14]. This size corresponds to half of the ultrasonic wavelength.
When using a radiator with a uniform distribution of vibration amplitude over the surface [25] (piston emitter), there is a single vortex with transverse dimensions coinciding with the dimensions of the sounded volume. The speed of such a vortex does not exceed a fraction of cm/s and does not make a noticeable contribution to the efficiency of coagulation.
During bending vibrations of the emitter surface mentioned in the Introduction, there are many vortices with sizes corresponding to the length of the bending waves of vibrations of the emitter surface.
The speed of vortex flows under the influence of a bending–oscillating emitter can reach over 10 cm/s at a sound pressure level of 150 dB near the emitter (when radiation occurs in an unlimited space) [24].
Next, under the optimal conditions determined for the formation of nonlinear velocity disturbances, a numerical analysis of the contribution of disturbances to the rate of ultrasonic coagulation was carried out. Calculations were carried out using a flat distribution of vibrations of the emitter when the nonlinear gas velocity disturbances did not affect the efficiency of ultrasonic coagulation (classical ultrasonic coagulation), and bending vibrations of the emitter surface when the nonlinear velocity disturbances had a significant effect (ultrasonic coagulation + nonlinear velocity disturbances).
By analogy with nonlinear pressure disturbances, the dependences were given starting with particle sizes of 0.5 μm, at which rarefaction shock waves do not provide increased efficiency compared to compression shock waves (Figure 5).
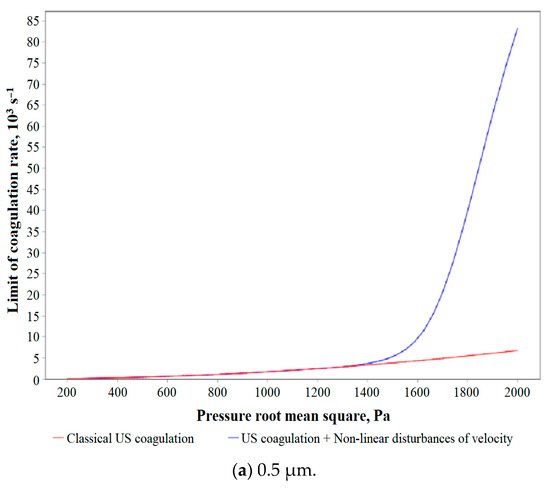
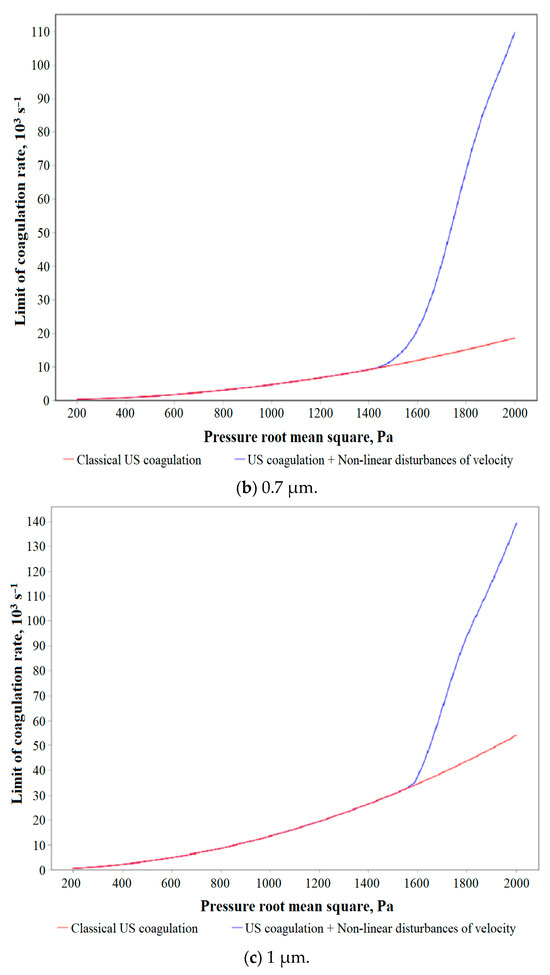
Figure 5.
Dependences of the maximum speed of ultrasonic coagulation on the root-mean-square value of sound pressure in the presence and absence of nonlinear disturbances of the gas velocity for various initial particle sizes (counting concentration: 1 × 1013 m−3).
The obtained dependencies (Figure 5) made it possible to establish that, in the range of root-mean-square sound pressure values from 200 to 1400 Pa, nonlinear gas velocity disturbances have no effect, whereas they can increase the coagulation efficiency by more than 10 times for particles with a size of 0.5 microns and more than 2.5 times for particles with a size of 1 microns. The influence of nonlinear velocity disturbances is manifested for a similar counting concentration, only starting from a root-mean-square sound pressure of more than 1400 Pa. However, since nonlinear velocity disturbances determine the transfer of individual particles regardless of their concentration, and since the final speed of ultrasonic coagulation is directly proportional to the concentration because it is determined by pairwise collisions of particles, it follows that, at lower concentrations, the contribution of nonlinear velocity disturbances should increase. Meanwhile, at lower concentrations, the efficiency of ultrasonic coagulation, even in a nonlinearly disturbed pressure field, which directly affects the probability of collision of individual particles (see Section 3), will decrease proportionally.
Therefore, further studies were carried out on the speed of ultrasonic coagulation at a reduced counting concentration of 1 × 1012 m−3 (Figure 6).
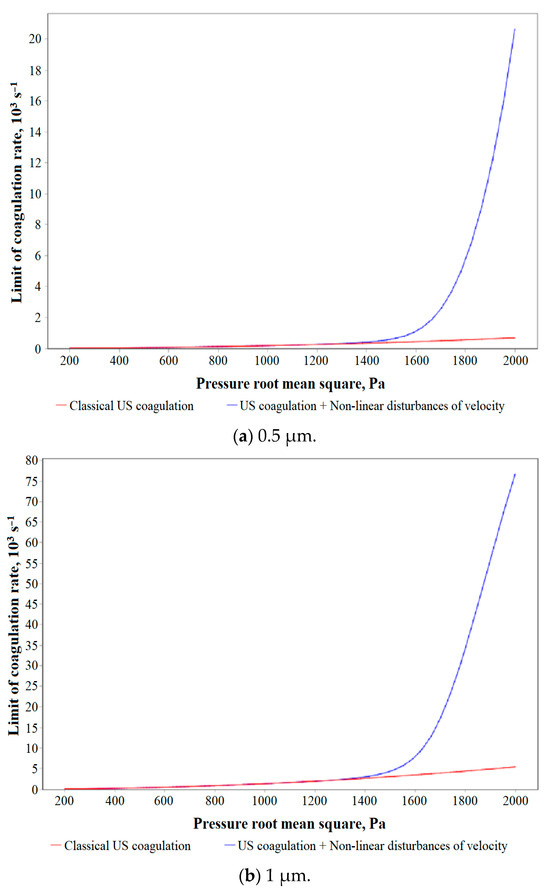
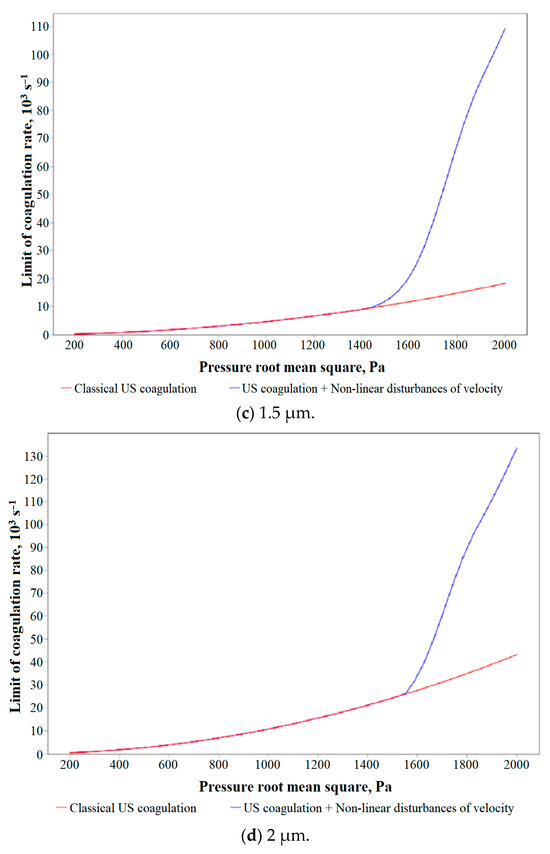
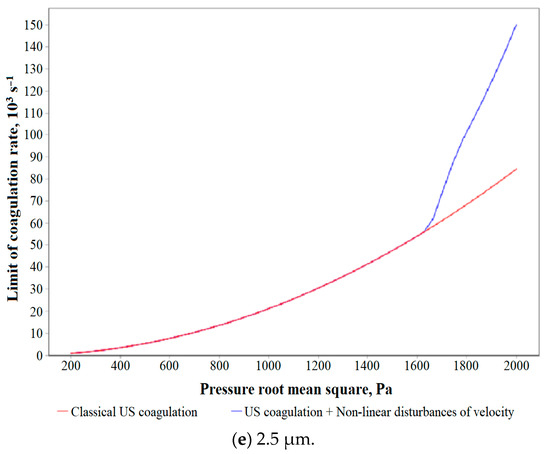
Figure 6.
Dependences of the maximum speed of ultrasonic coagulation on the root-mean-square value of sound pressure in the presence and absence of nonlinear disturbances of the gas velocity for various initial particle sizes (counting concentration: 1 × 1012 m−3).
It has been established that, in the presence of vortex acoustic flows, the rate of ultrasonic coagulation at a reduced concentration turns out to be comparable to the rate at an increased concentration (see Section 3). Thus, for particles of 1 µm in size, the coagulation rate reaches 0.14 s−1 at concentration 1 × 1013 m−3, and at a concentration 10 times lower (1 × 1012 m−3) the coagulation speed reaches 0.08 s−1 at the same sound pressure. This is explained by local compaction of particles as a result of inertia in a nonlinearly disturbed field of gas velocities.
In turn, the influence of nonlinear velocity disturbances for small particles is enhanced compared to that for large ones. This is due to the fact that the relaxation time of a particle in a laminar gas flow is proportional to the square of its size, and the probability of a particle collision under the influence of ultrasound is a quantity that multiplicatively depends on the cross-sectional area of the collision (proportional to the square of the particle size) and the ratio of the force of hydrodynamic interaction to the force of viscous flow (linearly proportional to particle size)—the cube of particle size.
In Figure 7, the dependences of the coagulation rate on concentration are presented.
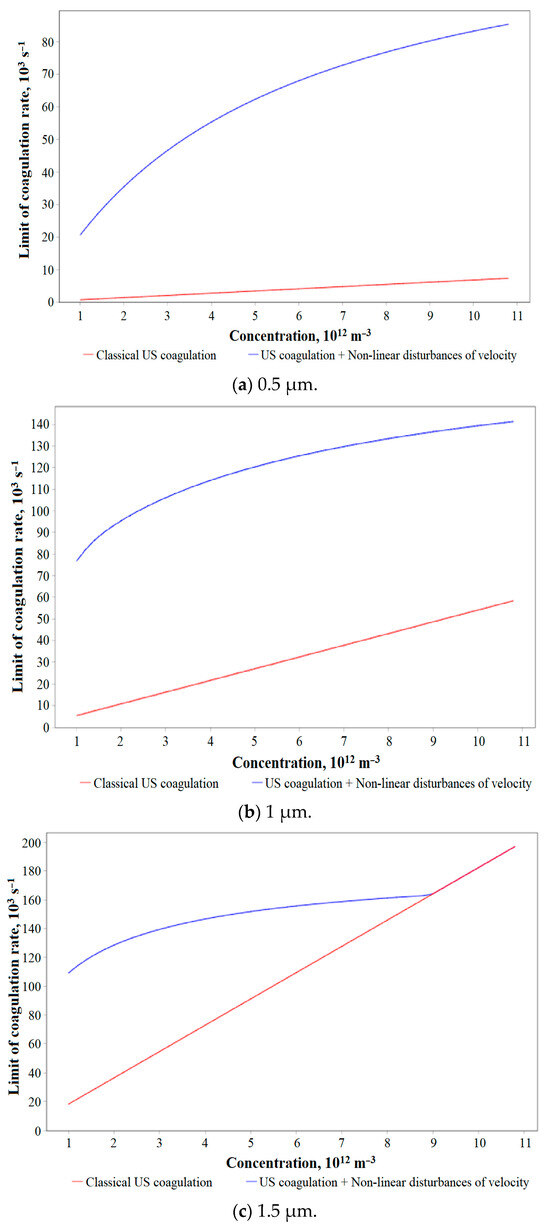
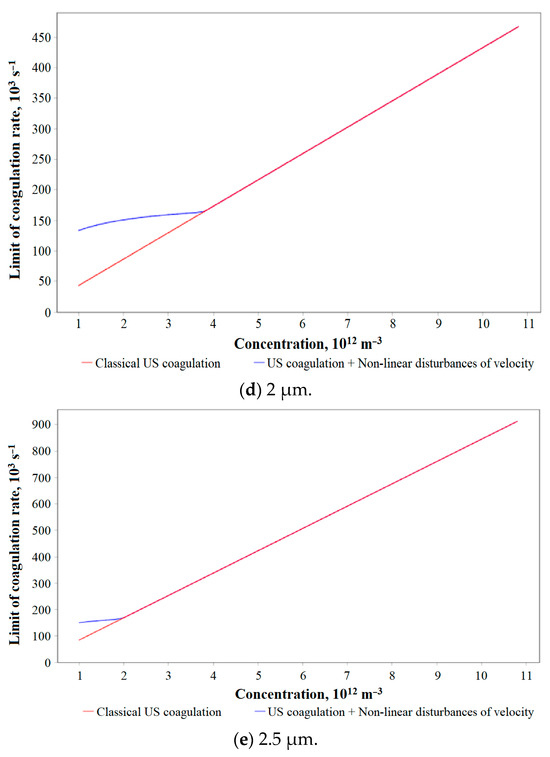
Figure 7.
Dependences of the maximum speed of ultrasonic coagulation on the particles’ initial concentration in the presence and absence of nonlinear disturbances of the gas velocity for various initial particle sizes (RMS pressure: 2000 Pa).
The dependences indicate that nonlinear disturbances of the ultrasonic field are effective for lower concentrations of particles across the whole range of PM2.5 diameters (a diameter of 1 micron and concentration of 1012 m−3 correspond to a volume fraction of 5.2 × 10−7 m−3).
This means that nonlinear velocity disturbances can provide an increase in coagulation efficiency at low concentrations due to local compaction of the aerosol cloud. Then, when nonlinear velocity disturbances increase the particle concentration, the aerosol cloud can be effectively coagulated in the nonlinearly disturbed pressure field, which has a predominant effect at elevated concentrations.
The effect of nonlinear velocity on coagulation has been confirmed by experimental work [24]. According to that work, at a sound pressure of about 140 dB, which corresponds to an RMS pressure of 200 Pa, the effect is absent. There is no difference between the coagulation efficiencies in the presence and absence of acoustic vortices (the presence and absence of acoustic vortices were obtained by different ultrasonic radiators). However, at 160 dB (RMS pressure: 2000 Pa), there is a higher coagulation rate at acoustic vortices, which is also present in the theoretical dependences.
Thus, the influence of nonlinear effects on the rate of ultrasonic coagulation of PM2.5 has been theoretically analyzed, and ways have been found to increase the efficiency of ultrasonic coagulation, thereby bringing it closer to the maximum possible, due to the following mechanisms:
- -
- Local compaction of an aerosol cloud of particles at low concentrations in a nonlinearly disturbed gas velocity field;
- -
- Effective coagulation of a dense aerosol cloud in a nonlinearly disturbed pressure field with predominant rarefaction waves, which make the greatest contribution to the enlargement of particles less than 0.5 microns in size.
7. Conclusions
As a result of our studies, the ineffectiveness of ultrasonic coagulation for PM2.5 by classical sinusoidal action was substantiated, due to the peculiarities of the physical mechanisms of hydrodynamic and orthokinetic interaction realized in gaseous media.
Ways to increase the efficiency of ultrasonic coagulation have been proposed and theoretically substantiated, based on the creation of special conditions for the occurrence of nonlinear disturbances of the main parameters characterizing the flow of the gas phase—i.e., the pressure and velocity of the medium.
A numerical model of the coagulation of individual particles in a nonlinearly disturbed pressure field is proposed here, which, for the first time, unlike previous models, takes into account the influence of non-equilibrium and molecular effects not only on the force of the hydrodynamic interaction of particles, but also on the effective cross-sectional area of the collision. A new method has been proposed for calculating the probability of particle collisions while taking these effects into account.
Using the proposed model, it has been established that the coagulation rate can be increased up to 13 times for submicron-sized particles by creating periodic rarefaction shock waves, which not only increase the force of hydrodynamic interaction of particles due to non-equilibrium and molecular effects, but also increase the effective cross-sectional area of the collision up to 2.5 times or more on account of Brownian motion. At the same time, it has been shown that for particles ranging in size from 0.1 μm to 0.5 μm, periodic shock-wave exposure (with a rarefaction amplitude of at least 10,000 Pa) allows the coagulation rate to be increased by up to 20 times compared to classical sinusoidal exposure.
For an ensemble of aerosol particles, a new numerical model is proposed that allows one to calculate the spatially inhomogeneous evolution of an aerosol in vortex acoustic flows. A method for reducing the dimensionality of the initial boundary value problem is proposed. This method is based on averaging the aerosol concentrations along a streamline. The validity of using this method is due to the high speed of the vortices compared to the speed of ultrasonic coagulation of aerosols at low concentrations. The possibility of additionally increasing the efficiency of aerosol coagulation by up to 2-fold due to the occurrence of vortex acoustic flows has been established.
The results obtained here could be used to develop technology for highly effective gas purification from the most dangerous and difficult to detect PM2.5 particles.
Author Contributions
Conceptualization, V.K. and A.S.; methodology, R.G. and A.S.; software, R.G.; validation, R.G., A.S. and V.K.; formal analysis, R.G.; investigation, R.G.; resources, V.K.; data curation, V.K.; writing—original draft preparation, R.G.; writing—review and editing, V.K. and A.S.; visualization, R.G.; supervision, V.K.; project administration, A.S.; funding acquisition, V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, No. 19-19-00121 (https://rscf.ru/en/project/19-19-00121/) (accessed on 19 September 2023).
Data Availability Statement
The data are available from the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Y.; Yang, Y.; Chen, J.; Shi, M. Spatiotemporal heterogeneity of the relationships between PM 2.5 concentrations and their drivers in China’s coastal ports. J. Environ. Manag. 2023, 345, 118698. [Google Scholar] [CrossRef]
- Hassan, M.S.; Gomes, R.; Bhuiyan, M.; Rahman, M. Land Use and the Climatic Determinants of Population Exposure to PM2.5 in Central Bangladesh. Pollutants 2023, 3, 381–395. [Google Scholar] [CrossRef]
- Ihsan, I.; Oktivia, R.; Anjani, R.; Zahroh, N. Health risk assessment of PM2.5 and PM10 in KST BJ Habibie, South Tangerang, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2023, 1201, 012033. [Google Scholar] [CrossRef]
- Ma, Y.; Zang, E.; Liu, Y.; Lu, Y.; Krumholz, H.; Bell, M.; Chen, K. Wildfire smoke PM2.5 and mortality in the contiguous United States. medRxiv 2023. [Google Scholar] [CrossRef]
- Riera, E.; González-Gómez, I.; Corral, G.; Gallego-Juarez, J. Ultrasonic agglomeration and preconditioning of aerosol particles for environmental and other applications. In Power Ultrasonics, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2023; pp. 861–886. [Google Scholar]
- Song, L. Modelling of Acoustic Agglomeration of Fine Aerosol Particles. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 1990. [Google Scholar]
- Moldavsky, L.; Gutfinger, C.; Oron, A.; Fichman, M. Effect of sonic waves on gas filtration by granular beds. J. Aerosol Sci. 2013, 57, 125–130. [Google Scholar] [CrossRef]
- Moldavsky, L.; Gutfinger, C.; Fichman, M. Effect of acoustic waves on the performance of a multi-cyclone—Filter system. Filtration 2011, 11, 229–232. [Google Scholar]
- Sheng, C.; Shen, X. Simulation of Acoustic Agglomeration Processes of Poly-Disperse Solid Particles. Aerosol Sci. Technol. 2007, 41, 1–13. [Google Scholar] [CrossRef]
- Shaw, D.T.; Tu, K.W. Acoustic particle agglomeration due to hydrodynamic interaction between monodisperse aerosols. J. Aerosol Sci. 1979, 10, 317–328. [Google Scholar] [CrossRef]
- Dong, S.; Lipkens, B.; Cameron, T. The effects of orthokinetic collision, acoustic wake, and gravity on acoustic agglomeration of polydisperse aerosols. J. Aerosol Sci. 2006, 37, 540–553. [Google Scholar] [CrossRef]
- Shi, Y.; Bai, W.; Zhao, Z.; Ayantobo, O.; Wang, G. Theoretical analysis of acoustic and turbulent agglomeration of droplet aerosols. Adv. Powder Technol. 2023, 34, 104145. [Google Scholar] [CrossRef]
- Khmelyov, V.N.; Golykh, R.N.; Nesterov, V.A.; Shalunov, A.V. Numerical Model of Ultrasonic Agglomeration of Submicron Particles in Resonant Gas Gaps. J. Eng. Phys. Thermophy 2023, 96, 255–265. [Google Scholar] [CrossRef]
- Khmelev, V.N.; Golykh, R.N.; Shalunov, A.V.; Nesterov, V.A. Numerical model of ultrasonic coagulation of dispersed particles in Eckart flows. Interfac. Phenom. Heat Transf. 2022, 10, 1–23. [Google Scholar] [CrossRef]
- Brysev, A.P.; Krutyanskiy, L.M.; Perno, F.; Preobrazhenskiy, V.L. Non-linear ultrasonic beams with reversed front and its application in acoustoscopy. J. Acoust. 2004, 50, 725–743. (In Russian) [Google Scholar]
- Kurosaka, M. Acoustic streaming in swirling flow and the Ranque—Hilsch (vortex-tube) effect. J. Fluid Mech. 1982, 124, 139–172. [Google Scholar] [CrossRef]
- Konnova, E.O.; Khokhlova, V.A.; Yuldashev, P.V. The using of graphical accelerators for simulation of non-linear ultrasonic beams with shock fronts based on Westervelt equation. Acoust. Phys. 2023, 68, 529–536. (In Russian) [Google Scholar] [CrossRef]
- Tyurina, A.V.; Yuldashev, P.V.; Esipov, I.B.; Khokhlova, V.A. Generation of acoustic wave at difference frequency in diffracting beam of pump waves in quasi-linear approximation. J. Acoust. 2023, 69, 13–21. (In Russian) [Google Scholar]
- Shuster, K.; Fichman, M.; Goldshtein, A.; Gutfinger, C. Agglomeration of submicrometer particles in weak periodic shock waves. Phys. Fluids 2002, 14, 1802–1805. [Google Scholar] [CrossRef]
- Goldshtein, A.; Shuster, K.; Vainshtein, P.; Fichman, M.; Gutfinger, C. Particle motion in resonance tubes. J. Fluid Mech. 1998, 360, 1–20. [Google Scholar] [CrossRef]
- Michaelides, E.E. Brownian movement and thermophoresis of nanoparticles in liquids. Int. J. Heat Mass Transf. 2015, 81, 179–187. [Google Scholar] [CrossRef]
- Sharpe, J.; Greated, C.; Gray, C. The Measurement of Acoustic Streaming using Particle Image Velocimetry. Acta Acust. United Acust. 1989, 68, 168–172. [Google Scholar]
- Desjouy, C.; Penelet, G.; Lotton, P.; Blondeau, J. Measurement of acoustic streaming in a closed-loop traveling wave resonator using laser Doppler velocimetry. J. Acoust. Soc. Am. 2009, 126, 2176–2183. [Google Scholar] [CrossRef] [PubMed]
- Khmelev, V.; Shalunov, A.; Bochenkov, A.; Nesterov, V. Development and research of a new method of gas cleaning from particles less than 2.5 micron in size. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2021, 332, 127–139. [Google Scholar] [CrossRef]
- Khmelev, V.N.; Shalunov, A.V.; Nesterov, V.A. Summation of high-frequency Langevin transducers vibrations for increasing of ultrasonic radiator power. Ultrasonics 2021, 114, 106413. [Google Scholar] [CrossRef] [PubMed]
- Khmelev, V.N.; Shalunov, A.V.; Nesterov, V.A. Ultrasonic Transducer with Increased Exposure Power and Frequency up to 100 kHz. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 1773–1782. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.; Xu, X.; Zhang, S.; Su, M. Modeling of particle interaction dynamics in standing wave acoustic field. Aerosol Sci. Technol. 2019, 53, 1204–1216. [Google Scholar] [CrossRef]
- Riera, E.; Gallego-Juarez, J.A. Ultrasonic agglomeration of micron aerosols under standing wave conditions. J. Sound Vib. 1986, 110, 413–427. [Google Scholar] [CrossRef]
- Protodyakonov, I.O.; Tsibarov, V.A.; Chesnokov, Y.G. Kinetic Theory of Gas Suspensions; Publishing of Leningrad University, USSR: St. Petersburg, Russian, 1985. [Google Scholar]
- Tsibarov, V. Kinetic Method in the Theory of Gas Mixtures; Publishing House of St. Petersburg University: St. Petersburg, Russian, 1997. [Google Scholar]
- Iddo, E.; Arutkin, M. Weird Brownian Motion. J. Phys. A Math. Theor. 2023, 56, 325002. [Google Scholar]
- Katori, M. Brownian Motion and Theta Functions. Elliptic Extensions in Statistical and Stochastic Systems; Springer Nature: Singapore, 2023. [Google Scholar]
- Zagidullin, R.R.; Smirnov, A.P.; Matveev, S.A.; Tyrtyshnikov, E.E. An efficient numerical method for a mathematical model of a transport of coagulating particles. Mosc. Univ. Comput. Math. Cybern. 2017, 41, 179–186. [Google Scholar] [CrossRef]
- Sevryukova, E.A. Models of coagulation and mechanism of growth of agglomerates in clean rooms of microelectronics. Appl. Phys. 2012, 5, 37–41. [Google Scholar]
- Sommerfeld, M.; Stübing, S. Lagrangian modeling of agglomeration for applications to spray drying. In Proceedings of the 9th International ERCOFTAC Symposium on Engineering Turbulence Modeling and Measurements, Thessaloniki, Greece, 6–8 June 2012. [Google Scholar]
- Beg, S.; Kaushal, D.R. Experimental and Numerical (Fluent-VOF, k-ϵ, DPM) Study of Variation of Trap Efficiency of Irregular Hexagonal SIT (Sediment Invert Trap) for Particle Removal in Rectangular Open Drains and Sewers. J. Irrig. Drain. Eng. 2023, 149, 04022049. [Google Scholar] [CrossRef]
- Khmelev, V.N.; Shalunov, A.V.; Golykh, R.N. Increasing The Efficiency of Coagulation of Submicron Particles under Ultrasonic Action. Theor. Found. Chem. Eng. 2020, 54, 539–550. [Google Scholar] [CrossRef]
- Jennings, S.G. The mean free path in air. J. Aerosol Sci. 1988, 19, 159–166. [Google Scholar] [CrossRef]
- Elizarova, T.G. Quasi-Gasdynamic Equations and Methods for Calculating Viscous Flows; Lectures on mathematical models and numerical methods in gas and liquid dynamics; Scientific World: Moscow, Russian, 2007. (In Russian) [Google Scholar]
- Hecht, F. FreeFEM Documentation. Release 4.13. 2023. Available online: https://github.com/FreeFem/FreeFem-doc/raw/pdf/FreeFEM-documentation.pdf (accessed on 19 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).