Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations
Abstract
:1. Introduction
2. Description and Assumptions of the System
2.1. Mathematical Model of the System
- This system consists of three components and a repairer.
- The system operates normally when there are no or only one failed component. However, if two components fail, the system may fail and stop working.
- During system failure, the functioning components stop working and will not resume until the failed component is repaired. Once the failure has been repaired, the normal components will resume operations and the system will return to its operational state.
- When the system is properly functioning, the repairer operates on a round of WVs. If the component fails during the vacation period, the repairer will repair it, but at a lower rate than during a normal working period.
- If a component fails within the system by the end of the repairer’s WV, it will be immediately repaired and returned to operational status. Once the repair is complete, if there are no other failures, the repairer will then advance to the subsequent round of WVs. Conversely, the repairer will move directly to the next round of WVs until a failed component is detected in the system at the end of the vacation.
- If the system fails and the repairer is idle, the repair is immediately accepted. However, if the repairer is busy, the failed component is placed on a retrial orbit. After a certain period, the repair is requested again, and the retrying process continues until it is successful.
- The component failure rate, the retry rate for components in orbit, and the repairer’s vacation time are each governed by exponential distributions with the respective parameters , and .
- The repair rates of the components follow a general distribution. denotes the repair rate during the repairer’s WV, and represents the repair rate during a regular busy period. Both satisfy .
- The failure probability of each component is independent of the others. All the above five random variables are independent of each other.
2.2. Reset the Model
3. Well−Posedness of System
4. Asymptotic Behavior of the TDS of System
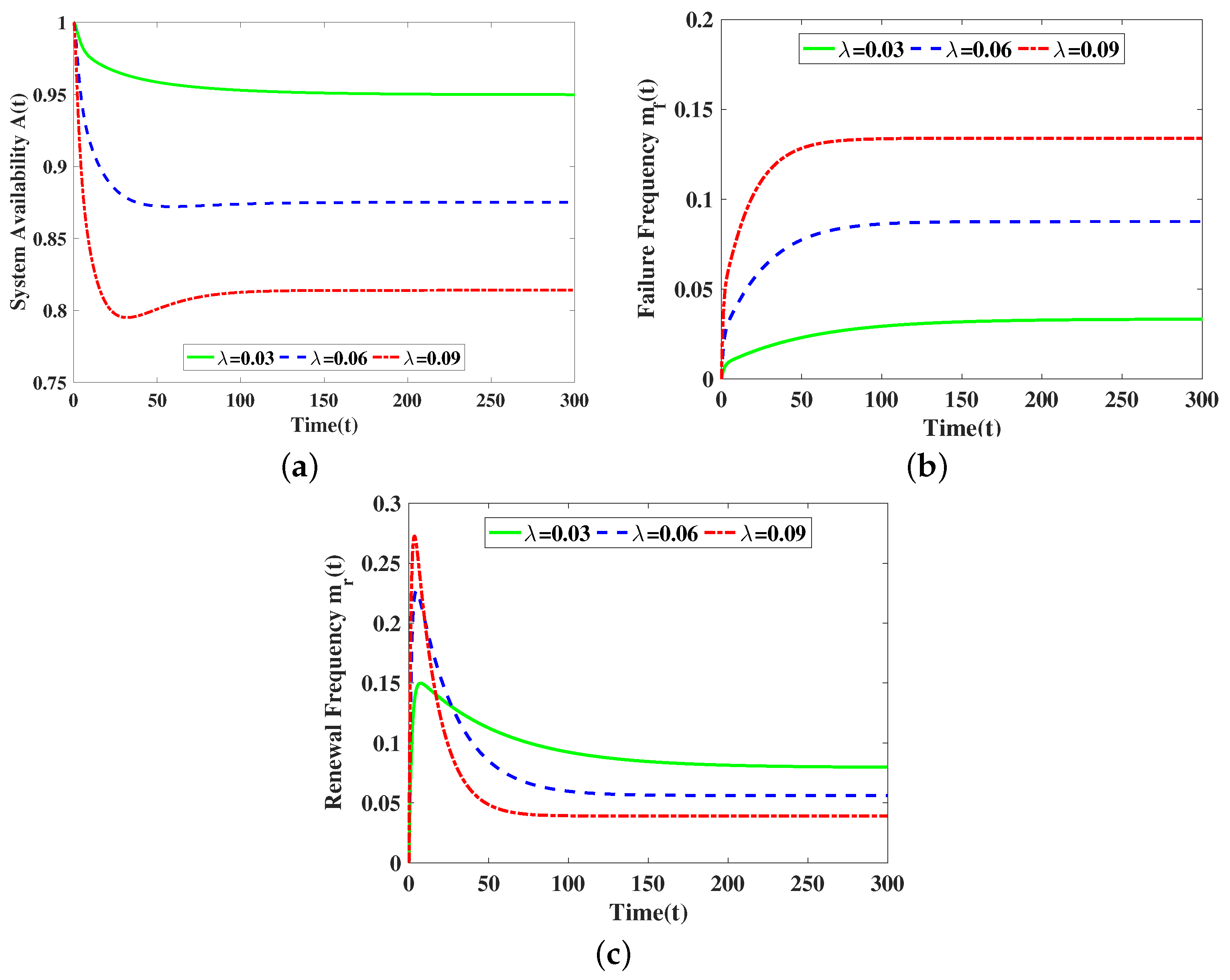
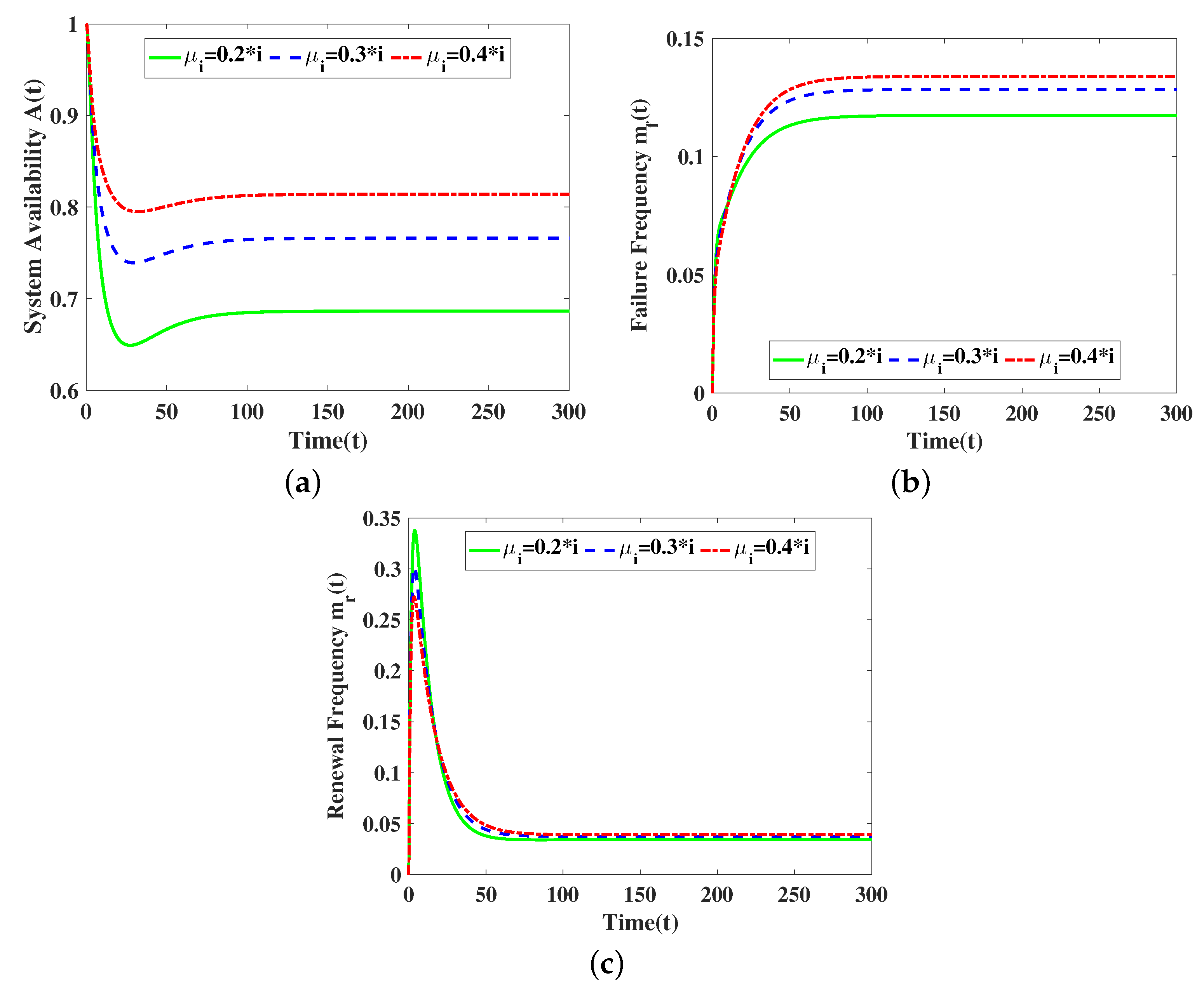
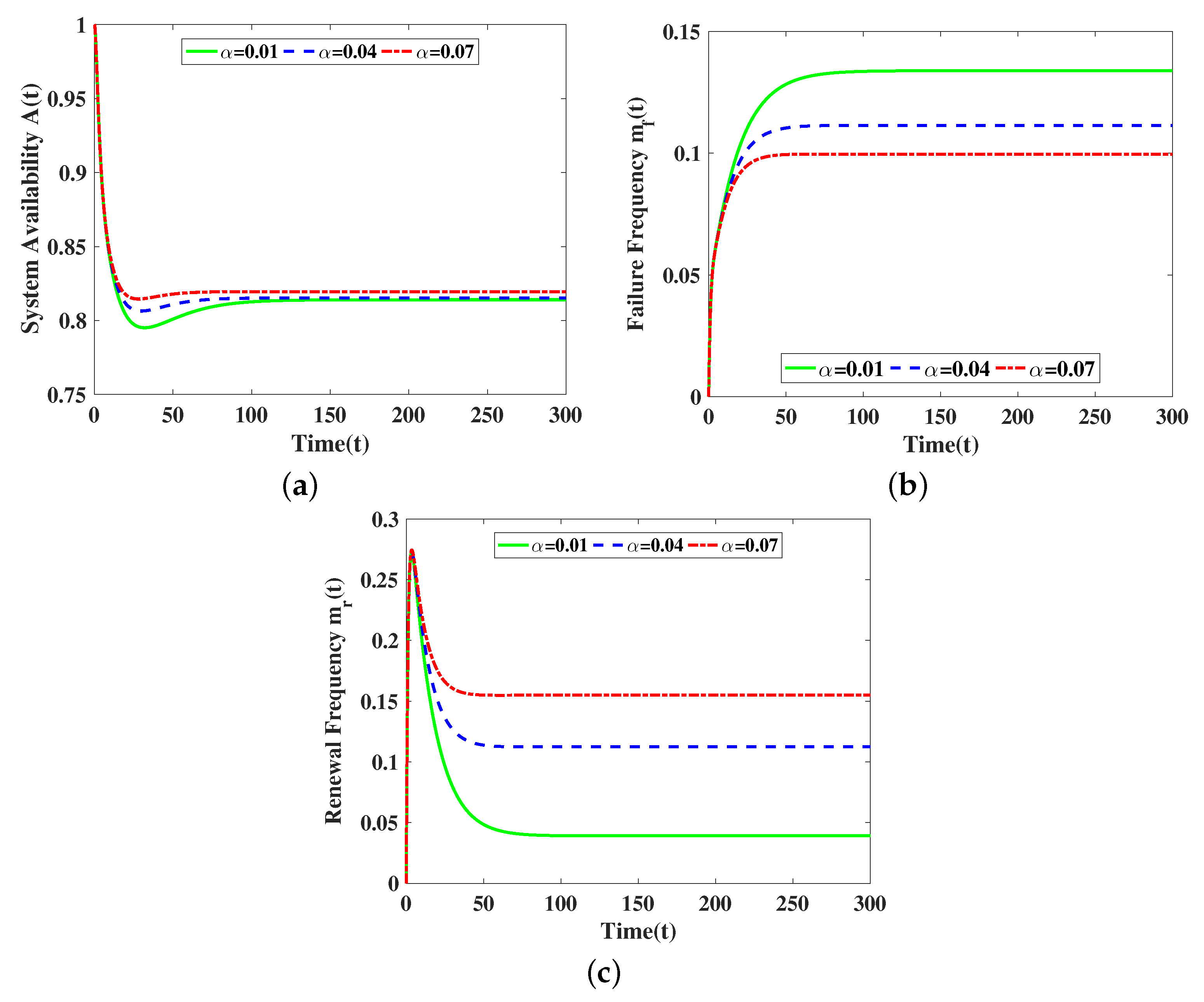
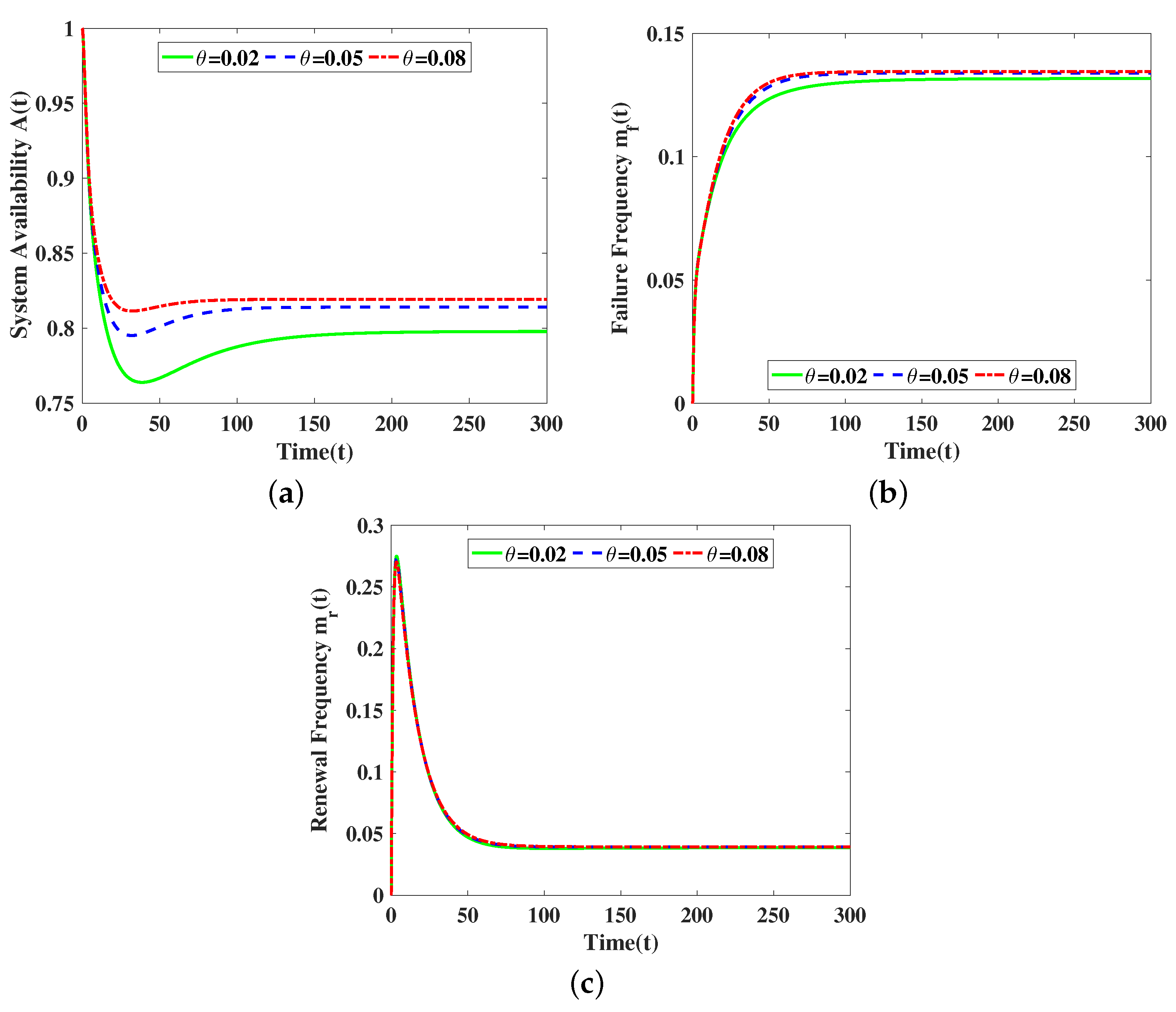
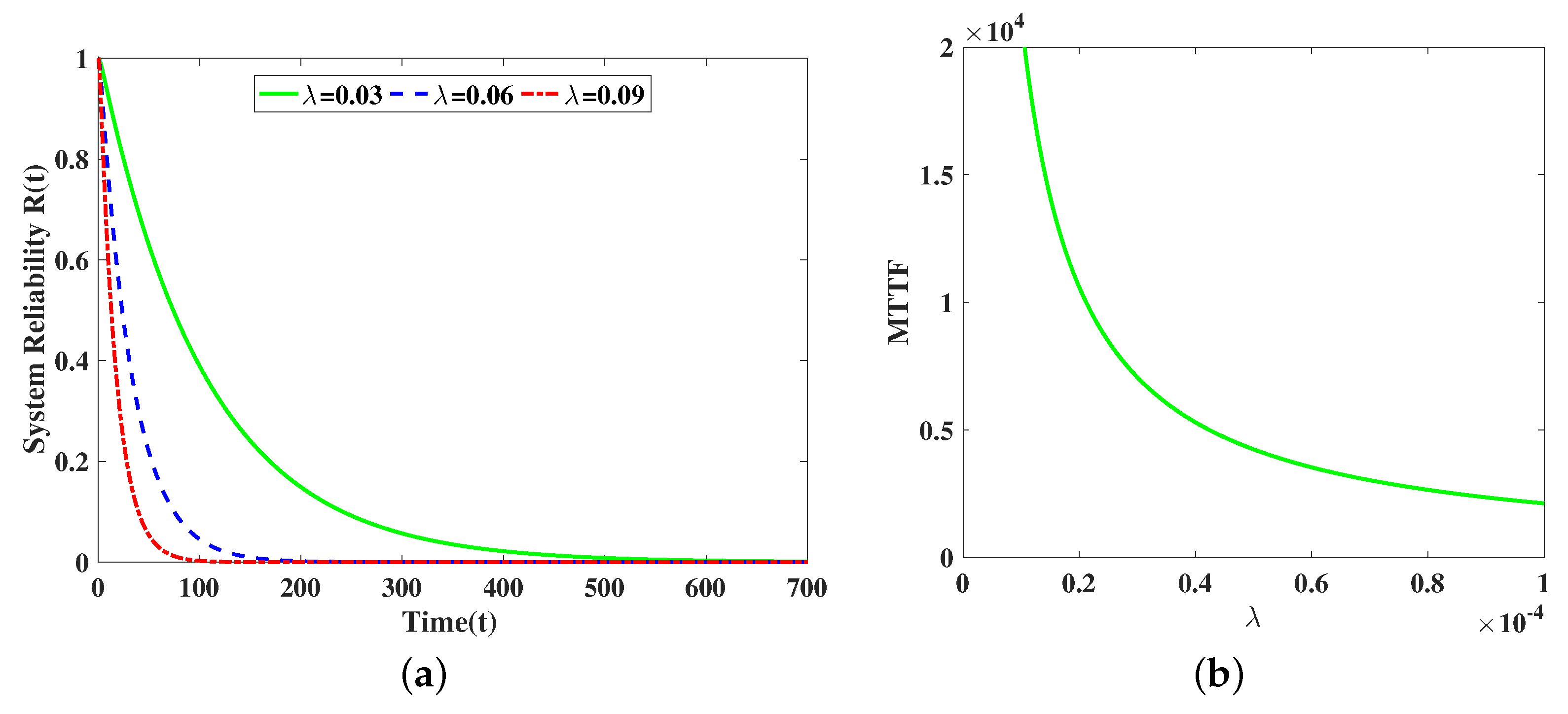
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WV | working vacation |
| ACP | abstract Cauchy problem |
| TDS | time−dependent solution |
| SSS | steady−state solution |
| SVM | supplementary variable method |
| GM | geometric multiplicity |
Appendix A
Appendix B
References
- Servi, L.D.; Finn, S.G. M/M/1 queues with working vacations (m/m/1/wv). Perform. Eval. 2002, 50, 41–52. [Google Scholar] [CrossRef]
- Baba, Y. Analysis of a GI/M/1 queue with multiple working vacations. Oper. Res. Lett. 2005, 33, 201–209. [Google Scholar] [CrossRef]
- Wu, D.; Takagi, H. M/G/1 queue with multiple working vacations. Perform. Eval. 2006, 63, 654–681. [Google Scholar] [CrossRef]
- Jain, M.; Agrawal, P.K. M/Ek/1 queueing system with working vacation. Qual. Technol. Quant. Manag. 2007, 4, 455–470. [Google Scholar] [CrossRef]
- Jain, M.; Jain, A. Working vacations queueing model with multiple types of server breakdowns. Appl. Math. Model. 2010, 34, 1–13. [Google Scholar] [CrossRef]
- Yang, D.Y.; Wu, C.H. Cost-minimization analysis of a working vacation queue with N-policy and server breakdowns. Comput. Ind. Eng. 2015, 82, 151–158. [Google Scholar] [CrossRef]
- Jeganathan, K.; Reiyas, M.A. Two parallel heterogeneous servers Markovian inventory system with modified and delayed working vacations. Math. Comput. Simul. 2020, 172, 273–304. [Google Scholar] [CrossRef]
- Yang, D.Y.; Chung, C.H.; Wu, C.H. Sojourn times in a Markovian queue with working breakdowns and delayed working vacations. Comput. Ind. Eng. 2021, 156, 107239. [Google Scholar] [CrossRef]
- Wang, K.H.; Chen, W.L.; Yang, D.Y. Optimal management of the machine repair problem with working vacation: Newton’s method. J. Comput. Appl. Math. 2009, 233, 449–458. [Google Scholar] [CrossRef]
- Liu, B.; Cui, L.; Wen, Y.; Shen, J. A cold standby repairable system with working vacations and vacation interruption following Markovian arrival process. Reliab. Eng. Syst. Saf. 2015, 142, 1–8. [Google Scholar] [CrossRef]
- Deora, P.; Kumari, U.; Sharma, D.C. Cost analysis and optimization of machine repair model with working vacation and feedback-policy. Int. J. Appl. Comput. Math. 2021, 7, 1–14. [Google Scholar] [CrossRef]
- Wu, C.H.; Yang, D.Y.; Ko, M.H. Performance Sensitivity Analysis for Machine Repair Problem with Two Failure Modes and Working Vacation. Int. J. Reliab. Qual. Saf. Eng. 2024, 2350040. [Google Scholar] [CrossRef]
- Fayolle, G. A simple telephone exchange with delayed feedbacks. In Proceedings of the International Seminar on Teletraffic Analysis and Computer Performance Evaluation, Amsterdam, The Netherlands, 2–6 June 1986; pp. 245–253. [Google Scholar]
- Falin, G.; Templeton, J.G. Retrial Queues; Chapman and Hall: London, UK, 1997. [Google Scholar]
- Artalejo, J.R.; Gómez-Corral, A. Retrial Queueing Systems. Math. Comput. Model. 1999, 30, 13–15. [Google Scholar]
- Wang, J.; Zhang, F. Strategic joining in M/M/1 retrial queues. Eur. J. Oper. Res. 2013, 230, 76–87. [Google Scholar] [CrossRef]
- Gao, S.; Wang, J. Reliability and availability analysis of a retrial system with mixed standbys and an unreliable repair facility. Reliab. Eng. Syst. Saf. 2021, 205, 107240. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Ushakumari, P.V. Reliability of a k-out-of-n system with repair and retrial of failed units. Top 1999, 7, 293–304. [Google Scholar] [CrossRef]
- Wu, W.; Tang, Y. A Study of the k/n(G) Voting Repairable System with Repairers on Multiple Leave and Repairable Equipment Replacement. Syst. Eng.-Theory Pract. 2013, 33, 2604–2614. (In Chinese) [Google Scholar]
- Sharma, R.; Kumar, G. Availability improvement for the successive k-out-of-n machining system using standby with multiple working vacations. Int. J. Reliab. Saf. 2017, 11, 256–267. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, L.; Yang, L.; Li, J. Reliability modeling and analysis for linear consecutive-k-out-of-n: F retrial systems with two maintenance activities. Reliab. Eng. Syst. Saf. 2022, 226, 108665. [Google Scholar] [CrossRef]
- Kumar, S.; Gupta, R. Working vacation policy for load sharing K-out-of-N: G system. J. Reliab. Stat. Stud. 2022, 583–616. [Google Scholar] [CrossRef]
- Hu, L.; Liu, S.; Peng, R.; Liu, Z. Reliability and sensitivity analysis of a repairable k-out-of-n: G system with two failure modes and retrial feature. Commun. Stat.-Theory Methods 2022, 51, 3043–3064. [Google Scholar] [CrossRef]
- Yu, X.; Hu, L.; Ma, M. Reliability measures of discrete time k-out-of-n: G retrial systems based on Bernoulli shocks. Reliab. Eng. Syst. Saf. 2023, 239, 109491. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, C.; Wang, X.; Sun, J. Reliability analysis of k-out-of-n: F balanced systems with multiple functional sectors. Appl. Math. Model. 2020, 82, 108–124. [Google Scholar] [CrossRef]
- Li, M.; Hu, L.; Peng, R.; Bai, Z. Reliability modeling for repairable circular consecutive-k-out-of-n: F systems with retrial feature. Reliab. Eng. Syst. Saf. 2021, 216, 107957. [Google Scholar] [CrossRef]
- Dui, H.; Tian, T.; Zhao, J.; Wu, S. Comparing with the joint importance under consideration of consecutive-k-out-of-n system structure changes. Reliab. Eng. Syst. Saf. 2022, 219, 108255. [Google Scholar] [CrossRef]
- Li, J.T.; Li, T.; An, M. An M/M/1 retrial queue with working vacation, orbit search and balking. Eng. Lett. 2019, 27, 97–102. [Google Scholar]
- Yang, D.Y.; Tsao, C.L. Reliability and availability analysis of standby systems with working vacations and retrial of failed components. Reliab. Eng. Syst. Saf. 2019, 182, 46–55. [Google Scholar] [CrossRef]
- Do, N.H.; Do, T.V.; Melikov, A. Equilibrium customer behavior in the M/M/1 retrial queue with working vacations and a constant retrial rate. Oper. Res. 2020, 20, 627–646. [Google Scholar] [CrossRef]
- Kumar, P.; Jain, M.; Meena, R.K. Transient analysis and reliability modeling of fault-tolerant system operating under admission control policy with double retrial features and working vacation. ISA Trans. 2023, 134, 183–199. [Google Scholar] [CrossRef]
- Cox, D.R. The analysis of non-Markovian stochastic processes by the inclusion of supplementary variables. Math. Proc. Camb. Philos. Soc. 1955, 51, 433–441. [Google Scholar] [CrossRef]
- Gaver, D.P. Time to failure and availability of paralleled systems with repair. IEEE Trans. Reliab. 1963, 12, 30–38. [Google Scholar] [CrossRef]
- Gupur, G. Well-posedness of the system consisting of two repairable units. Acta Anal. Funct. Appl. 2001, 3, 188–192. [Google Scholar]
- Gupur, G. Asymptotic property of the solution of a repairable, standby, human and machine system. Int. J. Pure Appl. Math. 2006, 8, 35–54. [Google Scholar]
- Gupur, G.; Wong, M.W. On a dynamical system for a reliability model. J. -Pseudo-Differ. Oper. Appl. 2011, 2, 509–542. [Google Scholar] [CrossRef]
- Kasim, E.; Gupur, G. Dynamic analysis of a complex system under preemptive repeat repair discipline. Bound. Value Probl. 2020, 2020, 71. [Google Scholar] [CrossRef]
- Yiming, N.; Guo, B.Z. Asymptotic behavior of a retrial queueing system with server breakdowns. J. Math. Anal. Appl. 2023, 520, 126867. [Google Scholar] [CrossRef]
- Yumaier, A.; Kasim, E. Dynamic Analysis of the Multi-state Reliability System with Priority Repair Discipline. Acta Math. Appl. Sin. Engl. Ser. 2023, 40, 665–694. [Google Scholar] [CrossRef]
- Gupur, G. Functional Analysis Methods for Reliability Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Greiner, G. Perturbing the boundary-conditions of a generator. Houst. J. Math. 1987, 13, 213–229. [Google Scholar]
- Fattorini, H.O. The Cauchy Problem; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Adams, R.A.; Fournier, J.J. Sobolev Spaces; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Haji, A.; Radl, A. A semigroup approach to queueing systems. Semigroup Forum 2007, 75, 609–623. [Google Scholar] [CrossRef]
- Nagel, R. One-Parameter Semigroups of Positive Operators; Springer: Berlin, Germany, 1986. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, C.; Kasim, E.; Muhammadhaji, A. Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations. Mathematics 2024, 12, 3999. https://doi.org/10.3390/math12243999
Lai C, Kasim E, Muhammadhaji A. Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations. Mathematics. 2024; 12(24):3999. https://doi.org/10.3390/math12243999
Chicago/Turabian StyleLai, Changjiang, Ehmet Kasim, and Ahmadjan Muhammadhaji. 2024. "Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations" Mathematics 12, no. 24: 3999. https://doi.org/10.3390/math12243999
APA StyleLai, C., Kasim, E., & Muhammadhaji, A. (2024). Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations. Mathematics, 12(24), 3999. https://doi.org/10.3390/math12243999




