Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations

Abstract

In this paper, we developed a new standby system that combines a retrial strategy with multiple working vacations, and we performed a dynamic analysis of the system. We investigated its well−posedness and asymptotic behavior using the theory of the $C_0-$semigroup in the functional analysis. First, the corresponding model was transformed into an abstract Cauchy problem in Banach space by introducing the state space, the main operator, and its domain of definition. Second, we demonstrated that the model had a unique non−negative time−dependent solution. Using Greiner’s boundary perturbation idea and the spectral properties of the corresponding operator, the non−negative time−dependent solution strongly converged to its steady−state solution. We also provide numerical examples to illustrate the effect of different parameters on the system’s reliability metrics.

1. Introduction

Reliability theory is the study of the universal quantitative laws of the operational reliability of systems and the theory and methods of their analysis, evaluation, design, and control. The problem of reliability was first identified as a consequence of the need for large−scale industrial production and the development and use of complex military equipment during the Second World War. Although the reliability of units continues to improve significantly, the quantitative evaluation and improvement of the system’s reliability have become important issues due to the increasing structural complexity of large systems and the wide range of functions that they must execute. The concept of a WV was first introduced in queuing systems in 2002 by Servi and Finn [1], who studied the M/M/1 queuing system with a WV. In this system, attendants served customers at a lower rate during the vacation period instead of stopping the service altogether. In 2005, Baba [2] expanded the M/M/1 queuing system [1] to a GI/M/1 queuing system. In 2006, Wu and Takagi [3] extended the results of Servi and Finn [1] to M/G/1 queuing systems with multiple WVs. In 2007, Jain and Agrawal [4] used a probability−generating function to investigate the M/$E^k$/1 queue with WV and derive the average queue length. In 2010, Jain and Jain [5] studied a WV queuing model with multiple server breakdown types. In 2015, Yang and Wu [6] studied N−policy M/M/1 queuing systems with WV and server breakdowns. In 2020, Jeganathan and Reiyas [7] studied parallel heterogeneous server inventory management systems with modified and delayed WVs. In 2021, Yang et al. [8] investigated service queues with working breakdowns and delayed WVs, and they derived the Laplace−Stilgers transform of sojourn times.

The subject of WV strategies has been the focus of considerable research in the field of queuing models and in the context of reliability models. In 2009, Wang et al. [9] investigated the M/M/1 machine repair problem using a WV policy and determined the optimal number of machines and two different repair rates using a direct search method and Newton’s method. In 2015, Liu et al. [10] used the matrix−analytic method to study a cold standby repairable system with multiple WVs and vacation interruptions. In 2021, Deora et al. [11] used particle swarm for the cost optimization of the machine repair problem with WV. In 2024, Wu et al. [12] conducted a sensitivity analysis of a machine repair problem with two failure modes and WV.

In 1986, Fayolle [13] first introduced the constant retrial rate to build telephone exchange systems. Falin and Templeton [14] and Artalejo and G$\acute{o}$mez−Corral [15] comprehensively summarized the main models and approaches to retrial queuing. In 2013, Wang and Zhang [16] investigated equilibrium strategic behavior and social optimization in the M/M/1 retrial queues. In 2021, Gao and Wang [17] conducted a reliability analysis of a retrial system with mixed standbys and an unreliable repair facility.

In the field of reliability modeling, the k/n(G) system represents a significant redundant system with a diverse range of applications, including those in aerospace, materials science, weapons systems, nuclear reactor safety systems, and beyond. In 1999, Krishnamoorthy and Ushakumari [18] studied the k/n(G) repairable system with retries, where both repair and retrial rates followed an exponential distribution. In 2013, Wu and Tang [19] studied k/n(G) repairable systems with multiple vacations for repairmen and replaceable repair equipment, where the repair rate followed an exponential distribution. In 2017, Sharma and Kumar [20] studied a k/n(G) repairable system with multiple WVs and standby. In 2022, Wang et al. [21] conducted a linear consecutive k/n(F) repairable retrial system with an unreliable repair facility. In 2022, Kumar and Gupta [22] studied load−sharing k/n(G) repairable systems with WVs and suggested closed structure analytic expressions for the reliability and other performance measures. In 2022, Hu et al. [23] performed a reliability analysis of a repairable k/n(G) system with two failure modes and a retrial feature. In 2023, Yu et al. [24] conducted a reliability analysis of a discrete−time k/n(G) retrial system based on Bernoulli shocks. Furthermore, the k/n(G) system containing different strategies have all been studied in depth by Zhao et al. [25], Li et al. [26], and Dui et al. [27].

In recent years, the WV strategy combined with the retrial strategy has been the subject of extensive discussion among experts and scholars in queuing models and reliability models to satisfy the needs of engineering practice. In 2019, Li et al. [28] investigated the M/M/1 queuing model with retries and WVs with feedback scenarios. In this model, the service rate and retrial rate were assumed to be following an exponential distribution. In 2019, Yang and Tsao [29] conducted a reliability analysis of a standby system with WV and retrial of failed parts. In 2020, Do et al. [30] studied a constant−retrial−rate queuing system with WVs. They used a matrix analysis to determine the steady−state probability distribution of the system. In 2023, Kumar et al. [31] studied the reliability model of a fault−tolerant system with double retrial features and WVs.

Several studies have been conducted on the subject of reliability modeling with WVs and retrial strategies. However, to the best of our knowledge, no studies have been conducted on the application of multiple WVs in combination with retrial strategies to k/n(G) systems. In this paper, we generalize the model in [18] with the assumption that the repair rate follows a general distribution and introduce the WV strategy into this model. We also improve the model in [19] with the assumption that the repair rate follows a general distribution and introduce the retrial strategy into that model.

The SVM was initially proposed by Cox [32] in 1955 as a pivotal approach to analyze the reliability of repairable systems. It was subsequently integrated into the field of reliability theory by Gaver [33] in 1963, which addressed the case where the repair distribution was not negatively exponential. In 2001, Gupur [34] used the $C_0-$semigroup theory to conduct a dynamic analysis of a reliability model constructed using SVM with two components connected in parallel. In 2006, Gupur [35] initially investigated the asymptotic behavior of the TDS of a reliability model. In 2011, Gupur and Wong [36] conducted a reliability analysis of a system that comprised a reliable machine, an unreliable machine, and a storage buffer with infinite capacity. In 2020, Kasim and Gupur [37] studied a complex system consisting of two units, one of which had priority and a preemptive repeated repair discipline. In 2023, Yiming and Guo [38] studied the asymptotic behavior of an M/G/1 retrial queuing system with server breakdowns. In 2023, Yumaier and Kasim [39] performed a dynamic analysis of a multi−state reliability system with the priority repair discipline.

In this paper, we first extend the mathematical model presented in the literature [18,19], Our model differs from that of [18], as we add multiple WV strategies and assume that repair times follow a general distribution. In contrast to [19], we integrate WVs and retrial strategies, with repair times following a general distribution. Overall, we have developed a new mathematical model that includes retrial strategies and multiple WVs, using the supplementary variable technique. Then, we use the $C_0-$semigroup theory to investigate the well−posedness of the model and asymptotic behavior of the dynamic solutions. We apply concepts and methodologies from the existing literature [34,40] to demonstrate that the model has a unique, non−negative, TDS that satisfies the probabilistic properties. Subsequently, we use Greiner’s boundary perturbation techniques [41] and the spectral properties of the corresponding operators [40] to demonstrate that the TDS of the model strongly converges to the SSS.

2. Description and Assumptions of the System

2.1. Mathematical Model of the System

The following assumptions have been made about the system:

• This system consists of three components and a repairer.
• The system operates normally when there are no or only one failed component. However, if two components fail, the system may fail and stop working.
• During system failure, the functioning components stop working and will not resume until the failed component is repaired. Once the failure has been repaired, the normal components will resume operations and the system will return to its operational state.
• When the system is properly functioning, the repairer operates on a round of WVs. If the component fails during the vacation period, the repairer will repair it, but at a lower rate than during a normal working period.
• If a component fails within the system by the end of the repairer’s WV, it will be immediately repaired and returned to operational status. Once the repair is complete, if there are no other failures, the repairer will then advance to the subsequent round of WVs. Conversely, the repairer will move directly to the next round of WVs until a failed component is detected in the system at the end of the vacation.
• If the system fails and the repairer is idle, the repair is immediately accepted. However, if the repairer is busy, the failed component is placed on a retrial orbit. After a certain period, the repair is requested again, and the retrying process continues until it is successful.
• The component failure rate, the retry rate for components in orbit, and the repairer’s vacation time are each governed by exponential distributions with the respective parameters $\lambda ,\theta$, and $\alpha$.
• The repair rates of the components follow a general distribution. ${\varsigma }_1\left(x\right)$ denotes the repair rate during the repairer’s WV, and ${\varsigma }_2\left(x\right)$ represents the repair rate during a regular busy period. Both satisfy ${\varsigma }_l\left(x\right)\ge 0,{\int }_0^{\infty }{\varsigma }_l\left(x\right)\mathrm{d}x=\infty ,(l=1,2)$.
• The failure probability of each component is independent of the others. All the above five random variables are independent of each other.

Before introducing the system model, we provide the following definitions.

$G_{i,0}\left(t\right)(i=0,1)$ is the probability that there is no failed component on the orbit and the repairer is in a WV period at time t.

$G_{i,1}(t,x)\mathrm{d}x(i=0,1)$ represents the probability that at time t the repairer is in a WV period, with i failed components on the orbit, and the consumed repair time falls in the interval $[x,x+\mathrm{d}x)$.

$G_{1,2}\left(t\right)(i=0,1)$ is the probability that at time t, there is one failed component on the orbit, and the repairer is idle during a regular busy period.

$G_{i,3}(t,x)\mathrm{d}x(i=0,1)$ represents the probability that at time t the repairer is in a regular busy period, there are i failed components on the orbit, and the elapsed repair time for the failed component is in $[x,x+\mathrm{d}x)$.

Taking into account the assumptions of the system outlined above, and using the SVM, we derive the following system of equations:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}{G}_{0,0}\left(t\right)}{\mathrm{d}t}}=-3\lambda G_{0,0}\left(t\right)+{\int }_0^{\infty }{G}_{0,1}(t,x){\varsigma }_1\left(x\right)\mathrm{d}x+{\int }_0^{\infty }{G}_{0,3}(t,x){\varsigma }_2\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}{G}_{1,0}\left(t\right)}{\mathrm{d}t}}=-(2\lambda +\alpha +\theta )G_{1,0}\left(t\right)+{\int }_0^{\infty }{G}_{1,1}(t,x){\varsigma }_1\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial G_{0,1}(t,x)}{\partial t}}+{\displaystyle \frac{\partial G_{0,1}(t,x)}{\partial x}}=-[2\lambda +\theta +{\varsigma }_1\left(x\right)]G_{0,1}(t,x),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial G_{1,1}(t,x)}{\partial t}}+{\displaystyle \frac{\partial G_{1,1}(t,x)}{\partial x}}=-[\theta +{\varsigma }_1\left(x\right)]G_{1,1}(t,x)+2\lambda G_{0,1}(t,x),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}{G}_{1,2}\left(t\right)}{\mathrm{d}t}}=-(2\lambda +\alpha )G_{1,2}\left(t\right)+{\int }_0^{\infty }{G}_{1,3}(t,x){\varsigma }_2\left(x\right)\mathrm{d}x+\theta G_{1,0}\left(t\right),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial G_{0,3}(t,x)}{\partial t}}+{\displaystyle \frac{\partial G_{0,3}(t,x)}{\partial x}}=-[2\lambda +{\varsigma }_2\left(x\right)]G_{0,3}(t,x),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial G_{1,3}(t,x)}{\partial t}}+{\displaystyle \frac{\partial G_{1,3}(t,x)}{\partial x}}=-{\varsigma }_2\left(x\right)G_{1,3}(t,x)+2\lambda G_{0,3}(t,x).\hfill \end{array}$$

(7)

with the boundary and initial conditions being as follows:

$$\begin{array}{cc}\hfill & G_{0,1}(t,0)=3\lambda G_{0,0}\left(t\right)+\alpha G_{1,0}\left(t\right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & G_{1,1}(t,0)=2\lambda G_{1,0}\left(t\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & G_{0,3}(t,0)=\alpha G_{1,2}\left(t\right)+\theta {\int }_0^{\infty }{G}_{0,1}(t,x)\mathrm{d}x,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & G_{1,3}(t,0)=2\lambda G_{1,2}\left(t\right)+\theta {\int }_0^{\infty }{G}_{1,1}(t,x)\mathrm{d}x,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & G_{0,0}\left(0\right)=1,G_{1,0}\left(0\right)=G_{1,2}\left(0\right)=G_{i,j}(0,x)=0,(i=0,1j=1,3).\hfill \end{array}$$

(12)

where $(t,x)\in [0,\infty )\times [0,\infty ).$

2.2. Reset the Model

Let us consider the state space to be as for:

$$\begin{array}{c}\hfill X=\left\{\mathbf{G}\left|\begin{array}{c}\mathbf{G}=(G_{0,0},G_{1,0},G_{0,1},G_{1,1},G_{1,2},G_{0,3},G_{1,3}),\hfill \\ G_{0,0},G_{1,0},G_{1,2}\in \mathbb{R},\hfill \\ G_{0,1}\left(x\right),G_{1,1}\left(x\right),G_{0,3}\left(x\right),G_{1,3}\left(x\right)\in L^1[0,\infty ),\hfill \\ \parallel \mathbf{G}\parallel ={\displaystyle \sum _{i=0}^1}|G_{i,0}|+{\displaystyle \sum _{i=0}^1}\parallel G_{i,1}{\parallel }_{L^1[0,\infty )}+|G_{1,2}|+{\displaystyle \sum _{i=0}^1}{\parallel G_{i,3}\parallel }_{L^1[0,\infty )}\hfill \end{array}\right.\right\}.\end{array}$$

X is a Banach space.

The maximal operator $({\mathcal{S}}_m,D\left({\mathcal{S}}_m\right))$ (see Greiner [41]) is defined as follows:

$$\begin{array}{c}\hfill {\mathcal{S}}_m\mathbf{G}=\left(\begin{array}{ccccccc}-3\lambda & 0& {\psi }_1& 0& 0& {\psi }_2& 0\\ 0& -(2\lambda +\alpha +\theta )& 0& {\psi }_1& 0& 0& 0\\ 0& 0& {\varphi }_0^1& 0& 0& 0& 0\\ 0& 0& 2\lambda & {\varphi }^1& 0& 0& 0\\ 0& \theta & 0& 0& -(2\lambda +\alpha )& 0& {\psi }_2\\ 0& 0& 0& 0& 0& {\varphi }_0^2& 0\\ 0& 0& 0& 0& 0& 2\lambda & {\varphi }^2\end{array}\right)\mathbf{G},\end{array}$$

$$\begin{array}{c}\hfill D\left({\mathcal{S}}_m\right)=\left\{\mathbf{G}\in X\left|\begin{array}{c}{\displaystyle \frac{\mathrm{d}{G}_{i,j}}{\mathrm{d}x}}\in L^1[0,\infty ),G_{i,j}\left(x\right)\mathrm{are}\mathrm{absolutely}\mathrm{continuous}\mathrm{functions}\mathrm{and}\hfill \\ {\displaystyle \sum _{i=0}^1}\parallel {\displaystyle \frac{\mathrm{d}{G}_{i,1}}{\mathrm{d}x}}{\parallel }_{L^1[0,\infty )}+{\displaystyle \sum _{i=0}^1}\parallel {\displaystyle \frac{\mathrm{d}{G}_{i,3}}{\mathrm{d}x}}{\parallel }_{L^1[0,\infty )}<\infty \hfill \end{array}\right.\right\}.\end{array}$$

Then, let us consider

$$\begin{array}{cc}\hfill {\psi }_1\varrho :& ={\int }_0^{\infty }{\varsigma }_1\left(x\right)\varrho \left(x\right)\mathrm{d}x,{\psi }_1:L^1[0,\infty )\to \mathbb{R},\forall \varrho \in L^1(0,\infty ),\hfill \\ \hfill {\psi }_2\varrho :& ={\int }_0^{\infty }{\varsigma }_2\left(x\right)\varrho \left(x\right)\mathrm{d}x,{\psi }_2:L^1[0,\infty )\to \mathbb{R},\forall \varrho \in L^1(0,\infty ),\hfill \\ \hfill {\varphi }_0^1\varrho :& =-{\displaystyle \frac{\mathrm{d}\varrho \left(x\right)}{\mathrm{d}x}}-[2\lambda +\theta +{\varsigma }_1\left(x\right)]\varrho \left(x\right),\forall \varrho \in W^{1,1}[0,\infty ),\hfill \\ \hfill {\varphi }^1\varrho :& =-{\displaystyle \frac{\mathrm{d}\varrho \left(x\right)}{\mathrm{d}x}}-[\theta +{\varsigma }_1\left(x\right)]\varrho \left(x\right),\forall \varrho \in W^{1,1}[0,\infty ),\hfill \\ \hfill {\varphi }_0^2\varrho :& =-{\displaystyle \frac{\mathrm{d}\varrho \left(x\right)}{\mathrm{d}x}}-[2\lambda +{\varsigma }_2\left(x\right)]\varrho \left(x\right),\forall \varrho \in W^{1,1}[0,\infty ),\hfill \\ \hfill {\varphi }^2\varrho :& =-{\displaystyle \frac{\mathrm{d}\varrho \left(x\right)}{\mathrm{d}x}}-{\varsigma }_2\left(x\right)\varrho \left(x\right),\forall \varrho \in W^{1,1}[0,\infty ).\hfill \end{array}$$

Following boundary space and operators:

$$\partial X={\mathbb{R}}^4,\mathsf{\Theta }:D\left({\mathcal{S}}_m\right)\to \partial X,$$

$$\begin{array}{c}\hfill \mathsf{\Theta }\mathbf{G}=\left(\begin{array}{c}{G}_{0,1}\left(0\right)\\ G_{1,1}\left(0\right)\\ G_{0,3}\left(0\right)\\ G_{1,3}\left(0\right)\end{array}\right),\end{array}$$

and

$$\mathsf{\Psi }:D\left({\mathcal{S}}_m\right)\to \partial X,$$

$$\mathsf{\Psi }\mathbf{G}=\left.\left(\begin{array}{ccccccc}\hfill 3\lambda & \hfill \alpha & \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 2\lambda & \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill \theta \phi & \hfill 0& \hfill \alpha & \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill \theta \phi & \hfill 2\lambda & \hfill 0& \hfill 0\end{array}\right.\right)\mathbf{G},$$

where

$$\phi \varrho :={\int }_0^{\infty }\varrho \left(x\right)\mathrm{d}x,\forall \varrho \in L^1(0,\infty ).$$

If we define operator $\overline{\mathcal{S}}$ as

$$\begin{array}{c}\hfill \overline{\mathcal{S}}\mathbf{G}={\mathcal{S}}_m\mathbf{G},D\left(\overline{\mathcal{S}}\right)=\left\{\mathbf{G}\in D\left({\mathcal{S}}_m\right)|\mathsf{\Theta }\mathbf{G}=\mathsf{\Psi }\mathbf{G}\right\}.\end{array}$$

The aforementioned Equations (1)–(12) can be rewritten as an ACP in the X.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}\mathbf{G}\left(t\right)}{\mathrm{d}t}}={\mathcal{S}}_m\mathbf{G}\left(t\right),\forall t\in (0,\infty ),\hfill \\ \mathbf{G}\left(0\right)=(1,0,0,0,0,0,0).\hfill \end{array}\right.\end{array}$$

(13)

3. Well−Posedness of System

Firstly, we demonstrate that the operator $\overline{\mathcal{S}}$ generates a positive contraction $C_0-$semigroup $T\left(t\right)$. Next we show that $\overline{\mathcal{S}}$ is a conservative operator and furthermore obtain that $T\left(t\right)$ is isometric. This establishes the well−posedness of the system.

Theorem 1. 

Let ${\varsigma }_l=\underset{x\in [0,\infty )}{sup}{\varsigma }_l\left(x\right)<\infty (l=1,2)$; then, $\overline{\mathcal{S}}$ generates a positive contraction $C_0-$semigroup $T\left(t\right)$.

The proof can be found in Appendix A.

The dual space $X^{*}$ of X is defined as follows:

$$\begin{array}{c}\hfill X^{*}=\left\{{\mathbf{G}}^{*}\left|\begin{array}{c}{\mathbf{G}}^{*}=(G_{0,0}^{*},G_{1,0}^{*},G_{0,1}^{*},G_{1,1}^{*},G_{1,2}^{*},G_{0,3}^{*},G_{1,3}^{*}),\hfill \\ G_{0,0}^{*},G_{1,0}^{*},G_{1,2}^{*}\in \mathbb{R},\hfill \\ G_{0,1}^{*}\left(x\right),G_{1,1}^{*}\left(x\right),G_{0,3}^{*}\left(x\right),G_{1,3}^{*}\left(x\right)\in L^{\infty }[0,\infty ),\hfill \\ \left|\right||{\mathbf{G}}^{*}\left|\right||=max\{|G_{0,0}^{*}|,|G_{1,0}^{*}|,|G_{1,2}^{*}|,\parallel G_{0,1}^{*}{\parallel }_{L^{\infty }[0,\infty )},\hfill \\ \parallel G_{1,1}^{*}{\parallel }_{L^{\infty }[0,\infty )},\parallel G_{0,3}^{*}{\parallel }_{L^{\infty }[0,\infty )},{\parallel G_{1,3}^{*}\parallel }_{L^{\infty }[0,\infty )}\}\hfill \end{array}\right.\right\}.\end{array}$$

$X^{*}$ is a Banach space. In space X, we define the subset

$$\begin{array}{c}\hfill \mathcal{Y}=\left\{\begin{array}{cc}\mathbf{G}\in X\hfill & \begin{array}{c}\mathbf{G}=(G_{0,0},G_{1,0},G_{0,1}\left(x\right),G_{1,1}\left(x\right),G_{1,2},G_{0,3}\left(x\right),G_{1,3}\left(x\right)),\hfill \\ G_{i,0}\ge 0,G_{1,2}\ge 0,G_{i,j}\left(x\right)\ge 0,i=0,1,j=1,3,\forall x\in [0,\infty )\hfill \end{array}\hfill \end{array}\right\}.\end{array}$$

According to Theorem 1, we can conclude that $T\left(t\right)\mathcal{Y}\subset \mathcal{Y}.$ For $\mathbf{G}\in D\left(\overline{\mathcal{S}}\right)\bigcap \mathcal{Y},$ we take ${\mathbf{G}}^{*}=\parallel \mathbf{G}\parallel (1,1,1,1,1,1,1)$; then, ${\mathbf{G}}^{*}\in X^{*}$ and

$$\begin{array}{cc}\hfill & ⟨\overline{\mathcal{S}}\mathbf{G},{\mathbf{G}}^{*}⟩\hfill \\ \hfill & =\left\{-3\lambda G_{0,0}+{\int }_0^{\infty }{G}_{0,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+{\int }_0^{\infty }{G}_{0,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x\right\}\parallel \mathbf{G}\parallel \hfill \\ \hfill & +\left\{-(2\lambda +\alpha +\theta )G_{1,0}+{\int }_0^{\infty }{G}_{1,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x\right\}\parallel \mathbf{G}\parallel \hfill \\ \hfill & +{\int }_0^{\infty }\left\{-{\displaystyle \frac{\mathrm{d}{G}_{0,1}\left(x\right)}{\mathrm{d}x}}-[2\lambda +\theta +{\varsigma }_1\left(x\right)]G_{0,1}\left(x\right)\right\}\parallel \mathbf{G}\parallel \mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }\left\{-{\displaystyle \frac{\mathrm{d}{G}_{1,1}\left(x\right)}{\mathrm{d}x}}-[\theta +{\varsigma }_1\left(x\right)]G_{1,1}\left(x\right)+2\lambda G_{0,1}\left(x\right)\right\}\parallel \mathbf{G}\parallel \mathrm{d}x\hfill \\ \hfill & +\left\{-(2\lambda +\alpha )G_{1,2}+{\int }_0^{\infty }{G}_{1,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x+\theta G_{1,0}\right\}\parallel \mathbf{G}\parallel \hfill \\ \hfill & +{\int }_0^{\infty }\left\{-{\displaystyle \frac{\mathrm{d}{G}_{0,3}\left(x\right)}{\mathrm{d}x}}-[2\lambda +{\varsigma }_2\left(x\right)]G_{0,3}\left(x\right)\right\}\parallel \mathbf{G}\parallel \mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }\left\{-{\displaystyle \frac{\mathrm{d}{G}_{1,3}\left(x\right)}{\mathrm{d}x}}-{\varsigma }_2\left(x\right)G_{1,3}\left(x\right)+2\lambda G_{0,3}\left(x\right)\right\}\parallel \mathbf{G}\parallel \mathrm{d}x\hfill \\ \hfill & =-\parallel \mathbf{G}\parallel 3\lambda G_{0,0}+\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{0,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{0,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x\hfill \\ \hfill & -\parallel \mathbf{G}\parallel (2\lambda +\alpha +\theta )G_{1,0}+\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{1,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+\parallel \mathbf{G}\parallel G_{0,1}\left(0\right)\hfill \\ \hfill & -\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{0,1}\left(x\right)[2\lambda +\theta +{\varsigma }_1\left(x\right)]\mathrm{d}x+\parallel \mathbf{G}\parallel G_{1,1}\left(0\right)\hfill \\ \hfill & -\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{1,1}\left(x\right)[\theta +{\varsigma }_1\left(x\right)]\mathrm{d}x+\parallel \mathbf{G}\parallel {\int }_0^{\infty }2\lambda G_{0,1}\left(x\right)\mathrm{d}x\hfill \\ \hfill & -\parallel \mathbf{G}\parallel (2\lambda +\alpha )G_{1,2}+\parallel \mathbf{G}\parallel \theta G_{1,0}+\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{1,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x\hfill \\ \hfill & +\parallel \mathbf{G}\parallel G_{0,3}\left(0\right)-\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{0,3}\left(x\right)[2\lambda +{\varsigma }_2\left(x\right)]\mathrm{d}x+\parallel \mathbf{G}\parallel G_{1,3}\left(0\right)\hfill \\ \hfill & -\parallel \mathbf{G}\parallel {\int }_0^{\infty }{G}_{1,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x+\parallel \mathbf{G}\parallel {\int }_0^{\infty }2\lambda G_{0,3}\left(x\right)\mathrm{d}x\hfill \\ \hfill & =0.\hfill \end{array}$$

Thus, $\overline{\mathcal{S}}$ is conservative for the set

$$\varpi \left(\mathbf{G}\right)=\{{\mathbf{G}}^{*}\in X^{*}|⟨\mathbf{G},{\mathbf{G}}^{*}⟩=\parallel \mathbf{G}{\parallel }^2=\left|\right|\left|{\mathbf{G}}^{*}\right|\left|{|}^2\right\}.$$

Since $\mathbf{G}\left(0\right)\in D\left({\overline{\mathcal{S}}}^2\right)\bigcap \mathcal{Y}$, the following result was obtained by applying Fattorini’s method [42].

Theorem 2. 

$T\left(t\right)$ is isometric for $\mathbf{G}\left(0\right)$, i.e.,

$$\begin{array}{c}\hfill \parallel T\left(t\right)\mathbf{G}\left(0\right)\parallel =\parallel \mathbf{G}\left(0\right)\parallel ,\forall t\in [0,\infty ).\end{array}$$

By combining Theorem 1 with Theorem 2 we obtain the desired result in this section.

Theorem 3. 

Let ${\varsigma }_l=\underset{x\in [0,\infty )}{sup}{\varsigma }_l\left(x\right)<\infty (l=1,2)$; then system (13) has a unique nonnegative TDS $\mathbf{G}(t,x)$ that satisfies

$$\parallel \mathbf{G}(t,·)\parallel =1,\forall t\in [0,\infty ).$$

Proof. 

Since $\mathbf{G}\left(0\right)\in D\left({\overline{\mathcal{S}}}^2\right)\bigcap \mathcal{Y}$, by Theorems 1 and 1.81 [40], we obtain that system (13) has a unique positive TDS $\mathbf{G}(t,x)$ which can be expressed as

$$\begin{array}{c}\hfill \mathbf{G}(t,x)=T\left(t\right)\mathbf{G}\left(0\right),\forall t\in [0,\infty ).\end{array}$$

By Theorem 2, it has

$$\begin{array}{c}\hfill \parallel \mathbf{G}(t,·)\parallel =\parallel T\left(t\right)\mathbf{G}\left(0\right)\parallel =\parallel \mathbf{G}\left(0\right)\parallel =1,\forall t\in [0,\infty ).\end{array}$$

This justifies the physics reflected by $\mathbf{G}(t,x)$. □

4. Asymptotic Behavior of the TDS of System

By looking at the system (13), we realize that the key to the solution lies in the boundary conditions. In 1987, Greiner [41] introduced the idea of studying the spectrum of $\overline{\mathcal{S}}$ by perturbing the boundary conditions. In this section, we use this method to obtain the spectrum of $\overline{\mathcal{S}}$ on the imaginary axis, thus obtaining the asymptotic behavior of the TDS of system (13).

Lemma 1. 

Let

$$2\lambda +\alpha +\theta >{\int }_0^{\infty }[2\lambda +\alpha (1-e^{-2\lambda x})]e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x,$$

$${\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x<\infty ,$$

then, $0\in {\sigma }_p\left(\overline{\mathcal{S}}\right)$ and the geometric multiplicity is 1.

Proof. 

For the Equation $\overline{\mathcal{S}}\mathbf{G}=0,$ i.e.,

$$\begin{array}{cc}\hfill 3\lambda G_{0,0}& ={\int }_0^{\infty }{G}_{0,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+{\int }_0^{\infty }{G}_{0,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill (2\lambda +\alpha +\theta )G_{1,0}& ={\int }_0^{\infty }{G}_{1,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{0,1}\left(x\right)}{\mathrm{d}x}}& =-\left[2\lambda +\theta +{\varsigma }_1\left(x\right)\right]G_{0,1}\left(x\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{1,1}\left(x\right)}{\mathrm{d}x}}& =-\left[\theta +{\varsigma }_1\left(x\right)\right]G_{1,1}\left(x\right)+2\lambda G_{0,1}\left(x\right),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill (2\lambda +\alpha )G_{1,2}& ={\int }_0^{\infty }{G}_{1,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x+\theta G_{1,0},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{0,3}\left(x\right)}{\mathrm{d}x}}& =-\left[2\lambda +{\varsigma }_2\left(x\right)\right]G_{0,3}\left(x\right),\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{1,3}\left(x\right)}{\mathrm{d}x}}& =-{\varsigma }_2\left(x\right)G_{1,3}\left(x\right)+2\lambda G_{0,3}\left(x\right),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill G_{0,1}\left(0\right)& =3\lambda G_{0,0}+\alpha G_{1,0},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill G_{1,1}\left(0\right)& =2\lambda G_{1,0},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill G_{0,3}\left(0\right)& =\alpha G_{1,2}+\theta {\int }_0^{\infty }{G}_{0,1}\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill G_{1,3}\left(0\right)& =2\lambda G_{1,2}+\theta {\int }_0^{\infty }{G}_{1,1}\left(x\right)\mathrm{d}x.\hfill \end{array}$$

(24)

By solving Equations (16), (17), (19) and (20) and using Equations (21)–(24) we obtain

$$\begin{array}{cc}\hfill G_{0,1}\left(x\right)=& e^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }(3\lambda G_{0,0}+\alpha G_{1,0}),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill G_{1,1}\left(x\right)=& e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\left[2\lambda G_{1,0}+(1-e^{-2\lambda x})(3\lambda G_{0,0}+\alpha G_{1,0})\right],\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill G_{0,3}\left(x\right)=& e^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\left[\alpha G_{1,2}+\theta {\int }_0^{\infty }{G}_{0,1}\left(x\right)\mathrm{d}x\right],\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill G_{1,3}\left(x\right)=& e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }[2\lambda G_{1,2}+\theta {\int }_0^{\infty }{G}_{1,1}\left(x\right)\mathrm{d}x\hfill \\ \hfill & +(1-e^{-2\lambda x})\left(\alpha G_{1,2}+\theta {\int }_0^{\infty }{G}_{0,1}\left(x\right)\mathrm{d}x\right)].\hfill \end{array}$$

(28)

Substituting Equations (25) and (26) into Equations (27) and (28) gives

$$\begin{array}{cc}\hfill G_{0,3}\left(x\right)=& e^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times \left[\alpha G_{1,2}+\theta (3\lambda G_{0,0}+\alpha G_{1,0}){\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\right],\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill G_{1,3}\left(x\right)=& e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }[2\lambda G_{1,2}+\alpha G_{1,2}(1-e^{-2\lambda x})\hfill \\ \hfill & +2\lambda \theta G_{1,0}{\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +\theta (3\lambda G_{0,0}+\alpha G_{1,0}){\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & -\theta \left(3\lambda G_{0,0}+\alpha G_{1,0}\right)e^{-2\lambda x}{\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x].\hfill \end{array}$$

(30)

Combining Equations (26) and (30) with Equations (15) and (18) we have

$$\begin{array}{cc}\hfill & G_{1,0}={\displaystyle \frac{3\lambda {\int }_0^{\infty }(1-e^{-2\lambda x})e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x}{2\lambda +\alpha +\theta -{\int }_0^{\infty }[2\lambda +\alpha (1-e^{-2\lambda x})]e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x}}{G}_{0,0},\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & G_{1,2}={\displaystyle \frac{\mathsf{\Pi }}{\alpha {\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x}}{G}_{0,0}.\hfill \end{array}$$

(32)

where

$$\begin{array}{cc}\hfill \mathsf{\Pi }=& 3\lambda \theta \left\{\right[{\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & -{\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x{\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x]\hfill \\ \hfill & +[1+(2\lambda +\alpha ){\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & -\alpha {\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x{\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x]\hfill \\ \hfill & \times {\displaystyle \frac{{\int }_0^{\infty }(1-e^{-2\lambda x})e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x}{2\lambda +\alpha +\theta -{\int }_0^{\infty }[2\lambda +\alpha (1-e^{-2\lambda x})]e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x}}\}.\hfill \end{array}$$

From Equations (25), (26), and (29)–(32) we estimate

$$\begin{array}{cc}\hfill \parallel \mathbf{G}\parallel \le & \left|G_{0,0}\right|+\left|G_{1,0}\right|+\left|G_{1,2}\right|+\left(3\lambda \left|G_{0,0}\right|+\alpha \left|G_{1,0}\right|\right){\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +\left[3\lambda \left|G_{0,0}\right|+(2\lambda +\alpha )\left|G_{1,0}\right|\right]{\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +\left(3\lambda \left|G_{0,0}\right|+\alpha \left|G_{1,0}\right|\right){\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +\left[\alpha \left|G_{1,2}\right|+\theta \left(3\lambda \left|G_{0,0}\right|+\alpha \left|G_{1,0}\right|\right){\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\right]\hfill \\ \hfill & \times {\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +(2\lambda +\alpha )\left|G_{1,2}\right|{\int }_0^{\infty }{e}^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +\theta \left[3\lambda \left|G_{0,0}\right|+(2\lambda +\alpha )\left|G_{1,0}\right|\right]{\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x{\int }_0^{\infty }{e}^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +\left[\alpha \left|G_{1,2}\right|+\theta \left(3\lambda \left|G_{0,0}\right|+\alpha \left|G_{1,0}\right|\right){\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\right]\hfill \\ \hfill & \times {\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill \le & \left\{\right[1+6\lambda {\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x+3\lambda {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +6\lambda \theta {\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x{\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +3\lambda \theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x{\int }_0^{\infty }{e}^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x]\hfill \\ \hfill & +[1+2\alpha {\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x+(2\lambda +\alpha ){\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +2\alpha \theta {\int }_0^{\infty }{e}^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x{\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +\theta (2\lambda +\alpha ){\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x{\int }_0^{\infty }{e}^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x]\hfill \\ \hfill & \times {\displaystyle \frac{3\lambda {\int }_0^{\infty }\left(1-e^{-2\lambda x}\right)e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x}{2\lambda +\alpha +\theta -{\int }_0^{\infty }\left[2\lambda +\alpha \left(1-e^{-2\lambda x}\right)\right]e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x}}\hfill \\ \hfill & +\left[1+2\alpha {\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x+(2\lambda +\alpha ){\int }_0^{\infty }{e}^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\right]\hfill \\ \hfill & \times {\displaystyle \frac{\mathsf{\Pi }}{\alpha {\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x}}\}\left|G_{0,0}\right|\hfill \\ \hfill <& \infty .\hfill \end{array}$$

This demonstrates that 0 is an eigenvalue of $\overline{\mathcal{S}}$. Furthermore, Equations (25), (26), and (29)–(32) mean that the GM of 0 is 1. □

Subsequently, we apply Greiner’s ideas [41] to investigate the resolvent set of $\overline{\mathcal{S}}$ on the imaginary axis. If we define $({\mathcal{S}}_0,D\left({\mathcal{S}}_0\right))$ as

$$\begin{array}{c}\hfill {\mathcal{S}}_0\mathbf{G}={\mathcal{S}}_m\mathbf{G},D\left({\mathcal{S}}_0\right)=\left\{\mathbf{G}\in D\left({\mathcal{S}}_m\right)|\mathsf{\Theta }\mathbf{G}=0\right\},\end{array}$$

then for any given $W=(W_{0,0},W_{1,0},W_{0,1},W_{1,1},W_{1,2},W_{0,3},W_{1,3})\in X$, for the Equation $(\gamma I-{\mathcal{S}}_0)\mathbf{G}=W$, i.e.,

$$\begin{array}{cc}\hfill (\gamma +3\lambda )G_{0,0}& ={\int }_0^{\infty }{G}_{0,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+{\int }_0^{\infty }{G}_{0,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x+W_{0,0},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill (\gamma +2\lambda +\alpha +\theta )G_{1,0}& ={\int }_0^{\infty }{G}_{1,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+W_{1,0},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{0,1}\left(x\right)}{\mathrm{d}x}}& =-\left[\gamma +2\lambda +\theta +{\varsigma }_1\left(x\right)\right]G_{0,1}\left(x\right)+W_{0,1}\left(x\right),\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{1,1}\left(x\right)}{\mathrm{d}x}}& =-\left[\gamma +\theta +{\varsigma }_1\left(x\right)\right]G_{1,1}\left(x\right)+2\lambda G_{0,1}\left(x\right)+W_{1,1}\left(x\right),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill (\gamma +2\lambda +\alpha )G_{1,2}& ={\int }_0^{\infty }{G}_{1,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x+\theta G_{1,0}+W_{1,2},\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{0,3}\left(x\right)}{\mathrm{d}x}}& =-\left[\gamma +2\lambda +{\varsigma }_2\left(x\right)\right]G_{0,3}\left(x\right)+W_{0,3}\left(x\right),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{1,3}\left(x\right)}{\mathrm{d}x}}& =-\left[\gamma +{\varsigma }_2\left(x\right)\right]G_{1,3}\left(x\right)+2\lambda G_{0,3}\left(x\right)+W_{1,3}\left(x\right),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill G_{i,j}\left(0\right)& =0,i=0,1,j=1,3.\hfill \end{array}$$

(40)

Solving Equations (33)–(39) and combining them with Equation (40), we obtain

$$\begin{array}{cc}\hfill G_{0,0}=& {\displaystyle \frac{1}{\gamma +3\lambda }}{W}_{0,0}+{\displaystyle \frac{1}{\gamma +3\lambda }}{\int }_0^{\infty }{G}_{0,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+{\displaystyle \frac{1}{\gamma +3\lambda }}{\int }_0^{\infty }{G}_{0,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill G_{1,0}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}{W}_{1,0}+{\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}{\int }_0^{\infty }{G}_{1,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill G_{0,1}\left(x\right)=& e^{-{\int }_0^x[\gamma +2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x{W}_{0,1}\left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +2\lambda +\theta +{\varsigma }_1\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill G_{1,1}\left(x\right)=& e^{-{\int }_0^x[\gamma +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x{W}_{1,1}\left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +\theta +{\varsigma }_1\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta \hfill \end{array}$$

$$\begin{array}{cc}\hfill & +e^{-{\int }_0^x[\gamma +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^{x}2\lambda G_{0,1}\left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +\theta +{\varsigma }_1\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill G_{1,2}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}{W}_{1,2}+{\displaystyle \frac{\theta }{\gamma +2\lambda +\alpha }}{G}_{1,0}+{\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}{\int }_0^{\infty }{G}_{1,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill G_{0,3}\left(x\right)=& e^{-{\int }_0^x[\gamma +2\lambda +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x{W}_{0,3}\left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +2\lambda +{\varsigma }_2\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill G_{1,3}\left(x\right)=& e^{-{\int }_0^x[\gamma +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x{W}_{1,3}\left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +{\varsigma }_2\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta \hfill \\ \hfill & +e^{-{\int }_0^x[\gamma +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^{x}2\lambda G_{0,3}\left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +{\varsigma }_2\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta .\hfill \end{array}$$

(47)

For any $\varrho \in L^1[0,\infty ),$ if we set

$$\begin{array}{cc}\hfill E_1\varrho \left(x\right)=& e^{-{\int }_0^x[\gamma +2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x\varrho \left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +2\lambda +\theta +{\varsigma }_1\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill {\tilde{E}}_1\varrho \left(x\right)=& e^{-{\int }_0^x[\gamma +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x\varrho \left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +\theta +{\varsigma }_1\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill E_2\varrho \left(x\right)=& e^{-{\int }_0^x[\gamma +2\lambda +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x\varrho \left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +2\lambda +{\varsigma }_2\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill {\tilde{E}}_2\varrho \left(x\right)=& e^{-{\int }_0^x[\gamma +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }{\int }_0^x\varrho \left(\vartheta \right)e^{{\int }_0^{\vartheta }[\gamma +{\varsigma }_2\left(\omega \right)]\mathrm{d}\omega }\mathrm{d}\vartheta .\hfill \end{array}$$

(51)

By applying ${\psi }_l\varrho \left(x\right)={\int }_0^{\infty }\varrho \left(x\right){\varsigma }_l\left(x\right)\mathrm{d}x(l=1,2),$ Equations (41)–(47) can be simplified as follows:

$$\begin{array}{cc}\hfill G_{0,0}=& {\displaystyle \frac{1}{\gamma +3\lambda }}{W}_{0,0}+{\displaystyle \frac{1}{\gamma +3\lambda }}{\psi }_1{E}_1{W}_{0,1}\left(x\right)+{\displaystyle \frac{1}{\gamma +3\lambda }}{\psi }_2{E}_2{W}_{0,3}\left(x\right),\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill G_{1,0}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}{W}_{1,0}+{\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}{\psi }_1{\tilde{E}}_1{W}_{1,1}\left(x\right)\hfill \\ \hfill & +{\displaystyle \frac{2\lambda }{\gamma +2\lambda +\alpha +\theta }}{\psi }_1{\tilde{E}}_1{E}_1{W}_{0,1}\left(x\right),\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill G_{0,1}\left(x\right)=& E_1{W}_{0,1}\left(x\right),\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill G_{1,1}\left(x\right)=& {\tilde{E}}_1{W}_{1,1}\left(x\right)+2\lambda {\tilde{E}}_1{E}_1{W}_{0,1}\left(x\right),\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill G_{1,2}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}{W}_{1,2}+{\displaystyle \frac{\theta }{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}\hfill \\ \hfill & \times \left[W_{1,0}+{\psi }_1{\tilde{E}}_1{W}_{1,1}\left(x\right)+2\lambda {\psi }_1{\tilde{E}}_1{E}_1{W}_{0,1}\left(x\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}{\psi }_2{\tilde{E}}_2{W}_{1,3}\left(x\right)+{\displaystyle \frac{2\lambda }{\gamma +2\lambda +\alpha }}{\psi }_2{\tilde{E}}_2{E}_2{W}_{0,3}\left(x\right),\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill G_{0,3}\left(x\right)=& E_2{W}_{0,3}\left(x\right),\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill G_{1,3}\left(x\right)=& {\tilde{E}}_2{W}_{1,3}\left(x\right)+2\lambda {\tilde{E}}_2{E}_2{W}_{0,3}\left(x\right).\hfill \end{array}$$

(58)

According to Equations (52)–(58), we get

$$\begin{array}{cc}\hfill & {(\gamma I-{\mathcal{S}}_0)}^{-1}W\hfill \\ \hfill =& \left(\begin{array}{ccccccc}{\displaystyle \frac{1}{\gamma +3\lambda }}& 0& {\displaystyle \frac{{\psi }_1{E}_1}{\gamma +3\lambda }}& 0& 0& {\displaystyle \frac{{\psi }_2{E}_2}{\gamma +3\lambda }}& 0\\ 0& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}& {\displaystyle \frac{2\lambda {\psi }_1{\tilde{E}}_1{E}_1}{\gamma +2\lambda +\alpha +\theta }}& {\displaystyle \frac{{\psi }_1{\tilde{E}}_1}{\gamma +2\lambda +\alpha +\theta }}& 0& 0& 0\\ 0& 0& E_1& 0& 0& 0& 0\\ 0& 0& 2\lambda {\tilde{E}}_1{E}_1& {\tilde{E}}_1& 0& 0& 0\\ 0& {\displaystyle \frac{\theta }{\mathsf{\Lambda }}}& {\displaystyle \frac{2\lambda \theta {\psi }_1{\tilde{E}}_1{E}_1}{\mathsf{\Lambda }}}& {\displaystyle \frac{\theta {\psi }_1{\tilde{E}}_1}{\mathsf{\Lambda }}}& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}& {\displaystyle \frac{2\lambda {\psi }_2{\tilde{E}}_2{E}_2}{\gamma +2\lambda +\alpha }}& {\displaystyle \frac{{\psi }_2{\tilde{E}}_2}{\gamma +2\lambda +\alpha }}\\ 0& 0& 0& 0& 0& E_2& 0\\ 0& 0& 0& 0& 0& 2\lambda {\tilde{E}}_2{E}_2& {\tilde{E}}_2\end{array}\right)W,\hfill \end{array}$$

(59)

where $\mathsf{\Lambda }=(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta ).$

According to the definition of the resolvent set, we can obtain the following result.

Lemma 2. 

Let ${\varsigma }_l\left(x\right):[0,\infty )\to [0,\infty )$ be measurable and

$$\begin{array}{cc}\hfill 0& <\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)<\underset{x\in [0,\infty )}{sup}{\varsigma }_l\left(x\right)<\infty ,l=1,2,\hfill \end{array}$$

then,

$$\left\{\gamma \in \mathbb{C}\left|\mathrm{Re}\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)>0,l=1,2\right\}\subset \rho \left({\mathcal{S}}_0\right)\right.,$$

which shows that all points on the imaginary axis belong to $\rho \left({\mathcal{S}}_0\right)$.

Proof. 

For any $\varrho \in L^1[0,\infty )\cap C_0^{\infty }[0,\infty ),$ we estimate

$$\begin{array}{cc}\hfill {\int }_0^{\infty }\left|E_1\varrho \left(x\right)\right|\mathrm{d}x\le & {\int }_0^{\infty }{e}^{-(Re\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\int }_0^x\left|\varrho \left(\vartheta \right)\right|e^{(Re\gamma +2\lambda +\theta )\vartheta +{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta \mathrm{d}x\hfill \\ \hfill =& {\int }_0^{\infty }{\displaystyle \frac{-1}{Re\gamma +2\lambda +\theta +{\varsigma }_1\left(x\right)}}{\int }_0^x\left|\varrho \left(\vartheta \right)\right|e^{(Re\gamma +2\lambda +\theta )\vartheta +{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta \hfill \\ \hfill & \times \mathrm{d}{e}^{-(Re\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill =& {\displaystyle \frac{-1}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\{e^{-(Re\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times {\int }_0^x\left|\varrho \left(\vartheta \right)\right|e^{(Re\gamma +2\lambda +\theta )\vartheta +{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta {|}_{x=0}^{x=\infty }\hfill \\ \hfill & -{\int }_0^{\infty }{e}^{-(Re\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times e^{(Re\gamma +2\lambda +\theta )x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\left|\varrho \left(x\right)\right|\mathrm{d}x\}\hfill \\ \hfill =& {\displaystyle \frac{-1}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\{\underset{x\to \infty }{lim}{e}^{-(Re\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times {\int }_0^x\left|\varrho \left(\vartheta \right)\right|e^{(Re\gamma +2\lambda +\theta )\vartheta +{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta +{\int }_0^{\infty }\left|\varrho \left(x\right)\right|\mathrm{d}x\}\hfill \\ \hfill \le & {\displaystyle \frac{1}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}{\parallel \varrho \parallel }_{L^1[0,\infty )}.\hfill \end{array}$$

(60)

Similarly,

$$\begin{array}{c}\hfill {\int }_0^{\infty }\left|{\tilde{E}}_1\varrho \left(x\right)\right|\mathrm{d}x\le {\displaystyle \frac{1}{Re\gamma +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}{\parallel \varrho \parallel }_{L^1[0,\infty )}.\end{array}$$

(61)

$$\begin{array}{c}\hfill {\int }_0^{\infty }\left|E_2\varrho \left(x\right)\right|\mathrm{d}x\le {\displaystyle \frac{1}{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}{\parallel \varrho \parallel }_{L^1[0,\infty )}.\end{array}$$

(62)

$$\begin{array}{c}\hfill {\int }_0^{\infty }\left|{\tilde{E}}_2\varrho \left(x\right)\right|\mathrm{d}x\le {\displaystyle \frac{1}{Re\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}{\parallel \varrho \parallel }_{L^1[0,\infty )}.\end{array}$$

(63)

According to Adams [43], $C_0^{\infty }[0,\infty )$ is dense in $L^1[0,\infty )$, and it follows that Equations (60)–(63) hold for all $\varrho \in L^1[0,\infty )$.

By using Equations (59)–(63) with the condition $\mathrm{Re}\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)>0(l=1,2)$ we estimate, for $W\in X$,

$$\begin{array}{cc}\hfill & \parallel {(\gamma I-{\mathcal{A}}_0)}^{-1}W\parallel \hfill \\ \hfill \le & \left|{\displaystyle \frac{1}{\gamma +3\lambda }}{W}_{0,0}+{\displaystyle \frac{1}{\gamma +3\lambda }}{\psi }_1{E}_1{W}_{0,1}+{\displaystyle \frac{1}{\gamma +3\lambda }}{\psi }_2{E}_2{W}_{0,3}\right|\hfill \\ \hfill & +\left|{\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}{W}_{1,0}+{\displaystyle \frac{2\lambda }{\gamma +2\lambda +\alpha +\theta }}{\psi }_1{\tilde{E}}_1{E}_1{W}_{0,1}+{\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}{\psi }_1{\tilde{E}}_1{W}_{1,1}\right|\hfill \\ \hfill & +∥E_1{W}_{0,1}∥+∥2\lambda {\tilde{E}}_1{E}_1{W}_{0,1}+{\tilde{E}}_1{W}_{1,1}∥\hfill \\ \hfill & +|{\displaystyle \frac{\theta }{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}{W}_{1,0}+{\displaystyle \frac{2\lambda \theta }{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}{\psi }_1{\tilde{E}}_1{E}_1{W}_{0,1}\hfill \\ \hfill & +{\displaystyle \frac{\theta }{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}{\psi }_1{\tilde{E}}_1{W}_{1,1}\hfill \\ \hfill & +{\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}{W}_{1,2}+{\displaystyle \frac{2\lambda }{\gamma +2\lambda +\alpha }}{\psi }_2{\tilde{E}}_2{E}_2{W}_{0,3}+{\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}{\psi }_2{\tilde{E}}_2{W}_{1,3}|\hfill \\ \hfill & +∥E_2{W}_{0,3}∥+∥2\lambda {\tilde{E}}_2{E}_2{W}_{0,3}+{\tilde{E}}_2{W}_{1,3}∥\hfill \\ \hfill \le & {\displaystyle \frac{1}{|\gamma +3\lambda |}}\left|W_{0,0}\right|+\left[{\displaystyle \frac{1}{|\gamma +2\lambda +\alpha +\theta |}}+{\displaystyle \frac{\theta }{\left|\right(\gamma +2\lambda +\alpha \left)\right(\gamma +2\lambda +\alpha +\theta \left)\right|}}\right]\left|W_{1,0}\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{|\gamma +2\lambda +\alpha |}}\left|W_{1,2}\right|\hfill \\ \hfill & +\left[{\displaystyle \frac{1}{|\gamma +3\lambda |}}∥{\psi }_1∥∥E_1∥+{\displaystyle \frac{2\lambda }{|\gamma +2\lambda +\alpha +\theta |}}∥{\psi }_1∥{\tilde{E}}_1\parallel \parallel E_1\parallel +\parallel E_1\parallel +2\lambda \parallel {\tilde{E}}_1\parallel \parallel E_1\parallel \right.\hfill \\ \hfill & \left.+{\displaystyle \frac{2\lambda \theta }{\left|\right(\gamma +2\lambda +\alpha \left)\right(\gamma +2\lambda +\alpha +\theta \left)\right|}}∥{\psi }_1∥\parallel {\tilde{E}}_1\parallel ∥E_1∥\right]{∥W_{0,1}∥}_{L^1[0,\infty )}\hfill \\ \hfill & +\left[{\displaystyle \frac{1}{|\gamma +2\lambda +\alpha +\theta |}}∥{\psi }_1∥\parallel {\tilde{E}}_1\parallel +\parallel {\tilde{E}}_1\parallel +{\displaystyle \frac{\theta }{\left|\right(\gamma +2\lambda +\alpha \left)\right(\gamma +2\lambda +\alpha +\theta \left)\right|}}∥{\psi }_1∥\parallel {\tilde{E}}_1\parallel \right]\hfill \\ \hfill & \times {∥W_{1,1}∥}_{L^1[0,\infty )}\hfill \\ \hfill & +\left[{\displaystyle \frac{1}{|\gamma +3\lambda |}}∥{\psi }_2∥∥E_2∥+{\displaystyle \frac{2\lambda }{|\gamma +2\lambda +\alpha |}}∥{\psi }_2∥\parallel {\tilde{E}}_2\parallel ∥E_2∥+∥E_2∥+2\lambda \parallel {\tilde{E}}_2\parallel ∥E_2∥\right]\hfill \\ \hfill & \times {∥W_{0,3}∥}_{L^1[0,\infty )}\hfill \\ \hfill & +\left[{\displaystyle \frac{1}{|\gamma +2\lambda +\alpha |}}∥{\psi }_2∥\parallel {\tilde{E}}_2\parallel +\parallel {\tilde{E}}_2\parallel \right]{∥W_{1,3}∥}_{L^1[0,\infty )}\hfill \\ \hfill \le & sup\{{\displaystyle \frac{1}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}+{\displaystyle \frac{1}{|\gamma +3\lambda |}}{\displaystyle \frac{\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}{\displaystyle \frac{2\lambda }{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\hfill \\ \hfill & +{\displaystyle \frac{2\lambda }{|\gamma +2\lambda +\alpha +\theta |}}{\displaystyle \frac{1}{Re\gamma +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}{\displaystyle \frac{\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\hfill \\ \hfill & +{\displaystyle \frac{2\lambda }{\left|\right(\gamma +2\lambda +\alpha \left)\right(\gamma +2\lambda +\alpha +\theta \left)\right|}}{\displaystyle \frac{\theta }{Re\gamma +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}{\displaystyle \frac{\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}},\hfill \\ \hfill & {\displaystyle \frac{1}{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}+{\displaystyle \frac{1}{|\gamma +3\lambda |}}{\displaystyle \frac{\underset{x\in [0,\infty )}{sup}{\varsigma }_2\left(x\right)}{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}{\displaystyle \frac{2\lambda }{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\hfill \\ \hfill & +{\displaystyle \frac{2\lambda }{|\gamma +2\lambda +\alpha |}}{\displaystyle \frac{1}{Re\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}{\displaystyle \frac{\underset{x\in [0,\infty )}{sup}{\varsigma }_2\left(x\right)}{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\}\parallel W\parallel \hfill \\ \hfill <& \infty .\hfill \end{array}$$

Which completes the proof. □

Lemma 3. 

Let ${\varsigma }_l\left(x\right):[0,\infty )\to [0,\infty )$ be measurable and

$$\begin{array}{cc}\hfill 0& <\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)<\underset{x\in [0,\infty )}{sup}{\varsigma }_l\left(x\right)<\infty ,l=1,2,\hfill \end{array}$$

if

$$\gamma \in \left\{\gamma \in \mathbb{C}|\mathrm{Re}\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)>0,l=1,2\right\},$$

then,

$$\begin{array}{cc}\hfill \mathbf{G}\in & ker(\gamma I-{\mathcal{S}}_m)\hfill \\ \hfill ⟺& \hfill \\ \hfill \mathbf{G}=& \left(G_{0,0},G_{1,0},G_{0,1}\left(x\right),G_{1,1}\left(x\right),G_{1,2},G_{0,3}\left(x\right),G_{1,3}\left(x\right)\right)\hfill \\ \hfill G_{0,0}=& {\displaystyle \frac{1}{\gamma +3\lambda }}[{\int }_0^{\infty }{a}_{0,1}{e}^{-(\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }{a}_{0,3}{e}^{-(\gamma +2\lambda )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x],\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill G_{1,0}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}[{\int }_0^{\infty }{a}_{1,1}{e}^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }{a}_{0,1}\left(1-e^{-2\lambda x}\right)e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x],\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill G_{0,1}\left(x\right)=& a_{0,1}{e}^{-(\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill G_{1,1}\left(x\right)=& \left[a_{1,1}+a_{0,1}\left(1-e^{-2\lambda x}\right)\right]e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill G_{1,2}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}\{{\int }_0^{\infty }\left[a_{1,3}+a_{0,3}\left(1-e^{-2\lambda x}\right)\right]e^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x\hfill \\ \hfill & +{\displaystyle \frac{\theta }{\gamma +2\lambda +\alpha +\theta }}{\int }_0^{\infty }\left[a_{1,1}+a_{0,1}\left(1-e^{-2\lambda x}\right)\right]e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x\},\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill G_{0,3}\left(x\right)=& a_{0,3}{e}^{-(\gamma +2\lambda )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill G_{1,3}\left(x\right)=& \left[a_{1,3}+a_{0,3}\left(1-e^{-2\lambda x}\right)\right]e^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }.\hfill \end{array}$$

(70)

Proof. 

If $\mathbf{G}\in ker(\gamma I-{\mathcal{S}}_m)$, then $(\gamma I-{\mathcal{S}}_m)\mathbf{G}=0,$ i.e.,

$$\begin{array}{cc}\hfill (\gamma +3\lambda )G_{0,0}=& {\int }_0^{\infty }{G}_{0,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x+{\int }_0^{\infty }{G}_{0,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill (\gamma +2\lambda +\alpha +\theta )G_{1,0}=& {\int }_0^{\infty }{G}_{1,1}\left(x\right){\varsigma }_1\left(x\right)\mathrm{d}x,\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{0,1}\left(x\right)}{\mathrm{d}x}}=& -\left[\gamma +2\lambda +\theta +{\varsigma }_1\left(x\right)\right]G_{0,1}\left(x\right),\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{1,1}\left(x\right)}{\mathrm{d}x}}=& -\left[\gamma +\theta +{\varsigma }_1\left(x\right)\right]G_{1,1}\left(x\right)+2\lambda G_{0,1}\left(x\right),\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill (\gamma +2\lambda +\alpha )G_{1,2}=& {\int }_0^{\infty }{G}_{1,3}\left(x\right){\varsigma }_2\left(x\right)\mathrm{d}x+\theta G_{1,0},\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{0,3}\left(x\right)}{\mathrm{d}x}}=& -\left[\gamma +2\lambda +{\varsigma }_2\left(x\right)\right]G_{0,3}\left(x\right),\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{1,3}\left(x\right)}{\mathrm{d}x}}=& -\left[\gamma +{\varsigma }_2\left(x\right)\right]G_{1,3}\left(x\right)+2\lambda G_{0,3}\left(x\right).\hfill \end{array}$$

(77)

By solving Equations (73), (74), (76), and (77), we have

$$\begin{array}{cc}\hfill G_{0,1}\left(x\right)=& a_{0,1}{e}^{-(\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill G_{1,1}\left(x\right)=& a_{1,1}{e}^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }+e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times {\int }_0^{x}2\lambda G_{0,1}\left(\vartheta \right)e^{(\gamma +\theta )\vartheta +{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill G_{0,3}\left(x\right)=& a_{0,3}{e}^{-(\gamma +2\lambda )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \end{array}$$

(80)

$$\begin{array}{cc}\hfill G_{1,3}\left(x\right)=& a_{1,3}{e}^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }+e^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times {\int }_0^{x}2\lambda G_{0,3}\left(\vartheta \right)e^{\gamma \vartheta +{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta .\hfill \end{array}$$

(81)

Substituting Equations (78) and (80) into Equations (79) and (81) gives

$$\begin{array}{cc}\hfill G_{1,1}\left(x\right)=& \left[a_{1,1}+a_{0,1}\left(1-e^{-2\lambda x}\right)\right]e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill G_{1,3}\left(x\right)=& \left[a_{1,3}+a_{0,3}\left(1-e^{-2\lambda x}\right)\right]e^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }.\hfill \end{array}$$

(83)

Substituting Equations (78), (80), (82), and (83) into Equations (71), (72), and (75) we derive

$$\begin{array}{cc}\hfill G_{0,0}=& {\displaystyle \frac{1}{\gamma +3\lambda }}[{\int }_0^{\infty }{a}_{0,1}{e}^{-(\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }{a}_{0,3}{e}^{-(\gamma +2\lambda )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x],\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill G_{1,0}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha +\theta }}[{\int }_0^{\infty }{a}_{1,1}{e}^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }{a}_{0,1}\left(1-e^{-2\lambda x}\right)e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x],\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill G_{1,2}=& {\displaystyle \frac{1}{\gamma +2\lambda +\alpha }}\{{\int }_0^{\infty }\left[a_{1,3}+a_{0,3}\left(1-e^{-2\lambda x}\right)\right]e^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x\hfill \\ \hfill & +{\displaystyle \frac{\theta }{\gamma +2\lambda +\alpha +\theta }}{\int }_0^{\infty }\left[a_{1,1}+a_{0,1}\left(1-e^{-2\lambda x}\right)\right]e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x\}.\hfill \end{array}$$

(86)

In accordance with the imbedding theorem [43], the implication of $\mathbf{G}\in ker(\gamma I-{\mathcal{S}}_m)$, $\mathbf{G}\in D\left({\mathcal{S}}_m\right)$ is as follows:

$$\begin{array}{cc}\hfill \sum _{i=0}^1\left|a_{i,j}\right|& \le \sum _{i=0}^1{∥G_{i,j}∥}_{L^{\infty }[0,\infty )}\hfill \\ \hfill & \le \sum _{i=0}^1{∥G_{i,j}∥}_{L^1[0,\infty )}+\sum _{i=0}^1{∥{\displaystyle \frac{\mathrm{d}{G}_{i,j}}{\mathrm{d}x}}∥}_{L^1[0,\infty )}\hfill \\ \hfill & <\infty ,j=1,3.\hfill \end{array}$$

(87)

Then, Equation (87) shows $a_{i,j}\in \mathbb{R}(i=0,1,j=1,3),$ and from the above equations, it can be concluded that Equations (64)–(70) are correct.

Contrarily, if Equations (64)–(70) are valid, then the application of $a_{i,j}\in \mathbb{R}(i=0,1,j=1,3)$ and $\mathrm{Re}\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)>0(l=1,2)$ allows for the estimation of

$$\begin{array}{cc}\hfill {∥G_{0,1}∥}_{L^1[0,\infty )}\le & {\int }_0^{\infty }\left|a_{0,1}\right|e^{-(Re\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill \le & {\displaystyle \frac{1}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\left|a_{0,1}\right|\hfill \\ \hfill {∥G_{1,1}∥}_{L^1[0,\infty )}\le & {\int }_0^{\infty }\left|a_{1,1}\right|e^{-(Re\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }\left|a_{0,1}\right|e^{-(Re\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }\left|a_{0,1}\right|e^{-(Re\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill \le & {\displaystyle \frac{1}{Re\gamma +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\left|a_{1,1}\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\left|a_{0,1}\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\left|a_{0,1}\right|\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⟹& \hfill \\ \hfill \sum _{i=0}^1{\parallel G_{i,1}\parallel }_{L^1[0,\infty )}\le & {\displaystyle \frac{2}{Re\gamma +2\lambda +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\left|a_{0,1}\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +\theta +\underset{x\in [0,\infty )}{inf}{\varsigma }_1\left(x\right)}}\sum _{i=0}^1\left|a_{i,1}\right|<\infty .\hfill \end{array}$$

(88)

$$\begin{array}{cc}\hfill {∥G_{0,3}∥}_{L^1[0,\infty )}\le & {\int }_0^{\infty }\left|a_{0,3}\right|e^{-(Re\gamma +2\lambda )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill \le & {\displaystyle \frac{1}{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\left|a_{0,3}\right|\hfill \\ \hfill {∥G_{1,3}∥}_{L^1[0,\infty )}\le & {\int }_0^{\infty }\left|a_{1,3}\right|e^{-(Re\gamma )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }\left|a_{0,3}\right|e^{-(Re\gamma )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{\infty }\left|a_{0,3}\right|e^{-(Re\gamma +2\lambda )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\hfill \\ \hfill \le & {\displaystyle \frac{1}{Re\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\left|a_{1,3}\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\left|a_{0,3}\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\left|a_{0,3}\right|\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⟹& \hfill \\ \hfill \sum _{i=0}^1{\parallel G_{i,3}\parallel }_{L^1[0,\infty )}\le & {\displaystyle \frac{2}{Re\gamma +2\lambda +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\left|a_{0,3}\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{Re\gamma +\underset{x\in [0,\infty )}{inf}{\varsigma }_2\left(x\right)}}\sum _{i=0}^1\left|a_{i,3}\right|<\infty .\hfill \end{array}$$

(89)

From Equations (88) and (89) we obtain

$$\begin{array}{c}\hfill \sum _{i=0}^1\left|G_{i,0}\right|+\sum _{i=0}^1\parallel G_{i,1}{\parallel }_{L^1(0,\infty )}+\left|G_{1,2}\right|+\sum _{i=0}^1{\parallel G_{i,3}\parallel }_{L^1[0,\infty )}<\infty .\end{array}$$

(90)

According to Equations (66) and (67), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}{G}_{0,1}\left(x\right)}{\mathrm{d}x}}=& -\left[\gamma +2\lambda +\theta +{\varsigma }_1\left(x\right)\right]G_{0,1}\left(x\right),\hfill \\ \hfill {\displaystyle \frac{\mathrm{d}{G}_{1,1}\left(x\right)}{\mathrm{d}x}}=& -\left[\gamma +\theta +{\varsigma }_1\left(x\right)\right]G_{1,1}\left(x\right)+2\lambda G_{0,1}\left(x\right).\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⟹& \hfill \\ \hfill {∥{\displaystyle \frac{\mathrm{d}{G}_{0,1}}{\mathrm{d}x}}∥}_{L^1[0,\infty )}\le & {\int }_0^{\infty }\left[\left|\gamma \right|+2\lambda +\theta +\underset{x\in (0,\infty )}{sup}{\varsigma }_1\left(x\right)\right]\left|G_{0,1}\left(x\right)\right|\mathrm{d}x\hfill \\ \hfill =& \left[\left|\gamma \right|+2\lambda +\theta +\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)\right]\parallel G_{0,1}{\parallel }_{L^1[0,\infty )}.\hfill \end{array}$$

(91)

$$\begin{array}{cc}\hfill {∥{\displaystyle \frac{\mathrm{d}{G}_{1,1}}{\mathrm{d}x}}∥}_{L^1[0,\infty )}\le & {\int }_0^{\infty }\left[\left|\gamma \right|+\theta +\underset{x\in (0,\infty )}{sup}{\varsigma }_1\left(x\right)\right]\left|G_{1,1}\left(x\right)\right|\mathrm{d}x+{\int }_0^{\infty }2\lambda \left|G_{0,1}\left(x\right)\right|\mathrm{d}x\hfill \\ \hfill =& \left[\left|\gamma \right|+\theta +\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)\right]\parallel G_{1,1}{\parallel }_{L^1[0,\infty )}+2\lambda \parallel G_{0,1}{\parallel }_{L^1[0,\infty )}.\hfill \end{array}$$

(92)

From Equations (91) and (92), we immediately estimate

$$\begin{array}{cc}\hfill \sum _{i=0}^1{∥{\displaystyle \frac{\mathrm{d}{G}_{i,1}}{\mathrm{d}x}}∥}_{L^1(0,\infty )}\le & \left[\left|\gamma \right|+2\lambda +\theta +\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)\right]\parallel G_{0,1}{\parallel }_{L^1[0,\infty )}\hfill \\ \hfill & +\left[\left|\gamma \right|+\theta +\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)\right]\parallel G_{1,1}{\parallel }_{L^1[0,\infty )}+2\lambda \parallel G_{0,1}{\parallel }_{L^1[0,\infty )}\hfill \\ \hfill \le & \left[\left|\gamma \right|+4\lambda +\theta +\underset{x\in [0,\infty )}{sup}{\varsigma }_1\left(x\right)\right]\sum _{i=0}^1\parallel G_{i,1}{\parallel }_{L^1[0,\infty )}<\infty .\hfill \end{array}$$

(93)

Similarly, we estimate

$$\begin{array}{c}\hfill \sum _{i=0}^1{∥{\displaystyle \frac{\mathrm{d}{G}_{i,3}}{\mathrm{d}x}}∥}_{L^1(0,\infty )}<\infty .\end{array}$$

(94)

In summary, we can deduce that $\mathbf{G}\in ker(\gamma I-{\mathcal{S}}_m).$ □

Since $\mathsf{\Theta }$ is a surjective operator, for any $\gamma \in \rho \left({\mathcal{S}}_0\right)$,

$$\begin{array}{c}\hfill \mathsf{\Theta }{|}_{ker(\gamma I-{\mathcal{S}}_m)}:ker(\gamma I-{\mathcal{S}}_m)⟶\partial X\end{array}$$

is invertible. If for any $\gamma \in \rho \left({\mathcal{A}}_0\right)$, then the Dirichlet operator can be defined as

$$\begin{array}{c}\hfill {\mathcal{D}}_{\gamma }:={\left(\mathsf{\Theta }{|}_{ker(\gamma I-{\mathcal{S}}_m)}\right)}^{-1}:\partial X⟶ker(\gamma I-{\mathcal{S}}_m).\end{array}$$

Then Lemma 3 contains a specific expression for ${\mathcal{D}}_{\gamma }$:

$$\begin{array}{c}\hfill {\mathcal{D}}_{\gamma }\left(\begin{array}{c}{a}_{0,1}\\ a_{1,1}\\ a_{0,3}\\ a_{1,3}\end{array}\right)=\left(\begin{array}{cccc}{\displaystyle \frac{{\psi }_1{\eta }_{0,0}}{\gamma +3\lambda }}& 0& {\displaystyle \frac{{\psi }_2{\omega }_{0,0}}{\gamma +3\lambda }}& 0\\ {\displaystyle \frac{{\psi }_1{\eta }_{1,0}}{\gamma +2\lambda +\alpha +\theta }}& {\displaystyle \frac{{\psi }_1{\eta }_{1,1}}{\gamma +2\lambda +\alpha +\theta }}& 0& 0\\ {\eta }_{0,0}& 0& 0& 0\\ {\eta }_{1,0}& {\eta }_{1,1}& 0& 0\\ {\displaystyle \frac{\theta {\psi }_1{\eta }_{1,0}}{\mathsf{\Lambda }}}& {\displaystyle \frac{\theta {\psi }_1{\eta }_{1,1}}{\mathsf{\Lambda }}}& {\displaystyle \frac{{\psi }_2{\omega }_{1,0}}{\gamma +2\lambda +\alpha }}& {\displaystyle \frac{{\psi }_2{\omega }_{1,1}}{\gamma +2\lambda +\alpha }}\\ 0& 0& {\omega }_{0,0}& 0\\ 0& 0& {\omega }_{1,0}& {\omega }_{1,1}\end{array}\right)\left(\begin{array}{c}{a}_{0,1}\\ a_{1,1}\\ a_{0,3}\\ a_{1,3}\end{array}\right),\end{array}$$

(95)

where

$$\begin{array}{cc}\hfill & {\eta }_{0,0}=e^{-(\gamma +2\lambda +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \\ \hfill & {\eta }_{1,0}=(1-e^{-2\lambda x})e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \\ \hfill & {\eta }_{1,1}=e^{-(\gamma +\theta )x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \\ \hfill & {\omega }_{0,0}=e^{-(\gamma +2\lambda )x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \\ \hfill & {\omega }_{1,0}=(1-e^{-2\lambda x})e^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \\ \hfill & {\omega }_{1,1}=e^{-\gamma x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta },\hfill \\ \hfill & \mathsf{\Lambda }=(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta ).\hfill \end{array}$$

Using Equation (95) and the expression of $\mathsf{\Psi }$, we have

$$\begin{array}{cc}\hfill & \mathsf{\Psi }{\mathcal{D}}_{\gamma }\left(\begin{array}{c}{a}_{0,1}\\ a_{1,1}\\ a_{0,3}\\ a_{1,3}\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{cccc}{\displaystyle \frac{3\lambda {\psi }_1{\eta }_{0,0}}{\gamma +3\lambda }}+{\displaystyle \frac{\alpha {\psi }_1{\eta }_{1,0}}{\gamma +2\lambda +\alpha +\theta }}& {\displaystyle \frac{\alpha {\psi }_1{\eta }_{1,1}}{\gamma +2\lambda +\alpha +\theta }}& {\displaystyle \frac{3\lambda {\psi }_2{\omega }_{0,0}}{\gamma +3\lambda }}& 0\\ {\displaystyle \frac{2\lambda {\psi }_1{\eta }_{1,0}}{\gamma +2\lambda +\alpha +\theta }}& {\displaystyle \frac{2\lambda {\psi }_1{\eta }_{1,1}}{\gamma +2\lambda +\alpha +\theta }}& 0& 0\\ \theta \phi {\eta }_{0,0}+{\displaystyle \frac{\alpha \theta {\psi }_1{\eta }_{1,0}}{\mathsf{\Lambda }}}& {\displaystyle \frac{\alpha \theta {\psi }_1{\eta }_{1,1}}{\mathsf{\Lambda }}}& {\displaystyle \frac{\alpha {\psi }_2{\omega }_{1,0}}{\gamma +2\lambda +\alpha }}& {\displaystyle \frac{\alpha {\psi }_2{\omega }_{1,1}}{\gamma +2\lambda +\alpha }}\\ \theta \phi {\eta }_{1,0}+{\displaystyle \frac{2\lambda \theta {\psi }_1{\eta }_{1,0}}{\mathsf{\Lambda }}}& \theta \phi {\eta }_{1,1}+{\displaystyle \frac{2\lambda \theta {\psi }_1{\eta }_{1,1}}{\mathsf{\Lambda }}}& {\displaystyle \frac{2\lambda {\psi }_2{\omega }_{1,0}}{\gamma +2\lambda +\alpha }}& {\displaystyle \frac{2\lambda {\psi }_2{\omega }_{1,1}}{\gamma +2\lambda +\alpha }}\end{array}\right)\left(\begin{array}{c}{a}_{0,1}\\ a_{1,1}\\ a_{0,3}\\ a_{1,3}\end{array}\right).\hfill \end{array}$$

Lemma 4. 

Let ${\varsigma }_l\left(x\right):[0,\infty )\to [0,\infty )$ be measurable and

$$\begin{array}{cc}\hfill 0& <\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)<\underset{x\in [0,\infty )}{sup}{\varsigma }_l\left(x\right)<\infty ,l=1,2,\hfill \end{array}$$

then, all points on the imaginary axis except 0 belong to $\rho \left(\overline{\mathcal{S}}\right)$.

Proof. 

Let $\gamma =\mathrm{i}v,v\ne 0.$ From Riemann−Lebesgue lemma

$$\begin{array}{c}\hfill \underset{v\to \infty }{lim}{\int }_0^{\infty }\varrho \left(x\right)cos\left(vx\right)\mathrm{d}x=0,\underset{v\to \infty }{lim}{\int }_0^{\infty }\varrho \left(x\right)sin\left(vx\right)\mathrm{d}x=0,\varrho \in L^1(0,\infty ).\end{array}$$

There exists $J>0$ for $\left|v\right|>J$,

$$\begin{array}{cc}\hfill |{\int }_0^{\infty }\varrho \left(x\right)e^{-\mathrm{i}vx}\mathrm{d}x{|}^2& ={\left[{\int }_0^{\infty }\varrho \left(x\right)cos\left(vx\right)\mathrm{d}x\right]}^2+{\left[{\int }_0^{\infty }\varrho \left(x\right)sin\left(vx\right)\mathrm{d}x\right]}^2\hfill \\ \hfill & <{\left[{\int }_0^{\infty }\varrho \left(x\right)\mathrm{d}x\right]}^2,0<\varrho \left(x\right)\in L^1[0,\infty ).\hfill \end{array}$$

which applying the fact ${\int }_0^{\infty }{\varsigma }_l\left(x\right)e^{-{\int }_0^y{\varsigma }_l\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x=1(l=1,2),$ and

$$\begin{array}{cc}\hfill \left|{\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x[\mathrm{i}v+2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\right|& \le {\int }_0^{\infty }{\varsigma }_1\left(x\right)\left|e^{\mathrm{i}vx}\right|\left|e^{-{\int }_0^x[2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\right|\mathrm{d}x\hfill \\ \hfill & ={\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x[2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x,\hfill \\ \hfill \left|{\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x[\mathrm{i}v+\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\right|& \le {\int }_0^{\infty }{\varsigma }_1\left(x\right)\left|e^{\mathrm{i}vx}\right|\left|e^{-{\int }_0^x[\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\right|\mathrm{d}x\hfill \\ \hfill & ={\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x[\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x,\hfill \\ \hfill \left|{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x[\mathrm{i}v+2\lambda +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\right|& \le {\int }_0^{\infty }{\varsigma }_2\left(x\right)\left|e^{\mathrm{i}vx}\right|\left|e^{-{\int }_0^x[2\lambda +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }\right|\mathrm{d}x\hfill \\ \hfill & ={\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x[2\lambda +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x,\hfill \\ \hfill \left|{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x[\mathrm{i}v+{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\right|& \le {\int }_0^{\infty }{\varsigma }_2\left(x\right)\left|e^{\mathrm{i}vx}\right|\left|e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\right|\mathrm{d}x\hfill \\ \hfill & ={\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x.\hfill \end{array}$$

For $\forall a=(a_{0,1},a_{1,1},a_{0,3},a_{1,3})\in {\mathbb{R}}^4,$ we estimate

$$\begin{array}{cc}\hfill & \parallel \mathsf{\Psi }{\mathcal{D}}_{\gamma }(a_1,a_3)\parallel \hfill \\ \hfill \le & \left\{\left|{\displaystyle \frac{3\lambda {\psi }_1{\eta }_{0,0}}{\gamma +3\lambda }}\right|+\left|{\displaystyle \frac{\alpha {\psi }_1{\eta }_{1,0}}{\gamma +2\lambda +\alpha +\theta }}\right|\right\}|a_{0,1}|+\left|{\displaystyle \frac{\alpha {\psi }_1{\eta }_{1,1}}{\gamma +2\lambda +\alpha +\theta }}\right|\left|a_{1,1}\right|\hfill \\ \hfill & +\left|{\displaystyle \frac{3\lambda {\psi }_2{\omega }_{0,0}}{\gamma +3\lambda }}\right||a_{0,3}|+|{\displaystyle \frac{2\lambda {\psi }_1{\eta }_{1,0}}{\gamma +2\lambda +\alpha +\theta }}|\left|a_{0,1}\right|+\left|{\displaystyle \frac{2\lambda {\psi }_1{\eta }_{1,1}}{\gamma +2\lambda +\alpha +\theta }}\right|\left|a_{1,1}\right|\hfill \\ \hfill & +\left\{\left|\theta \phi {\eta }_{0,0}\right|+\left|{\displaystyle \frac{\alpha \theta {\psi }_1{\eta }_{1,0}}{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}\right|\right\}\left|a_{0,1}\right|\hfill \\ \hfill & +\left|{\displaystyle \frac{\alpha \theta {\psi }_1{\eta }_{1,1}}{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}\right|\left|a_{1,1}\right|+\left|{\displaystyle \frac{\alpha {\psi }_2{\omega }_{1,0}}{\gamma +2\lambda +\alpha }}\right|\left|a_{0,3}\right|+\left|{\displaystyle \frac{\alpha {\psi }_2{\omega }_{1,1}}{\gamma +2\lambda +\alpha }}\right|\left|a_{1,3}\right|\hfill \\ \hfill & +\left\{\left|\theta \phi {\eta }_{1,0}\right|+\left|{\displaystyle \frac{2\lambda \theta {\psi }_1{\eta }_{1,0}}{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}\right|\right\}\left|a_{0,1}\right|\hfill \\ \hfill & +\left\{\left|\theta \phi {\eta }_{1,1}\right|+\left|{\displaystyle \frac{2\lambda \theta {\psi }_1{\eta }_{1,1}}{(\gamma +2\lambda +\alpha )(\gamma +2\lambda +\alpha +\theta )}}\right|\right\}\left|a_{1,1}\right|\hfill \\ \hfill & +\left|{\displaystyle \frac{2\lambda {\psi }_2{\omega }_{1,0}}{\gamma +2\lambda +\alpha }}\right||a_{0,3}|+\left|{\displaystyle \frac{2\lambda {\psi }_2{\omega }_{1,1}}{\gamma +2\lambda +\alpha }}\right|\left|a_{1,3}\right|\hfill \\ \hfill =& \{{\displaystyle \frac{3\lambda \left|{\psi }_1{\eta }_{0,0}\right|}{|\gamma +3\lambda |}}+{\displaystyle \frac{(2\lambda +\alpha )\left|{\psi }_1{\eta }_{1,0}\right|}{|\gamma +2\lambda +\alpha +\theta |}}+{\displaystyle \frac{(2\lambda +\alpha )\theta \left|{\psi }_1{\eta }_{1,0}\right|}{\left|\right(\gamma +2\lambda +\alpha \left)\right(\gamma +2\lambda +\alpha +\theta \left)\right|}}\hfill \\ \hfill & +\theta \left|\phi {\eta }_{0,0}\right|+\theta \left|\phi {\eta }_{10}\right|\}\left|a_{0,1}\right|\hfill \\ \hfill & +\left\{{\displaystyle \frac{(2\lambda +\alpha )\left|{\psi }_1{\eta }_{1,1}\right|}{|\gamma +2\lambda +\alpha +\theta |}}+{\displaystyle \frac{(2\lambda +\alpha )\theta \left|{\psi }_1{\eta }_{1,1}\right|}{\left|\right(\gamma +2\lambda +\alpha \left)\right(\gamma +2\lambda +\alpha +\theta \left)\right|}}+\theta \left|\phi {\eta }_{1,1}\right|\right\}\left|a_{1,1}\right|\hfill \\ \hfill & +\left\{{\displaystyle \frac{(2\lambda +\alpha )\left|{\psi }_2{\omega }_{1,0}\right|}{|\gamma +2\lambda +\alpha |}}+{\displaystyle \frac{3\lambda \left|{\psi }_2{\omega }_{0,0}\right|}{|\gamma +3\lambda |}}\right\}\left|a_{0,3}\right|\hfill \\ \hfill & +{\displaystyle \frac{(2\lambda +\alpha )\left|{\psi }_2{\omega }_{1,1}\right|}{|\gamma +2\lambda +\alpha |}}\left|a_{1,3}\right|\hfill \\ \hfill \le & {\displaystyle \frac{3\lambda }{|\mathrm{i}v+3\lambda |}}\left|{\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x\left[\mathrm{i}v+2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{0,1}\right|\hfill \\ \hfill & +{\displaystyle \frac{(2\lambda +\alpha )(1+\theta )}{\left|\right(\mathrm{i}v+2\lambda +\alpha \left)\right(\mathrm{i}v+2\lambda +\alpha +\theta \left)\right|}}\hfill \\ \hfill & \times \left|{\int }_0^{\infty }{\varsigma }_1\left(x\right)\left(1-e^{-2\lambda x}\right)e^{-{\int }_0^x\left[\mathrm{i}v+\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{0,1}\right|\hfill \\ \hfill & +\theta \left|{\int }_0^{\infty }{e}^{-{\int }_0^x\left[\mathrm{i}v+2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{0,1}\right|\hfill \\ \hfill & +\theta \left|{\int }_0^{\infty }\left(1-e^{-2\lambda x}\right)e^{-{\int }_0^x\left[\mathrm{i}v+\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{0,1}\right|\hfill \\ \hfill & +{\displaystyle \frac{(2\lambda +\alpha )(1+\theta )}{\left|\right(\mathrm{i}v+2\lambda +\alpha \left)\right(\mathrm{i}v+2\lambda +\alpha +\theta \left)\right|}}\left|{\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x\left[\mathrm{i}v+\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{1,1}\right|\hfill \\ \hfill & +\theta \left|{\int }_0^{\infty }{e}^{-{\int }_0^x\left[\mathrm{i}v+\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{1,1}\right|\hfill \\ \hfill & +{\displaystyle \frac{3\lambda }{|\mathrm{i}v+3\lambda |}}\left|{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x\left[\mathrm{i}v+2\lambda +{\varsigma }_2\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{0,3}\right|\hfill \\ \hfill & +{\displaystyle \frac{2\lambda +\alpha }{|\mathrm{i}v+2\lambda +\alpha |}}\left|{\int }_0^{\infty }{\varsigma }_2\left(x\right)\left(1-e^{-2\lambda x}\right)e^{-{\int }_0^x\left[\mathrm{i}v+{\varsigma }_2\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{0,3}\right|\hfill \\ \hfill & +{\displaystyle \frac{2\lambda +\alpha }{|\mathrm{i}v+2\lambda +\alpha |}}\left|{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x\left[\mathrm{i}v+{\varsigma }_2\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\right|\left|a_{1,3}\right|\hfill \\ \hfill <& {\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x[2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|\hfill \\ \hfill & +{\int }_0^{\infty }{\varsigma }_1\left(x\right)\left(1-e^{-2\lambda x}\right)e^{-{\int }_0^x\left[\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|\hfill \\ \hfill & +\theta {\int }_0^{\infty }{e}^{-{\int }_0^x[2\lambda +\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|\hfill \\ \hfill & +\theta {\int }_0^{\infty }\left(1-e^{-2\lambda x}\right)e^{-{\int }_0^x\left[\theta +{\varsigma }_1\left(\vartheta \right)\right]\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|\hfill \\ \hfill & +{\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-{\int }_0^x[\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,1}\right|\hfill \\ \hfill & +\theta {\int }_0^{\infty }{e}^{-{\int }_0^x[\theta +{\varsigma }_1\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,1}\right|\hfill \\ \hfill & +{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x[2\lambda +{\varsigma }_2\left(\vartheta \right)]\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,3}\right|\hfill \\ \hfill & +{\int }_0^{\infty }{\varsigma }_2\left(x\right)\left(1-e^{-2\lambda x}\right)e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,3}\right|\hfill \\ \hfill & +{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,3}\right|\hfill \\ \hfill =& {\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|+\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|\hfill \\ \hfill & +{\int }_0^{\infty }{\varsigma }_1\left(x\right)e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,1}\right|+\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,1}\right|\hfill \\ \hfill & +{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,3}\right|+{\int }_0^{\infty }{\varsigma }_2\left(x\right)e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,3}\right|\hfill \\ \hfill =& -{\int }_0^{\infty }{e}^{-\theta x}d{e}^{-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\left|a_{0,1}\right|+\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|\hfill \\ \hfill & -{\int }_0^{\infty }{e}^{-\theta x}d{e}^{-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\left|a_{1,1}\right|+\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,1}\right|\hfill \\ \hfill & +\left|a_{0,3}\right|+\left|a_{1,3}\right|\hfill \\ \hfill =& \left|a_{0,1}\right|-\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|+\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{0,1}\right|\hfill \\ \hfill & +\left|a_{1,1}\right|-\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,1}\right|+\theta {\int }_0^{\infty }{e}^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\mathrm{d}x\left|a_{1,1}\right|\hfill \\ \hfill & +\left|a_{0,3}\right|+\left|a_{1,3}\right|\hfill \\ \hfill =& \left|a_{0,1}\right|+\left|a_{1,1}\right|+\left|a_{0,3}\right|+\left|a_{1,3}\right|\hfill \\ \hfill =& \parallel \left(a_1,a_3\right)\parallel .\hfill \end{array}$$

This shows

$$\begin{array}{c}\hfill \parallel \mathsf{\Psi }{\mathcal{D}}_{\gamma }\parallel <1\end{array}$$

(96)

Equation (96) implies that $1\notin \sigma \left(\mathsf{\Psi }{\mathcal{D}}_{\gamma }\right)$ for $\left|v\right|>J$, and in conjunction with Lemma 3.2 [44] we know that $\gamma =\mathrm{i}v\notin \sigma \left(\overline{\mathcal{S}}\right)$ as $\left|v\right|>J,$ i.e.,

$$\begin{array}{c}\hfill \left\{\mathrm{i}v\left|\right|v|>J\right\}\subset \rho \left(\overline{\mathcal{S}}\right),\left\{\mathrm{i}v\left|\right|v|\le J\right\}\subset \sigma \left(\overline{\mathcal{S}}\right)\cap \mathrm{i}\mathbb{R}.\end{array}$$

(97)

According to Theorem 1, the $C_0-$semigroup $T\left(t\right)$ is a positive contraction. Additionally, Nagel [45] shows that $\sigma \left(\overline{\mathcal{S}}\right)\cap \mathrm{i}\mathbb{R}$ is imaginary and additively cyclic, consequently, for any positive integer k, we have

$$\begin{array}{c}\hfill \mathrm{i}v\in \sigma \left(\overline{\mathcal{S}}\right)\cap \mathrm{i}\mathbb{R}\Rightarrow \mathrm{i}vk\in \sigma \left(\overline{\mathcal{S}}\right)\cap \mathrm{i}\mathbb{R}.\end{array}$$

In summary, combining Equation (97) and Lemma 1, we can deduce that $\sigma \left(\overline{\mathcal{S}}\right)\cap \mathrm{i}\mathbb{R}=\left\{0\right\}$. □

Further, we consider ${\overline{\mathcal{S}}}^{*}$, which is the conjugate operator of $\overline{\mathcal{S}}$, and then demonstrate that $0\in {\sigma }_p\left({\overline{\mathcal{S}}}^{*}\right)$ and the GM is 1.

Lemma 5. 

${\overline{\mathcal{S}}}^{*}$ is expressed as follows:

$$\begin{array}{cc}\hfill {\overline{\mathcal{S}}}^{*}{\mathbf{G}}^{*}=& \left(\begin{array}{ccccccc}-3\lambda & 0& 0& 0& 0& 0& 0\\ 0& -(2\lambda +\alpha +\theta )& 0& 0& \theta & 0& 0\\ {\varsigma }_1\left(x\right)& 0& {\omega }_1& 2\lambda & 0& 0& 0\\ 0& {\varsigma }_1\left(x\right)& 0& {\omega }_2& 0& 0& 0\\ 0& 0& 0& 0& -(2\lambda +\alpha )& 0& 0\\ {\varsigma }_2\left(x\right)& 0& 0& 0& 0& {\tilde{w}}_1& 2\lambda \\ 0& 0& 0& 0& {\varsigma }_2\left(x\right)& 0& {\tilde{w}}_2\end{array}\right){\mathbf{G}}^{*}\hfill \\ \hfill & +\left(\begin{array}{cccc}3\lambda & 0& 0& 0\\ \alpha & 2\lambda & 0& 0\\ 0& 0& \theta & 0\\ 0& 0& 0& \theta \\ 0& 0& \alpha & 2\lambda \\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)\left(\begin{array}{c}{G}_{0,1}^{*}\left(0\right)\\ G_{1,1}^{*}\left(0\right)\\ G_{0,3}^{*}\left(0\right)\\ G_{1,3}^{*}\left(0\right)\end{array}\right),\hfill \end{array}$$

$$\begin{array}{c}\hfill D\left({\overline{\mathcal{S}}}^{*}\right)=\left\{{\mathbf{G}}^{*}\in X^{*}\left|\begin{array}{c}{\displaystyle \frac{\mathrm{d}{P}_{i,j}^{*}\left(x\right)}{\mathrm{d}x}}\mathit{are}\mathit{exist}\mathit{and}\hfill \\ P_{i,j}^{*}(\infty )=\chi (i=0,1,j=1,3)\hfill \end{array}\right.\right\},\end{array}$$

where χ in $D\left({\overline{\mathcal{S}}}^{*}\right)$ is a constant which is irrelevant to $i,j$, and

$$\begin{array}{cc}\hfill w_1& ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}-\left[2\lambda +\theta +{\varsigma }_1\left(x\right)\right],{\tilde{w}}_1={\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}-\left[2\lambda +{\varsigma }_2\left(x\right)\right],\hfill \\ \hfill w_2& ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}-\left[\theta +{\varsigma }_1\left(x\right)\right],{\tilde{w}}_2={\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}-{\varsigma }_2\left(x\right).\hfill \end{array}$$

The proof can be found in Appendix B.

Lemma 6. 

Let

$$2\lambda +\alpha +\theta >{\int }_0^{\infty }[2\lambda +\alpha (1-e^{-2\lambda x})]e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_1\left(x\right)\mathrm{d}x,$$

$${\int }_0^{\infty }{e}^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\varsigma }_2\left(x\right)\mathrm{d}x<\infty ,$$

then $0\in {\sigma }_p\left({\overline{\mathcal{S}}}^{*}\right)$ and the GM is 1.

Proof. 

For the Equation ${\overline{\mathcal{S}}}^{*}{\mathbf{G}}^{*}=0,$ i.e.,

$$\begin{array}{cc}\hfill & -3\lambda G_{0,0}^{*}+3\lambda G_{0,1}^{*}\left(0\right)=0,\hfill \end{array}$$

(98)

$$\begin{array}{cc}\hfill & -(2\lambda +\alpha +\theta )G_{1,0}^{*}+\theta G_{1,2}^{*}+\alpha G_{0,1}^{*}\left(0\right)+2\lambda G_{1,1}^{*}\left(0\right)=0,\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}{G}_{0,1}^{*}\left(x\right)}{\mathrm{d}x}}-\left[2\lambda +\theta +{\varsigma }_1\left(x\right)\right]G_{0,1}^{*}\left(x\right)+{\varsigma }_1\left(x\right)G_{0,0}^{*}+2\lambda G_{1,1}^{*}\left(x\right)+\theta G_{0,3}^{*}\left(0\right)=0,\hfill \end{array}$$

(100)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}{G}_{1,1}^{*}\left(x\right)}{\mathrm{d}x}}-\left[\theta +{\varsigma }_1\left(x\right)\right]G_{1,1}^{*}\left(x\right)+{\varsigma }_1\left(x\right)G_{1,0}^{*}+\theta G_{13}^{*}\left(0\right)=0,\hfill \end{array}$$

(101)

$$\begin{array}{cc}\hfill & -(2\lambda +\alpha )G_{1,2}^{*}+\alpha G_{0,3}^{*}\left(0\right)+2\lambda G_{1,3}^{*}\left(0\right)=0,\hfill \end{array}$$

(102)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}{G}_{0,3}^{*}\left(x\right)}{\mathrm{d}x}}-\left[2\lambda +{\varsigma }_2\left(x\right)\right]G_{0,3}^{*}\left(x\right)+{\varsigma }_2\left(x\right)G_{0,0}^{*}+2\lambda G_{1,3}^{*}\left(x\right)=0,\hfill \end{array}$$

(103)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}{G}_{1,3}^{*}\left(x\right)}{\mathrm{d}x}}-{\varsigma }_2\left(x\right)G_{1,3}^{*}\left(x\right)+{\varsigma }_2\left(x\right)G_{1,2}^{*}=0,\hfill \end{array}$$

(104)

$$\begin{array}{cc}\hfill & G_{0,1}^{*}(\infty )=G_{1,1}^{*}(\infty )=G_{0,3}^{*}(\infty )=G_{1,3}^{*}(\infty )=\chi .\hfill \end{array}$$

(105)

Solving Equations (98)–(104) we obtain

$$\begin{array}{cc}\hfill G_{0,1}^{*}\left(x\right)=& b_{0,1}{e}^{2\lambda x+\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }-e^{2\lambda x+\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times {\int }_0^x\left[{\varsigma }_1\left(\vartheta \right)G_{0,0}^{*}+2\lambda G_{1,1}^{*}\left(\vartheta \right)+\theta G_{0,3}^{*}\left(0\right)\right]e^{-2\lambda \vartheta -\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(106)

$$\begin{array}{cc}\hfill G_{1,1}^{*}\left(x\right)=& b_{1,1}{e}^{\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }-e^{\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times {\int }_0^x\left[{\varsigma }_1\left(\vartheta \right)G_{1,0}^{*}+\theta G_{1,3}^{*}\left(0\right)\right]e^{-\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(107)

$$\begin{array}{cc}\hfill G_{0,3}^{*}\left(x\right)=& b_{0,3}{e}^{2\lambda x+{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }-e^{2\lambda x+{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \times {\int }_0^x\left[{\varsigma }_2\left(\vartheta \right)G_{0,0}^{*}+2\lambda G_{1,3}^{*}\left(\vartheta \right)\right]e^{-2\lambda \vartheta -{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(108)

$$\begin{array}{cc}\hfill G_{1,3}^{*}\left(x\right)=& b_{1,3}{e}^{{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }-e^{{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\int }_0^x{\varsigma }_2\left(\vartheta \right)G_{1,2}^{*}{e}^{-{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta .\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill G_{0,1}^{*}\left(0\right)=& G_{1,1}^{*}\left(0\right)=G_{0,3}^{*}\left(0\right)=G_{1,3}^{*}\left(0\right)=G_{0,0}^{*}=G_{1,0}^{*}=G_{1,2}^{*},\hfill \end{array}$$

(110)

We multiply the two sides of Equations (106)–(109), respectively, by

$$e^{-2\lambda x-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },e^{-\theta x-{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta },e^{-2\lambda x-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta },e^{-{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }.$$

Then, we take the limit at $x\to \infty$ and apply Equation (105) to obtain

$$\begin{array}{cc}\hfill b_{0,1}& ={\int }_0^{\infty }[{\varsigma }_1\left(\vartheta \right)G_{0,0}^{*}+2\lambda G_{1,1}^{*}\left(\vartheta \right)+\theta G_{0,3}^{*}\left(0\right)]e^{-2\lambda \vartheta -\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill b_{1,1}& ={\int }_0^{\infty }[{\varsigma }_1\left(\vartheta \right)G_{1,0}^{*}+\theta G_{1,3}^{*}\left(0\right)]e^{-\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(112)

$$\begin{array}{cc}\hfill b_{0,3}& ={\int }_0^{\infty }[{\varsigma }_2\left(\vartheta \right)G_{0,0}^{*}+2\lambda G_{1,3}^{*}\left(\vartheta \right)]e^{-2\lambda \vartheta -{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(113)

$$\begin{array}{cc}\hfill b_{1,3}& ={\int }_0^{\infty }{\varsigma }_2\left(\vartheta \right)G_{1,2}^{*}{e}^{-{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta .\hfill \end{array}$$

(114)

Inserting Equations (111)–(114) into Equations (106)–(109), respectively, we obtain

$$\begin{array}{cc}\hfill G_{0,1}^{*}\left(x\right)=& e^{2\lambda x+\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\hfill \\ \hfill & \hfill \times {\int }_x^{\infty }\left[{\varsigma }_1\left(\vartheta \right)G_{0,0}^{*}+2\lambda G_{1,1}^{*}\left(\vartheta \right)+\theta G_{1,2}^{*}\right]e^{-2\lambda \vartheta -\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\end{array}$$

(115)

$$\begin{array}{cc}\hfill G_{1,1}^{*}\left(x\right)=& e^{\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{\int }_x^{\infty }\left[{\varsigma }_1\left(\vartheta \right)G_{1,0}^{*}+\theta G_{1,2}^{*}\right]e^{-\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(116)

$$\begin{array}{cc}\hfill G_{0,3}^{*}\left(x\right)=& e^{2\lambda x+{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\int }_x^{\infty }\left[{\varsigma }_2\left(\vartheta \right)G_{0,0}^{*}+2\lambda G_{1,3}^{*}\left(\vartheta \right)\right]e^{-2\lambda \vartheta -{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta ,\hfill \end{array}$$

(117)

$$\begin{array}{cc}\hfill G_{1,3}^{*}\left(x\right)=& e^{{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{\int }_x^{\infty }{\varsigma }_2\left(\vartheta \right)G_{1,2}^{*}{e}^{-{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta .\hfill \end{array}$$

(118)

Solving for Equations (116) and (118) and combining Equation (110) and ${\int }_0^{\infty }{\varsigma }_l\left(x\right)\mathrm{d}x=\infty (l=1,2)$, we obtain

$$\begin{array}{cc}\hfill G_{1,1}^{*}\left(x\right)& =G_{0,0}^{*}{e}^{\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\left(-e^{-\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }{|}_x^{\infty }\right)\hfill \\ \hfill & =G_{0,0}^{*},\hfill \end{array}$$

(119)

$$\begin{array}{cc}\hfill G_{1,3}^{*}\left(x\right)& =G_{0,0}^{*}{e}^{{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\left(-e^{-{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }{|}_x^{\infty }\right)\hfill \\ \hfill & =G_{0,0}^{*}.\hfill \end{array}$$

(120)

Substituting Equations (119) and (120) into Equations (115) and (117), respectively, and then combining that with Equation (110) and ${\int }_0^{\infty }{\varsigma }_l\left(x\right)\mathrm{d}x=\infty (l=1,2),$ we deduce

$$\begin{array}{cc}\hfill G_{0,1}^{*}\left(x\right)& =e^{2\lambda x+\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }{G}_{0,0}^{*}{\int }_x^{\infty }\left[{\varsigma }_1\left(\vartheta \right)+2\lambda +\theta \right]e^{-2\lambda \vartheta -\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta \hfill \\ \hfill & =G_{0,0}^{*}{e}^{2\lambda x+\theta x+{\int }_0^x{\varsigma }_1\left(\vartheta \right)\mathrm{d}\vartheta }\left(-e^{-2\lambda \vartheta -\theta \vartheta -{\int }_0^{\vartheta }{\varsigma }_1\left(\omega \right)\mathrm{d}\omega }{|}_x^{\infty }\right)\hfill \\ \hfill & =G_{0,0}^{*},\hfill \end{array}$$

(121)

$$\begin{array}{cc}\hfill G_{0,3}^{*}\left(x\right)& =e^{2\lambda x+{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }{G}_{0,0}^{*}{\int }_x^{\infty }\left[{\varsigma }_2\left(\vartheta \right)+2\lambda \right]e^{-2\lambda \vartheta -{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }\mathrm{d}\vartheta \hfill \\ \hfill & =G_{0,0}^{*}{e}^{2\lambda x+{\int }_0^x{\varsigma }_2\left(\vartheta \right)\mathrm{d}\vartheta }\left(-e^{-2\lambda \vartheta -{\int }_0^{\vartheta }{\varsigma }_2\left(\omega \right)\mathrm{d}\omega }{|}_x^{\infty }\right)\hfill \\ \hfill & =G_{0,0}^{*}.\hfill \end{array}$$

(122)

Summarizing Equations (110), (119)–(122) gives

$$\begin{array}{cc}\hfill \left|\right||{\mathbf{G}}^{*}\left|\right||& =max\left\{\begin{array}{c}|G_{0,0}^{*}|,|G_{1,0}^{*}|,|G_{1,2}^{*}|,\parallel G_{0,1}^{*}{\parallel }_{L^{\infty }[0,\infty )},\hfill \\ \parallel G_{1,1}^{*}{\parallel }_{L^{\infty }[0,\infty )},\parallel G_{0,3}^{*}{\parallel }_{L^{\infty }[0,\infty )},{\parallel G_{1,3}^{*}\parallel }_{L^{\infty }[0,\infty )}\hfill \end{array}\right\}\hfill \\ \hfill & =|G_{0,0}^{*}|<\infty .\hfill \end{array}$$

(123)

It can be observed that Equation (123) demonstrates that 0 is an eigenvalue of ${\overline{\mathcal{S}}}^{*}.$ Furthermore, Equations (110), (119)–(122) indicate that the GM of 0 is 1. □

In summary, in conjunction with Theorem 1.96 [40], we can derive the following main result:

Theorem 4. 

Let ${\varsigma }_l\left(x\right):[0,\infty )\to [0,\infty )$ be measurable and

$$\begin{array}{cc}\hfill 0& <\underset{x\in [0,\infty )}{inf}{\varsigma }_l\left(x\right)<\underset{x\in [0,\infty )}{sup}{\varsigma }_l\left(x\right)<\infty ,l=1,2,\hfill \end{array}$$

then, the TDS of system (13) strongly converges to its SSS, i.e.,

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\parallel \mathbf{G}(·,t)-\wp \mathbf{G}(·)\parallel =0,\end{array}$$

where $\wp =⟨{\mathbf{G}}^{*},\mathbf{G}\left(0\right)⟩$ and $\mathbf{G}$ is the eigenvector corresponding to eigenvalue 0 in Lemma 1.

5. Numerical Results

In this section, we discuss some reliability metrics of the system, such as system availability $A\left(t\right)$, system reliability $R\left(t\right)$, failure frequency $m_f\left(t\right)$, renewal frequency $m_r\left(t\right)$, and mean time to failure (MTTF), by means of specific examples. Moreover, we analyze the impact of variations in the system parameters on the system reliability metrics. First, we assume that the repair time of the system is distributed exponentially and the repair rate is constant, i.e., ${\mu }_1\left(x\right)={\mu }_1,{\mu }_2\left(x\right)={\mu }_2$, for both the WV period and the normal working period. The system parameters are fixed as $\lambda =0.09,\alpha =0.01,\theta =0.05,\mathrm{and}{\mu }_i=0.4\ast i(i=1,2)$. The influence of the parameter changes on the instantaneous reliability index of the system is discussed below.

From Figure 1, it can be seen that these reliability metrics converge to a fixed value as time increases. In addition, $m_f\left(t\right)$ (Figure 1b) increases as $\lambda$ increases, and $A\left(t\right)$ (Figure 1a) and $m_r\left(t\right)$ (Figure 1c) decrease as $\lambda$ increases.

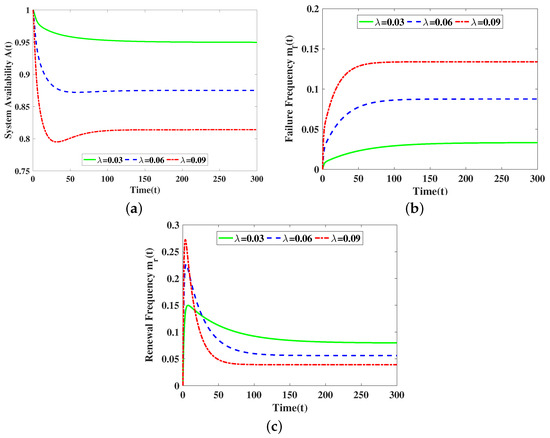
Figure 1. Influence of parameter $\lambda$ on the transient reliability index of the system. (a) $A\left(t\right)$ for different $\lambda$; (b) $m_f\left(t\right)$ for different $\lambda$; (c) $m_r\left(t\right)$ for different $\lambda$.

From Figure 2, it can be seen that these reliability metrics converge to a fixed value as time increases. In addition, $A\left(t\right)$ (Figure 2a), $m_f\left(t\right)$ (Figure 2b), and $m_r\left(t\right)$ (Figure 2c) all increase as ${\mu }_i(i=1,2)$ increases, but the effect of ${\mu }_i(i=1,2)$ on $m_r\left(t\right)$ (Figure 2c) is not significant.

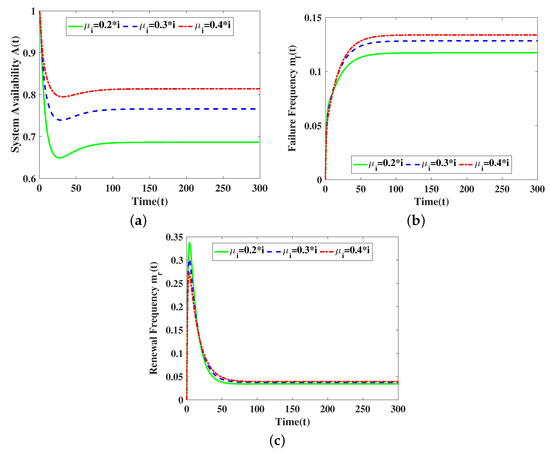
Figure 2. Influence of parameter ${\mu }_i(i=1,2)$ on the transient reliability index of the system. (a) $A\left(t\right)$ for different ${\mu }_i(i=1,2)$; (b) $m_f\left(t\right)$ for different ${\mu }_i(i=1,2)$; (c) $m_r\left(t\right)$ for different ${\mu }_i(i=1,2)$.

From Figure 3, it can be seen that these reliability metrics converge to a fixed value as time increases. In addition, $m_f\left(t\right)$ (Figure 3b) decreases as $\alpha$ increases, and $A\left(t\right)$ (Figure 3a) and $m_r\left(t\right)$ (Figure 3c) increase as $\alpha$ increases, but the effect of $\alpha$ on $A\left(t\right)$ (Figure 3a) is not significant.

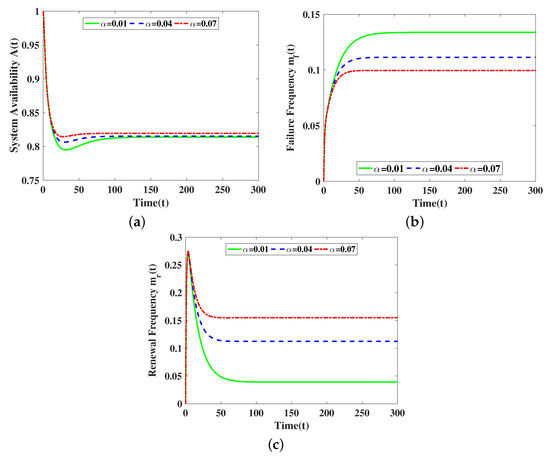
Figure 3. Influence of parameter $\alpha$ on the transient reliability index of the system. (a) $A\left(t\right)$ for different $\alpha$; (b) $m_f\left(t\right)$ for different $\alpha$; (c) $m_r\left(t\right)$ for different $\alpha$.

From Figure 4, it can be seen that these reliability metrics converge to a fixed value as time increases. In addition, $A\left(t\right)$ (Figure 4a), $m_f\left(t\right)$ (Figure 4b), and $m_r\left(t\right)$ (Figure 4c) all increase as $\theta$ increases, but the effect of $\theta$ on $m_f\left(t\right)$ (Figure 4b) and $m_r\left(t\right)$ (Figure 4c) are not significant.

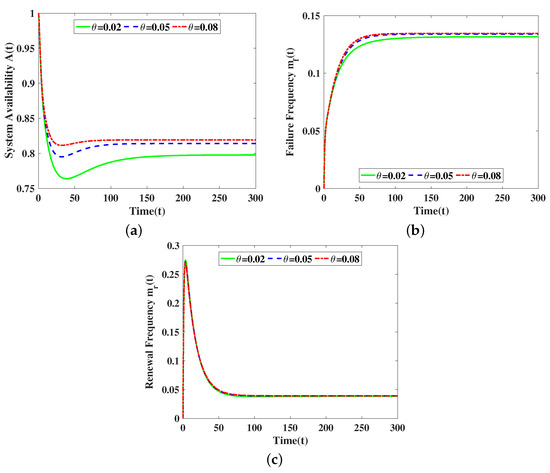
Figure 4. Influence of parameter $\theta$ on the transient reliability index of the system. (a) $A\left(t\right)$ for different $\theta$; (b) $m_f\left(t\right)$ for different $\theta$; (c) $m_r\left(t\right)$ for different $\theta$.

From Figure 5a, it can be seen that $R\left(t\right)$ decreases with time and eventually tends to 0, and the larger $\lambda$ is, the smaller the reliability is. From Figure 5b it can be seen that MTTF decreases with an increase in $\lambda$.

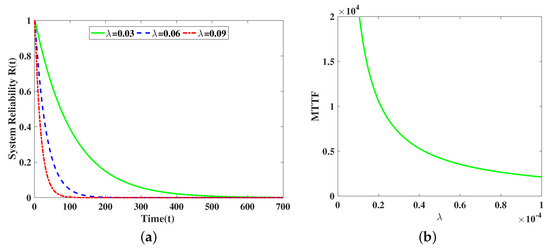
Figure 5. Reliability and MTTF for exponentially distributed repair time. (a) Reliability for different $\lambda$; (b) effect of $\lambda$ on MTTF.

6. Conclusions

In this paper, we have extended the mathematical models previously discussed in the literature [18,19] by introducing multiple working vacations and retrial strategies, under the assumption that repair times follow a general distribution. By applying the $C_0-$semigroup theory, we have analyzed the well−posedness and asymptotic behavior of the dynamic solutions of the model. Our results demonstrate that the dynamic solutions converge strongly to the SSS. In addition, the influence of each parameter on system reliability is elucidated through specific examples. Obviously, the findings of this study not only encompass the results from the literature [18,19] as a special case but also validate the accuracy of the hypotheses established therein.

By deriving the spectral distribution of the main operator, we may obtain an asymptotic expressions for the system’s dynamical solution. However, due to the intricacy of the derivation process, we have yet to reach this conclusion, and this will be addressed in a future study.