Abstract
A time stepping quasilinearization approach to the mixed (or coupled) form of one and two dimensional Richards’ equations is developed. For numerical solution of the linear ordinary differential equation (ODE) for 1D case and elliptic for 2D case, obtained after this semidiscretization, a finite volume method is used for direct problems arising on each time level. Next, we propose a version of the decomposition method for the numerical solution of the inverse ODE and 2D elliptic boundary problems. Computational results for some soil types and its related parameters reported in the literature are presented.
Keywords:
soil-water flow; Richards’ equation; inverse boundary condition problem; ODE system; Bellman-Kalaba quasilinearization; decomposition of the solution; finite difference scheme MSC:
65M06; 65M32
1. Introduction
Richards’ equation serves as a fundamental model for water movement in non-swelling unsaturated soils, see e.g., [,,,,,,,,]. It exclusively hinges on soil water content as the sole dependent variable. L. Richards [] derived it in an effort to construct a model of groundwater dynamics that includes actions of gravity and nonlinear capillary effects without having to model the non-wetting phase (air) as an unknown itself. Applications for computer simulations based on this equation include nuclear waste disposal, geochemical, and agricultural, etc.
Due to its nonlinear nature and transition of the type in different parts of the problem domain, this equation is difficult to solve by analytical techniques and closed form solutions can be obtained only in some particular cases [,].
In [], the author investigates a class of analytical solutions to describe moisture flow in unsaturated porous materials. These solutions hinge on an exponential connection between hydraulic conductivity and moisture content with respect to water pressure. Well-posedness of Richards’ equation and an explicit solution for the corresponding steady-state problem are established in []. Uniqueness of the solution to a parabolic inverse problem with an unknown boundary condition upon a single internal measurement is established in [].
Other difficulties in solving Richards’ equation arise from practical initial and boundary conditions, and water constitutive relations that can lead to solutions with low regularity. Additionally, when dry soils experience infiltration, it frequently triggers distinct wetting boundaries characterized by exceptionally steep spatial gradients in soil hydraulic characteristics [,,].
Overcoming all these complexities make Richards’ equation challenging to solve, even numerically. In [], the authors discuss the numerical behavior of standard approximation methods—finite difference and finite element methods for the unsaturated flow equation in different forms. Recently, variety numerical methods for solving Richards’ equation are developed: adaptive higher-order discontinuous Galerkin method [], finite volume discretization realized by nested, Newton-type algorithm [], Padé approximants for simplifying the analytical form of hydraulic parameters and Adomian’s decomposition [], finite difference method by local balance of mass [], monotone finite volume method [], fitted finite volume method on graded spatial mesh [], modified Picard algorithm with adaptive strategy in time and mass-conservative switching algorithm involving the mass-conservative mixed form and the pressure head-based form in different zones of the flow problem [], etc.
In [], an adaptive discontinuous Galerkin method for solving the model that combines Richards’ equation with a surface water balance is constructed to simulate the rate of recharge from rainwater in a zone with roots, an intermediate storage layer with high conductivity, and a lower water table. A numerical model is employed in [] to simulate both mechanical root reinforcement and hydrological influences, encompassing evapotranspiration with various root configurations and alterations induced by roots in soil water retention and hydraulic conductivity.
Richards’ equation indirectly connects even to honeybee populations through its impact on plant growth (as soybean, rapeseed, sunflower) and the availability of nectar-producing flowers. Proper irrigation and soil moisture management play a role in ensuring a suitable environment for both plants and honeybees [,]. The paper [] studies model verification both for classical and fractional Richardsons’ equations using measurements data for soybean sprinkling irrigation.
Inverse problems have important practical applications, since they involve the determination of initial function or boundary conditions and parameters that are unknown and cannot be measured in a satisfactory way. These problems are challenging to solve because, in general, they are ill-posed [,,,,,,,,,].
A more intensively studied class of inverse problems for Richards’ equation involves the identification of parameter(s). Necessary conditions for uniqueness of the solutions of parameter identification inverse problems of water flow through multi-dimensional variably saturated porous media are derived in []. In [], an inverse problem is discussed for the determination of the two coefficients within the pressure head formulation of the porous flow equation. The parameter estimation problem for the hydraulic properties (the nonlinear coefficients) of porous media is studied in []. The problem is solved numerically by least-squares functional minimization. The authors of [] solve the numerically parameter determination inverse problem for recovering hydrological parameters in Richards’ equation with given measurements of pressure. They apply optimal control approach, derive time discretization of the corresponding state problem, and solve the generated nonlinear state problem by finite difference scheme and Picard’s iteration procedure. In [], authors discuss numerically solving two parameter identification inverse problems for Richards’ equation. In the first problem, soil parameters are restored, while in the second problem, hydraulic permeability, longitudinal dispersivity, and adsorption isotherms are determined. Stochastic parameterization and Monte Carlo methods are employed in [] in order to determine saturated hydraulic conductivity fields. In [], the Levenberg–Marquardt algorithm is utilized to minimize least-square functional in order to restore two parameters in the constitutive relations of the exponential model of Richards’ equation. Compensated nonlinear root water uptake is developed and soil hydraulic parameters are estimated in [,].
A technique for determining the saturation coefficients linked to relative hydraulic conductivity and water content is suggested in [] on the basis of the simulation outcomes. In [], the parameters are estimated by fitting the experimental data exclusively to the retention curve. The authors of [] performed a model calibration in order to simulate water and nitrogen transport for two furrow irrigation technologies. In [], the authors propose mathematical modeling for the groundwater recharge estimation problem.
In an irrigation setting, an optimal control approach was implemented in [] for Richards’ equation, focusing on the reduction of water consumption and the enhancement of root water absorption.
There are few results in the literature for identifying boundary conditions in Richards’ problems. In [], the authors construct an algorithm for recovering boundary conditions at the lower end of the domain from observations at the surface. Simultaneous recovering of multiple boundary heat flux parameters is achieved in [] by solving nonlinear transient inverse heat conduction problems, applying a modified Levenberg–Marquardt algorithm.
In our previous paper [], decomposition method is applied in order to determine external boundary conditions in a lime-fractional linear fluid-porous interface problem, defined on disjoint domains.
In this work, we construct and examine a numerical method for solving an inverse problem to identify the left Dirichlet boundary condition and the pressure head in Richards’ initial boundary value problem with additional measurements of the pressure within the domain. The algorithm is based on a quazilinearization approach and on decomposition of the inverse problem solution.
The remaining part of the paper is organized as follows: In the next section, we discuss the basic forms of the famous Richards’ equation. In Section 3, direct and inverse problems are formulated. The main results, numerical solution of 1D and 2D inverse problems, are obtained in Section 4 and Section 5. Computational simulations are presented in Section 6 and the paper is finalized with some conclusions.
2. Mathematical Models
Richards’ equation incorporates a diffusion term into a mass balance equation. The conservation of mass within a small uniform volume of unsaturated soil is represented by the equality
The fluid motion is considered as incompressible and the soil structure as robust and unyielding. The Equation (1) correlates the volumetric soil water content [] with the specific flow vector q [] and t is time.
The governing principle that defines the flow of water through an unsaturated porous medium is modeled by
It can be seen as an expansion of Darcy’s law that takes unsaturated conditions into account. Here, [] represents the hydraulic conductivity, and H is the total head, , where is the capillary heights and z is geometric altitude.
In the case of flow along the z-direction, where the z-axis is oriented vertically upwards, an extra gravitational factor must be incorporated, leading to the inclusion of a gravitational term
In the scientific literature, Richards’ equation is represented in three principal formulations: the mixed form, the pressure -based form, and the water content -based form. We discuss these formulations in 1D case. Combining (1) and (3), we obtain the mixed formulation
Further, the utilization of the concept of differential water capacity, expressed as the derivative of the soil water retention curve
from (4) and (5), we derive the -based formulation of Richards’ equation
Here, [] is the specific fluid capacity.
In the saturated environment, the -based formulation of Richards’ equation can be formulated [,]. Namely, introducing the diffusion coefficient D []
we obtain
In the same fashion, the three formulations of 3D Richards’ equation are derived:
- -
- mixed formulation
- -
- -based formulation
- -
- head or -based formulation
A different type of empirical constitutive relation for the moisture content and hydraulic conductivity are used in the literature. For example, the exponential model or Gardner model [,,,], given by
where [] and [], are saturation and residual water content, respectively, is the saturated hydraulic conductivity, and [] is soil pore-size distribution parameter.
The most popular constitutive relations are those described in studies conducted by van Genuchten []
Here, is a pore-size distribution index, and are fitting parameters.
3. Direct and Inverse Problems
In this section, we formulate inverse problems for recovering the boundary condition in 1D and 2D problems, described by Richards’ equation in mixed form (4) and (8), respectively.
First, we consider 1D case. The model problem is formulated for mixed form of the Richards’ equation in the spatial domain with height [,,]
where is the external time-dependent surface flow.
The direct problem is the problem (15) with known parameters, boundary, and initial conditions.
The following assertion presents a brief analysis of the solution of this problem.
Theorem 1.
Let us assume that the functions and are piecewise continuous and there are constants , , such that
Then, the problem (15) has a unique solution .
Proof.
We follow the idea of [] to apply the results of []. To this end, we perform the change
and reduce the problem (15) as follows:
Now, in a usual way, see e.g., [], we define a weak solution of the problem (16) as follows
for all , such that and . Now, the statement of the theorem directly follows from the main result in []. □
We study the inverse problem (IP-1D) for identifying the left boundary condition and solution in (15) under given point measurements.
Next, we consider the initial boundary value problem for 2D Richards’ equation in mixed form (8) [,,,]
The inverse problem (IP-2D) for identifying the function in the left boundary condition and solution in (18) is formulated under given point measurements
4. Numerical Solution of the Inverse Problem—1D Case
In this section, we discuss numerically solving the IP-1D. The numerical approach is constructed in four steps—time semidiscretization, linearization, decomposition, and full discretization.
We introduce uniform temporal mesh with grid nodes , , . Applying implicit-explicit time-stepping (Rothe method) to the direct problem (15), we derive the following ODE system for unknown solution ,
where and .
For a general quasilinear parabolic equation, the convergence of the Rothe method is studied in []. This study is based on the proof of a priori estimates for the corresponding differential-difference nonlinear system (20). Then, using these estimates, the author of [] proves the existence of a smooth solution of the original differential problem. The next theorem immediately follows from the main result in [].
Theorem 2.
For , any ψ, , the input data of the problem (15) are uniformly bounded, where for the derivatives and hold:
The function , are continuous and is continuously differentiable and they all satisfy compatibility conditions. Then, Richards’ parabolic nonlinear problem (15) has a unique smooth solution, which is the limit of the Rothe solution (20) as the time step τ goes to zero.
Further, we apply Belman and Kalaba quazilinearization [,,,]. Let us denote
and suppose that , are the initial approximations of the corresponding exact values of and at the -th time layers.
Then
We consider and as independent variables and assume that and are small values. Using the notation , we represent
and therefore
In the same manner, we treat the the function in the evolution term in (20)
where .
From (24) and (25), substituting in (20), rearranging and taking into account (21), we obtain
where ,
The problem is completed by initial and boundary conditions in (20). The flux-type right boundary condition is handled as in (23). At point , we have
We proceed with the third step. In order to solve the inverse problem IP-1D, we apply the following decomposition of the solution
Substituting in (26) with the corresponding Dirichlet or flux boundary conditions (27) and initial condition, we obtain two problems for the unknown functions and
and
Finally, we define uniform spatial mesh with grid nodes , , and denote by the values of the mesh function v at grid node . We use also the notations
For the discretization of (29) and (30), we apply finite volume method. To this aim, we define also the dual mesh
and denote by the values of the mesh function v at grid node .
The full discrete scheme of the direct problem (26) and (27) associated with the corresponding Dirichlet boundary conditions and initial conditions (20) is
where , , , and similarly for the functions , and
Let denote . In order to solve the problems (31)–(33), we initiate iteration process, replacing by the solution at old iteration and is the solution at new iteration , . Suppose that the points of measurements are grid nodes. Thus, for the numerical recovering of the solution and left boundary condition, the computations are performed by the following steps
Algorithm IP-1D
- 1.
- Start with initial function , measurements , and set the accuracy .
- 2.
- Set .
- 3.
- Set .
- 4.
- Solve the problem (32), , to find .
- 5.
- Solve the problem (33), , to find .
- 6.
- 7.
- From (28), determine
- 8.
- Ifthen , , ;if ,then and go to step 3;or else, stop the computations.or else and go to step 4.
We use the iterative solution of the direct problem (31) in the numerical tests only to generate measurements and to estimate the accuracy of the inverse method.
5. Numerical Solution of the Inverse Problem—2D Case
In this section we briefly discuss the construction of the numerical method for solving inverse problem IP-2D. We follow the same steps as for the 1D case.
First, we apply weighed semidiscretization in time to obtain the ODE system. Next, we linearize the terms .
In this framework, for , using the notations (21), (22), we derive (24). In the same manner, we treat the term . Involving the notation , we obtain
Therefore
Then, in view of (25), the linearized problem (18) became
where , , , are defined as before, replacing by and
To solve the inverse problem IP-2D, we decompose the solution
Further, we define primal and dual uniform spatial meshes also in x-direction with grid nodes
Denote by , and the values of the mesh function v at grid node , and , respectively. We use also the notations
For clarity of the exposition, we simplify the notations for the mesh function v
Taking
the same for and , the full discrete iterative finite volume scheme of the direct problem (36) is
where and are defined as before, replacing by . Then, and are obtained applying (40)
Algorithm IP-2D
We follow the same steps 1–8 as in Algorithm IP-1D, but the norm is defined by and instead of (32) and (33), we compute (42) and (43), respectively. Also, steps 6 and 7 are based on the decomposition (37) and measurements (19), namely
- ......
- 6.
- 7.
- From (28), determine
- ...
6. Computational Results
In this section, we illustrate the efficiency of the constructed Algorithm IP-1D and Algorithm IP-2D for numerical determination of the left boundary condition and the solution in problems (15) and (18). The stability is investigated by adding a different level of random noise on the over-specified boundary data.
We set hydraulic parameters for clay loam texture [,]
All computations are performed for , and = 1 . To solve the linear systems of algebraic equations generated after full discretization, we apply direct method, using the ’mldivide’ toolbox of MATLAB R2022a for sparse matrices.
Example 1 (1D inverse problem: exact data).
We verify the order of convergence of the Algorithm IP-1D. The test problem is the inverse problem for (15), , .
We take the measurements from the numerical solution of the direct problem (31) at each time layer and at three different space points , , . The averaging number of iterations is denoted by .
First, we consider constitutive relations of the exponential model (11). We add residual functions in the right-hand side of the differential equation in (15), choose appropriate function , initial condition, and Dirichlet boundary conditions, such that to be the exact solution of the modified direct problem (15).
The error and order of convergence are estimated in maximal discrete norm
where is the solution, obtained by Algorithm IP-1D at final time, and is the exact solution of the direct problem (15) at , computed by (31).
In Table 1 and Table 2 we give errors, order of convergence, and average number of iterations for and .

Table 1.
Errors and order of convergence of the solution of Algorithm IP-1D, exponential problem with Dirichlet right boundary condition, Example 1.

Table 2.
Errors and order of convergence of the solution of Algorithm IP-1D, exponential problem with Neumann right boundary condition, Example 1.
We observe that the location of the measurements does not influence the accuracy of the Algorithm IP-1D and the order of convergence is .
Further, all computations are performed for the case of right Neumann boundary condition in (15). In Figure 1, we plot the absolute difference between the numerical solution of the inverse problem and direct problem at final time for . In Figure 2, we depict exact and recovered function . The results show that Algorithm IP-1D recovers numerical solution and left boundary condition of the direct problem exactly. Therefore, considering also the results in Table 1 and Table 2, both numerical solution of the direct and inverse problems are second order accurate in space and time.
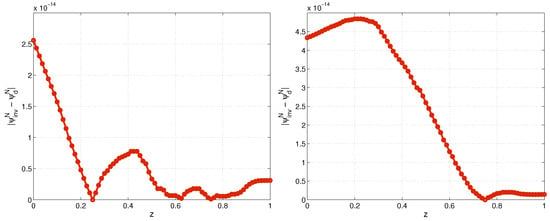
Figure 1.
Exponential model. Absolute difference between the numerical solution of the inverse problem and numerical solution of the direct problem at final time for , (left) and (right), Example 1.
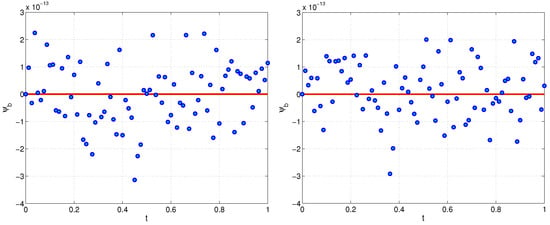
Figure 2.
Exponential model. Exact and recovered function for , (left) and (right), Example 1.
Now, we examine constitutive relations of the Genuchten model. We solve original problem (15), (12)–(14) for with [cm/h], [cm/h] and [h], see [], and initial function
In Figure 3, we illustrate the numerical solution of the inverse problem and direct problems and absolute error at final time for . In Figure 4, we depict exact function and numerically restored by Algorithm IP-1D function and the absolute difference between these two solutions. Note that for this test example . The computations show that the numerical solution of the direct problem is recovered exactly.
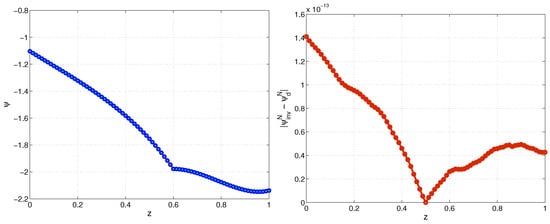
Figure 3.
Genuchten model. Numerical solution of the direct and inverse problems (left) and the corresponding absolute difference (right) at final time for , , Example 1.
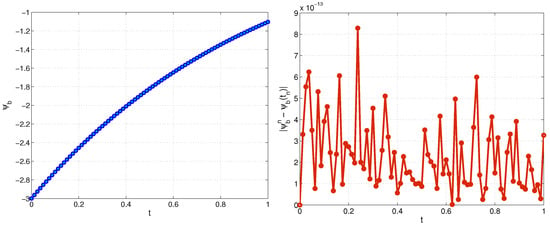
Figure 4.
Genuchten model. Exact and restored left boundary (left) and the corresponding absolute difference (right) for , , Example 1.
Example 2 (1D inverse problem: noisy data).
We repeat the same computations as in Example 1, but with perturbed measurements , , generated from numerical solution of the direct problem (31), by adding noise
where ε is the noise level and is a random function, uniformly distributed on the interval . For the test examples, we set and .
We consider exponential model (11) and (15). In Figure 5 and Figure 6, we plot numerical solution of the direct and inverse problems for and , respectively. Figure 7 illustrates the exact and recovered left boundary for and . For these test examples, the average number of iterations are for and for .
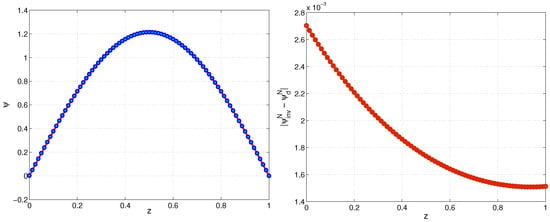
Figure 5.
Exponential model. Numerical solution of the direct and inverse problems, (left) and the corresponding absolute difference (right) at final time for , , Example 2.
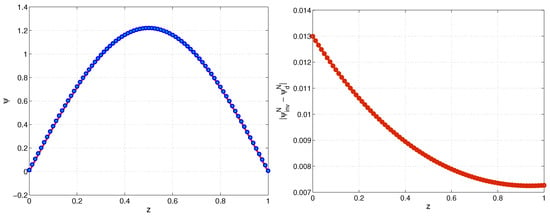
Figure 6.
Exponential model. Numerical solution of the direct and inverse problems, (left) and the corresponding absolute difference (right) at final time for , , Example 2.
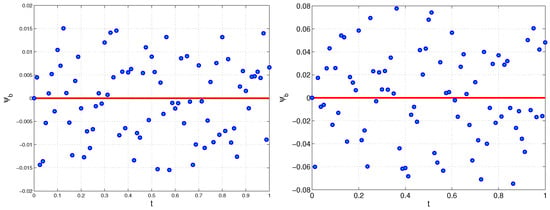
Figure 7.
Exponential model. Exact and restored left boundary for (left) and (right), , , Example 2.
Next, we examine Genuchten model (12)–(14) and (15). In Figure 8 and Figure 9, we depict numerical solution of the direct and inverse problems for and , respectively. Figure 10 represents the exact and recovered left boundary for and . In the case of , the average number of iterations is , while for it is .
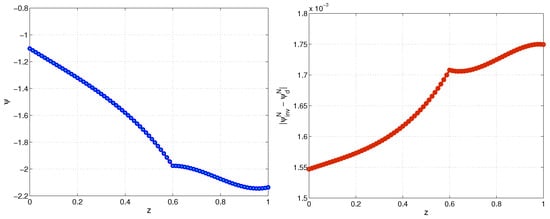
Figure 8.
Genuchten model. Numerical solution of the direct and inverse problems, (left) and the corresponding absolute difference (right) at final time for , , Example 2.
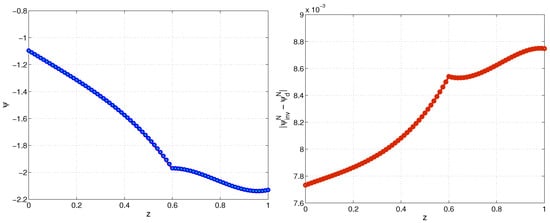
Figure 9.
Genuchten model. Numerical solution of the direct and inverse problems, (left) and the corresponding absolute difference (right) at final time for , , Example 2.
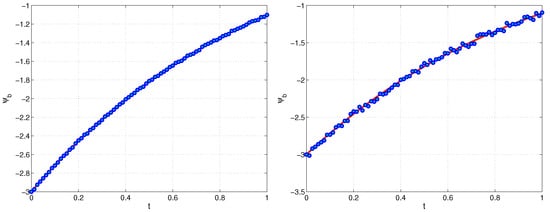
Figure 10.
Genuchten model. Exact and restored left boundary for (left) and (right), , , Example 2.
As can be expected, the bigger deviation leads to bigger error. Nevertheless, it is evident that even for perturbed data for both models, the Algorithm IP-1D recovers successfully the numerical solution of the direct problem with optimal accuracy.
Example 3 (2D inverse problem: exact data).
In Table 3, we give errors and orders of convergence, estimated in maximal discrete norm by (44), average number of iterations, and CPU times (in seconds). As for 1D case, we observe second temporal and spatial order convergence and rapid increasing of the computational time as the mesh become finer, since the large matrix inversion requires much more computational time.

Table 3.
Errors and order of convergence of the solution of the exponential problem, computed by Algorithm IP-2D, Example 3.
In Figure 11, we plot absolute difference between the numerical solution of the inverse problem , obtained by Algorithm IP-2D and direct problem , computed by (41) at final time, and recovered boundary and exact boundary for .
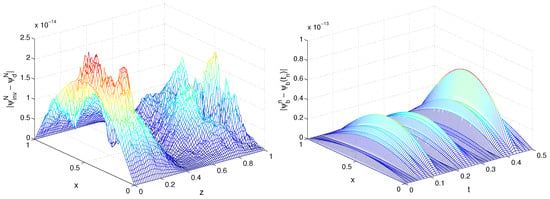
Figure 11.
Exponential model. Absolute difference between recovered solution and numerical solution of the direct problem at final time (left) and recovered boundary and exact boundary (right), , , , Example 3.
Now, we consider Genuchten model (8), (12)–(14) with initial solution and Dirichlet boundary conditions formed from the function at the corresponding boundary nodes. The function is the same as in Example 1.
We compare the recovered solution with the numerical solution of the direct problem. The solution, solved by Algorithm IP-2D, and absolute difference between this solution and numerical solution of the direct problem, are depicted in Figure 12. The average number of iterations is .
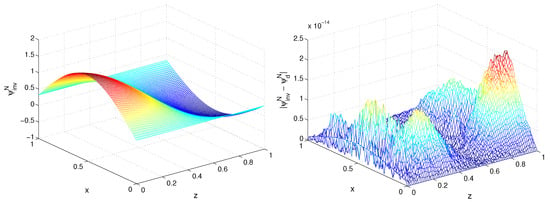
Figure 12.
Genuchten model. Recovered solution (left) and absolute difference between this solution and numerical solution of the direct problem (right), , , , Example 3.
As in 1D case, we conclude that the order of convergence of the numerical solution of the inverse and direct problems is . Moreover, the solution obtained by Algorithm IP-2D recovers exactly the numerical solution of the direct problem.
Example 4 (2D inverse problem: noisy data).
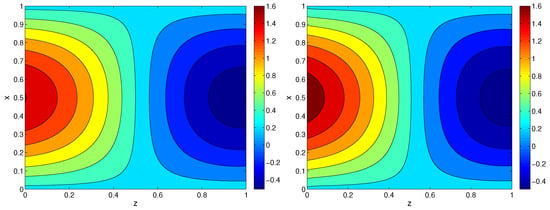
We consider the same Genuchten problem as in Example 3, but for perturbed data generated from numerical solution of the direct problem as in (45) for , , . In Figure 13, we plot numerical solution of the direct problem at final time, computed by (41), and the corresponding recovered solution, obtained by Algorithm IP-2D, for . We observe that the recovering is quite satisfactory. The average number of iterations is .

Figure 13.
Genuchten model. Numerical solution of the direct problem (left) and recovered solution (right) at final time, , , , , Example 4.
The computational simulations, presented in this section to test the developed method, are implemented by MATLAB R2022a on a computer with an Intel® Core i5-7500 Processor, DDR4 2133 MHz.
7. Summary and Conclusions
In this paper, we solved numerically inverse boundary condition problems upon internal measurements for 1D and 2D mixed forms of Richards’ equation. First, time discretization is performed and then at each time layer for the resulting elliptic boundary-value problems we apply quazilinearization. For the numerical solution of the inverse problem, the decomposition of the solution is realized. Numerical examples are presented to illustrate the efficiency of the proposed method.
The computational tests for exponential and Genuchten 1D and 2D problems illustrate that for noisy-free measurements the order of convergence of the restored solution is the same as for the numerical solution of the direct problem, namely second order in space and time for Crank–Nicolson time discretization. Moreover, the numerical solution of the inverse problem recovers exactly the numerical solution of the direct problem and unknown boundary.
In the case of perturbed observations, the proposed algorithms recover successfully the solution of the direct problem and unknown Dirichlet boundary with optimal accuracy.
The developed approach is stable and reaches satisfactory and relevant precision in a moderate number of iterations.
Our next aim is to develop other numerical methods for solving inverse boundary conditions and source problems for initial boundary values problems for Richards’ equation.
Author Contributions
Conceptualization, M.N.K. and L.G.V.; methodology, M.N.K. and L.G.V.; investigation, M.N.K. and L.G.V.; resources, M.N.K. and L.G.V.; writing—original draft preparation, M.N.K. and L.G.V.; writing—review and editing, M.N.K. and L.G.V.; validation, M.N.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Bulgarian National Science Fund under the Project KP-06-N 62/3 “Numerical methods for inverse problems in evolutionary differential equations with applications to mathematical finance, heat-mass transfer, honeybee population, and environmental pollution”, 2022.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to give special thanks to the anonymous reviewers whose valuable comments and suggestions have significantly improved the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chakib, A.; Johri, M.; Nachaoui, A.; Nachaoui, M. On a numerical approxiamtion of highly non-linear parabolic inverse problem in hydrology. Ann. Univ. Craiova, Math. Comput. Sci. Ser. 2015, 42, 192–201. [Google Scholar]
- Dostert, P.; Efendiev, Y.; Mohanty, B. Efficient uncertainty quantification techniques in inverse problems for Richards’ equation using coarse-scale simulation models. Adv. Water Resour. 2009, 32, 329–339. [Google Scholar] [CrossRef]
- Furtado, I.C.; Bodmann, B.E.J.; Vilhena, M.T. On the construction of a functional solution method for the infiltration in porous media problems. Phys. A Stat. Mech. Its Appl. 2016, 450, 18–29. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Weighted time-semidiscretization quasilinearization method for solving Richards’ equation. Lect. Notes Comput. Sci. 2020, 11958, 123–130. [Google Scholar]
- Popova, Z.; Crevoisier, D.; Mailhol, J.; Ruelle, P. Assessment and simulation of water and nitrogen transfer under furrow irrigation: Application of hydrus 2D model to simulate nitrogen transfer. In Proceedings of the ICID 22nd European Regional Conference 2007, Pavia, Italy, 2–7 September 2007. [Google Scholar] [CrossRef]
- Romashchenko, M.I.; Bohaienko, V.O.; Matiash, T.V.; Kovalchuk, V.P.; Krucheniuk, A.V. Numerical simulation of irrigation scheduling using fractional Richards equation. Irrig. Sci. 2021, 39, 385–396. [Google Scholar] [CrossRef]
- Sun, N.-Z. Inverse Problems in Groundwater Modeling; Springer: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Vocciante, M.; Reverberi, A.P.; Dovì, V.G. Approximate solutionof the inverse Richards’ problem. Appl. Math. Model. 2016, 40, 5364–5376. [Google Scholar] [CrossRef]
- Zadeh, K.S. A mass-conservative switching algorithm for modeling fluid flow in variably saturated porous media. J. Comput. Phys. 2011, 230, 664–679. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Basha, H.A. Multidimensional linearized nonsteady infiltration with prescribed boundary conditions at the soil surface. Water Resour. Res. 1999, 35, 75–93. [Google Scholar] [CrossRef]
- Farthing, M.W.; Ogden, F.L. Numerical solution of Richards’ equation: A review of advances and challenges. Soil Sci. Soc. Am. J. 2017, 81, 1257–1269. [Google Scholar] [CrossRef]
- Misiats, O.; Lipnikov, K. Second-order accurate monotone finite volume scheme for Richards’ equation. J. Comput. Phys. 2013, 239, 123–137. [Google Scholar] [CrossRef]
- Rundell, W.; Yin, H.-M. A parabolic inverse problem with an unknown boundary condition. J. Differ. Equations 1990, 86, 234–242. [Google Scholar] [CrossRef][Green Version]
- Gray, W.G.; Hassanizadeh, S. Paradoxes and realities in unsaturated flow theory. Water Resour. Res. 1991, 27, 1847–1854. [Google Scholar] [CrossRef]
- Miller, C.T.; Dawson, C.N.; Farthing, M.W.; Hou, T.Y.; Huang, J.F.; Kees, C.E.; Kelley, C.T.; Langtangen, H.P. Numerical simulation of water resources problems: Models, methods, and trends. Adv. Water Resour. 2013, 51, 405–437. [Google Scholar] [CrossRef]
- Zha, Y.; Yang, J.; Yin, L.; Zhang, Y.; Zeng, W.; Shi, L. A modified Picard iteration scheme for overcoming numerical difficulties of simulating infiltration into dry soil. J. Hydrol. 2017, 551, 56–69. [Google Scholar] [CrossRef]
- Celia, M.; Boulout, F.; Zarba, R.L. A general mass-conservativ numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Dolejší, V.; Kurazb, M.; Solin, P. Adaptive higher-order space-time discontinuous Galerkin method for the computer simulation of variably-saturated porous media flows. Appl. Math. Model. 2019, 72, 276–305. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. A nested Newton-type algorithm for finite volume methods solving Richards’ equation in mixed form. SIAM J. Sci. Comput. 2010, 32, 2255–2273. [Google Scholar] [CrossRef]
- Fuentes, S.; Trejo-Alonso, J.; Quevedo, A.; Fuentes, C.; Chavez, C. Modeling soil water redistribution under gravity irrigation with the Richards equation. Mathematics 2020, 8, 1581. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Fitted finite volume method for unsaturated flow parabolic problems with space degeneration. In Large-Scale Scientific Computing; Lirkov, I., Margenov, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; Volume 13127, pp. 524–532. [Google Scholar]
- Dussaillant, A.R.; Wu, C.H.; Potter, K.W. Richards Equation Model of a Rain Garden. J. Hydrol. Eng. 2004, 9, 219–225. [Google Scholar] [CrossRef]
- Ni, J.J.; Leung, A.K.; Ng, C.W.W.; Shao, W. Modelling hydro-mechanical reinforcements of plants to slope stability. Comput. Geotech. 2018, 95, 99–109. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.V.; Guglielmi, R. A preliminary model for optimal control of moisture content in unsaturated soils. Comput Geosci. 2023, 27, 1133–1144. [Google Scholar] [CrossRef]
- de O. Milfont, M.; Rocha, E.E.M.; Lima, A.O.N.; Freitas, B.M. Higher soybean production using honeybee and wild pollinators, a sustainable alternative to pesticides and autopollination. Environ. Chem. Lett. 2013, 11, 335–341. [Google Scholar] [CrossRef]
- Beck, J.V.; Arnold, K.J. Parameter Estimation in Engineering and Science; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Bitterlich, S.; Knabner, P. An efficient method for solving an inverce problem for Richards equation. J. Comput. Appl. Math. 2002, 147, 153–173. [Google Scholar] [CrossRef][Green Version]
- Constales, D.; Kačur, J. On the solution of some inverse problems in porous media flow. Acta Math. Univ. Comen. 2001, LXX, 1–13. [Google Scholar]
- Lesnic, D. Inverse Problems with Applications in Science and Engineering; CRC Press: Abingdon, UK, 2021; p. 349. [Google Scholar]
- Marchuk, G.I.; Agoshkov, P.V.; Shutyaev, I.V. Adjoint Equations and Perturbation Algorithms in Nonlinear Problems; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Mao, D.; Yeh, T.-C.J.; Wan, L.; Hsu, K.-C.; Lee, C.-H.; Wen, J.-C. Necessary conditions for inverse modeling of flow through variably saturated porous media. Adv. Water Resour. 2013, 52, 50–61. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Vabishchevich, P.N. Numerical Methods for Solving Inverse Problems in Mathematical Physics; de Gruyter: Berlin, Germany, 2007; p. 438. [Google Scholar]
- Duchateau, P. An inverse problem for the hydraulic properties of porous media. SIAM J. Math. Anal. 1997, 28, 611–632. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical material identification of subsurface flow in unsaturated soil. AIP Conf. Proc. 2021, 2333, 090005. [Google Scholar]
- Sonkar, I.; Kotnoor, H.P.; Sen, S. Estimation of root water uptake and soil hydraulic parameters from root zone soil moisture and deep percolation. Agric. Water Manag. 2019, 222, 38–47. [Google Scholar] [CrossRef]
- Sonkar, I.; Sudesan, S.; Suryanarayana Rao Kotnoor, H.P. Compensated non-linear root water uptake model and identification of soil hydraulic and root water uptake parameters. Irrig. Drain. 2022, 71, 157–174. [Google Scholar] [CrossRef]
- Chen, S.; Mao, X.; Wang, C. A Modified Green-Ampt model and parameter determination for water infiltration in fine-textured soil with coarse interlayer. Water 2019, 11, 787. [Google Scholar] [CrossRef]
- Bouchemella, S.; Ichola, I.A.; Séridi, A. Estimation of the empirical model parameters of unsaturated soils. E3S Web Conf. 2016, 9, 16007. [Google Scholar] [CrossRef]
- Nitcheva, O. Hydrology models approach to estimation of the groundwater recharge: Case study in the Bulgarian Danube watershed. Environ. Earth Sci. J. 2018, 77, 464. [Google Scholar] [CrossRef]
- Cui, M.; Yang, K.; Xu, X.; Wang, S.; Gao, X. A modified Levenberg-Marquardt algorithm for simultaneous estimation of multi-parameters of boundary heat flux by solving transient nonlinear inverse heat conduction problems. Int. J. Heat Mass Transf. 2016, 97, 908–916. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical identification of external boundary conditions for time fractional parabolic equations on disjoint domains. Fractal Fract. 2023, 7, 326. [Google Scholar] [CrossRef]
- Ngnepieba, P.; Desmond, S.; Le Dimet, F.-X. The Newton method in problems of variational data assimilation: Application to an infiltration model. Int. J. Pure Appl. Math. 2011, 69, 15–32. [Google Scholar]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- van Genuchten, M. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Otto, F. L1-contraction and uniquiness for quasilinear elliptic-parabolic equation. J. Differ. Equations 1996, 131, 20–38. [Google Scholar] [CrossRef]
- Evans, L.C. Partial Differential Equations, 2nd ed.; AMS: Providence, RI, USA, 2010. [Google Scholar]
- Gol’dman, N.L. Boundary value problems for a quasilinear parabolic equation with an unknown coefficient. J. Differ. Equations 2019, 266, 4925–4952. [Google Scholar] [CrossRef]
- Bellman, R.; Kalaba, R. Quasilinearization and Nonlinear Boundary-Value Problems; Elsevier Publishing Company: New York, NY, USA, 1965. [Google Scholar]
- Koleva, M.N.; Vulkov, L.G. Two-grid quasilinearization approach to ODEs with applications to model problems in physics and mechanics. Comput. Phys. Commun. 2010, 181, 663–670. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).