Fictitious Point Technique Based on Finite-Difference Method for 2.5D Direct-Current Resistivity Forward Problem
Abstract
1. Introduction
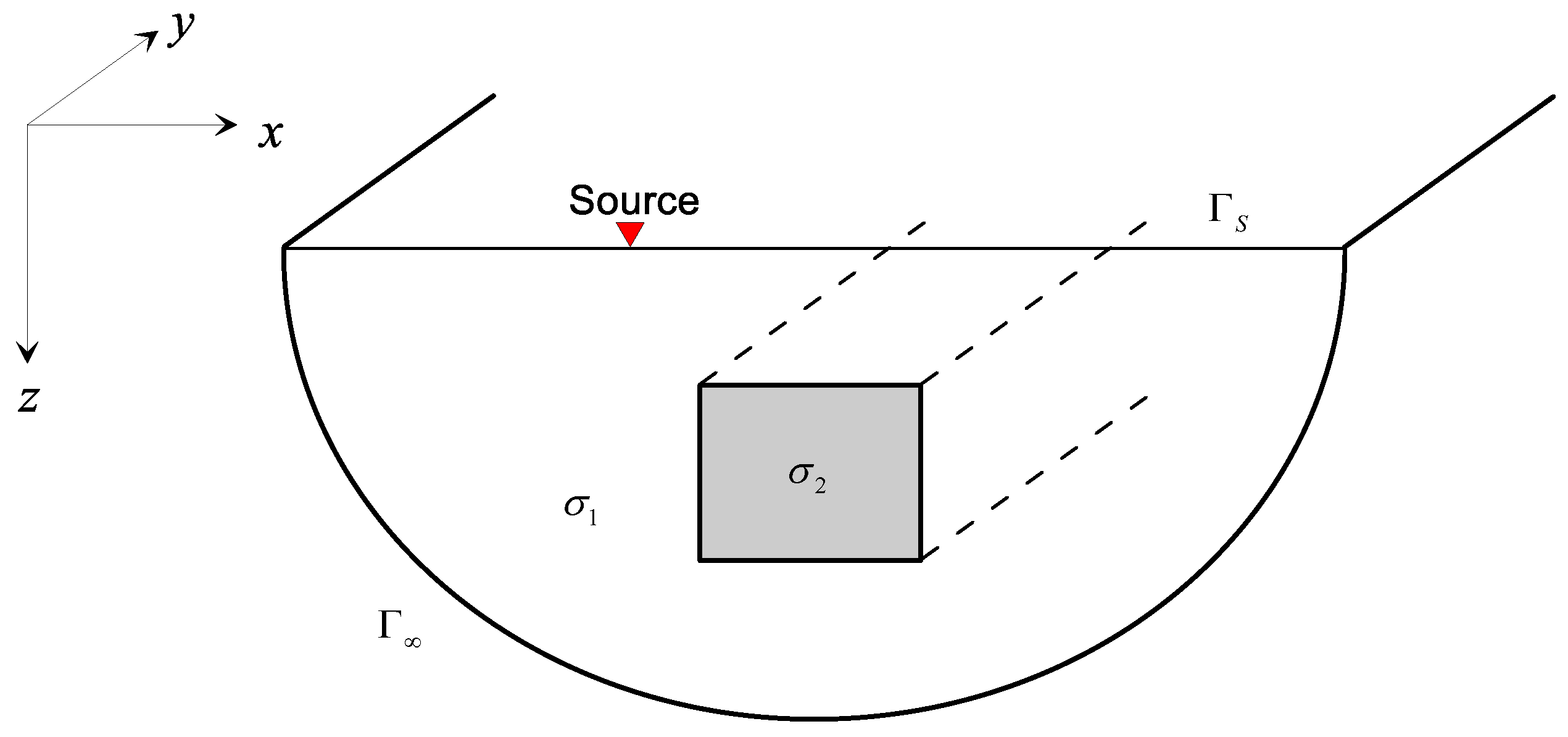
2. Statement of 2.5D Direct-Current Resistivity Forward Problem
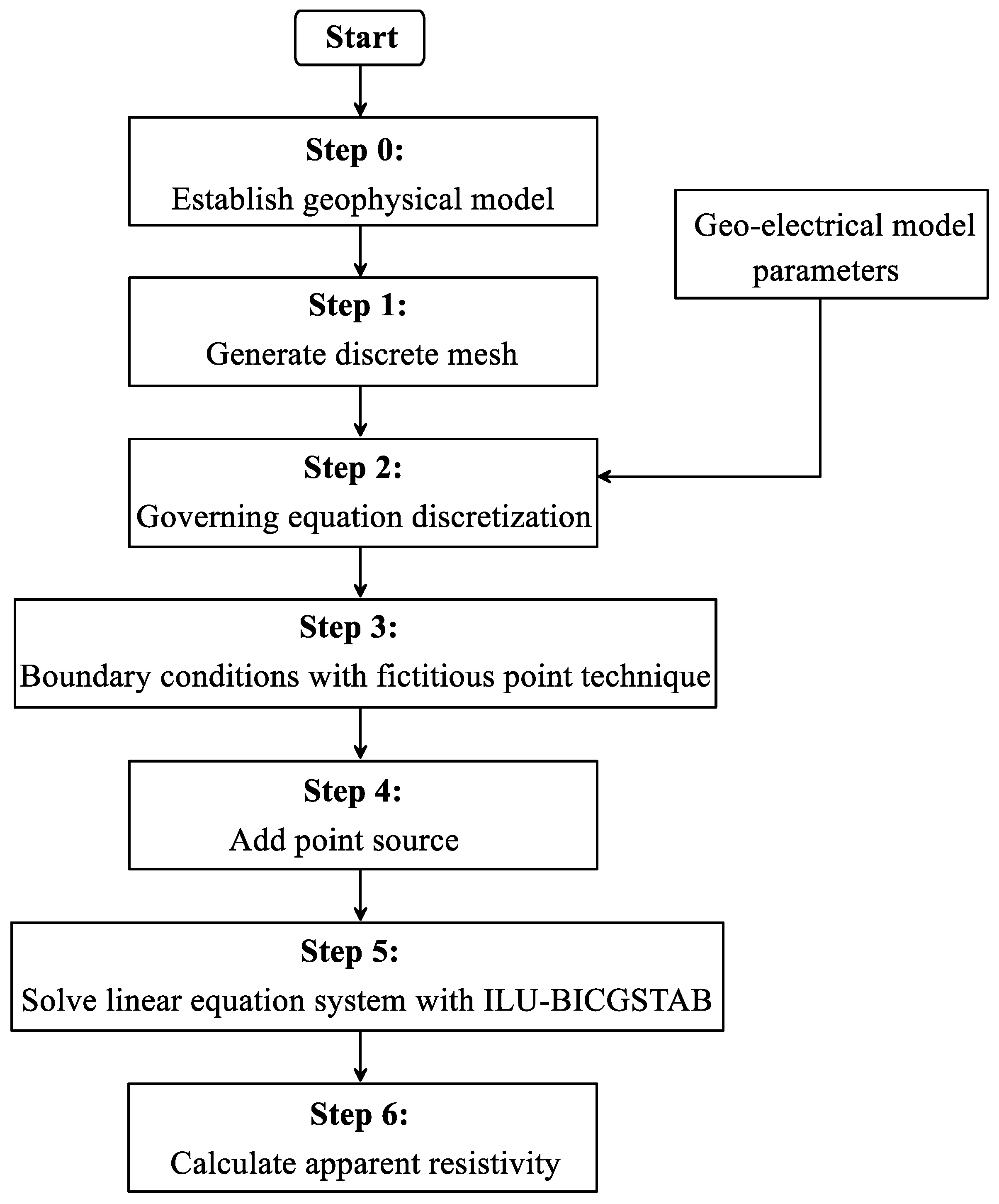
3. Methodology
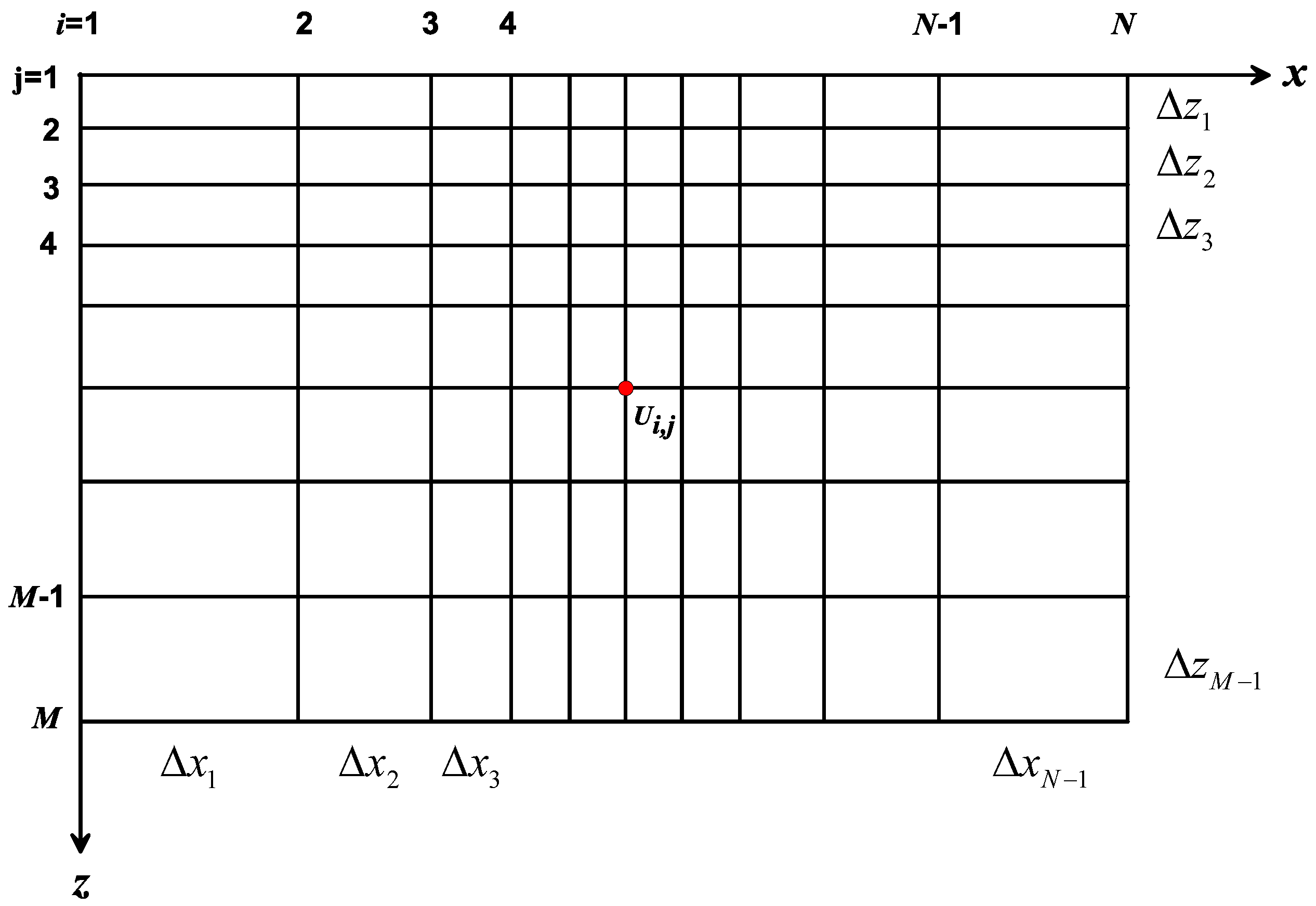
3.1. Discretization of the Helmholtz Governing Equation
3.2. Fictitious Point Technique for Boundary Conditions
3.2.1. Boundary Nodes Located on the Top Edge
3.2.2. Boundary Nodes Located on the Bottom Edge
3.2.3. Boundary Nodes Located on the Left Edge
3.2.4. Boundary Nodes Located on the Right Edge
3.2.5. Corner Nodes with Fictitious Point Technique
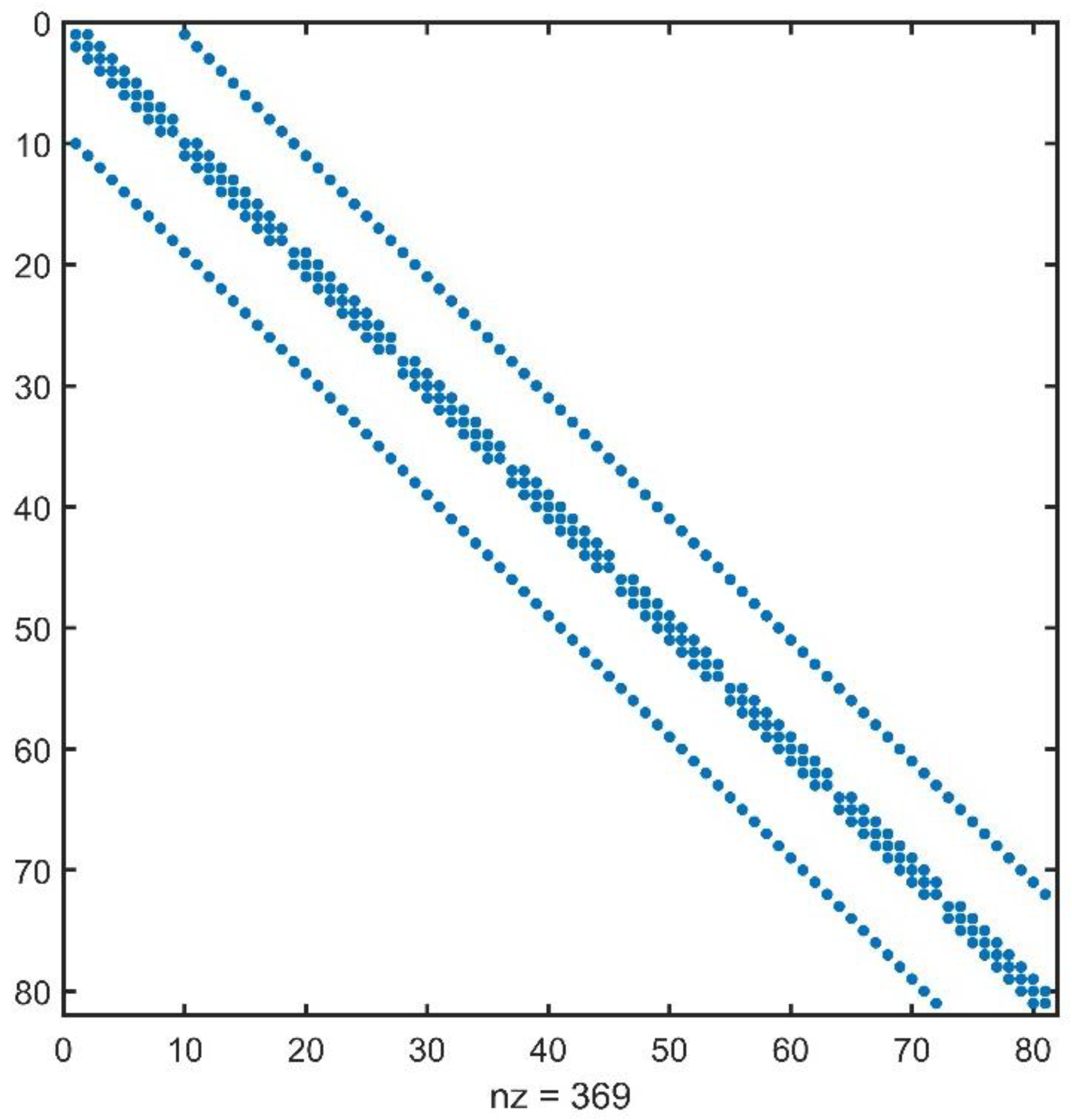
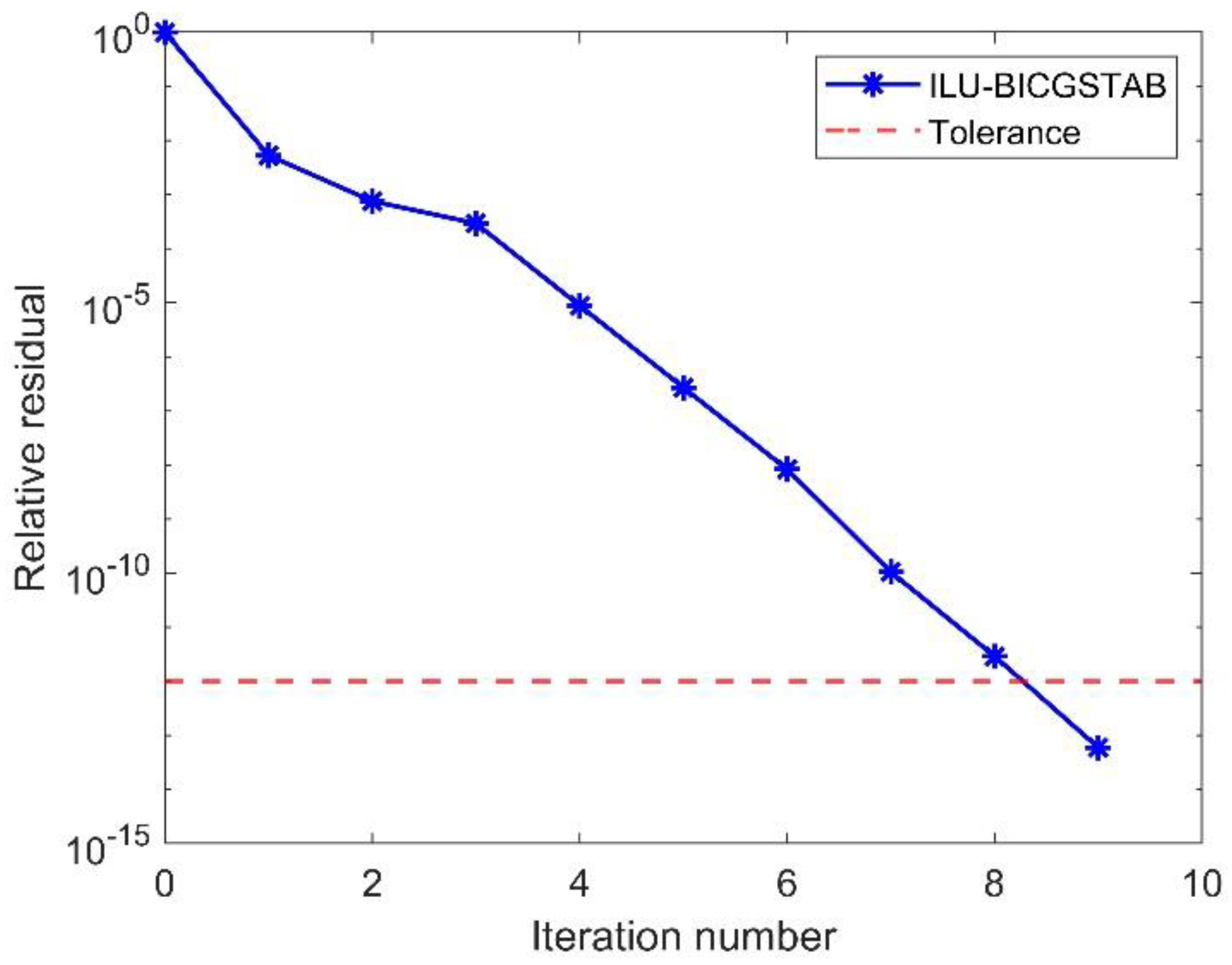
3.3. Solution of the Discrete Forward Equation System
3.4. Calculation of Spatial-Domain Electrical Potential and Apparent Resistivity
4. Numerical Experiments
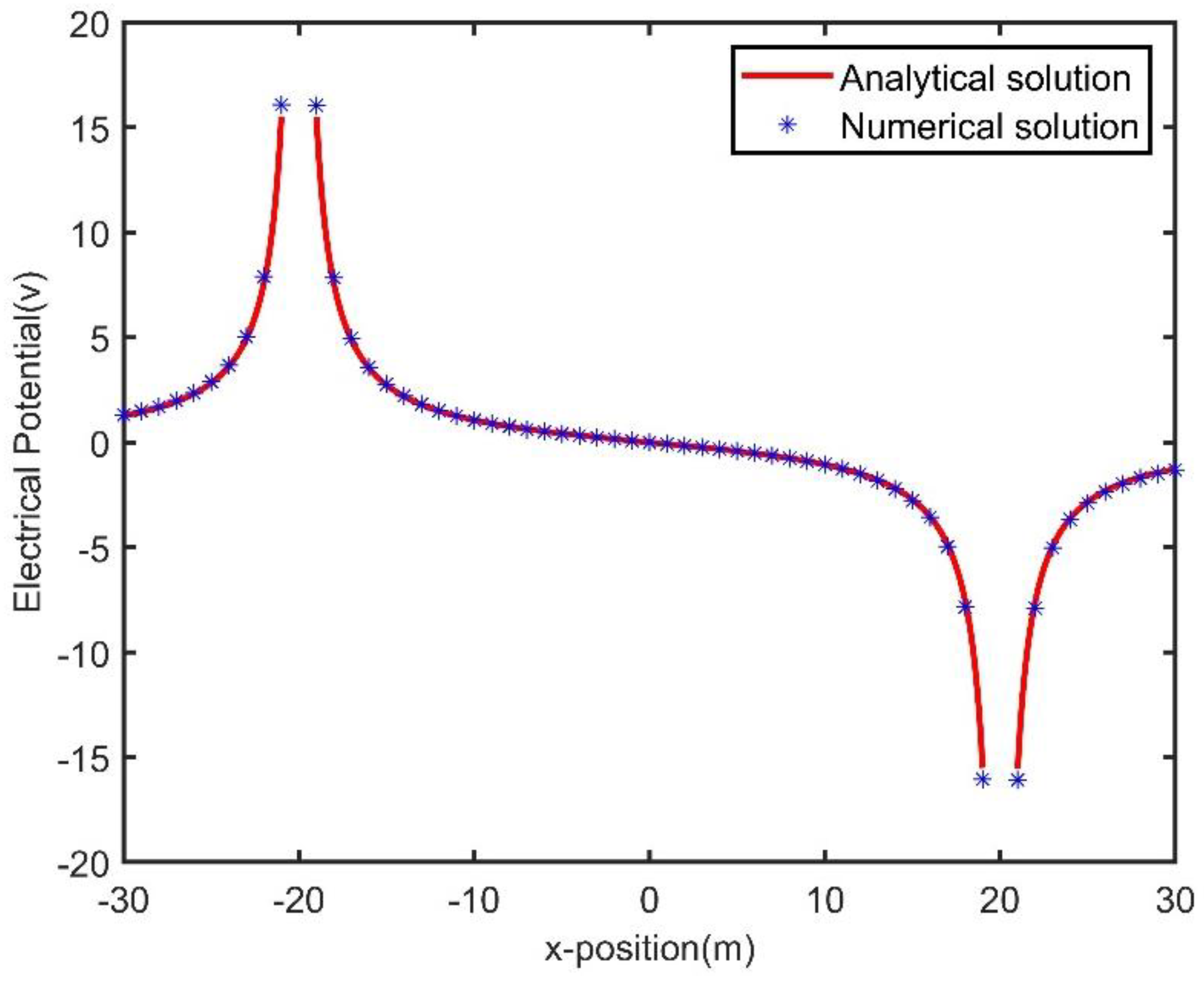
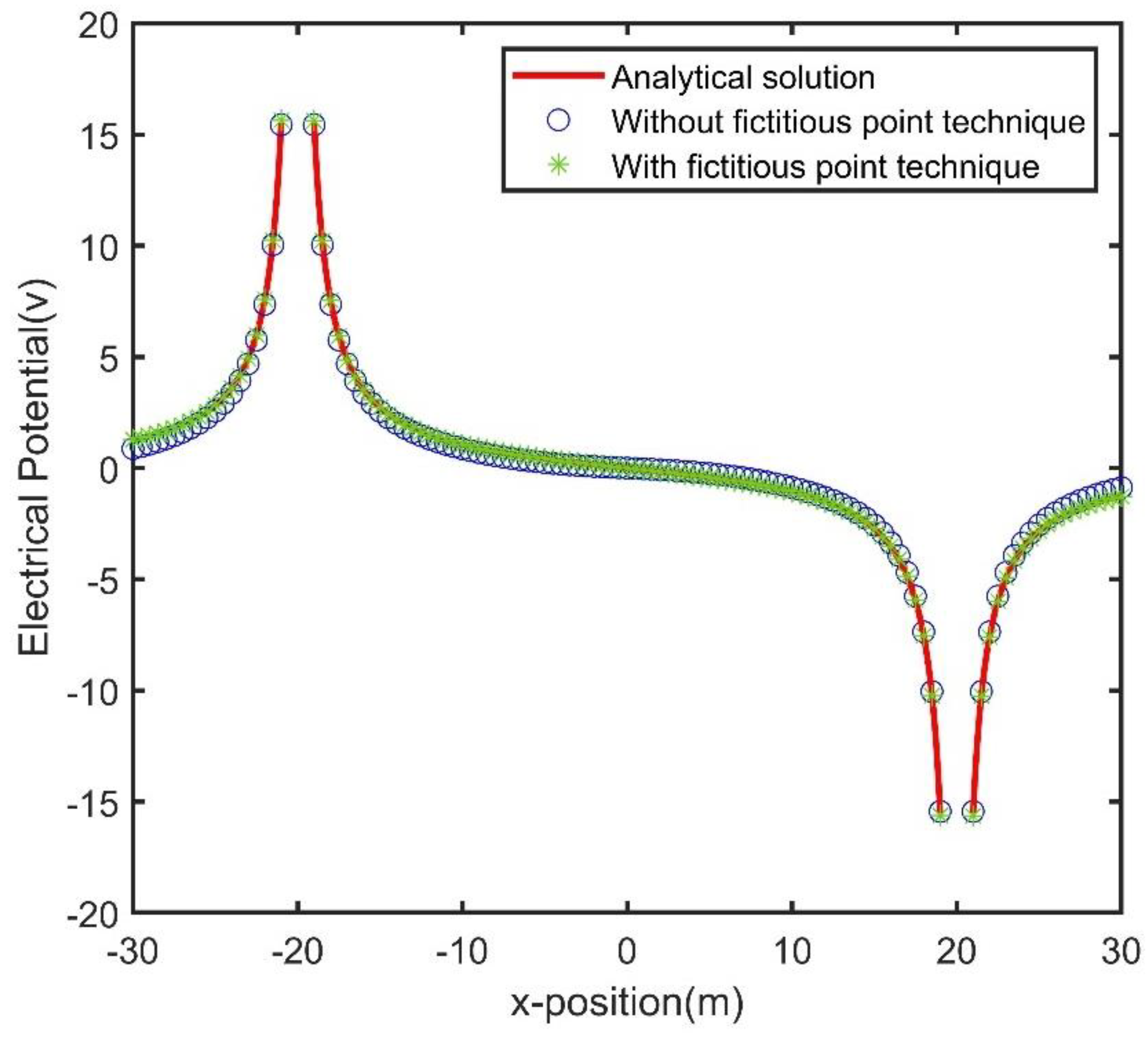
4.1. Benchmark with Homogeneous Half-Space
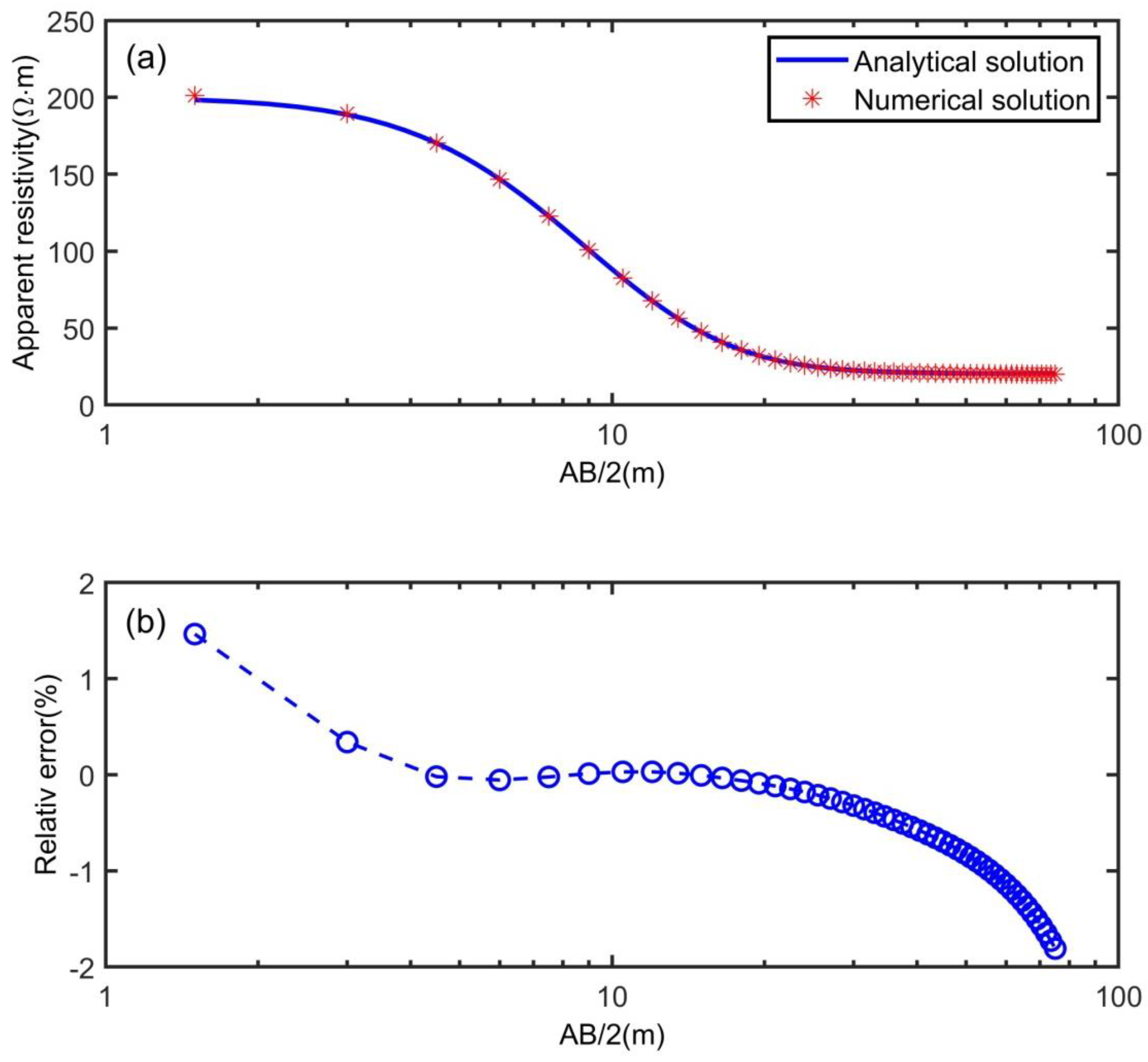
4.2. Two-Layer Conductivity Model
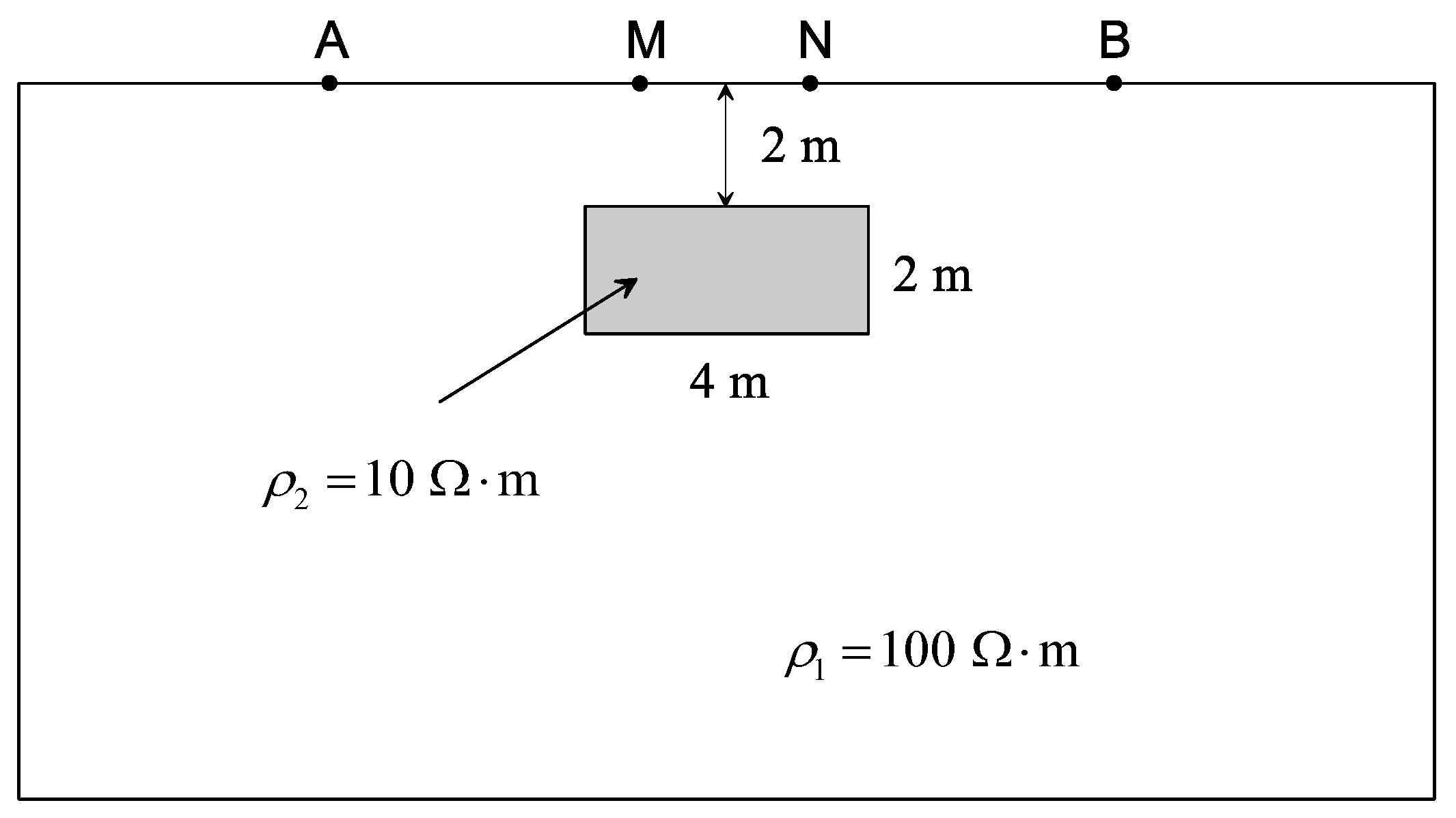
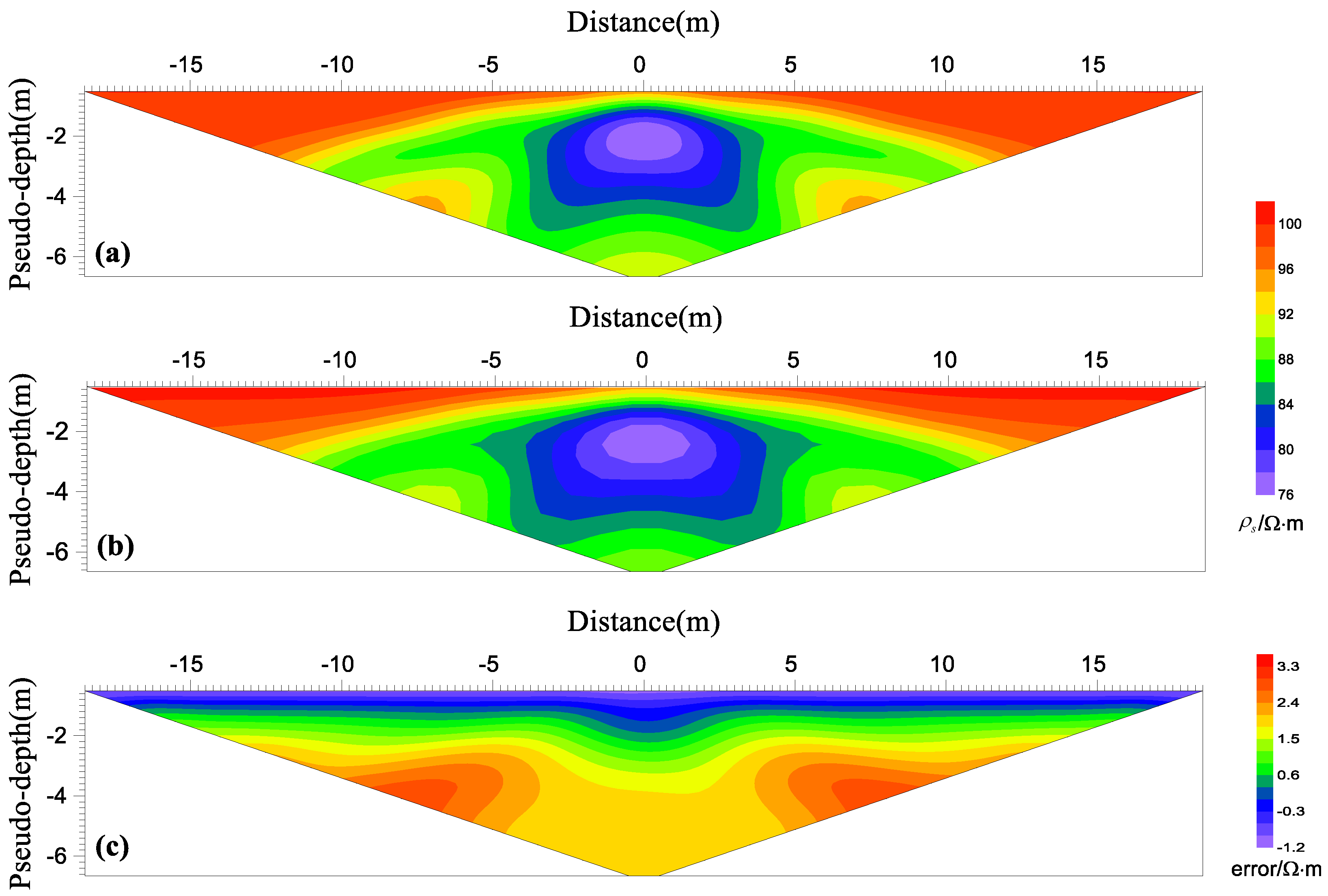
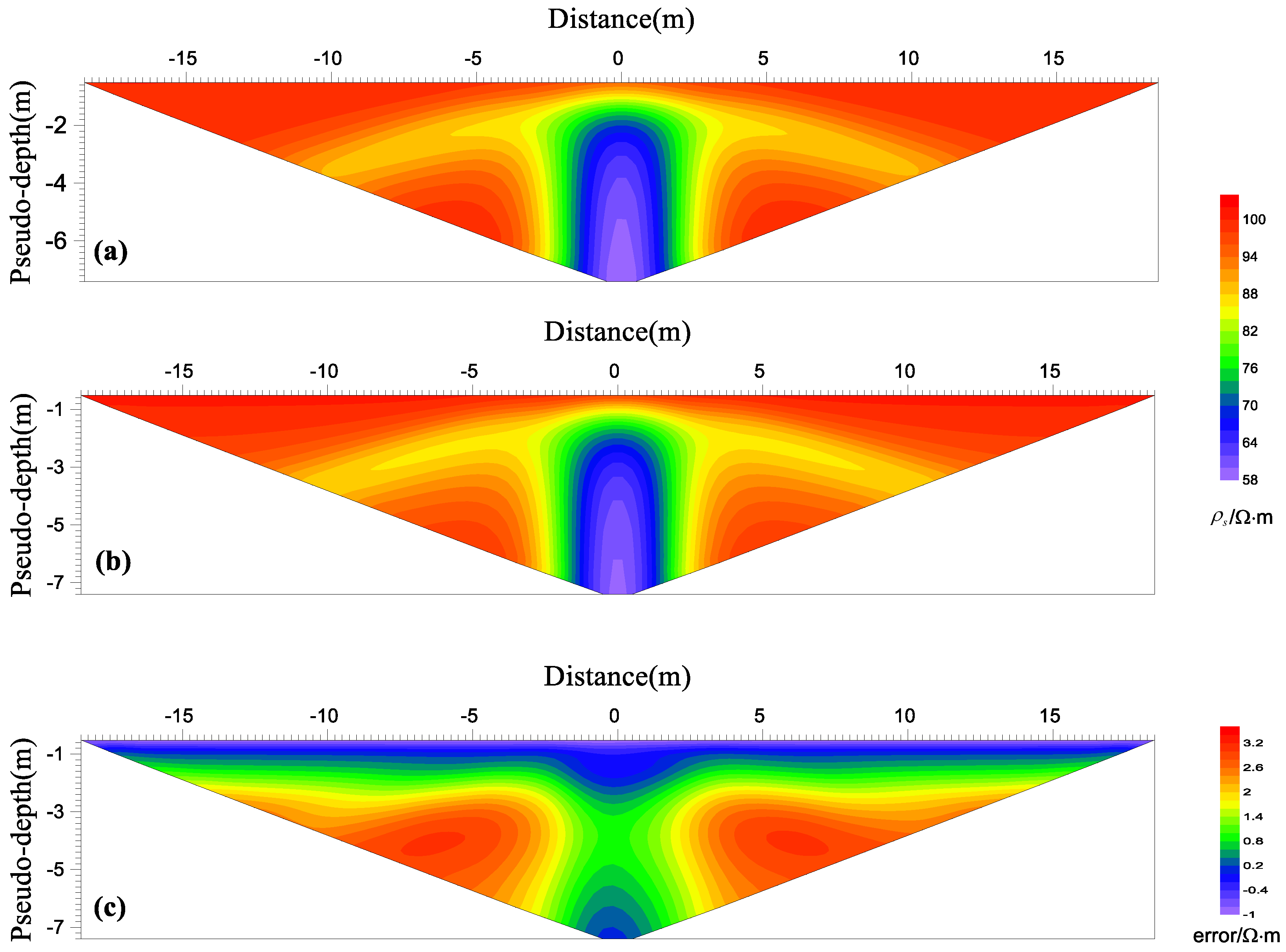
4.3. A Rectangular Conductive Body in Half-Space
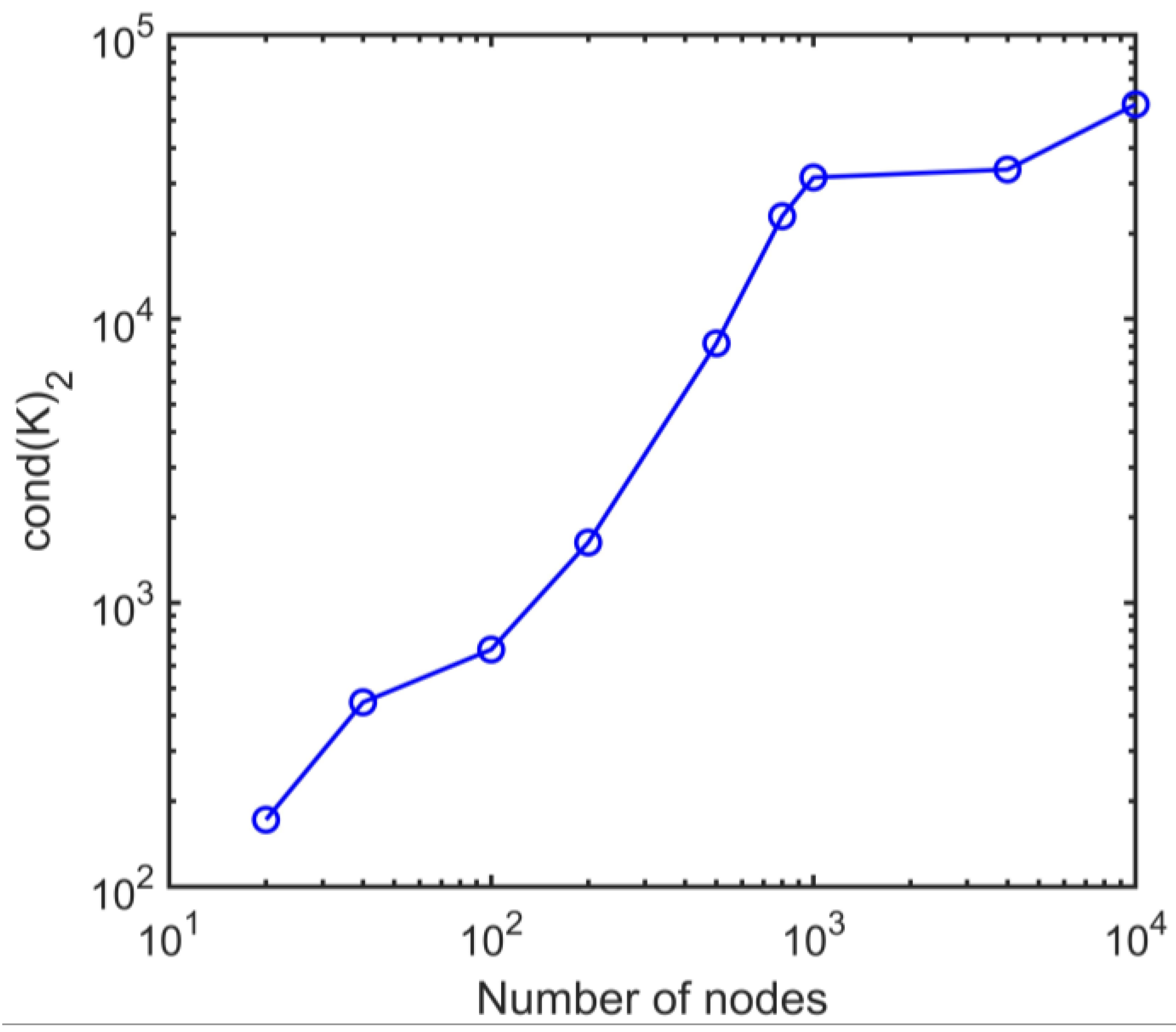
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
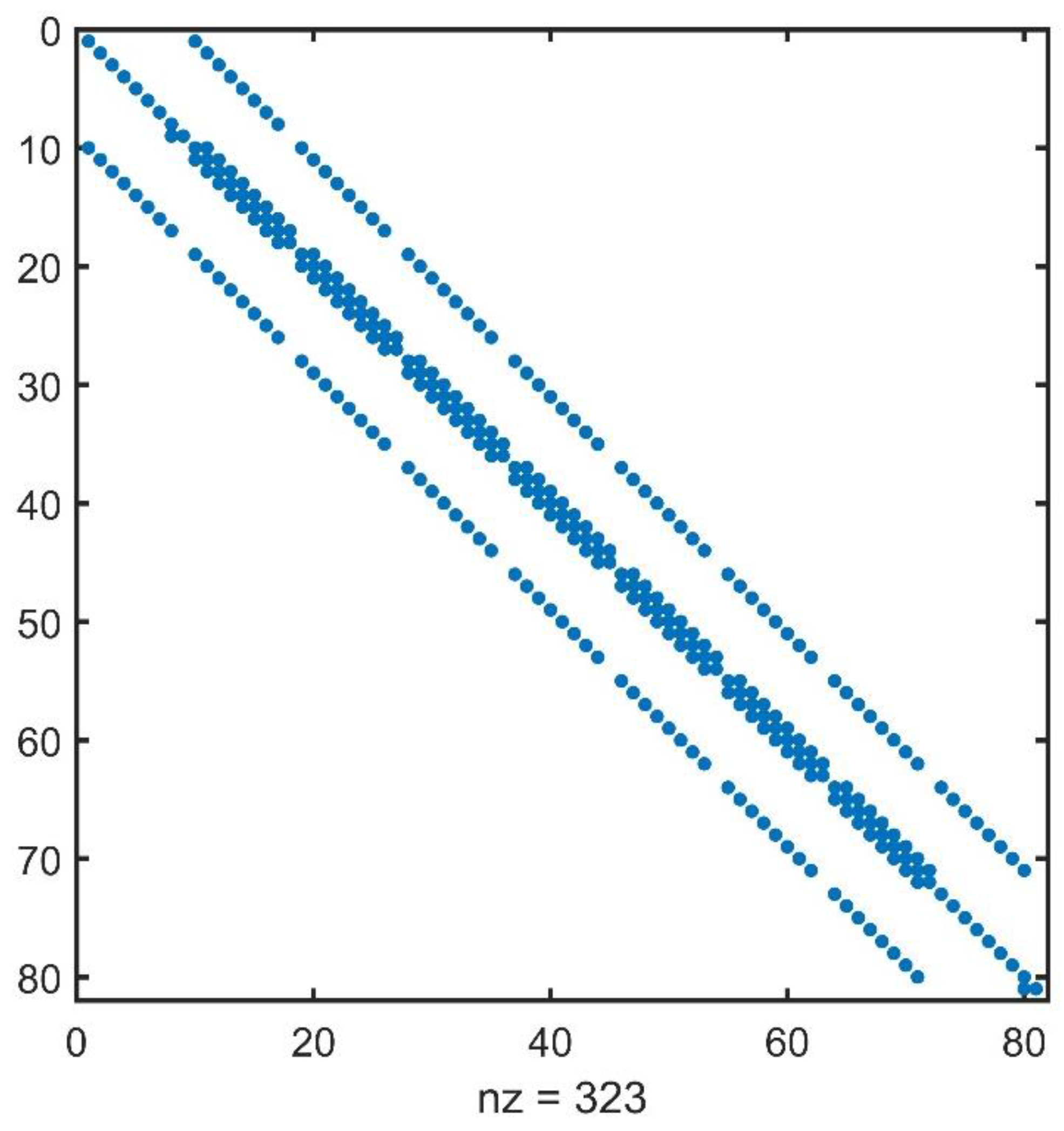
Appendix A. MATLAB Program for 2.5D Direct-Current Resistivity Modeling
Functio n [U]=fdm_25DC_Neumann(x,dx,z,dz,t,I,sigm) %Input arguments %x: x-direction coordinate vector %dx Mesh size in x-direction %z: z-direction coordinate vector %dz: Mesh size in z-direction %t: The locattion of the surce %I: The current value %sigm: The conductivity matrix %Output argument %U: Space-domain electrical Potential dA=(x(t+1)-x(t-1))*dz(1)/4; M=length(x); N=length(z); % Number of rows in the model matrix q(M*N,1)=0; xs=x(t); zs=0; q((t-1)*N+1)=2*I/(2*dA); Ky = [0.00669536185444851, 0.516011331129247,... 0.23888121181836100, 0.129592031420649,... 0.99183940749273000, 0.062370794321097,... 0.35152894553111700, 2.086382045795400,... 0.02821971094872780, 6.95492402823451]; Gy = [0.00990316118235839, 0.175904762136477,... 0.07604192559029110, 0.057858976242153,... 0.44830432193231000, 0.029248474429237,... 0.06787363490235750, 1.145172473298260,... 0.01703221854812900, 7.950172047416480]; A=sparse(M*N,M*N); for k=1:length(Ky) for i=1:N for j=1:M m=(j-1)*N+i; if i~=1 && i~=N && j~=1 && j~=M aW=-2*(sigm(i,j-1)+sigm(i,j))/(dx(j)+dx(j-1))/dx(j-1); aE=-2*(sigm(i,j+1)+sigm(i,j))/(dx(j)+dx(j-1))/dx(j); aN=-2*(sigm(i-1,j)+sigm(i,j))/(dz(i)+dz(i-1))/dz(i-1); aS=-2*(sigm(i+1,j)+sigm(i,j))/(dz(i)+dz(i-1))/dz(i); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aE+aW+aN+aS)+AA; A(m,m)=aP; A(m,m-1)=aN; A(m,m+1)=aS; A(m,m-N)=aW; A(m,m+N)=aE; elseif i==1 && j~=1 && j~=M aW=-2*(sigm(i,j-1)+sigm(i,j))/(dx(j)+dx(j-1))/dx(j-1); aE=-2*(sigm(i,j+1)+sigm(i,j))/(dx(j)+dx(j-1))/dx(j); aS=-2*(sigm(i+1,j)+sigm(i,j))/dz(i)/dz(i); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aE+aW+aS)+AA; A(m,m)=aP; A(m,m+1)=aS; A(m,m-N)=aW; A(m,m+N)=aE; elseif i==N && j~=1 && j~=M aW=-2*(sigm(i,j-1)+sigm(i,j))/(dx(j)+dx(j-1))/dx(j-1); aE=-2*(sigm(i,j+1)+sigm(i,j))/(dx(j)+dx(j-1))/dx(j); aN=-2*(sigm(i-1,j)+sigm(i,j))/dz(i-1)/dz(i-1); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aW+aN+aE)+AA; A(m,m)=aP; A(m,m-1)=aN; A(m,m-N)=aW; A(m,m+N)=aE; elseif j==1 && i~=1 && i~=N aE=-2*(sigm(i,j+1)+sigm(i,j))/dx(j)/dx(j); aN=-2*(sigm(i-1,j)+sigm(i,j))/(dz(i)+dz(i-1))/dz(i-1); aS=-2*(sigm(i+1,j)+sigm(i,j))/(dz(i)+dz(i-1))/dz(i); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aE+aN+aS)+AA; A(m,m)=aP; A(m,m-1)=aN; A(m,m+1)=aS; A(m,m+N)=aE; elseif j==M && i~=1 && i~=N aW=-2*(sigm(i,j-1)+sigm(i,j))/dx(j-1)/dx(j-1); aN=-2*(sigm(i-1,j)+sigm(i,j))/(dz(i)+dz(i-1))/dz(i-1); aS=-2*(sigm(i+1,j)+sigm(i,j))/(dz(i)+dz(i-1))/dz(i); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aW+aN+aS)+AA; A(m,m)=aP; A(m,m-1)=aN; A(m,m+1)=aS; A(m,m-N)=aW; elseif i==N && j==1 aE=-2*(sigm(i,j+1)+sigm(i,j))/dx(j)/dx(j); aN=-2*(sigm(i-1,j)+sigm(i,j))/dz(i-1)/dz(i-1); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aE+aN)+AA; A(m,m)=aP; A(m,m-1)=aN; A(m,m+N)=aE; elseif i==N && j==M aW=-2*(sigm(i,j-1)+sigm(i,j))/dx(j-1)/dx(j-1); aN=-2*(sigm(i-1,j)+sigm(i,j))/dz(i-1)/dz(i-1); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aW+aN)+AA; A(m,m)=aP; A(m,m-1)=aN; A(m,m-N)=aW; elseif i==1 && j==1 aE=-2*(sigm(i,j+1)+sigm(i,j))/dx(j)/dx(j); aS=-2*(sigm(i+1,j)+sigm(i,j))/dz(i)/dz(i); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aE+aS)+AA; A(m,m)=aP; A(m,m+1)=aS; A(m,m+N)=aE; elseif i==1 && j==M aW=-2*(sigm(i,j-1)+sigm(i,j))/dx(j-1)/dx(j-1); aS=-2*(sigm(i+1,j)+sigm(i,j))/dz(i)/dz(i); AA= 2*Ky(k)^2*sigm(i,j); aP=-(aW+aS)+AA; A(m,m)=aP; A(m,m+1)=aS; A(m,m-N)=aW; end end end [L,U] = ilu(A); [VV(:,k),fl1,rr1,it1,rv1] = bicgstab(A,q,1e-10,20,L,U); V(:,:,k) = reshape(VV(:,k),N,M); end U=zeros(N,M); for k=1:length(Gy) U=U+V(:,:,k)*Gy(k); end
Appendix B. Mathematical Expressions of the Electrical Potential in Homogenous Half-Space
Appendix C. Apparent Resistivity Formula of Two-Layer Resistivity Model
References
- Mosaad, A.H.; Farag, M.M.; Wei, Q.; Fahad, A.; Mohamed, S.A.; Hussein, A.S. Integration of electrical resistivity tomography and induced polarization for characterization and mapping of (Pb-Zn-Ag) sulfide deposits. Minerals 2023, 13, 986. [Google Scholar] [CrossRef]
- Mitchell, M.A.; Oldenburg, D.W. Using DC resistivity ring array surveys to resolve conductive structures around tunnels or mine-workings. J. Appl. Geophys. 2022, 211, 104949. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y.; Ellis, R.G. Inversion of geophysical data over a copper gold porphyry deposit: A case history for Mt. Milligan. Geophysics 1997, 62, 1419–1431. [Google Scholar] [CrossRef]
- Chambers, J.C.; Kuras, O.; Meldrum, P.I.; Ogilvy, R.D.; Hollands, J. Electrical resistivitytomography applied to geologic, hydrogeologic, and engineering investigations at a former waste-disposal site. Geophysics 2006, 71, 231–239. [Google Scholar] [CrossRef]
- Rucker, D.; Loke, M.H.; Levitt, M.T.; Noonan, G.E. Electrical resistivity characterization of an industrial site using long electrodes. Geophysics 2010, 75, 95–104. [Google Scholar] [CrossRef]
- Kim, J.H.; Tsourlos, P.; Karmis, P.; Vargemezis, G.; Yi, M.J. 3D inversion of irregular gridded 2D electrical resistivity tomography lines: Application to sinkhole mapping at the Island of Corfu (West Greece). Near Surf. Geophys. 2018, 14, 275–285. [Google Scholar] [CrossRef]
- Plank, Z.; Polgar, D. Application of the DC resistivity method in urban geological problems of karstic areas. Near Surf. Geophys. 2019, 17, 547–561. [Google Scholar] [CrossRef]
- Sirota, D.; Shragge, J.; Krahenbuhl, R.; Swidinsky, A.; Yalo, N.; Bradford, J. Development and validation of a low-cost direct current resistivity meter for humanitarian geophysics applications. Geophysics 2022, 87, 1–4. [Google Scholar] [CrossRef]
- Zhou, B.; Greenhalgh, M.; Greenhalgh, S.A. 2.5-D/3-D resistivity modelling in anisotropic media using Gaussian quadrature grids. Geophys. J. Int. 2009, 176, 63–80. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Yang, X. An efficient ADI difference scheme for the nonlocal evolution problem in three-dimensional space. J. Appl. Math. Comput. 2023, 69, 651–674. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, H.; Yang, X. H1-norm error analysis of a robust ADI method on graded mesh for three-dimensional subdiffusion problems. Numer. Algorithms 2023, 94, 1–19. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Tian, Q.; Yang, X.; Zhang, H.; Xu, D. An implicit robust numerical scheme with graded meshes for the modified Burgers model with nonlocal dynamic properties. Comput. Appl. Math. 2023, 42, 246. [Google Scholar] [CrossRef]
- Mufti, I.R. Finite-difference resistivity modeling for arbitrarily shaped two-dimensional structures. Geophysics 1976, 41, 62–78. [Google Scholar] [CrossRef]
- Vachiratienchai, C.; Boonchaisuk, S.; Siripunvaraporn, W. A hybrid finite difference-finite element method to incorporate topography for 2D direct current (DC) resistivity modeling. Phys. Earth Planet. Interiors 2010, 183, 426–434. [Google Scholar] [CrossRef]
- Gernez, S.; Bouchedda, A.; Gloaguen, E.; Paradis, D. AIM4RES, an open-source 2.5D finite difference MATLAB library for anisotropic electrical resistivity modeling. Comput. Geosci. 2020, 135, 104401. [Google Scholar] [CrossRef]
- Jahandari, H.; Lelièvre, P.; Farquharson, C.G. Forward modeling of direct-current resistivity data on unstructured grids using an adaptive mimetic finite-difference method. Geophysics 2023, 88, 123–134. [Google Scholar] [CrossRef]
- Suryavanshi, D.; Dehiya, R. A mimetic finite-difference method for two-dimensional DC resistivity modeling. Math. Geosci. 2023, 55, 1189–1216. [Google Scholar] [CrossRef]
- Zhou, B.; Greenhalgh, S.A. Finite element three-dimensional direct current resistivity modelling: Accuracy and efficiency considerations. Geophys. J. Int. 2001, 145, 679–688. [Google Scholar] [CrossRef]
- Pan, K.J.; Tang, J. 2.5-D and 3-D DC resistivity modelling using an extrapolation cascadic multigrid method. Geophys. J. Int. 2014, 197, 1459–1470. [Google Scholar] [CrossRef]
- Chou, T.K.; Chouteau, M.; Dubé, J.S. Intelligent meshing technique for 2D resistivity inverse problems. Geophysics 2016, 81, 45–56. [Google Scholar] [CrossRef]
- Yan, B.; Li, Y.; Liu, Y. Adaptive finite element modeling of direct current resistivity in 2-D generally anisotropic structures. J. Appl. Geophys. 2016, 130, 169–176. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Qiu, L.; Tang, J. 3D direct current resistivity anisotropic modelling by goal-oriented adaptive finite element methods. Geophys. J. Int. 2018, 212, 76–87. [Google Scholar] [CrossRef]
- Doyoro, Y.G.; Chang, P.Y.; Puntu, J.M.; Puntu, J.M.; Lin, D.J.; Huu, T.V.; Rahmalia, D.A.; Shie, M.S. A review of open software resources in python for electrical resistivity modelling. Geosci. Lett. 2022, 9, 3. [Google Scholar] [CrossRef]
- Pidlisecky, A.; Knight, R. FW2_5D: A MATLAB 2.5-D electrical resistivity modelling code. Comput. Geosci. 2008, 34, 1645–1654. [Google Scholar] [CrossRef]
- Ma, C.; Liu, J.; Liu, H.; Guo, R.; Musa, B.; Cui, Y. 2.5D electric resistivity forward modeling with element-free Galerkin method. J. Appl. Geophys. 2019, 162, 47–57. [Google Scholar] [CrossRef]
- Xu, S.Z.; Zhou, H. Modelling the 2D terrain effect on MT by the boundary-element method. Geophys. Prospect. 1997, 45, 931–943. [Google Scholar] [CrossRef]
- Dey, A.; Morrisson, H.F. Resistivity modeling for arbitrarily shaped three-dimensional structures. Geophysics 1979, 44, 753–780. [Google Scholar] [CrossRef]
- Liu, J.; Liu, P.; Tong, X. Three-dimensional land FD-CSEM forward modeling using edge finite-element method. J. Cent. South Univ. 2018, 25, 131–140. [Google Scholar] [CrossRef]
- Chen, J.; Haber, E.; Oldenburg, D.W. Three-dimensional numerical modelling and inversion of magnetometric resistivity data. Geophys. J. Int. 2002, 149, 679–697. [Google Scholar] [CrossRef]
- Pan, K.; Wang, J.; Hu, S.; Ren, Z.; Cui, T.; Guo, R.; Tang, J. An efficient cascadic multigrid solver for 3-D magnetotelluric forward modelling problems using potentials. Geophys. J. Int. 2022, 230, 1834–1851. [Google Scholar] [CrossRef]
- Xu, S.Z.; Duan, B.C.; Zhang, D.H. Selection of the wavenumbers k using an optimization method for the inverse Fourier transform in 2.5D electrical modeling. Geophys. Prospect. 2000, 48, 789–796. [Google Scholar] [CrossRef]
- Pan, K.; Zhang, Z.; Hu, S.; Ren, Z.; Guo, R.; Tang, J. Three-dimensional forward modelling of gravity field vector and its gradient tensor using the compact difference schemes. Geophys. J. Int. 2021, 224, 1272–1286. [Google Scholar] [CrossRef]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Loke, M.H.; Barker, R.D. Rapid least-squares inversion of apparent resistivity pseudosections by a quasi-Newton method. Geophys. Prospect. 1996, 44, 131–152. [Google Scholar] [CrossRef]

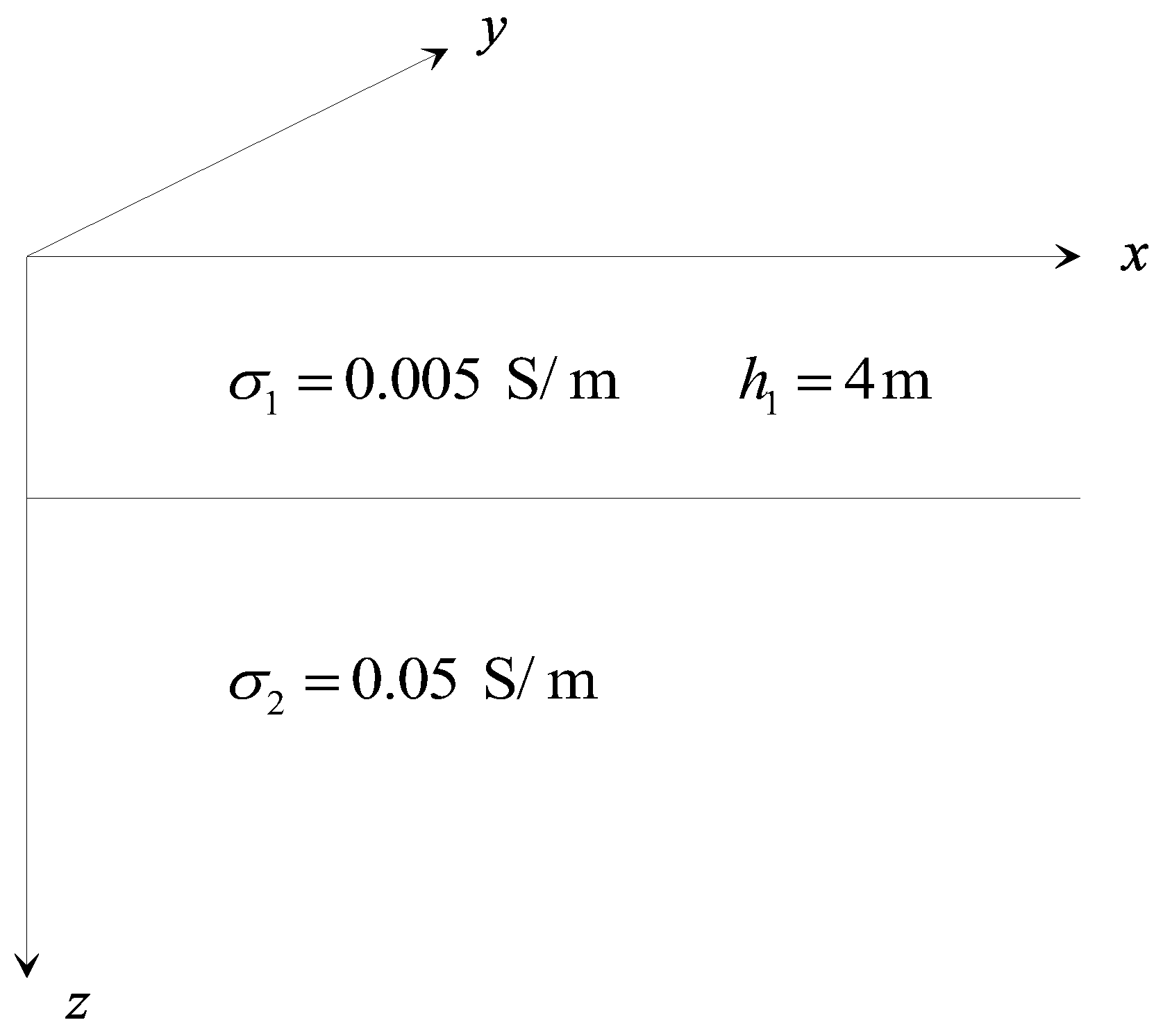
| i | λi | gi |
|---|---|---|
| 1 | 0.0066954 | 0.0099032 |
| 2 | 0.5160113 | 0.1759048 |
| 3 | 0.2388812 | 0.0760419 |
| 4 | 0.1295920 | 0.0578590 |
| 5 | 0.9918394 | 0.4483043 |
| 6 | 0.0623708 | 0.0292485 |
| 7 | 0.3515289 | 0.0678736 |
| 8 | 2.0863820 | 1.1451725 |
| 9 | 0.0282197 | 0.0170322 |
| 10 | 6.9549240 | 7.9501720 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, X.; Sun, Y. Fictitious Point Technique Based on Finite-Difference Method for 2.5D Direct-Current Resistivity Forward Problem. Mathematics 2024, 12, 269. https://doi.org/10.3390/math12020269
Tong X, Sun Y. Fictitious Point Technique Based on Finite-Difference Method for 2.5D Direct-Current Resistivity Forward Problem. Mathematics. 2024; 12(2):269. https://doi.org/10.3390/math12020269
Chicago/Turabian StyleTong, Xiaozhong, and Ya Sun. 2024. "Fictitious Point Technique Based on Finite-Difference Method for 2.5D Direct-Current Resistivity Forward Problem" Mathematics 12, no. 2: 269. https://doi.org/10.3390/math12020269
APA StyleTong, X., & Sun, Y. (2024). Fictitious Point Technique Based on Finite-Difference Method for 2.5D Direct-Current Resistivity Forward Problem. Mathematics, 12(2), 269. https://doi.org/10.3390/math12020269








