Second-Order Approximate Reflection Coefficient of Thin Interbeds with Vertical Fractures

Abstract

The horizontal fractures in the strata will close in the compaction effect of overlying strata, while the vertical cracks are widely developed, which can be equivalent to HTI (transverse isotropy with a horizontal axis of symmetry) medium. When an S-wave propagates into HTI media, the shear wave will divide into two types of waves: a fast S-wave and slow S-wave. When the strata of HTI are thin and overlapping, called the thin interbeds model, the wave field exhibits complex primary reflections, converted waves, and multiples. We introduce a new second-order approximation of the total reflection coefficient, with the incidence angle lower than the critical angle in thin-interbed HTI media using a recursive algorithm. We verify the effectiveness of the second-order approximation by analyzing the energy of multiples. Comparing the second-order approximate solution that degenerates the HTI medium into isotropic and Kennett’s exact solution, we find that our solution has an accuracy of over 99.9% in any azimuth, with the incidence angle lower than the critical angle under P-wave incidence. However, our solution of the SP wave field is suitable for incidence azimuth angles between 0–75° and 120–180°, with the lowest accuracy occurring at an incidence angle of 25° and a relative error of 6.4%. The approximate solution in the SS wave field has the same applicable range as the SP wave, with the maximum error of 6.3% occurring at the incident angle of 1°. This new second-order approximate formula for the total reflection coefficient of thin interbeds composed of HTI helps us to understand the reflection characteristics of complex thin interbeds. It also lays a theoretical foundation for the development of AVO (Amplitude Versus Offset) analysis and inversion techniques for lithological and stratigraphic oil and gas reservoirs.

1. Introduction

In recent years, with the advancement of lithological stratigraphic oil and gas reservoir development, some terrestrial oil-bearing basins composed of thin layers of sandy mudstone in China have formed thin carbonate interbeds with high-angle fractures. Xie, through the derivation of reflection coefficients for monoclinic media, demonstrated that media with high-angle fractures exhibit complex fast and slow shear-wave wavefields [1]. For the reservoirs with vertical fractures mentioned above, we can simulate them using thin interbeds composed of HTI media. The fractures in the HTI medium are perpendicular to the bedding of the interbeds, which makes the shear wave separate into two waves with perpendicular polarization directions [2,3,4]. The splitting shear waves lead to a more complex wavefield in the thin interbeds, including reflected waves, transmitted waves, interbed multiples, and converted waves, compared to isotropic thin interbeds. This complexity poses challenges in effectively separating interference wavefields in thin layers. Utilizing the traditional Zoeppritz equations to calculate seismic wave reflection coefficients for a single interface may cause a loss of some information regarding internal reflection and transmitted waves within thin layers [5,6,7]. Therefore, reflection coefficients in anisotropic thin interbeds are of great significance for the exploration of lithologic stratigraphic oil–gas reservoirs.

Postma demonstrated that periodic thin interbeds can be equivalent to horizontally isotropic media [8]. Geophysicists generally define thin layers with a thickness of less than one-quarter of a wavelength. The thin interbeds are formed by the overlaying of these single thin layers [9]. By 1962, Backus proposed that the combination of thin interbeds could induce anisotropy based on the foundation of a PTL (Periodic Thin Layer), enriching the theoretical framework provided by Postma [10]. Zhang and He equated the N-thin layer medium to a single-layer anisotropic medium and derived its macroscopic elastic parameters [11]. They analyzed the characteristics of wave velocity changing with the propagation direction in the equivalent anisotropic medium. Carcione provided conditions for periodic thin interbeds that can be equivalent to a horizontally isotropic model with uniform variations. He also explored the dispersion and scattering patterns of the equivalent model [12]. Wang considered the thin interbeds as a VTI (Vertical Transversely Isotropic) layer sandwiched with the target single layer under the assumption of a single layer to be extremely thin. However, the accuracy of this approximation is highly dependent on frequency in the inversion [13,14]. The internal structure of VTI media is shown in Figure 1.

All the above theories consider the entire set of thin interbeds as equivalent to a VTI medium and study the propagation characteristics of wavefields. They do not take into account the transmission losses, multiples, and converted waves within and between thin layers. Simmons and Backus, respectively studied the converted waves inside thin layers and analyzed the role of converted waves in the seismic response of thin layers. It was confirmed that converted waves and multiples contribute to seismic response [15]. Kennett’s recursive algorithm considers the wave field of each layer in a layered isotropic medium when calculating the reflection coefficient [16,17,18,19,20]. Yang and Lu made second-order approximations based on this algorithm, which have the advantages of high accuracy and low computational complexity in isotropic conditions [21]. Zhang derived the reflection coefficients for P-wave incidence in orthorhombic anisotropic media, which is similar to the reflection coefficients for thin interbeds containing vertical fractures [22]. However, it lacks the contribution of interbed multiples to the reflection coefficients. Huang employed the Kennett recursive method to construct thin interbeds composed of VTI (Vertical Transverse Isotropic) media, demonstrating that thin interbeds with VTI media exhibit differences in wavefield responses compared to isotropic thin interbeds [23]. However, this formula is not suitable for the anisotropic thin interbedded reservoirs with closed horizontal fractures and widely developed vertical fractures. We extended the second-order approximate equation of the isotropic single thin-layer reflection coefficients proposed by Yang and Lu to an HTI single thin layer in this paper. Then, we obtained the approximate total reflection coefficient of the HTI thin interbeds using a recursive algorithm. Subsequently, we analyzed the relative error between the HTI thin-layer approximation formula and the exact formula and determined the application range of incident angles and azimuth angles in the approximation results.

Reflection seismic amplitude interpretation techniques (such as AVO techniques) are crucial methods for reservoir seismic prediction. The core of these techniques involves studying the variation in the reflection coefficients of seismic waves at reservoir interfaces with changes in the incident angle [24]. In contemporary oil and gas seismic exploration, the precise description of reservoirs and the prediction of reservoirs with thin interbeds containing fractures pose challenging problems. Reservoirs are typical fractured media, and conducting reservoir seismic prediction research based on the model of wave propagation in fractured thin interbeds media is more in line with the actual morphology of the medium. Approximate reflection coefficients can be used for AVO inversion and forward modeling. AVO inversion is a more rational approach to extracting rock parameters hidden in seismic information. Many seismologists have delved into AVO inversion, typically using approximate expressions for reflection coefficients and estimating rock seismic parameters based on the relationship between amplitude and incident angle in actual seismic traces [25]. For instance, parameters such as density, P-wave velocity, S-wave velocity, or Poisson’s ratio are estimated for lithology analysis or the direct detection of hydrocarbons. The reflection coefficients changing with incident angle can be synthesized into seismic records for AVO forward modeling. By simulating AVO phenomena through model forward modeling, combined with the characteristics of the reservoir in the study area, different AVO features for oil, gas, water, and special lithologies are analyzed. This establishes corresponding AVO detection markers, allowing for the direct identification of lithology and hydrocarbons in actual seismic records. Therefore, forward modeling methods can be used for qualitative reservoir characterization [26]. In summary, the approximate reflection coefficients for thin interbeds are highly meaningful for studying the AVO (Amplitude-Versus-Offset) characteristics of thin interbeds.

2. Methodology and Theory

2.1. Second-Order Approximate Reflection Coefficient of the Isotropic Single Thin Layer

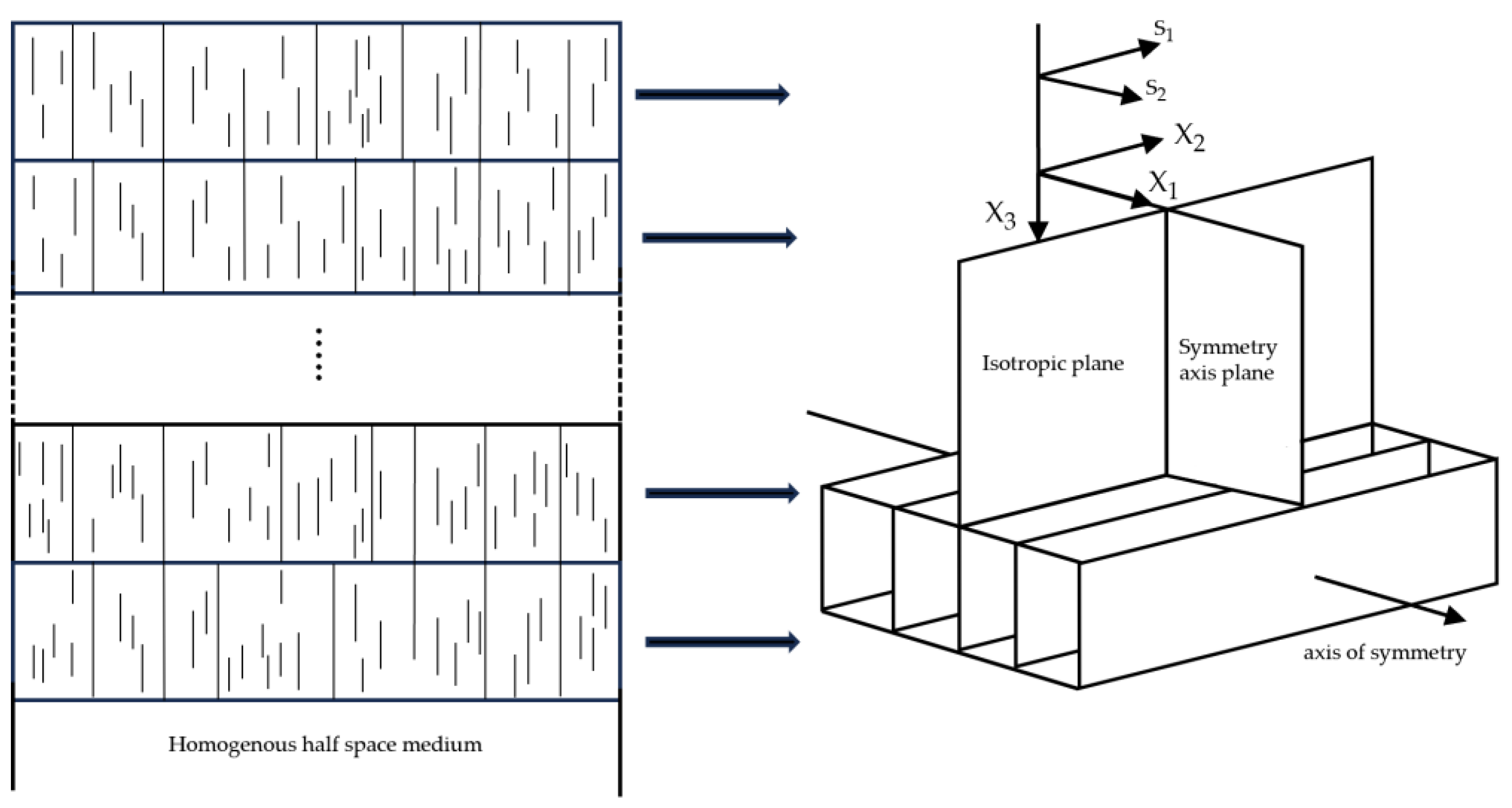
When solving the reflection coefficient of thin interbeds with widely developed vertical fractures, the single thin layer of interbeds cannot be considered an isotropic medium. We replace the single layer with an HTI medium, shown in Figure 2. HTI media can be separated into two symmetry planes based on their relative relationship with the fracture surface. One is perpendicular to the fracture surface, and the other is parallel to the fracture surface [27]. When a shear wave propagates in this anisotropy medium, it will split into two types: the fast shear-wave S1 with the polarization parallel to the fracture surface and the slow shear-wave S2 with the polarization perpendicular to the fracture surface, shown in Figure 2.

Kennett proposed the reflection coefficient of isotropic layered media [17,18], where the reflection coefficient on the top of any layer n in the interbeds medium is

$$R_{\mathrm{Down}}^{\left(n\right)}=r_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{[I-r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}]}^{-1}{t}_{\mathrm{Down}}^{(n)}.$$

(1)

Yang and Lu proposed a method for calculating the reflection coefficient of layered media based on Kennett [21]. Under the assumption of small incidence angles and moderate impedance contrasts (Figure 3), they introduced the reflection coefficient for an isotropic single thin layer in the slowness–frequency domain:

$$R_{\mathrm{Down}}^{\left(n\right)}=r_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}[I+r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}+{(r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)})}^2]t_{\mathrm{Down}}^{(n)},$$

(2)

where I is the unit diagonal matrix of elements, and $r_{\mathrm{Down}}^{\left(n\right)}$ and $t_{\mathrm{Down}}^{\left(n\right)}$ represent a single interface reflection and transmission coefficient matrices on interface n for the downward waves, respectively. They can be represented as

$$I=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],r_{\mathrm{Down}}^{\left(n\right)}={\left[\begin{array}{cc}{r}_{\mathrm{pp}}& r_{\mathrm{ps}}\\ r_{\mathrm{sp}}& r_{\mathrm{ss}}\end{array}\right]}_{\mathrm{Down}}^{(n)},t_{\mathrm{Down}}^{\left(n\right)}={\left[\begin{array}{cc}{t}_{\mathrm{pp}}& t_{\mathrm{ps}}\\ t_{\mathrm{sp}}& t_{\mathrm{ss}}\end{array}\right]}_{\mathrm{Down}}^{(n)},$$

(3)

$r_{\mathrm{Up}}^{\left(n\right)}$ and $t_{\mathrm{Up}}^{\left(n\right)}$ represent the single interface reflection and transmission coefficient matrices on interface n for the upward wave waves, respectively. They can be represented as

$$r_{\mathrm{Up}}^{\left(n\right)}={\left[\begin{array}{cc}{r}_{\mathrm{pp}}& r_{\mathrm{ps}}\\ r_{\mathrm{sp}}& r_{\mathrm{ss}}\end{array}\right]}_{\mathrm{Up}}^{(n)},t_{\mathrm{Up}}^{\left(n\right)}={\left[\begin{array}{cc}{t}_{\mathrm{pp}}& t_{\mathrm{ps}}\\ t_{\mathrm{sp}}& t_{\mathrm{ss}}\end{array}\right]}_{\mathrm{Up}}^{(n)}.$$

(4)

$R_{\mathrm{D}}^{(n+1)}$ is total reflection coefficient matrix on interface n + 1:

$${\tilde{R}}_{\mathrm{D}}^{(n+1)}=E^{(n)}{R}_{\mathrm{D}}^{(n+1)}{E}^{(n)},$$

(5)

$E^{(n)}$ is a phase-shift factor of layer n. It can be represented as

$$E^{\left(n\right)}=\left[\begin{array}{cc}{e}^{(i\omega q_{\mathrm{P} }^{\left(n\right)}{h}^{(n)})}& \\ & e^{(i\omega q_{\mathrm{S}}^{\left(n\right)}{h}^{(n)})}\end{array}\right],$$

(6)

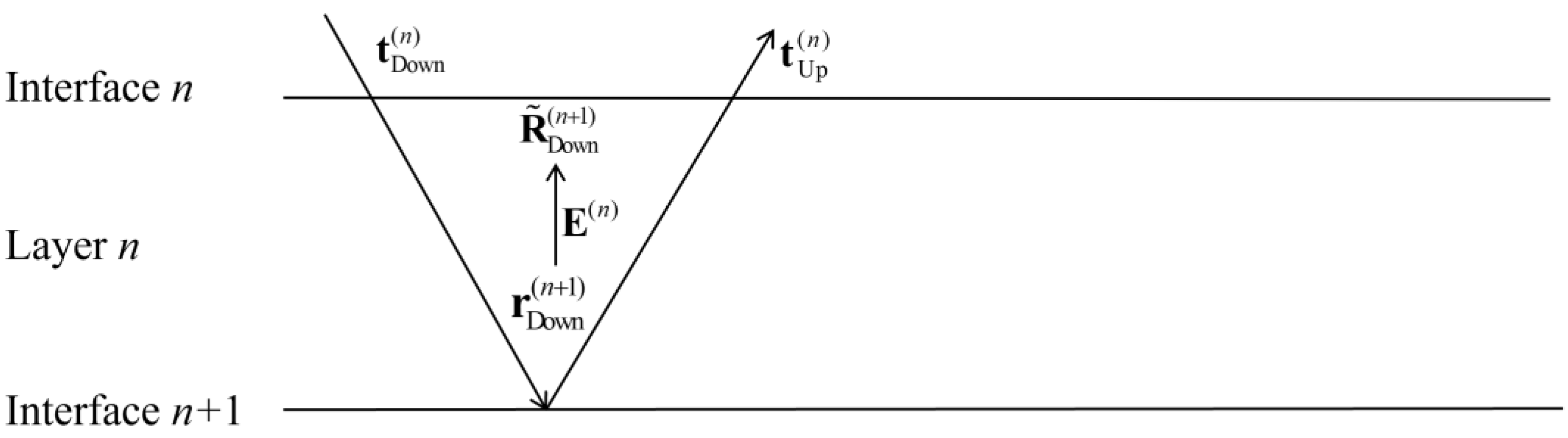
As shown in Figure 4, ${\tilde{R}}_{\mathrm{D}}^{(n+1)}$ is obtained by phase-shifting the total reflection coefficient matrix $R_{\mathrm{D}}^{(n+1)}$ from interface n + 1 to the bottom of interface n.

The symbol ω represents the angular frequency in Formula (6), and h(n) represents the thickness of layer n. The vertical slowness of the P-wave and S-wave for layer n can be represented as $q_{\mathrm{P}}^{\left(n\right)}$ and $q_{\mathrm{S}}^{\left(n\right)}$.

2.2. Reflection Coefficients of a Single Interface for HTI Media

According to Formulas (1)–(4) in the preceding section, it is obvious that if we want to obtain the total reflection coefficient of any single thin layer n, it is necessary to calculate the single interface reflection and transmission coefficients of the thin layer. We then replace the isotropic term in the isotropic approximate reflection coefficient formula with the anisotropic term in Formulas (1) and (2), transforming the isotropic single interface reflection coefficient in Formulas (1) or (2) into the reflection coefficient of HTI medium.

Rokhlin first proposed a precise reflection coefficient and transmission coefficient of the TI medium for P-waves incident from above the interface [28,29]. The incident wave function is

$$U_{\mathrm{Down}}^{\mathrm{P}}=P_{\mathrm{Down}}^{\mathrm{P}}\cdot \exp [ik\left((n_1{x}_1+n_2{x}_2+n_3{x}_3)-V_{\mathrm{Down}}^{\mathrm{P}}t\right)].$$

(7)

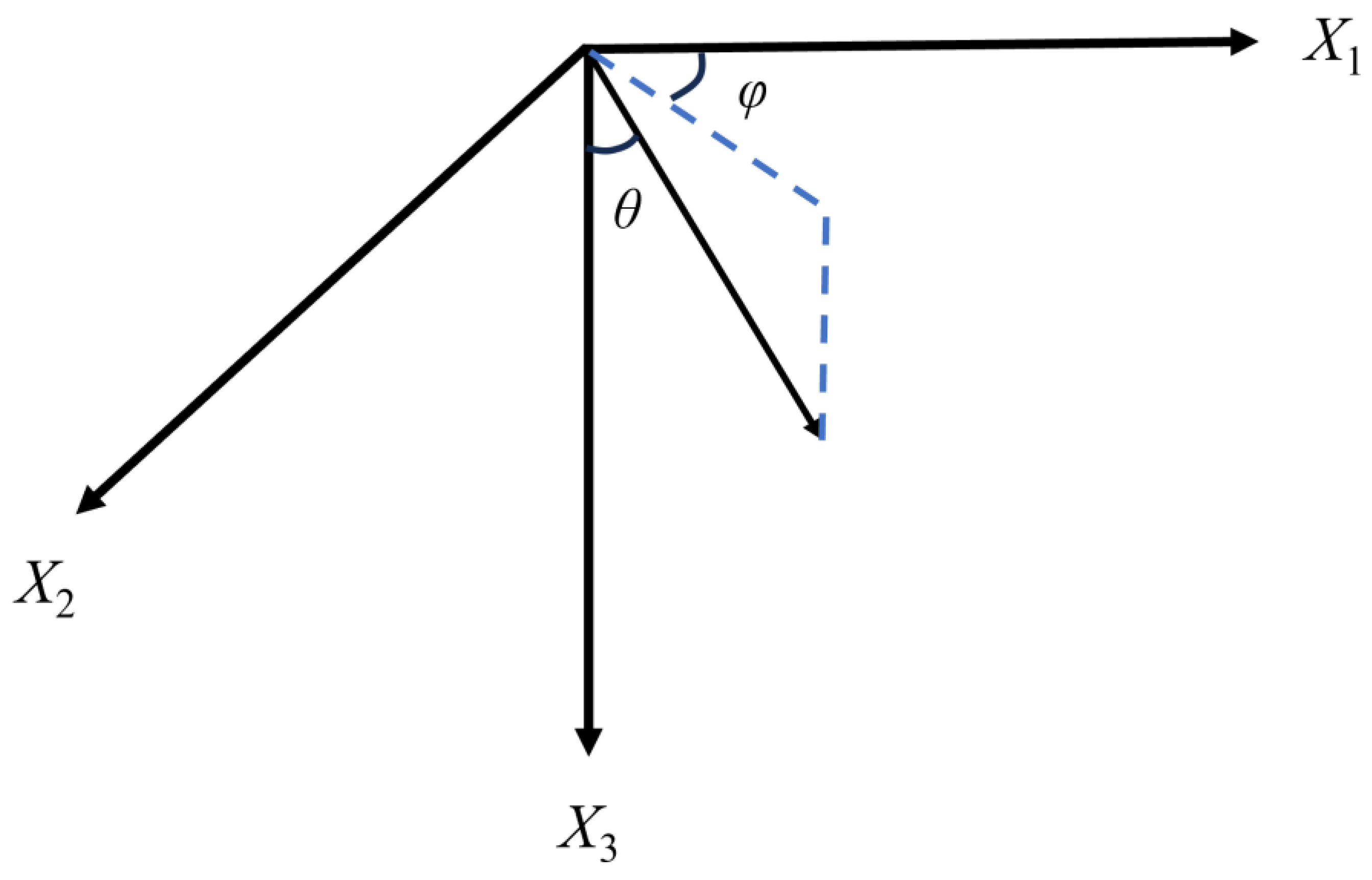
where the symbol $P_{\mathrm{Down}}^{\mathrm{P}}$ represents the polarization vector of the incident P-wave, k is the wave number, n₁, n₂, and n₃ are the three components of the normal vector of the wavefront, $n={(\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )}^{\mathrm{T}}$, and x₁, x₂, x₃, are the three components of the position vector. $V_{\mathrm{Down}}^{\mathrm{P}}$ represents the phase velocity of the P-wave incident.

Based on the boundary conditions of stress and displacement continuity on both sides of the interface, we can conclude

$$\{\begin{array}{l}{P}_{0l}+{\displaystyle \sum _{\alpha =1}^6{R}_{\alpha }{P}_{\alpha l}=0}\\ {\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{13kl}^{\mathrm{I}}{m}_{0k}{P}_{0l}}}+{\displaystyle \sum _{\alpha =1}^3{R}_{\alpha }\left({\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{13kl}^{\mathrm{I}}{m}_{\alpha k}{P}_{\alpha l}}}\right)+}{\displaystyle \sum _{\alpha =4}^6{R}_{\alpha }\left({\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{13kl}^{\mathrm{II}}{m}_{\alpha k}{P}_{\alpha l}}}\right)=0}\\ {\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{23kl}^{\mathrm{I}}{m}_{0k}{P}_{0l}}}+{\displaystyle \sum _{\alpha =1}^3{R}_{\alpha }\left({\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{23kl}^{\mathrm{I}}{m}_{\alpha k}{P}_{\alpha l}}}\right)+}{\displaystyle \sum _{\alpha =4}^6{R}_{\alpha }\left({\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{23kl}^{\mathrm{II}}{m}_{\alpha k}{P}_{\alpha l}}}\right)=0}\\ {\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{33kl}^{\mathrm{I}}{m}_{0k}{P}_{0l}}}+{\displaystyle \sum _{\alpha =1}^3{R}_{\alpha }\left({\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{33kl}^{\mathrm{I}}{m}_{\alpha k}{P}_{\alpha l}}}\right)+}{\displaystyle \sum _{\alpha =4}^6{R}_{\alpha }\left({\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{33kl}^{\mathrm{II}}{m}_{\alpha k}{P}_{\alpha l}}}\right)=0}\end{array}.$$

(8)

When the subscript α = 0, it represents the elastic properties of the incident wave. For α = 1, 2, 3, they, respectively, represent the elastic properties of the reflected P-wave, S1-wave, and S2-wave. Similarly, α = 4, 5, 6 represent the elastic properties of reflected P-wave, S1-wave, and S2-wave, respectively. The superscripts I and II represent the overlying medium and underlying medium at the interface, respectively. The subscript k = 1, 2, 3 represents the components of the slowness vector along the X₁, X₂, and X₃ directions, and m stands for slowness. R represents interface reflection coefficient, and c represent the elements of the HTI elastic stiffness matrix.

We then converted Equation (8) into a matrix form:

$$\begin{gathered} \begin{array}{l}\left[\begin{array}{cccccc}{P}_{11}& P_{21}& P_{31}& -P_{41}& -P_{51}& -P_{61}\\ P_{12}& P_{22}& P_{32}& -P_{42}& -P_{52}& -P_{62}\\ P_{13}& P_{23}& P_{33}& -P_{43}& -P_{53}& -P_{63}\\ I_{41}& I_{42}& I_{43}& I_{44}& I_{45}& I_{46}\\ I_{51}& I_{52}& I_{53}& I_{54}& I_{55}& I_{56}\\ I_{61}& I_{62}& I_{63}& I_{64}& I_{65}& I_{66}\end{array}\right]\left[\begin{array}{c}{R}_1\\ R_2\\ R_3\\ R_4\\ R_5\\ R_6\end{array}\right]=\left[\begin{array}{c}-P_{01}\\ -P_{02}\\ -P_{03}\\ -I_{40}\\ -I_{50}\\ -I_{60}\end{array}\right],\hfill \end{array} \\ \begin{array}{c}\begin{array}{ll}{I}_{ia}={\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{(i-3)3kl}^{\mathrm{I}}{m}_{\alpha k}{P}_{\alpha l}}}& \hspace{1em}(i=4,5,6;\alpha =0,1,2,3;)\end{array}\hfill \\ \begin{array}{ll}{I}_{ia}=-{\displaystyle \sum _{k=1}^3{\displaystyle \sum _{l=1}^3{c}_{(i-3)3kl}^{\mathrm{II}}{m}_{\alpha k}{P}_{\alpha l}}}& (i=4,5,6;\alpha =4,5,6;)\end{array}\hfill \end{array}. \end{gathered}$$

(9)

When the wave function Equation (7) incident is downwards from the interface, it can be solved as

$$\begin{array}{ll}\hfill R_{\mathrm{Down}}^{\mathrm{P}-}& ={\left[\begin{array}{cccccc}{R}_1& R_2& R_3& R_4& R_5& R_6\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Down}}\hfill \\ & ={\left[\begin{array}{cccccc}{r}_{\mathrm{Down}}^{\mathrm{PP}}& r_{\mathrm{Down}}^{\mathrm{PS}1}& r_{\mathrm{Down}}^{\mathrm{PS}2}& t_{\mathrm{Down}}^{\mathrm{PP}}& t_{\mathrm{Down}}^{\mathrm{PS}1}& t_{\mathrm{Down}}^{\mathrm{PS}2}\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Down}}\hfill \end{array}.$$

(10)

However, according to Equations (3) and (4), only the interface reflection coefficient for P-wave downward incidence is not enough. We also need to solve the single-interface reflection coefficient for P-wave upward incidence and S-wave incidence.

From Equations (3) and (4), it can be seen that we not only needed the reflection coefficient of the downward incident P-wave but also the reflection coefficient of the upward incident P-wave and the upward and downward incident S-wave. Therefore, we modified the polarization and phase velocity of the incident wave function (7) to simulate different types of wave incidence. Therefore, based on the calculation approach of Rokhlin P-wave incidence, we extended it to the calculation of the reflection coefficients of various waveforms in HTI media, including upward and downward waves.

When incident P-waves propagate upwards from the bottom of the interface, the incident wave function is

$$U_{\mathrm{Up}}^{\mathrm{P}}=P_{\mathrm{Up}}^{\mathrm{P}}\cdot \exp [ik\left((n_1{x}_1+n_2{x}_2-n_3{x}_3)-V_{\mathrm{Up}}^{\mathrm{P}}t\right)].$$

(11)

Due to the upward incidence of P-waves, the components n₁ and n₂ of the wavefront propagation direction remain unchanged. Adding a negative sign before n₃ represents the upward incidence from below the interface. The polarization vector $P_{\mathrm{Up}}^{\mathrm{P}}$ and phase velocity vector $V_{\mathrm{Up}}^{\mathrm{P}}$ change in the same way as n, so we just added a negative sign before the component on the X₃ axis. The detailed information for calculating the polarization vector and phase velocity of P-wave, S1-wave, and S2 wave in the HTI medium is shown in Appendix A.

The interface reflection and transmission coefficient matrix of the single interface can be written as

$$\begin{array}{ll}\hfill R_{\mathrm{Up}}^{\mathrm{P}-}& ={\left[\begin{array}{cccccc}{R}_1& R_2& R_3& R_4& R_5& R_6\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Up}}\hfill \\ & ={\left[\begin{array}{cccccc}{r}_{\mathrm{Up}}^{\mathrm{PP}}& r_{\mathrm{Up}}^{\mathrm{PS}1}& r_{\mathrm{Up}}^{\mathrm{PS}2}& t_{\mathrm{Up}}^{\mathrm{PP}}& t_{\mathrm{Up}}^{\mathrm{PS}1}& t_{\mathrm{Up}}^{\mathrm{PS}2}\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Up}}\hfill \end{array}.$$

(12)

The wave functions for the upward and downward waves of S1 and S2 wave sources are described as follows:

$$U_{\mathrm{Down}}^{\mathrm{S}1}=P_{{}_{\mathrm{Down}}}^{\mathrm{S}1}\cdot \exp [ik\left((n_1{x}_1+n_2{x}_2+n_3{x}_3)-V_{{}_{\mathrm{Down}}}^{\mathrm{S}1}t\right)].$$

(13)

$$U_{\mathrm{Up}}^{\mathrm{S}1}=P_{\mathrm{Up}}^{\mathrm{S}1}\cdot \exp [ik\left((n_1{x}_1+n_2{x}_2-n_3{x}_3)-V_{\mathrm{Up}}^{\mathrm{S}1}t\right)].$$

(14)

$$U_{\mathrm{Down}}^{\mathrm{S}2}=P_{{}_{\mathrm{Down}}}^{\mathrm{S}2}\cdot \exp [ik\left((n_1{x}_1+n_2{x}_2+n_3{x}_3)-V_{{}_{\mathrm{Down}}}^{\mathrm{S}2}t\right)].$$

(15)

$$U_{\mathrm{Up}}^{\mathrm{S}2}=P_{{}_{\mathrm{Up}}}^{\mathrm{S}2}\cdot \exp [ik\left((n_1{x}_1+n_2{x}_2-n_3{x}_3)-V_{{}_{\mathrm{Up}}}^{\mathrm{S}2}t\right)].$$

(16)

when the waves are incident on the interface, the reflection and transmission coefficients can be obtained through Equation (9):

$$\begin{array}{ll}\hfill R_{\mathrm{Down}}^{\mathrm{S}1-}& ={\left[\begin{array}{cccccc}{R}_1& R_2& R_3& R_4& R_5& R_6\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Down}}\hfill \\ & ={\left[\begin{array}{cccccc}{r}_{\mathrm{Down}}^{\mathrm{S}1\mathrm{P}}& r_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}1}& r_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}2}& t_{\mathrm{Down}}^{\mathrm{S}1\mathrm{P}}& t_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}1}& t_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}2}\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Down}}\hfill \end{array}.$$

(17)

$$\begin{array}{ll}\hfill R_{\mathrm{Up}}^{\mathrm{S}1-}& ={\left[\begin{array}{cccccc}{R}_1& R_2& R_3& R_4& R_5& R_6\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Up}}\hfill \\ & ={\left[\begin{array}{cccccc}{r}_{\mathrm{Up}}^{\mathrm{S}1\mathrm{P}}& r_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}1}& r_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}2}& t_{\mathrm{Up}}^{\mathrm{S}1\mathrm{P}}& t_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}1}& t_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}2}\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Up}}\hfill \end{array}.$$

(18)

$$\begin{array}{ll}\hfill R_{\mathrm{Down}}^{\mathrm{S}2-}& ={\left[\begin{array}{cccccc}{R}_1& R_2& R_3& R_4& R_5& R_6\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Down}}\hfill \\ & ={\left[\begin{array}{cccccc}{r}_{\mathrm{Down}}^{\mathrm{S}2\mathrm{P}}& r_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}1}& r_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}2}& t_{\mathrm{Down}}^{\mathrm{S}2\mathrm{P}}& t_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}1}& t_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}2}\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Down}}\hfill \end{array}.$$

(19)

$$\begin{array}{ll}\hfill R_{\mathrm{Up}}^{\mathrm{S}2-}& ={\left[\begin{array}{cccccc}{R}_1& R_2& R_3& R_4& R_5& R_6\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Up}}\hfill \\ & ={\left[\begin{array}{cccccc}{r}_{\mathrm{Up}}^{\mathrm{S}2\mathrm{P}}& r_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}1}& r_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}2}& t_{\mathrm{Up}}^{\mathrm{S}2\mathrm{P}}& t_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}1}& t_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}2}\end{array}\right]}^{\mathrm{T}}{}_{\mathrm{Up}}\hfill \end{array}.$$

(20)

The interface reflection and transmission coefficient matrices (3) and (4) can be rewritten as follows:

$$\begin{gathered} r_{\mathrm{Down}}^{\left(n\right)}={\left[\begin{array}{ccc}{r}_{\mathrm{Down}}^{\mathrm{PP}}& r_{\mathrm{Down}}^{\mathrm{PS}1}& r_{\mathrm{Down}}^{\mathrm{PS}2}\\ r_{\mathrm{Down}}^{\mathrm{S}1\mathrm{P}}& r_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}1}& r_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}2}\\ r_{\mathrm{Down}}^{\mathrm{S}2\mathrm{P}}& r_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}1}& r_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}2}\end{array}\right]}_{\mathrm{Down}}^{(n)}, r_{\mathrm{Up}}^{\left(n\right)}={\left[\begin{array}{ccc}{r}_{\mathrm{Up}}^{\mathrm{PP}}& r_{\mathrm{Up}}^{\mathrm{PS}1}& r_{\mathrm{Up}}^{\mathrm{PS}2}\\ r_{\mathrm{Up}}^{\mathrm{S}1\mathrm{P}}& r_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}1}& r_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}2}\\ r_{\mathrm{Up}}^{\mathrm{S}2\mathrm{P}}& r_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}1}& r_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}2}\end{array}\right]}_{\mathrm{Up}}^{(n)}, \\ {t}_{\mathrm{Down}}^{\left(n\right)}={\left[\begin{array}{ccc}{t}_{\mathrm{Down}}^{\mathrm{PP}}& t_{\mathrm{Down}}^{\mathrm{PS}1}& t_{\mathrm{Down}}^{\mathrm{PS}2}\\ t_{\mathrm{Down}}^{\mathrm{S}1\mathrm{P}}& t_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}1}& t_{\mathrm{Down}}^{\mathrm{S}1\mathrm{S}2}\\ t_{\mathrm{Down}}^{\mathrm{S}2\mathrm{P}}& t_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}1}& t_{\mathrm{Down}}^{\mathrm{S}2\mathrm{S}2}\end{array}\right]}_{\mathrm{Down}}^{(n)}, t_{\mathrm{Up}}^{\left(n\right)}={\left[\begin{array}{ccc}{t}_{\mathrm{Up}}^{\mathrm{PP}}& t_{\mathrm{Up}}^{\mathrm{PS}1}& t_{\mathrm{Up}}^{\mathrm{PS}2}\\ t_{\mathrm{Up}}^{\mathrm{S}1\mathrm{P}}& t_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}1}& t_{\mathrm{Up}}^{\mathrm{S}1\mathrm{S}2}\\ t_{\mathrm{Up}}^{\mathrm{S}2\mathrm{P}}& t_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}1}& t_{\mathrm{Up}}^{\mathrm{S}2\mathrm{S}2}\end{array}\right]}_{\mathrm{Up}}^{(n)}. \end{gathered}$$

(21)

We modified the single-layer phase shift factor in Formula (6). The detailed information for calculating the phase shift factor of the P-wave, S1-wave, and S2 wave in the HTI medium is shown in Appendix B. The phase shift factor in the thin interbed of HTI medium should consider the influence of shear wave splitting, such as

$$E^{(n)}=\left[\begin{array}{ccc}{e}^{i\omega q_{\mathrm{p}}^{(n)}(\theta )h^{(n)}}& & \\ & e^{i\omega q_{\mathrm{S}1}^{(n)}(\theta )h^{(n)}}& \\ & & e^{i\omega q_{\mathrm{S}2}^{(n)}(\theta )h^{(n)}}\end{array}\right].$$

(22)

where ω represents the angular frequency, h⁽ⁿ⁾ represents the thickness of layer n, and $q_{\mathrm{P}}^{\left(n\right)}({\theta }_{\mathrm{P}})$, $q_{\mathrm{S}1}^{\left(n\right)}({\theta }_{\mathrm{S}1})$, $q_{\mathrm{S}2}^{\left(n\right)}({\theta }_{\mathrm{S}2})$ represent the vertical slowness of Layer n’s P-wave, S1 wave, and S2 wave, respectively. We derived the analytical expression for the vertical slowness of HTI media by solving the Christoffel equation [30]:

$$q_{\mathrm{P}}^{\left(n\right)}({\theta }_{\mathrm{P}})={\left[\begin{array}{c}\frac{1}{2\rho }(c_{33}+c_{66})·({\cos }^2{\theta }_{\mathrm{P}}+{\sin }^2{\theta }_{\mathrm{P}}{\sin }^2\phi )+(c_{11}+c_{66})·{(\sin {\theta }_{\mathrm{P}}·\cos \phi )}^2\hfill \\ +\left(\begin{array}{l}{[(c_{33}-c_{66})·({\cos }^2{\theta }_{\mathrm{P}}+{\sin }^2{\theta }_{\mathrm{P}}·{\sin }^2\phi )-(c_{11}-c_{66})·{(\sin {\theta }_{\mathrm{P}}·\cos \phi )}^2]}^2\hfill \\ +4{(c_{13}+c_{66})}^2·{(\sin {\theta }_{\mathrm{P}}·\cos \phi )}^2·{({\cos }^2{\theta }_{\mathrm{P}}+{\sin }^2{\theta }_{\mathrm{P}}{\sin }^2\phi )}^{1/2}\end{array}\right)\end{array}\right]}^{-1/2}·\begin{array}{c}\end{array}\cos ({\theta }_{\mathrm{P}}).$$

(23)

$$q_{\mathrm{S}1}^{\left(n\right)}({\theta }_{\mathrm{S}1})={\left[\begin{array}{c}\frac{1}{2\rho }(c_{33}+c_{66})·({\cos }^2{\theta }_{\mathrm{S}1}+{\sin }^2{\theta }_{\mathrm{S}1}{\sin }^2\phi )+(c_{11}+c_{66})·{(\sin {\theta }_{\mathrm{S}1}·\cos \phi )}^2\hfill \\ -{\left(\begin{array}{l}{[(c_{33}-c_{66})·({\cos }^2{\theta }_{\mathrm{S}1}+{\sin }^2{\theta }_{\mathrm{S}1}·{\sin }^2\phi )-(c_{11}-c_{66})·{(\sin {\theta }_{\mathrm{S}1}·\cos \phi )}^2]}^2\\ +4{(c_{13}+c_{66})}^2·{(\sin {\theta }_{\mathrm{S}1}·\cos \phi )}^2·({\cos }^2{\theta }_{\mathrm{S}1}+{\sin }^2{\theta }_{\mathrm{S}1}{\sin }^2\phi )\end{array}\right)}^{1/2}\end{array}\right]}^{-1/2}·\begin{array}{c}\end{array}\cos ({\theta }_{\mathrm{S}1}).$$

(24)

$$q_{\mathrm{S}2}^{\left(n\right)}({\theta }_{\mathrm{S}2})={\left[\begin{array}{c}\frac{1}{2\rho }(c_{33}+c_{66})·({\cos }^2{\theta }_{\mathrm{S}2}+{\sin }^2{\theta }_{\mathrm{S}2}{\sin }^2\phi )+(c_{11}+c_{66})·{(\sin {\theta }_{\mathrm{S}2}·\cos \phi )}^2\hfill \\ -{\left(\begin{array}{l}{[(c_{33}-c_{66})·({\cos }^2{\theta }_{\mathrm{S}2}+{\sin }^2{\theta }_{\mathrm{S}2}·{\sin }^2\phi )-(c_{11}-c_{66})·{(\sin {\theta }_{\mathrm{S}2}·\cos \phi )}^2]}^2\\ +4{(c_{13}+c_{66})}^2·{(\sin {\theta }_{\mathrm{S}2}·\cos \phi )}^2·({\cos }^2{\theta }_{\mathrm{S}2}+{\sin }^2{\theta }_{\mathrm{S}2}{\sin }^2\phi )\end{array}\right)}^{1/2}\end{array}\right]}^{-1/2}·\begin{array}{c}\end{array}\cos ({\theta }_{\mathrm{S}2}).$$

(25)

$${\theta }_{\mathrm{P}}=\arcsin \left(\sqrt{\frac{-4c_{33}{c}_{66}{\sin }^2\phi -A_1{\cos }^2\phi -A_2+\sqrt{{\left(4c_{33}{c}_{66}{\sin }^2\phi +A_1{\cos }^2\phi +A_2\right)}^2-16A{c}_{33}{c}_{66}}}{2A}}\right).$$

(26)

$${\theta }_{\mathrm{S}1}=\arcsin \left(\sqrt{\frac{-4c_{33}{c}_{66}{\sin }^2\phi -A_1{\cos }^2\phi -A_2-\sqrt{{\left(4c_{33}{c}_{66}{\sin }^2\phi +A_1{\cos }^2\phi +A_2\right)}^2-16A{c}_{33}{c}_{66}}}{2A}}\right).$$

(27)

$${\theta }_{\mathrm{S}2}=\arcsin \left(\sqrt{\frac{-P^2{c}_{44}}{(P^2{c}_{44}{\sin }^2\phi +P^2{c}_{66}{\cos }^2\phi -P^2{c}_{44}-\rho )}}\right).$$

(28)

$$\begin{array}{c}A=4c_{33}{c}_{66}{\sin }^4\phi +A_1{\sin }^2\phi {\cos }^2\phi +A_2{\sin }^2\phi +4c_{11}{c}_{66}{\cos }^4\phi +A_3{\cos }^2\phi +A_4\hfill \\ A_1=-4{(c_{13})}^2-8c_{66}{c}_{13}+4c_{11}{c}_{33},\hfill \\ A_2=-8c_{33}{c}_{66}-4\rho (c_{33}+c_{66})/{\rho }^2,\hfill \\ A_3=8c_{13}{c}_{66}-4c_{11}{c}_{33}+4{(c_{13})}^2-4\rho (c_{11}+c_{66})/{\rho }^2,\hfill \\ A_4=4(c_{13}{P}^2+\rho )(c_{66}{P}^2)/P^4.\hfill \end{array}$$

where ρ represents the thin layer’s density; c₁₁, c₃₃, c₅₅, and c₁₃ are independent stiffness coefficients, which can be determined through VTI parameters [31,32,33]. V_P0 and V_S0 represent the P- and S-wave velocities of isotropic surfaces, respectively, s ε^(v), δ^(v), and γ^(v) Represent the Thomsen anisotropic parameter.

$$\begin{gathered} c_{11}=\rho (1+2{\epsilon }^{(\mathrm{v})})V_{\mathrm{P}0}^2,c_{33}=\rho V_{\mathrm{P}0}^2,c_{44}=c_{55}=\rho V_{\mathrm{S}0}^2,c_{66}=\rho (1+2{\gamma }^{(\mathrm{v})})V_{\mathrm{S}0}^2, \\ {c}_{12}=\rho V_{\mathrm{P}0}^2[1+2{\epsilon }^{(\mathrm{v})}-2\left(\frac{c_{55}}{c_{33}}\right)](1+2{\gamma }^{(\mathrm{v})})], \\ {c}_{13}=c_{23}=\rho V_{\mathrm{P}0}^2\sqrt{1-\frac{c_{55}}{c_{33}}·\left(1-\frac{c_{55}}{c_{33}}+2{\delta }^{(\mathrm{v})}\right)}-\rho V_{\mathrm{S}0}^2. \end{gathered}$$

(29)

2.3. Second-Order Approximate Total Reflection Coefficient of Thin Interbeds with Vertical Fractures

The total reflection coefficient on the top of any nth thin layer within the thin interbeds can be obtained from Equations (21) and (22). We represent Equation (1) with Formulas (21) and (22) as

$$\begin{array}{ll}\hfill R_{\text{Down}}^{\left(n\right)}=& \left[\begin{array}{ccc}{r}_{\text{Down}}^{\text{PP}}& r_{\text{Down}}^{\text{PS1}}& r_{\text{Down}}^{\text{PS2}}\\ r_{\text{Down}}^{\text{S1P}}& r_{\text{Down}}^{\text{S1S1}}& r_{\text{Down}}^{\text{S1S2}}\\ r_{\text{Down}}^{\text{S2P}}& r_{\text{Down}}^{\text{S2S1}}& r_{\text{Down}}^{\text{S2S2}}\end{array}\right]+\left[\begin{array}{ccc}{t}_{\text{Up}}^{\text{PP}}& t_{\text{Up}}^{\text{PS1}}& t_{\text{Up}}^{\text{PS2}}\\ t_{\text{Up}}^{\text{S1P}}& t_{\text{Up}}^{\text{S1S1}}& t_{\text{Up}}^{\text{S1S2}}\\ t_{\text{Up}}^{\text{S2P}}& t_{\text{Up}}^{\text{S2S1}}& t_{\text{Up}}^{\text{S2S2}}\end{array}\right]\hfill \\ \hfill ·& \left[\begin{array}{ccc}{e}^{i\omega q_{\text{p}}^{(n)}(\theta )h^{(n)}}& & \\ & e^{i\omega q_{\text{S1}}^{(n)}(\theta )h^{(n)}}& \\ & & e^{i\omega q_{\text{S2}}^{(n)}(\theta )h^{(n)}}\end{array}\right]·R_{\text{Down}}^{(n+1)}·\left[\begin{array}{ccc}{e}^{i\omega q_{\text{p}}^{(n)}(\theta )h^{(n)}}& & \\ & e^{i\omega q_{\text{S1}}^{(n)}(\theta )h^{(n)}}& \\ & & e^{i\omega q_{\text{S2}}^{(n)}(\theta )h^{(n)}}\end{array}\right]\hfill \\ & ·{\left(\begin{array}{l}\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]-\left[\begin{array}{ccc}{r}_{\text{Up}}^{\text{PP}}& r_{\text{Up}}^{\text{PS1}}& r_{\text{Up}}^{\text{PS2}}\\ r_{\text{Up}}^{\text{S1P}}& r_{\text{Up}}^{\text{S1S1}}& r_{\text{Up}}^{\text{S1S2}}\\ r_{\text{Up}}^{\text{S2P}}& r_{\text{Up}}^{\text{S2S1}}& r_{\text{Up}}^{\text{S2S2}}\end{array}\right]·\left[\begin{array}{ccc}{e}^{i\omega q_{\text{p}}^{(n)}(\theta )h^{(n)}}& & \\ & e^{i\omega q_{\text{S1}}^{(n)}(\theta )h^{(n)}}& \\ & & e^{i\omega q_{\text{S2}}^{(n)}(\theta )h^{(n)}}\end{array}\right]\\ ·R_{\text{Down}}^{(n+1)}·\left[\begin{array}{ccc}{e}^{i\omega q_{\text{p}}^{(n)}(\theta )h^{(n)}}& & \\ & e^{i\omega q_{\text{S1}}^{(n)}(\theta )h^{(n)}}& \\ & & e^{i\omega q_{\text{S2}}^{(n)}(\theta )h^{(n)}}\end{array}\right]\end{array}\right)}^{-1}·\left[\begin{array}{ccc}{t}_{\text{Down}}^{\text{PP}}& t_{\text{Down}}^{\text{PS1}}& t_{\text{Down}}^{\text{PS2}}\\ t_{\text{Down}}^{\text{S1P}}& t_{\text{Down}}^{\text{S1S1}}& t_{\text{Down}}^{\text{S1S2}}\\ t_{\text{Down}}^{\text{S2P}}& t_{\text{Down}}^{\text{S2S1}}& t_{\text{Down}}^{\text{S2S2}}\end{array}\right]\hfill \end{array}.$$

(30)

In order to explain the physical meaning of each part in the above formula, we first expanded the Taylor series in Formula (1):

$$R_{\mathrm{Down}}^{\left(n\right)}=r_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}[I+{\displaystyle \sum _{n=1}^{\infty }{(r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)})}^m}]t_{\mathrm{Down}}^{(n)}.$$

(31)

The convergence region of the Taylor expansion is $-I<r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}<I$. Based on the provided elastic parameters such as layer medium wave velocity, density, and anisotropic parameters, we can observe that the absolute values of each element in matrices $r_{\mathrm{Up}}^{(n)}$ and ${\tilde{R}}_{\mathrm{Down}}^{(n+1)}$ are all below 1. The determinant of matrix $r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}$ is consistently less than 1. Therefore, replacing ${\left(I-r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}\right)}^{-1}$ with its mth-order Taylor expansion $I+{\displaystyle \sum _{n=1}^{\infty }{(r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)})}^m}$ is reasonable under condition $-I<r_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}<I$.

Equation (31) is the m-order approximation formula; m can take any positive integer.

We consider m as 3 to expand the above equation:

$$\begin{array}{ll}\hfill R_{\text{Down}}^{\left(n\right)}=& r_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}\hfill \\ & +t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}\hfill \end{array}.$$

(32)

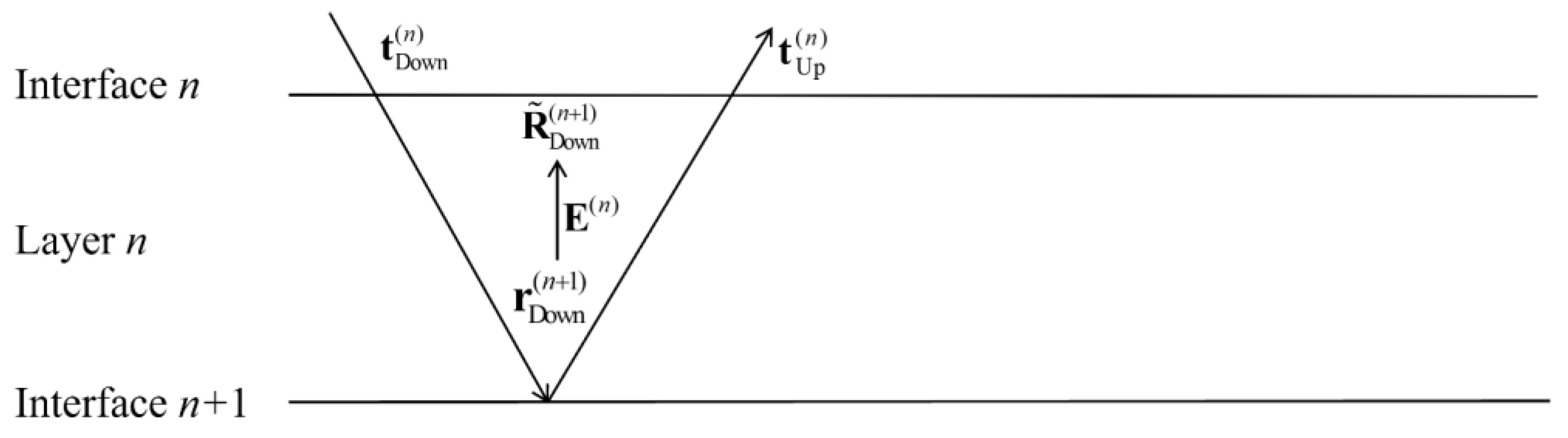
Each term of the third-order approximation formula has a clear physical meaning in Equation (32). Each term in the reflection coefficient represents a different propagation path of seismic waves. The first term $r_{\mathrm{Down}}^{(n)}$ is the reflection coefficient matrix of a reflected wave on the interface n, shown in Figure 5.

In Figure 6, $t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}$ illustrates the reflection coefficient matrix for the incident wave that passes through interface n, and reflect on interface n + 1, and then transmits back through interface n. The above-mentioned waves are called primary waves.

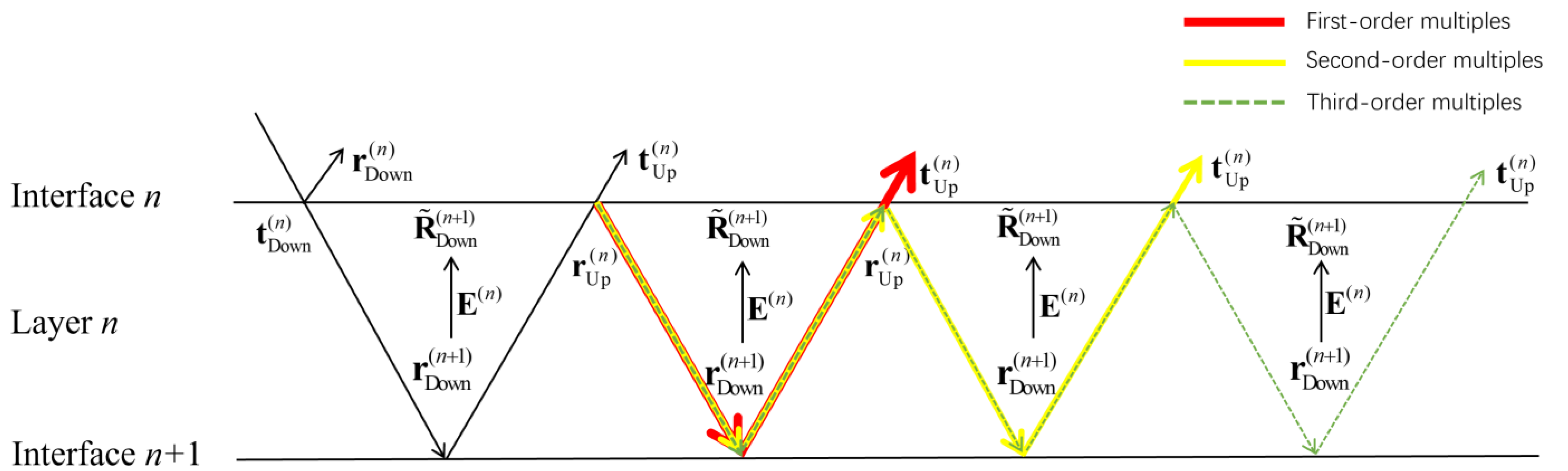
As shown in Figure 7, after completing primary-wave reflection in the thin layer n, the seismic wave does not directly transmit through the interface n. Instead, it continues to reflect within layer n, the reflections of which are called multiples.

• First-order multiples: $t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}$;
• Second-order multiples: $t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}$;
• Third-order multiples: $t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}$.

Combining the coefficient expressions for seismic wave propagation on interface n described in Figure 7, we can obtain all wave fields:

$$\begin{array}{l}{r}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}\\ +t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}\end{array}.$$

(33)

Formula (33) is the sum of the reflection coefficients of various wave fields under third-order multiples. This equation is completely consistent with Formula (32). This indicates that the order of Taylor expansion is consistent with the order of multiples. We can control the order of multiples by changing m.

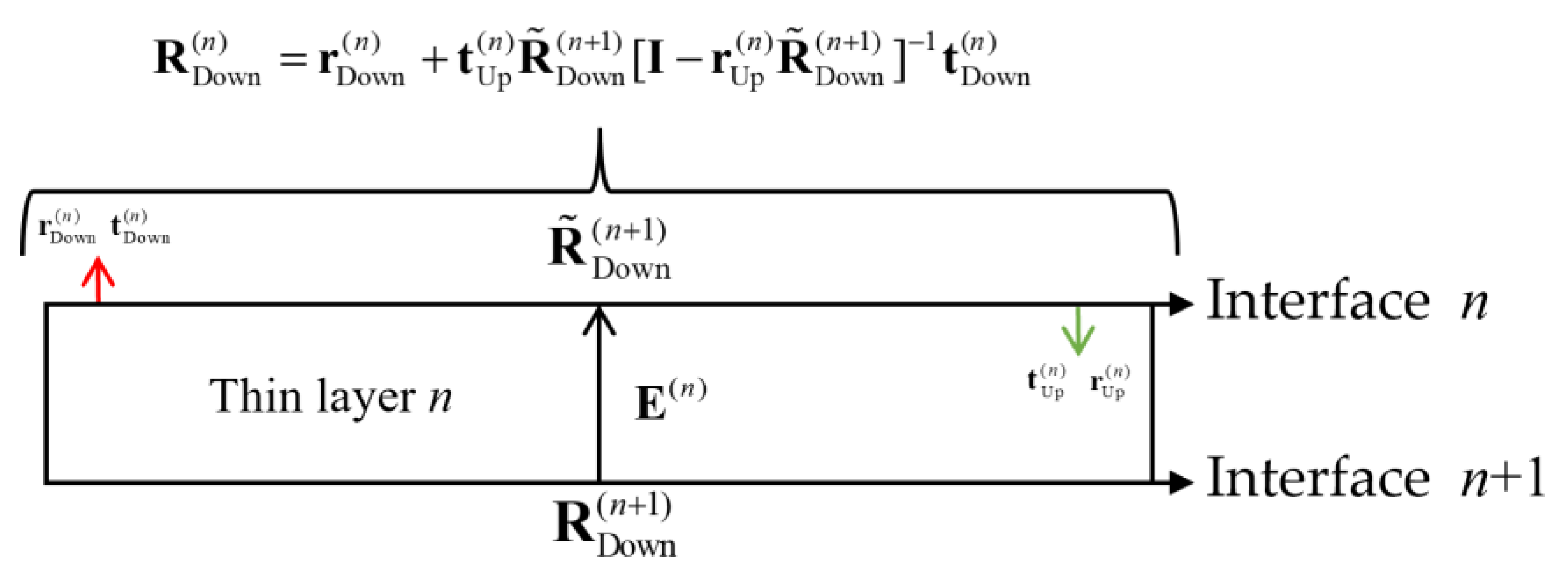
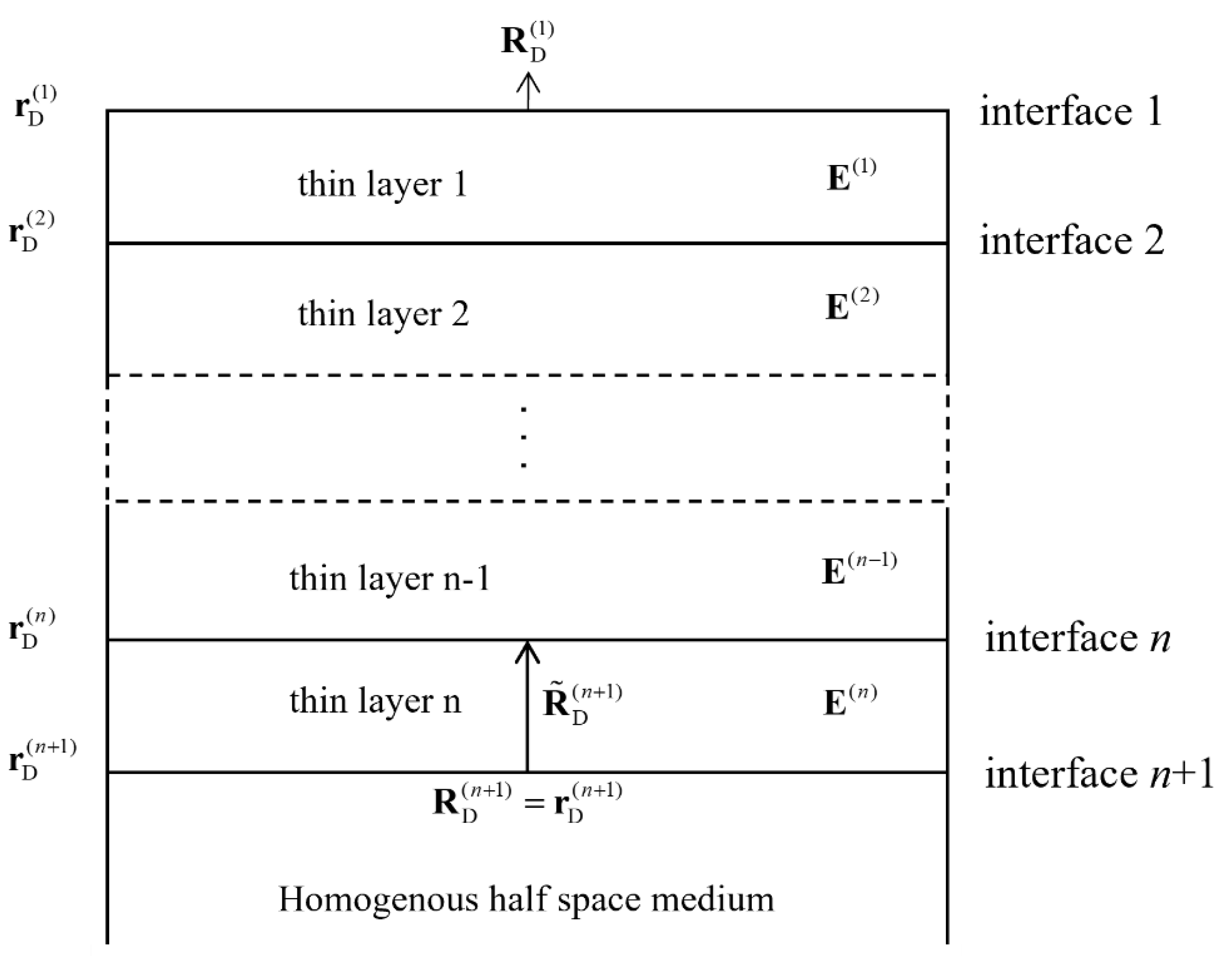
Taking the reflection coefficient of a single thin layer that retains third-order and fewer multiples as an example, as shown in Figure 8, we used Kennett’s reflection coefficient recursion method to iterate layer by layer from the reflection coefficient at the bottom of the thin interbed, and calculated the total reflection coefficient at the top of the thin interbed.

Since our model is based on the homogenous half-space assumption, there was no upward reflection transmission in the bottom half space. Therefore, the total reflection coefficient of the bottom single layer was equal to the single-interface reflection coefficient of the bottom interface:

$$R_{\mathrm{Down}}^{(n+1)}=r_{\mathrm{Down}}^{(n+1)}={\left[\begin{array}{ccc}{r}^{\mathrm{PP}}& r^{\mathrm{PS}1}& r^{\mathrm{PS}2}\\ r^{\mathrm{S}1\mathrm{P}}& r^{\mathrm{S}1\mathrm{S}1}& r^{\mathrm{S}1\mathrm{S}2}\\ r^{\mathrm{S}2\mathrm{P}}& r^{\mathrm{S}2\mathrm{S}1}& r^{\mathrm{S}2\mathrm{S}2}\end{array}\right]}_{\mathrm{Down}}^{(n+1)}.$$

(34)

$$E^{(n)}=\left[\begin{array}{ccc}{e}^{i\omega q_{\mathrm{p}}^{(n)}(\theta )h^{(n)}}& & \\ & e^{i\omega q_{\mathrm{S}1}^{(n)}(\theta )h^{(n)}}& \\ & & e^{i\omega q_{\mathrm{S}2}^{(n)}(\theta )h^{(n)}}\end{array}\right].$$

(35)

where $R_{\mathrm{Down}}^{(n+1)}$ is the contribution term of the reflection coefficient of the n + 1 interface to the top interface of the n layer; it can be calculated by

$${\tilde{R}}_{\mathrm{Down}}^{(n+1)}=E^{(n)}{R}_{\mathrm{Down}}^{(n+1)}{E}^{(n)}.$$

(36)

Given ${\tilde{R}}_{\mathrm{Down}}^{(n+1)}$, the total reflection coefficient on the top of the adjacent layer n can be obtained as follows:

$$\begin{array}{ll}\hfill R_{\text{Down}}^{\left(n\right)}=& r_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}\hfill \\ & +t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}\hfill \end{array}.$$

(37)

Similarly, at this point, the contribution term of $R_{\mathrm{Down}}^{\left(n\right)}$ to the reflection coefficient of the top interface of the n − 1 layer can be determined as ${\tilde{R}}_{\mathrm{Down}}^{(n)}$. At this time, it can be inferred that the total reflection coefficient of the n − 1 layer and its underlying strata is

$$\begin{array}{ll}\hfill R_{\text{Down}}^{(n-1)}=& r_{\text{Down}}^{(n-1)}+t_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{t}_{\text{Down}}^{(n-1)}+t_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{r}_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{t}_{\text{Down}}^{(n-1)}+t_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{r}_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{r}_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{t}_{\text{Down}}^{(n-1)}\hfill \\ & +t_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{r}_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{r}_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{r}_{\text{Up}}^{(n-1)}{\tilde{R}}_{\text{Down}}^{(n)}{t}_{\text{Down}}^{(n-1)}\hfill \end{array}.$$

(38)

Using the above method to recursively push each thin layer to the top of the thin interbeds, the third-order approximate total reflection coefficient of the thin interbeds can be

$$\begin{array}{ll}\hfill R_{\text{Down}}^{\left(1\right)}=& r_{\text{Down}}^{(1)}+t_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{t}_{\text{Down}}^{(1)}+t_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{r}_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{t}_{\text{Down}}^{(1)}+t_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{r}_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{r}_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{t}_{\text{Down}}^{(1)}\hfill \\ & +t_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{r}_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{r}_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{r}_{\text{Up}}^{(1)}{\tilde{R}}_{\text{Down}}^{(2)}{t}_{\text{Down}}^{(1)}\hfill \end{array}.$$

(39)

In order to analyze the energy proportion relationship between multiples of different orders, we chose the recursive method as an example to obtain the total reflection coefficient formula of thin interbeds with vertical fractures. In the reflection coefficient calculation formula, we retained first-order, second-order, and third-order multiples, while ignoring high-order multiples:

$$R_{\mathrm{Down}}^{\left(n\right)}=r_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}.$$

(40)

$$R_{\mathrm{Down}}^{\left(n\right)}=r_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}.$$

(41)

$$R_{\mathrm{Down}}^{\left(n\right)}=r_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}.$$

(42)

$$\begin{array}{ll}\hfill R_{\text{Down}}^{\left(n\right)}=& r_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}+t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}\hfill \\ & +t_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{r}_{\text{Up}}^{(n)}{\tilde{R}}_{\text{Down}}^{(n+1)}{t}_{\text{Down}}^{(n)}\hfill \end{array}.$$

(43)

The validation model was composed of four layers of 10 m thick HTI medium thin layers. The bottom of the model was an isotropic half-infinite space. The maximum incident angle was the critical angle, while the step size of the incident angle was taken as 0.1°. The azimuth angle of the crack was set to 45°. The density, velocity, and anisotropy parameter information of the thin layer are shown in

Table 1. Parameters of thin interbed model with vertical fractures.

	VP0 (km/s)	VS0 (km/s)	ρ (g/cm3)	ε(V)	δ(V)	γ(V)	φ (°)
First layer	2.361	1.381	2.36	0.01	0.018	0.023	45
Second layer	2.375	1.408	2.394	0.02	0.021	0.031	45
Third layer	2.404	1.428	3.061	0.03	0.032	0.034	45
Fourth layer	2.431	1.462	3.099	0.04	0.039	0.037	45
Bottom half space	2.473	1.478	3.2	0	0	0	45

.

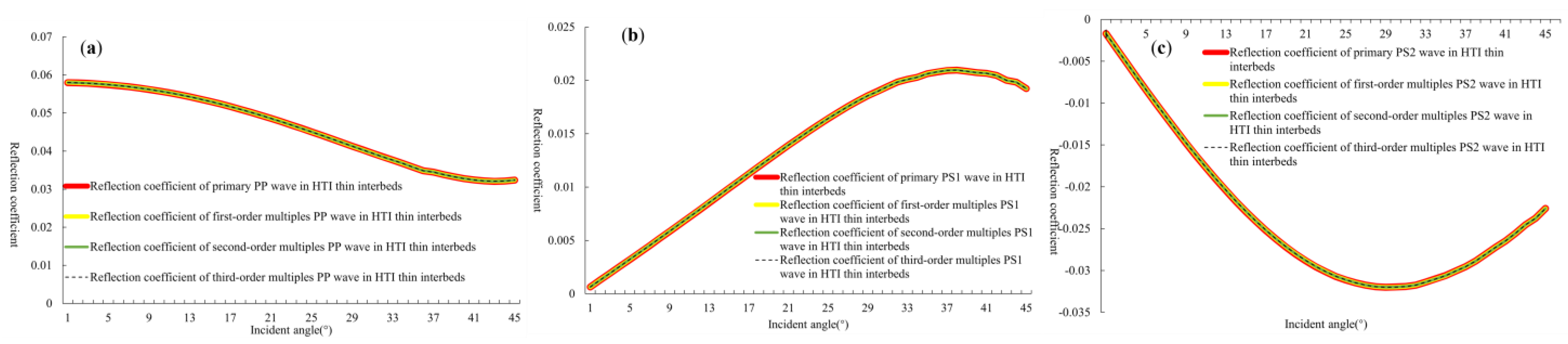
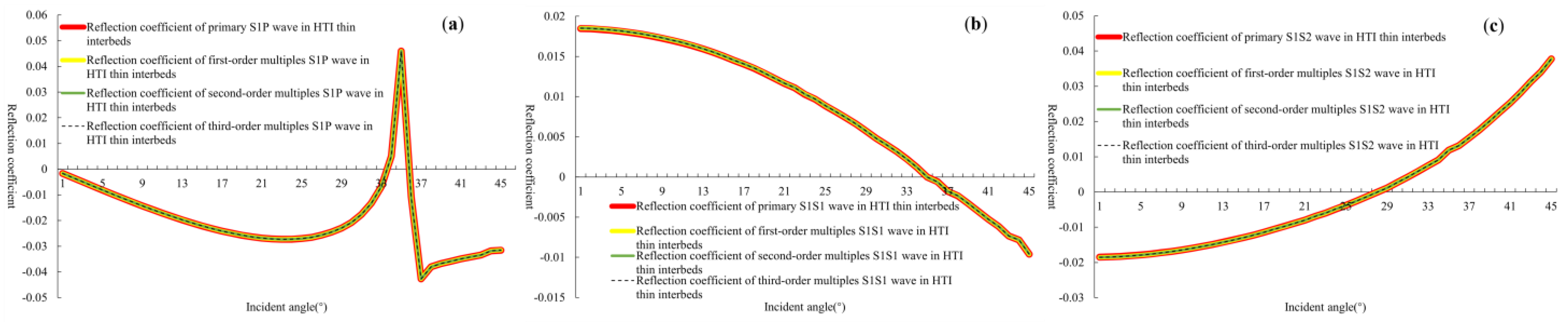
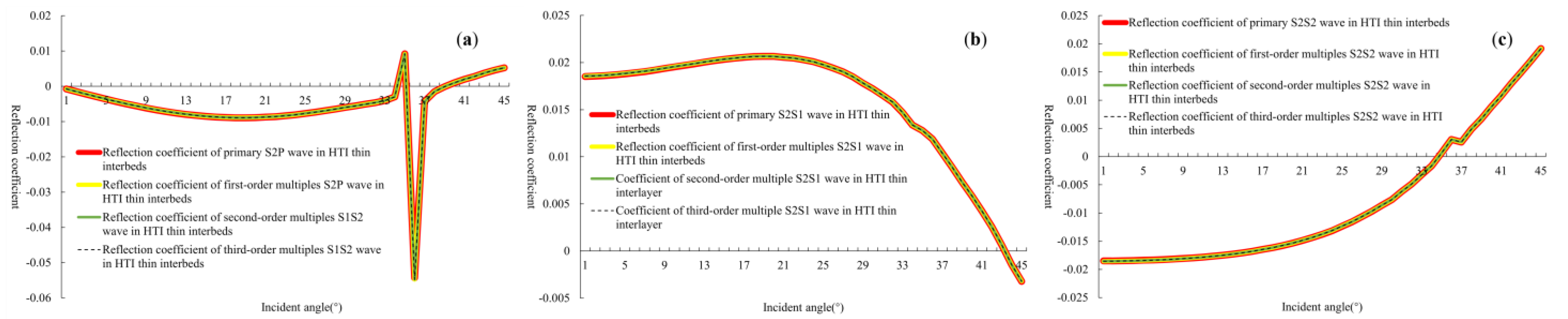
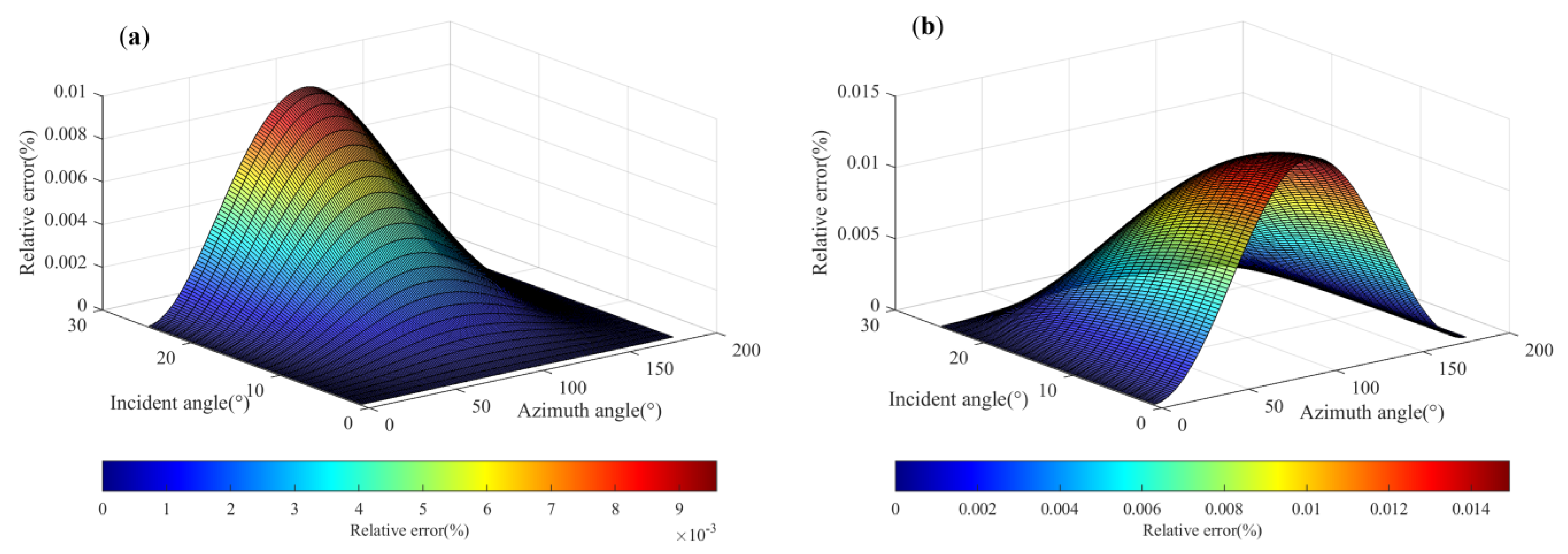
As shown in Figure 9, Figure 10 and Figure 11, it is evident that the relative error for the primary reflection coefficients of PP, PS1, PS2, S1P, S1S1, S1S2, S2P, S2S1, and S2S2 waves, in comparison to the reflection coefficients retaining first-, second-, and third-order multiples, was consistently below 0.1%. There is almost no difference between the four approximate reflection coefficients regarding retaining different order multiples.

The above indicates that under the model in Table 1, retaining multiples of different orders has little effect on the total reflection coefficient of thin interbeds with fractures. In order to verify the energy proportion relationship between different-order multiples in other models, we used the reflection coefficient on a single interface as a variable to simulate the energy relationship between different-order multiples in different thin-layer models.

Since the energy of a wave is proportional to the square of its amplitude, we analyzed its energy by studying the amplitudes between different-order multiples.

Based on the physical description of the multiples’ expression in a thin layer, we assumed that the amplitude of the incident wave was A_inc, and the reflection coefficient of the primary wave in the thin layer was R_Prim, while the reflection coefficient of first-order multiples in the thin layer was R_Muti. (R_Prim: $t_{\mathrm{Down}}^{\left(n\right)}\cdot t_{\mathrm{Up}}^{\left(n\right)}\cdot r_{\mathrm{Down}}^{(n+1)}$, R_Muti: $r_{\mathrm{Down}}^{\left(n\right)}\cdot r_{\mathrm{Down}}^{(n+1)}$).

The amplitude of a primary wave in a thin layer is

$${\mathrm{A}}_{\mathrm{Prim}}={\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}.$$

(44)

The amplitude of seismic waves reflected by second-order multiples within a thin layer is

$${\mathrm{A}}_{\mathrm{Muti}\_2}={\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot R_{\mathrm{Muti}}^2.$$

(45)

The amplitude of m-order multiples in a thin layer is

$${\mathrm{A}}_{\mathrm{Muti}\_\mathrm{n}}={\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot R_{\mathrm{Muti}}^m.$$

(46)

If infinite-order multiples are retained, i.e., m tends towards infinity, then the amplitude is

$${\mathrm{A}}_{\mathrm{Muti}\_\mathrm{infinte}}=\left({\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot R_{\mathrm{Muti}}^1\right)+\left({\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot R_{\mathrm{Muti}}^2\right)+\cdot \cdot \cdot +\left({\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot R_{\mathrm{Muti}}^m\right).$$

(47)

$${\mathrm{A}}_{\mathrm{Muti}\_\mathrm{infinte}}=\left({\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\right)\cdot \left(R_{\mathrm{Muti}}^{}+R_{\mathrm{Muti}}^2+\cdot \cdot \cdot +R_{\mathrm{Muti}}^m\right)={\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot \frac{R_{\mathrm{Muti}}^{}\left(1-R_{\mathrm{Muti}}^m\right)}{\left(1-R_{\mathrm{Muti}}^{}\right)}.$$

(48)

Since the reflection coefficient is between −1 and 1, when m tends to infinity, $R_{\mathrm{Muti}}^m$ tends to 0:

$${\mathrm{A}}_{\mathrm{Muti}\_\mathrm{infinte}}{=\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot \frac{R_{\mathrm{Muti}}^{}}{1-R_{\mathrm{Muti}}^{}}.$$

(49)

The ratio of the amplitude energy of first-order multiples to the amplitude energy of all multiples can be written as follows:

$$\frac{{\mathrm{A}}_{\mathrm{Muti}\_1}}{{\mathrm{A}}_{\mathrm{Muti}\_\mathrm{infinte}}}=\frac{{\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot R_{\mathrm{Muti}}^{}}{{\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot \frac{R_{\mathrm{Muti}}^{}}{1-R_{\mathrm{Muti}}^{}}}=1-R_{\mathrm{Muti}}^{}.$$

(50)

The ratio of the amplitude energy of second-order multiples to the amplitude energy of all multiples can be expressed as

$$\frac{{\mathrm{A}}_{\mathrm{Muti}\_2}}{{\mathrm{A}}_{\mathrm{Muti}\_\mathrm{infinte}}}=\frac{{\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\left(R_{\mathrm{Muti}}^{}+R_{\mathrm{Muti}}^2\right)}{{\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot \frac{R_{\mathrm{Muti}}^{}}{1-R_{\mathrm{Muti}}^{}}}=1-R_{\mathrm{Muti}}^2.$$

(51)

The ratio of the reflection amplitude of multiples within the third-order to the reflection amplitude of all multiples can be written as

$$\frac{{\mathrm{A}}_{\mathrm{Muti}\_3}}{{\mathrm{A}}_{\mathrm{Muti}\_\mathrm{infinte}}}=\frac{{\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\left(R_{\mathrm{Muti}}^{}+R_{\mathrm{Muti}}^2+R_{\mathrm{Muti}}^3\right)}{{\mathrm{A}}_{\mathrm{inc}}\cdot R_{\mathrm{Prim}}\cdot \frac{R_{\mathrm{Muti}}^{}}{1-R_{\mathrm{Muti}}^{}}}=\left(1+R_{\mathrm{Muti}}^{}+R_{\mathrm{Muti}}^2\right)\cdot \left(1-R_{\mathrm{Muti}}^{}\right).$$

(52)

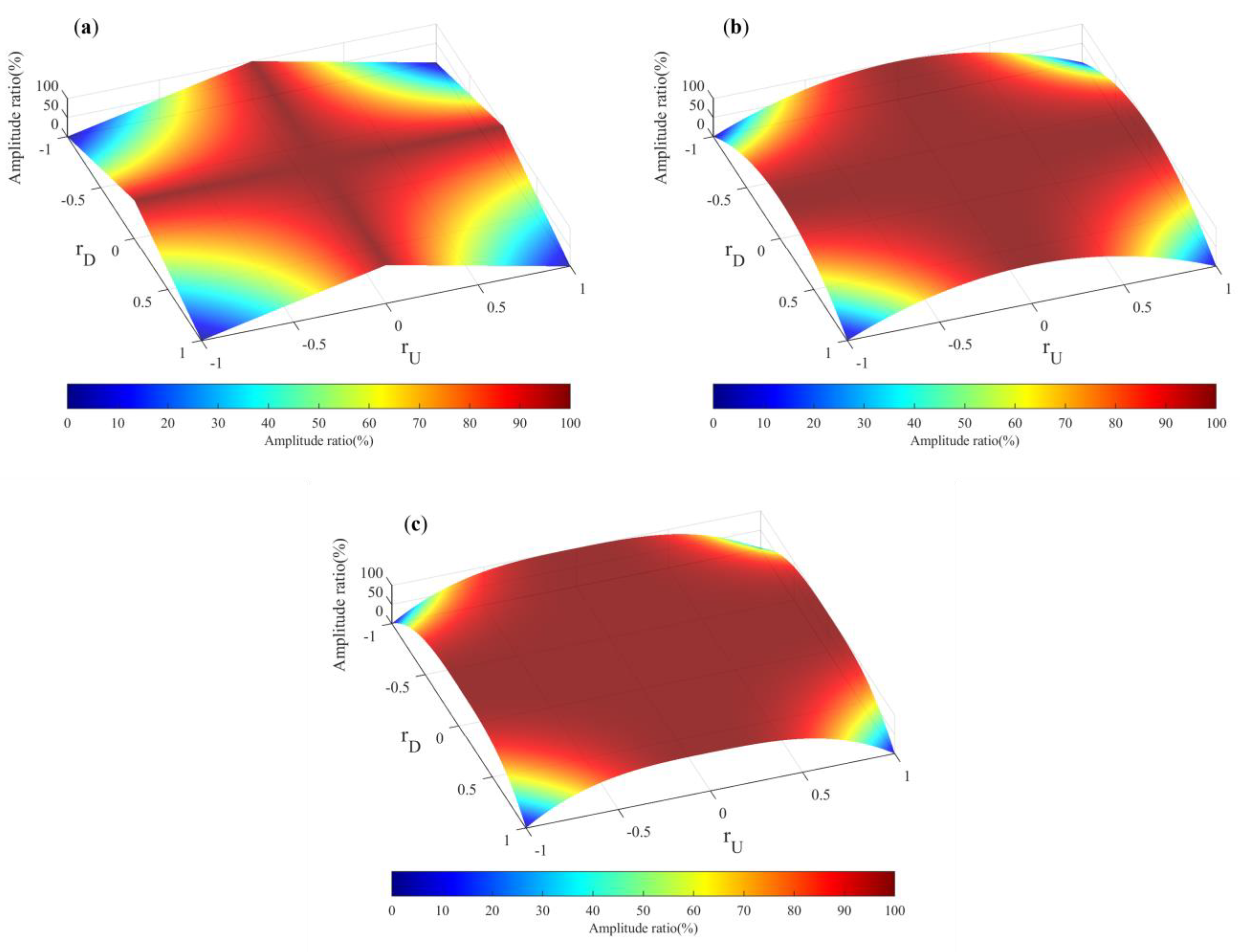
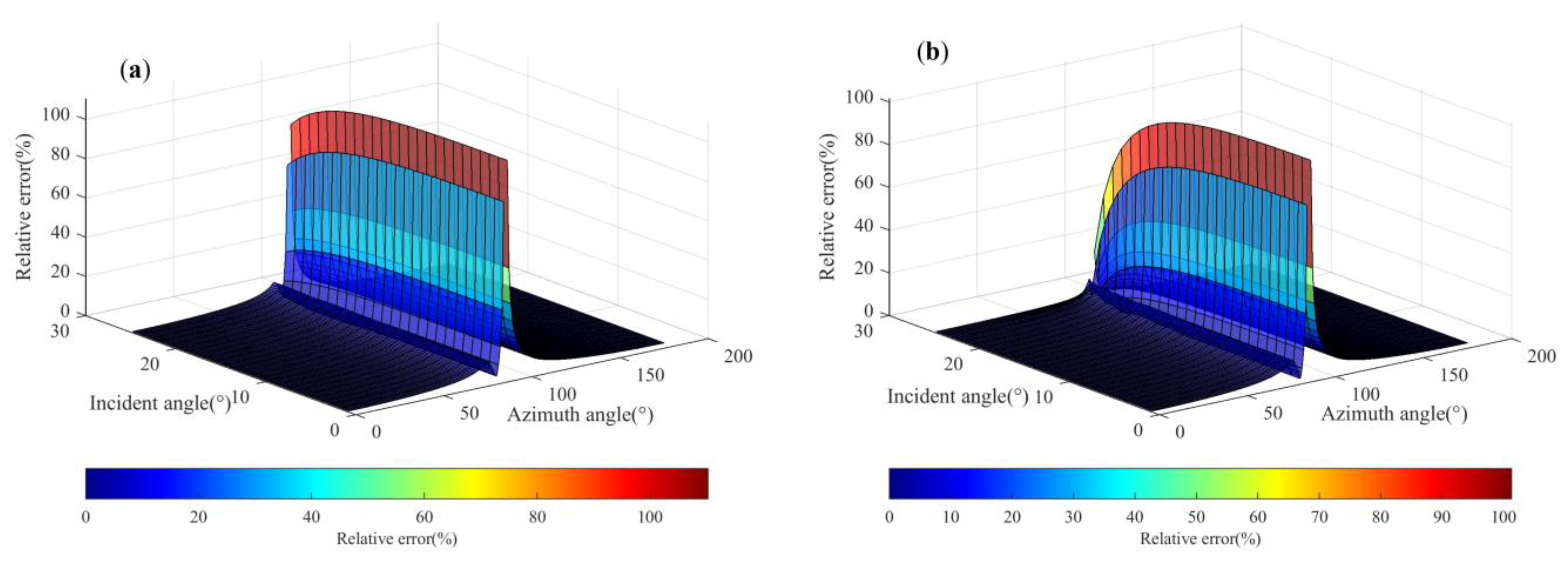
We can also draw the ratio of the seismic wave reflection amplitude of the first-order multiples with different conditions to the amplitude of all multiples in Figure 12.

In Figure 12a, it shows that when both of the absolute values of the reflection coefficients of upward $r_{\mathrm{Up}}^{\left(n\right)}$ and downward $r_{\mathrm{Down}}^{\left(n\right)}$ on a single interface are both less than 0.07, the energy of first-order multiples will occupy over 95% of the total energy. When the absolute values of $r_{\mathrm{Up}}^{\left(n\right)}$ and $r_{\mathrm{Down}}^{\left(n\right)}$ are greater than 0.2, the energy of higher-order multiples can exceed 15%. The absolute values of the reflection coefficients of the thin interbeds were less than 10⁻³ in this model, so the energy of the first-order multiples always accounted for the main part of the energy of multiples. As shown in Figure 12b, the energy of first-order and second-order multiples accounts for 98–99% of the high-order multiples in this model (absolute values of $r_{\mathrm{Up}}^{\left(n\right)}$ and $r_{\mathrm{Down}}^{\left(n\right)}$ both less than 0.1). In Figure 12c, it shows that the third-order and low-order multiples also account for over 99% of the total wave field amplitude, which is not significantly different from the results in Figure 13. When the absolute value of the thin-layer interface reflection coefficient is above 0.45, the energy of third-order and above multiples should be considered.

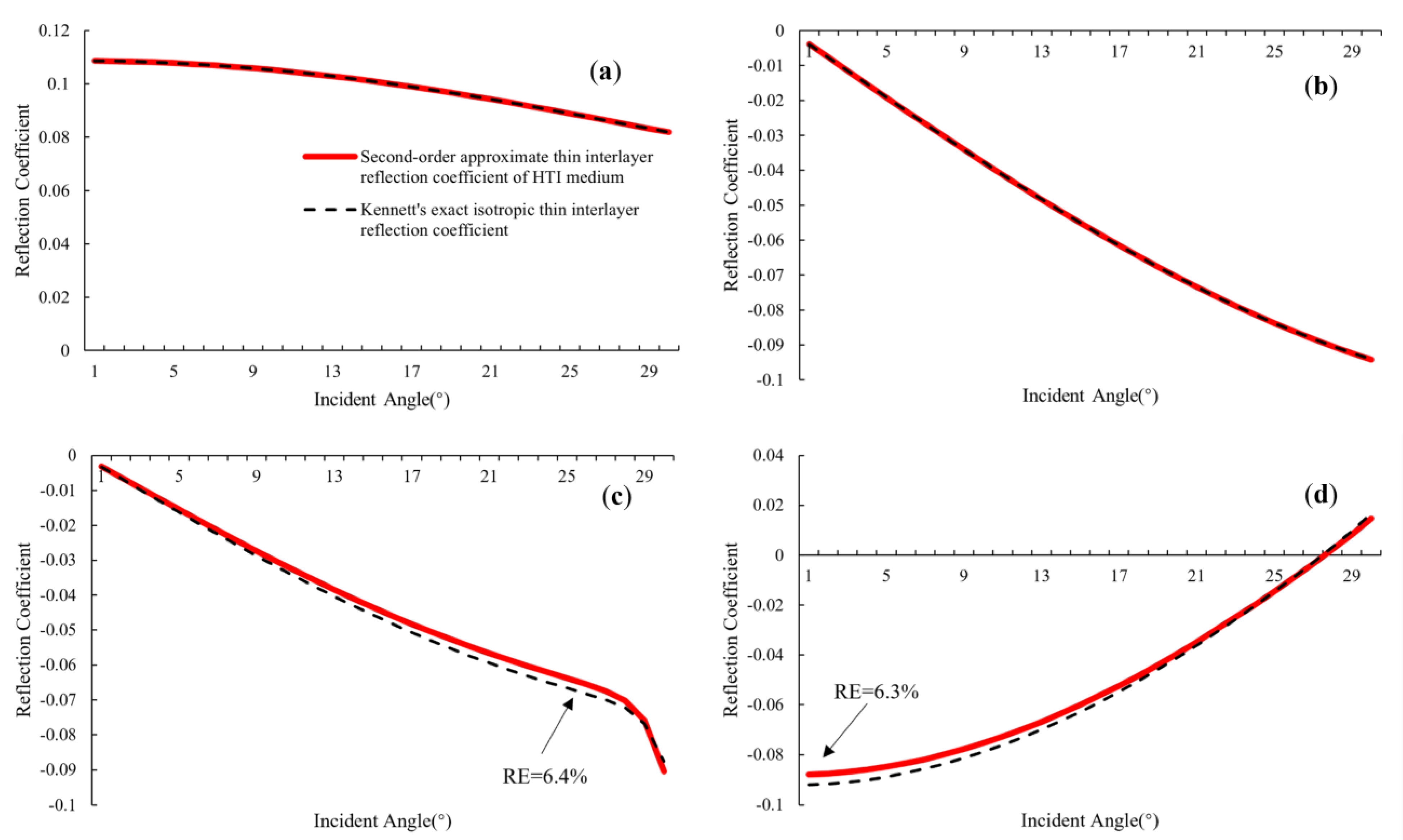
However, the reflection coefficient of actual strata rarely exceeds the degree to which third-order multiples need to be considered. Therefore, when calculating the reflection coefficient of thin interbeds with fractures, we mostly used a second-order approximation formula:

$$R_{\mathrm{Down}}^{\left(n\right)}=r_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}+t_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{r}_{\mathrm{Up}}^{(n)}{\tilde{R}}_{\mathrm{Down}}^{(n+1)}{t}_{\mathrm{Down}}^{(n)}.$$

(53)

3. Error Analysis

After verifying the rationality of the second-order approximation, we continued to test the accuracy of the second-order approximation Formula (53) using Kennett’s isotropic thin-layer formula. We were able to degenerate the second-order approximation formula into an isotropic formula by setting the Thomsen anisotropy parameter to 10⁻¹⁰. We abbreviated this technology as second-order DAF. The reflection coefficients of the PP wave, PS wave, SP wave, and SS wave can be calculated using Kennett’s exact formula and second-order DAF. We then quantitatively analyzed the reflection coefficients observed by two methods.

We firstly established a thin layer sandwiched in a homogeneous medium. The detailed information for the model is shown in

Table 2. Parameters of HTI medium thin-layer model.

	VP0 (km/s)	VS0 (km/s)	ρ (g/cm3)	ε(V)	δ(V)	γ(V)	φ (°)
Overlying medium	2.361	1.381	2.36	10−10	10−10	10−10	45
HTI medium layer	2.375	1.408	2.394	10−10	10−10	10−10	45
Underlying medium	2.404	1.428	3.061	10−10	10−10	10−10	45

. The overlying and underlying strata of the thin-layer model were isotropy. The incidence angle was less than the critical angle, and the azimuth angle was 45°. The comparison of the reflection coefficient observed by second-order DAF and Kennett’s exact isotropic of a thin layer are shown in Figure 13.

The maximum relative error between the second-order DAF and Kennett’s exact isotropic formula was less than 0.01% in both the PP and PS wave fields. In the SP wave field, the maximum error between Kennett’s exact formula and second-order DAF occurred at the seismic wave incident of 25°, with a relative error of 6.4%. In the SS wave field, the maximum error between second-order DAF and Kennett’s exact formula occurred at the incident angle of 0.1°, with a relative error of 6.3%. Within the critical angle, the relative error of SP-wave DAF exhibited a characteristic of increasing with the increase in incident angle. The relative error of SS wave DAF decreased with increasing incident angle.

In order to evaluate the relative error in the joint influence of different azimuth angles and incident angles, we varied the azimuth angles from 1° to 180° in steps of 0.1° and changed the incident angle from 1° to 25° in steps of 0.1°. The measured relative error between the two reflection coefficients for P-wave incidence and S-wave incidence is shown in Figure 14 and Figure 15, respectively.

Figure 14 shows that the relative errors of the reflection coefficient between the two methods for PP and PS waves at azimuth angles of 1–180° and incidence angles of 1–25° remained below 0.01%, which was lower than the upper limit of 1%. Therefore, in the PP and PS wave fields, the second-order approximation technique has high computational accuracy. The relative error surfaces of the PP wave and PS wave were both symmetrical around an azimuth angle of 90°. The relative error of the PP waves increased with the increase in incident angle, while the opposite was true for the PS waves.

Figure 15a shows that the SP wave relative error is only 1% with the azimuth varying in the range of 0–70° and 120–180°, and the incidence angle changing in the range of 1–25°. The relative error gradually increases with the azimuth angle increasing. When the azimuth is 75°, the relative error reaches 6.4%. The relative error increases from the azimuth of 75° to 100°, with the maximum relative error of 98.7% at an azimuth of 91°. However, when the azimuth exceeds 100°, the relative error gradually decreases from 15% to 6% in the range of 100–120°. For the relative error of SS wave in Figure 15b, when the incidence angle of S waves is less than the critical angle and the azimuth lies in the range of 0–75°, the relative errors are lower than 6.5%. The characteristics of the relative error of SS waves are like the SP wave field. It increases sharply following an azimuthal angle in the range of 75–100°, with the maximum relative error of 89% at the azimuth angle of 91°. The relative error drops sharply below 5% in the azimuth range of 120–180° and an incident angle of 25°. Especially when the azimuth angle is greater than 130°, the relative error is less than 2%.

4. Discussion

For single thin layers and thin interbeds, internal multiples reflections are mixed with primary reflections, and it is currently impossible to suppress multiples reflections without affecting the energy of primary reflections. Therefore, the impact of multiples reflections on reflection coefficients must be considered in seismic data processing and inversion of single thin layers and thin interbeds. The Kennett formula system explicitly calculates all types of multiples and also considers interbed transmission losses. The equation system has no limitations on layer thickness conditions, making it suitable for calculating the reflection coefficient of thin interbeds. We generalized the second-order approximation of the Kennett equation for the reflection coefficient of isotropic layered media and obtained a second-order approximation equation for the reflection coefficient of HTI thin interbeds. The rationality of retaining second-order multiples and the rationality of the formula results were verified. Therefore, in the subsequent simulation, analysis, and inversion of AVA response, it could be more time-saving and maintain good accuracy compared to accurate formulas when considering multiples. Due to the presence of high-angle fractures in the formation, there are not only vertical fractures, but also some oblique fractures that form a more complex azimuthal anisotropy. In the future, we will derive more complex second-order approximate reflection coefficients for thin interbeds. And we combined the reflection coefficient with Green’s function for wave field simulation, making the seismic wave response characteristics of anisotropic thin interlayers more intuitive.

5. Conclusions

This article proposed a new second-order approximate formula for the total reflection coefficient of thin interbeds composed of HTI. The rationality of the second-order approximation was verified by comparing the amplitude energy of multiples when the absolute value of the single interface reflection coefficient was less than 0.45. The formula is only applicable to the calculation of the reflection coefficient with the incidence angle less than the critical angle, and when the absolute value of the single interface reflection coefficient is below 0.45. Additionally, it is necessary for the thin interbeds to have a low impedance contrast, and weak anisotropy, and the method does not consider the influence of the electromagnetic field properties of the strata on the elastic properties. When the P-wave is incident, the relative error of the P-wave approximate reflection coefficient has an accuracy of 99%, while the relative error of the S-wave approximate reflection coefficient is relatively large between azimuth angles of 75–120°, with an accuracy of 95% at 1–45° and 120–180°. When the S-wave is incident, the relative error is less than 5% in the azimuth range. The calculation accuracy is mainly affected by the incident angle in the high-precision field (relative error < 5%). The accuracy decreases as the incident angle approaches the critical angle for SP waves, while for SS waves, the accuracy increases as the incident angle approaches the critical angle. Our second-order reflection coefficient approximation proves effective in simulating a more comprehensive seismic wavefield in thin-interbed environments. It holds significant potential for applications in thin-interbed AVO (Amplitude-Versus-Offset) inversion and stratigraphic structure prediction, where the influence of these complexities is crucial to consider. Therefore, this second-order approximation formula can guide the subsequent inversion work of complex thin interbeds, and has certain significance for searching for oil gas, reservoirs and predicting stratigraphic structures.