Optimization of an IPMSM for Constant-Angle Square-Wave Control of a BLDC Drive
Abstract
1. Introduction
2. Theoretical Background
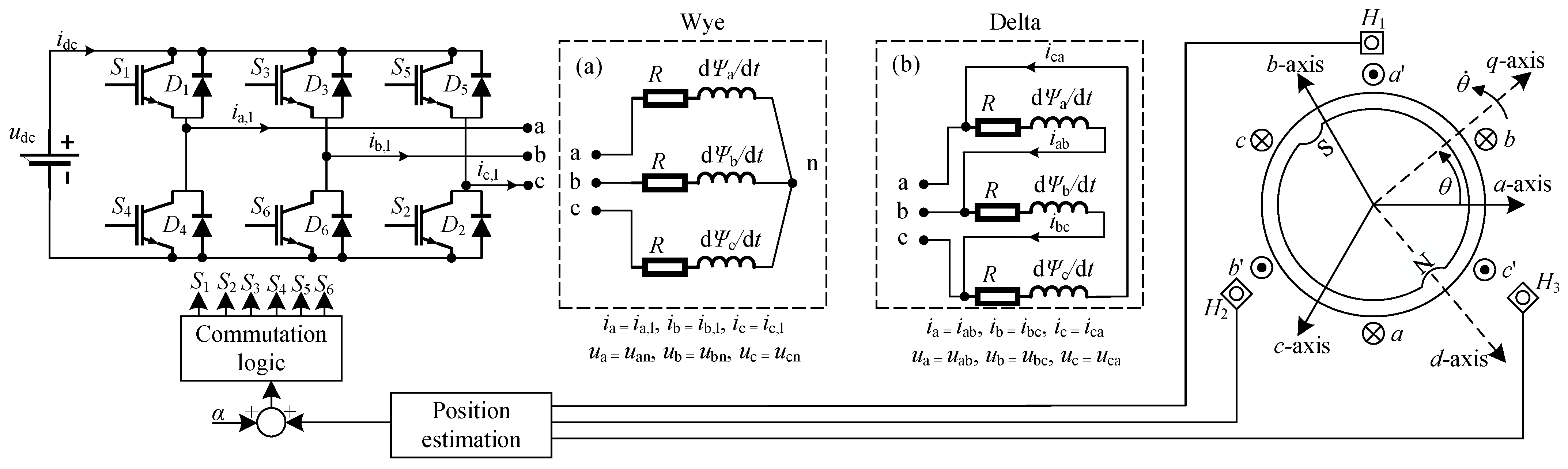
2.1. Dynamic Model of an IPMSM within BLDC Drives
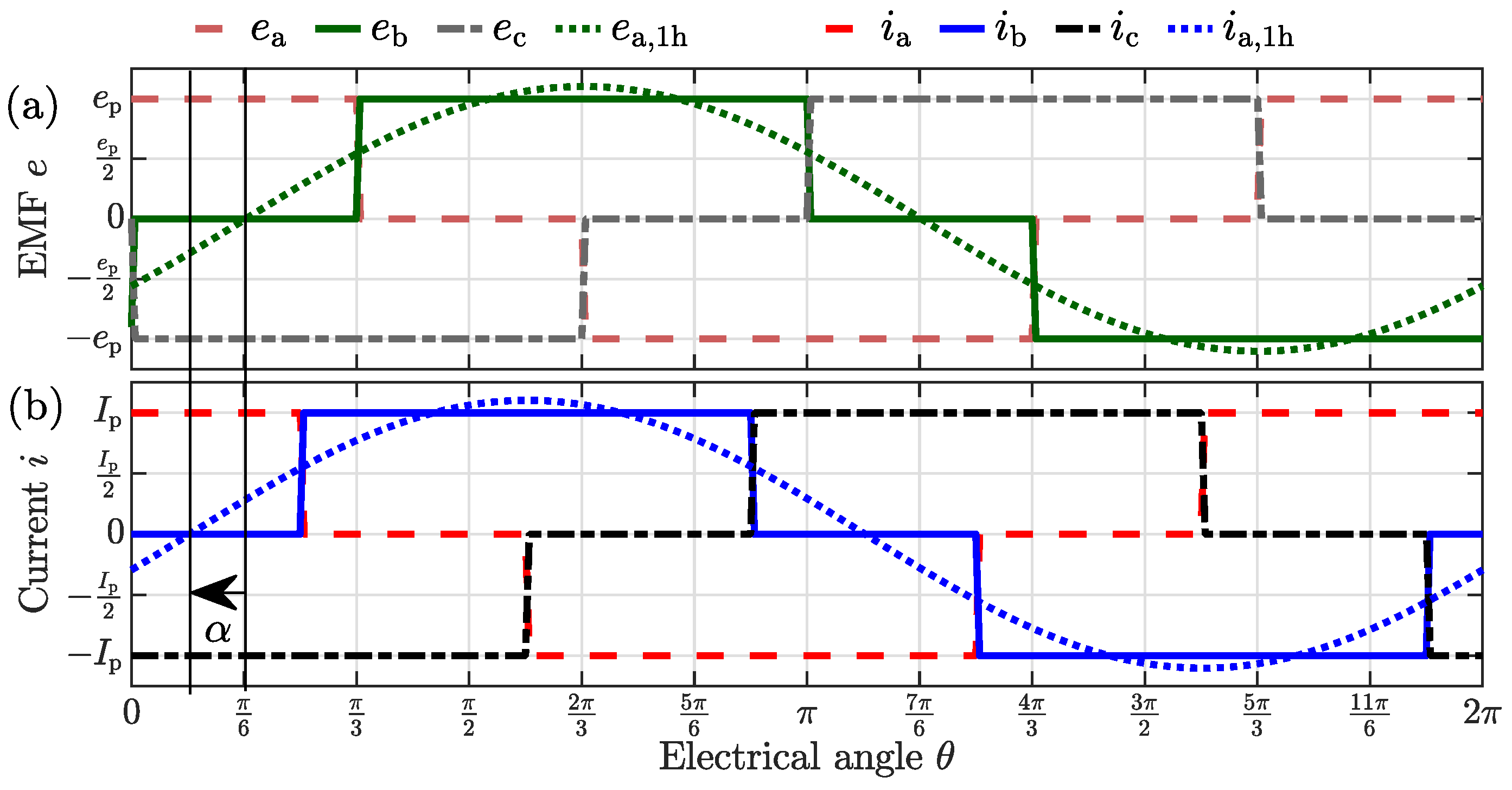
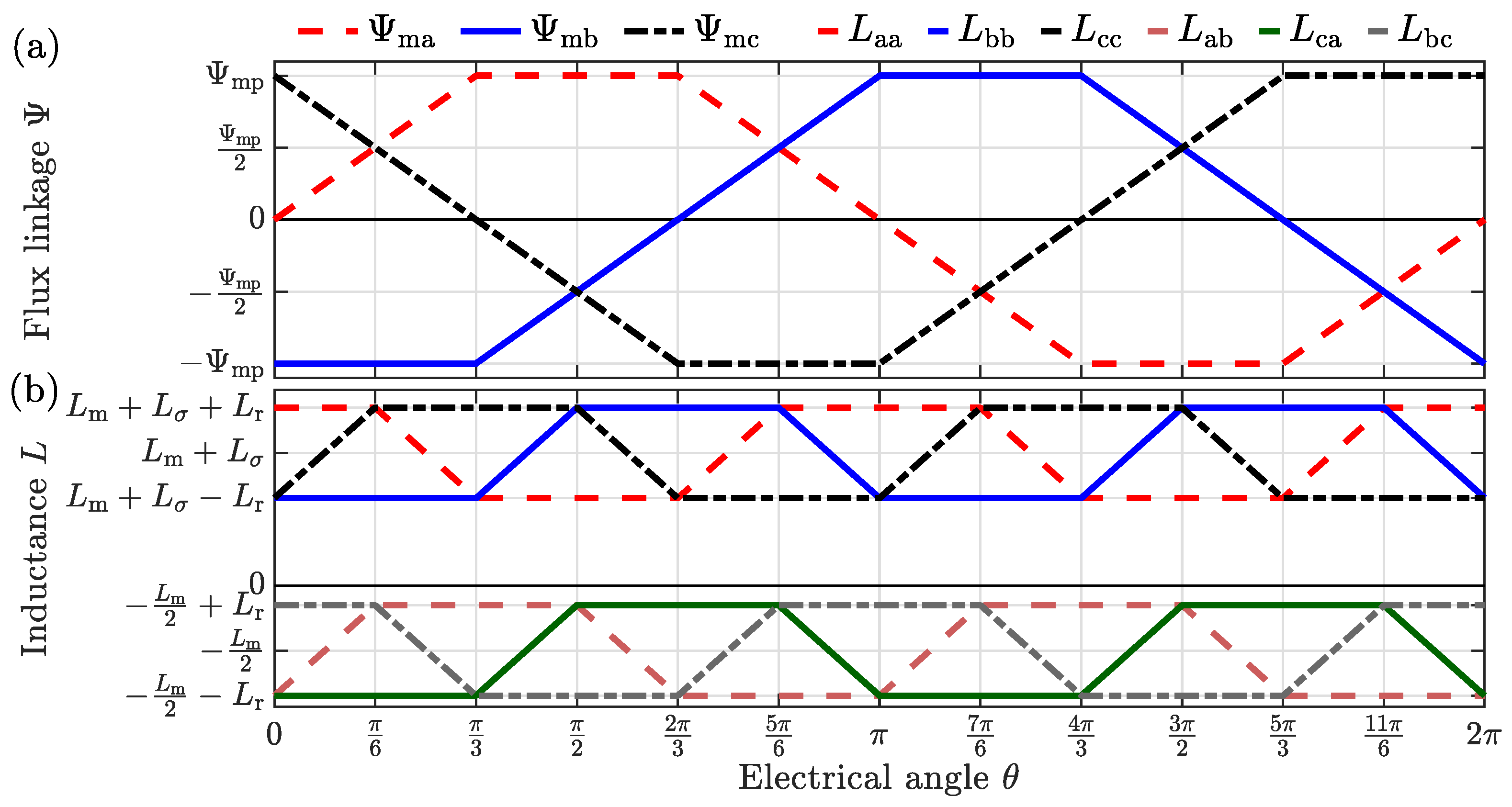
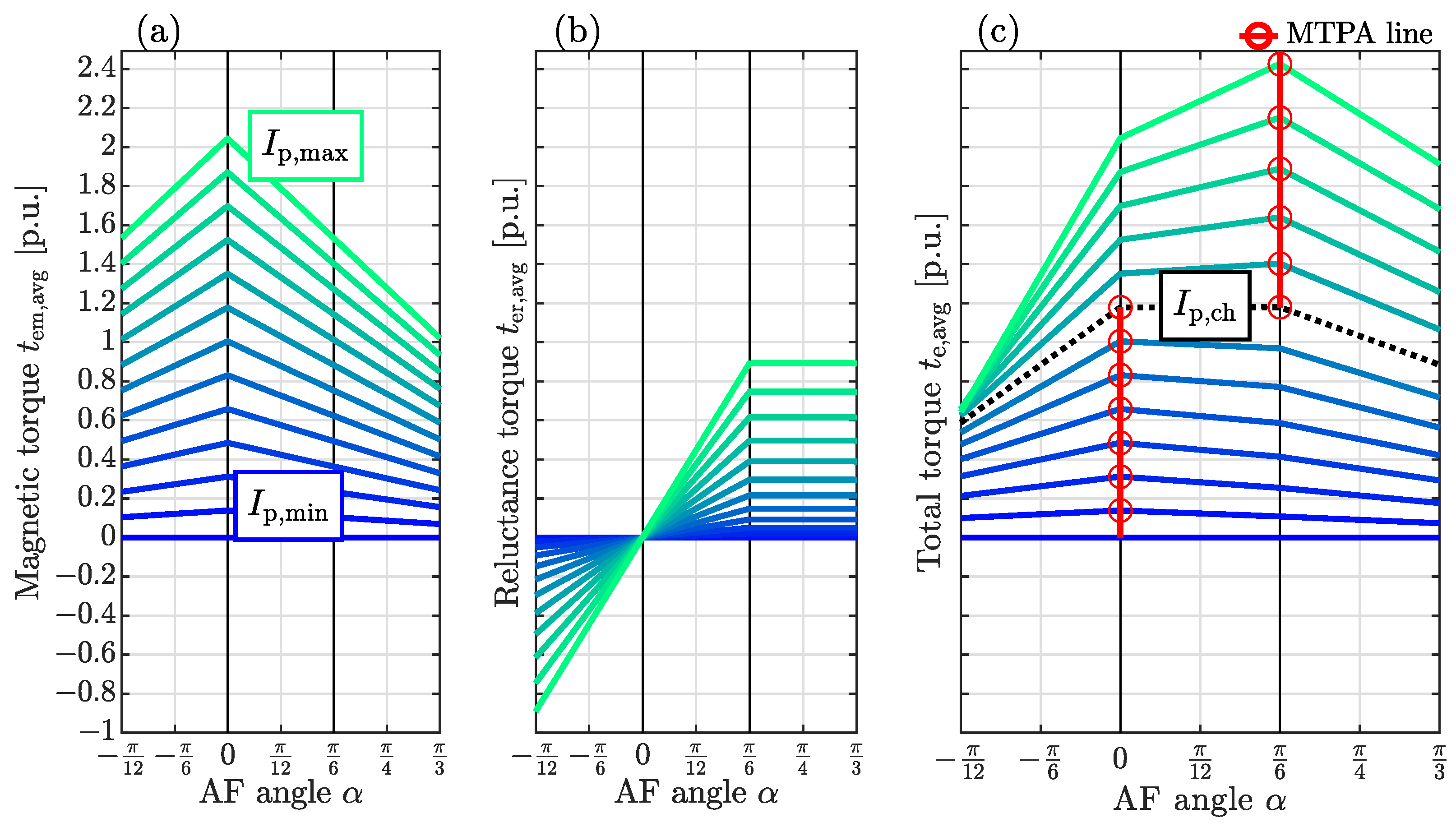
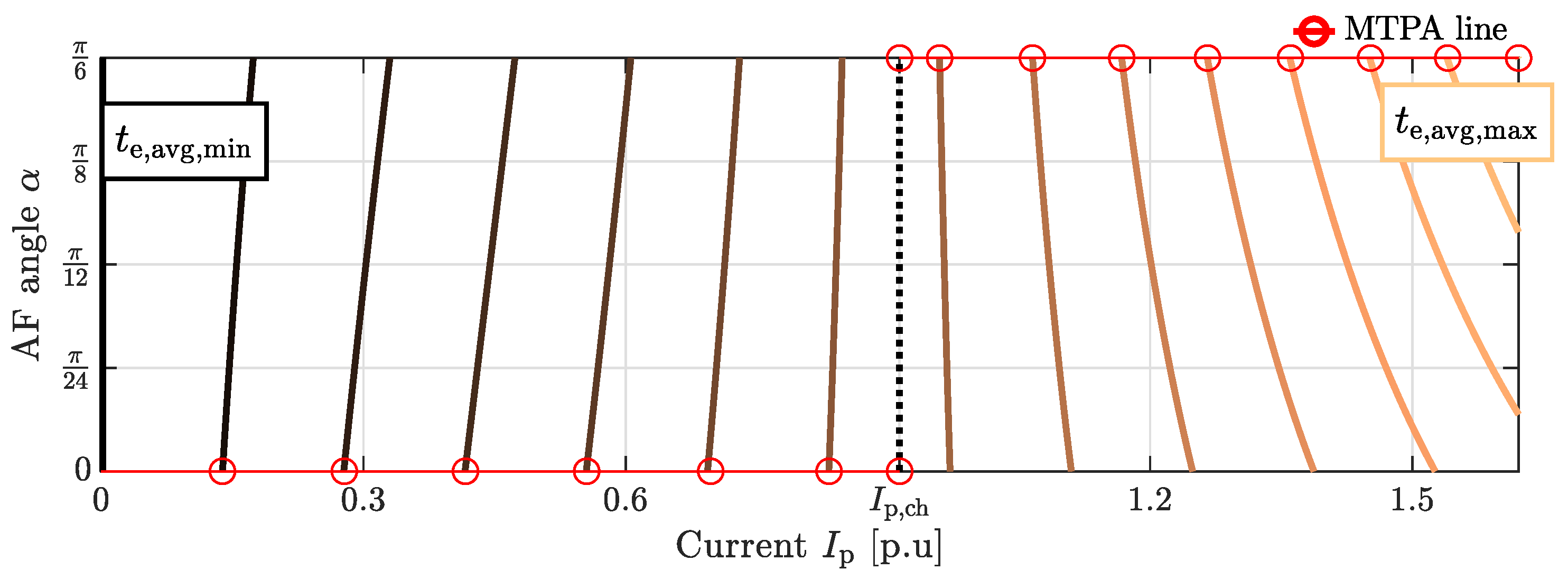
2.2. MTPA Angle of an Ideal BLDC Drive
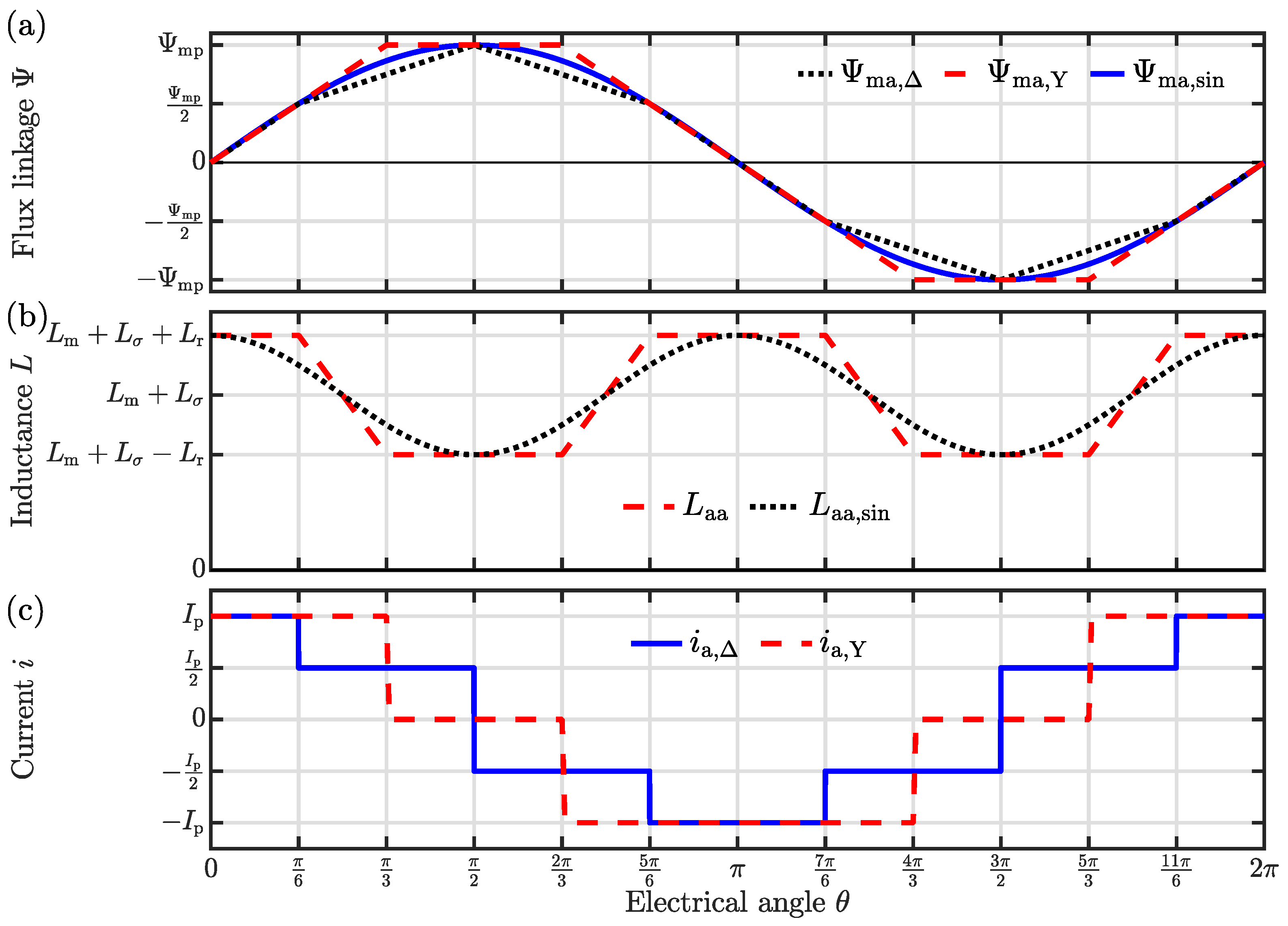
- Wye-connected windings of the IPMSM (i.e., phase currents , were identical to the line currents , as presented in Figure 2).
- The design of the IPMSM is such that and .
- The torque , exhibits periodic repetition every , reflecting the symmetry in a three-phase system, as demonstrated in [36]. Consequently, the analysis can be performed for a electrical rotation of the rotor.
- The analysis of the AF angle , was restricted to due to the definition of the involved variables.
2.3. Impact of the IPMSM Design on the MTPA Angle
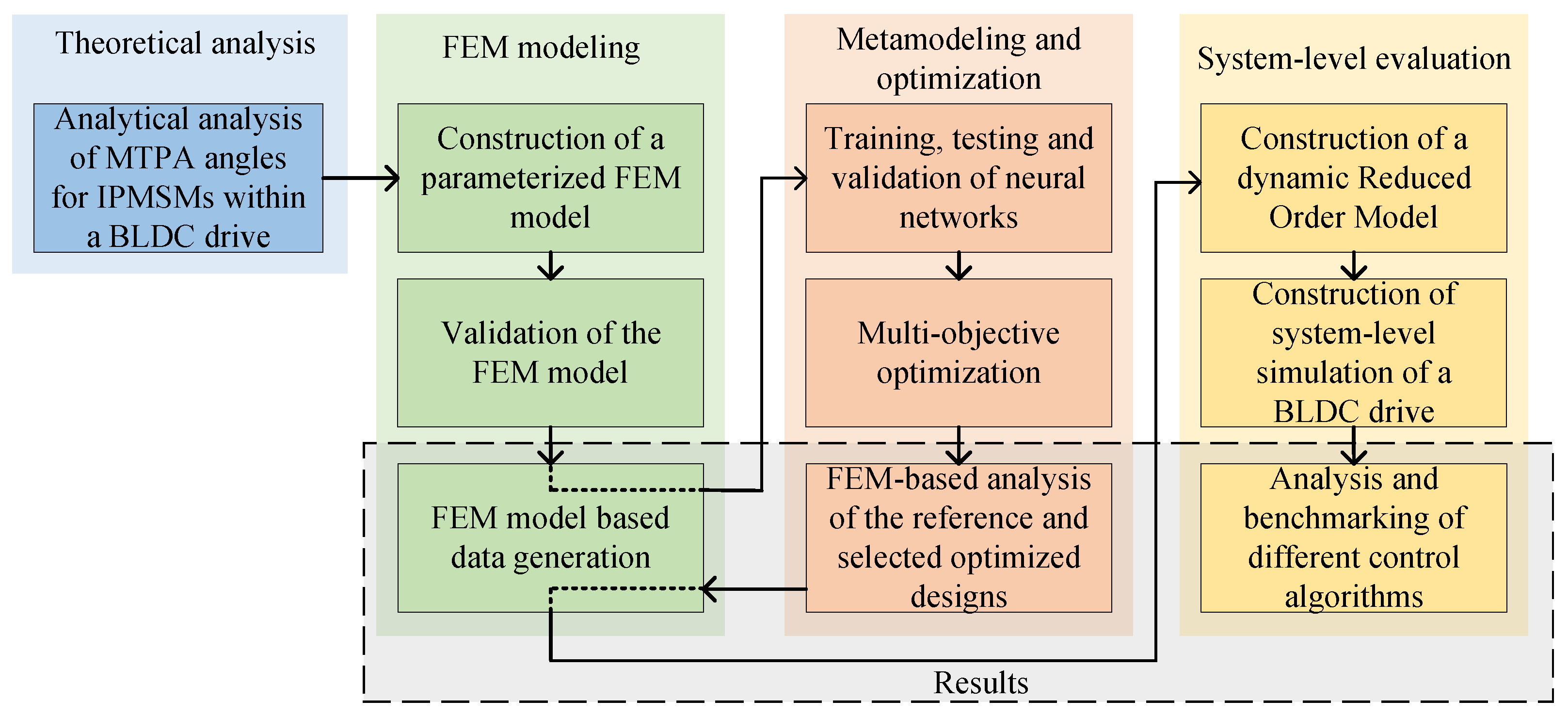
3. Optimization of an IPMSM for SWC
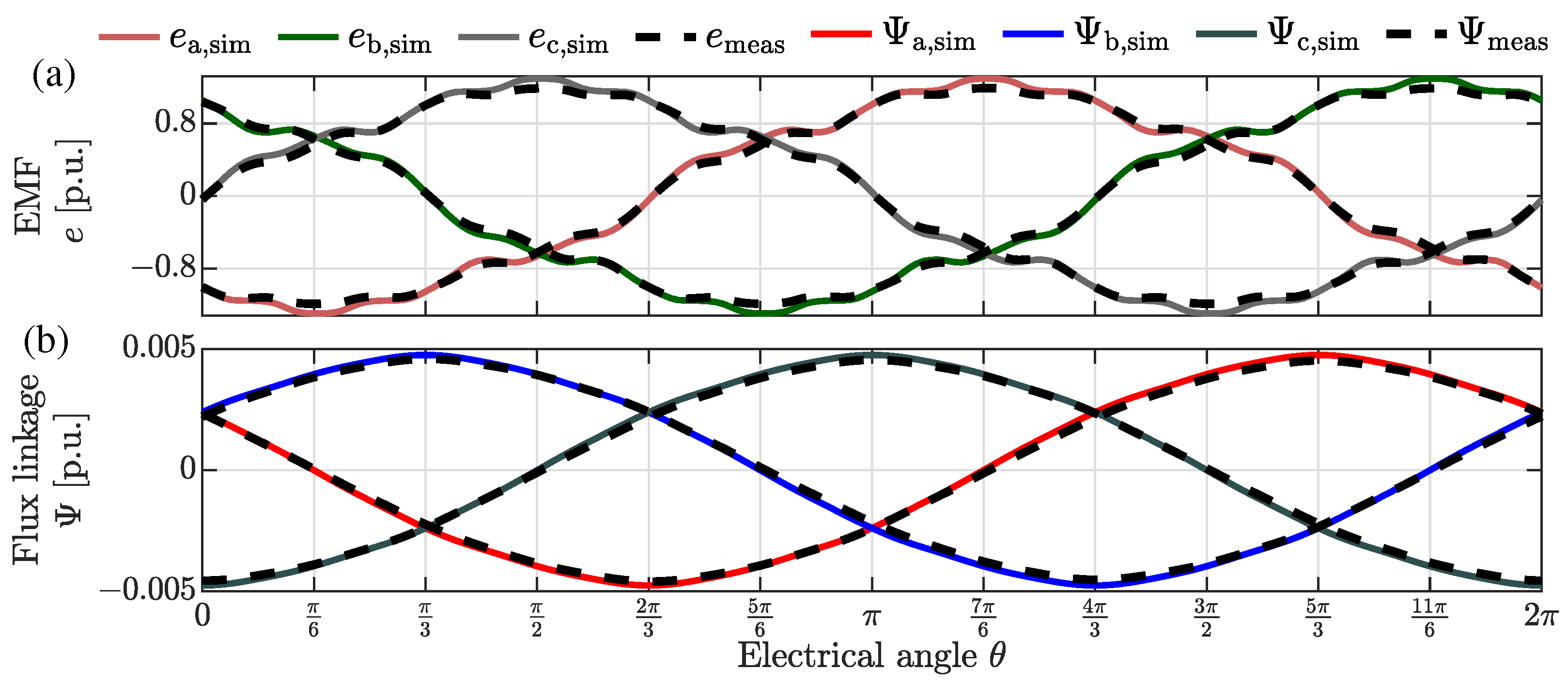
3.1. Experimental Validation of the Reference IPMSM Model
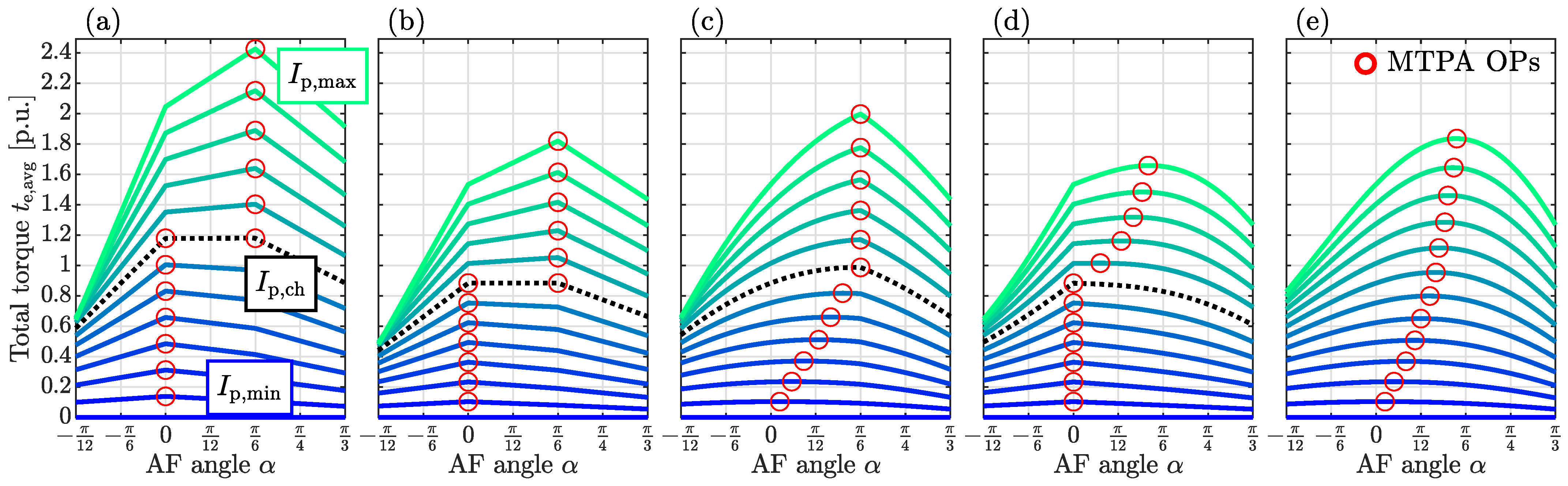
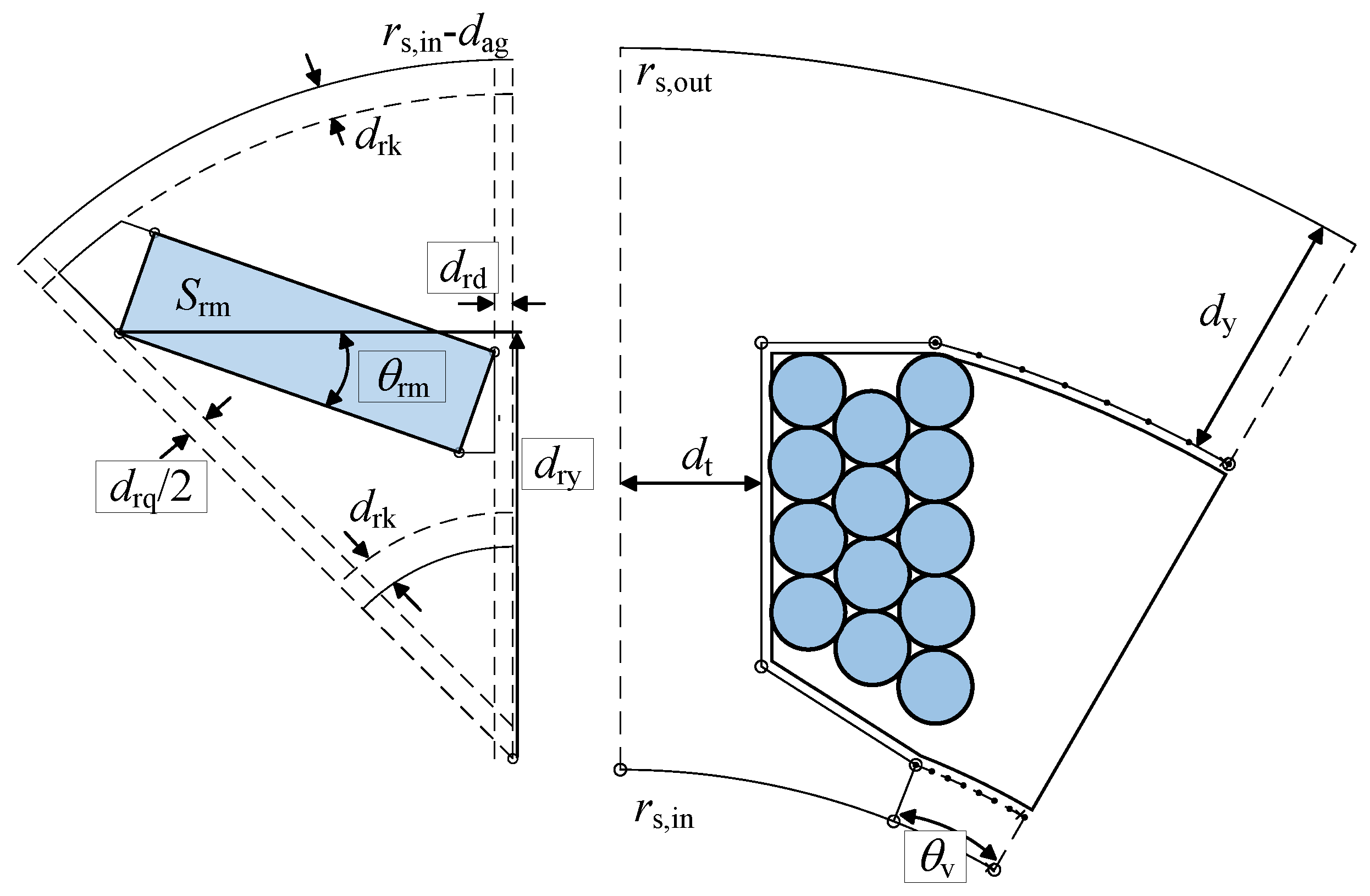
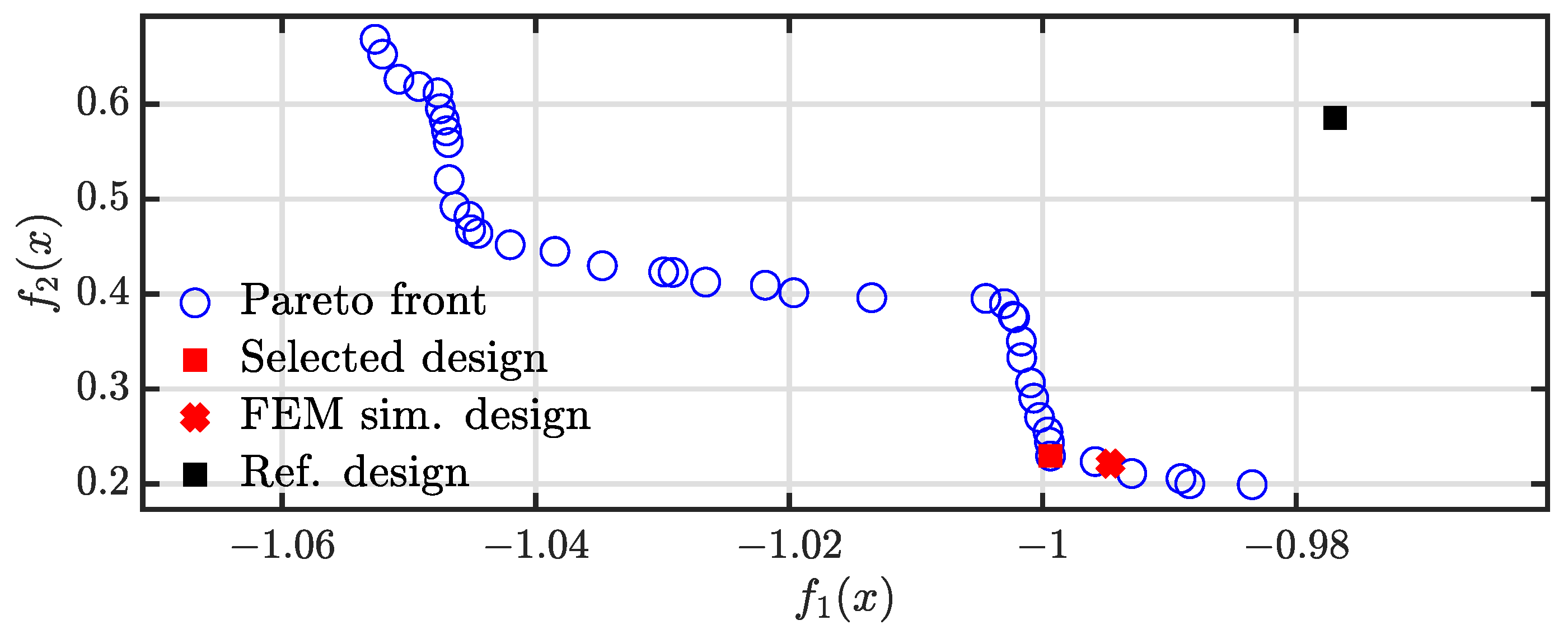
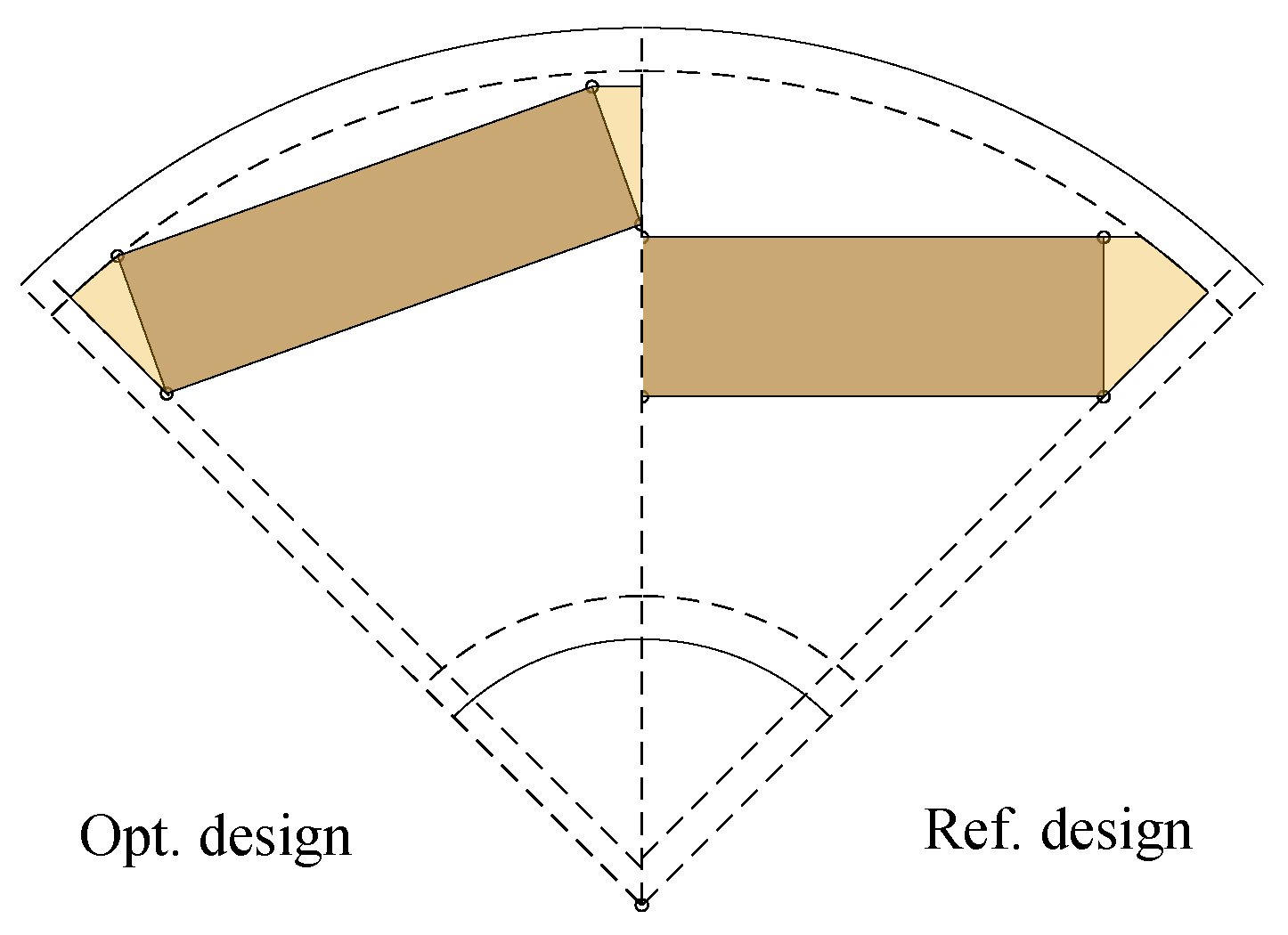
3.2. IPMSM Design Optimization
4. Results
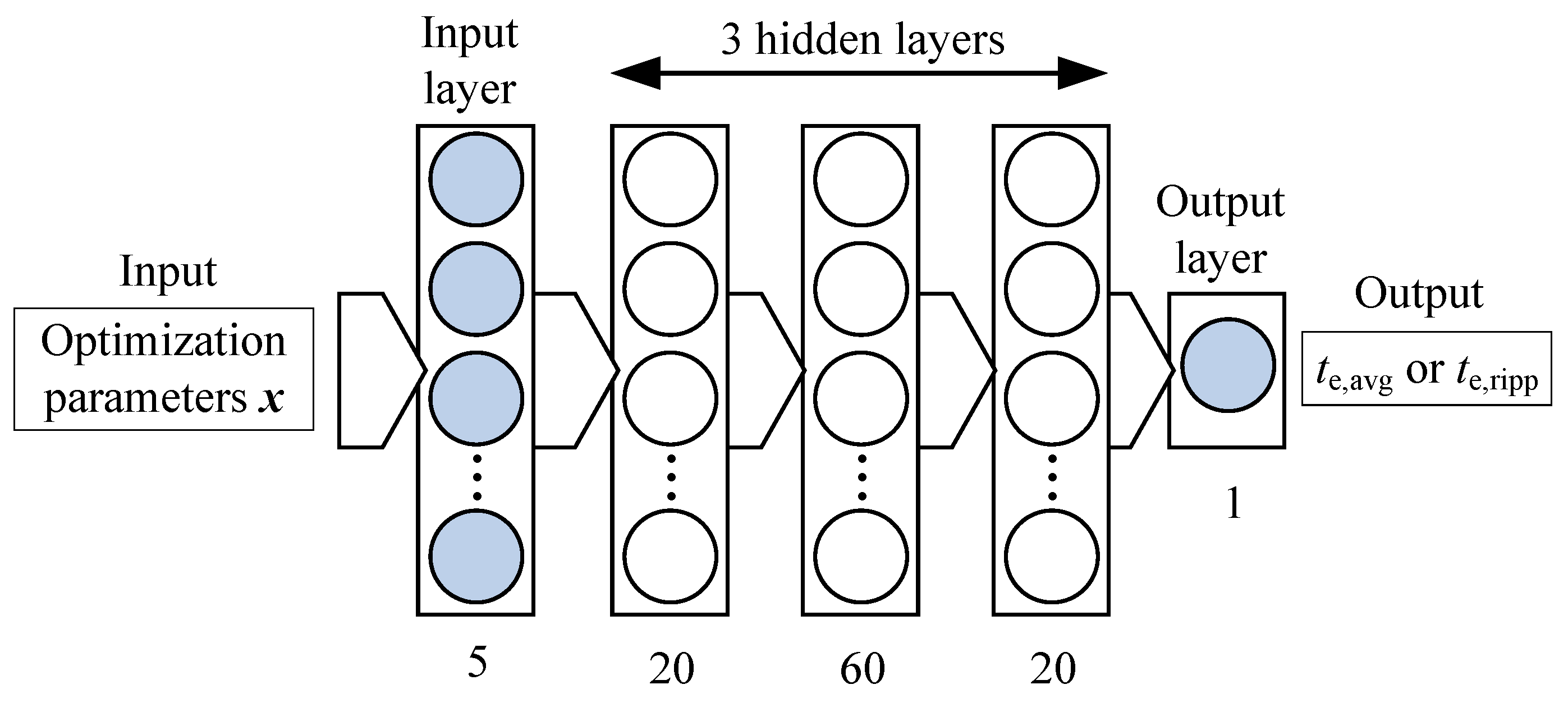
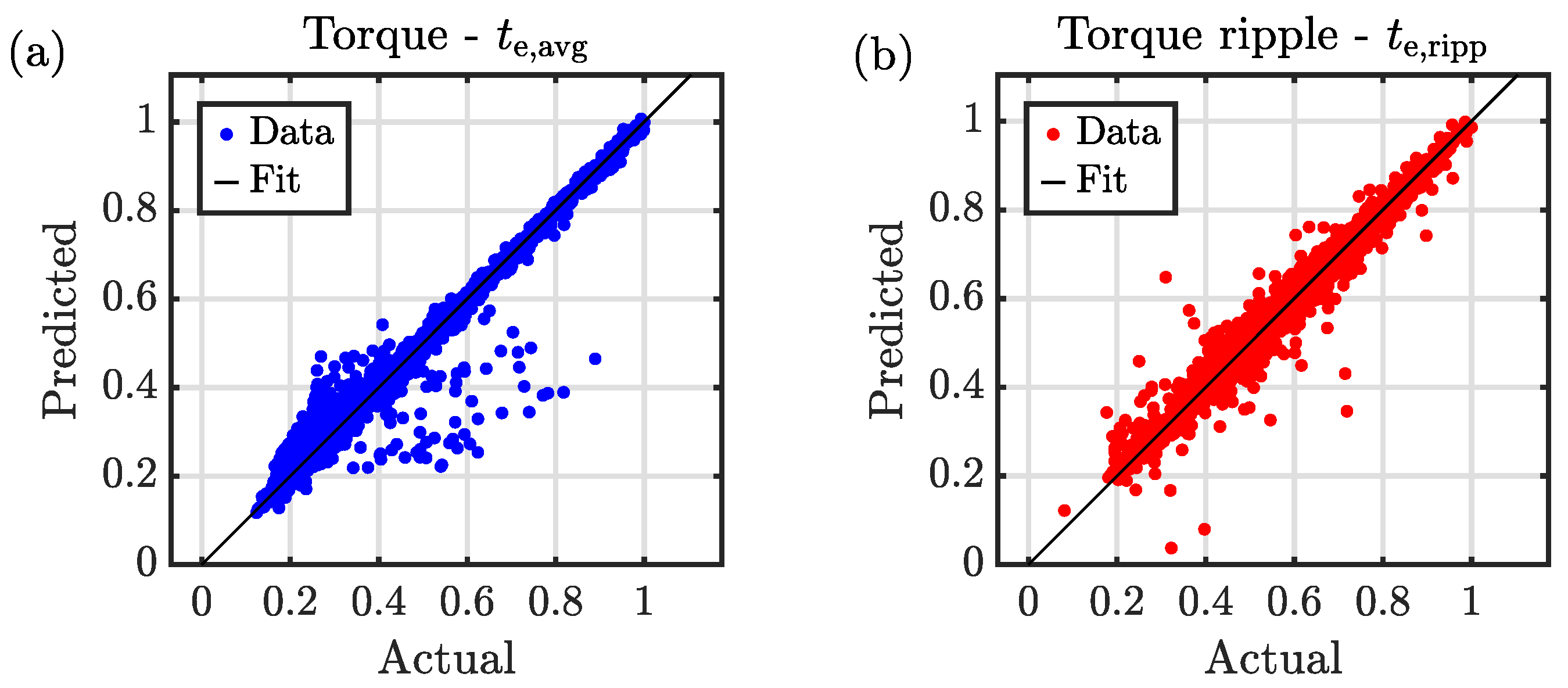
4.1. Design Optimization and Computational Efficiency
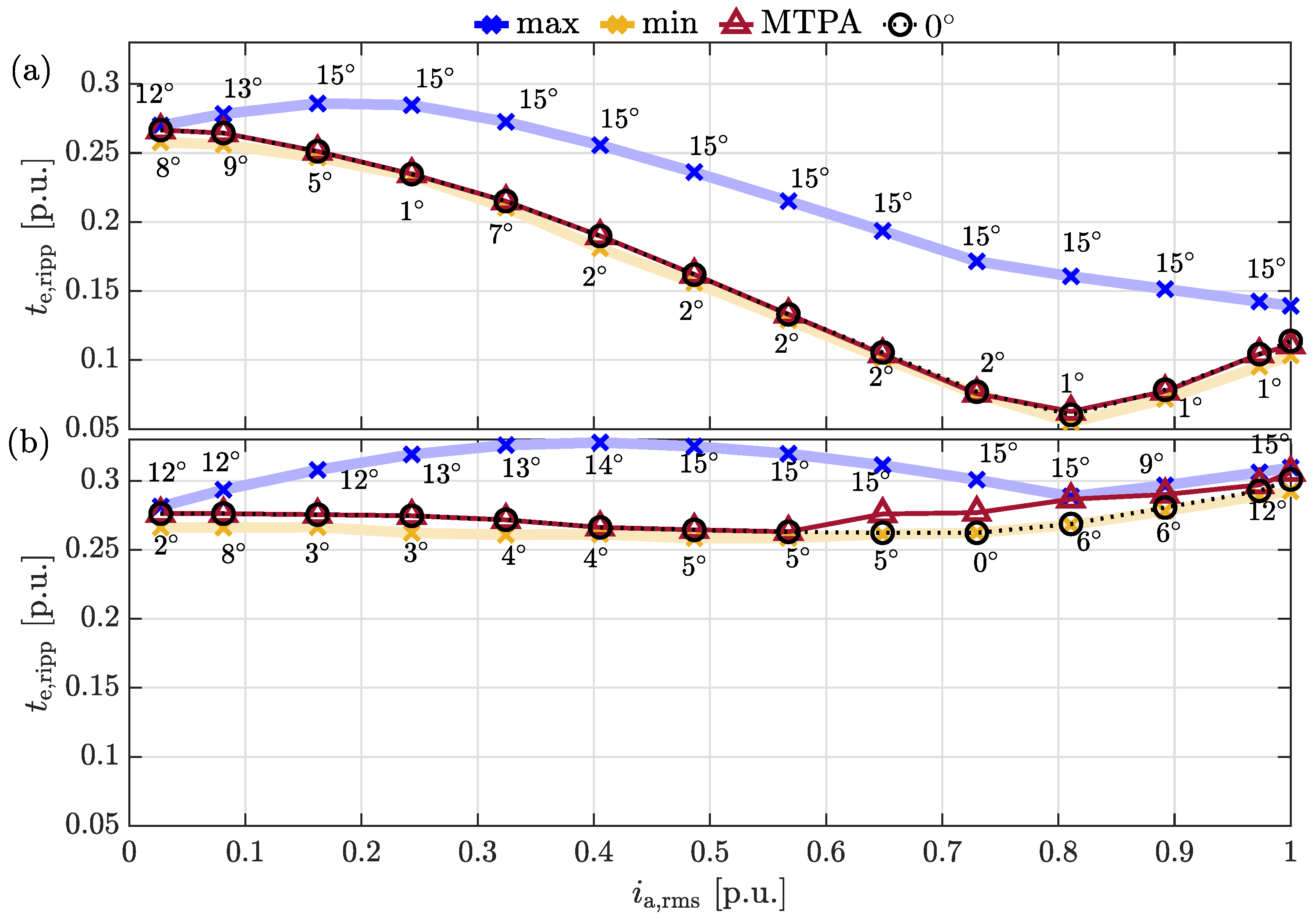
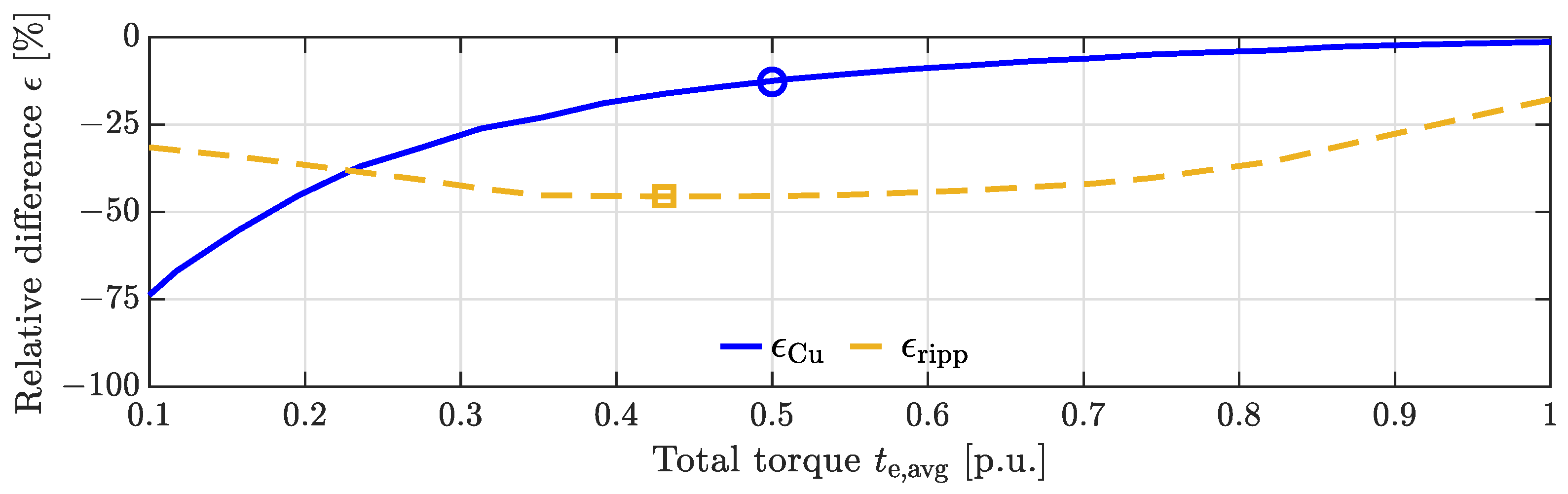
4.2. Analysis in the Case of an Ideally Shaped Current
4.3. System-Level Simulation Analysis
- It was possible to model the nonlinear electromagnetic behavior of discussed IPMSM designs according to the respective FEM models and reproduce all the related effects in the system-level simulation.
- By varying the DC at a set mechanical speed = 0.78 p.u., we analyzed the RMS phase currents , torque ripples , and electromagnetic torques .
- The AF angle , could be adjusted according to different strategies for benchmarking purposes.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AF | advance firing |
| BLAC | brushless alternating current |
| BLDC | brushless direct current |
| DC | direct current |
| EMF | electromotive force |
| FEM | finite element method |
| FOC | field-oriented control |
| IPMSM | interior permanent magnet synchronous machine |
| MOSFET | metal oxide semiconductor field effect transistor |
| MTPA | maximum torque per ampere |
| PMSM | permanent magnet synchronous machine |
| ROM | reduced order model |
| RMS | root mean square |
| SPMSM | surface permanent magnet synchronous machine |
| SWC | square-wave control |
References
- Hendershot, J.R.; Miller, T.J.E. Design of Brushless Permanent-Magnet Motors; Motor Design Books: Venice, FL, USA, 2010. [Google Scholar]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D.; Pekarek, S.D. Analysis of Electric Machinery and Drive Systems; IEEE Press and Wiley: Piscataway, NJ, USA, 2013. [Google Scholar]
- Han, Q.; Samoylenko, N.; Jatskevich, J. Average-Value Modeling of Brushless DC Motors with 120∘ Voltage Source Inverter. IEEE Trans. Energy Convers. 2008, 23, 423–432. [Google Scholar] [CrossRef]
- Zhou, J.; Ebrahimi, S.; Jatskevich, J. Extended Operation of Brushless DC Motors Beyond 120∘ Under Maximum Torque Per Amperee Control. IEEE Trans. Energy Convers. 2023, 38, 1280–1291. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, J.; Ebrahimi, S.; Jatskevich, J. A Compensation of Commutation Angle in Hall-Sensor-Controlled Brushless DC Motors for Maximum Torque per Ampere Operation. In Proceedings of the 21st International Symposium INFOTEH-JAHORINA, East Sarajevo, Bosnia and Herzegovina, 16–18 March 2022. [Google Scholar]
- Baby, B.K.; George, S. Torque ripple reduction in BLDC motor with 120 degree conduction inverter. In Proceedings of the 2012 Annual IEEE India Conference (INDICON), Kochi, Kerala, India, 7–9 December 2012. [Google Scholar]
- Zhang, P.; Shi, Z.; Yu, B.; Qi, H. Research on the Control Method of a Brushless DC Motor Based on Second-Order Active Disturbance Rejection Control. Machines 2024, 12, 244. [Google Scholar] [CrossRef]
- Mohanraj, D.; Aruldavid, R.; Verma, R.; Sathiyasekar, K.; Barnawi, A.B.; Chokkalingam, B.; Mihet-Popa, L. A Review of BLDC Motor: State of Art, Advanced Control Techniques, and Applications. IEEE Access 2022, 10, 54833–54869. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, H.; Wang, J.; Gao, Y.; Wang, L. Commutation analysis of brushless DC motor and reducing commutation torque ripple in the two-phase stationary frame. IEEE Trans. Power Electron. 2017, 32, 4675–4682. [Google Scholar] [CrossRef]
- Heidari, R.; Ahn, J.-W. Torque ripple reduction of BLDC motor with a low-cost fast-response direct DC-link current control. IEEE Trans. Ind. Electron. 2024, 71, 150–159. [Google Scholar] [CrossRef]
- Sudhoff, S.D.; Krause, P.C. Operating modes of the brushless DC motor with a 120 degrees inverter. IEEE Trans. Energy Convers. 1990, 5, 558–564. [Google Scholar] [CrossRef]
- Dianov, A.; Tinazzi, F.; Calligaro, S.; Bolognani, S. Review and Classification of MTPA Control Algorithms for Synchronous Motors. IEEE Trans. Power Electron. 2022, 37, 3990–4007. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator. IEEE Trans. Ind. Appl. 1994, 30, 920–926. [Google Scholar] [CrossRef]
- Eldeeb, H.; Hackl, C.M.; Horlbeck, L.; Kullick, J. A Unified Theory for Optimal Feedforward Torque Control of Anisotropic Synchronous Machines. Int. J. Control 2018, 91, 2273–2302. [Google Scholar] [CrossRef]
- Khazaee, A.; Zarchi, H.A.; Markadeh, G.A.; Mosaddegh Hesar, H. MTPA Strategy for Direct Torque Control of Brushless DC Motor Drive. IEEE Trans. Ind. Electron. 2021, 68, 6692–6700. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y. Maximum Torque per Ampere (MTPA) Control for IPMSM Drives Using Signal Injection and an MTPA Control Law. IEEE Trans. Ind. Inform. 2019, 15, 5588–5598. [Google Scholar] [CrossRef]
- Dianov, A.; Anuchin, A. Design of Constraints for Seeking Maximum Torque Per Ampere Techniques in an Interior Permanent Magnet Synchronous Motor. Mathematics 2021, 9, 2785. [Google Scholar] [CrossRef]
- Garmut, M.; Steentjes, S.; Petrun, M. Parameter identification for MTPA control based on a nonlinear d-q dynamic IPMSM model. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2022, 42, 846–860. [Google Scholar] [CrossRef]
- Jung, W.-S.; Lee, H.-K.; Lee, Y.-K.; Kim, S.-M.; Lee, J.-I.; Choi, J.-Y. Analysis and Comparison of Permanent Magnet Synchronous Motors According to Rotor Type under the Same Design Specifications. Energies 2023, 16, 1306. [Google Scholar] [CrossRef]
- Bertoluzzo, M.; Buja, G.; Keshri, R.K.; Menis, R. Sinusoidal Versus Square-Wave Current Supply of PM Brushless DC Drives: A Convenience Analysis. IEEE Trans. Ind. Electron. 2015, 62, 7339–7349. [Google Scholar] [CrossRef]
- Yan, M.; Wen, B.; Cui, Q.; Peng, X. Parameter Identification for Maximum Torque Per Ampere Control of Permanent Magnet Synchronous Machines Under Magnetic Saturation. Electronics 2024, 13, 699. [Google Scholar] [CrossRef]
- Elsherbiny, H.; Szamel, L.; Ahmed, M.K.; Elwany, M.A. High Accuracy Modeling of Permanent Magnet Synchronous Motors Using Finite Element Analysis. Mathematics 2022, 10, 3880. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Li, W.; Zhang, T.; Wang, R.; Huang, S.; Liang, J. Multimodal Multi-objective Optimization: Comparative Study of the State-of-the-art. Swarm Evol. Comput. 2023, 77, 101253. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Zavoianu, A.-C. Surrogate-Based Multi-Objective Optimization of Electrical Machine Designs Facilitating Tolerance Analysis. IEEE Trans. Magn. 2017, 53, 1–11. [Google Scholar] [CrossRef]
- Zheng, S.; Zhu, X.; Xu, L.; Xiang, Z.; Quan, L.; Yu, B. Multi-Objective Optimization Design of a Multi-Permanent-Magnet Motor Considering Magnet Characteristic Variation Effects. IEEE Trans. Ind. Electron. 2022, 69, 3428–3438. [Google Scholar] [CrossRef]
- Zarko, D.; Stipetic, S.; Martinovic, M.; Kovacic, M.; Jercic, T.; Hanic, Z. Reduction of Computational Efforts in Finite Element-Based Permanent Magnet Traction Motor Optimization. IEEE Trans. Ind. Electron. 2018, 65, 1799–1807. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Multi-Objective Design Optimization of an IPMSM Based on Multilevel Strategy. IEEE Trans. Ind. Electron. 2021, 68, 139–148. [Google Scholar] [CrossRef]
- Parekh, V.; Flore, D.; Schöps, S. Deep Learning-Based Prediction of Key Performance Indicators for Electrical Machines. IEEE Access 2021, 9, 21786–21797. [Google Scholar] [CrossRef]
- Gör, H. Feasibility of Six Metaheuristic Solutions for Estimating Induction Motor Reactance. Mathematics 2024, 12, 483. [Google Scholar] [CrossRef]
- Sasaki, H.; Hidaka, Y.; Igarashi, H. Prediction of IPM Machine Torque Characteristics Using Deep Learning Based on Magnetic Field Distribution. IEEE Access 2022, 10, 60814–60822. [Google Scholar] [CrossRef]
- Parekh, V.; Flore, D.; Schöps, S. Deep Learning-Based Meta-Modeling for Multi-Objective Technology Optimization of Electrical Machines. IEEE Access 2023, 11, 93420–93430. [Google Scholar] [CrossRef]
- Li, Y.; Lei, G.; Bramerdorfer, G.; Peng, S.; Sun, X.; Zhu, J. Machine Learning for Design Optimization of Electromagnetic Devices: Recent Developments and Future Directions. Appl. Sci. 2021, 11, 1627. [Google Scholar] [CrossRef]
- Weidenholzer, G.; Silber, S.; Jungmayr, G.; Bramerdorfer, G.; Grabner, H.; Amrhein, W. A flux-based PMSM motor model using RBF interpolation for time-stepping simulations. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013. [Google Scholar]
- Mohammed, O.A.; Liu, S.; Liu, Z. A phase variable model of brushless dc motors based on finite element analysis and its coupling with external circuits. IEEE Trans. Magn. 2005, 41, 1576–1579. [Google Scholar] [CrossRef]
- Sizov, G.Y.; Ionel, D.M.; Demerdash, N.A.O. Modeling and Parametric Design of Permanent-Magnet AC Machines Using Computationally Efficient Finite-Element Analysis. IEEE Trans. Ind. Electron. 2012, 59, 2403–2413. [Google Scholar] [CrossRef]
- Steentjes, S.; Leßmann, M.; Hameyer, K. Advanced iron-loss calculation as a basis for efficiency improvement of electrical machines in automotive application. In Proceedings of the Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012. [Google Scholar]
- Garmut, M.; Petrun, M. Influence of stator segmentation on iron losses in PMSMs for traction applications. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 644–658. [Google Scholar] [CrossRef]
- gamultiobj: Find Pareto front of Multiple Fitness Functions Using Genetic Algorithm. Available online: https://www.mathworks.com/help/gads/gamultiobj.html (accessed on 10 April 2024).



| SPMSMs | IPMSMs | |
|---|---|---|
| magnet position | mounted on the rotor surface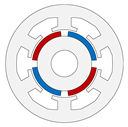 | embedded within the rotor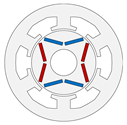 |
| magnetic circuit | constant reluctance, independent on the rotor position | varying reluctance, dependent on the rotor position |
| torque | due to permanent magnets | due to permanent magnets and varying reluctance |
| torque-to-current ratio | lower | higher |
| power density | lower | higher |
| flux-weakening capability | lower | higher |
| MTPA AF angle adjustment | none, | dependent on load current, i.e., |
| Design Case | Winding Connection Type | Shape of Figure 5a | Shape of Figure 5b | Current Figure 5c | Torque | Char. Current | AF Angle |
|---|---|---|---|---|---|---|---|
| 1 | Wye | Trap. (7) | Trap. (8) | (6) | (13) | (26) | (29) |
| 2 | Delta | Trap., (19) | Trap. (8), | (18) | (22) | (26) | (29) |
| 3 | Delta | Sin., (20) | Trap., (8) | (18) | (23) | (27) | (30) |
| 4 | Delta | Trap., (19) | Sin., (21) | (18) | (24) | (28) | (31) |
| 5 | Delta | Sin., (20) | Sin., (21) | (18) | (25) | / | (32) |
| Parameters | Description | Unit | Ref. Value | Min | Max |
|---|---|---|---|---|---|
| Slot opening angle | ° | 7.5 | 5 | 10 | |
| q-axis bridge width | p.u. | 0.074 | 0.026 | 0.184 | |
| d-axis bridge width | p.u. | 0 | 0 | 0.184 | |
| Magnet tip height | p.u. | 0.563 | 0.268 | 0.783 | |
| Magnet angle | ° | 0 | 25 | ||
| Stator outer radius | p.u. | 1.9 | / | / | |
| Stator inner radius | p.u. | 1 | / | / | |
| Yoke width | p.u. | 0.30 | / | / | |
| Tooth width | p.u. | 0.23 | / | / | |
| Minimal bridge width | p.u. | 0.05 | / | / | |
| Air gap width | p.u. | 0.03 | / | / | |
| Magnet area | p.u. | 1 | / | / |
| Par. | Unit | Ref. | Opt. |
|---|---|---|---|
| ° | 7.5 | 7.2 | |
| p.u. | 0.074 | 0.058 | |
| p.u. | 0 | 0 | |
| p.u. | 0.563 | 0.619 | |
| ° | 0 | 19.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garmut, M.; Steentjes, S.; Petrun, M. Optimization of an IPMSM for Constant-Angle Square-Wave Control of a BLDC Drive. Mathematics 2024, 12, 1418. https://doi.org/10.3390/math12101418
Garmut M, Steentjes S, Petrun M. Optimization of an IPMSM for Constant-Angle Square-Wave Control of a BLDC Drive. Mathematics. 2024; 12(10):1418. https://doi.org/10.3390/math12101418
Chicago/Turabian StyleGarmut, Mitja, Simon Steentjes, and Martin Petrun. 2024. "Optimization of an IPMSM for Constant-Angle Square-Wave Control of a BLDC Drive" Mathematics 12, no. 10: 1418. https://doi.org/10.3390/math12101418
APA StyleGarmut, M., Steentjes, S., & Petrun, M. (2024). Optimization of an IPMSM for Constant-Angle Square-Wave Control of a BLDC Drive. Mathematics, 12(10), 1418. https://doi.org/10.3390/math12101418








