A Review of Intelligent Airfoil Aerodynamic Optimization Methods Based on Data-Driven Advanced Models
Abstract
1. Introduction
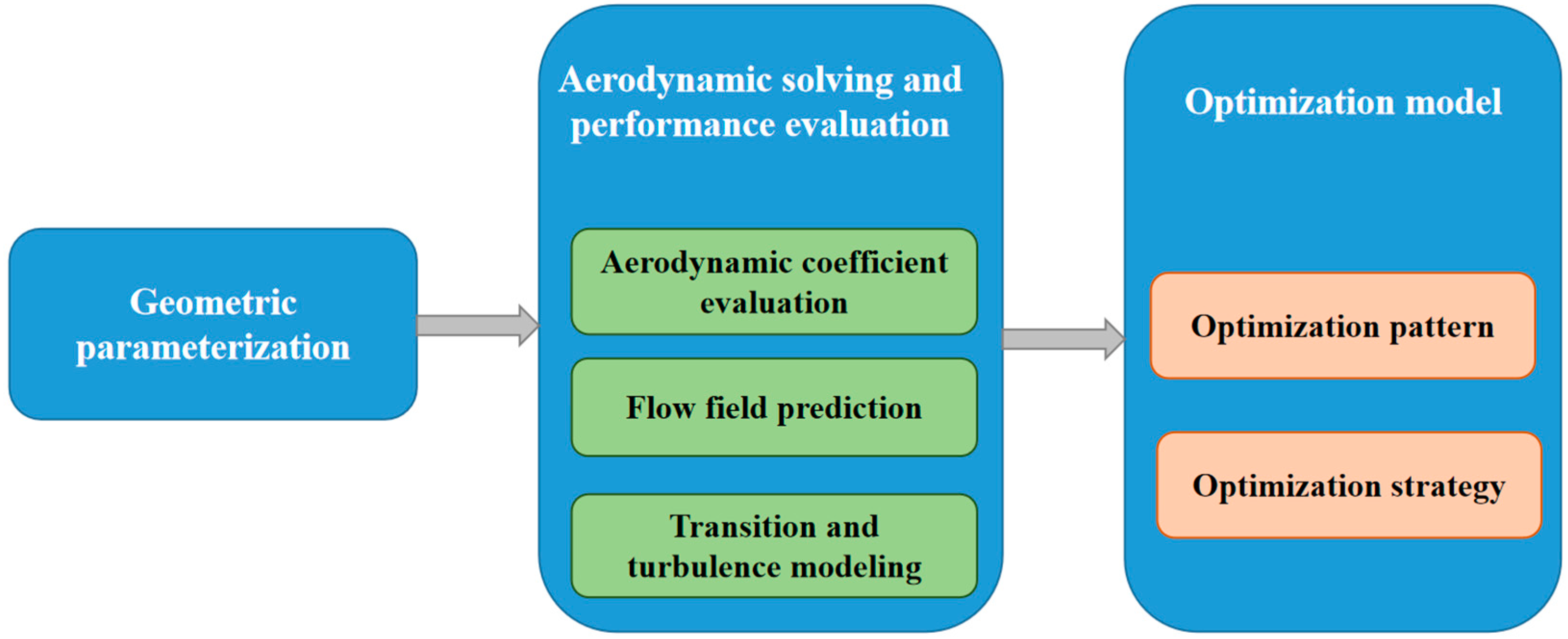
2. Data-Driven Advanced Model in Critical Steps of Airfoil Aerodynamic Optimization
2.1. Geometric Parameterization
2.2. Aerodynamic Solving and Performance Evaluation
2.2.1. Aerodynamic Coefficient Evaluation
2.2.2. Flow Field Prediction
2.2.3. Transition Modeling and Turbulence Modeling
2.3. Optimization Model
2.3.1. Optimization Pattern
2.3.2. Optimization Strategy
3. Conclusions
- (a)
- Expanding the database for aerodynamic modeling. A large and sufficient amount of data is the basis for aerodynamic modeling. There is no sufficient publicly available dataset with abundant flow field characteristics for aerodynamic optimization. The quantity and quality of data limit the further development and application of models. In order to address the above problem, it is recommended to develop aerodynamic modeling strategies applicable for small-scale data, e.g., data augmentation and meta-learning-based modeling methods. The construction of a large-scale aerodynamic database might also be enhanced, and the data fusion of wind tunnel test, flight test, and numerical simulation data could be considered.
- (b)
- Improving the interpretability and generalization of advanced models. Most of the current aerodynamic models are “black box” models, making it hard for researchers to understand the learning principle and process in the network. Improving the interpretability of advanced models and transforming models from the original “black box” to “gray box” or even “white box” will help to enhance the understanding of aerodynamics and realize the update of knowledge in the progress of optimization. On the other hand, improving the generalizability of advanced models is also significant for the expansion of application scenes and the improvement of optimization design efficiency.
- (c)
- Enhancing the ability of advanced models to solve 3D complex configuration optimization. The “dimensional disasters” by three-dimensional complex configurations are a great challenge for optimization design. Compared to aerodynamic optimization of 2D configurations, the difficulty of each process of 3D complex configuration optimization increases significantly. Most of the current advanced models focus on improving the efficiency of solving existing problems, and advanced models should be developed to address the unsolved issue by the traditional methods, especially to facilitate the aerodynamic optimization of 3D complex configurations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, G.; Wang, C.; Wang, L.; Tao, J.; Wang, S.; Wang, X.; Zhou, S.; Li, Z.; Hu, Y. Application and prospect of artificial intelligence in aerodynamic design. Civ. Aircr. Des. Res. 2021, 3, 1–9. [Google Scholar]
- Jameson, A. Aerodynamic design. In Computational Science for the 21st Century; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Van Leer, B. CFD education-Past, present, future. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999. [Google Scholar]
- Li, J.; Du, X.; Martins, J.R. Machine learning in aerodynamic shape optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, M.; Zhang, M. Review of large civil aircraft aerodynamic design. Acta Aeronaut. Astronaut. Sin. 2019, 40, 522759. [Google Scholar]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Conroy, G. Handbook of genetic algorithms by Lawrence Davis (Ed.), Chapman & Hall, London, 1991, pp 385, £ 32.50. Knowl. Eng. Rev. 1991, 6, 363–365. [Google Scholar]
- Shi, Y. Particle swarm optimization. IEEE Connect. 2004, 2, 8–13. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Approximating the nondominated front using the Pareto archived evolution strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef] [PubMed]
- Taguchi, G. Introduction to Quality Engineering, Asian Productivity Organization; American Supplier Institute Inc.: Dearborn, MI, USA, 1986. [Google Scholar]
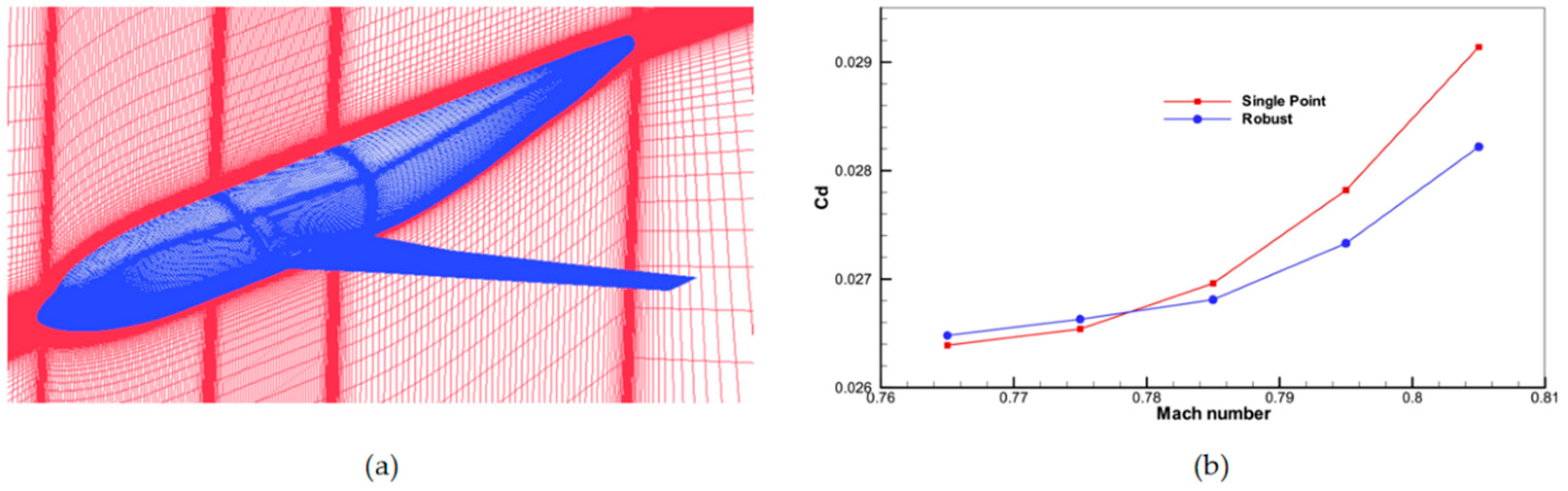
- Tao, J.; Sun, G.; Wang, X.; Guo, L. Robust optimization for a wing at drag divergence Mach number based on an improved PSO algorithm. Aerosp. Sci. Technol. 2019, 92, 653–667. [Google Scholar] [CrossRef]
- Lee, S.W.; Kwon, O.J. Robust airfoil shape optimization using design for six sigma. J. Aircr. 2006, 43, 843–846. [Google Scholar] [CrossRef]
- Papadimitriou, D.I.; Papadimitriou, C. Aerodynamic shape optimization for minimum robust drag and lift reliability constraint. Aerosp. Sci. Technol. 2016, 55, 24–33. [Google Scholar] [CrossRef]
- Schreiner, B.D.J.; Tejero, F.; MacManus, D.G.; Sheaf, C. Robust aerodynamic design of nacelles for future civil aero-engines. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, London, UK, 21–25 September 2020; p. V001T001A015. [Google Scholar]
- Wu, X.; Zhang, W.; Song, S. Robust aerodynamic shape design based on an adaptive stochastic optimization framework. Struct. Multidiscip. Optim. 2018, 57, 639–651. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Kou, J.; Liu, Y. Prospect of artificial intelligence empowered fluid mechanics. Acta Aeronaut. Astronaut. Sin. 2021, 42, 524689. [Google Scholar]
- Tang, Z.; Zhu, L.; Xiang, X. Some research progress and prospect of Intelligent Aerodynamics. Acta Aerodyn. Sin. 2023, 41, 1–35. [Google Scholar]
- Sekar, V.; Jiang, Q.; Shu, C.; Khoo, B.C. Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 2019, 31, 057103. [Google Scholar] [CrossRef]
- Kashefi, A.; Rempe, D.; Guibas, L.J. A point-cloud deep learning framework for prediction of fluid flow fields on irregular geometries. Phys. Fluids 2021, 33, 027104. [Google Scholar] [CrossRef]
- Mohan, A.T.; Gaitonde, D.V. A deep learning based approach to reduced order modeling for turbulent flow control using LSTM neural networks. arXiv 2018, arXiv:1804.09269. [Google Scholar]
- Nagawkar, J.; Leifsson, L. Multifidelity aerodynamic flow field prediction using random forest-based machine learning. Aerosp. Sci. Technol. 2022, 123, 107449. [Google Scholar] [CrossRef]
- Zuo, K.; Ye, Z.; Zhang, W.; Yuan, X.; Zhu, L. Fast aerodynamics prediction of laminar airfoils based on deep attention network. Phys. Fluids 2023, 35, 037127. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Duru, C.; Alemdar, H.; Baran, Ö.U. CNNFOIL: Convolutional encoder decoder modeling for pressure fields around airfoils. Neural Comput. Appl. 2021, 33, 6835–6849. [Google Scholar] [CrossRef]
- Renganathan, S.A.; Maulik, R.; Rao, V. Machine learning for nonintrusive model order reduction of the parametric inviscid transonic flow past an airfoil. Phys. Fluids 2020, 32, 047110. [Google Scholar] [CrossRef]
- Bhatnagar, S.; Afshar, Y.; Pan, S.; Duraisamy, K.; Kaushik, S. Prediction of aerodynamic flow fields using convolutional neural networks. Comput. Mech. 2019, 64, 525–545. [Google Scholar] [CrossRef]
- Peng, J.-Z.; Chen, S.; Aubry, N.; Chen, Z.-H.; Wu, W.-T. Time-variant prediction of flow over an airfoil using deep neural network. Phys. Fluids 2020, 32, 123602. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Machine-learning-based spatio-temporal super resolution reconstruction of turbulent flows. J. Fluid Mech. 2021, 909, A9. [Google Scholar] [CrossRef]
- Liu, B.; Tang, J.; Huang, H.; Lu, X.-Y. Deep learning methods for super-resolution reconstruction of turbulent flows. Phys. Fluids 2020, 32, 025105. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Won, S.; Lee, C. Unsupervised deep learning for super-resolution reconstruction of turbulence. J. Fluid Mech. 2021, 910, A29. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Liu, L.; Wu, X.; Hao, P.; Zhang, X.; He, F. Deep-learning-based super-resolution reconstruction of high-speed imaging in fluids. Phys. Fluids 2022, 34, 037107. [Google Scholar] [CrossRef]
- Jeon, Y.; You, D. Super-resolution reconstruction of transitional boundary layers using a deep neural network. Int. J. Aeronaut. Space Sci. 2023, 24, 1–17. [Google Scholar] [CrossRef]
- Kong, C.; Chang, J.; Wang, Z.; Li, Y.; Bao, W. Data-driven super-resolution reconstruction of supersonic flow field by convolutional neural networks. AIP Adv. 2021, 11, 065321. [Google Scholar] [CrossRef]
- Yousif, M.Z.; Yu, L.; Lim, H.-C. Super-resolution reconstruction of turbulent flow fields at various Reynolds numbers based on generative adversarial networks. Phys. Fluids 2022, 34, 015130. [Google Scholar] [CrossRef]
- Huang, S.; Sun, J.; Yang, Y.; Fang, Y.; Lin, P. Multi-frame super-resolution reconstruction based on gradient vector flow hybrid field. IEEE Access 2017, 5, 21669–21683. [Google Scholar] [CrossRef]
- Yu, L.; Yousif, M.Z.; Zhang, M.; Hoyas, S.; Vinuesa, R.; Lim, H.-C. Three-dimensional ESRGAN for super-resolution reconstruction of turbulent flows with tricubic interpolation-based transfer learning. Phys. Fluids 2022, 34, 125126. [Google Scholar] [CrossRef]
- Yousif, M.Z.; Yu, L.; Lim, H.-C. High-fidelity reconstruction of turbulent flow from spatially limited data using enhanced super-resolution generative adversarial network. Phys. Fluids 2021, 33, 125119. [Google Scholar] [CrossRef]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef] [PubMed]
- Schaeffer, H. Learning partial differential equations via data discovery and sparse optimization. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160446. [Google Scholar] [CrossRef]
- Long, Z.; Lu, Y.; Ma, X.; Dong, B. PDE-net: Learning PDEs from data. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 3208–3216. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Michoski, C.; Milosavljević, M.; Oliver, T.; Hatch, D.R. Solving differential equations using deep neural networks. Neurocomputing 2020, 399, 193–212. [Google Scholar] [CrossRef]
- Venkatachalapathy, P.; Mallikarjunaiah, S. A deep learning neural network framework for solving singular nonlinear ordinary differential equations. Int. J. Appl. Comput. Math. 2023, 9, 68. [Google Scholar] [CrossRef]
- Huang, K.; Krügener, M.; Brown, A.; Menhorn, F.; Bungartz, H.-J.; Hartmann, D. Machine learning-based optimal mesh generation in computational fluid dynamics. arXiv 2021, arXiv:2102.12923. [Google Scholar]
- Peng, L.; Nianhua, W.; Chang, X.; Zhang, L.; Yadong, W. An automatic isotropic/anisotropic hybrid grid generation technique for viscous flow simulations based on an artificial neural network. Chin. J. Aeronaut. 2022, 35, 102–117. [Google Scholar]
- Wang, N.; Lu, P.; Chang, X.; Zhang, L.; Deng, X. Unstructured mesh size control method based on artificial neural network. Chin. J. Theor. Appl. Mech. 2021, 53, 2682–2691. [Google Scholar]
- Wang, N.; Lu, P.; Chang, X.; Zhang, L. Preliminary investigation on unstructured mesh generation technique based on advancing front method and machine learning methods. Chin. J. Theor. Appl. Mech. 2021, 53, 740–751. [Google Scholar]
- Zhang, Z.; Wang, Y.; Jimack, P.K.; Wang, H. MeshingNet: A new mesh generation method based on deep learning. In Proceedings of the International Conference on Computational Science, Amsterdam, Netherlands, 3–5 June 2020; pp. 186–198. [Google Scholar]
- Lu, P.; Wang, N.; Lin, Y.; Zhang, X.; Wu, Y.; Zhang, H. A new unstructured hybrid mesh generation method based on BP-ANN. J. Phys. Conf. Ser. 2020, 2280, 012045. [Google Scholar] [CrossRef]
- Lu, X.; Huang, J.; Song, L.; Li, J. An improved geometric parameter airfoil parameterization method. Aerosp. Sci. Technol. 2018, 78, 241–247. [Google Scholar] [CrossRef]
- Liem, R.P.; Mader, C.A.; Martins, J.R. Surrogate models and mixtures of experts in aerodynamic performance prediction for aircraft mission analysis. Aerosp. Sci. Technol. 2015, 43, 126–151. [Google Scholar] [CrossRef]
- Shukla, K.; Oommen, V.; Peyvan, A.; Penwarden, M.; Bravo, L.; Ghoshal, A.; Kirby, R.M.; Karniadakis, G.E. Deep neural operators can serve as accurate surrogates for shape optimization: A case study for airfoils. arXiv 2023, arXiv:2302.00807. [Google Scholar]
- Pan, M.; Chen, F.; Tong, W. Volumetric spline parameterization for isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2020, 359, 112769. [Google Scholar] [CrossRef]
- Sobieszczanski-Sobieski, J.; Haftka, R.T. Multidisciplinary aerospace design optimization: Survey of recent developments. Struct. Optim. 1997, 14, 1–23. [Google Scholar] [CrossRef]
- Kulfan, B.; Bussoletti, J. “Fundamental” parameteric geometry representations for aircraft component shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VI, USA, 6–8 September 2006; p. 6948. [Google Scholar]
- De Boor, C.; De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978; Volume 27. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hicks, R.M.; Henne, P.A. Wing design by numerical optimization. J. Aircr. 1978, 15, 407–412. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 18–22 August 1986; pp. 151–160. [Google Scholar]
- Robinson, G.; Keane, A. Concise orthogonal representation of supercritical airfoils. J. Aircr. 2001, 38, 580–583. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Tao, J.; Sun, G.; Mao, J. A PCA–ANN-based inverse design model of stall lift robustness for high-lift device. Aerosp. Sci. Technol. 2018, 81, 272–283. [Google Scholar] [CrossRef]
- Poole, D.J.; Allen, C.B.; Rendall, T. Aerofoil design variable extraction for aerodynamic optimization. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 2705. [Google Scholar]
- Li, J.; Bouhlel, M.A.; Martins, J.R. Data-based approach for fast airfoil analysis and optimization. AIAA J. 2019, 57, 581–596. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Chen, W.; Chiu, K.; Fuge, M.D. Airfoil design parameterization and optimization using bézier generative adversarial networks. AIAA J. 2020, 58, 4723–4735. [Google Scholar] [CrossRef]
- Du, X.; He, P.; Martins, J.R. Rapid airfoil design optimization via neural networks-based parameterization and surrogate modeling. Aerosp. Sci. Technol. 2021, 113, 106701. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Cao, C.; Sun, G.; Huang, Y.; Zhou, S. Aerodynamic Optimization Framework for a Three-Dimensional Nacelle Based on Deep Manifold Learning-Assisted Geometric Multiple Dimensionality Reduction. Aerospace 2023, 10, 573. [Google Scholar] [CrossRef]
- Sóbester, A.; Keane, A.J. Supervised learning approach to parametric computer-aided design geometry repair. AIAA J. 2006, 44, 282–289. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Martins, J.R.; Shu, C. Efficient aerodynamic shape optimization with deep-learning-based geometric filtering. AIAA J. 2020, 58, 4243–4259. [Google Scholar] [CrossRef]
- Wu, H.; Liu, X.; An, W.; Chen, S.; Lyu, H. A deep learning approach for efficiently and accurately evaluating the flow field of supercritical airfoils. Comput. Fluids 2020, 198, 104393. [Google Scholar] [CrossRef]
- Wang, X.; Ni, B.; Zeng, L.; Liu, Y. An adaptive sampling strategy for construction of surrogate aerodynamic model. Aerosp. Sci. Technol. 2021, 112, 106594. [Google Scholar] [CrossRef]
- Han, Z.-H.; Zhang, K.-S. Surrogate-based optimization. Real-World Appl. Genet. Algorithms 2012, 343, 343–362. [Google Scholar]
- Eden, M.R.; Siirola, J.D.; Towler, G. Proceedings of the 8th International Conference on Foundations of Computer-Aided Process Design; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Ahn, J.; Kim, H.-J.; Lee, D.-H.; Rho, O.-H. Response surface method for airfoil design in transonic flow. J. Aircr. 2001, 38, 231–238. [Google Scholar] [CrossRef]
- Giunta, A.; Narducci, R.; Burgee, S.; Grossman, B.; Mason, W.; Watson, L.; Haftka, R. Variable-complexity response surface aerodynamic design of an HSCT wing. In Proceedings of the 13th Applied Aerodynamics Conference, Diego, CA, USA, 19–22 June 1995; p. 1886. [Google Scholar]
- Han, Z.-H.; Zhang, Y.; Song, C.-X.; Zhang, K.-S. Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization. AIAA J. 2017, 55, 4330–4346. [Google Scholar] [CrossRef]
- Han, Z.-H.; Chen, J.; Zhang, K.-S.; Xu, Z.-M.; Zhu, Z.; Song, W.-P. Aerodynamic shape optimization of natural-laminar-flow wing using surrogate-based approach. AIAA J. 2018, 56, 2579–2593. [Google Scholar] [CrossRef]
- Oktay, T.; Çelik, H.; Uzun, M. A novel learning algorithm to estimate the optimum fuselage drag coefficient. Sak. Univ. J. Sci. 2017, 21, 63–68. [Google Scholar]
- Bouhlel, M.A.; He, S.; Martins, J.R. Scalable gradient–enhanced artificial neural networks for airfoil shape design in the subsonic and transonic regimes. Struct. Multidiscip. Optim. 2020, 61, 1363–1376. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. Data-based approach for wing shape design optimization. Aerosp. Sci. Technol. 2021, 112, 106639. [Google Scholar] [CrossRef]
- Zhang, Y.; Sung, W.J.; Mavris, D.N. Application of convolutional neural network to predict airfoil lift coefficient. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1903. [Google Scholar]
- Yu, B.; Xie, L.; Wang, F. An improved deep convolutional neural network to predict airfoil lift coefficient. In Proceedings of the International Conference on Aerospace System Science and Engineering, Toronto, ON, Canada, 30 July–1 August 2019; pp. 275–286. [Google Scholar]
- Bakar, A.; Li, K.; Liu, H.; Xu, Z.; Alessandrini, M.; Wen, D. Multi-objective optimization of low reynolds number airfoil using convolutional neural network and non-dominated sorting genetic algorithm. Aerospace 2022, 9, 35. [Google Scholar] [CrossRef]
- Sun, Y.; Sengupta, U.; Juniper, M. Physics-informed deep learning for simultaneous surrogate modeling and PDE-constrained optimization of an airfoil geometry. Comput. Methods Appl. Mech. Eng. 2023, 411, 116042. [Google Scholar] [CrossRef]
- Holland, J.R.; Baeder, J.D.; Duraisamy, K. Field inversion and machine learning with embedded neural networks: Physics-consistent neural network training. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3200. [Google Scholar]
- Wang, J.; He, C.; Li, R.; Chen, H.; Zhai, C.; Zhang, M. Flow field prediction of supercritical airfoils via variational autoencoder based deep learning framework. Phys. Fluids 2021, 33, 086108. [Google Scholar] [CrossRef]
- Wu, H.; Liu, X.; An, W.; Lyu, H. A generative deep learning framework for airfoil flow field prediction with sparse data. Chin. J. Aeronaut. 2022, 35, 470–484. [Google Scholar] [CrossRef]
- Lan, X.; Wang, L.; Wang, C.; Sun, G.; Feng, J.; Zhang, M. Prediction of Transonic Flow over Cascades via Graph Embedding Methods on Large-Scale Point Clouds. Aerospace 2023, 10, 1029. [Google Scholar] [CrossRef]
- Tieghi, L.; Corsini, A.; Delibra, G.; Angelini, G. Assessment of a Machine-Learnt Adaptive Wall-Function in a Compressor Cascade With Sinusoidal Leading Edge. J. Eng. Gas Turbines Power 2020, 142, 121011. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Lan, X.; Sun, G.; You, B.; Zhong, Y.; Hu, Y. High-fidelity surface flow data-driven aerodynamic solution strategy for non-smooth configurations: Study of compressor cascade with micro riblet surface. Phys. Fluids 2022, 34, 127114. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Wang, S.; Sun, G.; You, B.; Hu, Y. A novel ANN-Based boundary strategy for modeling micro/nanopatterns on airfoil with improved aerodynamic performances. Aerosp. Sci. Technol. 2022, 121, 107347. [Google Scholar] [CrossRef]
- Zafar, M.I.; Xiao, H.; Choudhari, M.M.; Li, F.; Chang, C.-L.; Paredes, P.; Venkatachari, B. Convolutional neural network for transition modeling based on linear stability theory. Phys. Rev. Fluids 2020, 5, 113903. [Google Scholar] [CrossRef]
- Wang, J.-X.; Wu, J.-L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Yang, M.; Xiao, Z. Improving the k–ω–γ–Ar transition model by the field inversion and machine learning framework. Phys. Fluids 2020, 32, 064101. [Google Scholar] [CrossRef]
- Zhang, T.-X.; Chen, J.-Q.; Zeng, F.-Z.; Tang, D.-G.; Yan, C. Improvement of transition prediction model in hypersonic boundary layer based on field inversion and machine learning framework. Phys. Fluids 2023, 35, 024104. [Google Scholar] [CrossRef]
- Zhao, Y.; Akolekar, H.D.; Weatheritt, J.; Michelassi, V.; Sandberg, R.D. RANS turbulence model development using CFD-driven machine learning. J. Comput. Phys. 2020, 411, 109413. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Y. Enhancing the shear-stress-transport turbulence model with symbolic regression: A generalizable and interpretable data-driven approach. Phys. Rev. Fluids 2023, 8, 084604. [Google Scholar] [CrossRef]
- Sun, G.; Wang, S. A review of the artificial neural network surrogate modeling in aerodynamic design. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5863–5872. [Google Scholar] [CrossRef]
- Wu, M.-Y.; Yuan, X.-Y.; Chen, Z.-H.; Wu, W.-T.; Hua, Y.; Aubry, N. Airfoil shape optimization using genetic algorithm coupled deep neural networks. Phys. Fluids 2023, 35, 085140. [Google Scholar] [CrossRef]
- Liao, P.; Song, W.; Du, P.; Zhao, H. Multi-fidelity convolutional neural network surrogate model for aerodynamic optimization based on transfer learning. Phys. Fluids 2021, 33, 127121. [Google Scholar] [CrossRef]
- Sommovigo, S. Development of Airfoil Optimization Procedure Based on Convolutional Neural Networks. Master’s Thesis, Polytechnic University of Milan, Milan, Italy, 2022. [Google Scholar]
- Zhao, X.; Wu, W.; Chen, W.; Lin, Y.; Ke, J. Multi-network collaborative lift-drag ratio prediction and airfoil optimization based on residual network and generative adversarial network. Front. Bioeng. Biotechnol. 2022, 10, 927064. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Medida, S.; Duraisamy, K. Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils. AIAA J. 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
- Zuo, K.; Bu, S.; Zhang, W.; Hu, J.; Ye, Z.; Yuan, X. Fast sparse flow field prediction around airfoils via multi-head perceptron based deep learning architecture. Aerosp. Sci. Technol. 2022, 130, 107942. [Google Scholar] [CrossRef]
- Slotnick, J.P.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D.J. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; Langley Research Center: Hampton, VI, USA, 2014.
- Tani, I. Boundary-layer transition. Annu. Rev. Fluid Mech. 1969, 1, 169–196. [Google Scholar] [CrossRef]
- Li, B.; Yang, Z.; Zhang, X.; He, G.; Deng, B.-Q.; Shen, L. Using machine learning to detect the turbulent region in flow past a circular cylinder. J. Fluid Mech. 2020, 905, A10. [Google Scholar] [CrossRef]
- Meng, D.; Shi, M.; Shi, Y.; Zhu, Y. A machine learning method for transition prediction in hypersonic flows over a cone with angles of attack. AIP Adv. 2022, 12, 025116. [Google Scholar] [CrossRef]
- Paredes, P.; Venkatachari, B.S.; Choudhari, M.M.; Li, F.; Chang, C.-L.; Irfan, M.I.; Xiao, H. Toward Transition Modeling in a Hypersonic Boundary Layer at Flight Conditions. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0103. [Google Scholar]
- Foroozan, F.; Guerrero, V.; Ianiro, A.; Discetti, S. Unsupervised modelling of a transitional boundary layer. J. Fluid Mech. 2021, 929, A3. [Google Scholar] [CrossRef]
- Tracey, B.D.; Duraisamy, K.; Alonso, J.J. A machine learning strategy to assist turbulence model development. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1287. [Google Scholar]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, W.; Kou, J.; Liu, Y. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Phys. Fluids 2019, 31, 015105. [Google Scholar] [CrossRef]
- Vicini, A.; Quagliarella, D. Inverse and direct airfoil design using a multiobjective genetic algorithm. AIAA J. 1997, 35, 1499–1505. [Google Scholar] [CrossRef]
- Tanabi, N.; Silva Jr, A.M.; Pessoa, M.A.O.; Tsuzuki, M.S.G. Robust Algorithm Software for NACA 4-Digit Airfoil Shape Optimization Using the Adjoint Method. Appl. Sci. 2023, 13, 4269. [Google Scholar] [CrossRef]
- Chen, Y.; Rao, H.; Xiong, N.; Fan, J.; Shi, Y.; Yang, T. Adjoint-based robust optimization design of laminar flow airfoil under flight condition uncertainties. Aerosp. Sci. Technol. 2023, 140, 108465. [Google Scholar] [CrossRef]
- Hess, J.L.; Smith, A.M.O. Calculation of potential flow about arbitrary bodies. Prog. Aerosp. Sci. 1967, 8, 1–138. [Google Scholar] [CrossRef]
- Fujiwara, G.E.; Chaparro, D.; Nguyen, N.T. An Integral Boundary Layer Direct Method Applied to 2D Transonic Small-Disturbance Equations. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3568. [Google Scholar]
- Cheng, F.; Xu, Y.; Zhou, W. Nozzle Flow Simulation by Small Disturbance Approximation and Euler Method. J. Phys. Conf. Ser. 2021, 2012, 012048. [Google Scholar] [CrossRef]
- Fuglsang, D.; Williams, M. Non-isentropic unsteady transonic small disturbance theory. In Proceedings of the 26th Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 15–17 April 1985; p. 600. [Google Scholar]
- Owoyele, O.; Pal, P. A novel machine learning-based optimization algorithm (ActivO) for accelerating simulation-driven engine design. Appl. Energy 2021, 285, 116455. [Google Scholar] [CrossRef]
- Song, X.; Wang, L.; Luo, X. Airfoil optimization using a machine learning-based optimization algorithm. J. Phys. Conf. Ser. 2022, 2217, 012009. [Google Scholar] [CrossRef]
- Sun, G.; Sun, Y.; Wang, S. Artificial neural network based inverse design: Airfoils and wings. Aerosp. Sci. Technol. 2015, 42, 415–428. [Google Scholar] [CrossRef]
- Sekar, V.; Zhang, M.; Shu, C.; Khoo, B.C. Inverse design of airfoil using a deep convolutional neural network. AIAA J. 2019, 57, 993–1003. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, C.; Chen, H. An inverse design method for airfoils based on pressure gradient distribution. Energies 2020, 13, 3400. [Google Scholar] [CrossRef]
- Wang, J.; Li, R.; He, C.; Chen, H.; Cheng, R.; Zhai, C.; Zhang, M. An inverse design method for supercritical airfoil based on conditional generative models. Chin. J. Aeronaut. 2022, 35, 62–74. [Google Scholar] [CrossRef]
- Yang, S.; Lee, S.; Yee, K. Inverse design optimization framework via a two-step deep learning approach: Application to a wind turbine airfoil. Eng. Comput. 2023, 39, 2239–2255. [Google Scholar] [CrossRef]
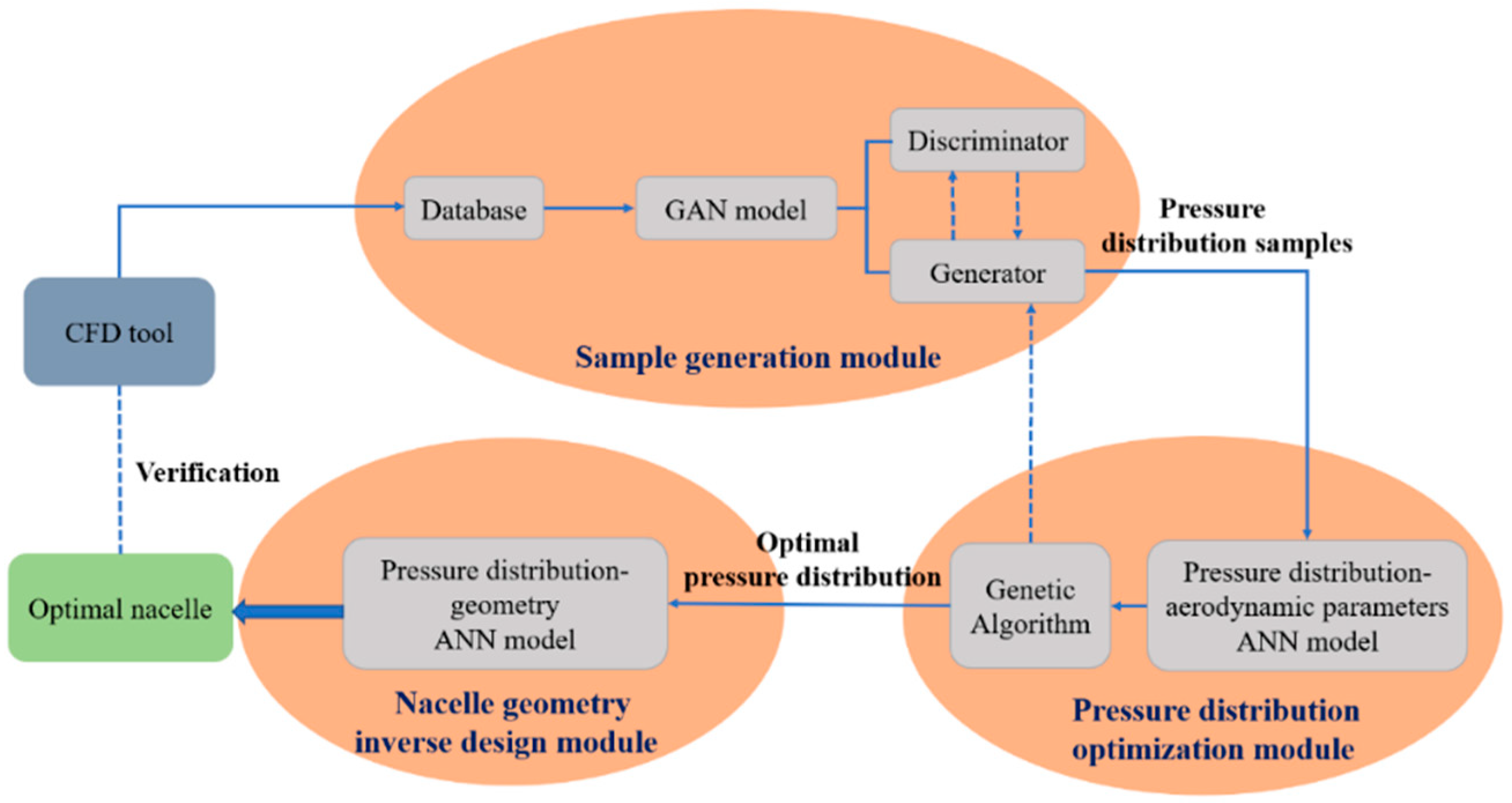
- Wang, C.; Wang, S.; Wang, L.; Cao, C.; Sun, G.; Li, C.; Yang, Y. Framework of nacelle inverse design method based on improved generative adversarial networks. Aerosp. Sci. Technol. 2022, 121, 107365. [Google Scholar] [CrossRef]
- Xing, Y.; Luo, D.; Yu, X. Optimization strategy of supercritical laminar flow airfoil design. J. Beijing Univ. Aeronaut. Astronsutics 2017, 43, 1616–1624. [Google Scholar]
- Hicks, R.M.; Vanderplaats, G.N. Application of Numerical Optimization to the Design of Supercritical Airfoils without Drag-Creep; SAE Technical Paper; SAE: Warrendale, PA, USA, 1977. [Google Scholar]
- Ye, J.; Sun, G. Supercritical Wing Aerodynamic Optimization Based on Multi-Strategy Method. Chin. Q. Mech. 2012, 33, 602–611. [Google Scholar]
- Wu, L.; Luc, H.; Sharon, P.; Bushnell, D.M. Robust airfoil optimization to achieve drag reduction over a range of Mach numbers. Struct. Multidiscip. Optim. 2001, 24, 38–50. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Tang, Z.; Zhang, L. Nash equilibrium and multi criterion aerodynamic optimization. J. Comput. Phys. 2016, 314, 107–126. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Q.; Han, Z. MOEA/D with gradient-enhanced kriging for expensive multiobjective optimization. Nat. Comput. 2023, 22, 329–339. [Google Scholar] [CrossRef]


| Target | Typical Advanced Models | References |
|---|---|---|
| Aerodynamic coefficient evaluation | Response surface method | Ahn et al. [81] Giunta et al. [82] |
| Kriging model | Han et al. [83,84] | |
| ANN/DNN | Oktay et al. [85] Wang et al. [67] Bouhlel et al. [86] Li and Zhang et al. [87] | |
| CNN | Zhang et al. [88] Yu et al. [89] Bakar et al. [90] | |
| Physical informed machine learning | Sun et al. [91] | |
| Flow field prediction | ANN/DNN | Renganathan et al. [28] |
| CNN | Bhatnagar et al. [29] | |
| LSTM | Mohan and Gaitonde [23] | |
| Physical informed machine learning | Raissi et al. [45,46] | |
| Field inversion and machine learning | Holland et al. [92] | |
| VAE | Wang et al. [93] | |
| GAN | Wu et al. [94] | |
| GCN | Lan et al. [95] | |
| Transition modeling and turbulence modeling | ANN/DNN | Tieghi et al. [96] Wang et al. [97,98] |
| CNN | Zafar et al. [99] | |
| Physical informed machine learning | Wang et al. [100] | |
| Field inversion and machine learning | Yang et al. [101] Zhang et al. [102] | |
| Symbolic regression | Zhao et al. [103] Wu and Zhang et al. [104] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, H.; Wang, C.; Tao, J.; Lan, X.; Sun, G.; Feng, J. A Review of Intelligent Airfoil Aerodynamic Optimization Methods Based on Data-Driven Advanced Models. Mathematics 2024, 12, 1417. https://doi.org/10.3390/math12101417
Wang L, Zhang H, Wang C, Tao J, Lan X, Sun G, Feng J. A Review of Intelligent Airfoil Aerodynamic Optimization Methods Based on Data-Driven Advanced Models. Mathematics. 2024; 12(10):1417. https://doi.org/10.3390/math12101417
Chicago/Turabian StyleWang, Liyue, Haochen Zhang, Cong Wang, Jun Tao, Xinyue Lan, Gang Sun, and Jinzhang Feng. 2024. "A Review of Intelligent Airfoil Aerodynamic Optimization Methods Based on Data-Driven Advanced Models" Mathematics 12, no. 10: 1417. https://doi.org/10.3390/math12101417
APA StyleWang, L., Zhang, H., Wang, C., Tao, J., Lan, X., Sun, G., & Feng, J. (2024). A Review of Intelligent Airfoil Aerodynamic Optimization Methods Based on Data-Driven Advanced Models. Mathematics, 12(10), 1417. https://doi.org/10.3390/math12101417






