General Approach to the Evolving Plasma Equilibria with a Resistive Wall in Tokamaks
Abstract
1. Introduction
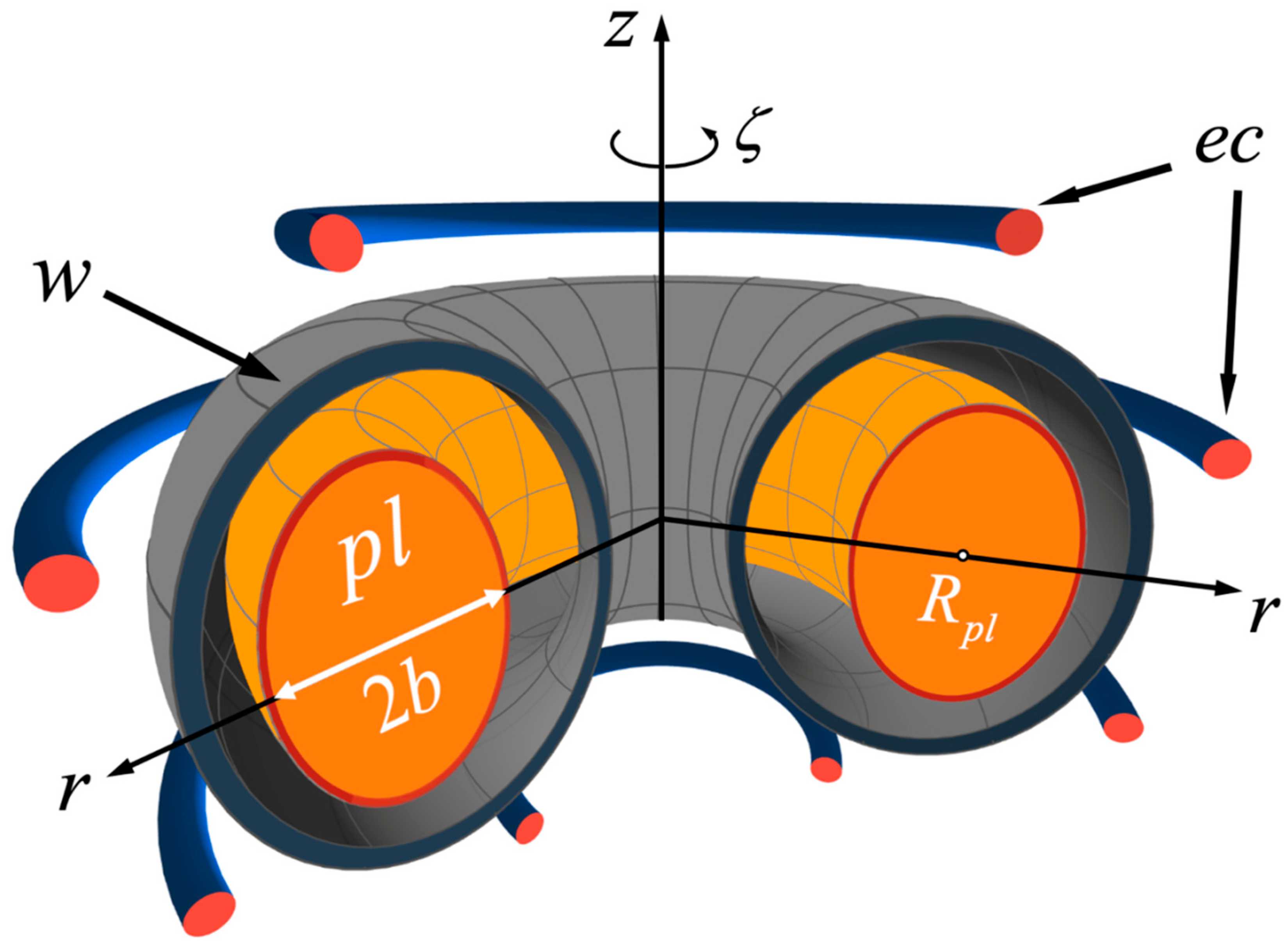
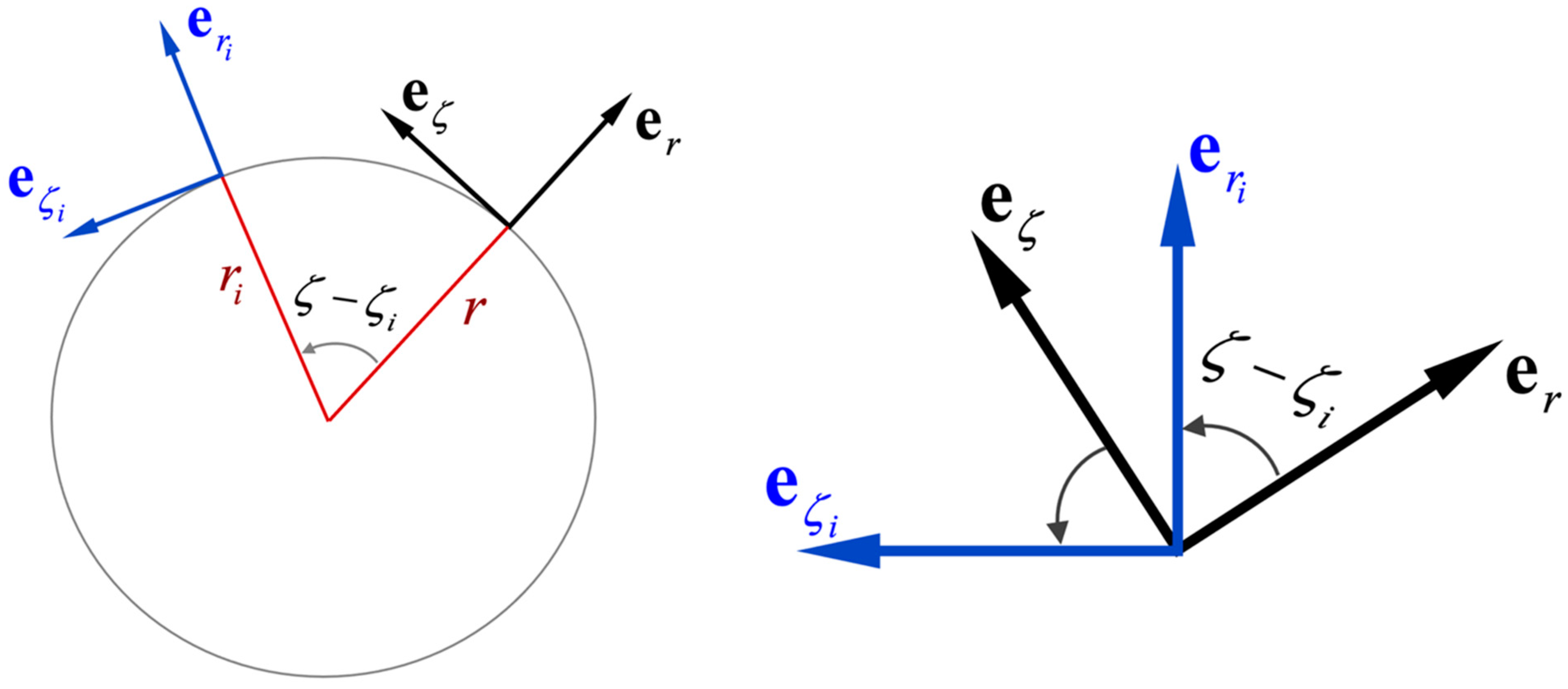
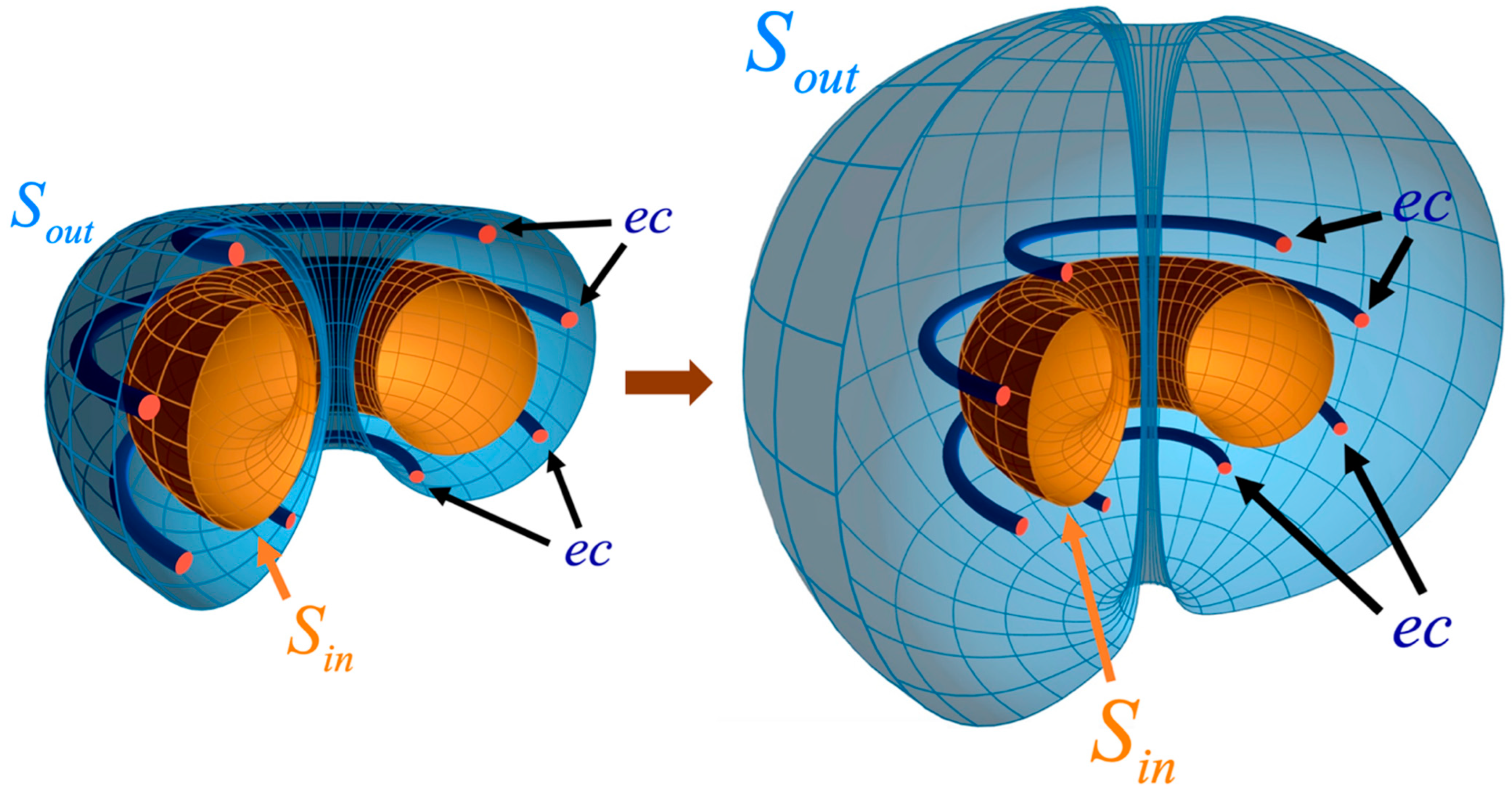
2. The Model
3. Expressions for with Account of Boundary Condition (18)
4. The Evolution Equation for
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Villone, F.; Ramogida, G.; Rubinacci, G. Electromagnetic disruption analysis in IGNITOR. Fusion Eng. Des. 2015, 93, 57–68. [Google Scholar] [CrossRef]
- Li, X.; Zakharov, L.E.; Galkin, S.A. Adaptive Grids in Simulations of Toroidal Plasma Starting from Magneto-Hydrodynamic Equilibrium. Plasma Sci. Technol. 2015, 17, 97–104. [Google Scholar] [CrossRef]
- Zakharov, L.E.; Li, X. Tokamak magneto-hydrodynamics and reference magnetic coordinates for simulations of plasma disruptions. Phys. Plasmas 2015, 22, 062511. [Google Scholar] [CrossRef]
- Pustovitov, V.D. Radial force on the vacuum chamber wall during thermal quench in tokamaks. Plasma Phys. Rep. 2015, 41, 952–960. [Google Scholar] [CrossRef]
- Pustovitov, V. General approach to the problem of disruption forces in tokamaks. Nucl. Fusion 2015, 55, 113032. [Google Scholar] [CrossRef]
- Khayrutdinov, R.R.; Lukash, V.; Pustovitov, V.D. Local and integral forces on the vacuum vessel during thermal quench in the ITER tokamak. Plasma Phys. Control. Fusion 2016, 58, 115012. [Google Scholar] [CrossRef]
- Pustovitov, V.; Rubinacci, G.; Villone, F. On the computation of the disruption forces in tokamaks. Nucl. Fusion 2017, 57, 126038. [Google Scholar] [CrossRef]
- Portone, A. Force scaling for n = 0 RWMs. Nucl. Fusion 2019, 59, 024002. [Google Scholar] [CrossRef]
- Sovinec, C.R.; Bunkers, K.J. Effects of asymmetries in computations of forced vertical displacement events. Plasma Phys. Control. Fusion 2019, 61, 024003. [Google Scholar] [CrossRef]
- Yanovskiy, V.; Isernia, N.; Pustovitov, V.; Villone, F.; Abate, D.; Bettini, P.; Chen, S.; Havlicek, J.; Herrmann, A.; Hromadka, J.; et al. Comparison of approaches to the electromagnetic analysis of Compass-U vacuum vessel during fast transients. Fusion Eng. Des. 2019, 146, 2338. [Google Scholar] [CrossRef]
- Isernia, N.; Pustovitov, V.D.; Villone, F.; Yanovskiy, V. Cross-validation of analytical models for computation of disruption forces in tokamaks. Plasma Phys. Control. Fusion 2019, 61, 115003. [Google Scholar] [CrossRef]
- Dubrov, M.L.; Lukash, V.E.; Khayrutdinov, R.R.; Dokuka, V.N. Analysis of Electromagnetic Forces in Tokamak Vacuum Chamber due to Induced Poloidal Current after Thermal Quench. Phys. At. Nucl. 2020, 83, 1058. [Google Scholar] [CrossRef]
- Khayrutdinov, R.R.; Lukash, V.E.; Pustovitov, V.D. Analysis of Electromagnetic Loads on the Vacuum Vessel during Thermal Quench in the TRT Tokamak. Plasma Phys. Rep. 2021, 47, 1128. [Google Scholar] [CrossRef]
- Pustovitov, V.D. Extension of Shafranov’s Equilibrium Theory to the Description of Current Quenches Affected by Resistive Wall Dissipation in Tokamaks. Plasma Phys. Rep. 2019, 45, 1114. [Google Scholar] [CrossRef]
- Shafranov, V.D. Equilibrium of a toroidal plasma in a magnetic field. J. Nucl. Energy. C 1963, 5, 251. [Google Scholar] [CrossRef]
- Mukhovatov, V.; Shafranov, V. Plasma equilibrium in a Tokamak. Nucl. Fusion 1971, 11, 605. [Google Scholar] [CrossRef]
- Zakharov, L.E.; Shafranov, V.D. Equilibrium of Current-Carrying Plasmas in Toroidal Configurations. In Reviews of Plasma Physics; Leontovich, M.A., Kadomtsev, B.B., Eds.; Consultants Bureau: New York, NY, USA, 1986; Volume 11, p. 153. [Google Scholar]
- Shafranov, V.D. Plasma Equilibrium in a Magnetic Field. In Reviews of Plasma Physics; Leontovich, M.A., Ed.; Consultants Bureau: New York, NY, USA, 1966; Volume 2, p. 103. [Google Scholar]
- Freidberg, J.P. Ideal Magnetohydrodynamics; Plenum: New York, NY, USA, 1987. [Google Scholar]
- Takeda, T.; Tokuda, S. Computation of MHD equilibrium of tokamak plasma. J. Comput. Phys. 1991, 93, 1. [Google Scholar] [CrossRef]
- Braams, B.J. The interpretation of tokamak magnetic diagnostics. Plasma Phys. Control. Fusion 1991, 33, 715–748. [Google Scholar] [CrossRef]
- Pustovitov, V.D. Theoretical Principles of the Plasma-Equilibrium Control in Stellarators. In Reviews of Plasma Physics; Kadomtsev, B.B., Shafranov, V.D., Eds.; Consultants Bureau: New York, NY, USA, 2000; Volume 21. [Google Scholar]
- Wesson, J.A. Tokamaks, 3rd ed.; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Goedbloed, J.P.; Keppens, R.; Poedts, S. Advanced Magnetohydrodynamics with Applications to Laboratory and Astrophysical Plasmas; Cambridge University Press: Oxford, UK, 2010. [Google Scholar]
- Lazarus, E.; Lister, J.; Neilson, G. Control of the vertical instability in tokamaks. Nucl. Fusion 1990, 30, 111. [Google Scholar] [CrossRef]
- Kiramov, D.I.; Breizman, B.N. Model of vertical plasma motion during the current quench. Phys. Plasmas 2017, 24, 100702. [Google Scholar] [CrossRef]
- Pfefferlé, D.; Bhattacharjee, A. Algebraic motion of vertically displacing plasmas. Phys. Plasmas 2018, 25, 022516. [Google Scholar] [CrossRef]
- Bardsley, O.P.; Hender, T.C. On the axisymmetric stability of tokamaks with ferromagnetic walls. Phys. Plasmas 2020, 27, 102508. [Google Scholar] [CrossRef]
- Porcelli, F.; Yolbarsop, A.; Barberis, T.; Fitzpatrick, R. Resonant Axisymmetric Modes. J. Phys. Conf. Ser. 2021, 1785, 012004. [Google Scholar] [CrossRef]
- Pustovitov, V.D.; Chukashev, N.V. Analytical Solution to External Equilibrium Problem for Plasma with Elliptic Cross Section in a Tokamak. Plasma Phys. Rep. 2021, 47, 956. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; McGrow-Hill Book Company, Inc.: New York, NY, USA, 1941. [Google Scholar]
- Smythe, W.R. Static and Dynamic Electricity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Morozov, A.I.; Solov’ev, L.S. The Structure of Magnetic Fields. In Reviews of Plasma Physics; Leontovich, M.A., Ed.; Consultants Bureau: New York, NY, USA, 1966; Volume 2, p. 1. [Google Scholar]
- Shafranov, V.; Zakharov, L. Use of the virtual-casing principle in calculating the containing magnetic field in toroidal plasma systems. Nucl. Fusion 1972, 12, 599. [Google Scholar] [CrossRef]
- Zakharov, L. Numerical methods for solving some problems of the theory of plasma equilibrium in toroidal configurations. Nucl. Fusion 1973, 13, 595. [Google Scholar] [CrossRef]
- Strumberger, E.; Günter, S.; Merkel, P.; Schwarz, E.; Tichmann, C.; Zehrfeld, H.-P. Numerical computation of magnetic fields of two- and three-dimensional equilibria with net toroidal current. Nucl. Fusion 2002, 42, 827. [Google Scholar] [CrossRef]
- Hirshman, S.P.; Lazarus, E.A.; Hanson, J.D.; Knowlton, S.F.; Lao, L.L. Magnetic diagnostic responses for compact stellarators. Phys. Plasmas 2004, 11, 595. [Google Scholar] [CrossRef]
- Lazerson, S.; Sakakibara, S.; Suzuki, Y. A magnetic diagnostic code for 3D fusion equilibria. Plasma Phys. Control. Fusion 2013, 55, 025014. [Google Scholar] [CrossRef]
- Li, X.; Zakharov, L.E.; Drozdov, V.V. Edge equilibrium code for tokamaks. Phys. Plasmas 2014, 21, 012505. [Google Scholar] [CrossRef]
- Hanson, J.D. The virtual-casing principle and Helmholtz’s theorem. Plasma Phys. Control. Fusion 2015, 57, 115006. [Google Scholar] [CrossRef]
- Sweeney, R.M.; Strait, E.J. Decomposing magnetic field measurements into internally and externally sourced components in toroidal plasma devices. Phys. Plasmas 2019, 26, 012509. [Google Scholar] [CrossRef]
- Malhotra, D.; Cerfon, A.J.; O’neil, M.; Toler, E. Efficient high-order singular quadrature schemes in magnetic fusion. Plasma Phys. Control. Fusion 2019, 62, 024004. [Google Scholar] [CrossRef]
- Clauser, C.F.; Jardin, S.C.; Ferraro, N. Vertical forces during vertical displacement events in an ITER plasma and the role of halo currents. Nucl. Fusion 2019, 59, 126037. [Google Scholar] [CrossRef]
- Krebs, I.; Artola, F.J.; Sovinec, C.R.; Jardin, S.C.; Bunkers, K.J.; Hoelzl, M.; Ferraro, N.M. Axisymmetric simulations of vertical displacement events in tokamaks: A benchmark of M3D-C1, NIMROD, and JOREK. Phys. Plasmas 2020, 27, 022505. [Google Scholar] [CrossRef]
- Artola, F.; Loarte, A.; Hoelzl, M.; Lehnen, M.; Schwarz, N.; The JOREK Team. Non-axisymmetric MHD simulations of the current quench phase of ITER mitigated disruptions. Nucl. Fusion 2022, 62, 056023. [Google Scholar] [CrossRef]
- Chance, M.S. Vacuum calculations in azimuthally symmetric geometry. Phys. Plasmas 1997, 4, 2161. [Google Scholar] [CrossRef]
- Pustovitov, V.D. General formulation of the resistive wall mode coupling equations. Phys. Plasmas 2008, 15, 072501. [Google Scholar] [CrossRef]
- Chu, M.S.; Okabayashi, M. Stabilization of the external kink and the resistive wall mode. Plasma Phys. Control. Fusion 2010, 52, 123001. [Google Scholar] [CrossRef]
- Pustovitov, V.D. Plasma stability theory including the resistive wall effects. J. Plasma Phys. 2015, 81, 905810609. [Google Scholar] [CrossRef]
- Jardin, S.; Pomphrey, N.; Delucia, J. Dynamic modeling of transport and positional control of tokamaks. J. Comput. Phys. 1986, 66, 481. [Google Scholar] [CrossRef]
- Lackner, K. Computation of ideal MHD equilibria. Comput. Phys. Commun. 1976, 12, 33. [Google Scholar] [CrossRef]
- Pustovitov, V.D. Resolution of the paradox discovered by Freidberg in the Shafranov’s theory on plasma equilibrium. Phys. Plasmas 2020, 27, 102503. [Google Scholar] [CrossRef]
- Wesson, J.; Ward, D.; Rosenbluth, M. Negative voltage spike in tokamak disruptions. Nucl. Fusion 1990, 30, 1011. [Google Scholar] [CrossRef]
- Takei, N.; Nakamura, Y.; Tsutsui, H.; Yoshino, R.; Kawano, Y.; Ozeki, T.; Tobita, K.; Tsuji-Iio, S.; Shimada, R.; Jardin, S.C. Numerical simulation on current spike behaviour of JT-60U disruptive plasmas. Plasma Phys. Control. Fusion 2004, 46, 1815. [Google Scholar] [CrossRef]
- Khayrutdinov, R.; Lukash, V. Studies of Plasma Equilibrium and Transport in a Tokamak Fusion Device with the Inverse-Variable Technique. J. Comput. Phys. 1993, 109, 193. [Google Scholar] [CrossRef]
- Sayer, R.; Peng, Y.-K.; Jardin, S.; Kellman, A.; Wesley, J. TSC plasma halo simulation of a DIII-D vertical displacement episode. Nucl. Fusion 1993, 33, 969. [Google Scholar] [CrossRef]
- Galkin, S.; Ivanov, A.; Medvedev, S.; Poshekhonov, Y. Comparison of tokamak axisymmetric mode growth rates from linear MHD and equilibrium evolution approaches. Nucl. Fusion 1997, 37, 1455. [Google Scholar] [CrossRef]
- Portone, A. The stability margin of elongated plasmas. Nucl. Fusion 2005, 45, 926. [Google Scholar] [CrossRef]
- Miyamoto, S.; Isayama, A.; Bandyopadhyay, I.; Jardin, S.; Khayrutdinov, R.; Lukash, V.; Kusama, Y.; Sugihara, M. Intercode comparison benchmark between DINA and TSC for ITER disruption modelling. Nucl. Fusion 2014, 54, 083002. [Google Scholar] [CrossRef]
- Qiu, Q.; Xiao, B.; Guo, Y.; Liu, L.; Xing, Z.; Humphreys, D. Simulation of EAST vertical displacement events by tokamak simulation code. Nucl. Fusion 2016, 56, 106029. [Google Scholar] [CrossRef]
- Jana, S.; Pradhan, S.; Dhongde, J.; Masand, H.; SST-1 Team. Vessel eddy current characteristics in SST-1 tokamak. Fusion Eng. Des. 2016, 112, 380. [Google Scholar] [CrossRef]
- Qiu, Q.; Guo, Y.; Gao, X.; Huang, J.; Sun, H.; Li, J.; Xiao, B.; Chen, D.; Luo, Z. Simulation of hot VDE disruption in EAST by using the TSC code. Fusion Eng. Des. 2020, 150, 111358. [Google Scholar] [CrossRef]
- Kumar, R.; Jha, S.; Aich, S.; Macwan, T.; Kumawat, D.; Tanna, R.; Ghosh, J.; Patel, K.; Jadeja, K. Estimation of vacuum vessel time-constant in ADITYA-U tokamak. Fusion Eng. Des. 2022, 177, 113055. [Google Scholar] [CrossRef]
- Morse, P.; Feshbach, H. Methods of Theoretical Physics; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- ITER Physics Expert Group on Disruptions, Plasma Control and MHD, ITER Physics Basis Editors. ITER EDA Chapter 3: MHD stability, operational limits and disruptions. Nucl. Fusion 1999, 39, 2251. [Google Scholar] [CrossRef]
- Hender, T.; Wesley, J.; Bialek, J.; Bondeson, A.; Boozer, A.; Buttery, R.; Garofalo, A.; Goodman, T.; Granetz, R.; Gribov, Y.; et al. Chapter 3: MHD stability, operational limits and disruptions. Nucl. Fusion 2007, 47, S128. [Google Scholar] [CrossRef]
- Riccardo, V.; Arnoux, G.; Cahyna, P.; Hender, T.C.; Huber, A.; Jachmich, S.; Kiptily, V.; Koslowski, R.; Krlin, L.; Lehnen, M.; et al. JET disruption studies in support of ITER. Plasma Phys. Control. Fusion 2010, 52, 124018. [Google Scholar] [CrossRef]
- Pautasso, G.; Giannone, L.; Gruber, O.; Herrmann, A.; Maraschek, M.; Schuhbeck, K.H.; The ASDEX Upgrade Team. The halo current in ASDEX Upgrade. Nucl. Fusion 2011, 51, 043010. [Google Scholar] [CrossRef]
- Myers, C.; Eidietis, N.; Gerasimov, S.; Gerhardt, S.; Granetz, R.; Hender, T.; Pautasso, G.; Contributors, J. A multi-machine scaling of halo current rotation. Nucl. Fusion 2017, 58, 016050. [Google Scholar] [CrossRef]
- Gerasimov, S.N.; Abreu, P.; Artaserse, G.; Baruzzo, M.; Buratti, P.; Carvalho, I.S.; Coffey, I.H.; De La Luna, E.; Hender, T.C.; Henriques, R.B.; et al. Overview of disruptions with JET-ILW. Nucl. Fusion 2020, 60, 066028. [Google Scholar] [CrossRef]
- Dialetis, D.; Len, L.K.; Golden, J.; Kapetanakos, C.A. Diffusion of magnetic fields in a toroidal conducting shell of circular cross section. J. Appl. Phys. 1991, 69, 1813. [Google Scholar] [CrossRef]
- Pustovitov, V.D. Reaction of the toroidal resistive wall on the magnetic field variations in tokamak-like systems. Phys. Plasmas 2018, 25, 062510. [Google Scholar] [CrossRef]
- Yanovskiy, V.; Isernia, N.; Pustovitov, V.; Scalera, V.; Villone, F.; Hromadka, J.; Imrisek, M.; Havlicek, J.; Hron, M.; Panek, R. Global forces on the COMPASS-U wall during plasma disruptions. Nucl. Fusion 2021, 61, 096016. [Google Scholar] [CrossRef]
- Abate, D.; Bettini, P. An inverse equilibrium tool to define axisymmetric plasma equilibria Plasma Phys. Control. Fusion 2019, 61, 105016. [Google Scholar] [CrossRef]
- Itagaki, M.; Fukunaga, T. Boundary element modelling to solve the Grad–Shafranov equation as an axisymmetric problem. Eng. Anal. Bound. Elements 2006, 30, 746–757. [Google Scholar] [CrossRef]
- Faugeras, B.; Heumann, H. FEM-BEM coupling methods for Tokamak plasma axisymmetric free-boundary equilibrium computations in unbounded domains. J. Comput. Phys. 2017, 343, 201. [Google Scholar] [CrossRef]
- López, O.E.; Guazzotto, L. High-beta analytic equilibria in circular, elliptical, and D-shaped large aspect ratio axisymmetric configurations with poloidal and toroidal flows. Phys. Plasmas 2017, 24, 032501. [Google Scholar] [CrossRef]
- López, O.E.; Guazzotto, L. Stability of a tokamak plasma with diffuse toroidal rotation. J. Plasma Phys. 2020, 86, 905860514. [Google Scholar] [CrossRef]
- Hole, M.J.; Qu, Z.; Pinches, S.D.; Schneider, M.; Arbina, I.L.; Mantsinen, M.; Sauter, O. The impact of anisotropy on ITER scenarios. Nucl. Fusion 2020, 60, 112010. [Google Scholar] [CrossRef]
- Faugeras, B. An overview of the numerical methods for tokamak plasma equilibrium computation implemented in the NICE code. Fusion Eng. Des. 2020, 160, 112020. [Google Scholar] [CrossRef]
- Guazzotto, L.; Freidberg, J.P. Simple, general, realistic, robust, analytic tokamak equilibria. Part 1. Limiter and divertor tokamaks. J. Plasma Phys. 2021, 87, 905870303. [Google Scholar] [CrossRef]
- Faugeras, B.; Blum, J.; Boulbe, C. First equilibrium reconstruction for ITER with the code NICE. J. Instrum. 2022, 17, C02024. [Google Scholar] [CrossRef]
- Goedbloed, J.; Zakharov, L. Helical equilibria of a plasma column with a diffuse current distribution. Nucl. Fusion 1980, 20, 1515. [Google Scholar] [CrossRef]
- Hölzl, M.; Merkel, P.; Huysmans, G.T.A.; Nardon, E.; Strumberger, E.; McAdams, R.; Chapman, I.; Günter, S.; Lackner, K. Coupling JOREK and STARWALL codes for non-linear resistive-wall simulations. J. Phys. Conf. Ser. 2012, 401, 012010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pustovitov, V.D.; Chukashev, N.V. General Approach to the Evolving Plasma Equilibria with a Resistive Wall in Tokamaks. Mathematics 2023, 11, 1885. https://doi.org/10.3390/math11081885
Pustovitov VD, Chukashev NV. General Approach to the Evolving Plasma Equilibria with a Resistive Wall in Tokamaks. Mathematics. 2023; 11(8):1885. https://doi.org/10.3390/math11081885
Chicago/Turabian StylePustovitov, Vladimir D., and Nikolay V. Chukashev. 2023. "General Approach to the Evolving Plasma Equilibria with a Resistive Wall in Tokamaks" Mathematics 11, no. 8: 1885. https://doi.org/10.3390/math11081885
APA StylePustovitov, V. D., & Chukashev, N. V. (2023). General Approach to the Evolving Plasma Equilibria with a Resistive Wall in Tokamaks. Mathematics, 11(8), 1885. https://doi.org/10.3390/math11081885






