Exergy Analysis for Combustible Third-Grade Fluid Flow through a Medium with Variable Electrical Conductivity and Porous Permeability

Abstract

A mathematical investigation of a thermodynamical system linked with energy management and its impact on the environment, especially climate change, is presented in this study. In this regard, a numerical investigation of the flow and heat transfer of hydromagnetic third-grade liquid through a porous medium. The permeability of the medium and electrical conductivity of the fluid are assumed to be temperature functions. The appropriate mathematical formulations for momentum, energy, and entropy equations are presented in both dimensional and dimensionless forms. We obtained the numerical solutions using the spectral version of the Chebyshev collocation method and compared the result with the shooting Runge–Kutta method. Numerical results for velocity, temperature, entropy, and Bejan profiles are communicated through tables and graphs with adequate physical interpretation. The thermal stability of the thermo-fluid system that guarantees the prevention of spontaneous fluid heating that fuels climate change is also included in the analysis.

1. Introduction

One typical relationship between some of the Sustainable Development Goals (SDG), including industrialization, a clean environment, and climate change is that of energy usage. In this context, the impact of thermodynamics in thermal engineering and other energy generation settings cannot be overemphasized due to the interconnectivity between heat generation, dissipation, and its net effect on climate change. Over the last few decades, the thermodynamics analysis of third-grade fluid (TGF) flow through a porous medium has been of interest to researchers, scientists, and engineers, due to its numerous and diverse applications in nature. The study finds its application in several branches of agriculture, science, and engineering, to mention just a few. Based on the aforementioned geophysical importance, Adesanya et al. [1] reported thermal analysis for a reactive third-grade liquid through a non-Darcian medium bounded by Riga walls subjected to Newtonian cooling. By applying the rapidly converging homotopy analysis method, Sajid and Hayat [2] presented the solution to a third-grade fluid flow in a porous channel filled with permeable materials by applying a modified Darcy law. Makinde et al. [3] reported a numerical approach to solving unsteady, fully developed flow problems in variable viscous TGF through a porous medium subjected to asymmetrical convective heating in which the fluid undergoes an exothermic chemical reaction. Hayat et al. [4] discussed the steady, fully developed flow of third-grade liquid in a porous space under no-slip and non-moving wall conditions using a homotopy analysis approach. Rundora and Makinde [5] examined the influence of vertical penetration on reactive TGF flow through a Darcian medium under heat-dependent viscosity. Baoku et al. [6] studied numerical solutions to heat and mass transfer in a boundary layer flow of a third-grade fluid flow in an enclosed porous region. Adesanya and Falade [7] analyzed the heat irreversibility inherent in the heat transfer of TGF through a porous medium using the perturbation method. Salawu and Fatunmbi [8] investigated the inherent heat irreversibility in the convective flow of variable, viscous, third-grade combustible liquid experiencing a transverse magnetic field. Magnhsoudi et al. [9] constructed an analytical solution to the heat transfer problem in TGF flowing steadily through a medium with flow barriers by applying the weighted residual least square method. Readers can see other exciting results on TGF through a restricted medium in reference [10,11,12,13] and references cited within the work.

Over the last few decades, studies on electrical conducting fluids are becoming more popular due to their wide range of applications in hydroponics, aquaponics, aquaculture, electrolytes, polymers, molten metals, and many more that are too numerous to be listed. Based on a wide application, Rahman et al. [14] used the linear dependence of electrical conductivity on flow velocity to obtain a numerical approximation of a micropolar fluid flow over an infinitely long inclined plane with a variable heat source. Additionally, Makinde and Onyejekwe [15] considered the heat-dependent electrical conductivity of the power law type for the flow and thermal analysis of a time-independent Couette flow. Hossain and Gorla [16] presented another variant of electrical conductivity relation based on free steam and tangential velocity for the developing flow analysis of hydromagnetic liquids. In a related study by Eguia et al. [17], electrical conductivity was assumed to be a linear function of temperature for unsteady dusty flow analysis. Similarly, Sivaraj and Kumar [18] studied the unsteady developing flow of reacting Walter-B fluid along a vertical cone. Eegunjobi and Makinde [19] utilized the power law dependence of electrical conductivity on temperature to study the hydromagnetic slip flow between leaking walls. Salawu et al. [20] presented the heat-dependent electrical conductivity property of an unsteady flow of Eyring–Powell fluid undergoing Arrhenius kinetics in a non-Darcian setting. Obalalu et al. [21] analyzed the convective magnetohydrodynamic flow of Casson nanofluid subjected to an exothermic chemical reaction. Adeosun and Ukaegbu [22] considered the squeezed flow of a reactive fluid experiencing variable electrical conductivity. The literature is inexhaustive when considering the variable electrical conductivity property of hydromagnetic fluid.

Motivated by the studies in [14,15,16,17,18,19,20,21,22], the first interest is in investigating variable electrical conductivity’s influence on the flow of third-grade liquid in the porous medium. Secondly, the studies in [1,2,3,4,5,6,7,8,9] assumed constant porous permeability. In the real sense, the permeability of any porous medium allowing the passage of viscous fluid depends on temperature, pressure/stress field, and non-homogeneity of the permeable material used. For example, in oil/well engineering, the flows of polymetric fluids in oil recovery/steam injection in petroleum engineering, groundwater, oil in geological flows, some areas involving water seepage in agricultural engineering, and lots more. As a result, the main objective of this paper is to study the steady flow of hydromagnetic third-grade fluid through a porous medium with temperature-dependent porous permeability and electrical conductivity. The problem will be formulated in the following section with some mathematical analysis. Section 3 will be dedicated to the numerical method of solution, and in the Section 4, the results will be presented and discussed while the Section 5 concludes the article.

2. Mathematical Formulation

This work studies the steady, unidirectional, fully developed flow of an electrically conducting, pressure-driven, third-grade fluid through a porous medium with no vertical wall penetration. The third-grade liquid is assumed to undergo a strong exothermic chemical reaction. A magnetic field of intensity $B_0$ is applied across the horizontal channel. It is further assumed that both electrical conductivity and porous permeability of the medium are nonlinear functions of temperature as shown in the flow geometry in Figure 1.

Neglecting the unsteadiness or temporal changes and the convective components of acceleration, the appropriate balanced pressure and viscous forces driving the flow can be written as:

$$0=-\frac{d{P}^{\prime }}{d{x}^{\prime }}+\frac{d}{d{y}^{\prime }}\left(\mu \frac{d{u}^{\prime }}{d{y}^{\prime }}+2{\beta }_3{\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^3\right) -\left(\mu +2{\beta }_3{\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^2\right)\frac{u^{\prime }}{K\left(T\right)}-\sigma \left(T\right)B_0^2{u}^{\prime },$$

(1)

and the energy balance equation

$$\begin{array}{l}0=k\frac{d^{2}T}{d{y^{\prime }}^2}+Q{C}_{0}A{\left(\frac{\hslash T}{\upsilon \iota }\right)}^m{e}^{-\frac{E}{RT}}+\left(\mu +2{\beta }_3{\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^2\right){\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(\left(\mu +2{\beta }_3{\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^2\right)\frac{u^{\prime }}{K\left(T\right)}+\sigma \left(T\right)B_0^2\right){u^{\prime }}^2\end{array},$$

(2)

Alongside the non-moving wall and no-slip conditions at the solid boundaries,

$$\begin{array}{l}{u}^{\prime }=0, T=T_a, \hspace{0.17em} y^{\prime }=a;\\ u^{\prime }=0, T=T_a, y^{\prime }=-a.\end{array}$$

(3)

While the wall shear stress for the determination of skin friction and heat transfer rate can be written as

$${\tau }_{xy}={\left.\mu \frac{d{u}^{\prime }}{d{y}^{\prime }}+2{\beta }_3{\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^3\right|}_{y=-1}, q_w=-k{\left.\frac{dT}{dy}\right|}_{y=-1}$$

(4)

Entropy changes from the spontaneous process due to heat transfer and viscous interaction can be written as

$$E_G=\frac{k}{T_0^2}{\left(\frac{d{T}^{\prime }}{d{Y}^{\prime }}\right)}^2+\frac{1}{T_0}\left\{\left(\mu +2{\beta }_3{\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^2\right){\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^2+\left(\frac{1}{K\left(T\right)}\left(\mu +2{\beta }_3{\left(\frac{d{u}^{\prime }}{d{y}^{\prime }}\right)}^2\right)+\sigma \left(T\right)B_0^2\right){u^{\prime }}^2\right\}$$

(5)

The first part of (5) is the heat transfer component of heat irreversibility while the other part arises from viscous interaction. The permeability of the porous medium is assumed to vary slightly with temperature, i.e., the thermal effect on permeability is of the form:

$$K\left(T\right)=K_0{e}^{\overline{\alpha }\left(T-T_0\right)}\approx K_0\left(1+\overline{\alpha }\left(T-T_0\right)\right) + H.O.T, 0< \overline{\alpha }<<1$$

(6)

While the dependence of electrical conductivity on temperature is given by [20,21,22]:

$$\sigma \left(T\right)={\sigma }_0{\left(\frac{E\left(T-T_0\right)}{T_0^{2}R}\right)}^r,$$

(7)

here, $\overline{\alpha }$ represents the coefficient of the temperature difference and $r$ is the exponent of temperature, $x^{\prime },y^{\prime }$ represents the Cartesian coordinates of the channel, $\left(P,\mu ,{\beta }_3\right)$ are fluid pressure, viscosity, and non-Newtonian material effect, $\left(u^{\prime },T,K\left(T\right)\right)$ are the dimensional velocity, temperature, and porous permeability. $\left(\sigma \left(T\right),B_0,k\right)$ are the electrical conductivity, magnetic field intensity, and thermal conductivity, $\left(Q,C_0,A\right)$ represents the heat of reaction, initial concentration, and rate constant. $\left(\iota ,m,\upsilon \right)$ are Plank’s constant, reaction exponent, and frequency of vibration. Using the following dimensionless parameters and variables,

$$\begin{array}{l}y=\frac{y^{\prime }}{a}, u=\frac{u^{\prime }}{UG}, \theta =\frac{E\left(T-T_0\right)}{R{T}_0^2}, H{a}^2=\frac{{\sigma }_0{B}_0^2{a}^2}{{\mu }_0}, \epsilon =\frac{R{T}_0}{E},\\ Da=\frac{K_0}{a^2}, S^2=\frac{1}{Da}, G=-\frac{a^2}{{\mu }_{0}U}\frac{dP}{dx}, \alpha =\frac{\overline{\alpha }R{T}_0^2}{E}, Ns=\frac{a^2{E}^2}{k{R}^2{T}_0^2},\kappa =\frac{{\beta }_3{U}^2{G}^2}{{\mu }_0{a}^2},\\ \lambda ={\left(\frac{h{T}_0}{\upsilon \iota }\right)}^m\frac{QEA{a}^2{C}_0}{kR{T}_0^2}{e}^{-\frac{E}{R{T}_0}},\gamma ={\left(\frac{\upsilon \iota }{h{T}_0}\right)}^m\frac{{\mu }_0{U}^2{G}^2}{QA{C}_0{a}^2}{e}^{\frac{E}{R{T}_0}}\end{array}$$

(8)

we arrive at the following dimensionless nonlinear and coupled boundary-value problem:

$$\left.\begin{array}{l}0=1+\frac{d}{dy}\left(\frac{du}{dy}+2\kappa {\left(\frac{du}{dy}\right)}^3\right)-\left(\left(1+2\kappa {\left(\frac{du}{dy}\right)}^2\right)\left(1-\alpha \theta \right)S^2+H^2{\theta }^r\right)u; u\left(\pm 1\right)=0\\ 0=\frac{d^2\theta }{d{y}^2}\\ +\lambda \left({\left(1+\epsilon \theta \right)}^m{e}^{\frac{\theta }{1+\epsilon \theta }}+\gamma \left\{{\left(\frac{du}{dy}\right)}^2\left(1+2\kappa {\left(\frac{du}{dy}\right)}^2\right)+\left(\left(1+2\kappa {\left(\frac{du}{dy}\right)}^2\right)\left(1-\alpha \theta \right)S^2+H^2{\theta }^r\right)u^2\right\}\right);\\ \hspace{1em}\hspace{1em}\hspace{1em}\theta \left(\pm 1\right)=0\\ N_S={\left(\frac{d\theta }{dy}\right)}^2+\frac{\lambda \gamma }{\epsilon }\left({\left(\frac{du}{dy}\right)}^2\left(1+2\kappa {\left(\frac{du}{dy}\right)}^2\right)+\left(\left(1+2\kappa {\left(\frac{du}{dy}\right)}^2\right)\left(1-\alpha \theta \right)S^2+H^2{\theta }^r\right)u^2\right).\end{array}\right\}$$

(9)

The contribution of each parameter to the entropy profile can be monitored using the ratio:

$$Be=\frac{{\left(\frac{d\theta }{dy}\right)}^2}{{\left(\frac{d\theta }{dy}\right)}^2+\frac{\lambda \gamma }{\epsilon }\left({\left(\frac{du}{dy}\right)}^2\left(1+2\kappa {\left(\frac{du}{dy}\right)}^2\right)+\left(\left(1+2\kappa {\left(\frac{du}{dy}\right)}^2\right)\left(1-\alpha \theta \right)S^2+H^2{\theta }^r\right)u^2\right)}$$

(10)

The dimensionless quantities $\left(u,\theta ,G\right)$ are velocity, temperature, and pressure gradient, $\left(H,\epsilon ,Da\right)$ are Hartmann number, activation energy parameter, and Darcy number, $\left(S^2,\alpha ,Ns\right)$ are shape factor, coefficient of electrical conductivity, and dimensionless entropy generation, $\left(\kappa ,\lambda ,Be\right)$ are the third-grade parameter, Frank–Kameneskii parameter, and Bejan ratio, respectively.

3. Spectral Collocation Method of Solution

To obtain the solution to the coupled boundary-value problem (9), we apply the idea of the dense set to take a polynomial approximation as suggested in the Weierstrass approximation theorem for the existence of a solution. In this way, we assume that the solution of (9) can be approximated by taking:

$$\left.\begin{array}{l}u\left(y\right)\approx u^N\left(y\right)={\displaystyle \sum _{j=0}^N{b}_j{\mathsf{\Phi }}_j\left(y\right)},\\ \theta \left(y\right)\approx {\theta }^N\left(y\right)={\displaystyle \sum _{j=0}^N{c}_j{\mathsf{\Phi }}_j\left(y\right)}\end{array}\right\}$$

(11)

where ${\mathsf{\Phi }}_j$(y) represents spectral Chebyshev polynomials and $\left(b_j,c_j\right)$ are the unknown coefficients to be determined. In this way, the residues that denote the difference between the exact solution of (9) and the approximated solutions are given by

$$\left.\begin{array}{l}{R}_1=1+{\left(u_y^N+2\kappa {\left(u_y^N\right)}^3\right)}_y-\left(\left(1+2\kappa {\left(u_y^N\right)}^2\right)\left(1-\alpha {\theta }^N\right)S^2+H^2{\theta }^{Nr}\right)u^N, \\ R_2={\theta }_{yy}^N+\lambda \left({\left(1+\epsilon {\theta }^N\right)}^m{e}^{\frac{{\theta }^N}{1+\epsilon {\theta }^N}}+\gamma \left\{{\left(u_y^N\right)}^2\left(1+2\kappa {\left(u_y^N\right)}^2\right)+\left(\left(1+2\kappa {\left(u_y^N\right)}^2\right)\left(1-\alpha {\theta }^N\right)S^2+H^2{\theta }^{Nr}\right)u^{2N}\right\}\right) \end{array}\right\}$$

(12)

with

$$u^N\left(-1\right)=0=u^N\left(1\right),{\left.{\theta }_y^N\right|}_{y=-1}=0 ={\left.{\theta }_y^N\right|}_{y=1}.$$

(13)

where $y_i$ are points within $[-1,1]=[y_{0,}{y}_N]$. Then the Gauss–Lobato points for the collocation points are

$$y_j=-\cos \left(\frac{j\pi }{N}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j=0,1,2,\dots ,N.$$

(14)

Which are evaluated at

$$R_1\left(y_j\right)=0=\hspace{0.17em}{R}_2\left(y_j\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}j=0,1,2,\dots ,N.$$

(15)

The derivatives for dependent variables are obtained as

$$\frac{d^{r}u}{d{y}^r}={\displaystyle \sum _{j=0}^N{b}_i\frac{d^r{u}_j}{d{y}^r}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{d^r\theta }{d{y}^r}={\displaystyle \sum _{j=0}^{Np}{c}_j\frac{d^r{\theta }_j}{d{y}^r}}.$$

(16)

The differentiation matrices at each Gauss–Lobato point are

$$\frac{d^r\overline{u}}{d^{r}y}=D^{(r)}\overline{u}=D^r\overline{u} r=1,2,3,\dots \mathrm{and}\frac{d^r\overline{\theta }}{d^{r}y}=D^{(r)}\overline{\theta }=D^r\overline{\theta }, r=1,2,3,\dots$$

(17)

So that the vector forms, defined as

$$\left.\begin{array}{l}\overline{u}={\left(u\left(y_0\right),u\left(y_1\right),\dots ,u\left(y_N\right)\right)}^T\\ \hspace{0.17em}\overline{\theta }={\left(\theta \left(y_0\right),\theta \left(y_1\right),\dots ,\theta \left(y_N\right)\right)}^T\end{array}\right\},$$

(18)

which are used to convert the coupled, nonlinear, boundary-value problem into a set of algebraic equations. By utilizing the NDSolve algorithm code in Wolfram Mathematica, the spectral collocation result for (9) is confirmed by the shooting Runge–Kutta method as reported in

Table 1. Numerical validation when $\lambda =0.5,ϵ=0.2,m=0.5,Bi=20,{\alpha }_1=0.1={\alpha }_2,\kappa =0.5,$ $G=\gamma =H=r=S=1$.

$\mathit{y}$	$\mathit{u}{\left(\mathit{y}\right)}_{\mathit{C}\mathit{W}\mathit{R}\mathit{M}}$	$\mathit{u}{\left(\mathit{y}\right)}_{\mathit{R}\mathit{K}45}$	$\left|\mathit{u}{\left(\mathit{y}\right)}_{\mathit{C}\mathit{W}\mathit{R}\mathit{M}}-\mathit{u}{\left(\mathit{y}\right)}_{\mathit{R}\mathit{K}4}\right|$
0	$0.29059333168978096$	$0.2905933626764475$	$3.098666651046855\times {10}^{-8}$
0.1	$0.2875531229984736$	$0.28755315707369733$	$3.407522375376004\times {10}^{-8}$
0.2	$0.2784580603387541$	$0.27845809831693963$	$3.797818554085452\times {10}^{-8}$
0.3	$0.26337977611466257$	$0.2633798176311869$	$4.151652432948793\times {10}^{-8}$
0.4	$0.24242311286613746$	$0.24242315706503897$	$4.419890151097228\times {10}^{-8}$
0.5	$0.21571064483575425$	$0.21571069190190728$	$4.70661530305172\times {10}^{-8}$
0.6	$0.18336924938712212$	$0.18336929955583225$	$5.016871013063806\times {10}^{-8}$
0.7	$0.14552094841986923$	$0.14552100275459876$	$5.433472952121043\times {10}^{-8}$
0.8	$0.10227800886883381$	$0.10227806869495099$	$5.982611717136876\times {10}^{-8}$
0.9	$0.05374120503311206$	$0.053741270769143465$	$6.573603140297424\times {10}^{-8}$
1.0	$-2.306642251952988\times {10}^{-20}$	$7.112594643000738\times {10}^{-8}$	$7.112594643003045\times {10}^{-8}$

and

Table 2. Numerical validation when $\lambda =0.5,ϵ=0.2,m=0.5,Bi=20,\alpha =0.1,\kappa =0.5,$ $G=\gamma =H=r=S=1$.

$\mathit{y}$	$\mathit{\theta }{\left(\mathit{y}\right)}_{\mathit{C}\mathit{W}\mathit{R}\mathit{M}}$	$\mathit{\theta }{\left(\mathit{y}\right)}_{\mathit{R}\mathit{K}45}$	$\left|\mathit{\theta }{\left(\mathit{y}\right)}_{\mathit{C}\mathit{W}\mathit{R}\mathit{M}}-\mathit{\theta }{\left(\mathit{y}\right)}_{\mathit{R}\mathit{K}4}\right|$
0	$0.38590264401948615$	$0.38590263681021386$	$7.209272290253921\times {10}^{-9}$
0.1	$0.38190747745163284$	$0.3819074704013799$	$7.050252937013113\times {10}^{-9}$
0.2	$0.36994346490495467$	$0.36994345794711025$	$6.957844411736858\times {10}^{-9}$
0.3	$0.3500734997990253$	$0.35007349292163265$	$6.877392655368908\times {10}^{-9}$
0.4	$0.322397158501689$	$0.3223971517395266$	$6.762162385598458\times {10}^{-9}$
0.5	$0.28704280983610114$	$0.28704280313984776$	$6.696253385118922\times {10}^{-9}$
0.6	$0.24415664136968146$	$0.24415663474092741$	$6.628754045667762\times {10}^{-9}$
0.7	$0.1938888308327938$	$0.19388882426219917$	$6.570594623944714\times {10}^{-9}$
0.8	$0.13637721443702794$	$0.13637720796479974$	$6.472228197829111\times {10}^{-9}$
0.9	$0.07172886591491089$	$0.07172885987750592$	$6.037404964853721\times {10}^{-9}$
1.0	$-2.853996136427998\times {10}^{-17}$	$-5.010838847582127\times {10}^{-9}$	$5.010838819042166\times {10}^{-9}$

.

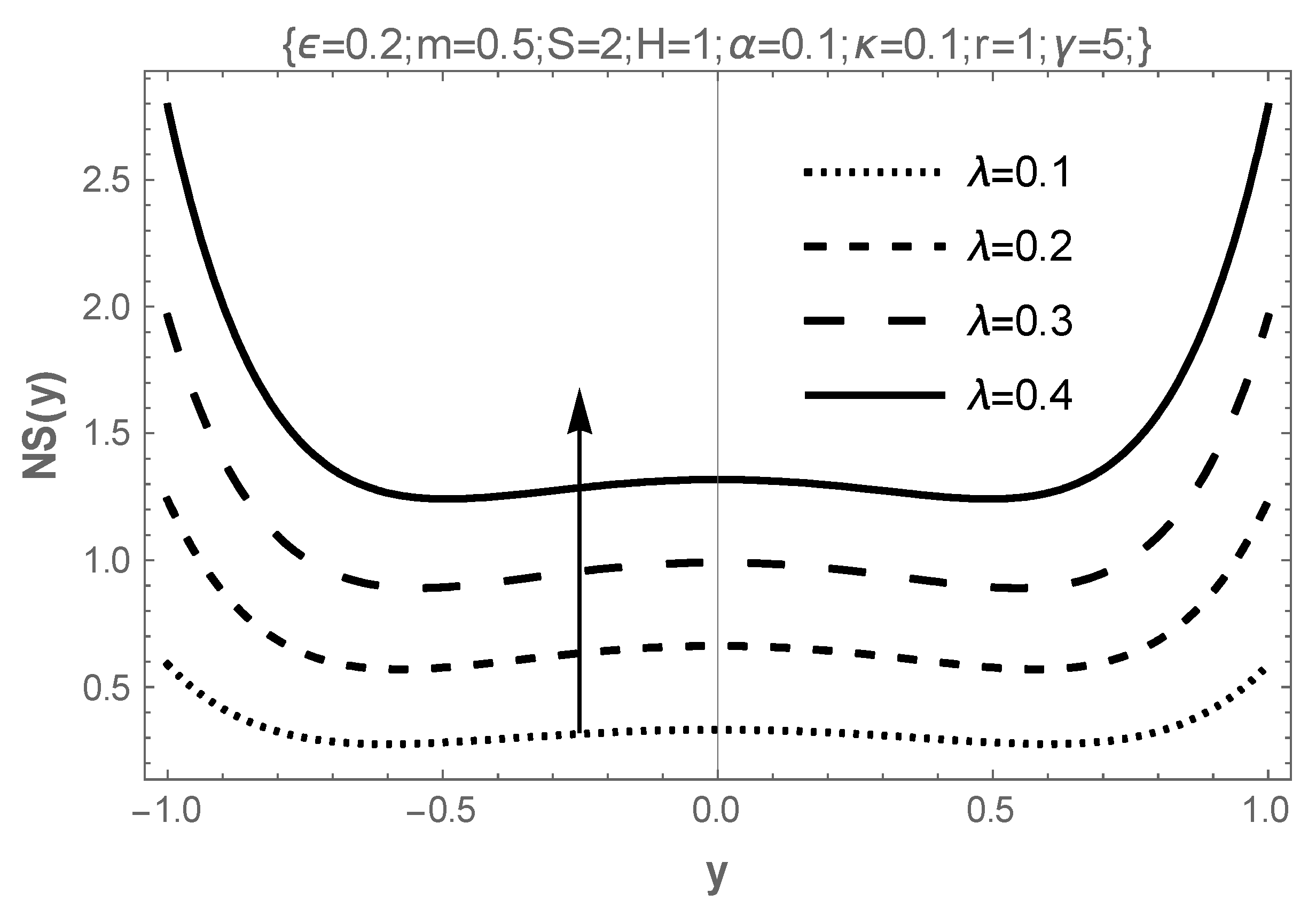
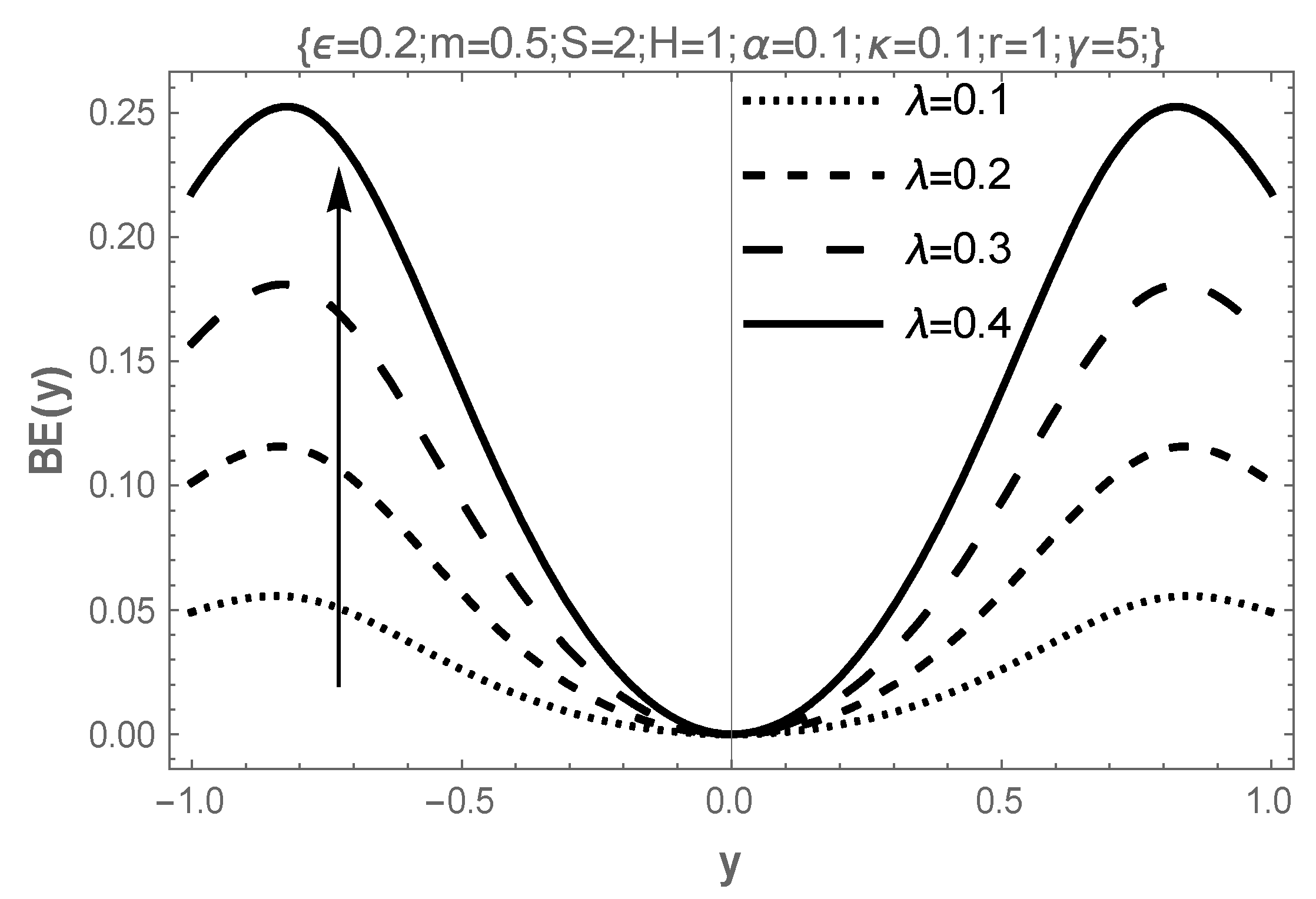
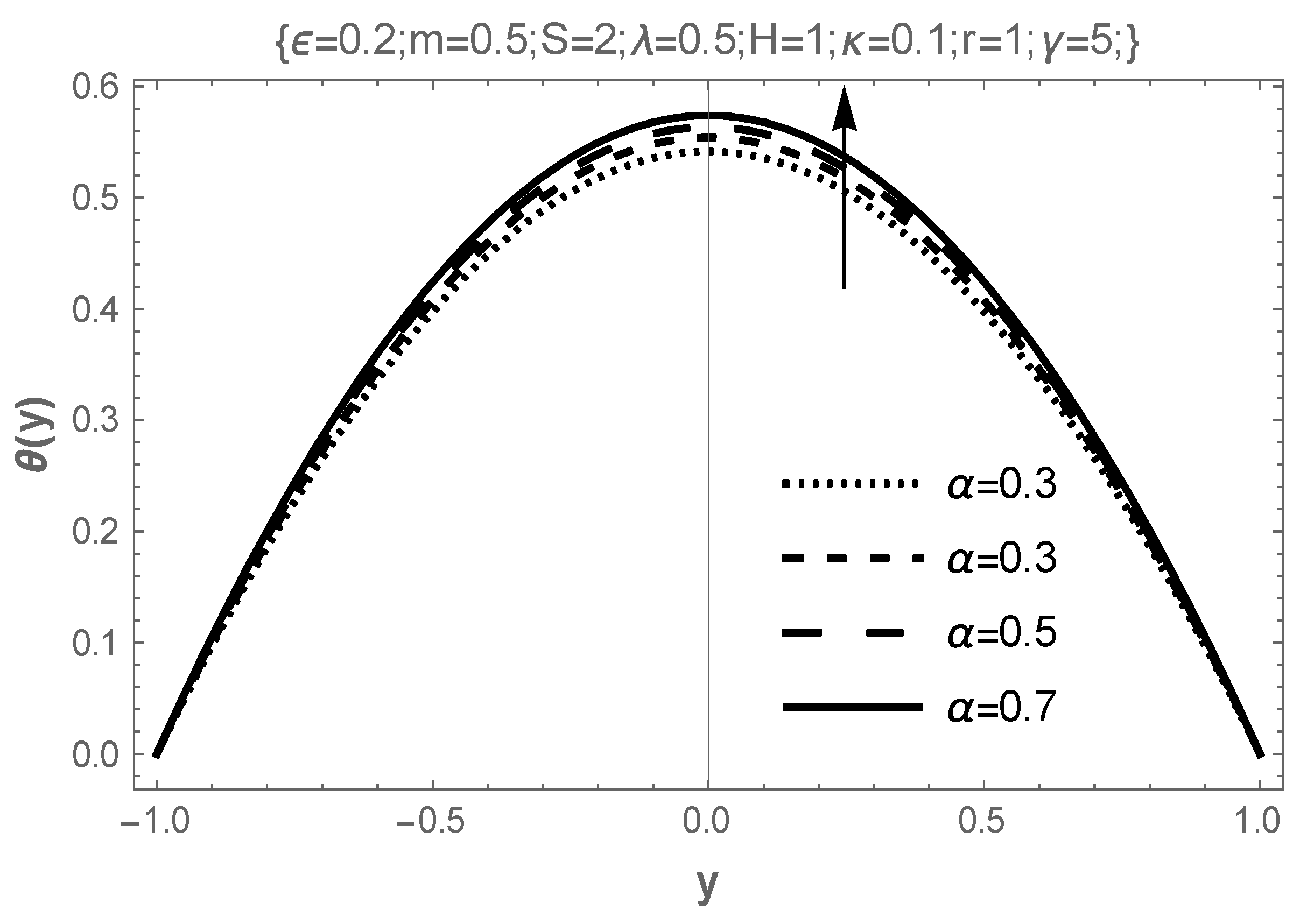
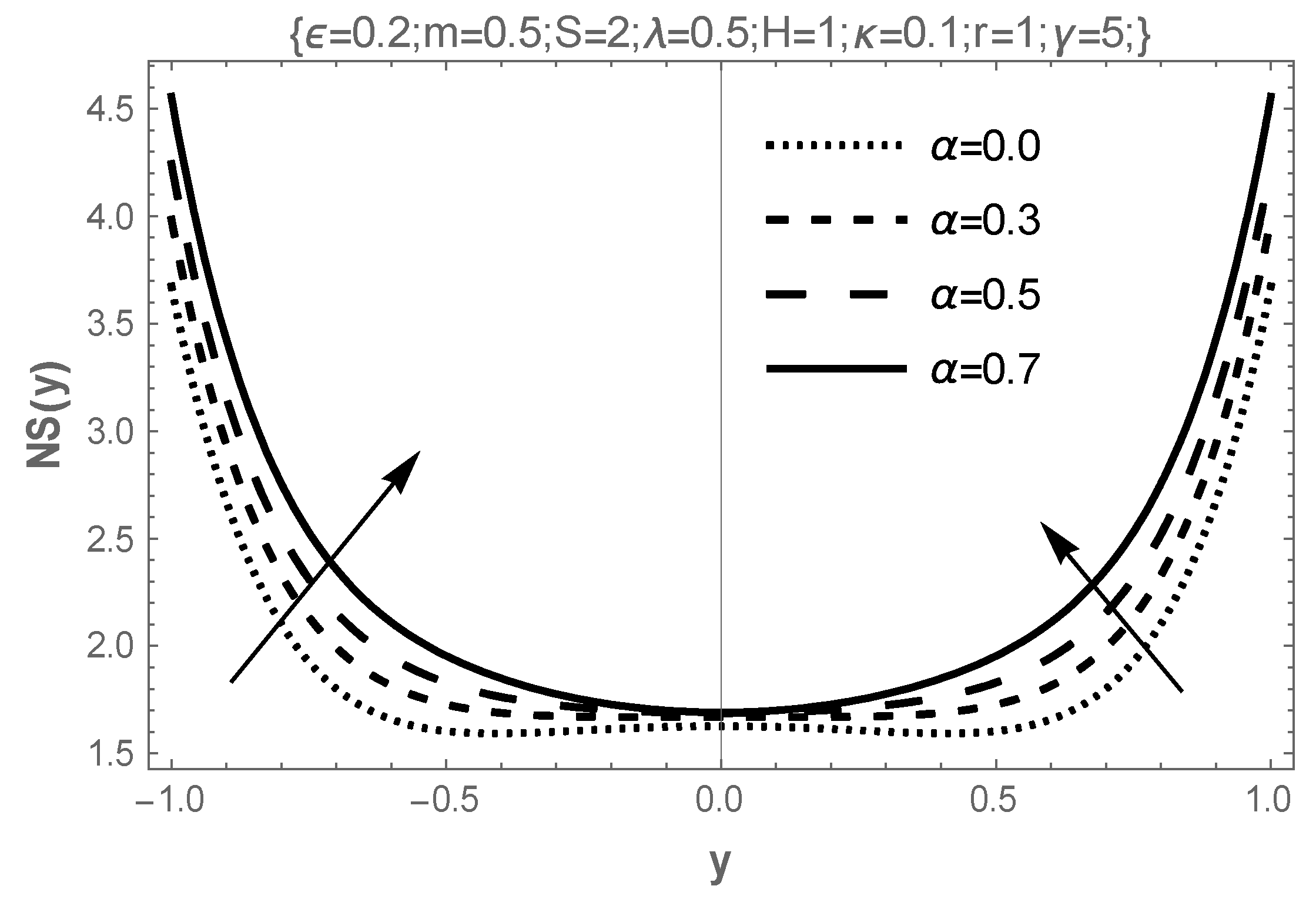
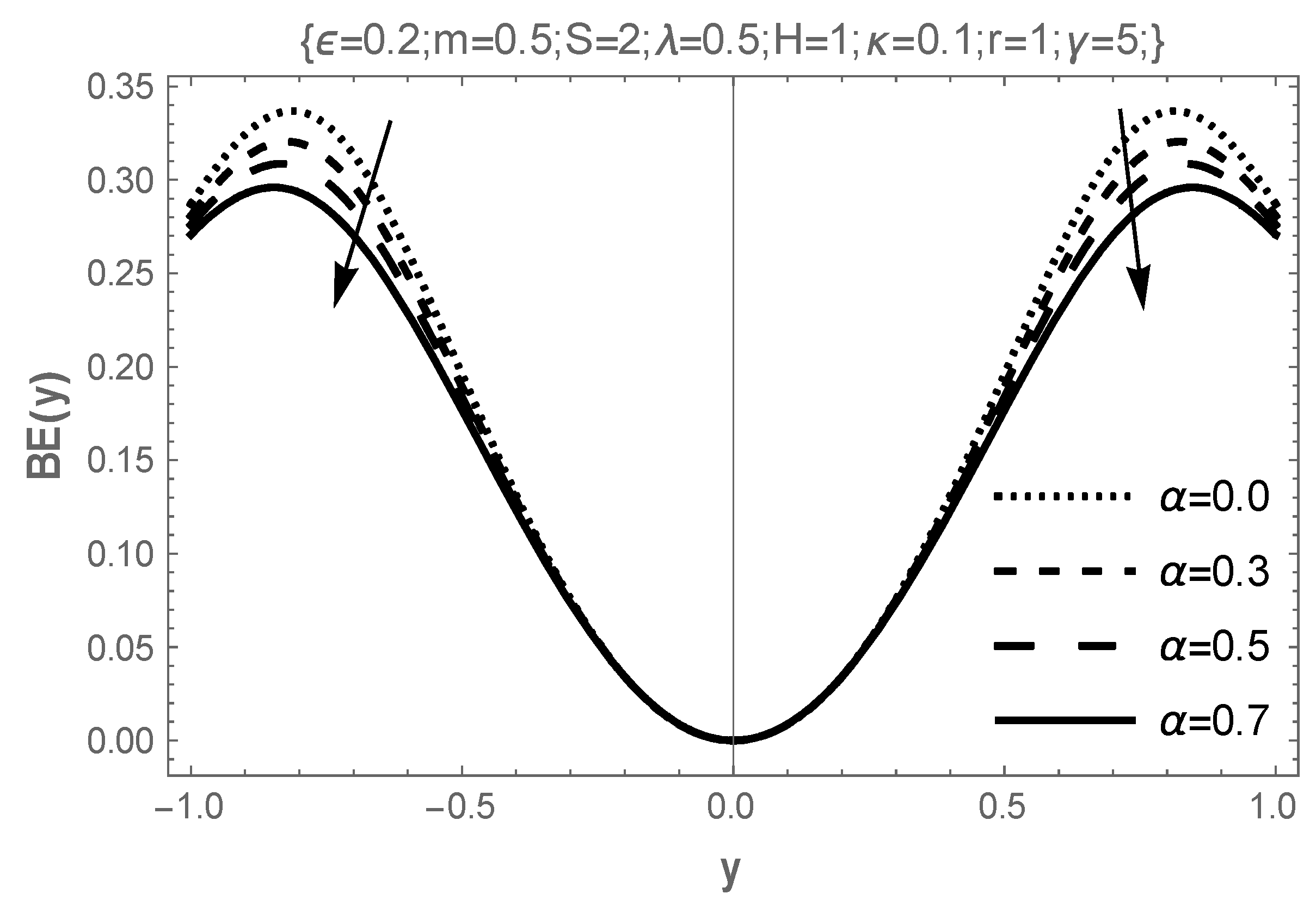
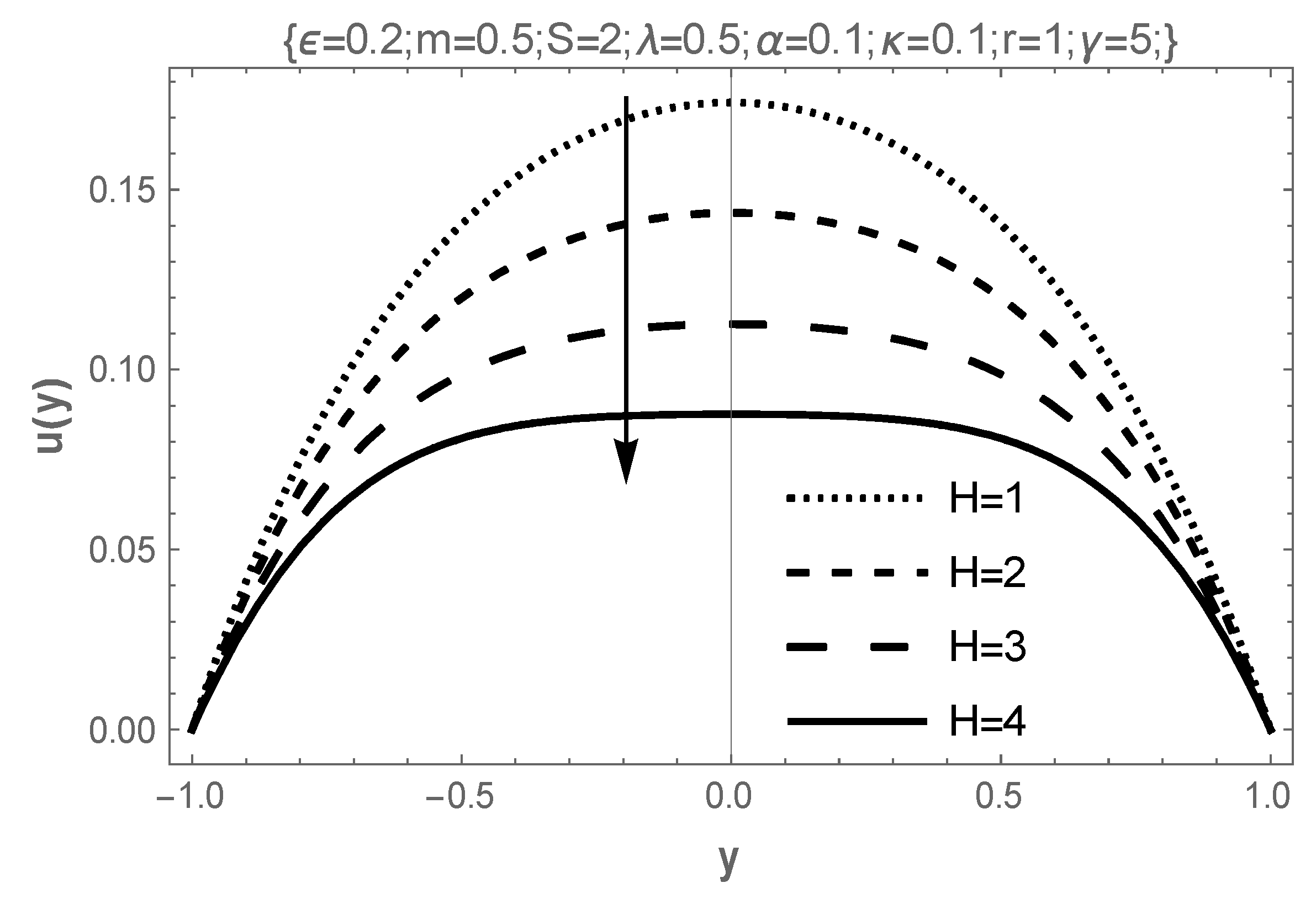
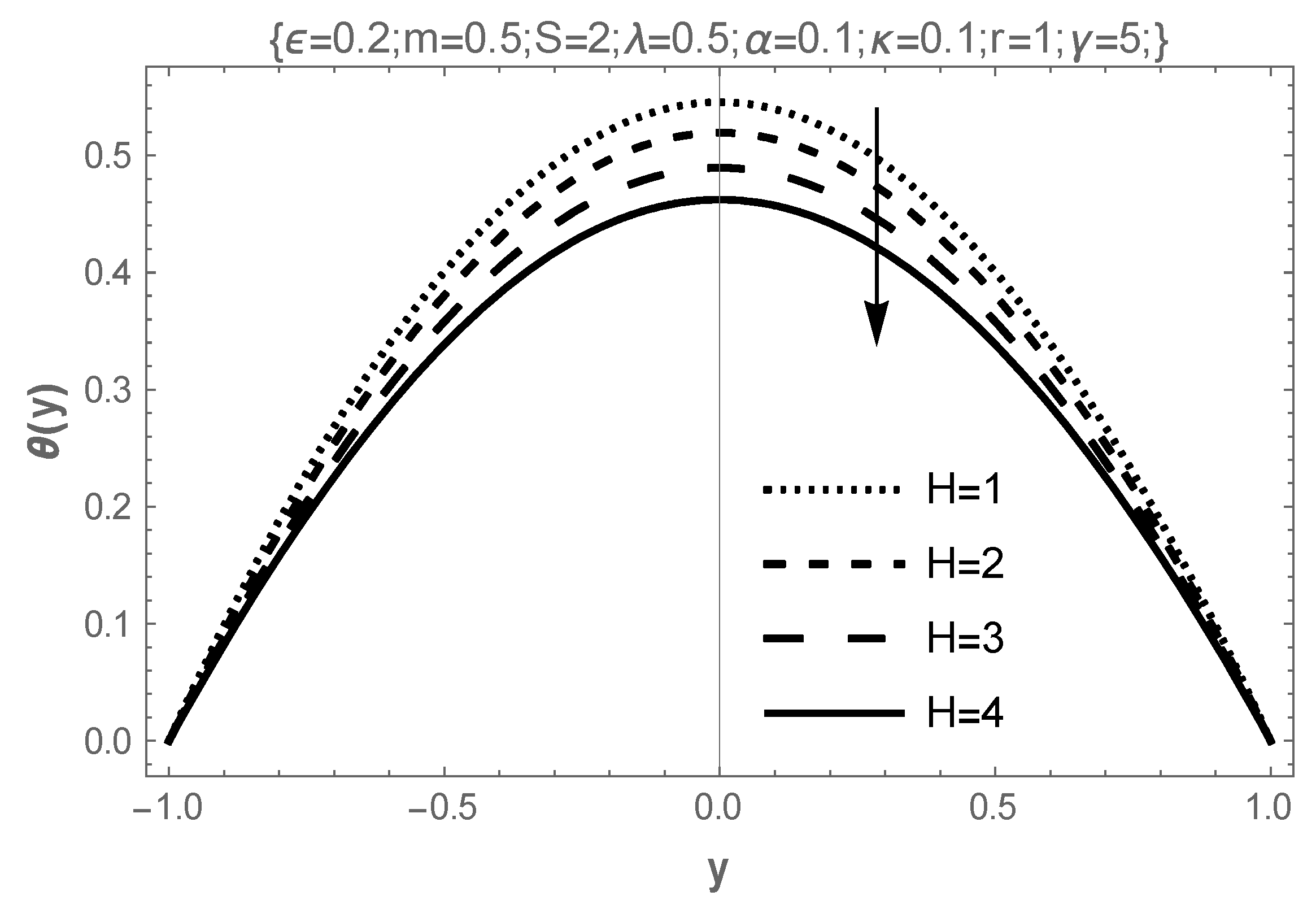
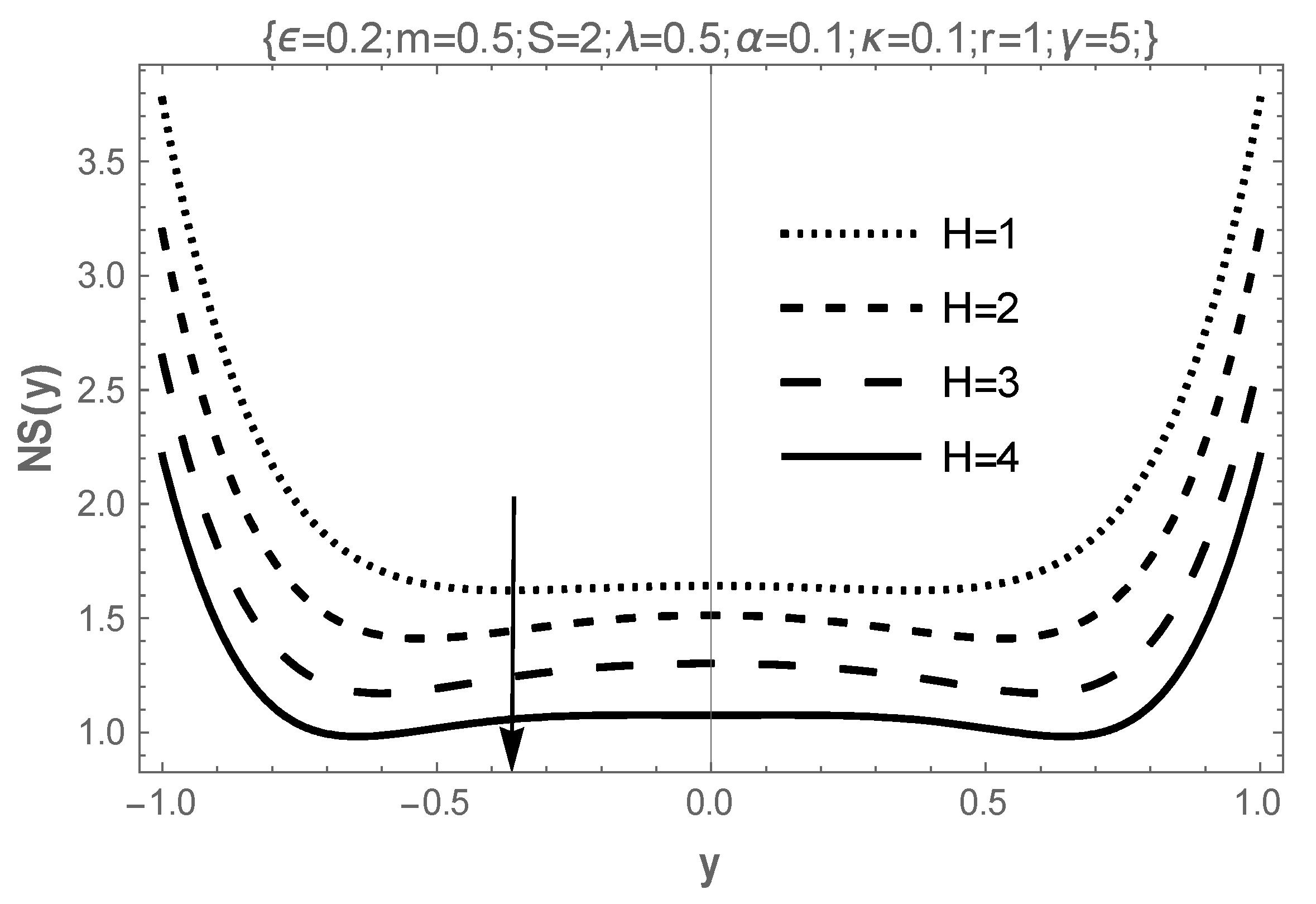
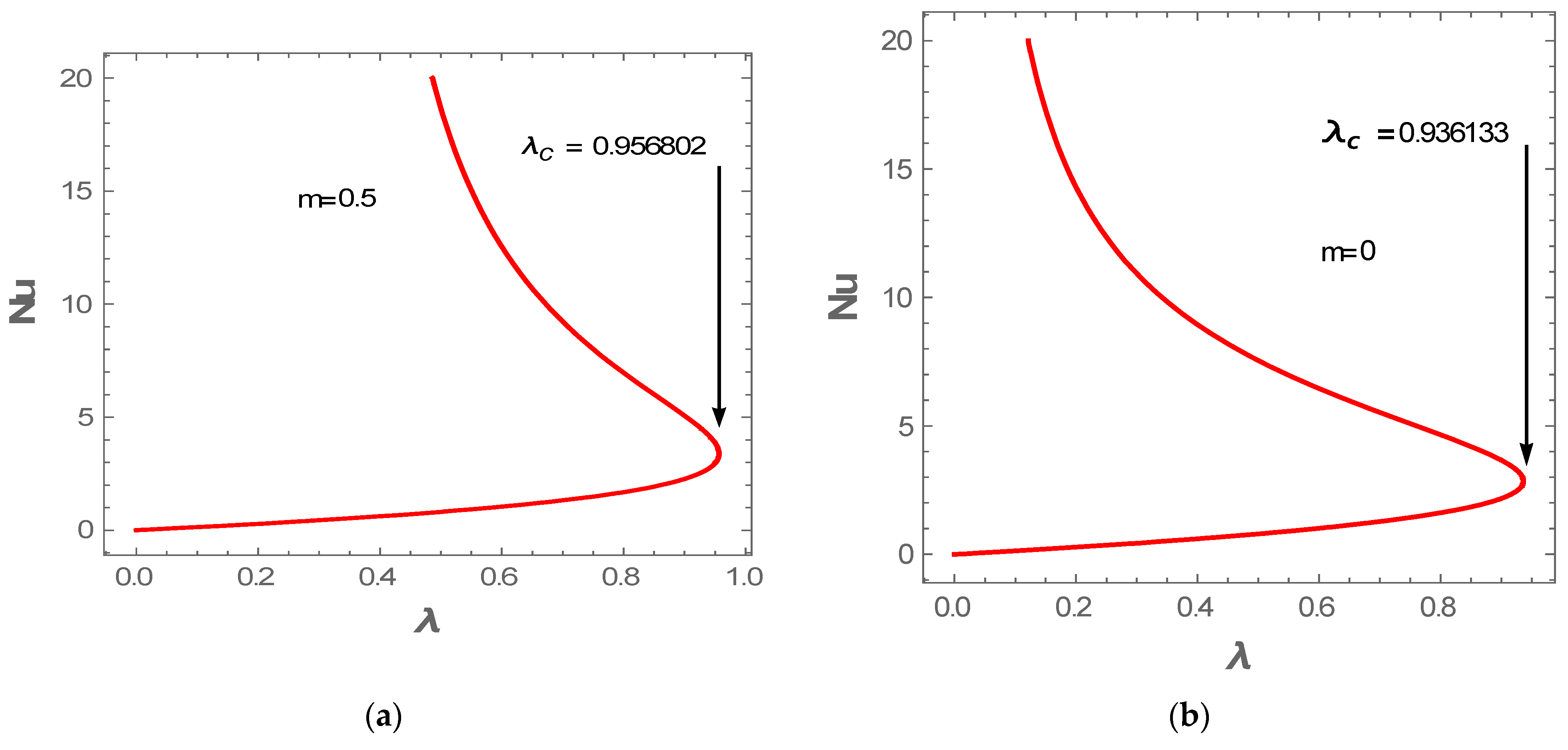
4. Results and Discussion

Table 1 and Table 2 reveal the results of comparing the two numerical methods used to solve (9) with parameter values used for the computation. The two results point to a unique numerical approximation.

Table 3. Convergence of critical values $\alpha =\kappa =H=S=0.1,\gamma =1=G=r$.

$\mathit{N}$	$\mathit{N}\mathit{u}\left(\mathit{\epsilon }=0.1,\mathit{m}=0\right)$	${\mathit{\lambda }}_{\mathit{c}}\left(\mathit{\epsilon }=0.1,\mathit{m}=0\right)$	$\mathit{N}\mathit{u}\left(\mathit{\epsilon }=0.2,\mathit{m}=0.5\right)$	${\mathit{\lambda }}_{\mathit{c}}\left(\mathit{\epsilon }=0.2,\mathit{m}=0.5\right)$
5	$2.846627970782652$	$0.9374126233474899$	$3.3625398187527153$	$0.9572961968391648$
10	$2.8501958216533407$	$0.9361333473082082$	$3.3789867582903286$	$0.9568015766586552$
15	$2.8501681280213513$	$0.9361332230608462$	$3.378984457190358$	$0.9568015916975717$
20	$2.8501680805234675$	$0.9361332229338021$	$3.3789844559157363$	$0.9568015917674281$
25	$2.8501680600340458$	$0.9361332229334971$	$3.3789844559157363$	$0.9568015917671002$
30	$2.850168051013584$	$0.9361332229334965$	$3.3789844559157363$	$0.9568015917670978$

shows the rapid convergence of the weighted residual method based on spectral collocation.

Table 4. Numerical result for stability analysis $r=1,\in =0.2$.

$\mathit{\alpha }$	$\mathit{\kappa }$	$\mathit{\gamma }$	$\mathit{H}$	$\mathit{S}$	${\mathit{\lambda }}_{\mathit{c}}$
0.1	0.1	1	0.1	0.1	$0.9568015917674281$
0.3	0.1	1	0.1	0.1	$0.9568150977269292$
0.5	0.1	1	0.1	0.1	$0.9568287821788171$
0.1	0.3	1	0.1	0.1	$0.9602351070037033$
0.1	0.5	1	0.1	0.1	$0.9624900150111185$
0.1	0.1	2	0.1	0.1	$0.9182714895582226$
0.1	0.1	1	0.3	0.1	$0.9563995116349202$
0.1	0.1	1	0.5	0.1	$0.9562084981492455$
0.1	0.1	1	0.1	0.5	$0.9563131736440517$
0.1	0.1	1	0.1	1	$0.9571020598593034$

presents the effects of various parameters on thermal flow stability. As seen from the table, porous permeability extends the critical value of the Frank–Kameneskii parameter, thus stabilizing the flow. Similarly, the third-grade parameter also delays the early occurrence of instability in the flow field. However, increasing magnetic field intensity and shape factor parameter values encourage thermal instability in the flow field.

Figure 2 reveals the Frank–Kameneskii parameter’s effect on the third-grade fluid’s temperature-dependent electrical conductivity. From the plot, an increase in the heat of the reaction from the initial liquid concentration produces a slight drop in the maximum flow velocity. This decline in flow peak is directly connected with the electrical resistance of the fluid to allow for passage of the electric current due to reduced ion formation in the liquid. In Figure 3, the rise in the Frank–Kameneskii parameter shows that the temperature distribution within the flow domain increases. This positive rise in temperature is due to a rise in the heat of the reaction, indicating that heat significantly flows into the flow domain from the surroundings. The significant increase in fluid temperature distribution (as shown in Figure 3) and the almost negligible decrease in the velocity maximum, as shown in Figure 2, reveal that the system’s entropy mainly depends on heat transfer rather than viscous interactions, as shown in Figure 4. Moreover, Figure 5 represents the effect of the Frank–Kameneskii parameter on the Bejan profile. From the plot, it is evident that the viscosity of the fluid becomes infinite at the center, thus $BE\left(\lambda ,y\right)=0$ at the core center. Beyond this point, towards the channel walls, the magnitude of attains $BE\left(\lambda ,y\right)=0.25$. This means that, at the walls, heat transfer irreversibility contributes to heat irreversibility.

Figure 6 represents the effect of the porous permeability variation parameter on flow velocity. The plot reveals that the flow velocity maximum rises with increasing values of the passable permeability parameter. This is because as temperature increases, there is a reduction in the viscosity of the third-grade fluid. This encourages flow due to the increased permeability of the porous matrix. The increase in porous permeability with the temperature of the fluid is presented in Figure 7. The result shows that the fluid’s porous permeability improves temperature distribution within the flow channel. This is connected with the reduced activation energy of the combustible liquid. Figure 8 shows the effect of variations in porous permeability on the entropy generation rate. The fact that flow velocity and temperature distribution increases with this parameter indicates that frictional interaction within the fluid layer is negligible. Therefore, the entropy profile is on the rise across the channel. Finally, fluid viscosity-related irreversibility dominates significantly over heat-transfer irreversibility at the core center of the flow channel. In contrast, heat transfer irreversibility is more prominent at the walls, as seen in Figure 9.

Figure 10 shows the effect of magnetization on the flow of third-grade fluid. The velocity peak declines with increasing magnetic field strength, as seen in the plot. This decline is physically correct since the spinning of fluid particles encourages fluid thickening; therefore, flow velocity declines with the increasing intensity of the magnetic field. Similarly, the kinetic energy of the fluid particles is expected to decrease due to fluid thickening. Therefore, the liquid temperature distribution declines, as seen in Figure 11. The combined effect of reducing flow velocity and temperature shows that heat transfer and fluid friction irreversibility will uniformly decrease across the flow channel, as observed in Figure 12. The Bejan ratio signifies the dominating viscous effect over heat transfer irreversibility at the core region of the flow channel, while irreversibility from heat transfer is more at the walls as seen in Figure 13. The bifurcation study in Figure 14a,b shows the variation of the Nusselt number with the Frank–Kameneskii parameter. The reaction exponent, m, has a stabilizing effect on third-grade fluid’s thermal stability.

5. Conclusions

In this work, numerical simulations have been conducted to study the heat irreversibility inherent in the steady flow of hydromagnetic third-grade fluid through a porous medium with temperature-dependent porous permeability and electrical conductivity. The spectral collocation method solved the dimensionless nonlinear equations and validated the results using the shooting Runge–Kutta method. The agreement between the two numerical results suggests the accuracy of the two numerical methods in handling the coupled nonlinear boundary-value problem. The significant contributions to knowledge from this study are:

• The effect of the increasing values of temperature-dependent porous permeability in the present study reveal that it stabilizes the flow and elevates both velocity and temperature while encouraging entropy generation;
• The influence of rising temperature-dependent electrical conductivity parameters destabilizes the flow, lowering both flow and temperature peaks while discouraging entropy generation in the flow field.