Developments of Electro-Osmotic Two-Phase Flows of Fourth-Grade Fluid through Convergent and Divergent Channels
Abstract
1. Introduction
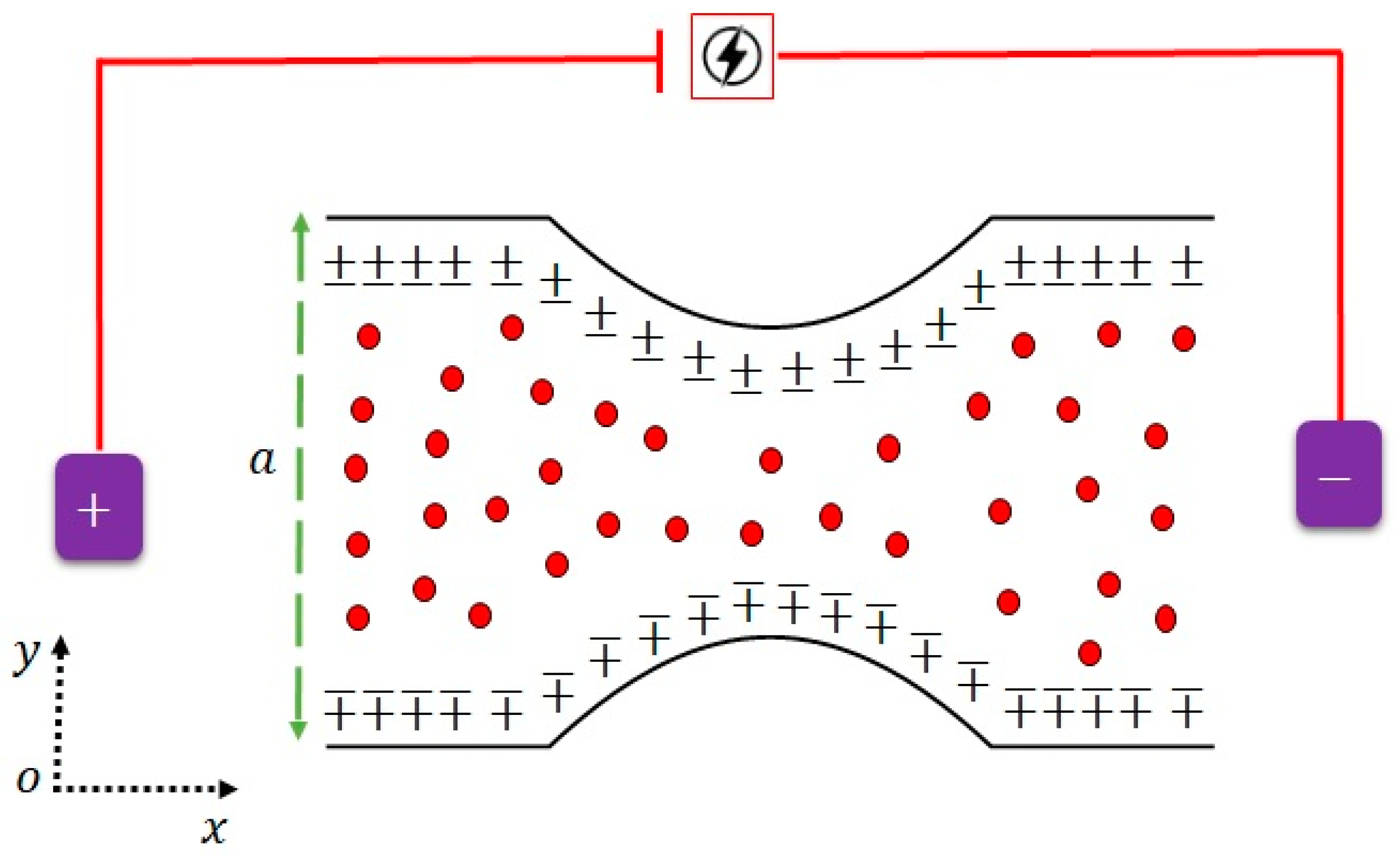
2. Development of a Mathematical Model of Multiphase Flow of Non-Newtonian Fluid with Electro-Osmotic Phenomena
2.1. Flow Equations for Fluid Phase
2.2. Governing Equations (Particle Phase)
3. Dimensionalization of the Problem
4. Perturbation Solution
5. Comparative Analysis
6. Results and Discussion
7. Concluding Remarks
- ❖
- An increase in the behavior of both particle and fluid phase velocities is viewed in convergent and divergent geometries when enhancement is made in the fourth-grade parameter;
- ❖
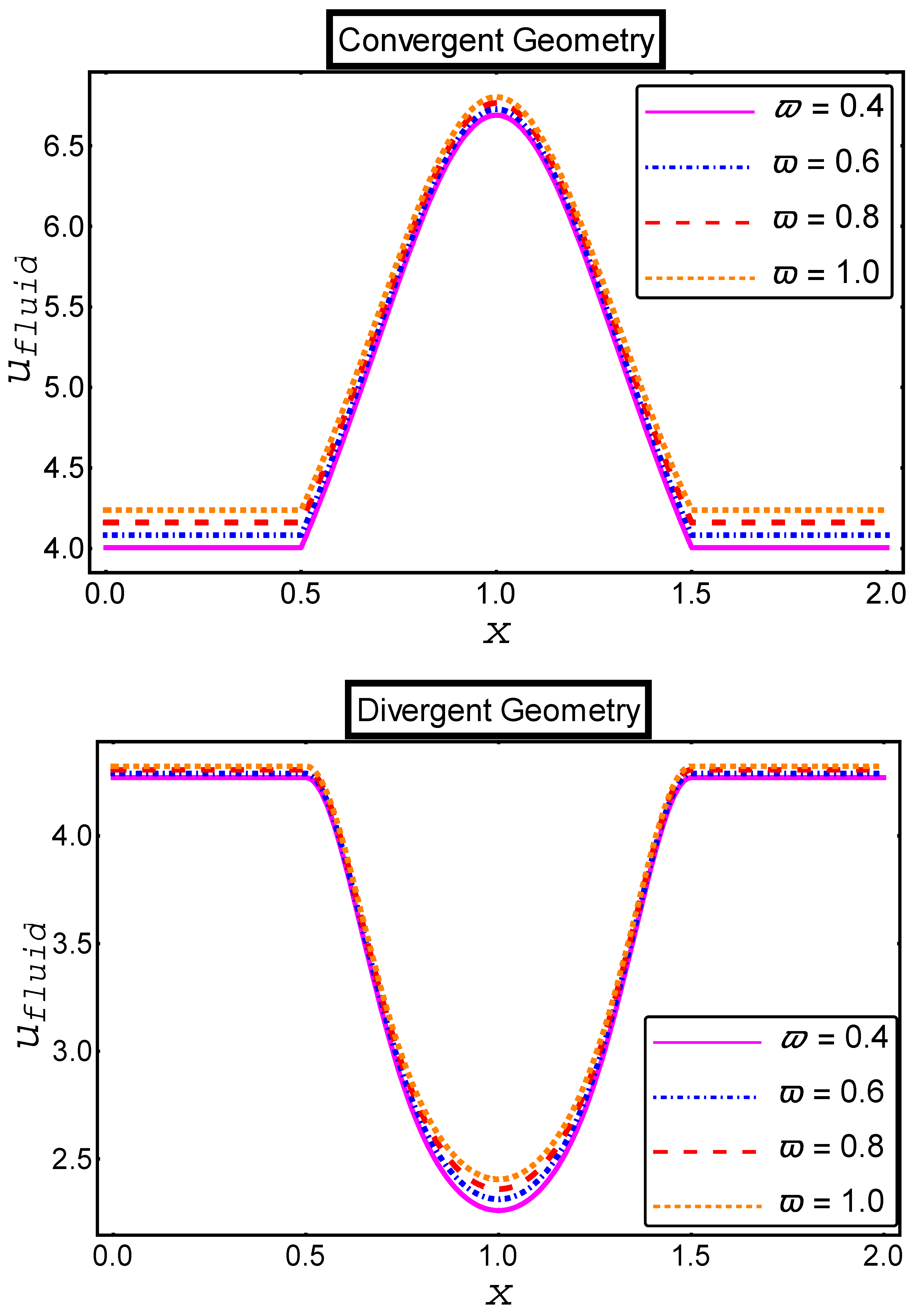
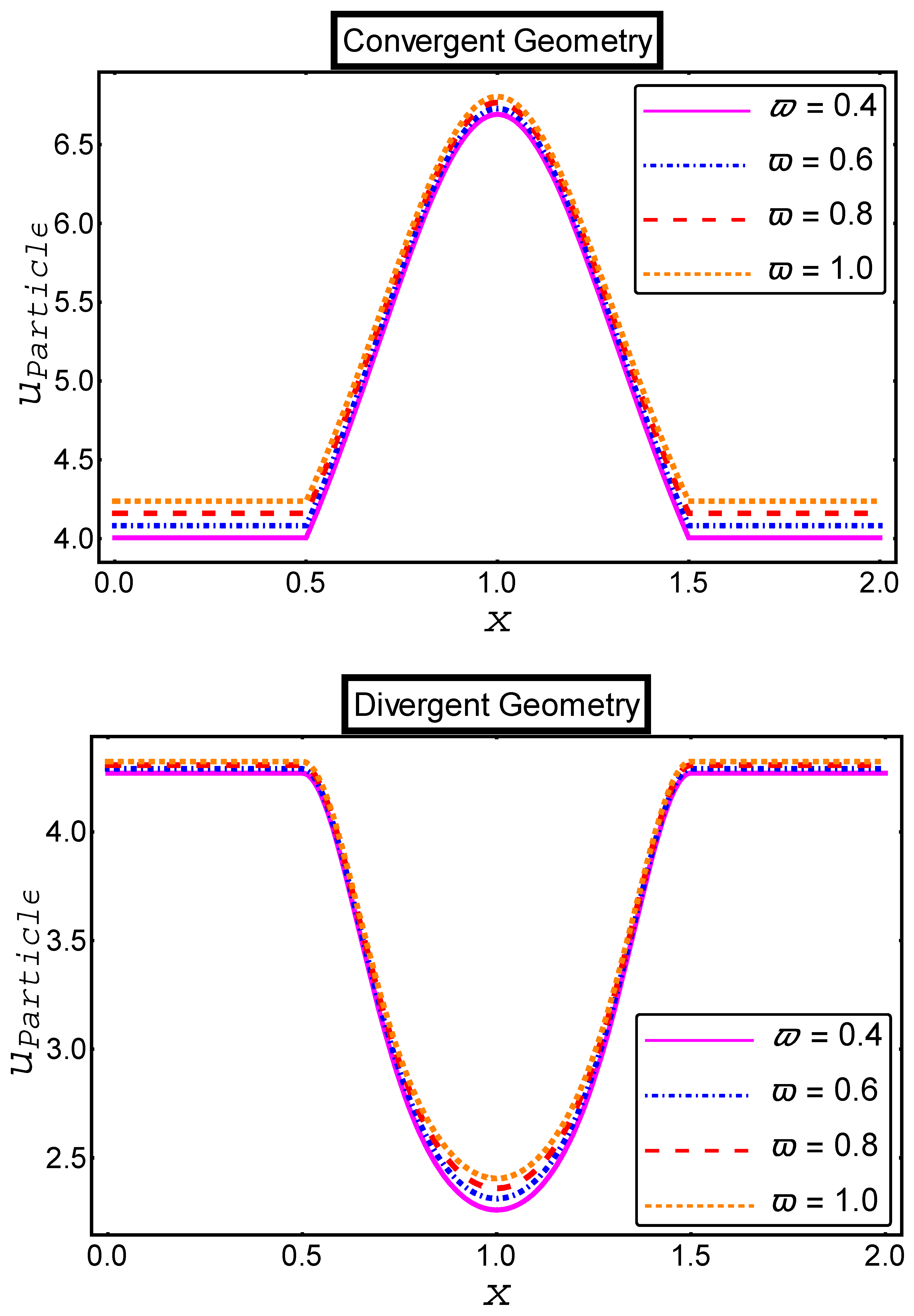
- A remarkable decrease in the velocity profiles of fluid and particle phases in both channels is noted when the value of the electro-osmotic parameter is enhanced;
- ❖
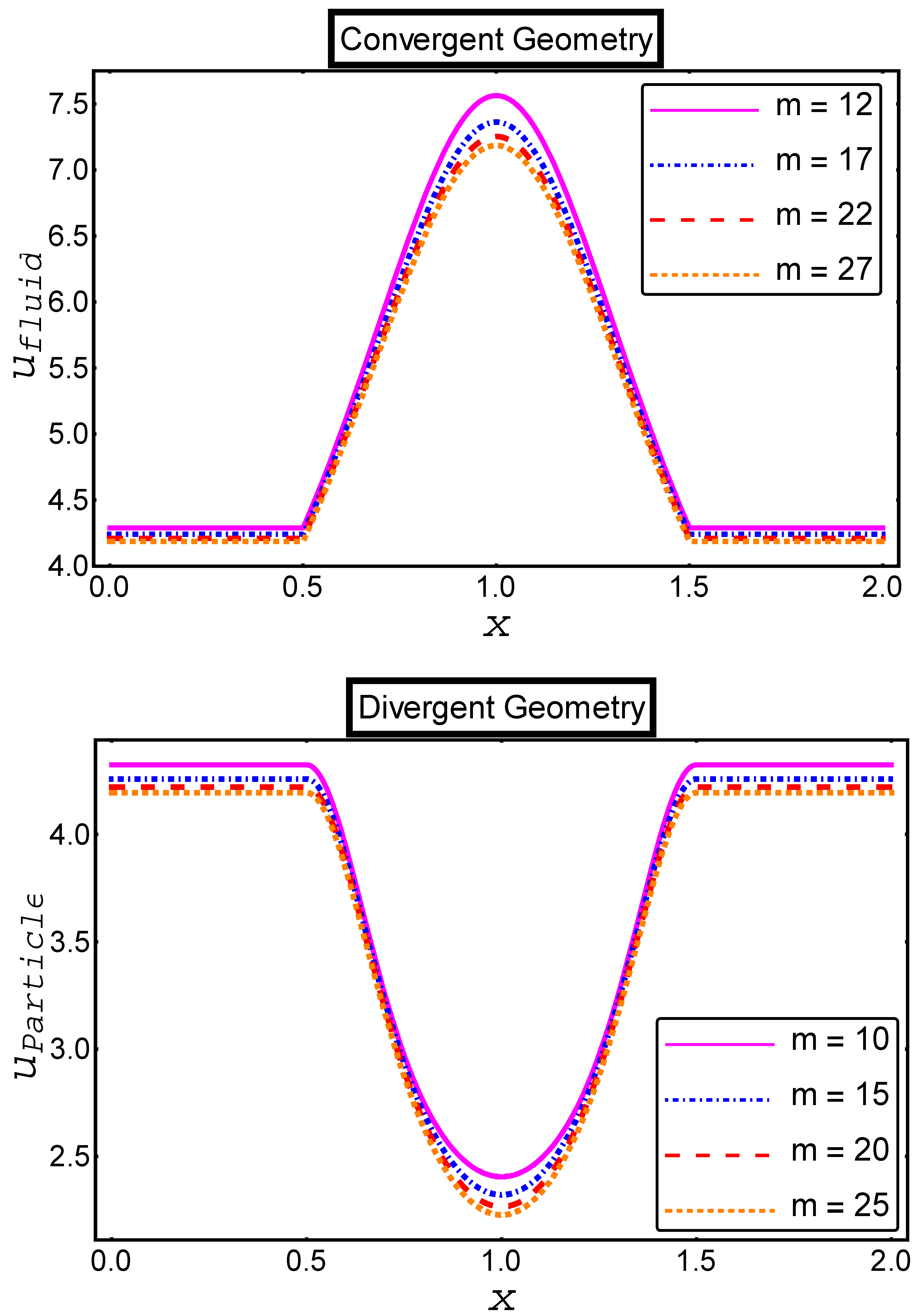
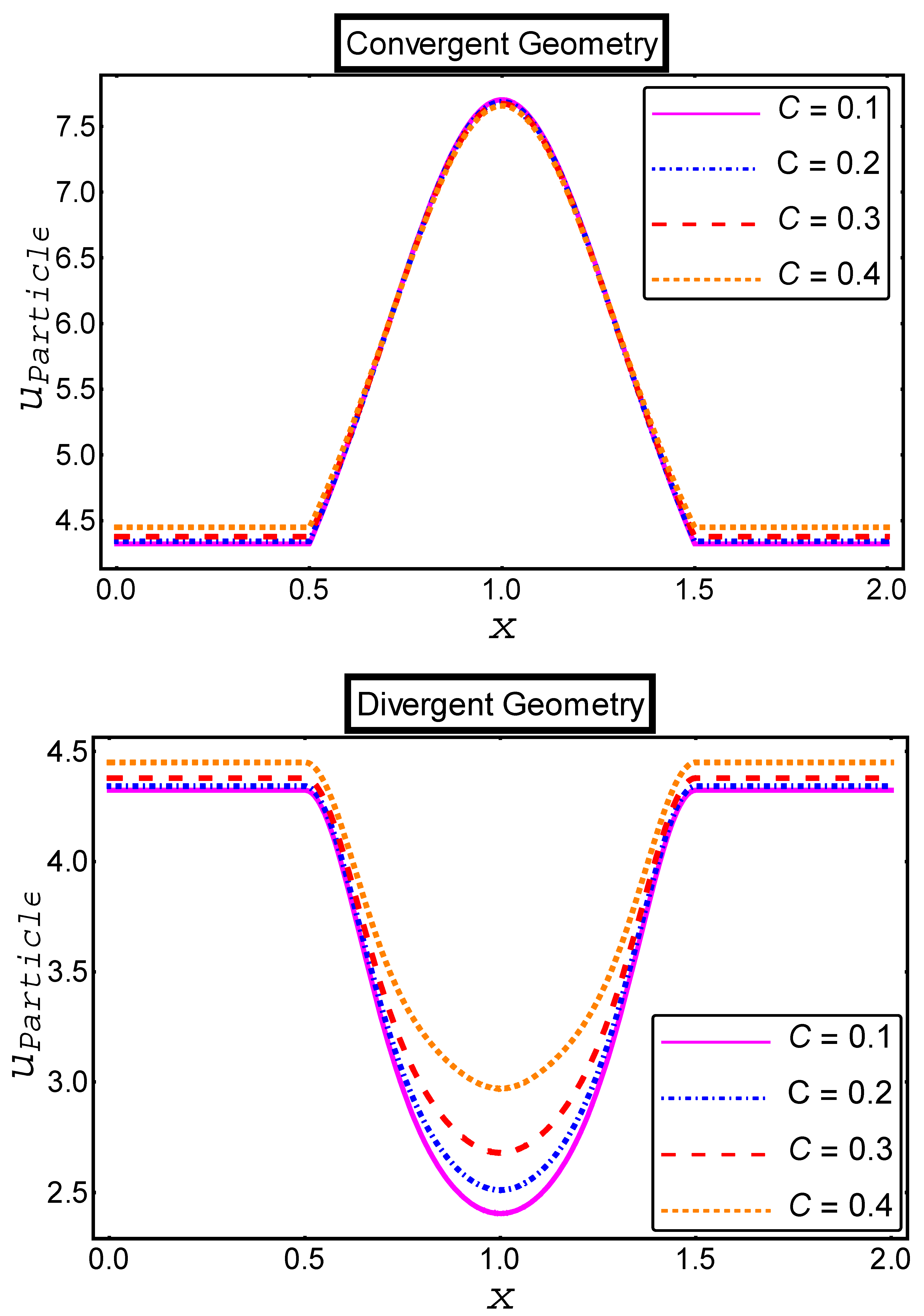
- The credible incline is measured in the velocity profile of both phases in the divergent channel when the value of particle concentration is increased, and a very dubious decline has been seen in the velocities of both phases in the convergent channel;
- ❖
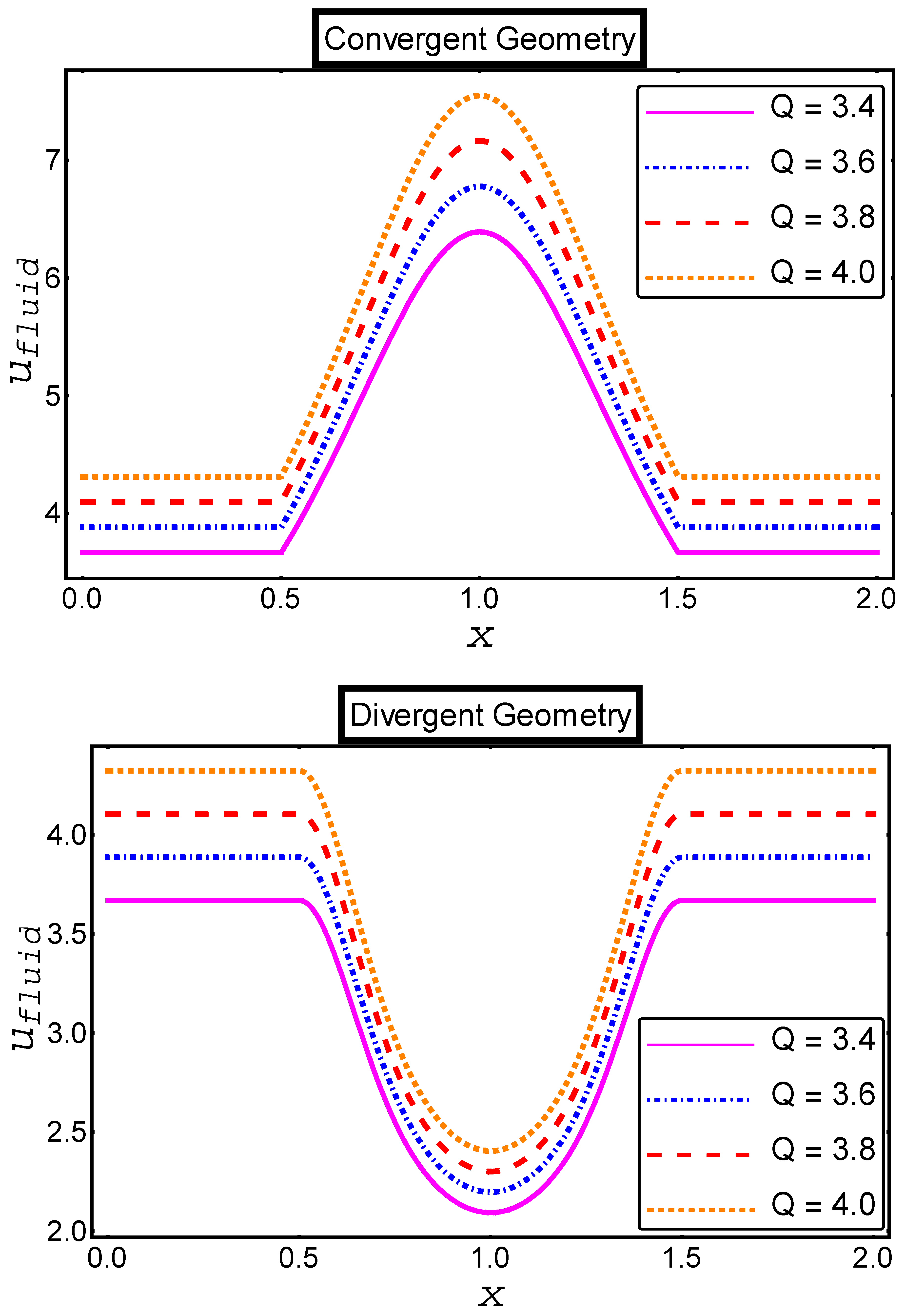
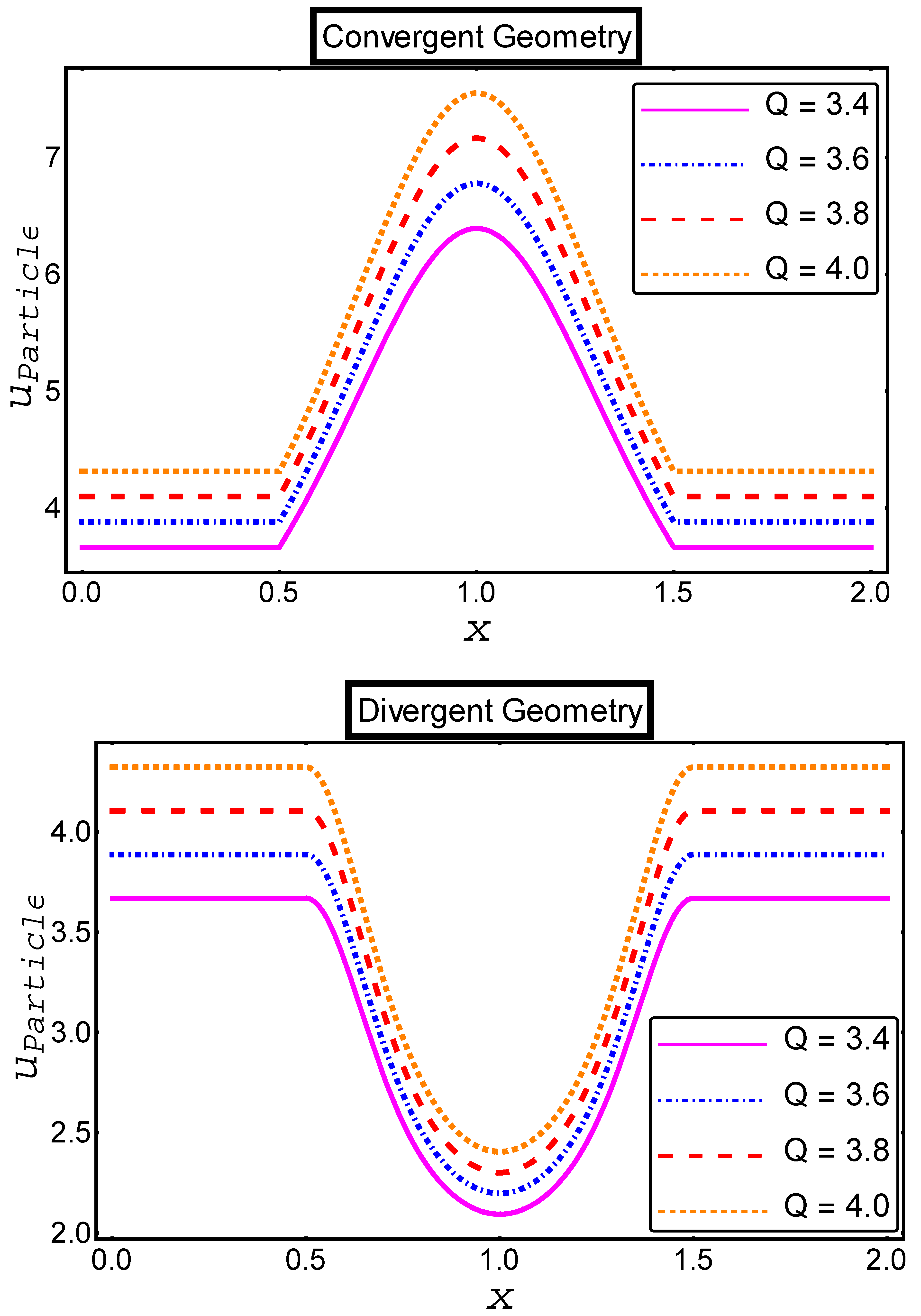
- When the volumetric flow rate upraised in both channels the velocity profile of fluid and particle phases improved as the volumetric flow rate more in velocities.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Islam, S.; Bano, Z.; Siddique, I.; Siddiqui, A. The optimal solution for the flow of a fourth-grade fluid with partial slip. Comput. Math. Appl. 2011, 61, 1507–1516. [Google Scholar] [CrossRef]
- Hayat, T.; Noreen, S. Peristaltic transport of fourth grade fluid with heat transfer and induced magnetic field. Comptes Rendus Mécanique 2010, 338, 518–528. [Google Scholar] [CrossRef]
- Sajid, M.; Hayat, T.; Asghar, S. On the analytic solution of the steady flow of a fourth grade fluid. Phys. Lett. A 2006, 355, 18–26. [Google Scholar] [CrossRef]
- Salawu, S.; Fatunmbi, E.; Ayanshola, A. On the diffusion reaction of fourth-grade hydromagnetic fluid flow and thermal criticality in a plane Couette medium. Results Eng. 2020, 8, 100169. [Google Scholar] [CrossRef]
- Khan, A.A.; Masood, F.; Ellahi, R.; Bhatti, M. Mass transport on chemicalized fourth-grade fluid propagating peristaltically through a curved channel with magnetic effects. J. Mol. Liq. 2018, 258, 186–195. [Google Scholar] [CrossRef]
- Sobamowo, M.; Akinshilo, A. Analysis of flow, heat transfer and entropy generation in a pipe conveying fourth grade fluid with temperature dependent viscosities and internal heat generation. J. Mol. Liq. 2017, 241, 188–198. [Google Scholar] [CrossRef]
- Nadeem, S.; Ali, M. Analytical solutions for pipe flow of a fourth grade fluid with Reynold and Vogel’s models of viscosities. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2073–2090. [Google Scholar] [CrossRef]
- Aziz, T.; Mahomed, F. Reductions and solutions for the unsteady flow of a fourth grade fluid on a porous plate. Appl. Math. Comput. 2013, 219, 9187–9195. [Google Scholar] [CrossRef]
- Yan, S.-R.; Toghraie, D.; Abdulkareem, L.A.; Alizadeh, A.; Barnoon, P.; Afrand, M. The rheological behavior of MWCNTs–ZnO/Water–Ethylene glycol hybrid non-Newtonian nanofluid by using of an experimental investigation. J. Mater. Res. Technol. 2020, 9, 8401–8406. [Google Scholar] [CrossRef]
- Palencia, J.L.D.; Rahman, S.U.; Redondo, A.N. Regularity and reduction to a Hamilton-Jacobi equation for a MHD Eyring-Powell fluid. Alex. Eng. J. 2022, 61, 12283–12291. [Google Scholar] [CrossRef]
- Subbarayudu, K.; Suneetha, S.; Ankireddy, B. The assessment of time dependent flow of Williamson fluid with radiative blood flow against a wedge. Propuls. Power Res. 2020, 9, 87–99. [Google Scholar] [CrossRef]
- Majeed, A.H.; Mahmood, R.; Shahzad, H.; Pasha, A.A.; Raizah, Z.; Hosham, H.A.; Reddy, D.S.K.; Hafeez, M.B. Heat and mass transfer characteristics in MHD Casson fluid flow over a cylinder in a wavy channel: Higher-order FEM computations. Case Stud. Therm. Eng. 2023, 42, 102730. [Google Scholar] [CrossRef]
- Asfour, H.A.H.; Ibrahim, M.G. Numerical simulations and shear stress behavioral for electro-osmotic blood flow of magneto Sutterby nanofluid with modified Darcy’s law. Therm. Sci. Eng. Prog. 2023, 37, 101599. [Google Scholar] [CrossRef]
- Asghar, Z.; Waqas, M.; Gondal, M.A.; Khan, W.A. Electro-osmotically driven generalized Newtonian blood flow in a divergent micro-channel. Alex. Eng. J. 2022, 61, 4519–4528. [Google Scholar] [CrossRef]
- Wang, X.; Xu, H.; Qi, H. Numerical analysis for rotating electro-osmotic flow of fractional Maxwell fluids. Appl. Math. Lett. 2020, 103, 106179. [Google Scholar] [CrossRef]
- Ali, F.; Iftikhar, M.; Khan, I.; Sheikh, N.A.; Aamina; Nisar, K.S. Time fractional analysis of electro-osmotic flow of Walters’s-B fluid with time-dependent temperature and concentration. Alex. Eng. J. 2019, 59, 25–38. [Google Scholar] [CrossRef]
- Trivedi, M.; Maurya, S.; Nirmalkar, N. Numerical simulations for electro-osmotic flow of PTT fluids in diverging microchannel. Mater. Today Proc. 2022, 57, 1765–1769. [Google Scholar] [CrossRef]
- Miao, H.; Dokhani, V.; Ma, Y.; Zhang, D. Numerical modeling of laminar and turbulent annular flows of power-law fluids in partially blocked geometries. Results Eng. 2023, 17, 100930. [Google Scholar] [CrossRef]
- Pan, T.-W.; Chiu, S.-H. A DLM/FD method for simulating balls settling in Oldroyd-B viscoelastic fluids. J. Comput. Phys. 2023, 484, 112071. [Google Scholar] [CrossRef]
- Tahraoui, Y.; Cipriano, F. Optimal control of two dimensional third grade fluids. J. Math. Anal. Appl. 2023, 523, 127032. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; El Shehawey, E.F.; Elaw, A.M. Peristaltic Motion of a Particle-Fluid Suspension in a Planar Channel. Int. J. Theor. Phys. 1998, 37, 2895–2920. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical Models of Electro-Magnetohydrodynamic Multiphase Flows Synthesis with Nano-Sized Hafnium Particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Thermally Charged MHD Bi-Phase Flow Coatings with Non-Newtonian Nanofluid and Hafnium Particles along Slippery Walls. Coatings 2019, 9, 300. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Two-Phase Couette Flow of Couple Stress Fluid with Temperature Dependent Viscosity Thermally Affected by Magnetized Moving Surface. Symmetry 2019, 11, 647. [Google Scholar] [CrossRef]



| Perturbation Solution | Numerical Solution | Absolute Error | ||||
|---|---|---|---|---|---|---|
| 1.0 | 1.45064 | 1.45089 | 1.45198 | 1.45001 | ||
| 2.0 | 1.35730 | 1.35744 | 1.35598 | 1.35671 | ||
| 3.0 | 1.21666 | 1.21680 | 1.21549 | 1.21612 | ||
| 4.0 | 1.04626 | 1.04638 | 1.04519 | 1.04590 | ||
| 5.0 | 0.86436 | 0.86446 | 0.86332 | 0.86399 | ||
| Pseudo-Spectral Collocation Method | Shooting Method | |||
|---|---|---|---|---|
| 0.1 | 1.41085 | 1.41110 | 1.41090 | 1.41001 |
| 0.2 | 1.33491 | 1.33506 | 1.33231 | 1.33325 |
| 0.3 | 1.23917 | 1.23932 | 1.23523 | 1.23567 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatima, N.; Nazeer, M.; Lashin, M.M.A.; Ghafar, M.M.; Gorji, M.R.; Hameed, M.K. Developments of Electro-Osmotic Two-Phase Flows of Fourth-Grade Fluid through Convergent and Divergent Channels. Mathematics 2023, 11, 1832. https://doi.org/10.3390/math11081832
Fatima N, Nazeer M, Lashin MMA, Ghafar MM, Gorji MR, Hameed MK. Developments of Electro-Osmotic Two-Phase Flows of Fourth-Grade Fluid through Convergent and Divergent Channels. Mathematics. 2023; 11(8):1832. https://doi.org/10.3390/math11081832
Chicago/Turabian StyleFatima, Nahid, Mubbashar Nazeer, Maha M. A. Lashin, M. M. Ghafar, M. R. Gorji, and M. K. Hameed. 2023. "Developments of Electro-Osmotic Two-Phase Flows of Fourth-Grade Fluid through Convergent and Divergent Channels" Mathematics 11, no. 8: 1832. https://doi.org/10.3390/math11081832
APA StyleFatima, N., Nazeer, M., Lashin, M. M. A., Ghafar, M. M., Gorji, M. R., & Hameed, M. K. (2023). Developments of Electro-Osmotic Two-Phase Flows of Fourth-Grade Fluid through Convergent and Divergent Channels. Mathematics, 11(8), 1832. https://doi.org/10.3390/math11081832







