The Effects of Heat Transfer through the Ends of a Cylindrical Cavity on Acoustic Streaming and Gas Temperature

Abstract

The longitudinal vibrational motion of a cylindrical cavity with gas, in which the acoustic streaming occurs, is considered. The motion is described by the system of equations for the dynamics and thermal conductivity of a viscous perfect gas, written in a cylindrical coordinate system associated with the cavity. The system of equations is solved numerically by the finite volume method with an implicit staggered grid scheme, while the convective–diffusion fluxes are approximated by the power law scheme. According to the boundary conditions, the lateral surface of the cavity is maintained at a constant equal initial temperature. The effects of heat transfer through the ends of the cavity are studied. Heat transfer is given by isothermal boundary conditions. The obtained solutions are compared with the solutions under adiabatic boundary conditions. It is shown for the first time that the effects of heat transfer manifest themselves with an increase in the nonlinearity of the process; when the frequency and amplitude of vibration increase, this is also facilitated by an increase in the radius of the cavity. The effects of heat transfer on the period average temperature, on the streaming velocity and on structure are established.

1. Introduction

In the presence of an oscillatory gas movement inside the cavity, a secondary flow called an acoustic stream can be observed. The streaming flow is formed by stable vortices that have a certain direction of rotation. In its theoretical description, the Schlichting streaming vortices are in the boundary layer. In these vortices, gas is transferred from the nodes of acoustic velocity to the antinode near the lateral surface. The Rayleigh streaming vortices are formed outside the boundary layer, and their direction of rotation is different from the direction of rotation of the Schlichting streaming vortices [1].

Features of acoustic streaming can be used in various engineering applications, such as mixing liquids, aerosol clearing, the coagulation and sedimentation of smoke and fog, technologies for increasing the extraction of oil and gas from the earth’s interior, biomedical applications, etc. [2,3,4,5]. Mathematical modeling of acoustic streaming can be carried out within the framework of the system of Navier–Stokes and energy equations, the solution of which is often found by numerical methods—for example, by the control volume method [6,7,8,9]. Note that this approach is also used to study other problems, for example, when modeling room ventilation, which is especially important for protecting hospitals from infection [10,11]. Several other classical methods and their applications can be noted: finite difference [12,13,14,15], the finite element [16], and the boundary element [17].

Acoustic streaming is one of the heat transfer mechanisms, and it is usually studied in closed cavities with the same thermal boundary conditions on all walls. The boundary conditions can be isothermal (constant temperature walls) [12,13,18,19,20], adiabatic (heat-insulated walls) [6], or without taking into account the change in gas temperature [14,15]. The type of boundary conditions for temperature strongly affects acoustic streaming and heat transfer [21,22,23]. The transition from adiabatic to isothermal boundary conditions by varying the heat transfer coefficient was described in [24]. Lin and Farouk [7] and Aktas and Ozgumus [8] showed a strong effect of the temperature difference between horizontal walls on acoustic streaming and its velocity for a rectangular cavity with thermally insulated vertical walls. Michel et al. [25] and Baran et al. [9] studied the baroclinic acoustic streaming phenomenon in channels with the temperature gradient between the upper and lower walls.

Due to the increase in the vibration amplitude, the wave motion becomes more intense. Nonlinear effects strongly influence the process. With increases in nonlinearity, the streaming vortices begin to differ from the vortices at low vibration amplitude. In addition, the period average temperature, pressure, and density become more inhomogeneous. In some cases, shock waves are generated [6,12,13,14,15,19,20,22,26].

In the study of acoustic streaming, the so-called nonlinear Reynolds number is used to determine the degree of the process nonlinearity:

$$R{e}_{NL}={\left(\frac{u_0{R}_0}{c_0{\delta }_{\nu }}\right)}^2.$$

In this formula, u₀ is the axial acoustic velocity amplitude, c₀ is the speed of sound in gas, R₀ is the cavity radius, ${\mathsf{\delta }}_{\nu }=\sqrt{2\nu /\mathsf{\omega }}$ is the acoustic boundary layer thickness, ν is the kinematic viscosity and ω is the angular frequency of vibration. Hence, it follows that the nonlinearity of the process increases not only with an increase in the axial velocity, but also with an increase in the cavity radius. In turn, the axial velocity increases with an increase in the frequency and amplitude of the cavity oscillations according to the equation of motion.

The effects of the cavity height and the vibration amplitude on the streaming structures in a gas-filled two-dimensional rectangular cavity with a vibrating wall are described by Aktas and Farouk [6]. Daru et al. [12] showed the coupling between acoustic streaming and mean temperature in a rectangular gas-filled channel when the parameter Re_NL is changed up to 27. Reyt et al. [13] considered acoustic streaming in a cylindrical tube for Re_NL up to 30 and described the displacement of the streaming vortices’ centers and the formation of new counter-rotating vortices. Daru et al. [14] experimentally and numerically obtained the dependence of the streaming velocity on the acoustic amplitude in a cylindrical tube at high Re_NL (up to Re_NL = 145).

Previously, in [23], it was found that in a weakly nonlinear oscillation mode, the results of solving the problem of the vibrational motion of a cylindrical cavity with gas under adiabatic and isothermal boundary conditions at the ends of the cavity practically coincide. Therefore, this work is devoted to the study of the question of whether this situation will change in a strongly nonlinear regime. Acoustic streaming in a vibrating air-filled cylindrical cavity is considered. The lateral surface of the cavity is kept at a constant temperature. The effects of heat transfer through the ends (isothermal or adiabatic boundary conditions) on the streaming structure, the streaming velocity, and the period average temperature in a strongly nonlinear regime are determined. The results are presented for two vibration frequencies and two values of the cavity radius (up to Re_NL = 114).

2. Governing Equations and Numerical Method

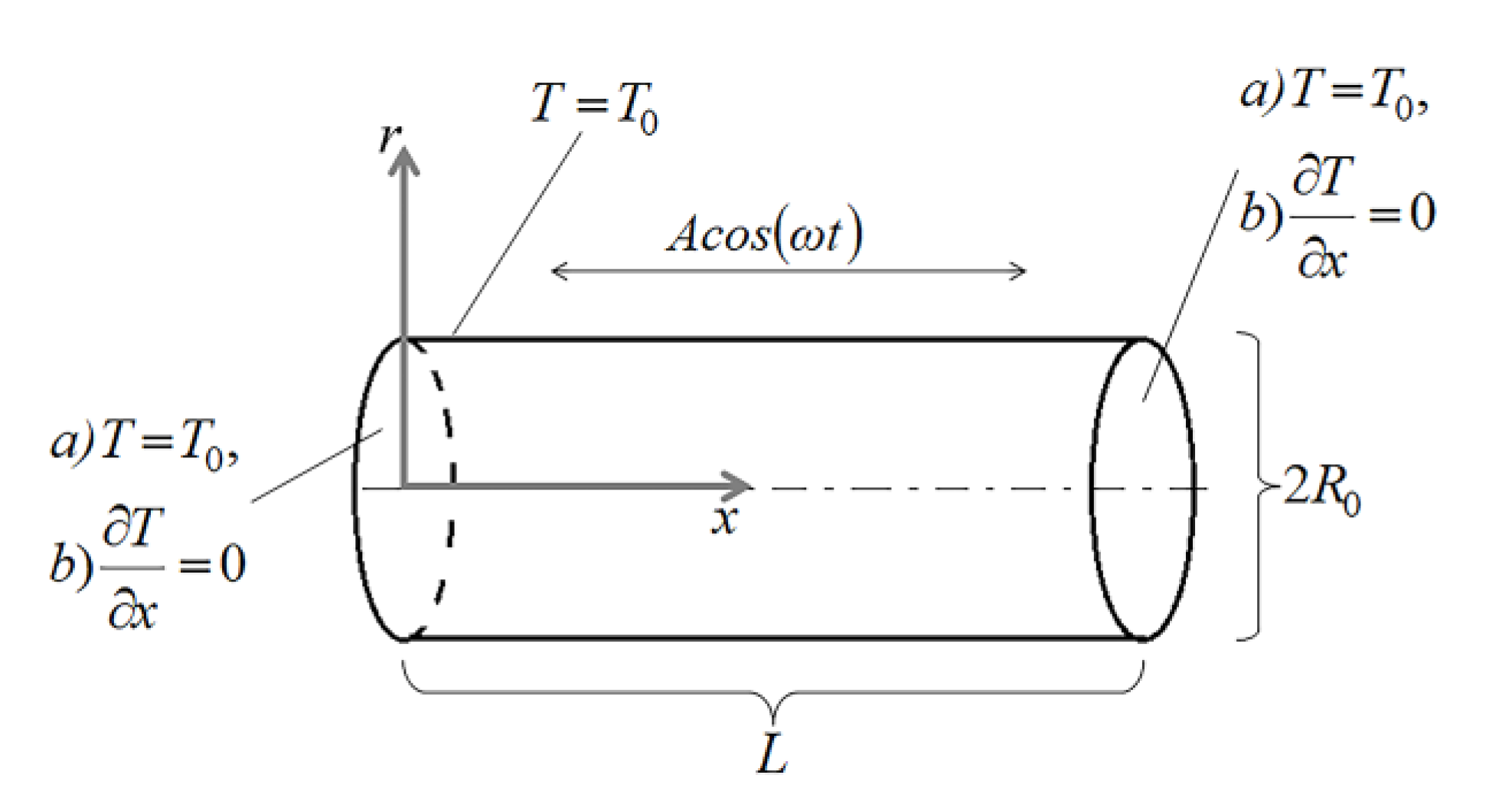
A cylindrical air filled cavity with length L and radius R₀ is shown in Figure 1. No-slip boundary conditions are specified on the walls of the cavity. A constant temperature is set on the cavity lateral surface, and two types of temperature boundary conditions at the ends are considered: isothermal and adiabatic. The cavity carries out vibration movement along its axis with frequency ω and amplitude A.

The problem is described by the continuity, momentum, and energy equations for a compressible fluid in an axisymmetric case with Clapeyron ideal gas law. This system of equations is presented below in dimensionless form in the cylindrical coordinate system (x, r) associated with the cavity.

$$\frac{\partial \tilde{\rho }}{\partial \tau }+\frac{\partial \tilde{\rho }U}{\partial X}+\frac{1}{R}\frac{\partial R\tilde{\rho }V}{\partial R}=0,$$

(1)

$$\frac{\partial \tilde{\rho }U}{\partial \tau }+\frac{\partial \tilde{\rho }UU}{\partial X}+\frac{1}{R}\frac{\partial R\tilde{\rho }UV}{\partial R}=-\frac{\partial P}{\partial X}+\mathrm{N}\left(\frac{{\partial }^{2}U}{\partial X^2}+\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial U}{\partial R}\right)\right)+\frac{1}{3}\mathrm{N}\left(\frac{{\partial }^{2}U}{\partial X^2}+\right.\frac{1}{R}\frac{\partial }{\partial X}\left.\left(\frac{\partial RV}{\partial R}\right)\right)+\tilde{\rho }\tilde{A}{\mathrm{\Omega }}^2\cos \left(\mathrm{\Omega }\tau \right),$$

(2)

$$\frac{\partial \tilde{\rho }V}{\partial \tau }+\frac{\partial \tilde{\rho }UV}{\partial X}+\frac{1}{R}\frac{\partial R\tilde{\rho }VV}{\partial R}=-\frac{\partial P}{\partial R}+N\left(\frac{{\partial }^{2}V}{\partial X^2}+\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial V}{\partial R}\right)\right)+\frac{1}{3}N\left(\frac{1}{R}\frac{\partial }{\partial R}\right.\left(R\frac{\partial V}{\partial R}\right)+\left.\frac{\partial }{\partial R}\left(\frac{\partial U}{\partial X}\right)\right)-\frac{4}{3}N\frac{V}{R^2},$$

(3)

$$\begin{array}{l}\frac{\partial \tilde{\rho }\Theta }{\partial \tau }+\frac{\partial \tilde{\rho }U\Theta }{\partial X}+\frac{1}{R}\frac{\partial R\tilde{\rho }V\Theta }{\partial R}=\gamma \Gamma \left(\frac{{\partial }^2\Theta }{\partial X^2}+\frac{1}{R}\frac{\partial }{\partial R}\left(R\frac{\partial \Theta }{\partial R}\right)\right)-\gamma \left(\gamma -1\right)P\left(\frac{\partial U}{\partial X}+\right.\left.\frac{1}{R}\frac{\partial RV}{\partial R}\right)-\frac{2}{3}\gamma \left(\gamma -1\right)N{\left(\frac{\partial U}{\partial X}+\frac{1}{R}\frac{\partial RV}{\partial R}\right)}^2+\\ \hspace{1em}\hspace{1em}+\gamma \left(\gamma -1\right)N{\left(\frac{\partial U}{\partial R}+\frac{\partial V}{\partial X}\right)}^2+2\gamma \left(\gamma -1\right)N\left({\left(\frac{\partial U}{\partial X}\right)}^2+{\left(\frac{\partial V}{\partial R}\right)}^2+\frac{V^2}{R^2}\right),\end{array}$$

(4)

$$P=\frac{\tilde{\rho }\left(\Theta +1\right)}{\gamma }.$$

(5)

The initial conditions are as follows:

$$\tau =0:\hspace{1em}U=0,\hspace{1em}V=0,\hspace{1em}\Theta =0,\hspace{1em}P=1/\gamma ,\hspace{1em}\tilde{\rho }=1.$$

(6)

Two types of boundary conditions are considered.

Isothermal boundary conditions:

$$X=0:\hspace{1em}U=0,\hspace{1em}V=0,\hspace{1em}\Theta =0,$$

$$X=1:\hspace{1em}U=0,\hspace{1em}V=0,\hspace{1em}\Theta =0,$$

(7)

$$R={\tilde{R}}_0:\hspace{1em}U=0,\hspace{1em}V=0,\hspace{1em}\Theta =0.$$

Isothermal boundary condition on the lateral surface and adiabatic boundary conditions at the ends:

$$X=0:\hspace{1em}U=0,\hspace{1em}V=0,\hspace{1em}\frac{\partial \Theta }{\partial X}=0,$$

$$X=1:\hspace{1em}U=0,\hspace{1em}V=0,\hspace{1em}\frac{\partial \Theta }{\partial X}=0,$$

(8)

$$R={\tilde{R}}_0:\hspace{1em}U=0,\hspace{1em}V=0,\hspace{1em}\Theta =0.$$

The following formulas for dimensionless variables and parameters were used: X = x/L, R = r/L, τ = tc₀/L, P = p/(γp₀), $\tilde{\rho }=\rho R_g{T}_0/p_0$, Θ = (T − T₀)/T₀, U = u/c₀, V = υ/c₀, N = ν/(c₀L), Γ = a/(c₀L), ${\tilde{R}}_0=R_0/L$, Ω = ωL/c₀, $\tilde{A}=A/L$.

Here, t is time, u and υ are the axial and radial velocity components, ρ is density, T is temperature, T₀ is the initial temperature, p is pressure, p₀ is the initial pressure, a is the thermal diffusivity, R_g is the gas constant, and γ is the ratio of specific heats.

The streaming velocity components U_st and V_st are calculated using the formulas [6]:

$$U_{\mathrm{st}}=\frac{〈\tilde{\rho }U〉}{〈\tilde{\rho }〉},V_{\mathrm{st}}=\frac{〈\tilde{\rho }V〉}{〈\tilde{\rho }〉},$$

(9)

where angle brackets denote averaging over the time period of the cavity vibrations.

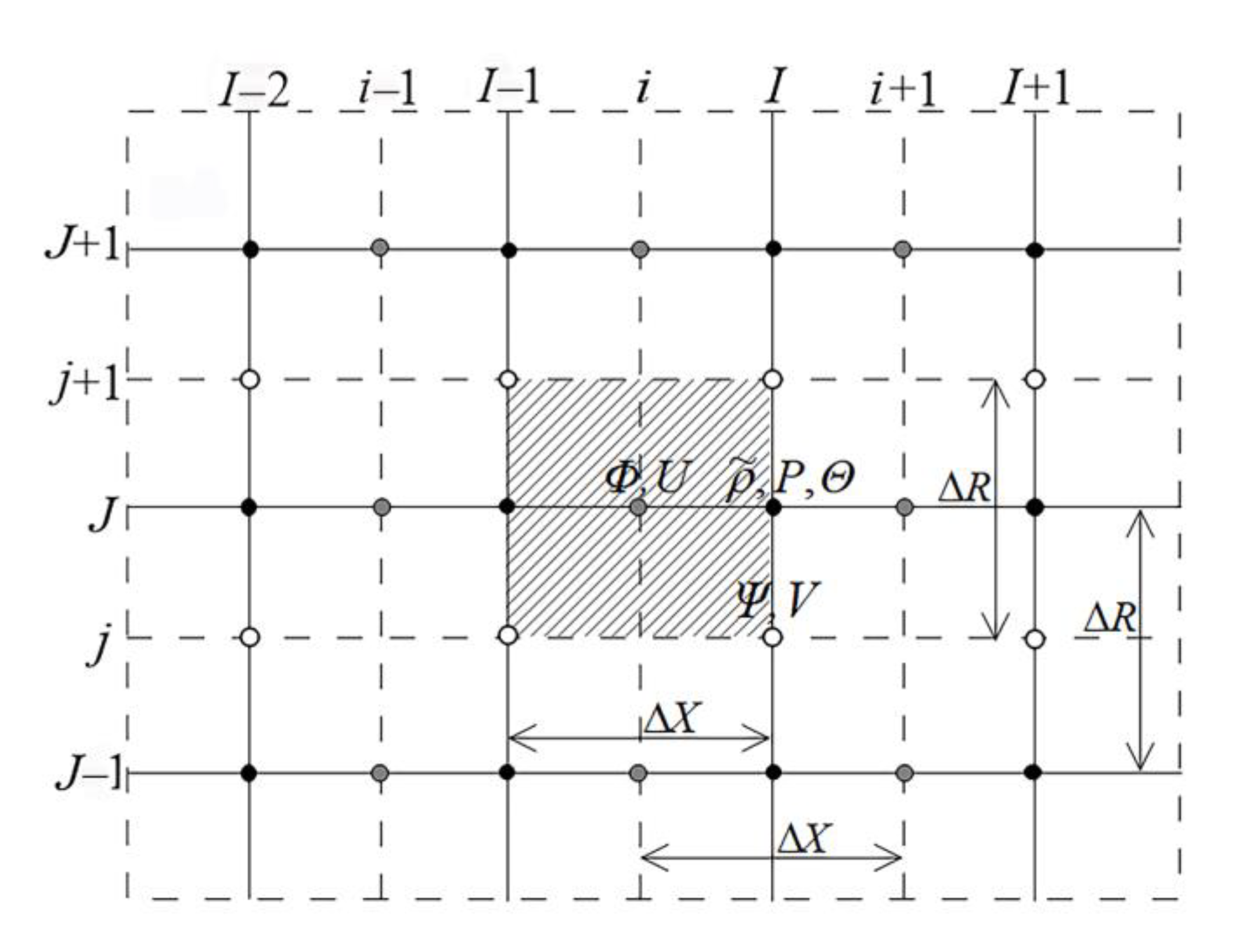
The system of Equations (1)–(5) was solved numerically using the calculation method, which is briefly presented by Gubaidullin and Pyatkova [21]. The finite volume method was taken as a basis, and a uniform staggered grid is used [27]. The calculation domain is divided into control volumes of size $\mathrm{\Delta }X$ × $\mathrm{\Delta }R$ (Figure 2). The faces of the main control volumes are shown with dashed lines. In the center of these volumes are nodes for density, temperature, and pressure (black circles indicated by capital letters, for example, I, J). The nodes for the mass flow $\Phi =\tilde{\rho }U$ and the velocity component U are shifted to the left relative to the main nodes by a distance of $\mathrm{\Delta }X/2$ (gray circles, for example, i and J; this control volume is shaded in Figure 2). The nodes for the mass flow $\Psi =\tilde{\rho }V$ and the velocity component V are shifted to the cylinder axis relative to the main nodes by a distance of $\mathrm{\Delta }R/2$ (white circles, for example, I, j).

The mass fluxes $\Phi$ and $\Psi$ are found from the momentum Equations (2) and (3), respectively. After that, the velocity components are recalculated. As an example, let us present the discretization of the momentum Equation (2), wherein an implicit numerical scheme will be used. After integrating Equation (2) over the shaded control volume (Figure 2) and passing to the variable $\Phi$, we obtain:

$$\begin{array}{l}\frac{{\Phi }_{i,J}-{\Phi }_{i,J}^{old}}{\mathrm{\Delta }\tau }{R}_J\mathrm{\Delta }X\mathrm{\Delta }R+F_{I,J}{\Phi }_{I,J}-F_{I-1,J}{\Phi }_{I-1,J}+F_{i,j+1}{\Phi }_{i,j+1}-F_{i,j}{\Phi }_{i,j}={\Gamma }_{I,J}{\left(\frac{\partial \Phi }{\partial X}\right)}_{I,J}-{\Gamma }_{I-1,J}{\left(\frac{\partial \Phi }{\partial X}\right)}_{I-1,J}+{\Gamma }_{i,j+1}{\left(\frac{\partial \Phi }{\partial R}\right)}_{i,j+1}-\\ -{\Gamma }_{i,j}{\left(\frac{\partial \Phi }{\partial R}\right)}_{i,j}+S_{i,J},\end{array}$$

(10)

where

$$F_{I,J}=\frac{U_{i,J}+U_{i+1,J}}{2}{R}_J\mathrm{\Delta }R,F_{I-1,J}=\frac{U_{i-1,J}+U_{i,J}}{2}{R}_J\mathrm{\Delta }R,F_{i,j+1}=\frac{V_{I-1,j+1}+V_{I,j+1}}{2}{R}_{j+1}\mathrm{\Delta }X,F_{i,j}=\frac{V_{I-1,j}+V_{I,j}}{2}{R}_j\mathrm{\Delta }X,$$

$${\Gamma }_{I,J}=\frac{{\rm N}}{{\tilde{\rho }}_{I,J}}{R}_J\mathrm{\Delta }R,{\Gamma }_{I-1,J}=\frac{{\rm N}}{{\tilde{\rho }}_{I-1,J}}{R}_J\mathrm{\Delta }R,{\Gamma }_{i,j+1}=\frac{N}{{\tilde{\rho }}_{i,j+1}}{R}_{j+1}\mathrm{\Delta }X,{\Gamma }_{i,j}=\frac{N}{{\tilde{\rho }}_{i,j}}{R}_j\mathrm{\Delta }X,$$

(11)

$$\begin{array}{l}{S}_{.i,J}=\left(P_{I-1,J}-P_{I,J}\right)R_J\mathrm{\Delta }R-{\rm N}\left[\frac{\left({\Phi }_{i,J}+{\Phi }_{i+1,J}\right)\left({\tilde{\rho }}_{I+1,J}-{\tilde{\rho }}_{I-1,J}\right)}{4{\rho }_{I,J}^2}-\right.\left.\frac{\left({\Phi }_{i-1,J}+{\Phi }_{i,J}\right)\left({\tilde{\rho }}_{I,J}-{\tilde{\rho }}_{I-2,J}\right)}{4{\rho }_{I-1,J}^2}\right]\frac{R_J\mathrm{\Delta }R}{\mathrm{\Delta }X}-\\ -N\left[\frac{R_{j+1}\left({\Phi }_{i,J}+{\Phi }_{i,J+1}\right)\left({\tilde{\rho }}_{I-1,J+1}+{\tilde{\rho }}_{I,J+1}-{\tilde{\rho }}_{I-1,J}-{\tilde{\rho }}_{I,J}\right)}{4{\rho }_{i,j+1}^2}-\right.\left.\frac{R_j\left({\Phi }_{i,J-1}+{\Phi }_{i,J}\right)\left({\tilde{\rho }}_{I-1,J}+{\tilde{\rho }}_{I,J}-{\tilde{\rho }}_{I-1,J-1}-{\tilde{\rho }}_{I,J-1}\right)}{4{\rho }_{i,j}^2}\right]\frac{\mathrm{\Delta }X}{\mathrm{\Delta }R}+\\ +\frac{1}{3}{\rm N}\left[\left(U_{i+1,J}-2U_{i,J}+U_{i-1,J}\right)\frac{R_J\mathrm{\Delta }R}{\mathrm{\Delta }X}+R_{j+1}\left(V_{I,j+1}-V_{I-1,j+1}\right)+\right.\left.R_j\left(V_{I-1,j}-V_{I,j}\right)\right]+\frac{{\tilde{\rho }}_{I-1,J}+{\tilde{\rho }}_{I,J}}{2}\cdot \tilde{A}{\mathrm{\Omega }}^2\cos (\mathrm{\Omega }\tau ).\end{array}$$

Here, $\mathsf{\Delta }\tau =0.2\mathsf{\Delta }X$ is the time step, R_J and R_j are the distances from the cylinder axis to the line indicated by the corresponding index (Figure 2), and the superscript old denotes the value of the variable from the previous time layer. Values ${\tilde{\rho }}_{i,j}$ and ${\tilde{\rho }}_{i,j+1}$ are calculated through the density values at nearby nodes. To approximate convective–diffusion fluxes, a power law scheme is used [27]:

$$F_{I,J}{\Phi }_{I,J}-{\Gamma }_{I,J}{\left(\frac{\partial \Phi }{\partial X}\right)}_{I,J}=\left[\frac{{\Gamma }_{I,J}}{\mathrm{\Delta }X}\cdot \max \left(0,{(1-0.1\frac{\left|F_{I,J}\right|\mathrm{\Delta }X}{{\Gamma }_{I,J}})}^5\right)+\max \left(-F_{I,J},0\right)\right]\left({\Phi }_{i,J}-{\Phi }_{i+1,J}\right)+F_{I,J}{\Phi }_{i,J},$$

$$F_{I-1,J}{\Phi }_{I-1,J}-{\Gamma }_{I-1,J}{\left(\frac{\partial \Phi }{\partial X}\right)}_{I-1,J}=\left[\frac{{\Gamma }_{I-1,J}}{\mathrm{\Delta }X}\cdot \max \left(0,{(1-0.1\frac{\left|F_{I-1,J}\right|\mathrm{\Delta }X}{{\Gamma }_{I-1,J}})}^5\right)+\max \left(F_{I-1,J},0\right)\right]\left({\Phi }_{i-1,J}-{\Phi }_{i,J}\right)+F_{I-1,J}{\Phi }_{i,J},$$

$$F_{i,j+1}{\Phi }_{i,j+1}-{\Gamma }_{i,j+1}{\left(\frac{\partial \Phi }{\partial R}\right)}_{i,j+1}=\left[\frac{{\Gamma }_{i,j+1}}{\mathrm{\Delta }R}\cdot \max \left(0,{(1-0.1\frac{\left|F_{i,j+1}\right|\mathrm{\Delta }R}{{\Gamma }_{i,j+1}})}^5\right)+\max \left(-F_{i,j+1},0\right)\right]\left({\Phi }_{i,J}-{\Phi }_{i,J+1}\right)+F_{i,j+1}{\Phi }_{i,J},$$

(12)

$$F_{i,j}{\Phi }_{i,j}-{\Gamma }_{i,j}{\left(\frac{\partial \Phi }{\partial R}\right)}_{i,j}=\left[\frac{{\Gamma }_{i,j}}{\mathrm{\Delta }R}\cdot \max \left(0,{(1-0.1\frac{\left|F_{i,j}\right|\mathrm{\Delta }R}{{\Gamma }_{i,j}})}^5\right)+\max \left(F_{i,j},0\right)\right]\left({\Phi }_{i,J-1}-{\Phi }_{i,J}\right)+F_{i,j}{\Phi }_{i,J}.$$

Thus, we obtain a discrete equation for the mass flow $\Phi$ in the form

$$a_{i,J}{\Phi }_{i,J}=b_{i,J}{\Phi }_{i+1,J}+c_{i,J}{\Phi }_{i-1,J}+d_{i,J}{\Phi }_{i,J+1}+e_{i,J}{\Phi }_{i,J-1},$$

(13)

where $a_{i,J},b_{i,J},c_{i,J},d_{i,J},e_{i,J}$ are the functions containing the unknown variable values from the previous iteration.

Similarly, other equation discretizations are performed. The system of algebraic equations is solved using the line-by-line method. After obtaining a convergent solution at a given time layer, a transition is made to a new time layer.

Note that the velocity components U and V are calculated by the formulas

$$U_{i,J}=\left\{\begin{array}{l}\frac{{\Phi }_{i,J}}{{\tilde{\rho }}_{I-1,J}},{\Phi }_{i,J}>0,\\ 0,{\Phi }_{i,J}=0,\\ \frac{{\Phi }_{i,J}}{{\tilde{\rho }}_{I,J}},{\Phi }_{i,J}<0,\end{array}\right.$$

(14)

$$V_{I,j}=\left\{\begin{array}{l}\frac{{\Psi }_{I,j}}{{\tilde{\rho }}_{I,J-1}},{\Psi }_{I,j}>0,\\ 0,{\Psi }_{I,j}=0,\\ \frac{{\Psi }_{I,j}}{{\tilde{\rho }}_{I,J}},{\Psi }_{I,j}<0.\end{array}\right.$$

(15)

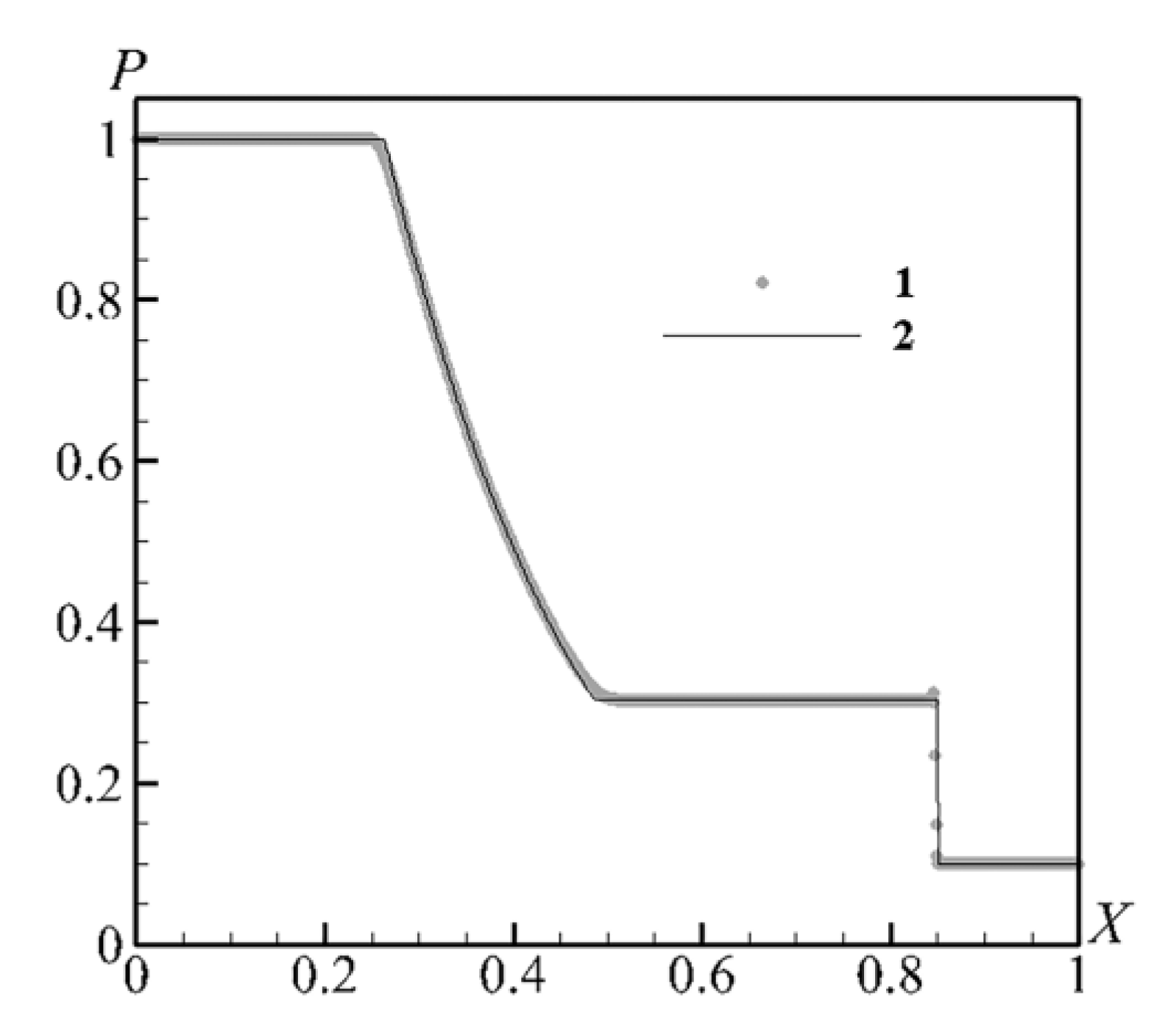
This method is implemented in program code written in Fortran. A number of test calculations were carried out to compare with known analytical solutions (the shock wave generation, the Riemann problem, the initial problem in the linear approximation). As an example, Figure 3 shows a comparison of the numerical solution with the analytical solution of the Sod shock tube problem [28]. At the initial moment of time, the ideal gas in the tube is at rest with the following parameters: the density and pressure in the left half of the tube are 1, and in the right half, the density is 0.125 and the pressure is 0.1. The result is shown at the time point equal to 0.2, and a good agreement between the analytical and numerical solutions can be seen.

A comparison was also made with experimental data by Reyt et al. [13]. In the experiment, the acoustic wave is generated by two loudspeakers at each end of the cylindrical air-filled tube. In numerical simulations, the length of the tube was taken to be less than in the experiment, but with a similar Shear number (Sh = δ_ν/R₀ = 0.0125). In Figure 4, the axial streaming velocity component along the symmetry axis of the tube is shown for the case of Re_NL = 4.8 at the first resonant mode. The velocity is normalized by U_Rayleigh = 3/8$u_0^2/{\mathrm{c}}_0$ (the amplitude of the streaming velocity in Rayleigh’s theory). It can be noted that the numerical solution is quite accurate.

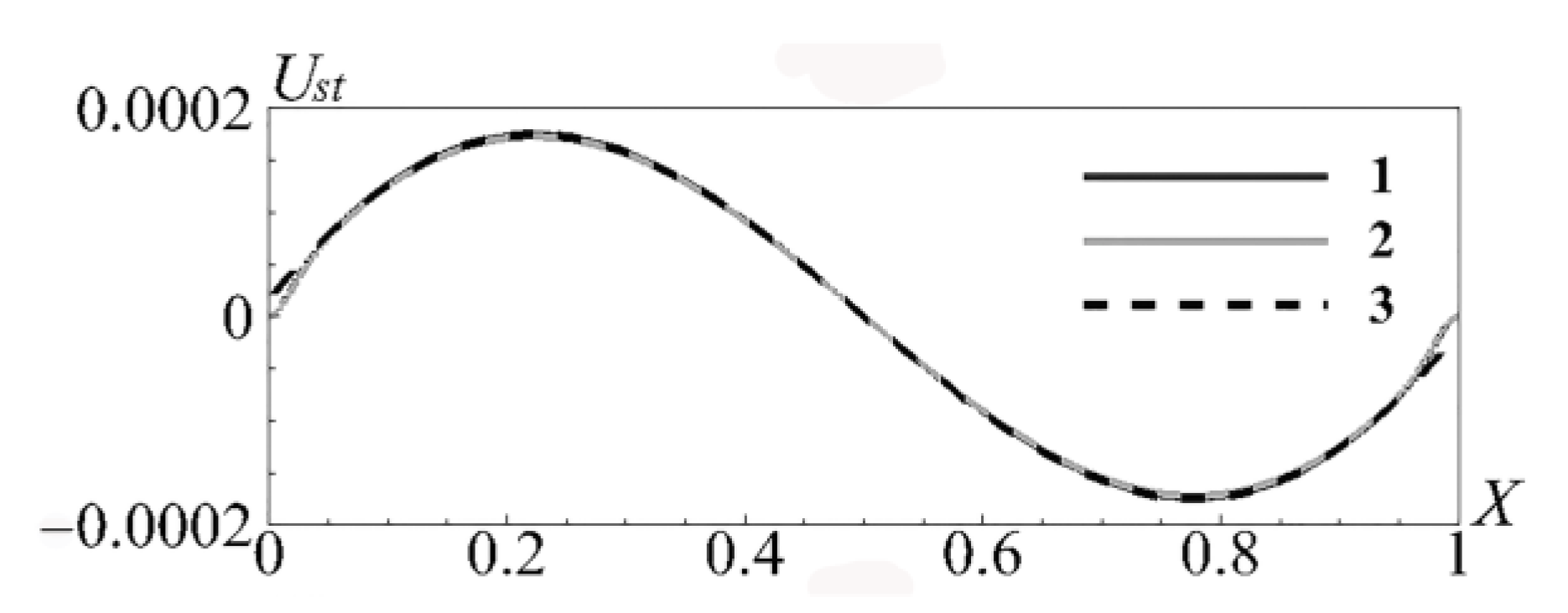
Let us compare our numerical solution of the problem of acoustic streaming in the vibrating air-filled cylindrical cavity with the analytical one. Figure 5 shows the distribution of the axial streaming velocity on the symmetry axis in comparison with the analytical solution obtained by Hamilton et al. [29] as a test. This analytical solution was obtained for the case of weak nonlinearity and of constant temperature on the lateral surface, but without the boundary conditions at the ends. At this small vibration amplitude, good agreement between the calculation results and the analytical solution is observed. Note that the numerical curves for the isothermal and adiabatic boundary conditions at the ends coincide.

3. Results and Discussion

This section describes the results of the numerical simulations obtained for sufficiently large values of the frequency and amplitude of the cavity vibration with a sufficiently large radius (strongly nonlinear regime of oscillations) when the effects of heat transfer on acoustic streaming and gas temperature are manifested.

The following values of the dimensionless parameters are set: Γ = 1.2·10⁻⁵, N = 8.6·10⁻⁶, and γ = 1.4, which correspond to air at a temperature of 300 K. The dimensional length of the cavity was L = 0.005 m. In this case, the first dimensionless resonance frequency is approximately equal to π. To compare the behavior of acoustic streaming in weakly nonlinear and strongly nonlinear modes of cavity vibrations, two vibration frequencies (Ω = 1 and 2) and two values of the cavity radius (${\tilde{R}}_0$ = 0.02 and 0.05) were chosen for the investigation. The vibration amplitude $\tilde{A}$ increased from 0.01 to the value depending on the frequency and radius. At Ω = 1 and ${\tilde{R}}_0$ = 0.02, the maximum vibration amplitude was 1, at Ω = 1 and ${\tilde{R}}_0$ = 0.05 or Ω = 2 and ${\tilde{R}}_0$ = 0.02, the maximum vibration amplitude was 0.5, and at Ω = 2 and ${\tilde{R}}_0$ = 0.05, the maximum vibration amplitude was 0.2. The ratios for R₀/δ_ν were 4.8, 6.8, 12, and 17. The parameter Re_NL in the cases considered did not exceed 114. This parameter is indicated in the captions for the figures below. The computational grid had 1002 × 42 and 1002 × 102 nodes for the cavities of ${\tilde{R}}_0$ = 0.02 and ${\tilde{R}}_0$ = 0.05, respectively. The grid size was selected based on the condition of fulfilling the accuracy of the calculations.

3.1. Acoustic Streaming Structure

Consider the streaming structure at small vibration amplitude ($\tilde{A}$ = 0.01). Assume also that a lot of time had passed since the start of the wave motion, and the process went on the regime of steady-state oscillations. In the narrow cavity of ${\tilde{R}}_0$ = 0.02 at vibration frequency Ω = 1, two Schlichting streaming vortices near the central part of the lateral surface and two Rayleigh streaming vortices are observed (Figure 6a). As the vibration frequency approaches the resonance frequency, the size of the Schlichting streaming vortices increases (Figure 6b). In the wider cavity of ${\tilde{R}}_0$ = 0.05 at vibration frequency Ω = 1, only Rayleigh streaming vortices are formed (Figure 6c), and at Ω = 2, in addition to the Rayleigh streaming vortices, there are also Schlichting vortices near the lateral surface (Figure 6d). The streaming patterns shown in Figure 6 correspond to both isothermal and adiabatic boundary conditions at the ends, since there is a weak nonlinear regime of oscillations at a given vibration amplitude. However, one can note differences in the streaming structure in this case and the case of the classical theory of acoustic streaming, since the presence of heat transfer through the lateral surface makes its contribution [21].

As the vibration amplitude increases, at ${\tilde{R}}_0$ = 0.02 and Ω = 1, the Schlichting streaming vortices increase and new vortices form in the center of the cavity (compare Figure 6a and Figure 7). For these values of the cavity radius and vibration frequency, no effect of heat transfer through the ends on acoustic streaming structure was found. However, the values of the streaming velocity may differ under isothermal and adiabatic boundary conditions at the ends in some areas of the cavity, which is manifested when the vibration amplitude increases.

With an increase in the frequency and amplitude of vibration, at ${\tilde{R}}_0$ = 0.02, Ω = 2, and $\tilde{A}$ = 0.2 the Schlichting streaming vortices increase in size and reach the symmetry axis of the cavity (compare Figure 6b and Figure 8a). At $\tilde{A}$ = 0.2, the streaming vortices at different boundary conditions at the ends differ insignificantly. With a further increase in the vibration amplitude, the streaming structure changes, and new vortices are formed (Figure 8b). In this case, the streaming patterns already significantly depend on heat transfer (Figure 8b,c). One can see differences in the shape and number of vortices (Figure 8b,c).

Nonlinearity is enhanced along with increases in the cavity radius. At ${\tilde{R}}_0$ = 0.05, Ω = 1, and $\tilde{A}$ = 0.5, the streaming structure also differs at different boundary conditions at the ends. As can be seen in Figure 9, small vortices at the ends disappear due to heat transfer. Note that these vortices also disappear with decreasing vibration amplitude (compare Figure 6c and Figure 9a). Further, in both cases, an increase in the vibration amplitude led to the appearance of small vortices in the central part of the cavity lateral surface.

In a strongly nonlinear case, at ${\tilde{R}}_0$ = 0.02, Ω = 2, $\tilde{A}$ = 0.2, the streaming structure strongly depends on the temperature boundary conditions at the ends and heat transfer, respectively. Differences are seen in the size, the shape of the vortices and the location of their centers; the number of vortices is also different (Figure 10).

3.2. The Axial Streaming Velocity

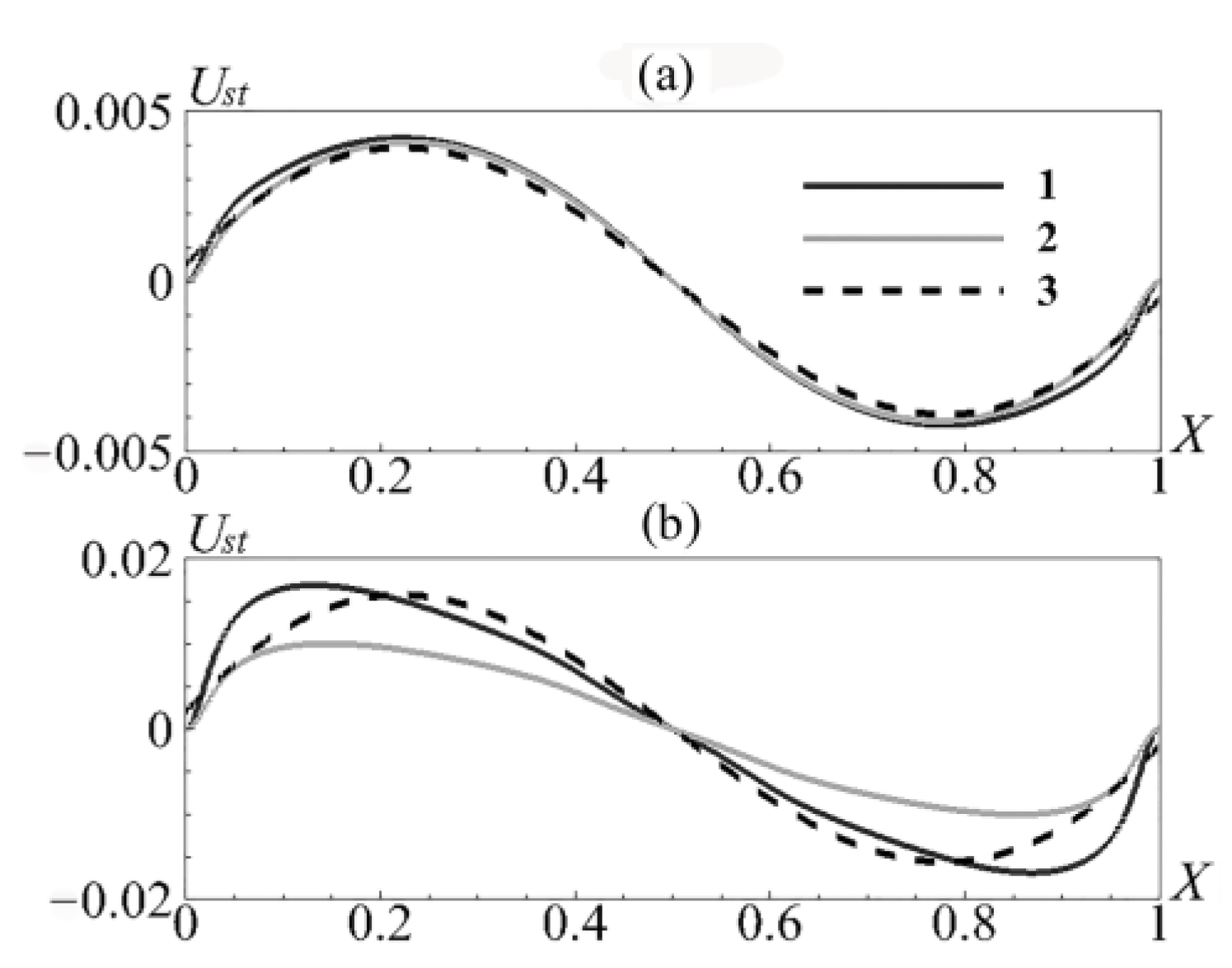
Consider the effect of heat transfer through the ends on the acoustic streaming velocity. The axial streaming velocity is much greater than the radial one, so let us consider the effect on the axial velocity. As an example, let us take the case of ${\tilde{R}}_0$ = 0.05 and Ω = 2. At $\tilde{A}$ = 0.01 (Figure 5), it was shown that the curves in the presence of heat transfer and with thermally insulated ends coincide. With an increase in the vibration amplitude, the nonlinearity of the process increases, and differences appear. At $\tilde{A}$ = 0.05 (Figure 11a), the difference between curves at isothermal and adiabatic boundary conditions at the ends is already visible. However, the nonlinearity is still weakly manifested. The curve under adiabatic boundary conditions at the ends is close to the analytical solution, which does not take into account the constant temperature at the ends. With a further increase in the vibration amplitude, the analytical solution begins to differ significantly from the calculation results (Figure 11b). Note that the shape of curve 1 correlates with the fact that the centers of the vortices are shifted towards the ends of the cavity. As the calculation results show, the analytical solution is valid only in the weakly nonlinear regime of cavity oscillations.

Let us consider the effect of heat transfer on the maximum value of the axial streaming velocity. Note that the streaming velocity in the radial direction is significantly lower than the streaming velocity in the axial direction. Figure 12 shows the maximum over the region axial component of the streaming velocity U_{st max}, depending on the vibration amplitude at different cavity radii, vibration frequencies, and thermal boundary conditions at the ends. It can be concluded that, in the wider cavity, an increase in the vibration amplitude leads to an increase in the streaming velocity under isothermal boundary conditions at the ends (due to heat transfer) in comparison with the case of adiabatic boundary conditions at the ends. It’s interesting that in the narrower cavity, the opposite behavior is observed, but the difference between the maximum values of the velocities is small.

3.3. Period Average Temperature

Let us consider the effect of heat transfer on the temperature averaged over the time period of the cavity vibration. Figure 13 shows a comparison of the period average temperature on the symmetry axis of the cavity under different boundary conditions at the ends at ${\tilde{R}}_0$ = 0.05, Ω = 2, and different vibration amplitudes. At a small vibration amplitude, the difference is observed only near the ends at a distance of approximately 0.13. Note that in the central part of the cavity period average temperature may be lower than the initial temperature. With an increase in the vibration amplitude, the gas in the cavity is heated on average over the period due to viscous dissipation, and the period average temperature of the entire axis of the cavity can become higher than the initial temperature in the case of adiabatic boundary conditions at the ends (Figure 13b,c). However, due to the heat transfer, the period average temperature on the entire symmetry axis decreases (Figure 13c).

Let us consider the bulk temperature of gas in the cavity. We define the bulk temperature as

$${\Theta }_b=\frac{{\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{0}{\overset{{\tilde{R}}_0}{\int }}\Theta \tilde{\rho }RdXdR}}}{{\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{0}{\overset{{\tilde{R}}_0}{\int }}\tilde{\rho }RdXdR}}}$$

(16)

Figure 14 shows the values of the period average bulk temperature $\langle {\Theta }_b\rangle$ (averaging over the time period) with an increasing vibration amplitude at different cavity radii, vibration frequencies, and thermal boundary conditions at the ends. In the case of heat transfer through the ends, gas is colder on average over the period in comparison with the case of adiabatic boundary conditions. Note that this difference is more noticeable at the higher vibration frequency.

Summing up the study, it should be noted that acoustic streaming is a nonlinear process. The degree of nonlinearity is determined by the value of the nonlinear Reynolds number, which is given by the following initial conditions: the frequency and amplitude of the cavity vibration and its size, density, compressibility, and the viscosity of the gas in the cavity. The mathematical model of the process consists of nonlinear differential equations of motion and energy. The problem statement includes initial and boundary conditions, including thermal boundary conditions. The main unknowns of the problem, or the parameters of motion and heat transfer, are the density, velocity and temperature of the gas, which are interconnected and change in a consistent manner, following the laws of conservation of mass, momentum, and energy. Acoustic streaming is a secondary flow. Its parameters (streaming velocity, temperature) are determined by averaging over the time period of cavity vibration. The streaming velocity determines the vortex structures.

The study showed for the first time that in a highly nonlinear mode of oscillations (Re_NL is approximately equal to 100), heat transfer through the ends of the cavity significantly affects the structure of acoustic streaming, its velocity, and its temperature.

4. Conclusions

Acoustic streaming that occurs in a gas-filled cylindrical cavity, which performs longitudinal vibration, was considered. The influence of heat transfer through the ends of the cavity was studied, while the lateral surface of the cavity was maintained at a constant temperature equal to the initial one. Heat transfer is determined by setting isothermal boundary conditions; under adiabatic boundary conditions, there is no heat transfer. It has been established for the first time that the effects of heat transfer manifest themselves with an increase in the nonlinearity of the process, when the vibration frequency approaches the resonant one and the vibration amplitude increases; this is also facilitated by an increase in the cavity radius. Due to heat transfer, both the structure and velocity of acoustic streaming, as well as the temperature of the gas, change. The heat transfer, on average over the period, leads to a slight cooling of the gas compared to the adiabatic boundary conditions. In the presence of heat transfer, an increase in the cavity radius leads to an increase in the acoustic streaming velocity. Heat transfer can affect the number, size and shape of the streaming vortices, and the location of their centers.

In future studies, it will be interesting to consider role of intensity of heat transfer through the cavity lateral surface and also to consider a situation when the lateral surface and the ends of cavity are isothermal, but as a result of different temperatures. How would this affect temperature difference?