Mathematical Modeling of the Wave Dynamics of an Encapsulated Perfluorocarbon Droplet in a Viscoelastic Liquid
Abstract
1. Introduction
2. Mathematical Model
3. Initial Conditions and Numerical Realization
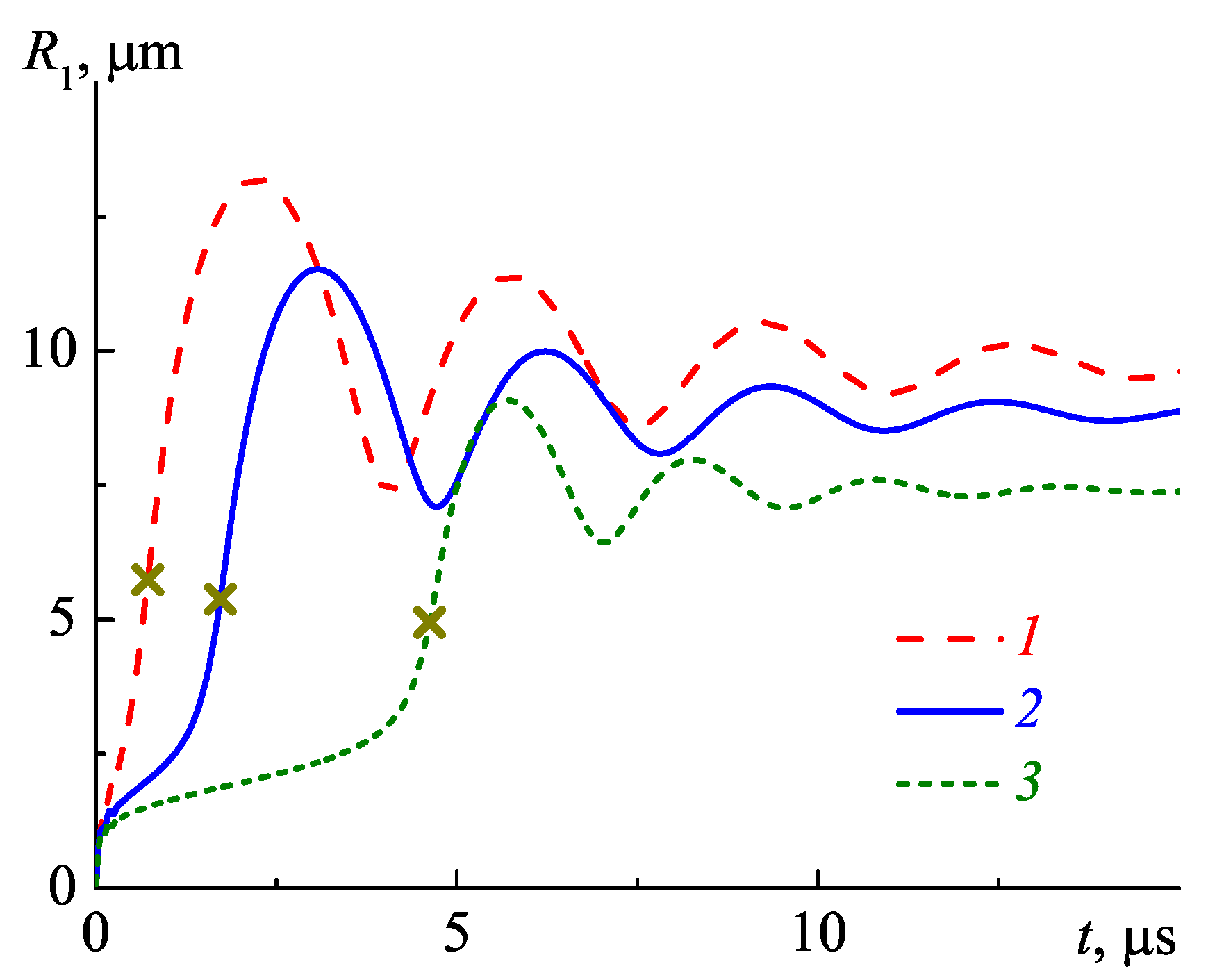
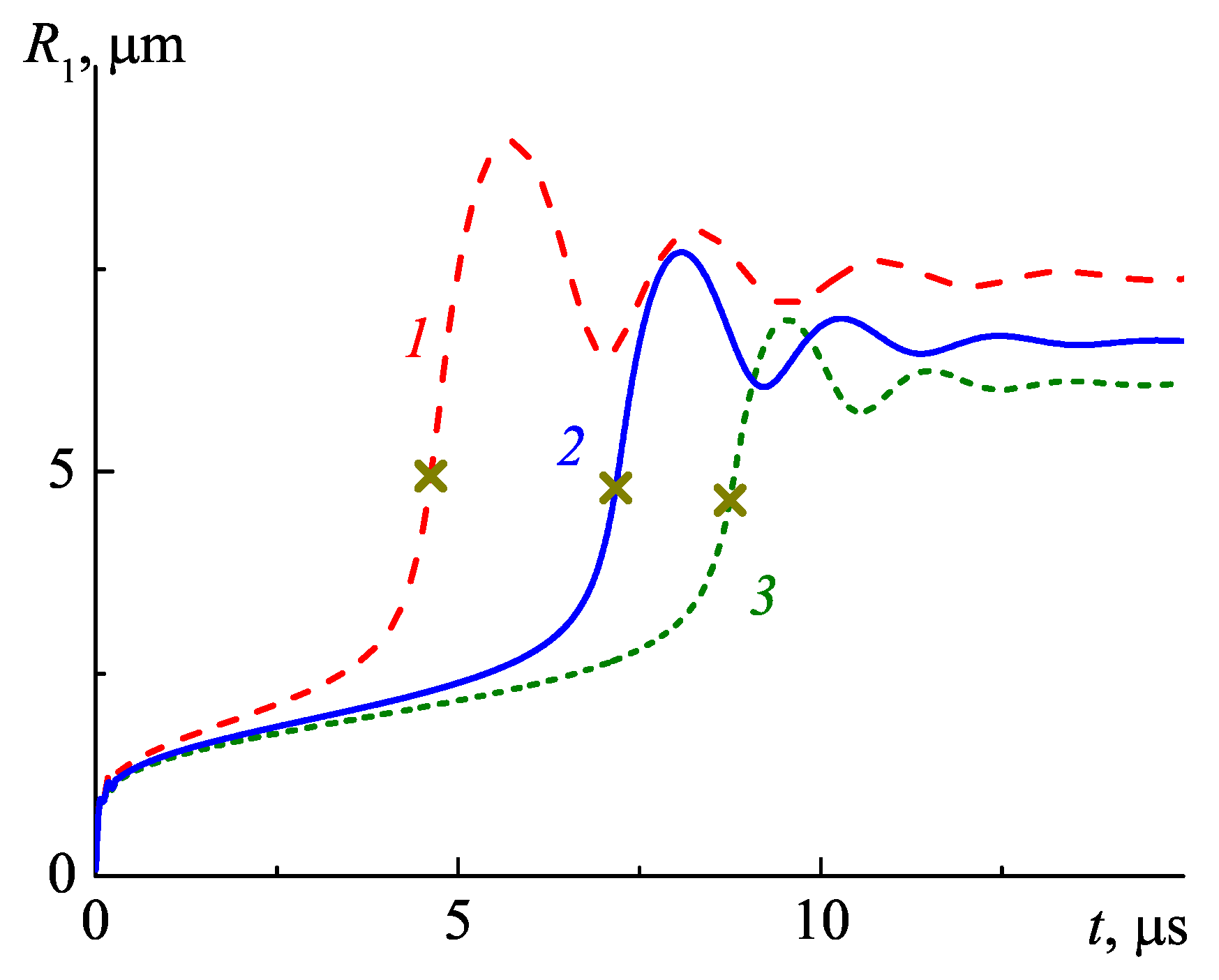
4. Results of Calculations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kripfgans, O.D.; Fowlkes, J.B.; Miller, D.L.; Eldevik, O.P.; Carson, P.L. Acoustic droplet vaporization for therapeutic and diagnostic applications. Ultrasound Med. Biol. 2000, 26, 1177–1189. [Google Scholar] [CrossRef] [PubMed]
- Sheeran, P.S.; Dayton, P.A. Phase-change contrast agents for imaging and therapy. Curr. Pharm. Des. 2012, 18, 2152–2165. [Google Scholar] [CrossRef] [PubMed]
- Kee, A.L.J.; Teo, B.M. Biomedical applications of acoustically responsive phase shift nanodroplets: Current status and future directions. Ultrason. Sonochem. 2019, 56, 37–45. [Google Scholar] [CrossRef]
- Rapoport, N.; Gao, Z.; Kennedy, A. Multifunctional nanoparticles for combining ultrasonic tumor imaging and targeted chemotherapy. J. Natl Cancer Inst. 2007, 99, 1095–1106. [Google Scholar] [CrossRef] [PubMed]
- Sheeran, P.S.; Wong, V.P.; Luois, S.; McFarland, R.J.; Ross, W.D.; Feingold, S.; Matsunaga, T.O.; Dayton, P.A. Decafluorobutane as a phase-change contrast agent for low-energy extravascular ultrasonic imaging. Ultrasound Med. Biol. 2011, 37, 1518–1530. [Google Scholar] [CrossRef] [PubMed]
- Sheeran, P.S.; Luois, S.; Dayton, P.A.; Matsunaga, T.O. Formulation and acoustic studies of a new phase-shift agent for diagnostic and therapeutic ultrasound. Langmuir 2011, 27, 10412–10420. [Google Scholar] [CrossRef] [PubMed]
- Sheeran, P.S.; Luois, S.; Mullin, L.B.; Matsunaga, T.O.; Dayton, P.A. Design of ultrasonically-activatable nanoparticles using low boiling point perfluorocarbons. Biomaterials 2012, 33, 3262–3269. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Sheeran, P.S.; Bouakaz, A.; Dayton, P.A. Vaporization dynamics of volatile perfluorocarbon droplets: A theoretical model and in vitro validation. Med. Phys. 2014, 41, 102901. [Google Scholar] [CrossRef]
- Shpak, O.; Stricker, L.; Versluis, M.; Lohse, D. The role of gas in ultrasonically driven vapor bubble growth. Phys. Med. Biol. 2013, 58, 2523–2535. [Google Scholar] [CrossRef]
- Cho, S.; Son, G. A. level set method for bubble growth in acoustic droplet vaporization. Int. Commun. Heat Mass Transf. 2018, 93, 83–92. [Google Scholar] [CrossRef]
- Cho, S.; Son, G. A. Numerical study of droplet vaporization under acoustic pulsing conditions. J. Mech. Sci. Technol. 2019, 33, 1673–1680. [Google Scholar] [CrossRef]
- Park, S.; Son, G. Numerical investigation of acoustic vaporization threshold of microdroplets. Ultrason. Sonochem. 2021, 71, 105361. [Google Scholar] [CrossRef]
- Rapoport, N. Phase-shift, stimuli-responsive perfluorocarbon nanodroplets for drug delivery to cancer. Wiley Interdiscip. Rev. Nanomed. Nanobiotecnol. 2012, 4, 492–510. [Google Scholar] [CrossRef] [PubMed]
- Gubaidullin, D.A.; Panin, K.A.; Fedorov, Yu.V. Acoustics of a liquid with droplets covered by a shell in the presence of phase transitions. Fluid Dyn. 2022, 57, 459–468. [Google Scholar] [CrossRef]
- Gubaidullin, D.A.; Fedorov, Yu.V. Acoustics of a viscoelastic medium with encapsulated bubbles. J. Hydrodyn. 2021, 33, 55–62. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Kanagawa, T.; Ayukai, T. Physico-mathematical model for multiple ultrasound-contrast-agent microbubbles encapsulated by a visco-elastic shell: Effect of shell compressibility on ultrasound attenuation. Chem. Eng. Sci. 2023, 269, 117541. [Google Scholar] [CrossRef]
- Kanagawa, T.; Honda, M.; Kikuchi, Y. Nonlinear acoustic theory on flowing liquid containing multiple microbubbles coated by a compressible visco-elastic shell: Low and high frequency cases. Phys. Fluids 2023, 35, 023303. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, D.; Cao, X.; He, X. Theoretical and experimental studies of acoustic reflection of bubbly liquid in multilayer media. Appl. Sci. 2022, 12, 12264. [Google Scholar] [CrossRef]
- Gordoa, P.R.; Pickering, A. Ultrasonic waves in bubbly liquids: An analytic approach. Mathematics 2021, 9, 1309. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, S.; Shan, Z.; Yin, M. Investigation of cavitation bubble dynamics considering pressure fluctuation induced by slap forces. Mathematics 2021, 9, 2064. [Google Scholar] [CrossRef]
- Prosperetti, A. Vapor bubbles. Annu. Rev. Fluid Mech. 2017, 49, 221–248. [Google Scholar] [CrossRef]
- Kwon, S.; Son, G. Experimental study of ultrasound-triggered vaporization of microdroplets on a wall. J. Mech. Sci. Technol. 2022, 36, 1329–1335. [Google Scholar] [CrossRef]
- Zhao, Y.; Qin, D.; Chen, J.; Hou, J.; Ilovitsh, T.; Wan, M.; Wu, L.; Feng, Y. On-demand regulation and enhancement of the nucleation in acoustic droplet vaporization using dual-frequency focused ultrasound. Ultrason. Sonochem. 2022, 90, 106224. [Google Scholar] [CrossRef]
- Qin, D.; Zou, Q.; Lei, S.; Wang, W.; Li, Z. Predicting initial nucleation events occurred in a metastable nanodroplet during acoustic droplet vaporization. Ultrason. Sonochem. 2021, 75, 105608. [Google Scholar] [CrossRef]
- Sojahrood, A.J.; Haghi, H.; Kolios, M.C.; Karshafian, R. Nonlinear dynamics and bifurcation structure of ultrasonically excited lipid coated microbubbles. Ultrason. Sonochem. 2021, 72, 105405. [Google Scholar] [CrossRef]
- Sojahrood, A.J.; Haghi, H.; Porter, T.M.; Karshafian, R.; Kolios, M.C. Experimental and numerical evidence of intensified non-linearity at the microscale: The lipid coated acoustic bubble. Phys. Fluids 2021, 33, 072006. [Google Scholar] [CrossRef]
- Sojahrood, A.J.; Haghi, H.; Karshafian, R.; Kolios, M.C. Nonlinear dynamics of acoustic bubbles excited by their pressure-dependent subharmonic resonance frequency: Influence of the pressure amplitude, frequency, encapsulation and multiple bubble interactions on oversaturation and enhancement of the subharmonic signal. Nonlinear Dyn. 2021, 103, 429. [Google Scholar]
- Sojahrood, A.J.; Haghi, H.; Rostam, S.N.; Kolios, M.C.; Karshafian, R. On the threshold of 1/2 order subharmonic emissions in the oscillations of ultrasonically excited bubbles. Ultrasonics 2021, 112, 106363. [Google Scholar] [CrossRef] [PubMed]
- Sojahrood, A.J.; Haghi, H.; Karshafian, R.; Kolios, M.C. Classification of the major nonlinear regimes of oscillations, oscillation properties, and mechanisms of wave energy dissipation in the nonlinear oscillations of coated and uncoated bubbles. Phys. Fluids 2021, 33, 016105. [Google Scholar] [CrossRef]
- Gubaidullin, D.A.; Fedorov, Yu.V. Acoustic waves in a liquid with gas inclusions containing a liquid layer and a viscoelastic shell. High Temp. 2022, in press. [CrossRef]
- Lacour, T.; Brasier, T.; Coulouvrat, F. Ultimate fate of a dynamical bubble/droplet system following acoustic vaporization. Phys. Fluids 2020, 32, 051702. [Google Scholar] [CrossRef]
- Hao, Y.; Prosperetti, A. The dynamics of vapor bubbles in acoustic pressure fields. Phys. Fluids 1999, 11, 2008. [Google Scholar] [CrossRef]
- Chabouh, G.; Dollet, B.; Quilliet, C.; Coupier, G. Spherical oscillations of encapsulated microbubbles: Effect of shell compressibility and anisotropy. J. Acoust. Soc. Am. 2021, 149, 1240–1257. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gubaidullin, D.A.; Gubaidullina, D.D.; Fedorov, Y.V. Mathematical Modeling of the Wave Dynamics of an Encapsulated Perfluorocarbon Droplet in a Viscoelastic Liquid. Mathematics 2023, 11, 1083. https://doi.org/10.3390/math11051083
Gubaidullin DA, Gubaidullina DD, Fedorov YV. Mathematical Modeling of the Wave Dynamics of an Encapsulated Perfluorocarbon Droplet in a Viscoelastic Liquid. Mathematics. 2023; 11(5):1083. https://doi.org/10.3390/math11051083
Chicago/Turabian StyleGubaidullin, Damir A., Dilya D. Gubaidullina, and Yuri V. Fedorov. 2023. "Mathematical Modeling of the Wave Dynamics of an Encapsulated Perfluorocarbon Droplet in a Viscoelastic Liquid" Mathematics 11, no. 5: 1083. https://doi.org/10.3390/math11051083
APA StyleGubaidullin, D. A., Gubaidullina, D. D., & Fedorov, Y. V. (2023). Mathematical Modeling of the Wave Dynamics of an Encapsulated Perfluorocarbon Droplet in a Viscoelastic Liquid. Mathematics, 11(5), 1083. https://doi.org/10.3390/math11051083




