A Novel Coupled Meshless Model for Simulation of Acoustic Wave Propagation in Infinite Domain Containing Multiple Heterogeneous Media
Abstract
1. Introduction
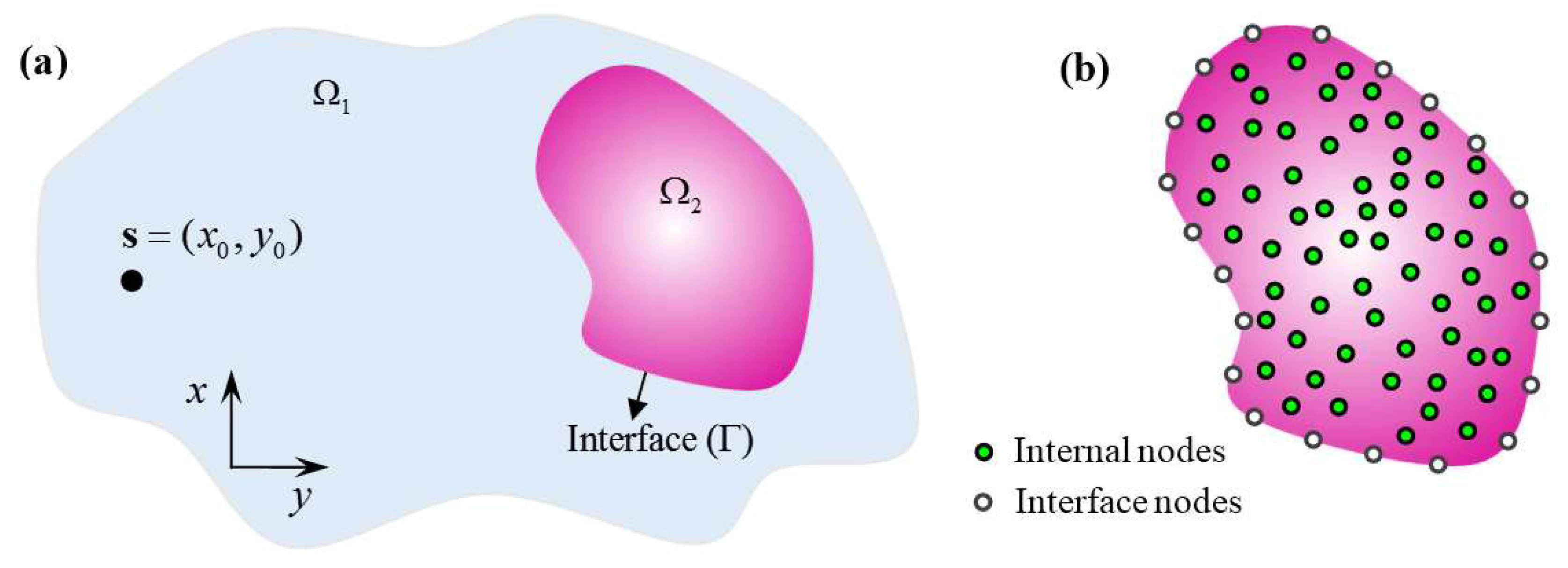
2. Problem Statement
3. Methodology
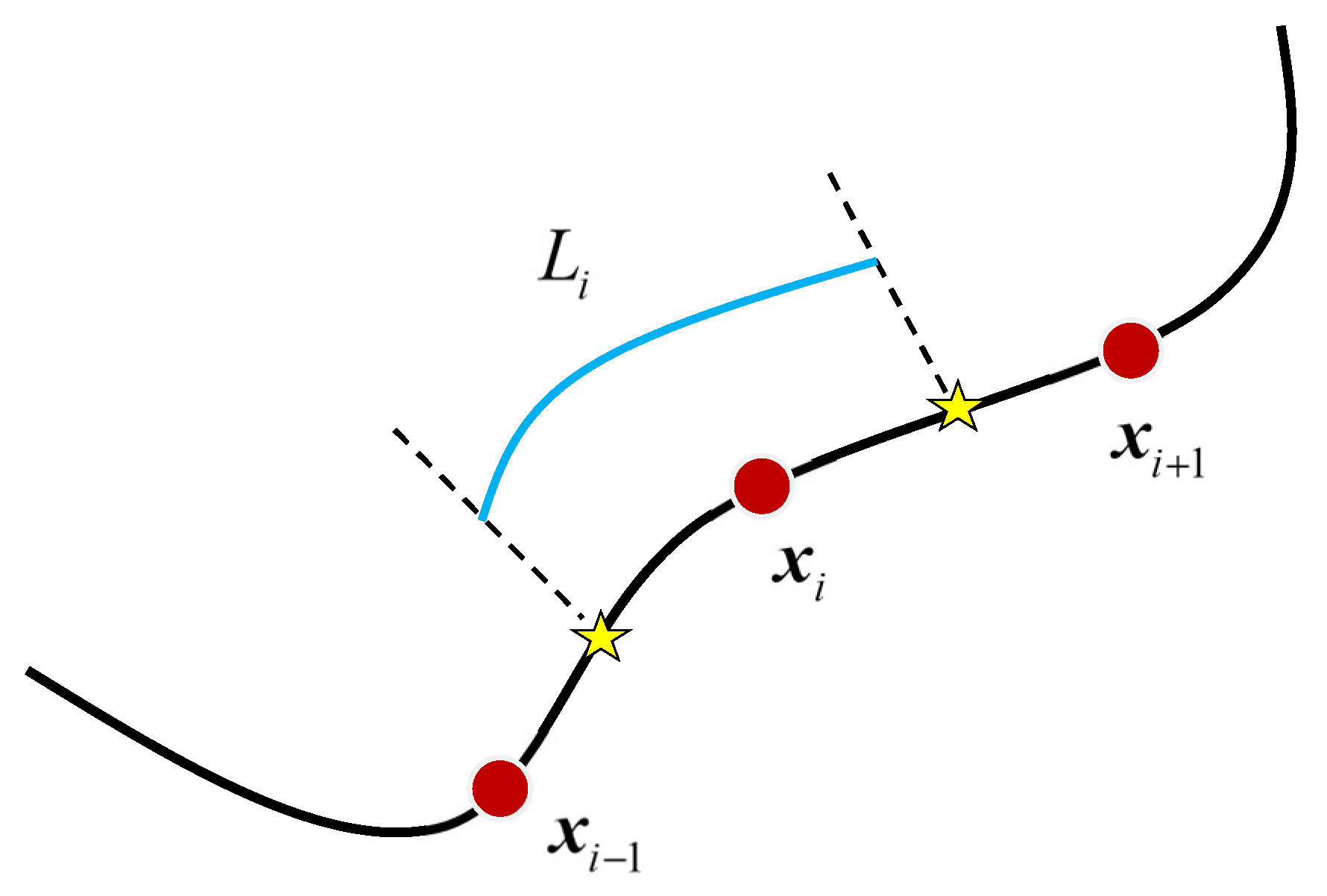
3.1. SBM for Unbounded Acoustic Medium
3.2. Kansa’s Method for Inhomogeneous Acoustic Medium
3.3. Coupled Model Dymamic System
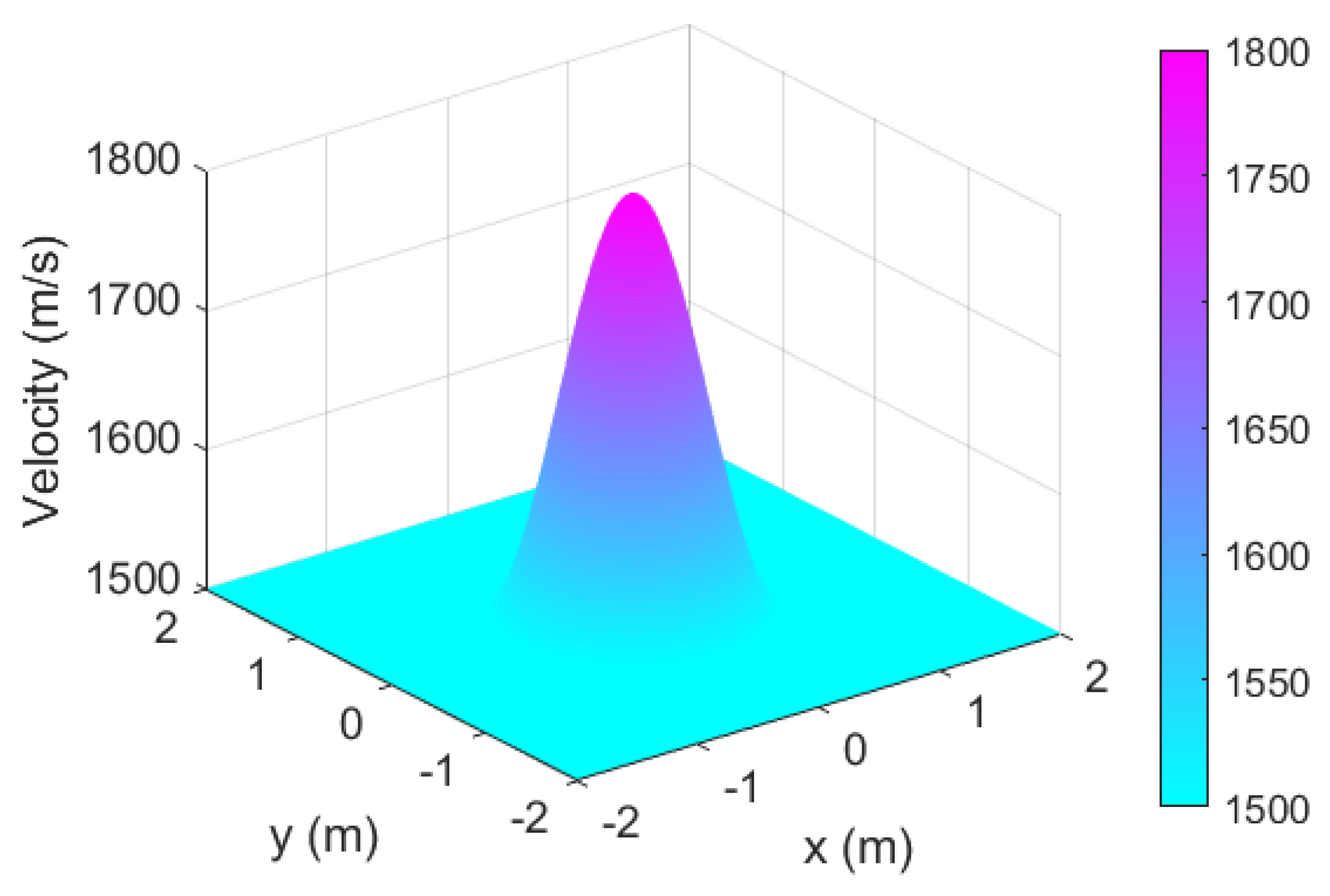
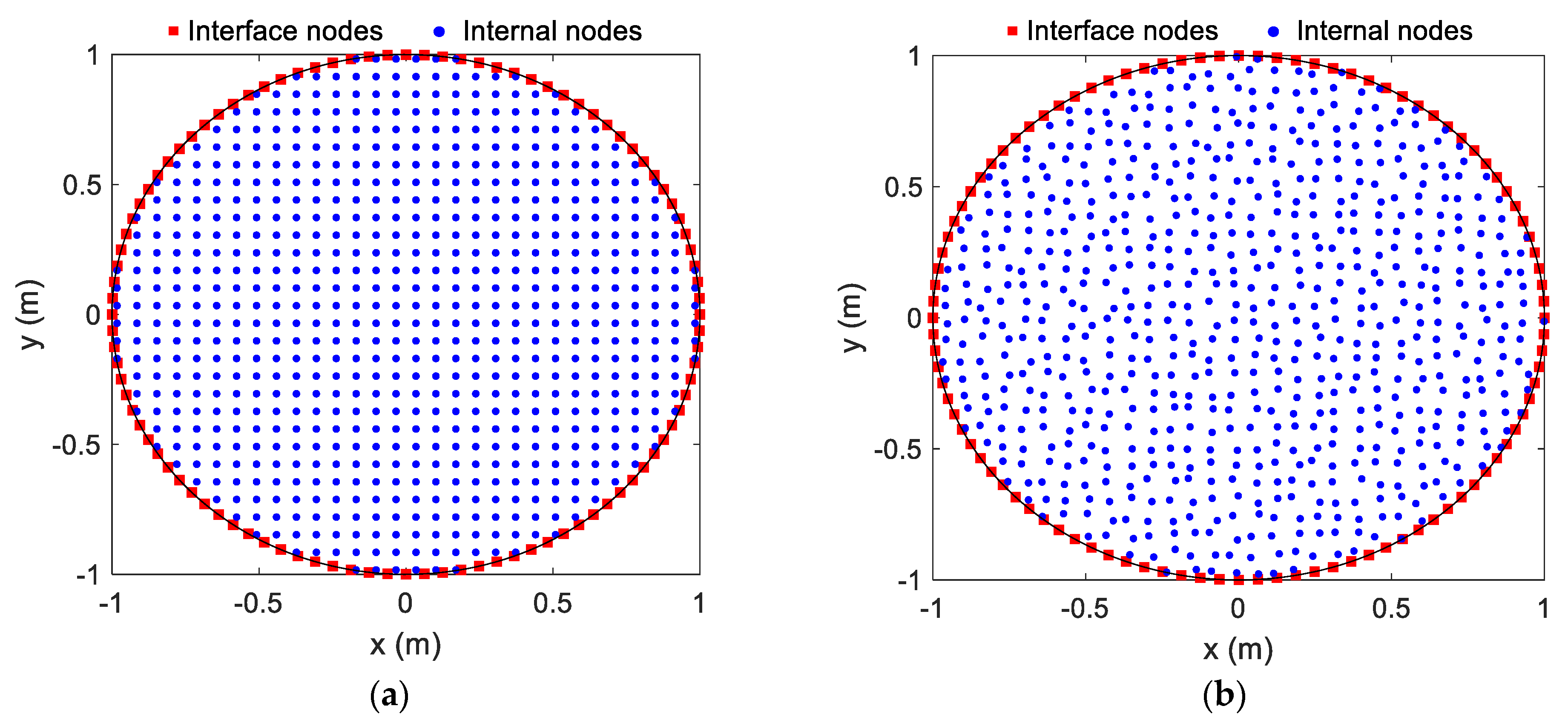
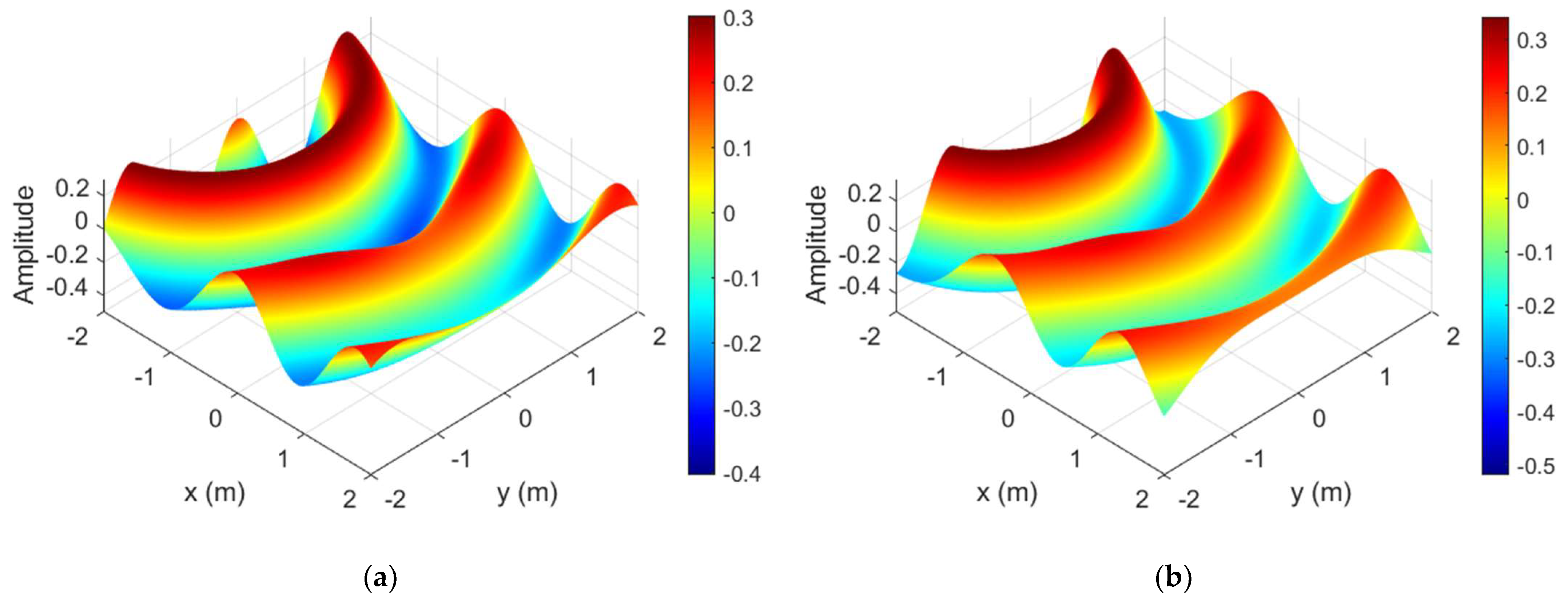
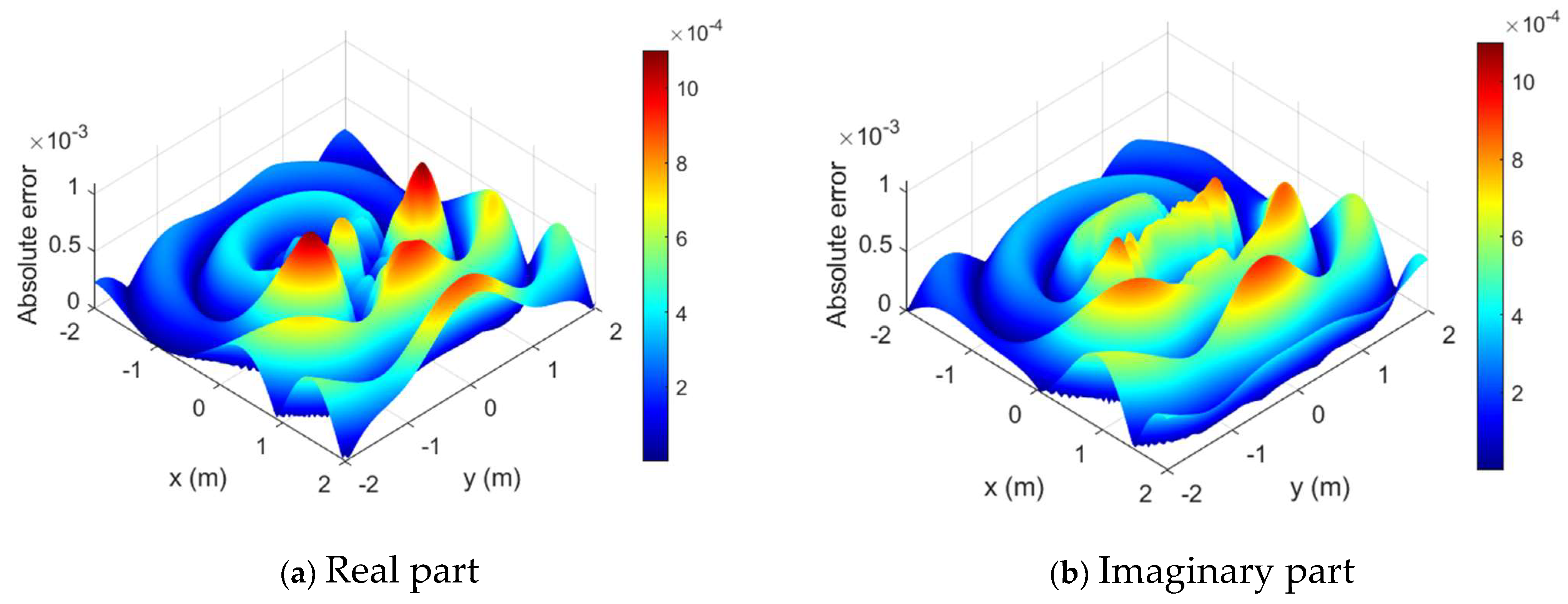
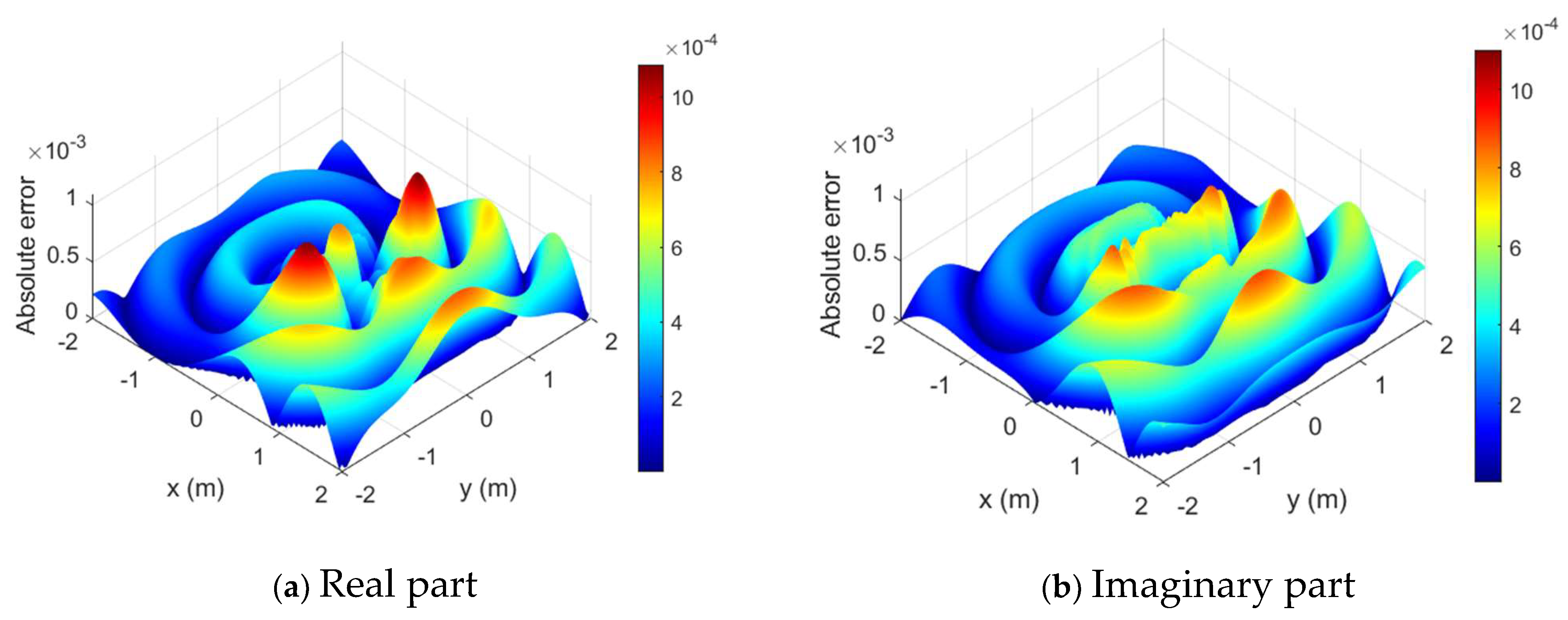
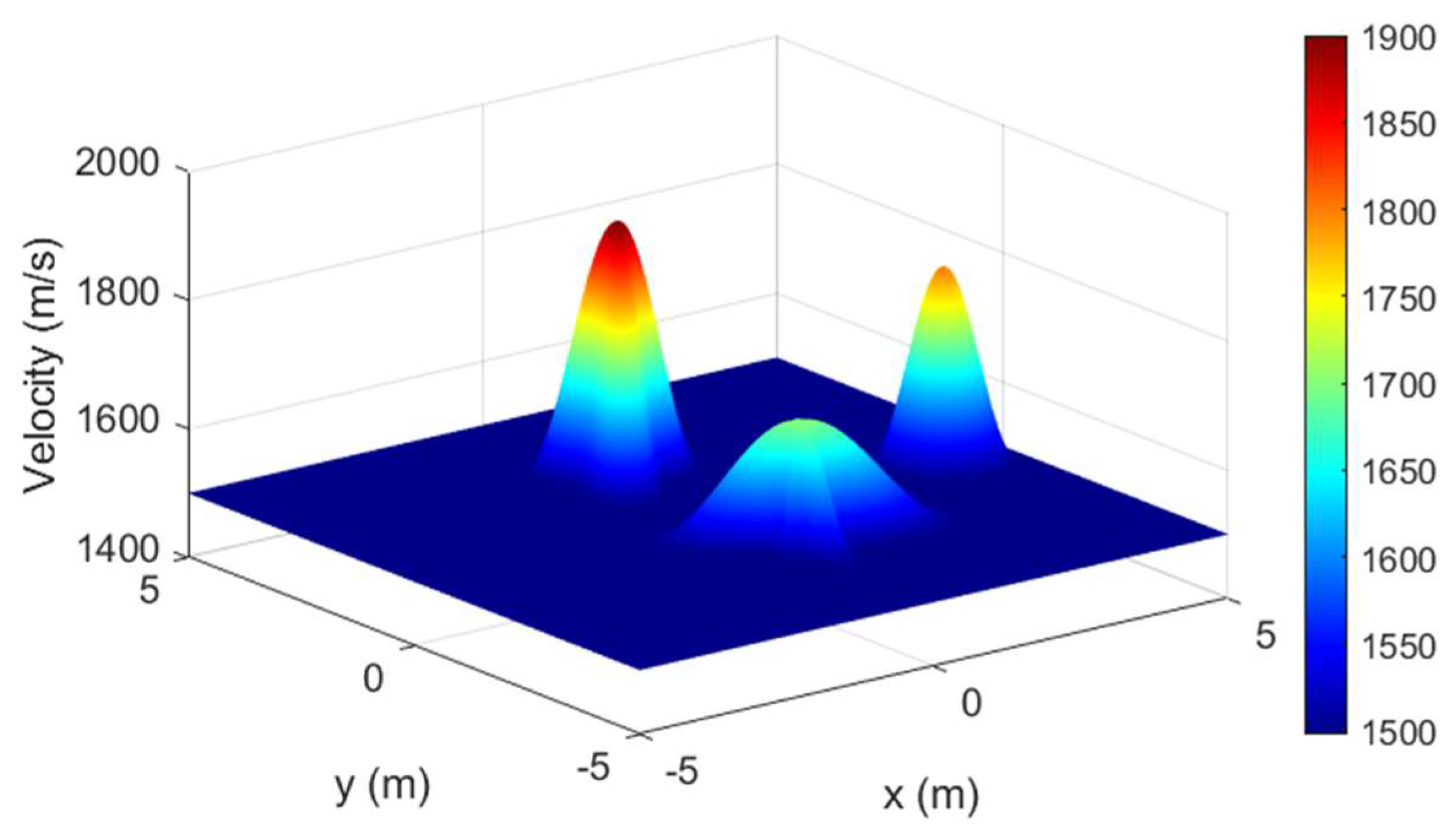
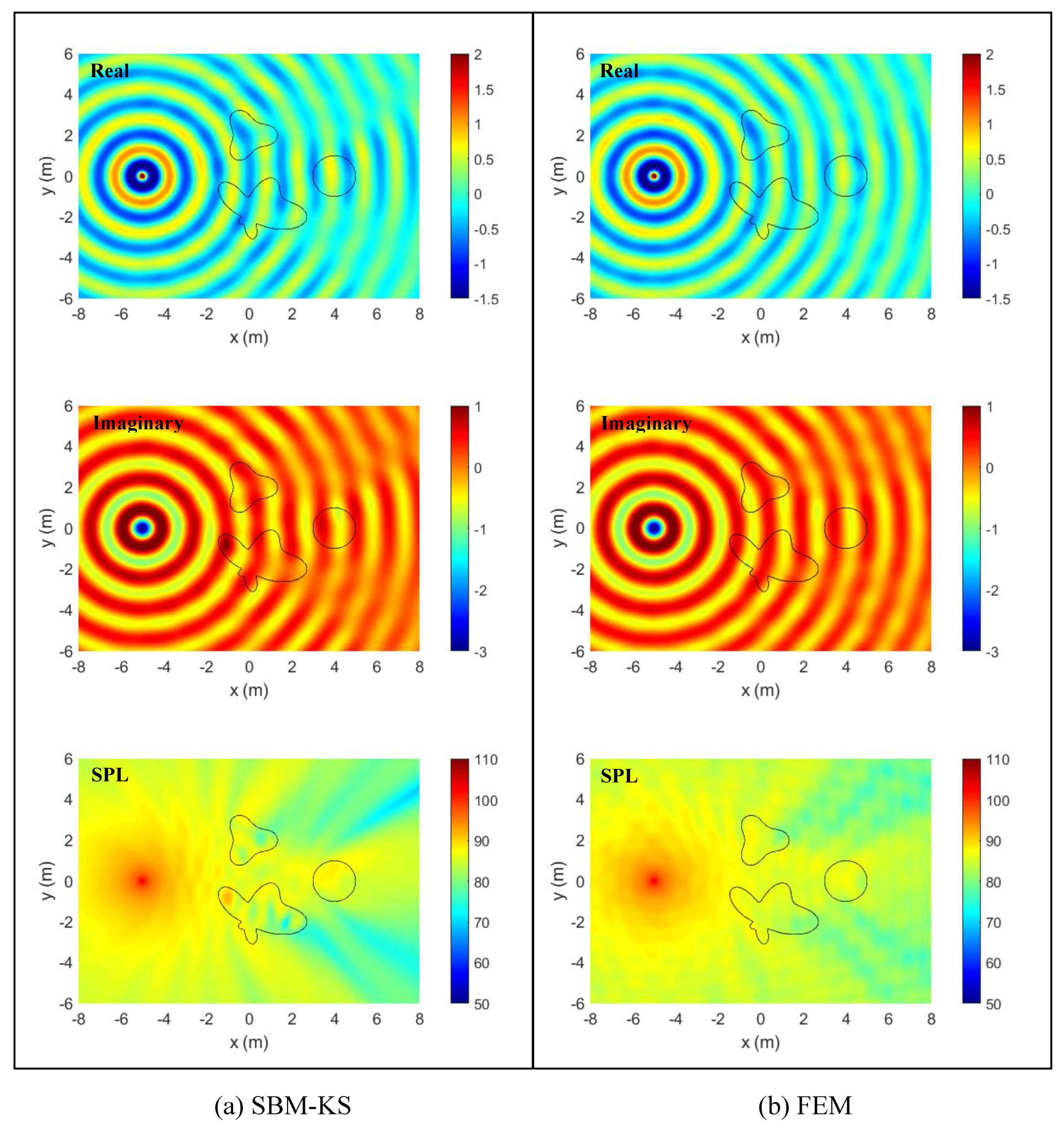
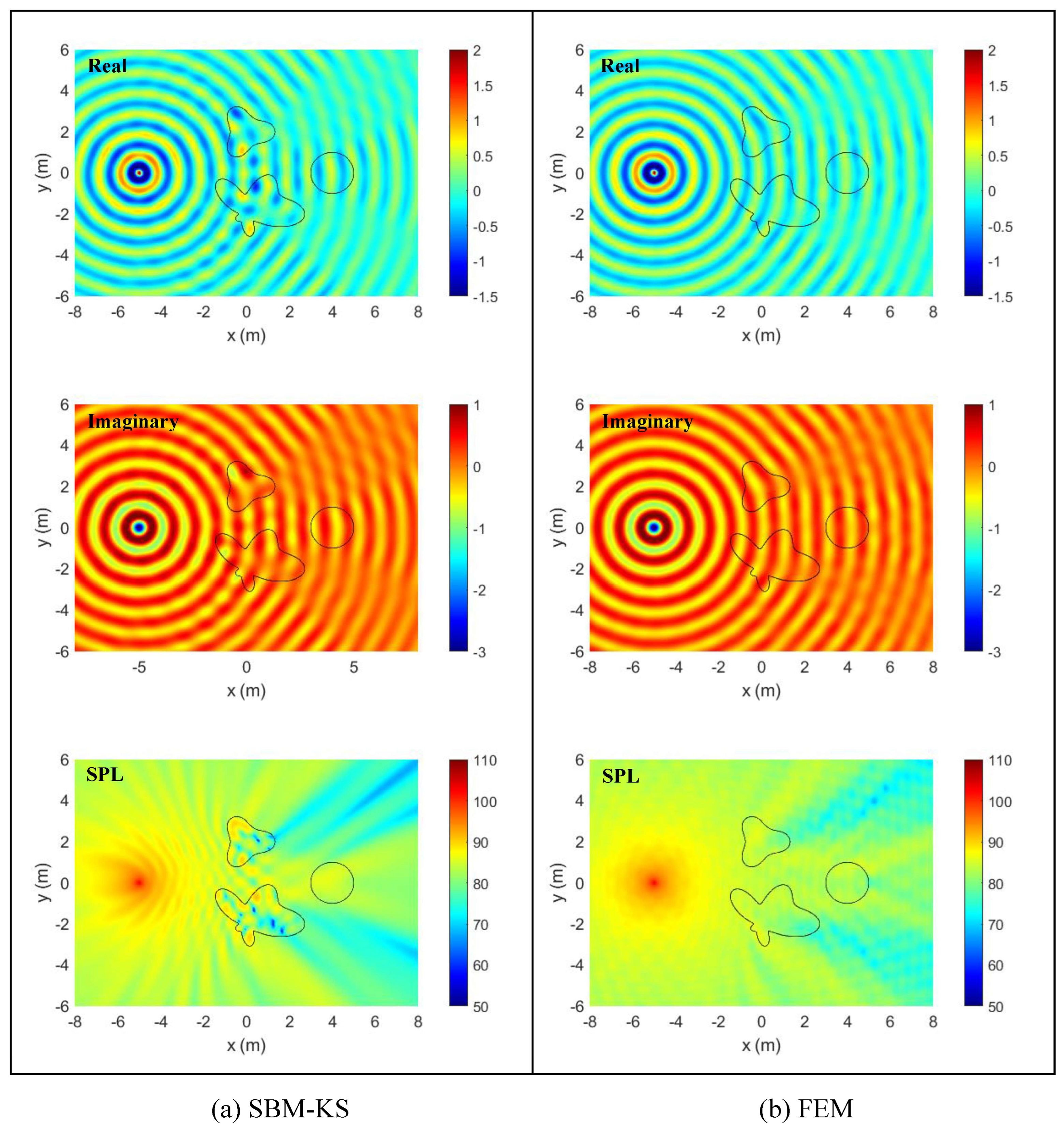
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Premat, E.; Gabillet, Y. A new boundary-element method for predicting outdoor sound propagation and application to the case of a sound barrier in the presence of downward refraction. J. Acoust. Soc. Am. 2000, 108, 2775–2783. [Google Scholar] [CrossRef]
- Liu, Y. On the BEM for acoustic wave problems. Eng. Anal. Boundary Elem. 2019, 107, 53–62. [Google Scholar] [CrossRef]
- Chen, X.; He, Q.; Zheng, C.-J.; Wan, C.; Bi, C.-X.; Wang, B. A parameter study of the Burton-Miller formulation in the BEM analysis of acoustic resonances in exterior configurations. J. Theor. Computat. Acous. 2021, 29, 2050023. [Google Scholar] [CrossRef]
- Aimi, A.; Boiardi, A.S. IGA-Energetic BEM: An effective tool for the numerical solution of wave propagation problems in space-time domain. Mathematics 2022, 10, 334. [Google Scholar] [CrossRef]
- Ganesh, M.; Morgenstern, C. High-order FEM domain decomposition models for high-frequency wave propagation in heterogeneous media. Comput. Math. Appl. 2018, 75, 1961–1972. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Gui, Q.; Chai, Y. A coupled FE-Meshfree triangular element for acoustic radiation problems. Int. J. Comp. Meth. 2021, 18, 2041002. [Google Scholar] [CrossRef]
- Chai, Y.; Li, W.; Liu, Z. Analysis of transient wave propagation dynamics using the enriched finite element method with interpolation cover functions. Appl. Math. Comput. 2022, 412, 126564. [Google Scholar] [CrossRef]
- Sun, T.; Wang, P.; Zhang, G.; Chia, Y. Transient analyses of wave propagations in nonhomogeneous mediaemploying the novel finite element method with the appropriate enrichment function. Comput. Math. Appl. 2023, 129, 90–112. [Google Scholar]
- Di Bartolo, L.; Dors, C.; Mansur, W.J. A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation. Geophysics 2012, 77, T187–T199. [Google Scholar] [CrossRef]
- Li, K.; Liao, W. An efficient and high accuracy finite-difference scheme for the acoustic wave equation in 3D heterogeneous media. J. Comput. Sci. 2020, 40, 101063. [Google Scholar] [CrossRef]
- Tadeu, A.; Stanak, P.; Sladek, J.; Sladek, V. Coupled BEM-MLPG acoustic analysis for non-homogeneous media. Eng. Anal. Boundary Elem. 2014, 44, 161–169. [Google Scholar] [CrossRef]
- Keuchel, S.; Hagelstein, N.C.; Zaleski, O.; von Estorff, O. Evaluation of hypersingular and nearly singular integrals in the Isogeometric Boundary Element Method for acoustics. Comput. Methods Appl. Mech. Eng. 2017, 325, 488–504. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Gong, Y. Analysis of 2D heat conduction in nonlinear functionally graded materials using a local semi-analytical meshless method. Aims Math. 2021, 6, 12599–12618. [Google Scholar] [CrossRef]
- Jiang, S.; Gu, Y.; Golub, M.V. An efficient meshless method for bimaterial interface cracks in 2D thin-layered coating structures. Appl. Math. Lett. 2022, 131, 108080. [Google Scholar] [CrossRef]
- Li, P.W. The space-time generalized finite difference scheme for solving the nonlinear equal-width equation in the long-time simulation. Appl. Math. Lett. 2022, 132, 108181. [Google Scholar] [CrossRef]
- Sun, L.; Fu, Z.; Chen, Z. A localized collocation solver based on fundamental solutions for 3D time harmonic elastic wave propagation analysis. Appl. Math. Comput. 2023, 439, 127600. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, F. Localized method of fundamental solutions for acoustic analysis inside a car cavity with sound-absorbing material. Adv. Appl. Math. Mech. 2023, 15, 182–201. [Google Scholar]
- Li, Y.; Liu, C.; Li, W.; Chai, Y. Numerical investigation of the element-free Galerkin method (EFGM) with appropriate temporal discretization techniques for transient wave propagation problems. Appl. Math. Comput. 2023, 442, 127755. [Google Scholar] [CrossRef]
- Ju, B.; Qu, W. Three-dimensional application of the meshless generalized finite difference method for solving the extended Fisher-Kolmogorov equation. Appl. Math. Lett. 2023, 136, 108458. [Google Scholar] [CrossRef]
- Wei, X.; Luo, W. 2.5D singular boundary method for acoustic wave propagation. Appl. Math. Lett. 2021, 112, 106760. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.; Wu, G.; Zhang, C. A semi-analytical and boundary-type meshless method with adjoint variable formulation for acoustic design sensitivity analysis. Appl. Math. Lett. 2022, 131, 108068. [Google Scholar] [CrossRef]
- Li, W.; Wang, F. Precorrected-FFT accelerated singular boundary method for high-frequency acoustic radiation and scattering. Mathematics 2022, 10, 238. [Google Scholar] [CrossRef]
- Fu, Z.; Xi, Q.; Gu, Y.; Li, J.; Qu, W.; Sun, L.; Wei, X.; Wang, F.; Lin, J.; Li, W.; et al. Singular boundary method: A review and computer implementation aspects. Eng. Anal. Boundary Elem. 2023, 147, 231–266. [Google Scholar] [CrossRef]
- Shojaei, A.; Hermann, A.; Seleson, P.; Silling, S.A.; Rabczuk, T.; Cyron, C.J. Peridynamic elastic waves in two-dimensional unbounded domains: Construction of nonlocal Dirichlet-type absorbing boundary conditions. Comput. Methods Appl. Mech. Eng. 2023, 407, 115948. [Google Scholar] [CrossRef]
- Shojaei, A.; Galvanetto, U.; Rabczuk, T.; Jenabi, A.; Zaccariotto, M. A generalized finite difference method based on the Peridynamic differential operator for the solution of problems in bounded and unbounded domains. Comput. Methods Appl. Mech. Eng. 2019, 343, 100–126. [Google Scholar] [CrossRef]
- Kansa, E. Multiquadrics-A scattered data approximation scheme with applications to computational fluid-dynamics-I: Surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Godinho, L.; Tadeu, A. Acoustic analysis of heterogeneous domains coupling the BEM with Kansa’s method. Eng. Anal. Boundary Elem. 2012, 36, 1014–1026. [Google Scholar] [CrossRef]
- Wang, F.; Chen, W.; Zhang, C.; Hua, Q. Kansa method based on the Hausdorff fractal distance for Hausdorff derivative Poisson equations. Fractals 2018, 26, 1850084. [Google Scholar] [CrossRef]
- Popczyk, O.; Dziatkiewicz, G. Kansa method for solving initial-value problem of hyperbolic heat conduction in nonhomogeneous medium. Int. J. Heat Mass Transf. 2022, 183, 122088. [Google Scholar] [CrossRef]
- Kumar, S.; Jiwari, R.; Mittal, R.C. Radial basis functions based meshfree schemes for the simulation of non-linear extended Fisher-Kolmogorov model. Wave Motion 2022, 109, 102863. [Google Scholar] [CrossRef]
- Jiwari, R. Local radial basis function-finite difference based algorithms for singularly perturbed Burgers’ model. Math. Comput. Simulat. 2022, 198, 106–126. [Google Scholar] [CrossRef]
- Jiwari, R.; Kumar, S.; Mittal, R.C. Meshfree algorithms based on radial basis functions for numerical simulation and to capture shocks behavior of Burgers’ type problems. Eng. Comput. 2019, 36, 1142–1168. [Google Scholar] [CrossRef]
- Pandit, S. Local radial basis functions and scale-3 Haar wavelets operational matrices based numerical algorithms for generalized regularized long wave model. Wave Motion 2022, 109, 102846. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.; Li, P.-W.; Qu, W. Singular boundary method for 2D and 3D acoustic design sensitivity analysis. Comput. Math. Appl. 2022, 119, 371–386. [Google Scholar] [CrossRef]
- Lan, L.; Cheng, S.; Sun, X.; Li, W.; Yang, C.; Wang, F. A fast singular boundary method for the acoustic design sensitivity analysis of arbitrary two-and three-dimensional structures. Mathematics 2022, 10, 3817. [Google Scholar] [CrossRef]
- Soares, D.; Godinho, L.; Pereira, A.; Dors, C. Frequency domain analysis of acoustic wave propagation in heterogeneous media considering iterative coupling procedures between the method of fundamental solutions and Kansa’s method. Int. J. Numer. Methods Eng. 2012, 89, 914–938. [Google Scholar] [CrossRef]
- Tadeu, A.; Godinho, L.; António, J. Benchmark solution for 3D scattering from cylindrical inclusions. J. Comput. Acoust. 2001, 9, 1311–1328. [Google Scholar] [CrossRef]
- Wei, X.; Chen, W.; Fu, Z.J. Solving inhomogeneous problems by singular boundary method. J. Mar. Sci. Tech. 2013, 21, 2. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, C.; Wang, F.; Qiu, L. A Novel Coupled Meshless Model for Simulation of Acoustic Wave Propagation in Infinite Domain Containing Multiple Heterogeneous Media. Mathematics 2023, 11, 1841. https://doi.org/10.3390/math11081841
Chi C, Wang F, Qiu L. A Novel Coupled Meshless Model for Simulation of Acoustic Wave Propagation in Infinite Domain Containing Multiple Heterogeneous Media. Mathematics. 2023; 11(8):1841. https://doi.org/10.3390/math11081841
Chicago/Turabian StyleChi, Cheng, Fajie Wang, and Lin Qiu. 2023. "A Novel Coupled Meshless Model for Simulation of Acoustic Wave Propagation in Infinite Domain Containing Multiple Heterogeneous Media" Mathematics 11, no. 8: 1841. https://doi.org/10.3390/math11081841
APA StyleChi, C., Wang, F., & Qiu, L. (2023). A Novel Coupled Meshless Model for Simulation of Acoustic Wave Propagation in Infinite Domain Containing Multiple Heterogeneous Media. Mathematics, 11(8), 1841. https://doi.org/10.3390/math11081841







