An Improved Relationship between the Solution and Its Corresponding Function in Fourth-Order Neutral Differential Equations and Its Applications

Abstract

This work aims to derive new inequalities that improve the asymptotic and oscillatory properties of solutions to fourth-order neutral differential equations. The relationships between the solution and its corresponding function play an important role in the oscillation theory of neutral differential equations. Therefore, we improve these relationships based on the modified monotonic properties of positive solutions. Additionally, we set new conditions that confirm the absence of positive solutions and thus confirm the oscillation of all solutions of the considered equation. We finally explain the importance of the new inequalities by applying our results to some special cases of the studied equation, as well as comparing them with previous results in the literature.

1. Introduction

It is easy to see the great importance of differential equations (DE) since their inception. It is well recognized that various types of DEs may frequently and accurately represent a very large number of physical, chemical, biological, financial, and economic phenomena (Ordinary DEs, Partial DEs, Stochastic DEs, dynamical systems, and so on). It is also easy to notice that the current technological and scientific development is accompanied by many phenomena and open problems. These problems and their innovative solutions also produced a huge amount of mathematical models and DEs. These models and equations are accompanied by many questions about their properties or the possibility of solving them numerically. Having answers to these questions leads to understanding, analyzing, and explaining phenomena and models, which in turn will contribute to the development of many sectors.

The development of fractional calculus followed that of classical calculus in 1695. The earliest systematic studies were attributed to Liouville, Riemann, Leibniz, etc. [1,2]. Fractional calculus has long been thought of as a purely mathematical field with few practical applications. However, this situation has changed in recent decades. Fractional calculus has been found to be both beneficial and effective. Many and varied sectors of engineering and research, including electromagnetics, viscoelasticity, fluid mechanics, electrochemistry, biological population models, optics, and signals processing, use fractional calculus. It has been used to simulate technical and physical processes that fractional differential equations have been determined to best describe.

Oscillation theory as a branch of qualitative theory answers many questions about oscillatory behavior and asymptotic properties of DE solutions. The theory of oscillation depends mainly on finding conditions that exclude the non-oscillatory solutions (positive or negative eventually). Therefore, it always needs to study and improve the asymptotic and monotonic properties of positive solutions. This resulted in many interesting analytical research questions and points.

Delay differential equations (DDE) are a type of functional DE that takes into account the temporal memory of phenomena. So, it is easy to see the many applications of these equations in physics, engineering, biology, and other sciences, see [3,4]. Monographs [5,6,7,8] collected several results, methods, and approaches to study the oscillation of solutions of DDEs.

Recently, the oscillation theory has expanded and developed greatly, as it includes the study of oscillation for solutions of ordinary, fractional, and partial DEs with delay, neutral, mixed, and damping. DEs with delay, especially in the non-canonical case, received the largest share of attention. For example, see [9,10] for delay equations, [11] for advanced equations, and [12,13,14,15,16] for neutral equations, while the evolution of the study of odd-order equations can be seen in [17,18,19,20]. On the other hand, the oscillation of fractional DEs can be traced in Survey [21]. Moreover, refs. [22,23,24,25] dealt with the study of mixed equations, while refs. [26,27,28] dealt with damping equations. DEs have also received a lot of attention over the past two decades, see for example [29,30,31,32].

The aim of this study is to improve the asymptotic and monotonic properties and establish oscillation conditions for solutions to the neutral DDE

$${\left(b\left(t\right){\left[x\left(t\right)+\rho \left(t\right)x\left(\tau \left(t\right)\right)\right]}^{‴}\right)}^{\prime }+q\left(t\right)x\left(\sigma \left(t\right)\right)=0,$$

(1)

where $t\ge t_0$. During this study, the following conditions must be satisfied:

(${\mathcal{H}}_1$)

$b,$$\rho ,$$\tau$ and $\sigma$ belong to ${\mathbf{C}}^1\left(\left[t_0,\infty \right)\right)$, and q belongs to $\mathbf{C}\left(\left[t_0,\infty \right)\right)$;

(${\mathcal{H}}_2$)

$b\left(t\right)>0$, $b^{\prime }\left(t\right)\ge 0$, $0<\rho \left(t\right)<{\rho }_0$, and $q\left(t\right)\ge 0$;

(${\mathcal{H}}_3$)

$\tau \left(t\right)\le t$, $\sigma \left(t\right)\le t$, ${\sigma }^{\prime }\left(t\right)\ge 0$, and ${lim}_{t\to \infty }\tau \left(t\right)=\infty ={lim}_{t\to \infty }\sigma \left(t\right)$.

Furthermore, we define the corresponding function to the solution x of the form $z\left(t\right):=x\left(t\right)+\rho \left(t\right)x\left(\tau \left(t\right)\right)$ and consider the non-canonical case, that is,

(${\mathcal{H}}_4$)

${\eta }_2\left(t_0\right)<\infty$, where

$${\eta }_0\left(t\right):={\int }_t^{\infty }{b}^{-1}\left(u\right)\mathrm{d}u$$

and

$${\eta }_j\left(t\right):={\int }_t^{\infty }{\eta }_{j-1}\left(u\right)\mathrm{d}u, \mathrm{for} j=1,2.$$

For a solution of (1), we mean a function $x$ in ${\mathbf{C}}^3\left(\left[t_{*},\infty \right)\right)$, $t_{*}\ge t_0$, which has the property $b·z^{‴}$ belongs to ${\mathbf{C}}^1\left(\left[t_0,\infty \right)\right),$ and $sup\{\left|x\left(t\right)\right|:t\ge t_x\}>0,$ for $t_x\ge t_{*},$ and x satisfies (1) on $\left[t_{*},\infty \right)$.

The relationship between the solution x and its corresponding function z plays an important role in studying the asymptotic and oscillatory behavior of solutions of differential equations of neutral type. For second-order equations, the traditional relationship

$$x>\left(1-\rho \right)z$$

(2)

is usually used in the canonical case, and the relationship

$$x>\left(1-\rho \frac{{\eta }_0\circ \tau }{{\eta }_0}\right)$$

(3)

is usually used for positive decreasing solutions in the non-canonical case, see [14,33]. In the canonical case, Moaaz et al. [34] studied the oscillatory behavior of

$${\left(b\left(t\right){\left({\left[x\left(t\right)+{\rho }_{0}x\left(\tau \left(t\right)\right)\right]}^{\prime }\left(t\right)\right)}^{\gamma }\right)}^{\prime }+\sum _{i=1}^L{q}_i\left(t\right)x^{\beta }\left({\sigma }_i\left(t\right)\right)=0,$$

(4)

where $\gamma ,\beta \in {\mathbb{Q}}^{+}$ are quotients of odd, and $L\in {\mathbb{Z}}^{+}$. They presented the following relationships as an improvement of (2):

$$x\left(t\right)>z\left(t\right)\sum _{m=1}^{n/2}\frac{1}{{\rho }_0^{2m-1}}\left(1-\frac{1}{{\rho }_0}\frac{A_{t_1}\left({\tau }^{-2m}\left(t\right)\right)}{A_{t_1}\left({\tau }^{-\left(2m-1\right)}\left(t\right)\right)}\right), \mathrm{for} \rho >1 \mathrm{and} n\in {\mathbb{Z}}^{+} \mathrm{is} \mathrm{even},$$

and

$$x\left(t\right)>z\left(t\right)\left(1-{\rho }_0\right)\sum _{m=0}^{\left(n-1\right)/2}{\rho }_0^{2m}\frac{A_{t_1}\left({\tau }^{2m+1}\left(t\right)\right)}{A_{t_1}\left(t\right)}, \mathrm{for} \rho <1, \mathrm{and} n\in {\mathbb{Z}}^{+} \mathrm{is} \mathrm{odd},$$

(5)

where ${\tau }^{\left[j\right]}\left(t\right)=\tau \left({\tau }^{\left[j-1\right]}\left(t\right)\right)$, for $j=1,2,\cdots ,2m$, and

$$A_{t_1}\left(t\right)={\int }_{t_1}^t{b}^{-1/\gamma }\left(u\right)\mathrm{d}u.$$

In a non-canonical case, Hassan et al. [35] investigated the oscillatory properties of (4) when $\gamma =\beta$ and $L=1$ and improved (3) by the relationship

$$x\left(t\right)>z\left(t\right)\sum _{r=0}^{\left(n-1\right)/2}{\rho }_0^{2r}\left(1-{\rho }_0\frac{{\eta }_0\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)}{{\eta }_0\left({\tau }^{2r}\left(t\right)\right)}\right).$$

Very recently, Bohner et al. [36] considered the neutral DDE

$${\left(b\left(t\right){\left(z^{\prime }\left(t\right)\right)}^{\beta }\right)}^{\prime }+q\left(t\right)x^{\beta }\left(\sigma \left(t\right)\right)=0$$

and improved (3) in both cases $\tau \left(t\right)\ge t$ and $\tau \left(t\right)\le t$.

For third-order neutral DDE

$${\left(b\left(t\right){\left(z^{″}\left(t\right)\right)}^{\alpha }\right)}^{\prime }+q\left(t\right)x^{\alpha }\left(\sigma \left(t\right)\right)=0,$$

Moaaz et al. [37] presented conditions for oscillation and improved (2) by the relationship

$$x\left(t\right)\ge \left(1-{\rho }_0\right)z\left(t\right)\sum _{r=0}^{\left(n-1\right)/2}{\rho }_0^{2r}{\left(\frac{{\tau }^{\left[2r+1\right]}\left(t\right)-t_1}{t-t_1}\right)}^2,$$

when $\rho \left(t\right)={\rho }_0$ (constant).

On the other hand, the oscillatory behavior of solutions to a higher order differential equation has been recently studied by many researchers. Moreover, the monotonic and asymptotic properties of solutions of these equations were improved, see [38,39,40].

For higher order neutral DDE

In the following, we review some results in the literature that will be useful to clarify the importance of our results through comparison with them.

Theorem 1

([39]). Suppose that $lim{inf}_{t\to \infty }\left({\eta }_0\left(\sigma \left(t\right)\right)/{\eta }_0\left(t\right)\right)=\lambda$ and

$$b\left(t\right){\eta }_0^2\left(t\right){\sigma }^{n-2}\left(t\right)q\left(t\right)\left(1-\rho \left(\sigma \left(t\right)\right)\right)\ge \left(n-2\right)!{\beta }_0 for some {\beta }_0\in \left(0,1\right).$$

If

$$\underset{t\to \infty }{liminf}{\int }_{\sigma \left(t\right)}^t{\sigma }^{n-2}\left(u\right){\eta }_0\left(u\right)q\left(u\right)\left(1-\rho \left(\sigma \left(u\right)\right)\right)\mathrm{d}u>\frac{\left(n-2\right)!\left(1-{\beta }_m\right)}{\mathrm{e}},$$

(6)

then there are no positive solutions of the DDE

$${\left(b\left(t\right)z^{\left(n-1\right)}\left(t\right)\right)}^{\prime }+q\left(t\right)x\left(\sigma \left(t\right)\right)=0,$$

whose corresponding function satisfies properties $z^{\prime }\left(t\right)>0$ and $z^{\left(n-1\right)}\left(t\right)<0$, where

$${\beta }_i=\frac{{\beta }_0{\lambda }^{{\beta }_{i-1}}}{1-{\beta }_{i-1}}, {\beta }_{i-1}\le {\beta }_i<1, for i=1,2,\cdots ,m.$$

Theorem 2

([40]). Suppose that ${\eta }_2\left(\sigma \left(t\right)\right)\ge \lambda {\eta }_2\left(t\right)$,

$${\int }_{t_0}^{\infty }\frac{1}{b\left(s\right)}\left({\int }_{t_2}^{s}q\left(u\right)\left(1-\rho \left(\sigma \left(u\right)\right)\frac{{\eta }_2\left(\tau \left(\sigma \left(u\right)\right)\right)}{{\eta }_2\left(\sigma \left(u\right)\right)}\right)\mathrm{d}u\right)\mathrm{d}s=\infty ,$$

(7)

and

$$q\left(t\right){\eta }_2^2\left(t\right){\eta }_1^{-1}\left(t\right)\left(1-\rho \left(\sigma \left(t\right)\right)\frac{{\eta }_2\left(\tau \left(\sigma \left(t\right)\right)\right)}{{\eta }_2\left(\sigma \left(t\right)\right)}\right)\ge {\alpha }_0, for some {\alpha }_0\in \left(0,1\right).$$

If the DDE

$$w^{\prime }\left(t\right)+\frac{1}{\left(1-{\alpha }_n\right)}q\left(t\right){\eta }_2\left(t\right)\left(1-\rho \left(\sigma \left(t\right)\right)\frac{{\eta }_2\left(\tau \left(\sigma \left(t\right)\right)\right)}{{\eta }_2\left(\sigma \left(t\right)\right)}\right)w\left(\sigma \left(t\right)\right)=0$$

(8)

is oscillatory, then there are no positive decreasing solutions of (1), where

$${\alpha }_i=\frac{{\alpha }_0{\lambda }^{{\alpha }_{i-1}}}{1-{\alpha }_{i-1}}, {\alpha }_{i-1}\le {\alpha }_i<1, for i=1,2,\cdots ,n.$$

The studied equation is a generalization of Emden–Fowler Differential Equations in fa ourth-order case and neutral delay case, see [41,42,43]. In this work, we start, as usual, by classifying the positive solutions of the studied equation according to the signs of its derivatives. Then, in some cases of positive solutions, we obtain new monotonic properties. Based on these characteristics, we improve the relationship between the solution and the corresponding function of the studied equation. Furthermore, we use these new relationships to rule out the existence of positive solutions. We also provide some examples and comparisons to illustrate the significance of our results.

2. Asymptotic and Monotonic Properties

In this section, we present some improved asymptotic and monotonic properties of the positive solutions of the studied equation. We start, as usual, by classifying positive solutions according to the sign of their derivatives. Assuming that the solution x is eventually positive, we obtain that $x\left(\tau \left(t\right)\right)$ and $x\left(\sigma \left(t\right)\right)$ are also eventually positive. Then, $z\left(t\right)>0,$ eventually. It follows from Equation (1) that $b·z^{‴}$ is nondecreasing, and z fulfills one of the following cases, based on Lemma 2.2.3 in [44]:

(${\mathbf{L}}_1$):

$z^{\left(i\right)}\left(t\right)>0 \mathrm{for} i=0,1,3 \mathrm{and} z^{\left(4\right)}\left(t\right)<0;$

(${\mathbf{L}}_2$):

$z^{\left(i\right)}\left(t\right)>0 \mathrm{for} i=0,1,2 \mathrm{and} z^{‴}\left(t\right)<0;$

(${\mathbf{L}}_3$):

${\left(-1\right)}^i{z}^{\left(i\right)}\left(t\right)>0 \mathrm{for} i=0,1,\cdots ,3.$

Notation 1.

We denote by the symbol ${\mathcal{S}}_i$ the class of all eventually positive solutions whose corresponding function satisfies $\left({\mathbf{L}}_i\right)$, for $i=1,2,3$. For convenience, we denote the increasing function F with the symbol $F\left[\uparrow \right]$ and the decreasing function G with the symbol $G\left[\downarrow \right]$. Additionally, we define

$$F^{\left[0\right]}\left(t\right):=t, F^{\left[j\right]}\left(t\right)=F\left(F^{\left[j-1\right]}\left(t\right)\right), for j=1,2,\cdots .$$

Notation 2.

For convenience, we define the functions, for any positive integer m,

$${\mathcal{P}}_1\left(t;m\right):=\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{1}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-1\right]{\left(\frac{{\tau }^{\left[2r\right]}\left(t\right)}{t}\right)}^{2/ϵ},$$

where $ϵ\in \left(0,1\right)$, and

$${\mathcal{P}}_2\left(t;m\right):=\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{1}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-\frac{{\eta }_2\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)}{{\eta }_2\left({\tau }^{\left[2r\right]}\left(t\right)\right)}\right].$$

Lemma 1.

Suppose that x is an eventually positive solution of (1). Then, eventually,

$$x\left(t\right)>\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{z\left({\tau }^{\left[2r\right]}\left(t\right)\right)}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-z\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)\right],$$

(9)

for any integer $m\ge 0$.

Proof. 

Using the relationship between x and z more than once,

$$\begin{array}{ccc}\hfill x\left(t\right)& =& z\left(t\right)-\rho \left(t\right)x\left(\tau \left(t\right)\right)\hfill \\ & =& z\left(t\right)-\rho \left(t\right)z\left(\tau \left(t\right)\right)+\rho \left(t\right)\rho \left(\tau \left(t\right)\right)x\left({\tau }^{\left[2\right]}\left(t\right)\right)\hfill \\ & =& z\left(t\right)-\rho \left(t\right)z\left(\tau \left(t\right)\right)+\rho \left(t\right)\rho \left(\tau \left(t\right)\right)z\left({\tau }^{\left[2\right]}\left(t\right)\right)-\rho \left(t\right)\rho \left(\tau \left(t\right)\right)\rho \left({\tau }^{\left[2\right]}\left(t\right)\right)x\left({\tau }^{\left[3\right]}\left(t\right)\right)\hfill \\ & =& z\left(t\right)-\rho \left(t\right)z\left(\tau \left(t\right)\right)+\rho \left(t\right)\rho \left(\tau \left(t\right)\right)z\left({\tau }^{\left[2\right]}\left(t\right)\right)-\rho \left(t\right)\rho \left(\tau \left(t\right)\right)\rho \left({\tau }^{\left[2\right]}\left(t\right)\right)z\left({\tau }^{\left[3\right]}\left(t\right)\right)\hfill \\ & & +\rho \left(t\right)\rho \left(\tau \left(t\right)\right)\rho \left({\tau }^{\left[2\right]}\left(t\right)\right)\rho \left({\tau }^{\left[3\right]}\left(t\right)\right)x\left({\tau }^{\left[4\right]}\left(t\right)\right),\hfill \end{array}$$

and so on. Thus,

$$x\left(t\right)>\sum _{r=0}^m{\left(-1\right)}^m\left(\prod _{l=0}^r\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\frac{z\left({\tau }^{\left[r\right]}\left(t\right)\right)}{\rho \left({\tau }^{\left[r\right]}\left(t\right)\right)},$$

for any odd positive integer m, or

$$x\left(t\right)>\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{z\left({\tau }^{\left[2r\right]}\left(t\right)\right)}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-z\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)\right],$$

for any integer $m\ge 0$. Hence, the proof ends. □

Lemma 2

([45]). Suppose that G belongs to ${\mathbf{C}}^{n+1}\left(\left[t_0,\infty \right)\right)$ and satisfies the following, eventually:

(i)

$G^{\left(i\right)}\left(t\right)>0$ for $i=0,1,\cdots ,n,$

(ii)

$G^{\left(n+1\right)}\left(t\right)\le 0.$

Then,

$$G\left(t\right)\ge \frac{ϵ}{n}t G^{\prime }\left(t\right),$$

for all $ϵ\in (0,1)$.

2.1. Category ${\mathcal{S}}_2$

Lemma 3.

Suppose that x belongs to ${\mathcal{S}}_2$. Then, eventually,

(A1-1) 

$z\left(t\right)\ge \frac{ϵ}{2}t z^{\prime }\left(t\right)$, for all $ϵ\in \left(0,1\right)$,

(A1-2) 

$z^{″}\left(t\right)\ge -{\eta }_0\left(t\right)b\left(t\right)z^{‴}\left(t\right)$,

(A1-3) 

$\left(z^{″}/{\eta }_0\right) \left[\uparrow \right]$.

Proof. 

Using Lemma 2 with $G=z$ and $n=2$, we obtain (A1-1). Now, based on the properties of solutions in the class ${\mathcal{P}}_2$, we conclude that

$$-z^{″}\left(t\right)\le {\int }_t^{\infty }{z}^{‴}\left(u\right)\mathrm{d}u\le {\eta }_0\left(t\right)b\left(t\right)z^{‴}\left(t\right).$$

Thus,

$${\left(\frac{z^{″}}{{\eta }_0}\right)}^{\prime }=\frac{1}{{\eta }_0^2}\left[{\eta }_0{z}^{‴}+\frac{1}{b}{z}^{″}\right]\ge 0.$$

Hence, the proof ends. □

Lemma 4.

Suppose that x belongs to ${\mathcal{S}}_2$. Then, eventually,

(A1-4) 

$x\left(t\right)>{\mathcal{P}}_1\left(t;m\right)z\left(t\right)$,

(A1-5) 

${\left(b\left(t\right)z^{‴}\left(t\right)\right)}^{\prime }\le -q\left(t\right){\mathcal{P}}_1\left(\sigma \left(t\right);m\right)z\left(\sigma \left(t\right)\right)$.

Proof. 

From Lemma 1, we have (9) holds. Based on the properties of solutions in the class ${\mathcal{S}}_2$, the fact $z\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)\le z\left({\tau }^{\left[2r\right]}\left(t\right)\right)$ for $r=0,1,\cdots$, is obtained. Thus, (9) becomes

$$x\left(t\right)>\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{1}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-1\right]z\left({\tau }^{\left[2r\right]}\left(t\right)\right).$$

(10)

It follows from (A1-1) that

$$z\left({\tau }^{\left[2r\right]}\left(t\right)\right)\ge {\left(\frac{{\tau }^{\left[2r\right]}\left(t\right)}{t}\right)}^{2/ϵ}z\left(t\right),$$

which with (10), gives (A1-4). Hence, it follows from (1) that (A1-5) holds. Therefore, the proof ends. □

Remark 1.

It is easy to verify that ${\mathcal{P}}_1\left(t;0\right)=1-\rho \left(t\right)$. Then, putting $m=0$ in (A1-4), the classical relation (2) is obtained.

The following results are obtained directly by replacing the function $Q\left(t\right)$ with $q\left(t\right){\mathcal{P}}_1\left(\sigma \left(t\right);m\right)$ in the results in [39].

Theorem 3.

Suppose that

(i) 

there is ${\mu }_{*}>0$ such that $b\left(t\right){\eta }_0^2\left(t\right){\sigma }^{n-2}\left(t\right)q\left(t\right){\mathcal{P}}_1\left(\sigma \left(t\right);m\right)\ge 2{\mu }_{*},$

(ii) 

$lim{inf}_{t\to \infty }\left({\eta }_0\left(\sigma \left(t\right)\right)/{\eta }_0\left(t\right)\right)=\delta <\infty ,$

(iii) 

there exists a positive integer n such that ${\mu }_{i-1}\le {\mu }_i$, for $i=1,\cdots ,n$, where ${\mu }_0=ϵ{\mu }_{*}$, for any $ϵ\in \left(0,1\right)$, and

$${\mu }_i:={\mu }_0\frac{{\delta }^{{\mu }_{i-1}}}{1-{\mu }_{i-1}}, for i=1,2,\cdots ,n.$$

If ${\mu }_n>1/2$, then ${\mathcal{S}}_2=\varnothing$.

Theorem 4.

Suppose that hypotheses (i)–(iii) in Theorem 3 are satisfied. If

$$\underset{t\to \infty }{liminf}{\int }_{\sigma \left(t\right)}^t{\sigma }^2\left(u\right){\eta }_0\left(u\right)q\left(u\right){\mathcal{P}}_1\left(\sigma \left(u\right);m\right)\mathrm{d}u>\frac{2\left(1-{\mu }_n\right)}{\mathrm{e}},$$

(11)

then ${\mathcal{S}}_2=\varnothing$.

Proof. 

This Theorem is obtained directly by replacing the function $Q\left(t\right)$ with $q\left(t\right){\mathcal{P}}_1\left(\sigma \left(t\right);m\right)$ in Theorem 2 in [39]. □

Example 1.

Consider the neutral DDE

$${\left(t^4{\left(x\left(t\right)+\frac{1}{2}x\left(0.9t\right)\right)}^{‴}\right)}^{\prime }+18x\left({\sigma }_{0}t\right)=0,$$

(12)

where $t>0,$ and ${\sigma }_0\in \left(0,1\right)$. It is simple to confirm that

$${\eta }_0\left(t\right)=\frac{1}{3t^3}, {\eta }_1\left(t\right)=\frac{1}{6t^2}, and {\eta }_2\left(t\right)=\frac{1}{6t}.$$

Then,

$${\mathcal{P}}_1\left(t;m\right):=\sum _{r=0}^{20}\left({\left(\frac{1}{2}\right)}^{2r+1}{\left(0.9\right)}^{\left(4/ϵ\right)r}\right)\approx 0.598.$$

We also note that ${\mu }_{*}=0.598{\sigma }_0^2$, $\delta =1/{\sigma }_0^3$, ${\mu }_0=0.5382{\sigma }_0^2$, with $ϵ=0.9$, and

$${\mu }_i=\frac{0.5382{\sigma }_0^{2-3{\mu }_{i-1}}}{1-{\mu }_{i-1}},$$

for $i=1,2,\cdots$. From Theorem 3, we have that ${\mathcal{S}}_2=\varnothing$ if ${\mu }_n>1/2$, for some $n\ge 0$, while Theorem 4 confirms that ${\mathcal{S}}_2=\varnothing$ if

$${\mu }_n>1-1.794\mathrm{e}{\sigma }_0^{2}ln\frac{1}{{\sigma }_0}:={\lambda }_1,$$

(13)

for some $n\ge 0$.

Remark 2.

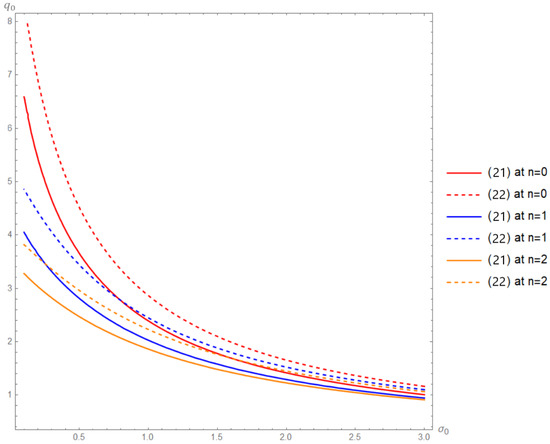
Considering Equation (12) and using Theorem 1 in [39], we obtain that ${\mathcal{S}}_2=\varnothing$ if ${\beta }_n>1/2$, for some $n\ge 0$, where ${\beta }_0=\frac{9}{20}{\sigma }_0^2$, and

$${\beta }_i=\frac{{\beta }_0}{1-{\beta }_{i-1}}{\left(\frac{1}{{\sigma }_0}\right)}^{3{\beta }_{i-1}}, for i=1,2,\cdots ,n.$$

Moreover, using Theorem 1, we obtain that ${\mathcal{S}}_2=\varnothing$ if

$${\beta }_n>1-\frac{3}{2}\mathrm{e}{\sigma }_0^{2}ln\frac{1}{{\sigma }_0}:={\lambda }_2,$$

(14)

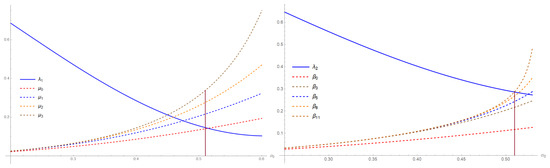
for some $n\ge 0$. Figure 1 shows that sequence ${\left\{{\mu }_i\right\}}_{i=0}^n$ crosses $1/2$ faster than sequence ${\left\{{\beta }_i\right\}}_{i=0}^n$, which means that it is possible to prove that ${\mathcal{S}}_2=\varnothing$ with fewer approximations. For example, we notice when ${\sigma }_0=0.6$ that the ${\mu }_3>1/2$, while ${\beta }_3<1/2.$ Figure 2 shows the difference between conditions (13) and (14). We notice when ${\sigma }_0=0.51$ that ${\mu }_2>{\lambda }_1,$ whereas the sequence ${\left\{{\beta }_i\right\}}_{i=0}^n$ needs the eleventh approximation to exceed ${\lambda }_2$.

2.2. Category ${\mathcal{S}}_3$

Lemma 5.

Suppose that x belongs to ${\mathcal{S}}_3$. Then, eventually,

(A2-1) 

$\left(z/{\eta }_2\right) \left[\uparrow \right]$,

(A2-2) 

${\left(-1\right)}^i{z}^{\left(i\right)}\left(t\right)\ge -b\left(t\right)z^{‴}\left(t\right){\eta }_{2-i}\left(t\right)$ for $i=0,1,2$.

Proof. 

The proof of this lemma comes directly from Lemma 3 and Theorem 1 in [40]. □

Lemma 6.

Suppose that x belongs to ${\mathcal{S}}_3$. Then, eventually,

(A2-3) 

$x\left(t\right)>{\mathcal{P}}_2\left(t;m\right)z\left(t\right)$,

(A2-4) 

${\left(b\left(t\right)z^{‴}\left(t\right)\right)}^{\prime }\le -q\left(t\right){\mathcal{P}}_2\left(\sigma \left(t\right);m\right)z\left(\sigma \left(t\right)\right)$.

Proof. 

From Lemma 1, we have (9) holds. From (A2-1), the following fact is obtained:

$$z\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)\le \frac{{\eta }_2\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)}{{\eta }_2\left({\tau }^{\left[2r\right]}\left(t\right)\right)}z\left({\tau }^{\left[2r\right]}\left(t\right)\right),$$

which with (9), gives

$$x\left(t\right)>\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{1}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-\frac{{\eta }_2\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)}{{\eta }_2\left({\tau }^{\left[2r\right]}\left(t\right)\right)}\right]z\left({\tau }^{\left[2r\right]}\left(t\right)\right).$$

(15)

It follows from the fact that $z\left[\downarrow \right]$ that (A2-3) holds. Hence, it follows from (1) that (A2-4) holds. Therefore, the proof ends. □

Remark 3.

It is easy to verify that

$${\mathcal{P}}_2\left(t;0\right)=1-\rho \left(t\right)\frac{{\eta }_2\left(\tau \left(t\right)\right)}{{\eta }_2\left(t\right)}.$$

Then, putting $m=0$ in (A2-3), we obtain the classical relation (3).

Lemma 7.

Suppose that x belongs to ${\mathcal{S}}_3$. Then, eventually,

(i) 

there is ${\kappa }_0>0$ such that ${\eta }_2^2\left(t\right){\eta }_1^{-1}\left(t\right)q\left(t\right){\mathcal{P}}_2\left(\sigma \left(t\right);m\right)\ge {\kappa }_0,$

(ii) 

$lim{inf}_{t\to \infty }\left({\eta }_2\left(\sigma \left(t\right)\right)/{\eta }_2\left(t\right)\right)=\ell <\infty ,$

(iii) 

there exists a positive integer n such that ${\kappa }_{i-1}\le {\kappa }_i<1$, for $i=1,\cdots ,n$, for any $ϵ\in \left(0,1\right)$, and

$${\kappa }_i:={\kappa }_0\frac{{\ell }^{{\kappa }_{i-1}}}{1-{\kappa }_{i-1}}, for i=1,2,\cdots ,n.$$

Then,

(A2-5) 

$\left(z/{\eta }_2^{{\kappa }_n}\right) \left[\downarrow \right],$

(A2-6) 

${lim}_{t\to \infty }\left(z\left(t\right)/{\eta }_2^{{\kappa }_n}\left(t\right)\right)=0.$

Proof. 

Assume that x belongs to ${\mathcal{S}}_3$. Since $z\left(t\right)>0$ and $z\left[\downarrow \right]$, we obtain that $z\left(t\right)\to c\ge 0$. Suppose the contrary that $c>0$. Hence, there exists a $t_1\ge t_0$ such that $z\left(t\right)\ge c$ for $t\ge t_1$. Then, from (A2-4), we find

$${\left(b\left(t\right)z^{‴}\left(t\right)\right)}^{\prime }\le -cq\left(t\right){\mathcal{P}}_2\left(\sigma \left(t\right);m\right).$$

(16)

By integrating from $t_1$ to t, (16) becomes

$$b\left(t\right)z^{‴}\left(t\right)\le -c{\int }_{t_1}^{t}q\left(u\right){\mathcal{P}}_2\left(\sigma \left(u\right);m\right)\mathrm{d}u.$$

It follows from (A2-2) at $i=1$ that

$$\frac{z^{\prime }\left(t\right)}{{\eta }_1\left(t\right)}\le b\left(t\right)z^{‴}\left(t\right)\le -c{\int }_{t_1}^{t}q\left(u\right){\mathcal{P}}_2\left(\sigma \left(u\right);m\right)\mathrm{d}u,$$

or

$$z^{\prime }\left(t\right)\le -c{\eta }_1\left(t\right){\int }_{t_1}^{t}q\left(u\right){\mathcal{P}}_2\left(\sigma \left(u\right);m\right)\mathrm{d}u.$$

Thus,

$$\begin{array}{ccc}\hfill z^{\prime }\left(t\right)& \le & -c{\kappa }_0{\eta }_1\left(t\right){\int }_{t_1}^t\frac{{\eta }_1\left(u\right)}{{\eta }_2^2\left(u\right)}\mathrm{d}u\hfill \\ & =& -c{\kappa }_0{\eta }_1\left(t\right)\left(\frac{1}{{\eta }_2\left(t\right)}-\frac{1}{{\eta }_2\left(t_1\right)}\right).\hfill \end{array}$$

(17)

Since ${\eta }_2\left(t\right)\to 0$ as $t\to \infty$, we obtain ${\eta }_2^{-1}\left(t\right)-{\eta }_2^{-1}\left(t_1\right)\ge ϵ{\eta }_2^{-1}\left(t\right)$ for $ϵ\in \left(0,1\right)$ and $t\ge t_2\ge t_1$, where $t_2$ is large enough. Then, (17) becomes

$$z^{\prime }\left(t\right)\le -cϵ{\kappa }_0\frac{{\eta }_1\left(t\right)}{{\eta }_2\left(t\right)}.$$

Integrating this inequality from $t_2$ to ∞, we obtain

$$z\left(t_2\right)\ge c+cϵ{\kappa }_{0}ln\frac{{\eta }_2\left(t_2\right)}{{\eta }_2\left(t\right)}\to \infty ,$$

a contradiction. Therefore, $z\left(t\right)\to c=0$ as $t\to \infty$.

The rest of the proof of this lemma is obtained directly by replacing the function $\left(1-\rho \left[\left({\eta }_2\circ \tau \right)/{\eta }_2\right]\right)$ with ${\mathcal{P}}_2\left(t;m\right)$ in the proof of Theorem 2 in [40]. □

Remark 4.

From the previous lemma, we notice in Theorem 2 that condition (7) is an extra condition and is satisfied from hypothesis (i) in Lemma 7.

Notation 3.

For convenience, we define the function for any positive integer m,

$${\widehat{\mathcal{P}}}_2\left(t;m\right):=\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{1}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-\frac{{\eta }_2\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)}{{\eta }_2\left({\tau }^{\left[2r\right]}\left(t\right)\right)}\right]\frac{{\eta }_2^{{\kappa }_n}\left({\tau }^{\left[2r\right]}\left(t\right)\right)}{{\eta }_2^{{\kappa }_n}\left(t\right)},$$

where ${\kappa }_n$ defined as in Lemma 7.

Lemma 8.

Suppose that hypotheses (i)–(iii) in Lemma 7 are satisfied. If x belongs to ${\mathcal{S}}_3$, then

(A2-7) 

$x\left(t\right)>{\widehat{\mathcal{P}}}_2\left(t;m\right)z\left(t\right)$.

Proof. 

As in the proof of Lemma 6, we arrive at (15). From (A2-5), we conclude that

$$z\left({\tau }^{\left[2r\right]}\left(t\right)\right)\ge \frac{{\eta }_2^{{\kappa }_n}\left({\tau }^{\left[2r\right]}\left(t\right)\right)}{{\eta }_2^{{\kappa }_n}\left(t\right)}z\left(t\right),$$

which with (15), gives

$$x\left(t\right)>z\left(t\right)\sum _{r=0}^m\left(\prod _{l=0}^{2r}\rho \left({\tau }^{\left[l\right]}\left(t\right)\right)\right)\left[\frac{1}{\rho \left({\tau }^{\left[2r\right]}\left(t\right)\right)}-\frac{{\eta }_2\left({\tau }^{\left[2r+1\right]}\left(t\right)\right)}{{\eta }_2\left({\tau }^{\left[2r\right]}\left(t\right)\right)}\right]\frac{{\eta }_2^{{\kappa }_n}\left({\tau }^{\left[2r\right]}\left(t\right)\right)}{{\eta }_2^{{\kappa }_n}\left(t\right)}.$$

Therefore, the proof ends. □

Theorem 5.

Suppose that hypotheses (i)–(iii) in Lemma 7 are satisfied. If

$$\underset{t\to \infty }{liminf}{\int }_{\sigma \left(t\right)}^{t}q\left(u\right){\eta }_2\left(u\right){\widehat{\mathcal{P}}}_2\left(\sigma \left(u\right);m\right)\mathrm{d}u>\frac{\left(1-{\kappa }_n\right)}{\mathrm{e}},$$

(18)

then ${\mathcal{S}}_3=\varnothing$.

Proof. 

This theorem is obtained directly by replacing the function $\left(1-\rho \left[\left({\eta }_2\circ \tau \right)/{\eta }_2\right]\right)$ with ${\widehat{\mathcal{P}}}_2\left(t;m\right)$ in Theorem 3 in [40]. □

Example 2.

Consider the neutral DDE

$${\left({\mathrm{e}}^t{\left[x\left(t\right)+{\rho }_{0}x\left(t-{\tau }_0\right)\right]}^{‴}\right)}^{\prime }+q_0{\mathrm{e}}^{t}x\left(t-{\sigma }_0\right)=0,$$

(19)

where ${\tau }_0,$${\rho }_0,$${\sigma }_0$, and $q_0$ are positive and ${\rho }_0<{\mathrm{e}}^{-{\tau }_0}$. We note that ${\eta }_i\left(t\right)={\mathrm{e}}^{-t}$ and ${\tau }^{\left[i\right]}\left(t\right)$ = $t-i{\tau }_0$. Then,

$${\mathcal{P}}_2\left(t;m\right)=\left[\frac{1}{{\rho }_0}-{\mathrm{e}}^{{\tau }_0}\right]\sum _{r=0}^m{\rho }_0^{2r+1}:={\mathcal{P}}_0$$

and

$${\widehat{\mathcal{P}}}_2\left(\sigma \left(t\right);m\right)=\left[\frac{1}{{\rho }_0}-{\mathrm{e}}^{{\tau }_0}\right]\sum _{r=0}^m{\rho }_0^{2r+1}{e}^{2r{\kappa }_n{\tau }_0}={\widehat{\mathcal{P}}}_0.$$

If we choose ${\kappa }_0=q_0{\mathcal{P}}_0$ and $\ell ={\mathrm{e}}^{{\sigma }_0}$, then (i) and (ii) in Lemma 7 are satisfied, where

$${\kappa }_i:=\frac{q_0{\mathcal{P}}_0{\mathrm{e}}^{{\sigma }_0{\kappa }_{i-1}}}{1-{\kappa }_{i-1}}, for i=1,2,\cdots ,n.$$

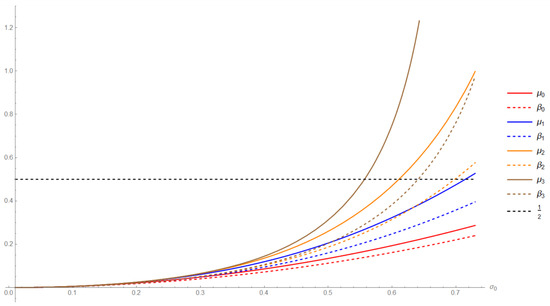
Condition (18) reduces to

$$q_0{\widehat{\mathcal{P}}}_0>\frac{\left(1-{\kappa }_n\right)}{\mathrm{e}{\sigma }_0}.$$

(20)

Thus, Theorem 4 confirms that ${\mathcal{S}}_3=\varnothing$, if (20) holds, for some $n\ge 0$.

Remark 5.

Considering the following special case of (19):

$${\left({\mathrm{e}}^t{\left[x\left(t\right)+\frac{1}{3}x\left(t-1\right)\right]}^{‴}\right)}^{\prime }+q_0{\mathrm{e}}^{t}x\left(t-{\sigma }_0\right)=0.$$

Theorem 4 confirms that ${\mathcal{S}}_3=\varnothing$ if

$$q_0\left[3-\mathrm{e}\right]\sum _{r=0}^m{\left(\frac{1}{3}\right)}^{2r+1}{e}^{2r{\kappa }_n}>\frac{\left(1-{\kappa }_n\right)}{\mathrm{e}{\sigma }_0},$$

(21)

where

$${\kappa }_0=0.10564q_0, {\kappa }_i=0.10564q_0\frac{{\mathrm{e}}^{{\sigma }_0{\kappa }_{i-1}}}{1-{\kappa }_{i-1}}, for i=1,2,\cdots ,n.$$

On the other hand, Theorem 2 confirms that ${\mathcal{S}}_3=\varnothing$ if

$$q_0\left(1-\frac{\mathrm{e}}{3}\right)>\frac{\left(1-{\alpha }_m\right)}{\mathrm{e}{\sigma }_0},$$

(22)

where

$${\alpha }_0=q_0\left(1-\frac{\mathrm{e}}{3}\right), {\alpha }_i=q_0\left(1-\frac{\mathrm{e}}{3}\right)\frac{{\mathrm{e}}^{{\sigma }_0{\alpha }_{i-1}}}{1-{\alpha }_{i-1}}, for i=1,2,\cdots ,n.$$

Figure 3 shows the difference between conditions (21) and (22) for $n=0,1,2.$ For example, at ${\sigma }_0=0.5$ and $n=0$, conditions (21) and (22) reduce to $q_0>3.6543$ and $q_0>4.5139,$ respectively.

Remark 6.

By using the new relationship between the solution and the corresponding function (A2-7), we can re-improve the monotonic property (A2-5) and then conduct another improvement for the condition (18), and this procedure can be repeated to obtain better approximations.

3. Oscillation Conditions

In this section, we use the results of the previous section to obtain new conditions for checking the oscillation of all solutions of (1).

Lemma 9.

Suppose that the DDE

$$\underset{t\to \infty }{liminf}{\int }_{\sigma \left(t\right)}^{t}q\left(u\right)\left(1-\rho \left(\sigma \left(u\right)\right)\right)\frac{{\sigma }^3\left(u\right)}{b\left(\sigma \left(u\right)\right)}\mathrm{d}u>\frac{6}{\mathrm{e}}$$

(23)

is oscillatory for some $ϵ\in \left(0,1\right)$. Then, ${\mathcal{S}}_1=\varnothing$.

Proof. 

Assume the contrary that $x\in {\mathcal{S}}_1$. In view of Theorem 2.1 in [46], the DDE

$$w^{\prime }\left(t\right)+ϵ\frac{{\sigma }^3\left(t\right)}{6b\left(\sigma \left(t\right)\right)}q\left(t\right)\left(1-\rho \left(\sigma \left(t\right)\right)\right)w\left(\sigma \left(t\right)\right)=0$$

(24)

has a positive solution, for all $ϵ\in \left(0,1\right)$. However, condition (23) ensures that DDE (24) oscillates, which is a contradiction. Therefore, the proof ends. □

Now, we have conditions that exclude all cases of positive solutions $\left({\mathbf{L}}_1\right)$–$\left({\mathbf{L}}_3\right)$. Combining these conditions, as in the following theorem, we can obtain conditions for oscillation.

Theorem 6.

All solutions of Equation (1) are oscillatory if all of the following conditions are satisfied:

(c${}_1$)

hypotheses (i)–(iii) in Theorem 3 and (11),

(c${}_2$)

hypotheses (i)–(iii) in Lemma 7 and (18),

(c${}_3$)

condition (23).

Example 3.

Consider the neutral DDE (19). It is easy to verify that conditions (11) and (23) are satisfied. In view of Theorem 6, all solutions of equation (19) are oscillatory if (21) holds for some $n\ge 0$.

4. Conclusions

In this study, we investigated the monotonic properties and oscillatory behavior of a class of functional differential equations of the neutral type. We presented a number of improved relationships that link the solution and its corresponding function in two of the three cases of the positive solutions of the studied equation. We then used these relationships to obtain conditions confirming that there are no solutions in Categories ${\mathcal{S}}_2$ and ${\mathcal{S}}_3$. Through comparisons and examples, we clarified that the new relationships contributed to the improvement of conditions that ensure that ${\mathcal{S}}_2$ and ${\mathcal{S}}_3$ are empty sets. Finally, we established a new condition to check the oscillation of Equation (1). It will be interesting, as a future proposal, to extend the results to half-linear higher order neutral DDEs.