A Novel Fractional-Order RothC Model
Abstract
1. Introduction
2. The Novel Fractional-Order Continuous RothC Model
2.1. Existence, Uniqueness, Positively Invariant Set, Equilibria
2.2. Analytic Solution
2.3. Soil Organic Carbon Content
3. Discretizations of the Fractional-Order Model
3.1. Stability Analysis of the Numerical Scheme
3.2. Convergence Testing on a Constructed Analytical Solution
4. Real-World Applications
4.1. The Case of “Hoosfield Spring Barley”
4.2. Solution Scheme Comparison
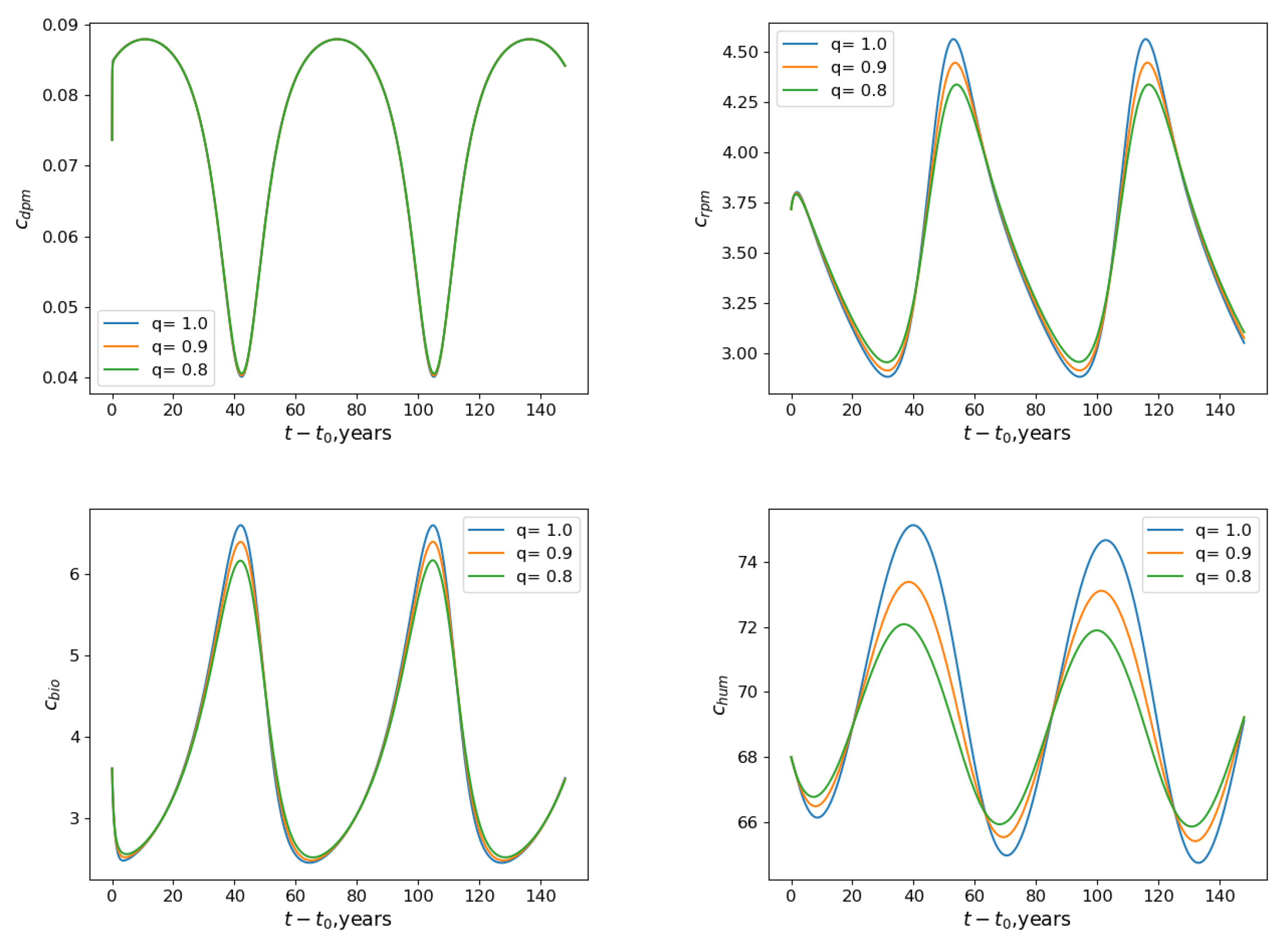
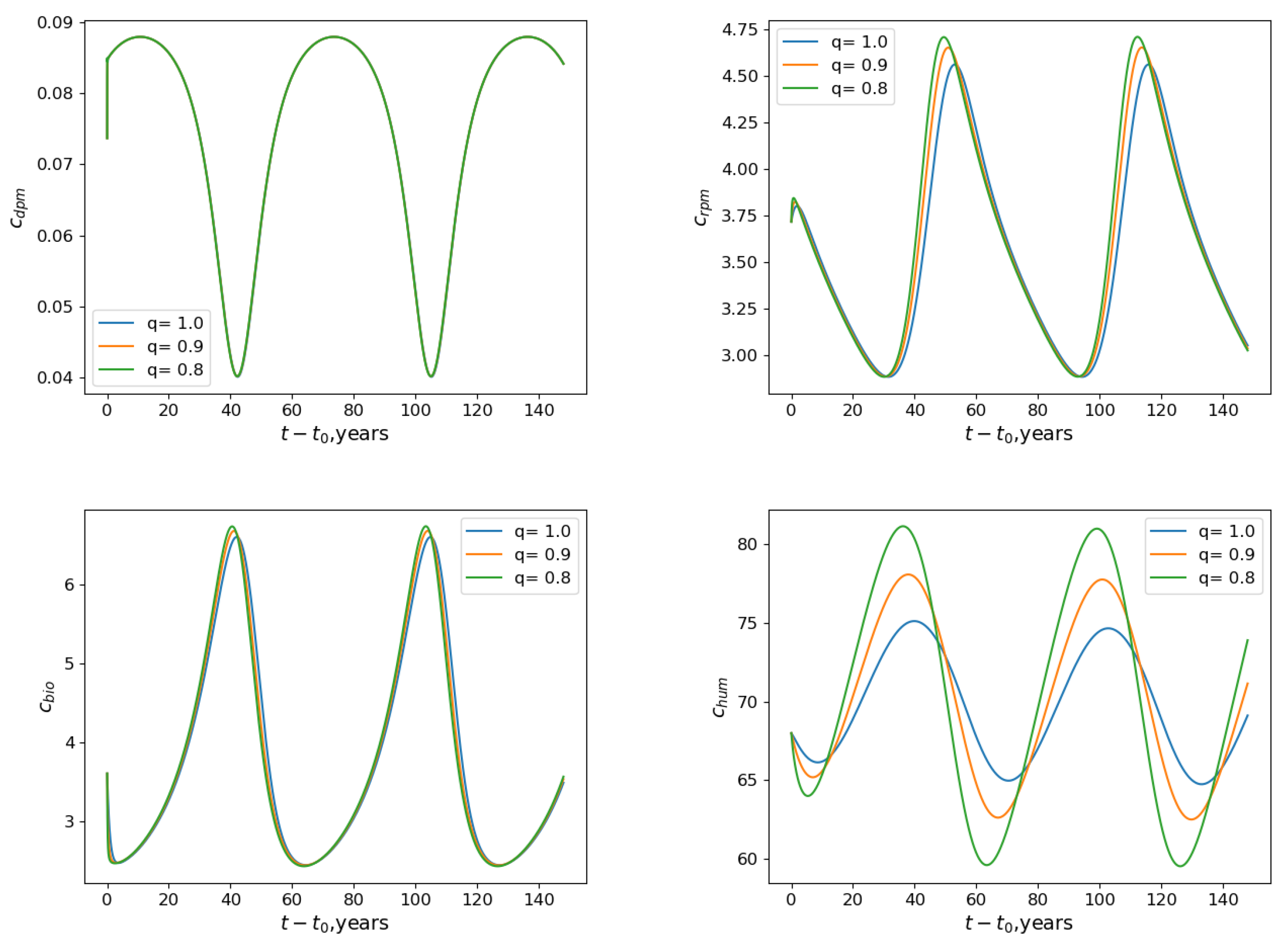
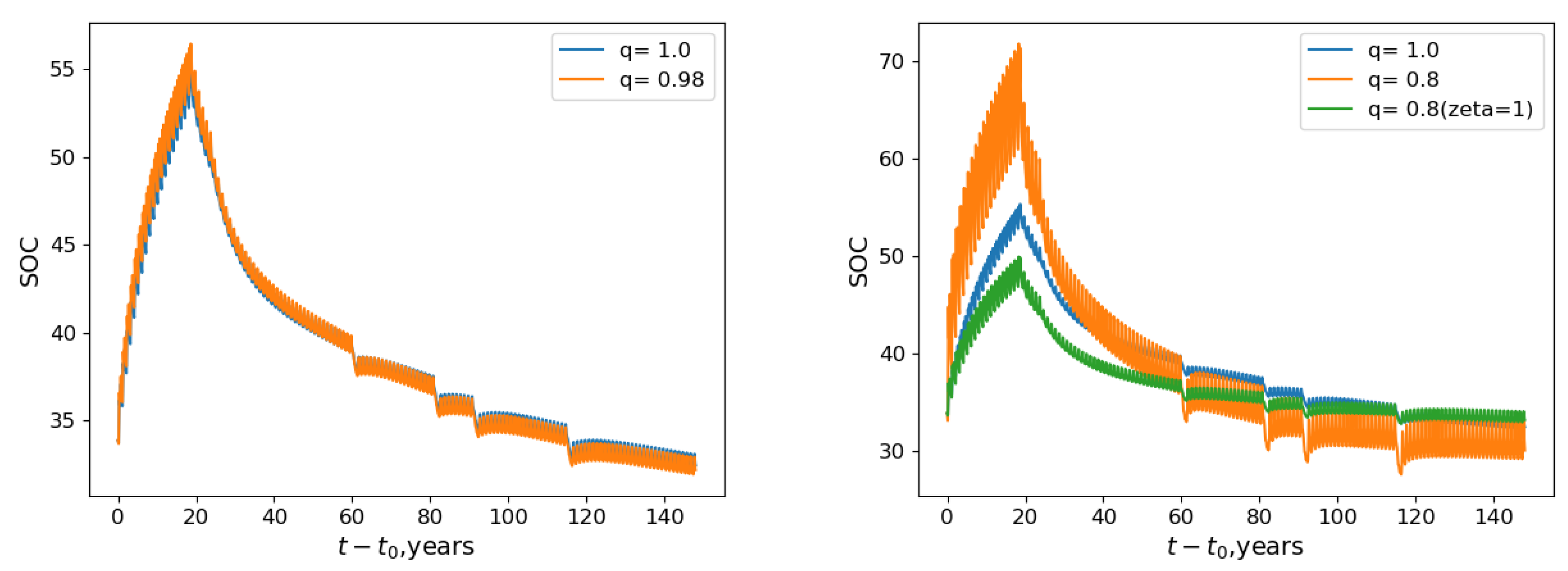
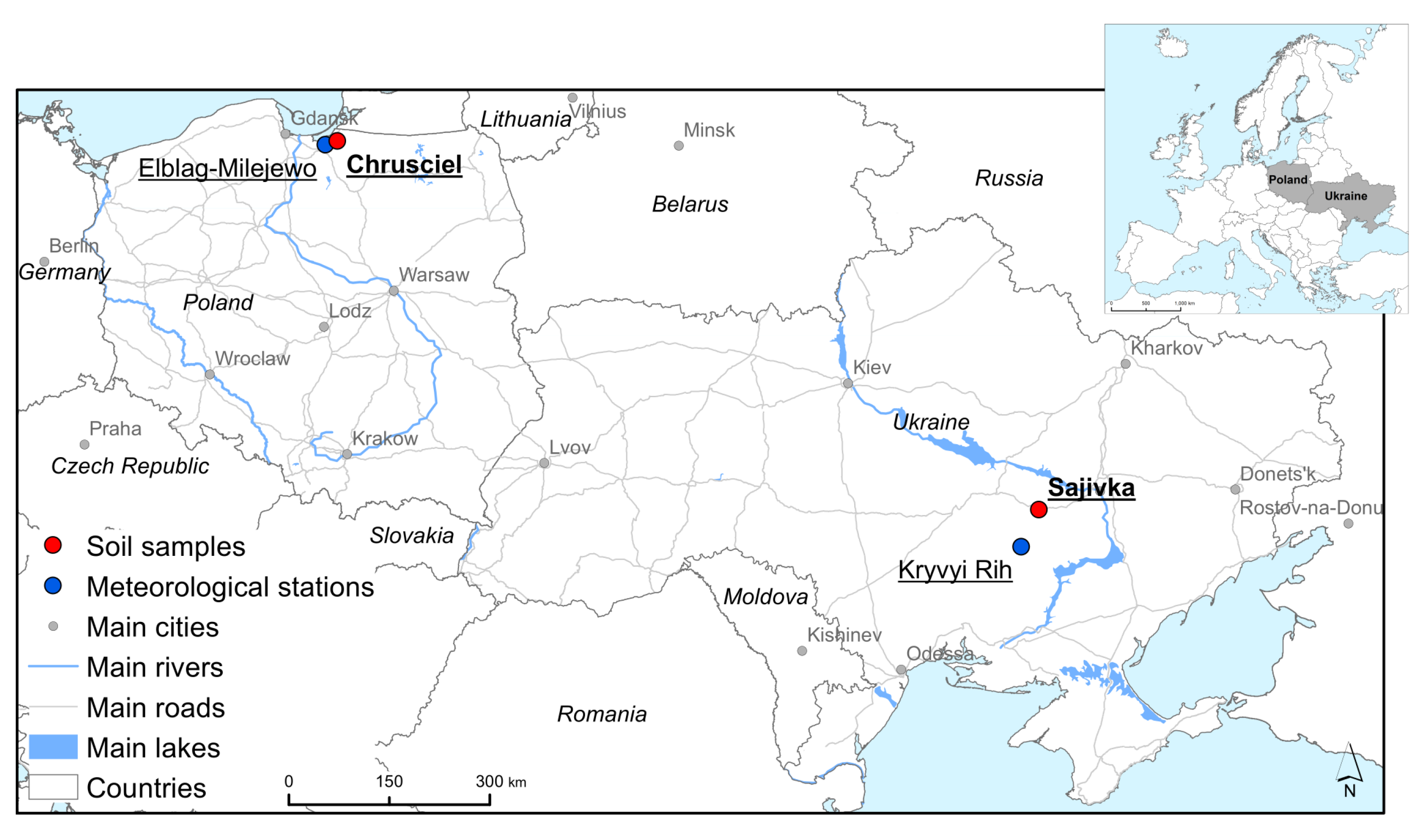
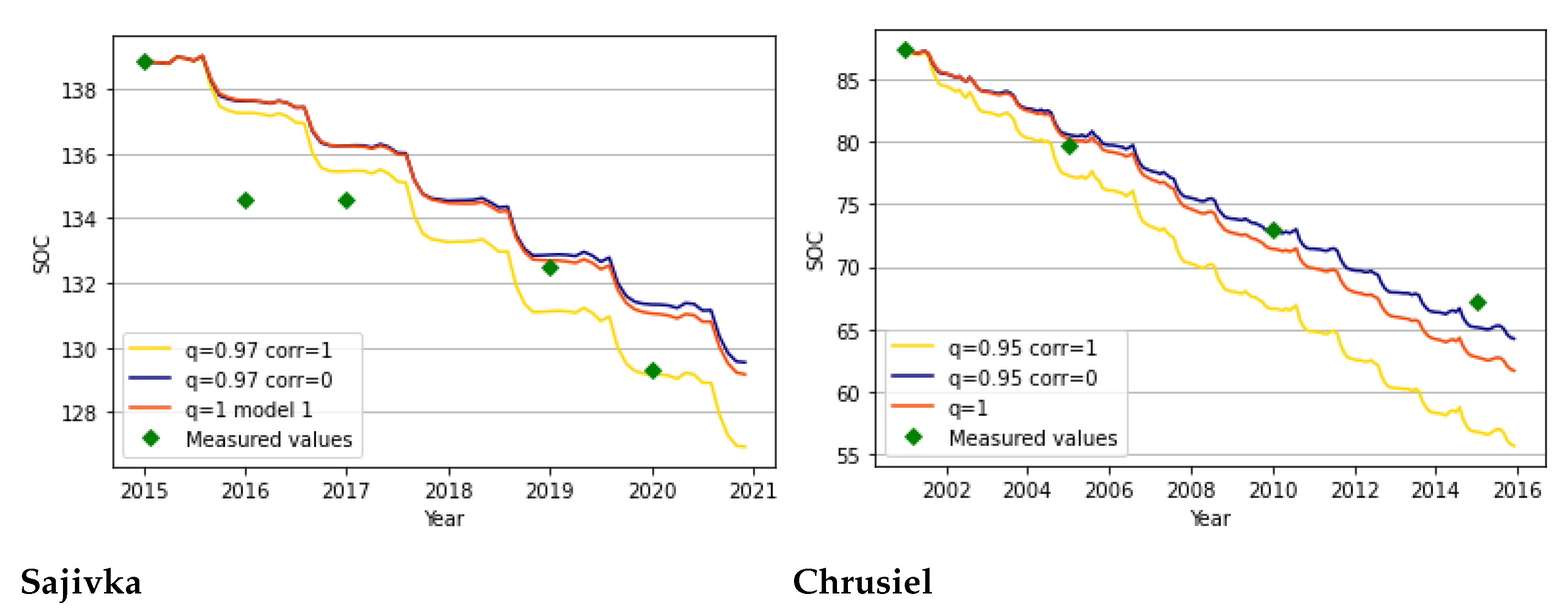
4.3. Ukrainian and Polish Scenarios
4.4. Ukrainian and Polish Numerical Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diele, F.; Luiso, I.; Marangi, C.; Martiradonna, A. SOC-reactivity analysis for a newly defined class of two-dimensional soil organic carbon dynamics. Appl. Math. Model. 2023, 118, 1–21. [Google Scholar] [CrossRef]
- Coleman, K.; Jenkinson, D.; Crocker, G.; Grace, P.; Klir, J.; Körschens, M.; Poulton, P.; Richter, D. Simulating trends in soil organic carbon in long-term experiments using RothC-26.3. Geoderma 1997, 81, 29–44. [Google Scholar] [CrossRef]
- Coleman, K.; Jenkinson, D.S. ROTHC-26.3: A Model for the Turnover of Carbon in Soil: Model Description and Users Guide: K. Coleman and DS Jenkinson; IACR: Santa Barbara, CA, USA, 1995. [Google Scholar]
- Diele, F.; Luiso, I.; Marangi, C.; Martiradonna, A.; Woźniak, E. Evaluating the impact of increasing temperatures on changes in Soil Organic Carbon stocks: Sensitivity analysis and non-standard discrete approximation. Comput. Geosci. 2022, 26, 1345–1366. [Google Scholar] [CrossRef]
- Marangi, C.; Diele, F.; Luiso, I.; Martiradonna, A.; Wozniak, E. SOC indicator of land-degradation: Responses of continuous and non-standard discrete RothC models to environmental changes. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22-5894. [Google Scholar]
- Diele, F.; Marangi, C.; Martiradonna, A. Non-standard discrete RothC models for soil carbon dynamics. Axioms 2021, 10, 56. [Google Scholar] [CrossRef]
- Parshotam, A. The Rothamsted soil-carbon turnover model—Discrete to continuous form. Ecol. Model. 1996, 86, 283–289. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Timlin, D. Water transport in soils as in fractal media. J. Hydrol. 1998, 204, 98–107. [Google Scholar] [CrossRef]
- Kong, B.; Dai, C.X.; Hu, H.; Xia, J.; He, S.H. The Fractal Characteristics of Soft Soil under Cyclic Loading Based on SEM. Fractal Fract. 2022, 6, 423. [Google Scholar] [CrossRef]
- Singh, A.; Das, S.; Ong, S. Study and analysis of nonlinear (2+1)-dimensional solute transport equation in porous media. Math. Comput. Simul. 2022, 192, 491–500. [Google Scholar] [CrossRef]
- Priya, P.; Sabarmathi, A. Caputo Fractal Fractional Order Derivative of Soil Pollution Model Due to Industrial and Agrochemical. Int. J. Appl. Comput. Math 2022, 8, 250. [Google Scholar] [CrossRef]
- Tanriverdi, T.; Baskonus, H.M.; Mahmud, A.A.; Muhamad, K.A. Explicit solution of fractional order atmosphere-soil-land plant carbon cycle system. Ecol. Complex. 2021, 48, 100966. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Ahmed, N.; Ali Shah, N. A generalized kinetic model of the advection-dispersion process in a sorbing medium. Math. Model. Nat. Phenom. 2021, 16, 39. [Google Scholar] [CrossRef]
- Krasnoschok, M.; Pereverzyev, S.; Siryk, S.; Vasylyeva, N. Determination of the fractional order in quasilinear subdiffusion equations. Fract. Calc. Appl. Anal. 2020, 23, 695–722. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: New York, NY, USA, 1993. [Google Scholar]
- Wheatcraft, S.; Meerschaert, M. Fractional conservation of mass. Adv. Water Resour. 2008, 31, 1377–1381. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.; Miranda-Hernandez, M.; Lopez-Lopez, M.; Alvarado-Martinez, V.; Baleanu, D. Modeling and simulation of the fractional space-time diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 115–127. [Google Scholar] [CrossRef]
- Wei, L. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar]
- Matychyn, I. Analytical Solution of Linear Fractional Systems with Variable Coefficients Involving Riemann–Liouville and Caputo Derivatives. Symmetry 2019, 11, 1366. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Computing the matrix Mittag-Leffler function with applications to fractional calculus. J. Sci. Comput. 2018, 77, 129–153. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. The Finite Difference Methods for Fractional Ordinary Differential Equations. Numer. Funct. Anal. Optim. 2013, 34, 149–179. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G. Exponentially accurate spectral and spectral element methods for fractional ODEs. J. Comput. Phys. 2014, 257, 460–480. [Google Scholar] [CrossRef]
- Langlands, T.; Henry, B. The accuracy and stability of an implicit solution method for the fractional diffusion equation. J. Comput. Phys. 2005, 205, 719–736. [Google Scholar] [CrossRef]
- Hundsdorfer, W. Unconditional convergence of some Crank-Nicolson LOD methods for initial-boundary value problems. Math. Comput. 1992, 58, 35–53. [Google Scholar]
- Rothamsted Experimental Station, Great Britain. Rothamsted: Guide to the Classical Field Experiments; AFRC Institute of Arable Crops Research: Harpenden, UK, 1991. [Google Scholar]
- Di Bene, C.; Marchetti, A.; Francaviglia, R.; Farina, R. Soil organic carbon dynamics in typical durum wheat-based crop rotations of Southern Italy. Ital. J. Agron. 2016, 11, 209–216. [Google Scholar] [CrossRef]
- Martens, B.; Miralles, D.; Lievens, H.; van der Schalie, R.; de Jeu, R.; Fernández-Prieto, D.; Beck, H.; Dorigo, W.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Wieder, W.R.; Allison, S.D.; Davidson, E.A.; Georgiou, K.; Hararuk, O.; He, Y.; Hopkins, F.; Luo, Y.; Smith, M.J.; Sulman, B.; et al. Explicitly representing soil microbial processes in Earth system models. Glob. Biogeochem. Cycles 2015, 29, 1782–1800. [Google Scholar] [CrossRef]
| h | 0.8 | 0.6 | 0.4 | 0.2 | 0.01 | |
|---|---|---|---|---|---|---|
| 0.08 | 0.00127 | 0.000717 | 0.000577 | 0.000413 | 0.000266 | 0.000176 |
| 0.04 | 0.000634 | 0.000356 | 0.000288 | 0.000206 | 0.000133 | |
| 0.02 | 0.000315 | 0.000177 | 0.000144 | 0.000103 | ||
| 0.01 | 0.000157 |
| Months | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Crop years | 0.3561 | 0.3723 | 0.5068 | 0.4471 | 0.7473 | 0.7779 | 0.2491 | 0.4151 | 0.6570 | 1.1277 | 0.6092 | 0.4594 |
Fallow years | 0.3561 | 0.3723 | 0.5068 | 0.7451 | 1.2454 | 1.2965 | 0.4151 | 0.4151 | 0.6570 | 1.1277 | 0.6092 | 0.4594 |
| Scenario | Integer-Order Model | Fractional-Order Model () | |
|---|---|---|---|
| 1 | 6.84 | 7.26 | 6.98 |
| 2 | 95.32 | 159 | 76.97 |
| 3 | 185 | 192 | 197 |
| Comparison between | SOC | DRM | DPM | BIO | HUM | Time, s | |
|---|---|---|---|---|---|---|---|
| C-N(1) | S | 1.98 | 211.87 | 7.68 | 5.09 | 0.16 | 0.23 |
| C-N(1) | NS | 2.04 | 229.89 | 7.71 | 5.66 | 0.17 | |
| S | NS | 0.18 | 25.97 | 0.44 | 1.11 | 0.02 | 0.37 |
| NS | 0.37 | ||||||
| F(1) () | NS | 2.06 | 211.19 | 7.81 | 5.14 | 0.76 | 4.9 |
| F(1) () | NS | 8.17 | 232.49 | 18.22 | 16.97 | 7.66 | |
| Point | Clay Content, % | Humified Layer Depth, cm | Mean Temperature, °C | Initial SOC, | |
|---|---|---|---|---|---|
| Sajivka | 55.0 | 40 | 10.57 | 1.6296 | 138.8 |
| Chrusciel | 11.83 | 30 | 8.46 | 1.11616 | 87.36 |
| Sajivka | Chrusiel | |||||
|---|---|---|---|---|---|---|
| , | , | , | , | |||
| EF | 0.851173 | 0.798365 | 0.808609 | 0.836487 | 0.922287 | 0.900954 |
| RMSE | 1.201889 | 1.398968 | 1.362967 | 3.044274 | 2.098715 | 2.369329 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bohaienko, V.; Diele, F.; Marangi, C.; Tamborrino, C.; Aleksandrowicz, S.; Woźniak, E. A Novel Fractional-Order RothC Model. Mathematics 2023, 11, 1677. https://doi.org/10.3390/math11071677
Bohaienko V, Diele F, Marangi C, Tamborrino C, Aleksandrowicz S, Woźniak E. A Novel Fractional-Order RothC Model. Mathematics. 2023; 11(7):1677. https://doi.org/10.3390/math11071677
Chicago/Turabian StyleBohaienko, Vsevolod, Fasma Diele, Carmela Marangi, Cristiano Tamborrino, Sebastian Aleksandrowicz, and Edyta Woźniak. 2023. "A Novel Fractional-Order RothC Model" Mathematics 11, no. 7: 1677. https://doi.org/10.3390/math11071677
APA StyleBohaienko, V., Diele, F., Marangi, C., Tamborrino, C., Aleksandrowicz, S., & Woźniak, E. (2023). A Novel Fractional-Order RothC Model. Mathematics, 11(7), 1677. https://doi.org/10.3390/math11071677






