Abstract
The explanation of risk contagion among economic players—not only in financial crises—and how they spread across the world has fascinated scholars and scientists in the last few decades. Inspired by the literature dealing with the analogy between financial systems and ecosystems, we model risk contagion by revisiting the mathematical approach of epidemiological models for infectious disease spread in a new paradigm. We propose a time delay differential system describing risk diffusion among companies inside an economic sector by means of a SIR dynamics. Contagion is modelled in terms of credit and financial risks with low and high levels. A complete theoretical analysis of the problem is carried out: well-posedness and solution positivity are proven. The existence of a risk-free steady state together with an endemic equilibrium is verified. Global asymptotic stability is investigated for both equilibria by the classical Lyapunov functional theory. The model is tested on a case study of some companies operating in the food economic sector in a specific Italian region. The analysis allows for understanding the crucial role of both incubation time and financial immunity period in the asymptotic behaviour of any solution in terms of endemic permanence of risk rather than its disappearance.
Keywords:
financial distress; financial immunity; bankruptcy; outbreak; SIR model; delay differential equation MSC:
91B05; 91B55; 34K05
1. Introduction
Understanding how financial and bank crises spread across the world has fascinated not only scholars and scientists, but also journalists and movie makers. In the musical fantasy “Mary Poppins”, directed by Robert Stevenson in 1964, when a fiduciary in a bank crashes, the bank closes its doors. As soon as the rumour spreads in Edwardian London, large groups of depositors rush to the door and ask for their money, but the bank door remains closed in an epic depiction of a banking crisis. According to [1], before 1997 the word “contagion” (which in “Mary Poppins” is represented by the well-known “bank run” that spreads by word of mouth) almost always referred to the spread of a biological disease. In July 1997, the currency crisis in Thailand overwhelmed first East Asia and then Russia and Brazil. By “infecting” various economies around the world like a spreading outbreak, the currency crisis caused the collapse of Long-Term Capital Management (LTCM), which was a U.S. hedge fund. Analogies between financial crises and the spread of a medical disease such as COVID-19 are often exaggerated, but this comparison can be used at several levels. In our paper, we consider contagion not only in terms of disease, but also as a transmission mechanism in a broad concept. In this respect, financial literature ranges from the importance of trade or the real linkages to investor behaviour or fear in financial markets when transmission mechanisms are considered. The linkage between financial systems and ecosystems has been pointed out by [2]. In [3], the authors apply the classical susceptible–infected–recovered (SIR) epidemic model to countries across the world by using ownership companies’ data. Financial distress spreads through networks as an epidemic outbreak and scholars evaluate the risk of transmission of the so-called default propagation. The scheme of risk propagation follows the topology of networks among banks, companies, and other economic actors. For example, many SMEs are not independent entities in terms of financial stability or distress, and often are interrelated in terms of financial flows in bidirectional ways; then, the default of one company could damage other SMEs and companies in their own supply chain (see [4]). This contagion scheme differs from that which started with the Lehman Brothers default (see [5]), but also from what happened to the European countries with the Greek sovereign crisis in 2009 (see [6]). In a wide definition of contagion, the spillover effect on financial markets could capture the contamination effects between markets and people’s attention to issues. Actually, these phenomena are checked in financial literature especially for nonfungible tokens, cryptocurrencies and for the so-called fintech sector (see [7]).
1.1. Contagion Risk in the Financial Sector
In the financial literature, contagion plays a key role in the so-called “systemic risk”, in which both endogenous and exogenous events could determine a large cascade of crises (see [8]). Starting from an outbreak with a domino effect, if a bank (or other financial intermediaries) moves toward a crisis or precrisis state, this could also cause a crisis or precrisis conditions for 50 other banks. Financial network interdependencies, such as the interbank market, are one of the most important determinants of default propagation (cfr. [9]), and are considered as a mechanism of contagion transmission. By using a probabilistic model, nodes, and Monte Carlo simulation, in [10], the authors study the default contagion risk in the Russian interbank market. The use of network analysis in economic analysis has a long history, according to [11], but it can also be used to explain financial crises. For the banking sector, Ref. [12] estimates the probability of systemic risk associated with a bank default in the interbank market, when this one is in an equilibrium status.
Financial networks are also analysed, among other things, by [13], which suggests that the interplay of network topology, capital requirements, and market liquidity are three important factors that could affect systemic risks. Under liquid risk perspective, the author in [14] outlines a model in which financial crisis propagation goes through illiquid assets and fire sales. Moreover, by accounting for the management effect, Ref. [15] considers other networks: the board and director networks, price correlations, and stock ownership. A sort of spillover effect is used in [16], in which the authors propose a model to study the contagion jump process in different regions by studying the equity market and focusing their findings on the stock price propagation mechanism. At the operative level, the investigation in [17] exploits quarterly client’s data from BBVA (i.e., a Spanish Bank) in order to study customer–supplier chain transactions. The authors consider a susceptible–infected–susceptible (SIS) model to evaluate the patterns that are similar to the ones used in a spreading epidemic. Starting from catastrophic events, Ref. [18] evaluates the effects on non-life insurance by using balance sheet analysis. Default contagion and default degree in capital chain are studied with the Copula metric for listed Chinese companies by [19]. Among the measures that can be applied by policy makers to contain the contagion effect on financial markets for banks, there is the short-selling ban for stocks and other financial instruments ( see [20]).
In the end, financial crises are boosted by psychological factors (see [21]), not only in their buildings but also in their spread in markets, instruments, and among economic players. For example, during the COVID-19 period, virus diffusion raised fear and uncertainty in the market (cfr. [22]). Generally, under more uncertain scenarios, the behaviours of financial players are characterized by: (i) actions more sensitive to investment losses than gains (cfr. [23]); (ii) players triggering risks, and emotional or sentimental behavior that drives decisions (cfr. [24]); and (iii) mostly damaging investment decisions (cfr. [25]).
1.2. Supply Chain Finance and Other Transmission Channels
The so-called spillover effects are measured not only on the financial market, when the correlation between indices and stocks is analysed, but also between firms. Among other contributions, Ref. [26] exploits event study methodologies to understand the stock reactions to disruption in the automobile industry supply chain, and it measures the contagion effect of the reduction of stock prices. The financial distress of a company caused by customer–supply chain relations is analysed by [27] from 1980 to 2014. The author finds that financial distress transfers from major customer firms to supplier firms, and the interfirm effect is persistent for up to two years. In [28], a credit default swap is used to evaluate credit shocks in the supply chain. Spatial analysis of the proximity effects of both financial distress and failure is considered in [29]. Local factors as determinants of default of a company also emerge in [30,31,32]. Starting from commonalities in banks’ balance sheets, Ref. [33] analyses China’s banking system by considering the vulnerability of each bank according to some channels of transmissions and complex relations among financial players.
1.3. Credit Channel Contagion
According to [34], there is another contagion mechanism through credit deterioration channels, in which the credit deterioration of a company could also deteriorate credit in other counterparties. The authors of [35] consider intraindustry bankruptcy and evaluate the consequences of distress both for customers and suppliers. They capture financial wealth effects on stock price reactions to distress and failures.
Furthermore, Ref. [36] analyses the default dependencies in a multisectoral framework starting from 1996 and evaluating the dot-com bubble and the global financial crisis (until 2015). The authors argue that the contagion effect between sectors manifests in two ways: (i) the “infectivity”, or the degree of transmission of default among sectors; and (ii) the “vulnerability” of each sector.
Moreover, Ref. [4] examines a dual-channel financing model in supply chain finance characterised by loans from the bank and trade credit from the manufacturer. In this paper, the credit risk is considered as a contagion channel from the supply chain perspective for small and medium enterprises (SMEs). Then, Ref. [37] studies the contagion effects of UK small business failures and finds that the geographical location and the industry group are significant.
In addition, the model in [38] considers analogies between medical disease and credit risk contagion. It describes a nonlinear dynamics in the SIR framework and accounts for the transitory immunity time lag before a bank becomes defaultable. Under another perspective, the authors in [39] study a contagion mechanism of associated credit risk with corporate senior executives’ alertness; they exploit the SIR approach to construct the interaction model between the corporate senior executive alertness and the associated credit risk contagion in the network.
1.4. Our Contribution
Inspired by the results provided in the previous literature, we describe risk contagion among companies in a given economic sector in the framework of SIR dynamics. Actually, we provide an ordinary differential system describing the evolution of contagion in terms of low- and high-level risk. Firms with lower risk are susceptible to be infected by other firms with extremely high risk. Among the infected ones, some enterprises get the capability of risk control (such as credit risk), so that they can keep their risk at a low level and are no longer infectious; in other words, these companies can be considered as recovered and get a temporary financial immunity ability after curing. They remain in a kind of recovery pool during the financial immunity period, which represents a time delay under the mathematical point of view.
Although SIR models are not a novelty, the paradigm is new and its application is worthy of attention. Actually, the time delay differential system we study is an original problem for modelling risk diffusion among firms in a sector. The phenomenon of contagion is modelled by a Holling Type II functional response. This kind of modelling originates in the framework of mathematical ecology. For instance, Holling’s response functions represent not only a very common tool for describing predator–prey dynamics (see [40,41,42]) but also for modelling the removal of invasive species from a given ecosystem (see [43,44,45,46]). As another example, these functions are involved in the analysis of epidemic behaviour described by dynamical models for disease transmission (see [47]). More recently, they have been introduced in financial models for modeling risk contagion among agents (see [48]). In this respect, we employ a Holling Type II response as a function of susceptible firms, which are interpreted as prey species; therefore, this term represents the reproduction rate of high-risk firms as a function of low-risk firms. As an original issue, this choice allows us to account for an incubation time that is implicitly involved in the contagion response function. We point out that this time is different from the immunity period after curing, but it corresponds to the so-called “handling time”, which represents the average time spent by high-risk enterprises on processing a low-risk item for contagion. On the other hand, immunity period is crucial when the recovered or restructured class of enterprises is modelled. In the model we propose, at any temporal step the recovered firm density is evaluated by integrating a given portion of high-risk companies during the previous immunity period. Then, we assume that a part of the firms recovered in the pool during the immunity period leaves the economic sector, whereas the remaining part again reverts to the class of firms that are susceptible of infection. As we point out in our discussion, both incubation time and immunity period play an important role in the long-run dynamics described by the model at stationary state.
The mathematical time-delayed model is described in detail in Section 2. In particular, a complete theoretical analysis is carried out concerning the differential problem’s well-posedness, based on the main results of delay differential equation theory (see [49,50]). Furthermore, as the variables at hand describes the evolution of firm populations, then it is crucial to prove that they remain positive for any time when they start from positive initial data. In this respect, the feature that solutions get positive values is proven in Section 2.1. In addition, we prove the existence of two equilibrium points in Section 2.2. The first equilibrium corresponds to a free-risk trivial steady state; on the other hand, the second equilibrium is nontrivial and represents an endemic state.
In Section 3, a complete analysis is performed regarding the global and local asymptotic stability of both steady states. Actually, in Section 3.1, we deal with the stability of the trivial equilibrium to understand whether default risk can be eliminated from the economic sector; on the other hand, the stability analysis is carried out in Section 3.2 for the nontrivial equilibrium, and some sufficient conditions are provided for assuring that risk will endemically continue to exist in the economy. The crucial role of both incubation and financial immunity periods is discussed in Section 3.3.
The model is validated in Section 4, in which some numerical simulations are performed on a sample of food industries operating in the economic sector of the Emilia Romagna region located in the northern part of Italy. This simulation is original and suggests some policy actions. A brief description of the sequence of commands involved in the numerical code are described in the Appendix A in order to let the reader be able to reproduce the results in MATLAB environment. Finally, our conclusions are drawn in Section 5.
We conclude by remarking that we are interested in the interconnection of companies in a general economic sector, and we focus on how financial distress of some firms could affect other companies, mostly via counterpart or credit risk. In our numerical simulation, we note that psychological factors are less important than those of both financial markets and financial players. These aspects could be captured by some parameters of the model, such as the attack rate involved in the contagion term.
2. Time-Delayed Dynamics
A nonlinear dynamical model consisting of a time delay differential system describes the risk contagion for any time . The problem is formulated from a SIR perspective; indeed, the economic sector consists of associated firms which are divided into three categories, as follows.
- Susceptible firms: This refers to some entities with lower risk that are vulnerable to infection by other firms with high risk, and therefore the possibility of becoming a high risk firm increase;
- Infected firms: This refers to firms which are infectious, whose risk is extremely high and who can infect other firms;
- Recovered firms: This refers to firms with the capability of risk control after infection, and which can keep their risk at a low level and be not infectious.
We denote by the density of susceptible firms at time t, i.e., the ratio between the total number of susceptible firms at time t and the initial level . In the same way, we denote by and the densities of infected and recovered firms, respectively, at time t. Actually, increases in time according to the new firms which come into the economic sector by a given growth rate . On the other hand, a portion of low-risk (for example, credit risk) firms leaves the class of susceptible ones at time t, due to contact with infectious firms. The contagion phenomenon is modeled by a Holling-II function such that the number of the newly infected is related to the following rate,
where represents the so-called attack rate, i.e., the average rate at which an infected firm gets in contact with a susceptible one, whereas is the so-called handling time, i.e., the average time which is spent for infecting a susceptible item. In other words, parameter a is related to the degree of association between the firms that transmit the risk; on the other hand, h indicates a sort of incubation time for the contagion that is the average time passing from the moment of contact between firms through any kind of financial contract up to the moment of actual financial distress. We notice that, as S becomes large, the term tends toward the value . This parameter models a kind of saturation level, such that the contagion effect is limited. Actually, as the number of susceptible firms increases, the same susceptible firms can gain protection against contagion because of the increased supervision, self-discipline, and collaboration. In this respect, a number of the newly infected related to the rate (1) leaves the susceptible class and joins the class of infected firms.
In the meantime, a portion of infected firms related to the term leaves the same class of infectives and is recovered. We assume . The contagion removal rate models a cure action and represents the rate at which contagious firms in the economic sector take the corresponding measures to become immune; therefore, may measure the intervention of internal and external policies aimed at overcoming the firm crisis.
We denote by the natural elimination rate, which models the regulatory authorities’ final elimination rate of the firms in the whole economic sector; we suppose . This implies that a portion of susceptible and infected firms related to the terms and , respectively, indefinitely leaves the economic sector. Anyway, we assume that recovered companies attain a temporary (but not lifelong) immunity after curing. Precisely, the immunity period represents the time lag of the model. When the firms are recovered from an extremely high level of risk at time , then they remain in a kind of recovery pool up to time t for a period of length . After that, a portion of the firms recovered at time related to the rate indefinitely leaves the economic sector, and the remaining part related to the rate reverts to the susceptible class. The choice of term is common in the literature (see for instance [47,48]); it allows us to account for the role of the financial immunity lag in the mechanism of reverting from recovery to survival or to failure. We notice that the rate toward bankruptcy decays as the temporary immunity delay increases.
In Figure 1, we show a graphical scheme of the whole dynamics. As a consequence, a time delayed model is established for the evolution of risk contagion among the classes of firms. More precisely, the susceptible and infected ones evolve according to the following equations,
for any . We assume that this differential system is completed by suitable initial conditions defined as
Condition (5) describes the history of the infected firms in the lag temporal interval . Once the infected dynamics is known, then it is possible to describe the recovered firm evolution according to the following rule,
which can be integrated in order to have
for any . We remark that, under this assumption, the initial value for the recovered corresponds to the value
which accounts for the whole history of infected firms during the lag immunity period before the initial time . As (2) and (3) do not depend on , then Equation (6) can be omitted without loss of generality. Hence, we focus on the solution of system (2) and (3), whose well-posedness is stated in the next result.
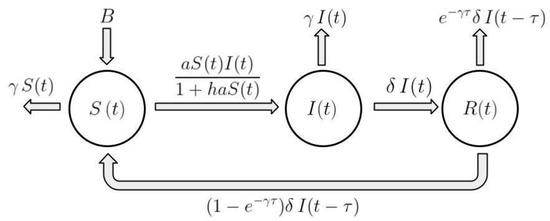
Figure 1.
Graphical scheme of the risk contagion dynamics.
Proposition 1.
Proof.
Consider the forcing term that characterizes the dynamical system; it is represented by such that
for any . We evaluate the Jacobian matrix related to as
Then we consider the compact set defined as
where is a constant value. We notice that all the entries of this Jacobian are continuous functions with respect to S and I; therefore, if and , then is also bounded from above and there exists a constant , such that
Then consider two arbitrary points , and note that
This relationship yields the following inequalities:
As a consequence, due to the fact that is arbitrary, the forcing term is Lipschitz-continuous in each compact set of .
In this framework, the dynamics of the firm system is described by Equations (2) and (3), under the assumption that initial conditions (4) and (5) hold and is a continuous function in . Once the solution of this model is available, then it is possible to evaluate the recovered firm density by (6).
2.1. Positivity of Solutions
The differential system (2) and (3) describes the evolution of firm populations; therefore, it is worthwhile to prove that and remain positive for all time when they start from positive initial data as supposed in (4) and (5). In this framework, we provide the next result whose proof is inspired to the approaches developed in [47,51], where the theory of dynamical systems takes application in biological phenomena.
Proposition 2.
Proof.
Assume the proposition is false. Let . First, suppose that . Therefore for . Due to the fact that is a differentiable function, then it is continuous and bounded over . In this respect, it is possible to define
Thus, for we obtain , which yields , which is a contradiction.
Finally, suppose that ; therefore for . Then, due to Equation (2), we have
Because , for , we must have , which is a contradiction. This completes the proof. It follows that Proposition 2 is true. □
As a consequence, due to the fact that function is integrated in (6), then we also get that is positive for all .
2.2. The Existence of Steady States
We notice that, at the steady state, an equilibrium point for (2) and (3) satisfies the following system of equations
It is easy to check that model (2) and (3) have the risk-free equilibrium
and one more nonzero steady state for certain parameter values. More precisely, it holds that
so that the nontrivial point represents an endemic equilibrium which is feasible under the assumption
which ensures both conditions and are satisfied. Therefore, we set
which represents the so-called basic reproduction number of the risk infection; actually, the endemic steady state is feasible in the case when . We would like to remark that, although the immunity period is involved in the relationship which defines in (9), does not affect endemic equilibrium feasibility. On the contrary, this feasibility strongly depends on incubation time magnitude; indeed, condition also implies that .
3. Steady-State Stability
In the model described so far, risk is affected by various factors and becomes complex due to its nonlinearity. Arguing whether the risk will continue to exist in or it will be eliminated from the economic sector is an issue which needs a specific analysis. Therefore, in this section we focus on the stability analysis of both steady states that characterize the dynamical system (2) and (3); then we discuss our results.
3.1. Free-Risk Steady-State Stability
We start our stability analysis with studying the behaviour of the original model (2) and (3) around the free-risk equilibrium . In the next proposition, we suppose that the basic reproduction number in (10) does not exceed 1 and prove that, as long as this condition holds, the risk-free steady state stays locally, asymptotically stable; in that case, no other equilibrium is feasible because it would be , as we have already remarked in the previous Section 2.2.
Proposition 3.
The risk-free equilibrium is locally, asymptotically stable if the following condition holds:
Under the opposite assumption , the steady state is unstable.
Proof.
As a further step, we go deep inside and investigate global stability conditions for risk-free equilibrium. In this respect, we provide and prove the following result.
Proposition 4.
Under the assumption that
the risk-free equilibrium is globally asymptotically stable.
Proof.
We adopt the following transformation
therefore, model (2) and (3) is equivalent to the system
Due to estimates , there exists a constant , such that Equation (14) yields
which can be integrated in order to obtain
for any time . Notice that assumption (12) assures ; in this respect, inequality (15) can be exploited in order to state the system behaviour in the long run.
First of all, we get in the case when . It follows that the original has the same behaviour: as .
On the other hand, (15) can be plugged into (13) in order to obtain
Then the previous inequality can be integrated so that:
- in the case when , we get
- in the opposite case when , we have
In both cases is bounded from above by the an exponentially decaying function at the long run. Therefore, as , it follows that , which is equivalent to have . Thus, we have proven that is globally, asymptotically stable. □
3.2. Endemic Steady-State Stability
In the previous Section 3.2, we have pointed out that, when condition (11) holds so that the trivial steady state is locally asymptotically stable, then the nontrivial equilibrium is not feasible. On the other hand, when (11) violates, then system (2) and (3) have the endemic equilibrium defined in (9) in addition to the risk-free one.
Then we focus on the endemic stability analysis and prove that, in the case when the basic reproduction number exceeds 1, then the trivial equilibrium is both feasible and locally stable. This result is stated in the next proposition.
Proposition 5.
Assume that the following condition holds:
Then endemic equilibrium defined in (9) is both feasible and locally, asymptotically stable.
Proof.
The Jacobian defined in (8) is evaluated at so that
Its characteristic equation in reads as
Assumption (16) yields that both the eigenvalues of the linearisation matrix cannot be purely imaginary and have negative real parts. As a consequence, the same assumption assures both the feasibility of endemic steady state and its local stability. □
As the next step, we study global stability conditions for endemic equilibrium and provide the following result, the assumptions of which are stronger than (16). The proof is inspired to the approach adopted in [47] to analyse a different SIR model, which aims to understand different scenarios for disease outbreak transmissions and the behaviour of epidemics.
Proposition 6.
Suppose that the following condition holds
where the constant value is defined by
under the further assumption that
Then endemic equilibrium defined in (9) is globally asymptotically stable.
Proof.
Condition (19) implies that , thus (17) assures that ; then, the endemic equilibrium is feasible. We center system (2) and (3) at by introducing new variables as
therefore, the problem can be rewritten in the following form:
We are going to prove that a trivial solution of system (20) and (21) is globally asymptotically stable, then it will immediately follow that the endemic equilibrium is globally asymptotically stable for model (2) and (3). With this aim, we are going to employ the Lyapunov functional technique (see, for instance [52]). Then we introduce the following functional,
where and is an arbitrary real constant. The derivative of V is
that is equivalent to have
Due to the fact that is defined by (9), then the last term can be rewritten according to the following relationship:
Thus, we exploit inequality for any time t and obtain
Due to assumptions (17)–(19), we may choose as
so that the term related to the product vanishes in the upper bound for . Then, we exploit the estimates for any time t and apply the Cauchy–Schwartz inequality in order to have
Because , then , which yields
We choose Lyapunov functional to be of the form
hence
Therefore, by exploiting the bound in (23), we get
As is defined in (22), then it follows that
From assumptions (17)–(19), it follows that the previous expression is negative-definite. A direct application of the Lyapunov–LaSalle type theorem (see Theorem 2.5.3 in [53], p. 30) implies that both and as . Then the proof is completed. □
3.3. Discussion
The previous results regarding the local and global stability of both steady states suggests some interesting comments and remarks. First of all, they allow for understanding that the risk-free equilibrium is globally, asymptotically stable and attracts all trajectories of the system under the assumption that incubation time h is large enough, such that . Indeed, this bound lets the basic reproduction number assume a negative value according to assumption (12) in Proposition 4. Actually, as expected, the incubation time period is so long that the infected class empties because the rate of susceptible capture by contagion is lower than the rate of bankruptcy and recovery. In this case, risk infection disappears from the economic sector in the long run.
On the other hand, when the incubation is shortened as , then the risk-free steady state stays locally stable as long as the basic reproduction number remains below 1, after which the nontrivial equilibrium becomes feasible as soon as exceeds 1. In addition, is globally asymptotically stable and attracts all trajectories of the system when the financial immunity period is sufficiently short according to condition (19) and the risk infection is characterized by a high value for so that condition (17) is satisfied. In that case, it continues to exist in the economy at the long run and represents an endemic equilibrium.
As another remark, the magnitude of both h and affects the partition between infected and susceptible firms at the endemic steady state. Indeed, it is possible to verify that condition
is equivalent to have assuming that endemic equilibrium is feasible. Notice that, if (24) is satisfied, then h is small enough so that and also is sufficiently large according to the following inequality:
As a conclusion, conditions (17)–(19) together with (24) assure that equilibrium is feasible, it attracts the trajectories which solve the model and, in addition, the level of infected companies exceeds the one of susceptible firms at steady state.
Remark 1.
We would like to make a brief final remark about the behaviour of recovered density over the long term. Under the assumption that an equilibrium is stable and attracts the trajectories that solve the system, i.e., and as , then it is easy to verify that is convergent toward . In other words, by applying the classical theory of real function limit, we obtain that as . As expected when the endemic equilibrium is feasible and stable, this last result implies that the magnitude of recovered companies tends to which increases when the financial immunity period τ becomes longer. On the other hand, as expected in the case when the risk-free equilibrium attracts the solution trajectory, the recovered density decays and the recovery pool becomes empty in the long run.
4. Numerical Simulation: The Case Study of Food Sector for the Emilia Romagna Italian Region
The model we propose is a nonlinear differential system, the solution for which is not available in closed form; therefore, its approximation is needed in order to provide numerical simulations. With this aim, we exploit the built-in function dde23 in the MATLAB environment, which integrates DDEs with constant delays, and focus our attention on the economic sector of food industries for the Emilia Romagna region located in the northern part of Italy. According to the Bank of Italy (https://www.bancaditalia.it/pubblicazioni/economie-regionali/?dotcache=refresh website consulted in 21 December 2022), this sector plays a key economic role in the entire territory of northern Italy.
In this respect, we exploit data about some firms obtained from AIDA (AIDA - BUREAU VAN DIJK collects complete information on companies in Italy, with a history of up to ten years, and it can be exploited in order to perform detailed analyses by searching for individual companies and peer clusters), which is a database containing comprehensive information on companies in Italy. We analyse a sample of 2606 of companies operating in the food sector. First, we select this economic sector for numerical simulation because it is among the sectors (such as the pharmaceutical and electronic industries) that have suffered less due to the COVID-19 crisis (see Bank of Italy), which gives more robustness to our elaboration and the selection of input data. Secondly, we choose a definite geographic area, because Bank of Italy analysis mostly focus on regional areas.
The parameters of the dynamical model are estimated by considering the time period between the years 2012 and 2021 in the AIDA database as a data sample. All companies in the sample, for each year, are considered as susceptible. Then we identify infected companies as those with high credit risk. Instead of a score approach, we measure credit risk by applying a logit model (the logit model is intended as a logistic regression in which the dependent variable can assume values between 0 and 1) starting from yearly balance sheet items, and taking into account companies with an early warning message. The logit model is estimated at the firm’s level, and on a year-by-year basis. It takes into account defaulting companies according to different financial distress meanings: bankruptcy, liquidation, arrangement with creditors, among others. By this approach, we measure the density of infected companies for each year of the period 2012–2021 and get the nodal values for history function in the lag period. Then, we exploit the built-in function polyfit in the MATLAB environment and evaluate a polynomial of degree as best fit (in a least-squares sense) for the nodal values of in a time interval of nine years, so that . The resulting best fit polynomial is plotted in Figure 2 and represents the history function , which is involved in initial condition (5). Therefore, the dynamics described by differential system (2) and (3) starts at time , which corresponds to the last year 2021 in the data sample. The initial value for the density of recovered companies is approximated by applying the trapezoidal quadrature rule to relationship (7); as a consequence, the initial value for susceptible class density in condition (4) is estimated as . Furthermore, risk evolves according to the values of the parameters estimated as , , , .
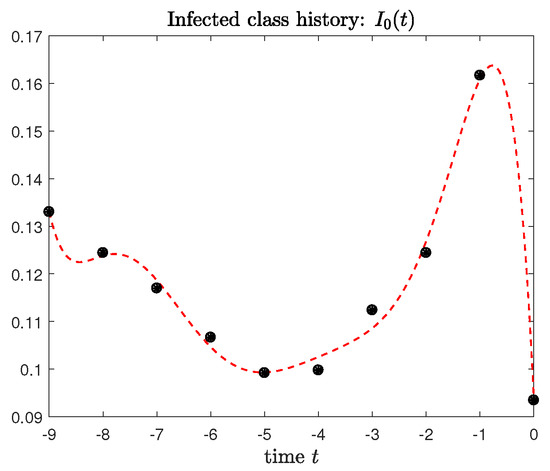
Figure 2.
Best−fit polynomial for the nodal values of infected density in the lag period. Red dashed line: plot of history function in the whole sample period . Black bullets: nodal values which are measured for infected density, they are obtained by relating the entries of the vector to the initial number of companies operating at .
As the incubation time and financial immunity period are not estimated, we simulate two different scenarios:
- immunity is set at and incubation gets different lengths as ;
- immunity is set at and incubation gets different lengths as .
In the first scenario, financial immunity lasts longer than in the second one; furthermore, in both cases incubation time starts small enough at levels and so that . Then it rises to a much higher value , such that . The results related to the first and second scenarios are shown in Figure 3 and Figure 4, respectively. In both scenarios the corresponding risk dynamics have a similar behaviour: the main difference is the trend in the recovered class density reaching a steady state that increases with the financial immunity period, as expected. In the case when , the endemic equilibrium is stable and attracts the solution trajectory: risk infection remains in the economy and the infected exceeds the susceptible at stationary state. On the other hand, when incubation becomes longer as , then infection still remains endemically stable. However, the density of susceptibles is greater than that of infected at the long run. On the other hand, overall bankruptcy risk disappears from the economic sector when incubation becomes longer and equal to , because in this case the risk-free equilibrium is asymptotically stable. It is evident that the period is both long and unrealistic; therefore it is realistic to deduce that the overall risk cannot be completely eliminated in our concrete and real context. Our elaboration could be improved in different ways. First, because we consider just one productive sector that is affected by a low degree of technological innovation and is featured by a low number of enterprises’ entries and departures from the market, it would be interesting to account for other economic sectors with different features. Secondly, future research could also analyze the cross-border channel of outbreak transmission and the features of the supply chain.
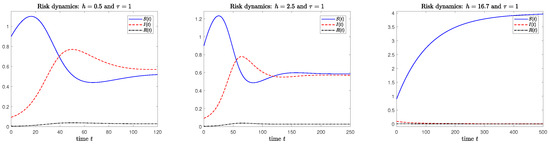
Figure 3.
Dynamics related to the first scenario: financial immunity period is . Incubation time varies from (on the left) to (in the middle) and (on the right). Solid blue line: susceptible dynamics. Dashed red line: infected dynamics. Dash dot black line: recovered dynamics.
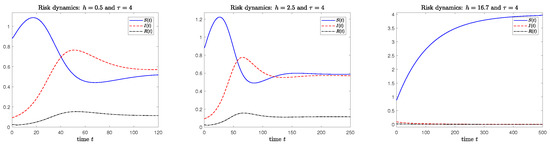
Figure 4.
Dynamics related to the second scenario: financial immunity period is , Incubation time varies from (on the left) to (in the middle) and (on the right). Dashed red line: infected dynamics. Dash dot black line: recovered dynamics.
5. Conclusions
In the present paper, we are concerned with the relevant problem of modelling how financial crises may spread across the world. As there exists a link between financial systems and ecosystems, it is possible to model risk contagion by exploiting the mathematical approach of epidemiological models that have been recognized as effective tools for describing infectious disease spread that starts as an outbreak. In the framework of SIR dynamics, we propose an original time delay dynamical model for risk diffusion among companies in an economic sector. The evolution of contagion is modelled in terms of credit and financial risks with low and high levels. After contagion, some companies become able to keep their risk at a low level and get a temporary financial immunity ability, which represents the time-delay lag in the differential system.
The approach we propose is inspired by the literature; to our knowledge, it differs from the other contributions. For instance, in [38] contagion is modelled by a nonlinear incidence rate in the variable corresponding to a high-risk level. As a relevant difference, in order to model contagion we apply a Holling Type II functional response in the other variable related to low-risk level. In our paradigm, the risk contagion phenomenon can be interpreted in a framework of two different populations, wherein the susceptible class represents the prey species which is captured by the predator species represented by the high-risk infected class. This approach can be an important tool of crisis investigation because it allows the model to implicitly take into account the incubation time for contagion, which represents the average time from the moment of contact between firms up to the moment of actual financial distress. We stress this topic over the whole paper.
We would also like to note that a nonlinear incidence rate with respect to the susceptible class variable has been used by [48], in which the authors state a completely different SEIR model that finds application in the specific framework of credit risk spreading over a P2P lending platform. On the other hand, the financial and economic application of the model we introduce is broader as it is designed to describe the diffusion of both credit and financial risk in a generic segment of any economic sector.
As a consequence, due to the fact that the paradigm of the model we propose and its discussion can be considered as worthy of attention, then we go deep inside and perform a complete theoretical analysis in terms of well-posedness and positivity of solutions. We also investigate the behaviour of the solution at the long run. Actually, we prove that two steady states can be determined: they represent a risk-free equilibrium and an endemic one. The Lyapunov functional theory is employed to prove global stability for both steady states. In this respect, as already pointed out, an important and original issue of our analysis consists of understanding the crucial role of both incubation time and financial immunity period in the asymptotic stability behaviour. We stress and prove that a sufficiently long incubation makes trivial risk-free equilibrium be globally stable. On the other hand, a sufficiently short incubation, together with a short immunity period lets the endemic steady state be locally stable so that risk remains in the economy in the long run. This analysis is confirmed by numerical simulation on a case study of some companies operating in the food economic sector in a specific Italian region. Even though this simulation starts from some simplifying assumptions, it is carried out by paying particular attention to the evaluation of the history function related to the infected class. This is another original topic which is faced by fitting the data from the database and following their trend well.
As a conclusion, our simulation provides interesting findings that could be deepened for future research. If we take into account parameters drawn from a traditional economic sector, the risk-free equilibrium could be reached only for sufficiently high values of the incubation period. In the opposite case, when incubation is short enough, the endemic steady state attracts trajectories of risk contagion. These results have important implications for policy makers in order to focus on their financial actions to provide a certain delay in the incubation time and financial distress. These issues could be investigated in future research, considering other economic sectors and geographical areas.
We conclude our discussion and notice that another interesting topic for future research could consist of considering specific psychological factors in the spread mechanism that affects managers and other players according to the different economic sectors at hand.
Author Contributions
Conceptualization, M.A. and S.R.; methodology, S.R.; software, M.A.; validation, G.C. and L.C.; formal analysis, S.R.; investigation, M.A.; data curation, G.C. and L.C.; writing—original draft preparation, M.A., L.C., G.C. and S.R.; writing—review and editing, M.A., L.C., G.C. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank four anonymous referees for careful reading of the manuscript and making useful comments which helped to improve the paper. The authors also thank Massimiliano Ferrara for his encouraging and valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Evaluating the History Function I0 (·)
With the aim of letting the reader be able to reproduce Figure 2, we briefly describe the sequence of commands and function calls for evaluating the dynamics of history function in the MATLAB environment. First of all, we account for the nodal values, which are measured for infected density. They are obtained by relating the entries of the vector to the initial number of companies operating at . In other words, we evaluate the vector
so that its generic entry corresponds to the estimated value for with ().
As the next step, we exploit the built-in function polyfit to obtain the coefficients for a polynomial of degree n that is a best fit (in a least-squares sense) for the data in : after carrying out some tests with different values of n, we have empirically verified that the polynomial with degree fits the data following their trend well. Then is evaluated at m time instants equally spaced between and 0 (for instance ) by employing the built-in function polyval. In this way, history function is approximated by and plotted in . The sequence of commands is
- n = 7; P = polyfit([-9:1:0],V,n);
- m = 100; t = linspace(-9,0,m); I0 = polyval(P,t);
- plot(t,I0,’r–’,[-9:1:0],V,’ok’,[-9:1:0],V,’*k’).
References
- Claessens, S.; Forbes, K. International Financial Contagion; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- May, R.M.; Levin, S.A.; Sugihara, G. Complex systems: Ecology for bankers. Nature 2008, 451, 893–895. [Google Scholar] [CrossRef]
- Garas, A.; Argyrakis, P.; Rozenblat, C. Worldwide spreading of economic crisis. New J. Phys. 2012, 12, 185–188. [Google Scholar] [CrossRef]
- Xie, X.; Shi, X.; Gu, J.; Xu, X. Examining the Contagion Effect of Credit Risk in a Supply Chain under Trade Credit and Bank Loan Offering. Omega 2023, 115, 102751. [Google Scholar] [CrossRef]
- Jiang, S.; Fan, H. Credit risk contagion coupling with sentiment contagion. Phys. A Stat. Mech. Its Appl. 2018, 512, 186–202. [Google Scholar] [CrossRef]
- Jorion, P.; Zhang, G. Credit contagion from counterparty risk. J. Financ. 2009, 64, 2053–2087. [Google Scholar] [CrossRef]
- Boido, C.; Aliano, M. Digital art and non-fungible-token: Bubble or revolution? Financ. Res. Lett. 2022. in Press. [Google Scholar] [CrossRef]
- Haldane, A.G.; May, R.M. Systemic risk in banking ecosystems. Nature 2011, 469, 351–355. [Google Scholar] [CrossRef] [PubMed]
- Roukny, T.; Bersini, H.; Pirotte, H.; Caldarelli, G.; Battiston, S. Default cascades in complex networks: Topology and systemic risk. Sci. Rep. 2013, 3, 2759. [Google Scholar] [CrossRef]
- Leonidova, A.V.; Rumyantsevb, E.L. Default contagion risks in Russian interbank market. Phys. A Stat. Mech. Its Appl. 2016, 451, 36–48. [Google Scholar] [CrossRef]
- Callon, M. Techno-economic Networks and Irreversibility. Sociol. Rev. 1990, 38, 132–161. [Google Scholar] [CrossRef]
- Babus, A. The formation of financial networks. Rand. J. Econ. 2016, 47, 239–272. [Google Scholar] [CrossRef]
- Battiston, S.; Caldarelli, G. Systemic risk in financial networks. J. Financ. Manag. Mark. Inst. 2013, 1, 129–154. [Google Scholar]
- Feinstein, Z. Financial contagion and asset liquidation strategies. Oper. Res. Lett. 2017, 45, 109–114. [Google Scholar] [CrossRef]
- Caldarelli, G.; Battiston, S.; Garlaschelli, D.; Catanzaro, M. Emergence of Complexity in Financial Networks; Ben-Naim, E., Frauenfelder, H., Toroczkai, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 399–423. [Google Scholar]
- Aït-Sahalia, Y.; Cacho-Diaz, J.; Laeven, R.J.A. Modeling financial contagion using mutually exciting jump processes. J. Financ. Econ. 2015, 117, 585–606. [Google Scholar] [CrossRef]
- Barja, A.; Martínez, A.; Arenas, A.; Fleurquin, P.; Nin, J.; Ramasco, J.J.; Tomás, E. Assessing the risk of default propagation in interconnected sectoral financial networks. EPJ Data Sci. 2019, 8, 32. [Google Scholar] [CrossRef]
- Torri, G.; Radi, D.; Dvořáčková, H. Catastrophic and systemic risk in the non-life insurance sector: A micro-structural contagion approach. Financ. Res. Lett. 2022, 47, 102718. [Google Scholar] [CrossRef]
- Han, L. Controlling Default Contagion Through Small-World Networks. Procedia Comput. Sci. 2019, 154, 47–53. [Google Scholar] [CrossRef]
- Previati, A.D.; Aliano, M.; Galloppo, G.; Paimanova, V. Why do banks react differently to short-selling bans? Evidence from the Asia-Pacific area and the United States. Q. Rev. Econ. Financ. 2021, 80, 144–158. [Google Scholar] [CrossRef]
- Akerlof, G.A.; Shiller, R.J. Animal Spirits: How Human Psychology Drives the Economy, and Why It Matters for Global Capitalism; Princeton University: Princeton, NJ, USA, 2009. [Google Scholar]
- Adekoya, O.B.; Oliyide, J.A. Commodity and financial markets’ fear before and during COVID-19 pandemic: Persistence and causality analyses. Resour. Policy 2022, 76, 102598. [Google Scholar] [CrossRef]
- Giot, P. Relationships between implied volatility indexes and stock index returns. J. Portfolio Manag. 2005, 31, 92–100. [Google Scholar] [CrossRef]
- Economou, F.; Panagopoulos, Y.; Tsouma, E. Uncovering asymmetries in the relationship between fear and the stock market using a hidden-co-integration approach. Res. Int. Bus. Financ. 2018, 44, 459–470. [Google Scholar] [CrossRef]
- Chen, X.; Chiang, T.C. Empirical investigation of changes in policy uncertainty on stock returns- Evidence from China’s market. Res. Int. Bus. Financ. 2020, 53, 101183. [Google Scholar] [CrossRef]
- Filbeck, G.; Kumar, S.; Liu, J.; Zhao, X. Supply chain finance and financial contagion from disruptions evidence from the automobile industry. Int. J. Phys. Distrib. Logist. Manag. 2016, 46, 414–438. [Google Scholar] [CrossRef]
- Lian, Y. Financial distress and customer-supplier relationships. J. Corp. Financ. 2017, 43, 397–406. [Google Scholar] [CrossRef]
- Agca, S.; Babich, V.; Birge, J.R.; Wu, J. Credit shock propagation along supply chains: Evidence from the CDS market. Manag. Sci. 2021, 68, 6506–6538. [Google Scholar] [CrossRef]
- Barro, D.; Basso, A. Credit contagion in a network of firms with spatial interaction. Eur. J. Oper. Res. 2010, 205, 459–468. [Google Scholar] [CrossRef]
- Barreto, G.; Artes, F. Spatial correlation in credit risk and its improvement in credit scoring. Eur. J. Oper. Res. 2016, 249, 517–524. [Google Scholar]
- Calabrese, R.; Andreeva, G.; Ansell, J. ’Birds of a feather’ fail together: Exploring the nature of dependency in SME defaults. Risk Anal. 2019, 39, 71–84. [Google Scholar] [CrossRef]
- Maté-Sánchez-Val, M.; Lóopez-Hernandez, F.; Rodriguez Fuentes, C.C. Geographical factors and business failure: An empirical study from the Madrid metropolitan area. Econ. Model. 2018, 74, 275–283. [Google Scholar] [CrossRef]
- Shi, Q.; Sun, X.; Jiang, Y. Concentrated commonalities and systemic risk in China’s banking system: A contagion network approach. Int. Rev. Financ. Anal. 2022, 83, 102253. [Google Scholar] [CrossRef]
- Egloff, D.; Leippold, M.; Vanini, P. A simple model of credit contagion. J. Bank. Financ. 2007, 31, 2475–2492. [Google Scholar] [CrossRef]
- Hertzel, M.G.; Li, Z.; Officer, M.S.; Rodgers, K.J. Inter-firm linkages and the wealth effects of financial distress along the supply chain. J. Financ. Econ. 2008, 87, 374–387. [Google Scholar] [CrossRef]
- Escribano, E.; Maggi, M. Intersectoral default contagion: A multivariate Poisson autoregression analysis. Econ. Model. 2016, 82, 376–400. [Google Scholar] [CrossRef]
- Calabrese, R. Contagion effects of UK small business failures: A spatial hierarchical autoregressive model for binary data. Eur. J. Oper. Res. 2022, 305, 989–997. [Google Scholar] [CrossRef]
- Fanelli, V.; Maddalena, L. A nonlinear dynamic model for credit risk contagion. Math. Comput. Simul. 2020, 170, 45–58. [Google Scholar] [CrossRef]
- Xua, K.; Qianb, Q.; Xiec, X.; Zhoud, Z. Study on the contagion mechanism of associated credit risk with corporate senior executives’ alertness. Procedia Comput. Sci. 2022, 199, 207–214. [Google Scholar] [CrossRef]
- Dawes, J.H.P.; Souza, M.O. A derivation of Holling’s type I, II and III functional responses in predator–prey systems. J. Theor. Biol. 2013, 327, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Holling, C.S. The components of predation as revealed by a study of small-mammal predation of the European sawfly. Can. Entomol. 1959, 91, 293–320. [Google Scholar] [CrossRef]
- Holling, C.S. Some characteristics of simple types of predation and parasitism. Can. Entomol. 1959, 91, 385–398. [Google Scholar] [CrossRef]
- Baker, C.M.; Armsworth, P.R.; Lenhart, S.M. Handling overheads: Optimal multi-method invasive species control. Theor. Ecol. 2017, 10, 493–501. [Google Scholar] [CrossRef]
- Baker, C.M.; Diele, F.; Marangi, C.; Martiradonna, A.; Ragni, S. Optimal spatiotemporal effort allocation for invasive species removal incorporating a removal handling time and budget. Nat. Resour. Model. 2018, 31, e12190. [Google Scholar] [CrossRef]
- Marangi, C.; Casella, F.; Diele, F.; Lacitignola, D.; Martiradonna, A.; Provenzale, A.; Ragni, S. Mathematical tools for controlling invasive species in protected areas. In Mathematical Approach to Climate Change and Its Impacts; Springer: Berlin/Heidelberg, Germany, 2020; pp. 211–237. [Google Scholar]
- Marangi, C.; Martiradonna, A.; Ragni, S. Optimal resource allocation for spatiotemporal control of invasive species. Appl. Math. Comput. 2023, 439, 127614. [Google Scholar] [CrossRef]
- Kyrychko, Y.N.; Blyuss, K.B. Global properties of a delayed SIR model with temporary immunity and nonlinear incidence rate. Nonlinear Anal. Real World Appl. 2005, 6, 495–507. [Google Scholar] [CrossRef]
- Zhao, C.; Li, M.; Wang, J.; Ma, S. The mechanism of credit risk contagion among internet P2P lending platforms based on a SEIR model with time-lag. Res. Int. Bus. Financ. 2021, 57, 101407. [Google Scholar] [CrossRef]
- Diekmann, O.; Van Gils, S.A.; Lunel, S.M.; Walther, H.O. Delay Equations: Functional-, Complex-, and Nonlinear Analysis; Springer: Berlin/Heidelberg, Germany, 2012; Volume 110. [Google Scholar]
- Richard, J.P. Time-delay systems:an overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- Li, B.; Kuang, Y. Simple food chain in a chemostat with distinct removal rates. J. Math. Anal. Appl. 2000, 242, 75–92. [Google Scholar] [CrossRef]
- Beretta, E.; Kuang, Y. Modeling and analysis of a marine bacteriophage infection with latency period. Nonlinear Anal. 2001, 2, 35–74. [Google Scholar] [CrossRef]
- Kuang, Y. Delay Differential Equations with Applications in Population Biology; Academic Press: NewYork, NJ, USA, 1993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).