Splines Parameterization of Planar Domains by Physics-Informed Neural Networks
Abstract
1. Introduction
- The discrete description of the computational domain is achieved by using PINNs.
- The continuous representation of the computational domain is then obtained by using a suitable QI operator which provides a spline parameterization, i.e., a continuous description, of the desired smoothness.
2. Preliminaries
3. The Method
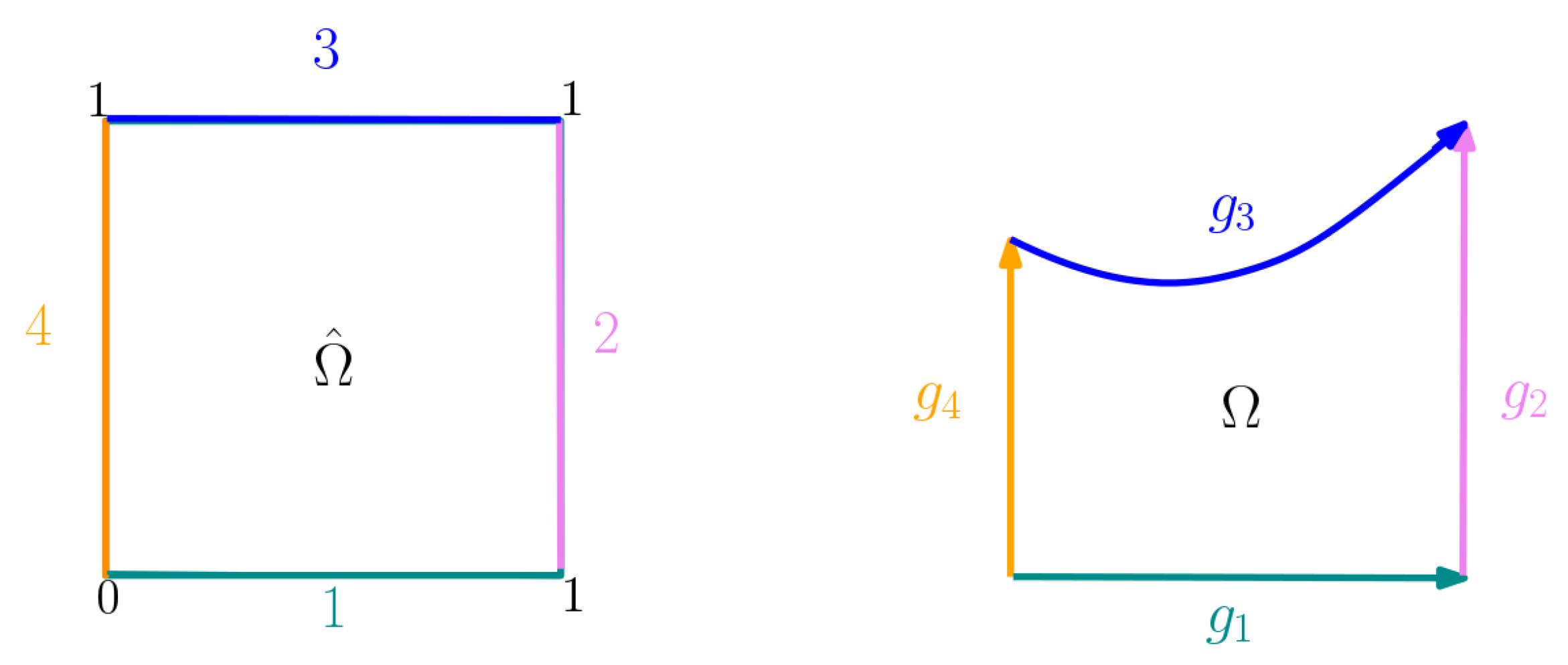
- The boundary is split into 4 pieces , for , by performing for example knot-insertion.
- Each is then parametrized as a Bspline curve .
- PINNs are trained to minimize the loss functional in Equation (4) over a set of boundary points and over the Laplace equation.
- The trained network represents an approximation of the sought parameterization map .
- Uniformly spaced grid points are generated in and mapped by to .
- A continuous spline approximation of is obtained by using a Hermite Quasi-Interpolation operator (QI).
| Algorithm 1 Pseudo-code for the proposed algorithm |
 |
4. Numerical Examples
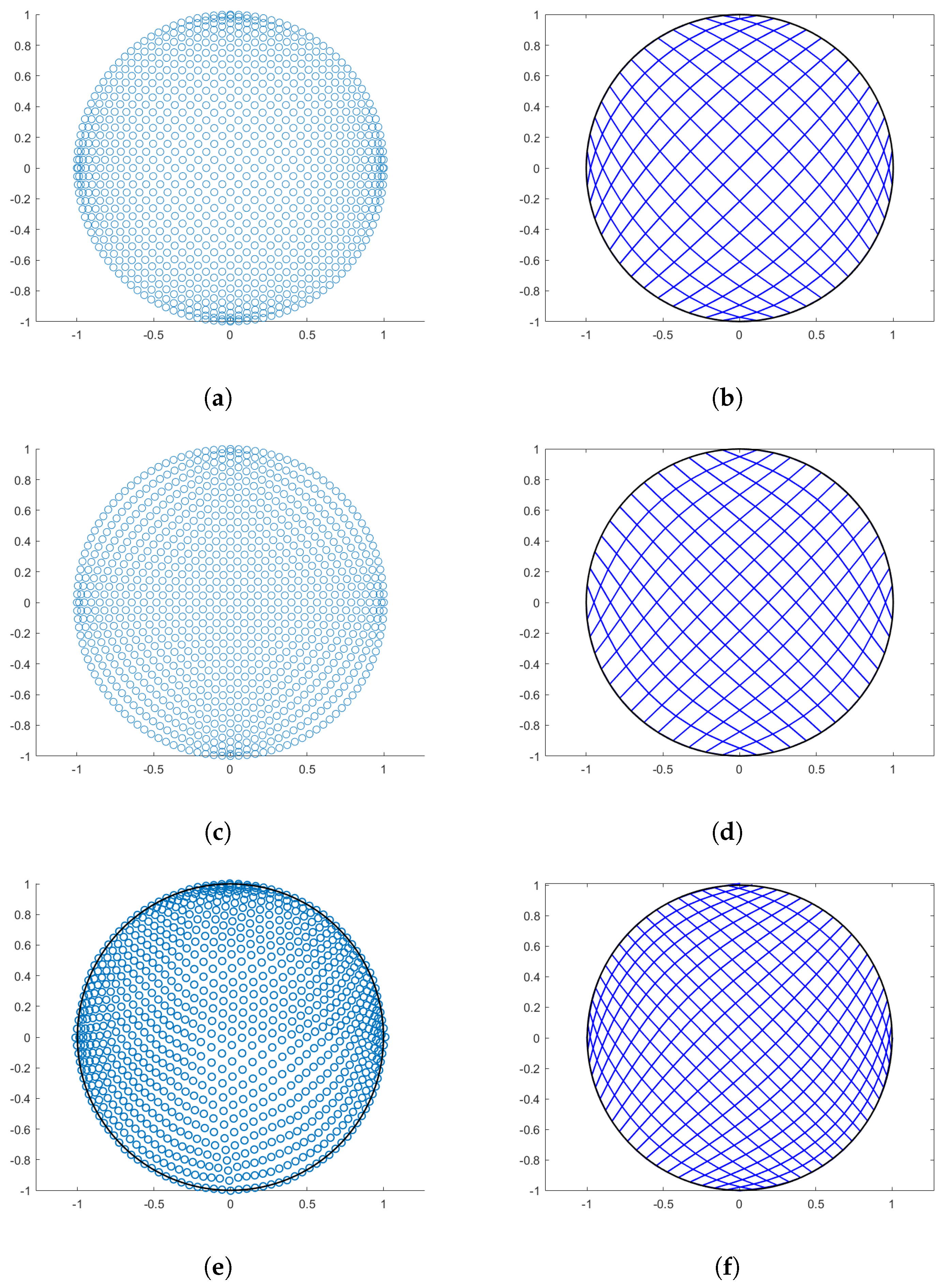
4.1. Circle
4.2. Wedge-Shape
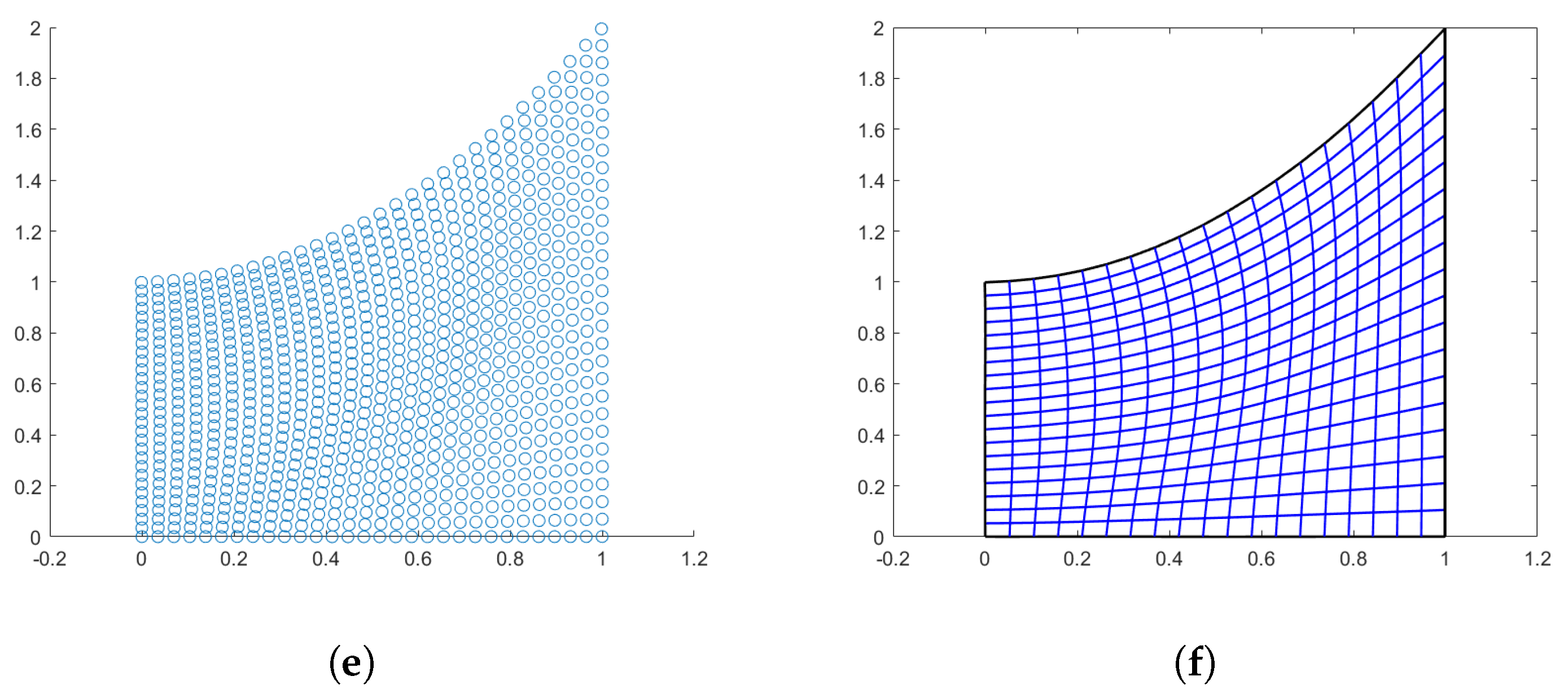
4.3. Quarter-Annulus-Shaped Domain
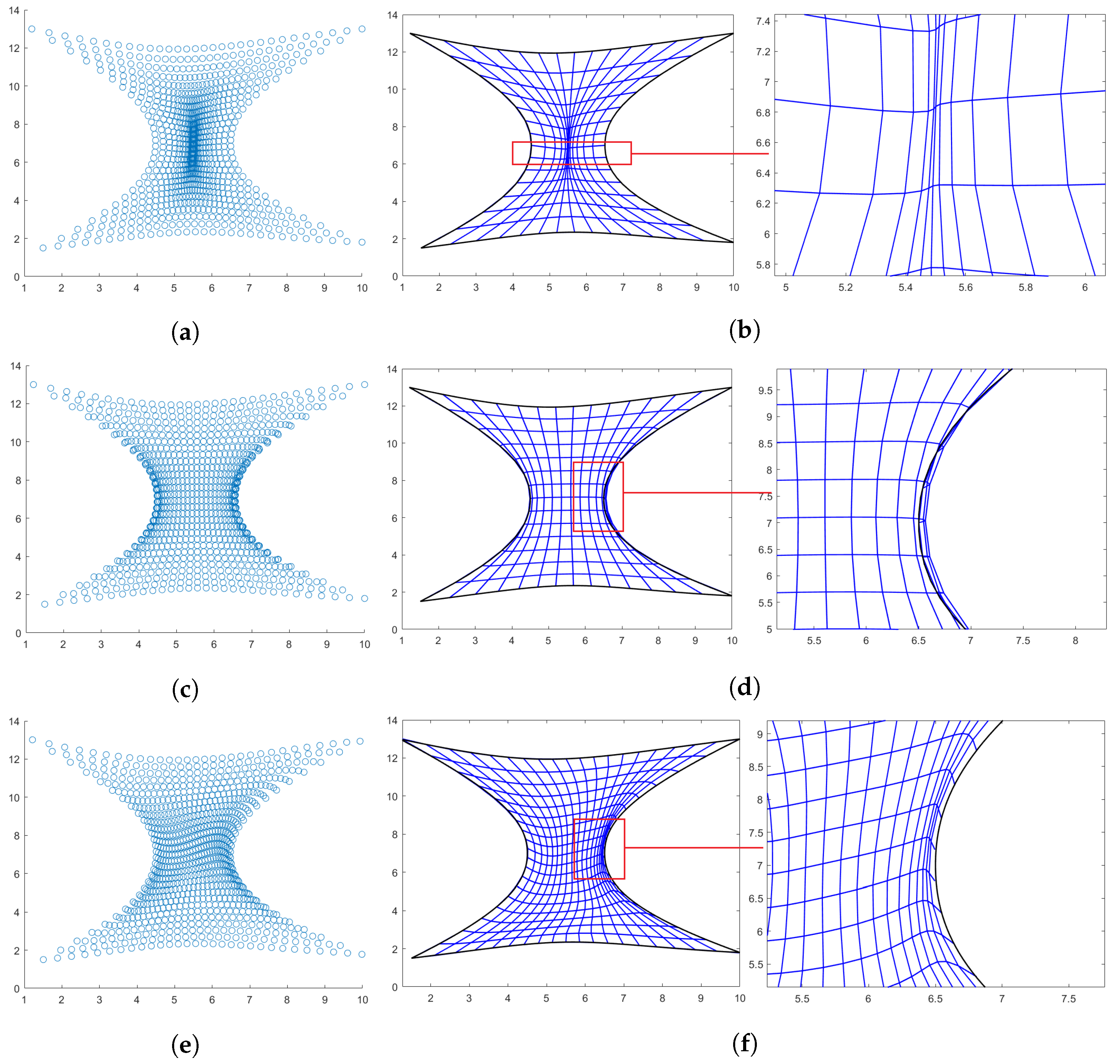
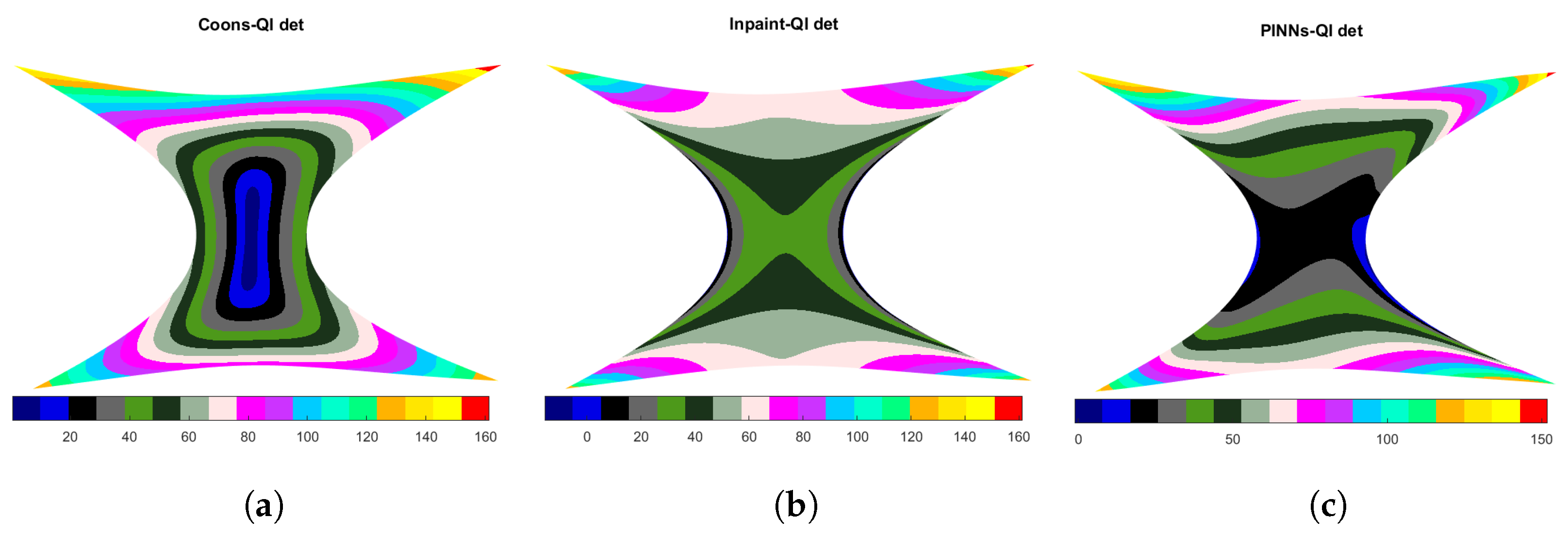
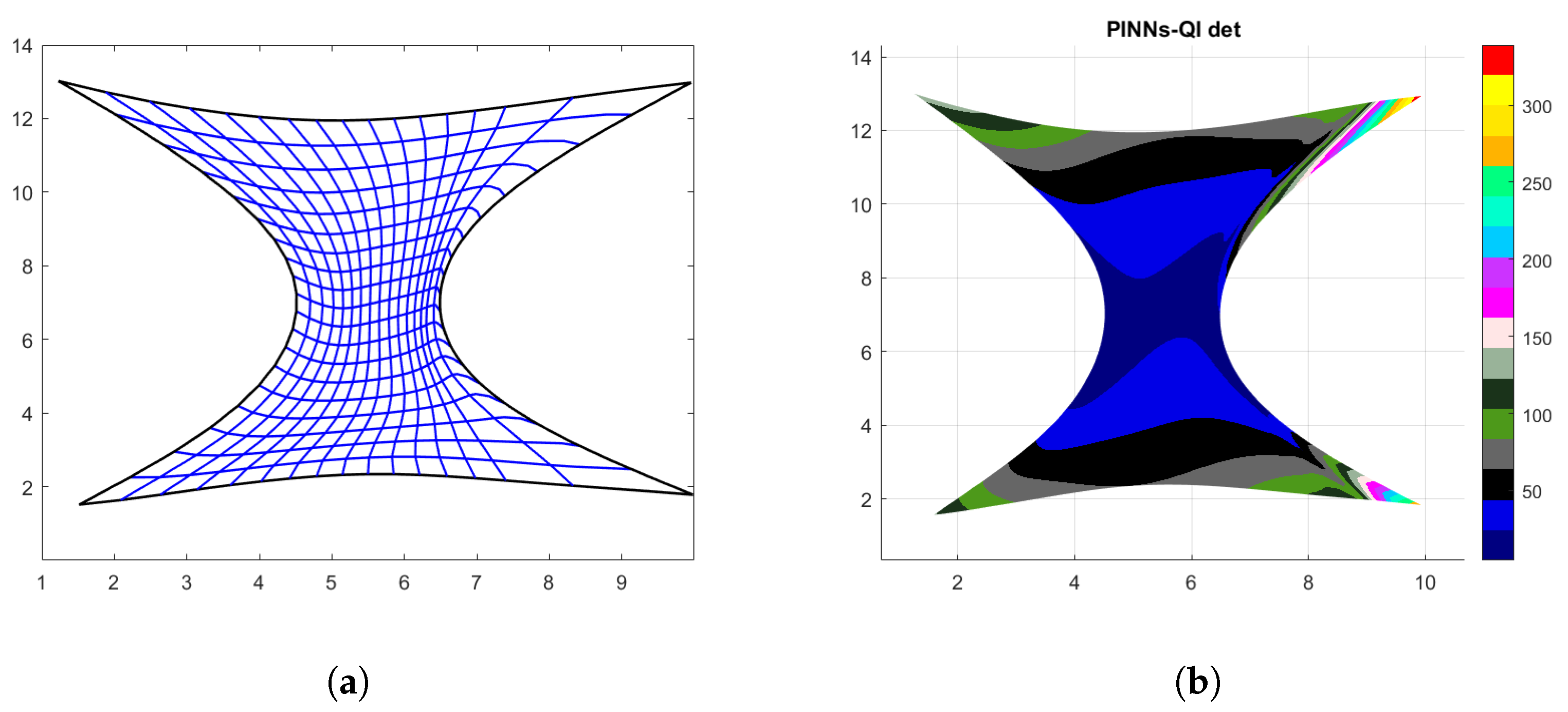
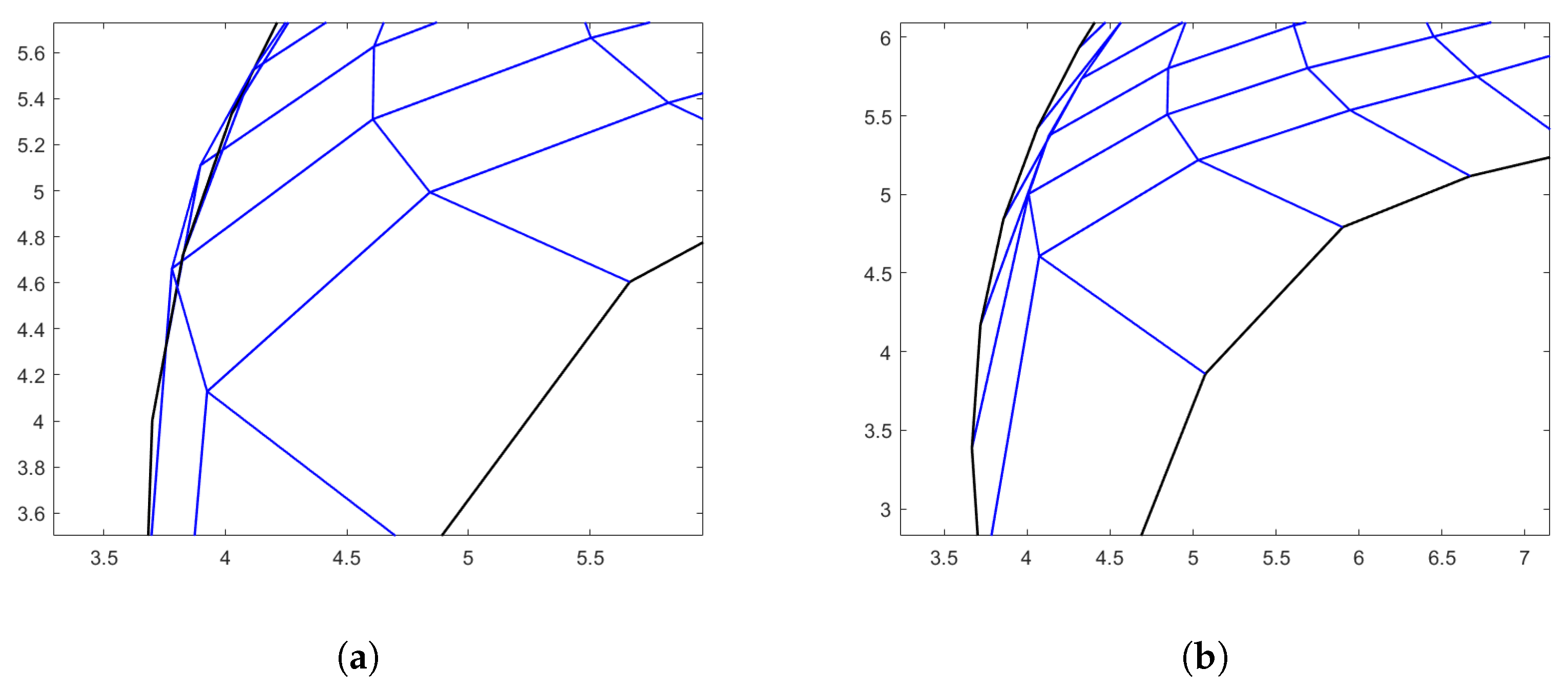
4.4. Hourglass-Shaped Domain
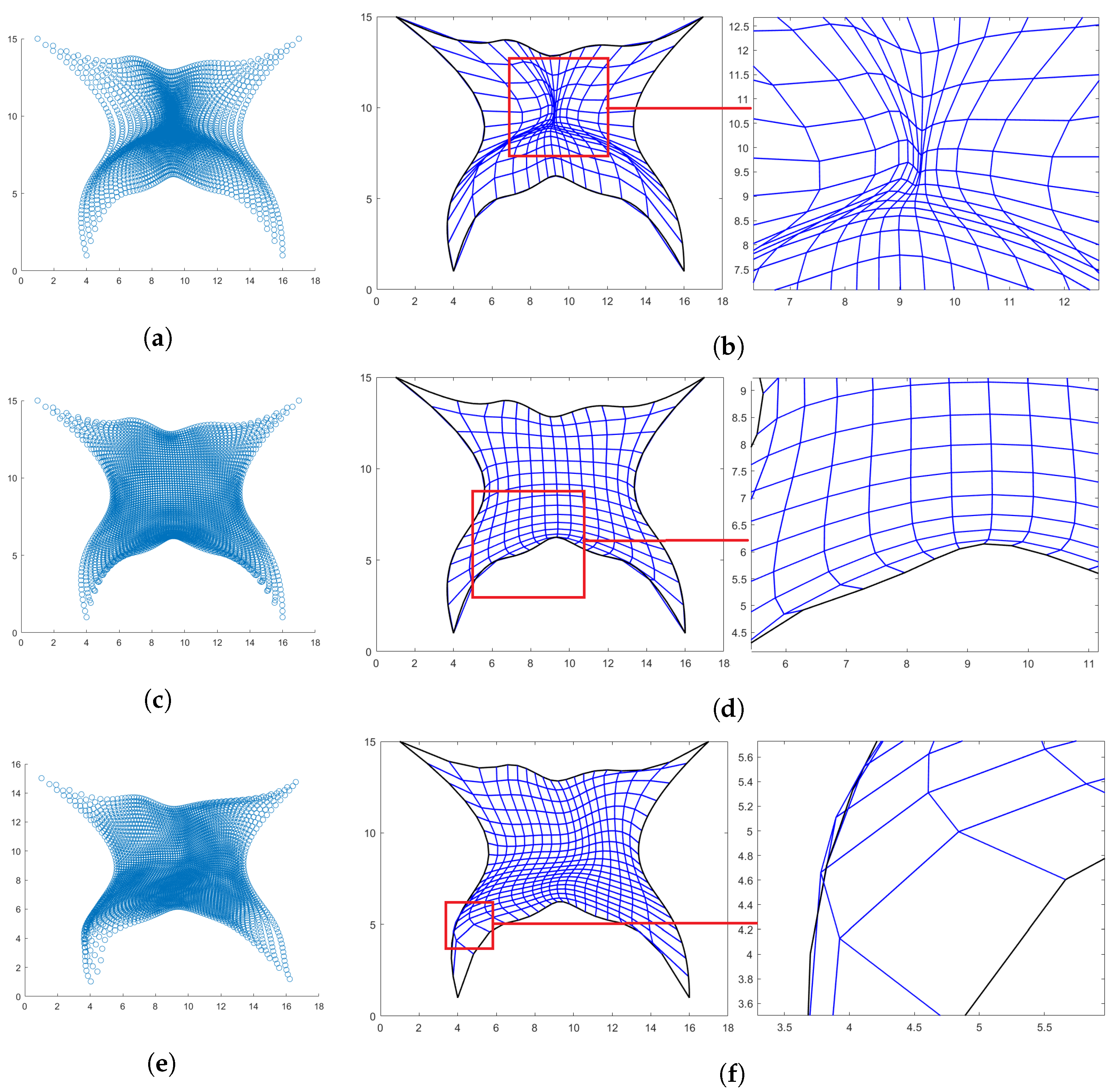
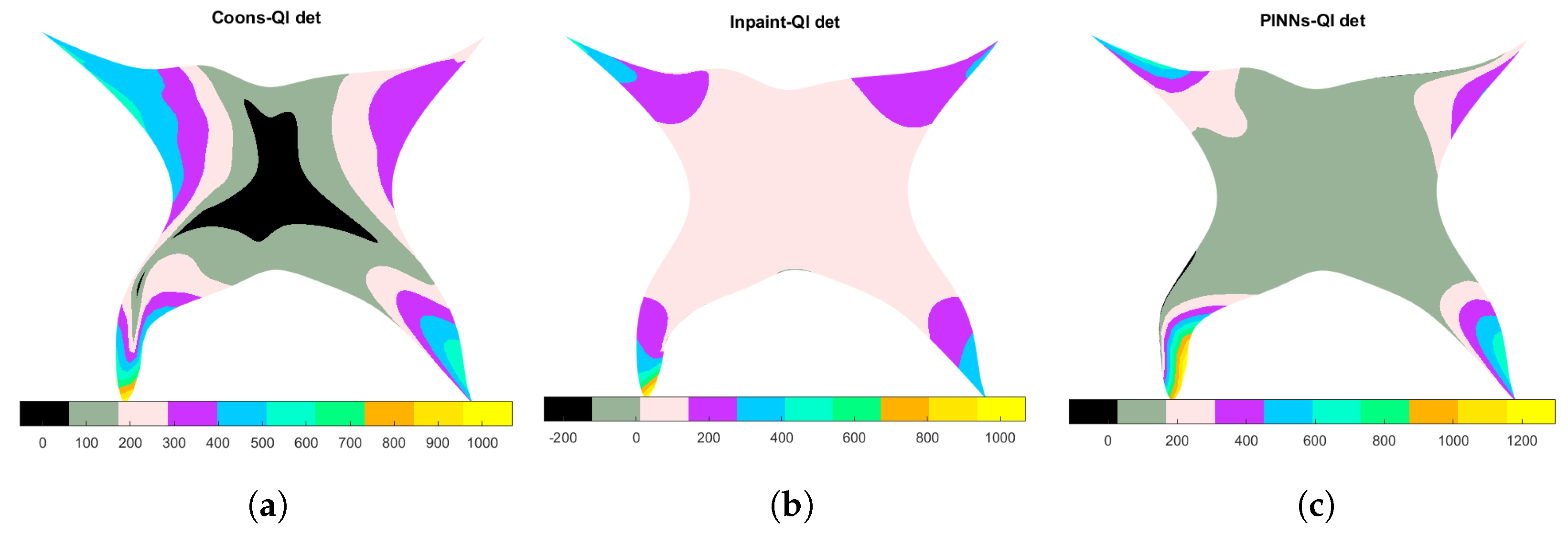
4.5. Butterfly-Shaped Domain
5. Post-Processing Correction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schöberl, J. NETGEN An advancing front 2D/3D-mesh generator based on abstract rules. Comput. Vis. Sci. 1997, 1, 41–52. [Google Scholar] [CrossRef]
- Shewchuk, J.R. Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator. In Proceedings of the Applied Computational Geometry Towards Geometric Engineering: FCRC’96 Workshop (WACG’96), Philadelphia, PA, USA, 27–28 May 2005; pp. 203–222. [Google Scholar]
- Beer, G.; Bordas, S. (Eds.) Isogeometric Methods for Numerical Simulation; Springer: Berlin/Heidelberg, Germany, 2015; Volume 240. [Google Scholar]
- Pelosi, F.; Giannelli, C.; Manni, C.; Sampoli, M.L.; Speleers, H. Splines over regular triangulations in numerical simulation. Comput. Aided Des. 2017, 82, 100–111. [Google Scholar] [CrossRef]
- Farin, G.; Hansford, D. Discrete coons patches. Comput. Aided Geom. Des. 1999, 16, 691–700. [Google Scholar] [CrossRef]
- Gravesen, J.; Evgrafov, A.; Nguyen, D.M.; Nørtoft, P. Planar Parametrization in Isogeometric Analysis. In Proceedings of the Mathematical Methods for Curves and Surfaces: 8th International Conference (MMCS 2012), Oslo, Norway, 28 June–3 July 2012; Revised Selected Papers 8. Springer: Berlin/Heidelberg, Germany, 2014; pp. 189–212. [Google Scholar]
- Xu, G.; Mourrain, B.; Duvigneau, R.; Galligo, A. Parameterization of computational domain in isogeometric analysis: Methods and comparison. Comput. Methods Appl. Mech. Eng. 2011, 200, 2021–2031. [Google Scholar] [CrossRef]
- Falini, A.; Špeh, J.; Jüttler, B. Planar domain parameterization with THB-splines. Comput. Aided Geom. Des. 2015, 35, 95–108. [Google Scholar] [CrossRef]
- Winslow, A.M. Adaptive-Mesh Zoning by the Equipotential Method; Technical Report; Lawrence Livermore National Lab.: Livermore, CA, USA, 1981.
- Nguyen, T.; Jüttler, B. Parameterization of Contractible Domains Using Sequences of Harmonic Maps. Curves Surfaces 2010, 6920, 501–514. [Google Scholar]
- Nian, X.; Chen, F. Planar domain parameterization for isogeometric analysis based on Teichmüller mapping. Comput. Methods Appl. Mech. Eng. 2016, 311, 41–55. [Google Scholar] [CrossRef]
- Pan, M.; Chen, F. Constructing planar domain parameterization with HB-splines via quasi-conformal mapping. Comput. Aided Geom. Des. 2022, 97, 102133. [Google Scholar] [CrossRef]
- Castillo, J.E. Mathematical Aspects of Numerical Grid Generation; SIAM: Philadelphia, PA, USA, 1991. [Google Scholar]
- Golik, W.L. Parallel solvers for planar elliptic grid generation equations. Parallel Algorithms Appl. 2000, 14, 175–186. [Google Scholar] [CrossRef]
- Hinz, J.; Möller, M.; Vuik, C. Elliptic grid generation techniques in the framework of isogeometric analysis applications. Comput. Aided Geom. Des. 2018, 65, 48–75. [Google Scholar] [CrossRef]
- Buchegger, F.; Jüttler, B. Planar multi-patch domain parameterization via patch adjacency graphs. Comput. Aided Des. 2017, 82, 2–12. [Google Scholar] [CrossRef]
- Falini, A.; Jüttler, B. THB-splines multi-patch parameterization for multiply-connected planar domains via template segmentation. J. Comput. Appl. Math. 2019, 349, 390–402. [Google Scholar] [CrossRef]
- Sajavičius, S.; Jüttler, B.; Špeh, J. Template mapping using adaptive splines and optimization of the parameterization. Adv. Methods Geom. Model. Numer. Simul. 2019, 35, 217–238. [Google Scholar]
- Pauley, M.; Nguyen, D.M.; Mayer, D.; Špeh, J.; Weeger, O.; Jüttler, B. The Isogeometric Segmentation Pipeline. In Isogeometric Analysis and Applications 2014; Springer: Berlin/Heidelberg, 2015; pp. 51–72. [Google Scholar]
- Chan, C.L.; Anitescu, C.; Rabczuk, T. Strong multipatch C1-coupling for isogeometric analysis on 2D and 3D domains. Comput. Methods Appl. Mech. Eng. 2019, 357, 112599. [Google Scholar] [CrossRef]
- Farahat, A.; Jüttler, B.; Kapl, M.; Takacs, T. Isogeometric analysis with C1-smooth functions over multi-patch surfaces. Comput. Methods Appl. Mech. Eng. 2023, 403, 115706. [Google Scholar] [CrossRef]
- Cai, W.; Li, X.; Liu, L. A phase shift deep neural network for high frequency approximation and wave problems. SIAM J. Sci. Comput. 2020, 42, A3285–A3312. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Burger, M.; Ruthotto, L.; Osher, S. Connections between deep learning and partial differential equations. Eur. J. Appl. Math. 2021, 32, 395–396. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Yu, J.; Lu, L.; Meng, X.; Karniadakis, G.E. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114823. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what is next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- De Boor, C.; Fix, G. Spline approximation by quasi-interpolants. J. Approx. Theory 1973, 8, 19–45. [Google Scholar] [CrossRef]
- Lee, B.G.; Lyche, T.; Mørken, K. Some examples of quasi-interpolants constructed from local spline projectors. Math. Methods Curves Surfaces 2000, 2000, 243–252. [Google Scholar]
- Lyche, T.; Schumaker, L.L. Local spline approximation methods. J. Approx. Theory 1975, 15, 294–325. [Google Scholar] [CrossRef]
- Sablonniere, P. Recent progress on univariate and multivariate polynomial and spline quasi-interpolants. Trends Appl. Constr. Approx. 2005, 151, 229–245. [Google Scholar]
- Mazzia, F.; Sestini, A. The BS class of Hermite spline quasi-interpolants on nonuniform knot distributions. BIT Numer. Math. 2009, 49, 611–628. [Google Scholar] [CrossRef]
- Mazzia, F.; Sestini, A. Quadrature formulas descending from BS Hermite spline quasi-interpolation. J. Comput. Appl. Math. 2012, 236, 4105–4118. [Google Scholar] [CrossRef]
- Bertolazzi, E.; Falini, A.; Mazzia, F. The object oriented C++ library QIBSH++ for Hermite spline quasi interpolation. arXiv 2022, arXiv:2208.03260. [Google Scholar]
- Shin, Y.; Darbon, J.; Karniadakis, G.E. On the convergence of physics informed neural networks for linear second-order elliptic and parabolic type PDEs. arXiv 2020, arXiv:2004.01806. [Google Scholar] [CrossRef]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A System forLarge-Scale Machine Learning. In Proceedings of the Operational Suitability Data, Savannah, GA, USA, 2–4 November 2016; Volume 16, pp. 265–283. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch. In Proceedings of the Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Bettencourt, J.; Johnson, M.J.; Duvenaud, D. Taylor-Mode Automatic Differentiation for Higher-Order Derivatives in JAX. In Proceedings of the Program Transformations for ML Workshop at NeurIPS 2019, Vancouver, BC, USA, 8–14 December 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics—JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Pang, G.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional physics-informed neural networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Learning parameters and constitutive relationships with physics informed deep neural networks. arXiv 2018, arXiv:1808.03398. [Google Scholar]
- Winslow, A.M. Numerical solution of the quasilinear Poisson equation in a nonuniform triangle mesh. J. Comput. Phys. 1966, 1, 149–172. [Google Scholar] [CrossRef]
- Pan, M.; Chen, F.; Tong, W. Low-rank parameterization of planar domains for isogeometric analysis. Comput. Aided Geom. Des. 2018, 63, 1–16. [Google Scholar] [CrossRef]
- Zheng, Y.; Pan, M.; Chen, F. Boundary correspondence of planar domains for isogeometric analysis based on optimal mass transport. Comput. Aided Des. 2019, 114, 28–36. [Google Scholar] [CrossRef]


| Method | Bij | W | min(det J) | max(det J) |
|---|---|---|---|---|
| Coons | yes | 2.1640 | 0.3150 | 4.7044 |
| Inpaint | yes | 2.1598 | 0.4141 | 3.7948 |
| PINNs | yes | 2.1639 | 0.3125 | 4.3160 |
| Method | Bij | W | min(det J) | max(det J) |
|---|---|---|---|---|
| Coons | yes | 2.0834 | 0.9927 | 1.9635 |
| Inpaint | yes | 2.0812 | 0.6329 | 2.0284 |
| PINNs | yes | 2.0819 | 0.9928 | 1.8355 |
| Curve | KV | ||
|---|---|---|---|
| Method | Bij | W | min(det J) | max(det J) |
|---|---|---|---|---|
| Coons | yes | 2.4242 | 5.0519 | 31.7624 |
| Inpaint | yes | 2.1631 | 2.1631 | 2.5388 |
| PINNs | yes | 2.2287 | 3.3262 | 31.1962 |
| Curve | ||
|---|---|---|
| Method | Bij | W | min(det J) | max(det J) |
|---|---|---|---|---|
| Coons | yes | 6.7636 | 0.4713 | 161.3302 |
| Inpaint | no | 8.2491 | −15.7232 | 161.3302 |
| PINNs | no | 2.1853 | −1.1140 | 151.6974 |
| PINNs-Post | yes | 4.0696 | 4.7709 | 339.1136 |
| Curve | KV | ||
|---|---|---|---|
| Method | Bij | W | min(detJ) | max(det J) |
|---|---|---|---|---|
| Coons | no | ∞ | −51.7043 | |
| Inpaint | no | ∞ | −254.3629 | |
| PINNs | no | 2.9064 | −114.9197 | |
| PINNs-Post | yes | 2.6513 | 0.045 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falini, A.; D’Inverno, G.A.; Sampoli, M.L.; Mazzia, F. Splines Parameterization of Planar Domains by Physics-Informed Neural Networks. Mathematics 2023, 11, 2406. https://doi.org/10.3390/math11102406
Falini A, D’Inverno GA, Sampoli ML, Mazzia F. Splines Parameterization of Planar Domains by Physics-Informed Neural Networks. Mathematics. 2023; 11(10):2406. https://doi.org/10.3390/math11102406
Chicago/Turabian StyleFalini, Antonella, Giuseppe Alessio D’Inverno, Maria Lucia Sampoli, and Francesca Mazzia. 2023. "Splines Parameterization of Planar Domains by Physics-Informed Neural Networks" Mathematics 11, no. 10: 2406. https://doi.org/10.3390/math11102406
APA StyleFalini, A., D’Inverno, G. A., Sampoli, M. L., & Mazzia, F. (2023). Splines Parameterization of Planar Domains by Physics-Informed Neural Networks. Mathematics, 11(10), 2406. https://doi.org/10.3390/math11102406







