Analysis and Optimal Control of the Tungro Virus Disease Spread Model in Rice Plants by Considering the Characteristics of the Virus, Roguing, and Pesticides
Abstract
1. Introduction
2. Mathematical Models
3. Dynamic Analysis
3.1. Positivity
3.2. Non-Endemic Equilibrium Point
3.3. Basic Reproduction Numbers
3.4. Stability Analysis
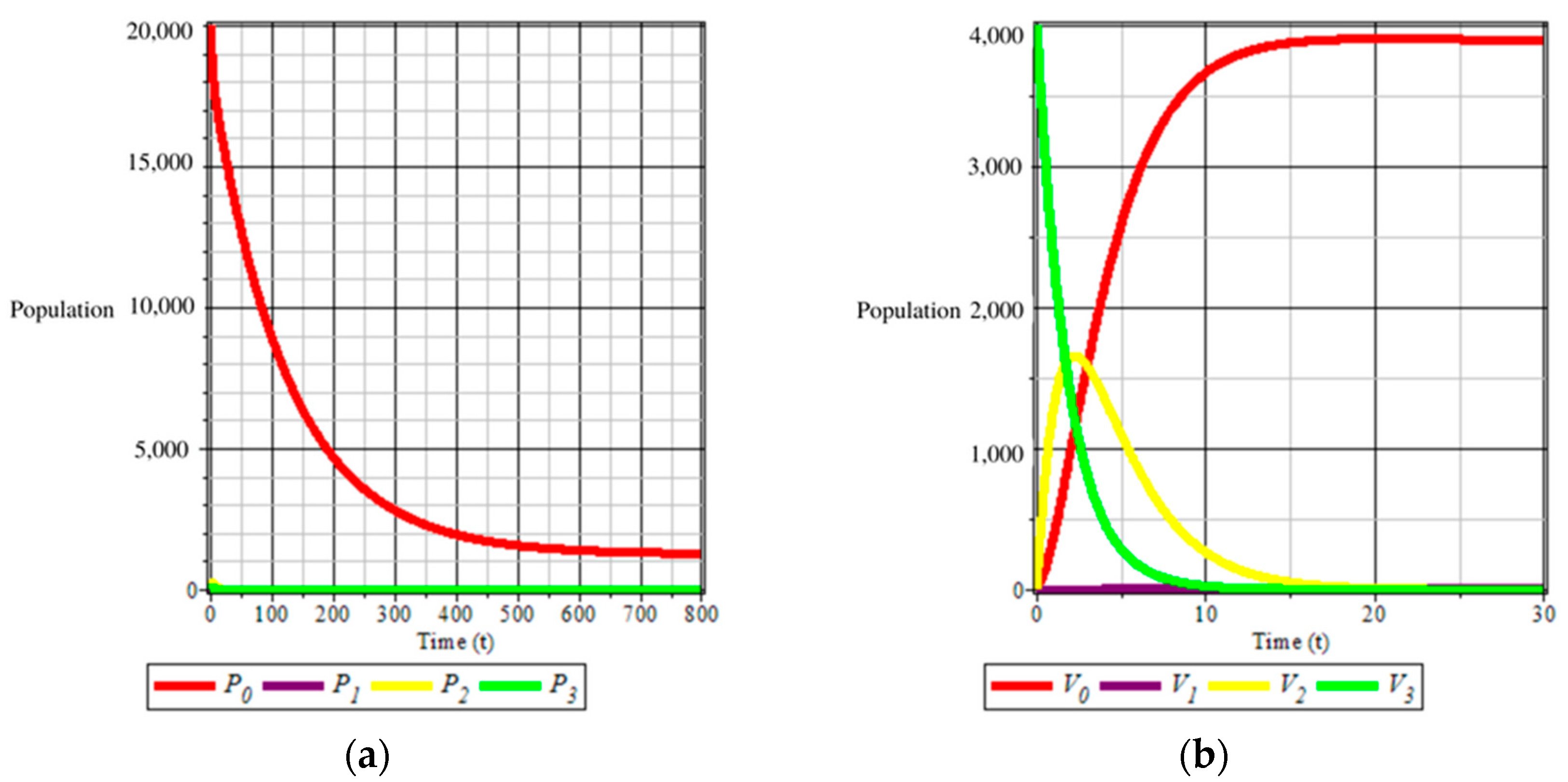
3.5. Numerical Simulation
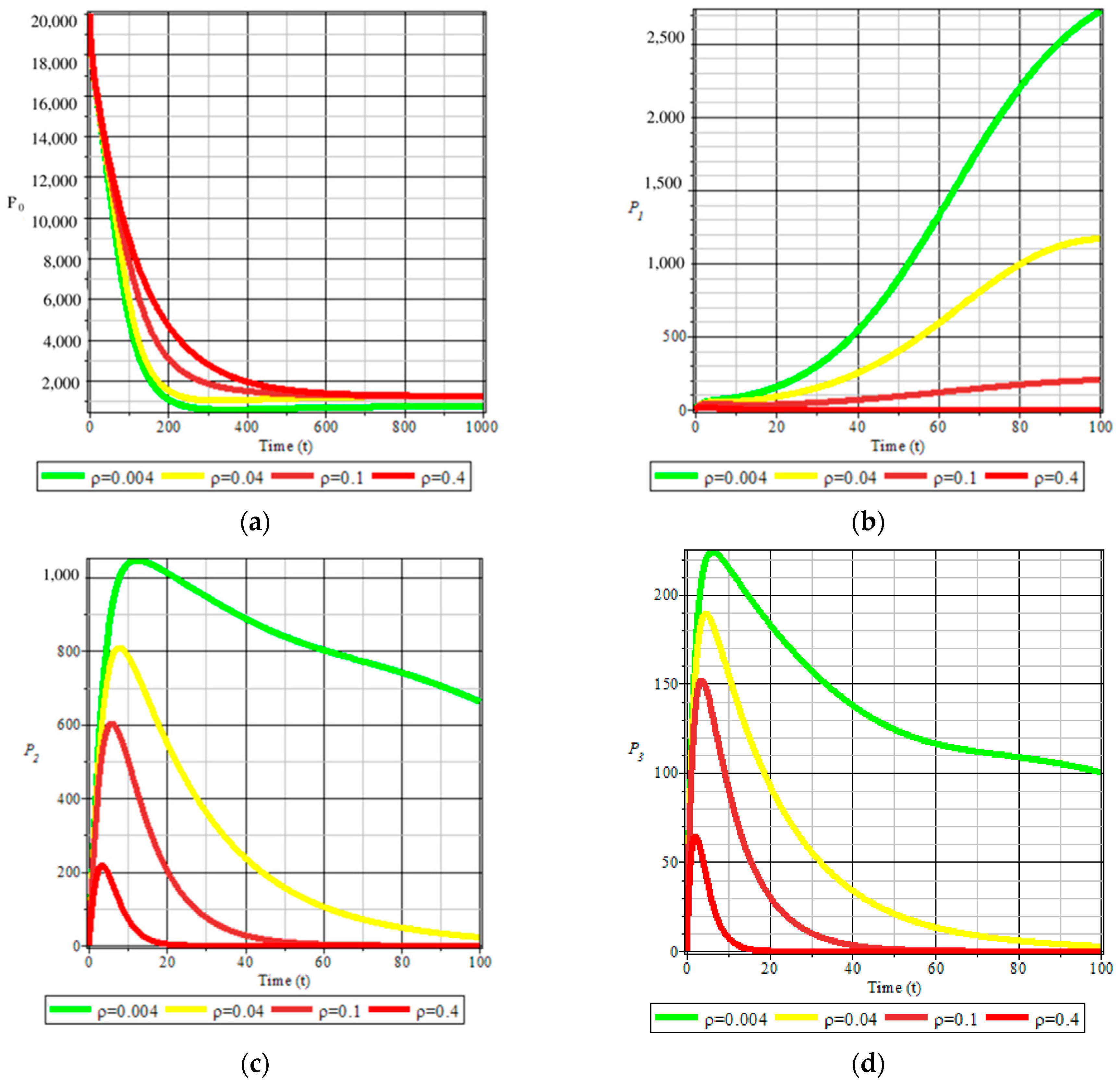
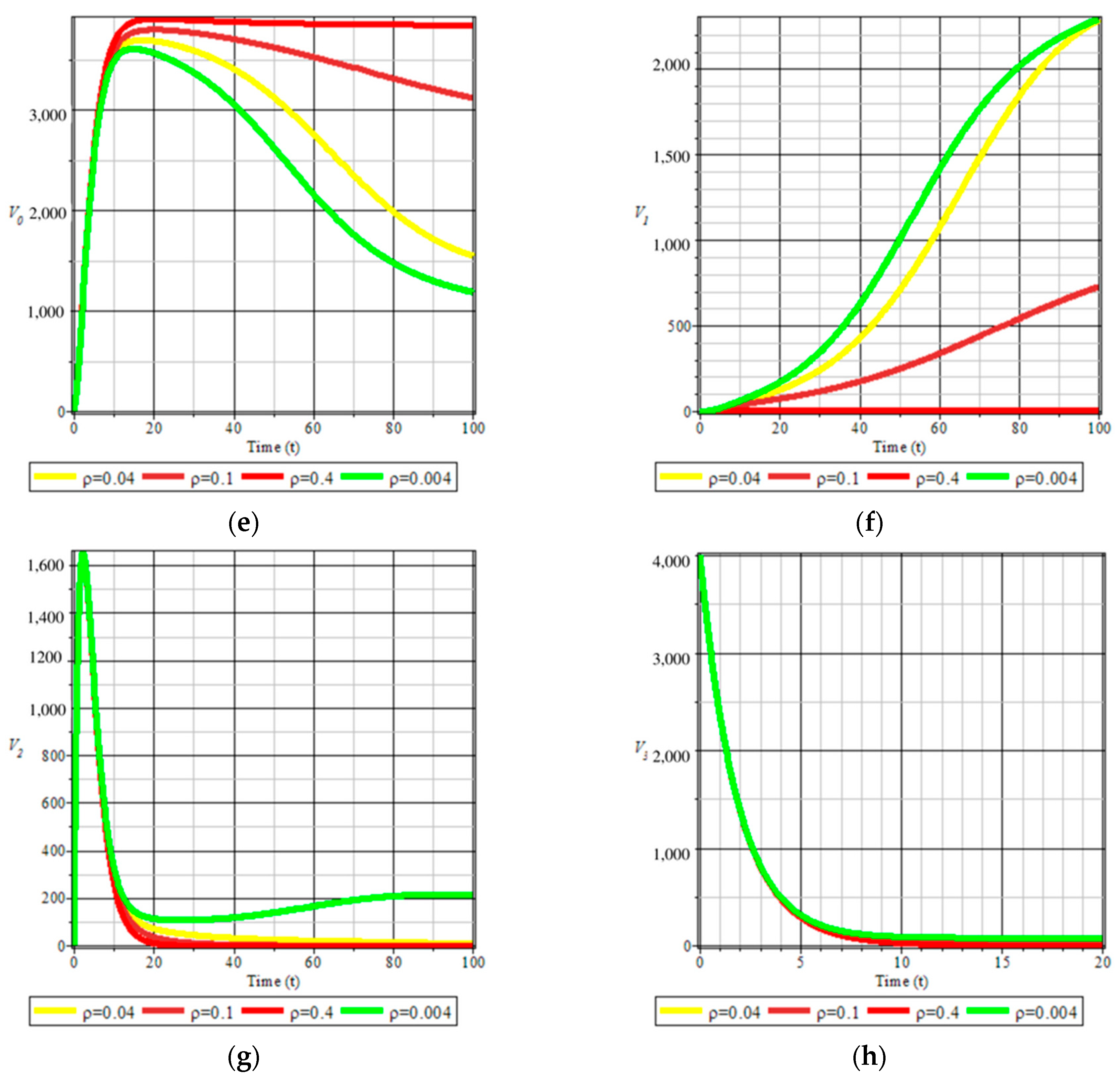
4. Sensitivity Analysis
5. Optimal Control
5.1. Optimal Control Model
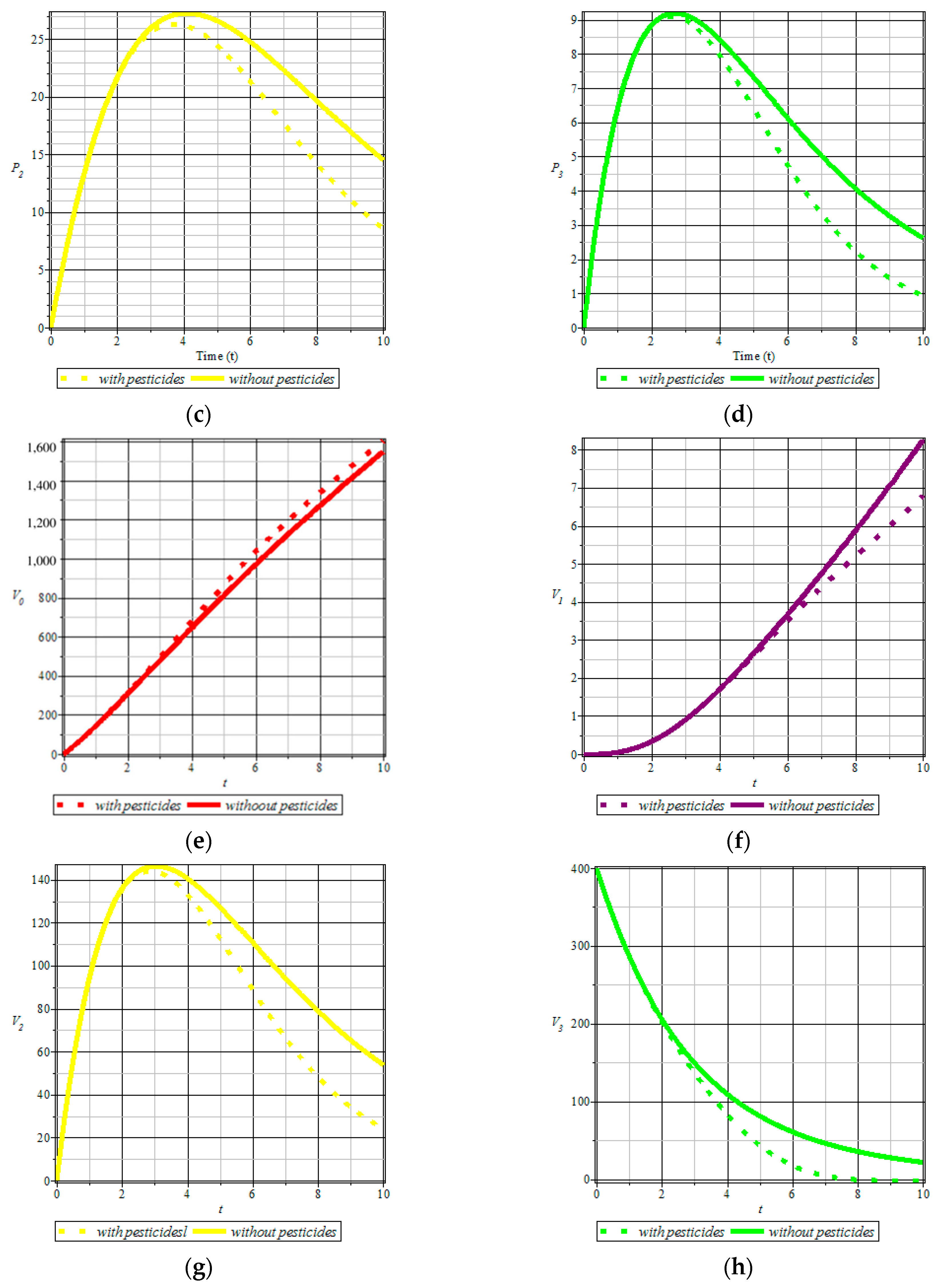
5.2. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bárcena, A.; Cimoli, M.; García-Buchaca, R.; Yáñez, L.F. The 2030 Agenda and the Sustainable Development Goals an Opportunity for Latin America and the Caribbean; United Nations Publication: Santiago, CA, USA, 2018. [Google Scholar]
- Jones, P.; Wynn, M.; Hillier, D.; Comfort, D. The Sustainable Development Goals and Information and Communication Technologies. Indones. J. Sustain. Account. Manag. 2017, 1, 1–15. [Google Scholar] [CrossRef]
- BBPOPT. Prakiraan Serangan OPT Padi Jagung Kedelai MT; Direktorat Jendral Tanaman Pangan: Jatisari, Indonesia, 2020. [Google Scholar]
- Umagapi, J.L. Identifying Factors to Solve Hunger: Reflecting on the Experience in Indonesia. J. Agric. Sci. Food Res. 2018, 9, 1–4. [Google Scholar]
- Suryadi, R.; Anindita, B.; Setiawan, S. Impact of The Rising Rice Prices on Indonesian Economy. J. Econ. Sustain. Dev. 2014, 5, 71–79. [Google Scholar]
- Rahmadanih, S.; Bulkis, M.; Arsyad, A.; Amrullah; Viantika, N.M. Role of farmer group institutions in increasing farm production and household food security. IOP Conf. Ser. Earth Environ. Sci. 2018, 157, 012062. [Google Scholar] [CrossRef]
- Merang, O.P.; Lahjie, A.M.; Yusuf, S.; Ruslim, Y. Productivity of three varieties of local upland rice on swidden agriculture field in Setulang village, North Kalimantan, Indonesia. Biodiversitas 2020, 1, 49–56. [Google Scholar]
- Sutardi. The Transformation of Rice Crop Technology in Indonesia: Innovation and Sustainable Food Security. Agronomy 2023, 13, 1. [Google Scholar] [CrossRef]
- Andika, Y.A. Determinants of Production of Agricultural Commodities of Food Crops in Bojonegoro Regency (Case Study of Farmers Accessing Tani Card and Non-Accessing Tani Card). East Java Econ. J. 2021, 5, 58–74. [Google Scholar] [CrossRef]
- Aqiel, M.; Maimun; Aman, F.; Ardy, S. Growth, Yield and Analysis of Rice (Oryza Sativa) Farming Due to the Application of PT.PIM Commercial Fertilizer. In Proceedings of the 2nd International Conference on Social Science, Political Science, and Humanities (ICoSPOLHUM 2021), Lhokseumawe, Indonesia, 26–27 November 2021. [Google Scholar]
- Soelaiman, V.; Ernawati, A. Pertumbuhan dan Perkembangan Cabai Keriting (Capsicum annuum L.) secara In Vitro pada beberapa Konsentrasi BAP dan IAA. Bul. Agrohorti 2013, 1, 62–66. [Google Scholar] [CrossRef]
- Sebayang, L. Teknik Pengendalian Penyakit Kuning pada Tanaman Cabai; BPTP: Sumatra Utara, Indonesia, 2013. [Google Scholar]
- Agrios, G.N. Plant Pathology, 5th ed.; Elsivier Academic Press: Gainesville, FL, USA, 2004. [Google Scholar]
- Kannan, M.; Saad, M.M.; Talip, N.; Baharum, S.N.; Bunawan, H. Complete Genome Sequence of Rice Tungro Bacilliform Virus Infecting Asian Rice (Oryza sativa) in Malaysia. Am. Soc. Microbiol. 2019, 8, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Budot, B.O. Suppression of cell wall-related genes associated with stunting of Oryza glaberrima infected with Rice tungro spherical virus. Front. Microbiol. 2014, 5, 1–9. [Google Scholar] [CrossRef]
- Bunawan, H.; Dusik, L.; Bunawan, S.N.; Amin, N.M. Rice Tungro Disease: From Identification to Disease Control. World Appl. Sci. J. 2014, 31, 1221–1226. [Google Scholar]
- Azzam, O.; Chancellor, T.C.B. The Biology, Epidemiology, and Management of Rice Tungro Disease in Asia. Plant Dis. 2002, 86, 88–100. [Google Scholar] [CrossRef] [PubMed]
- Azzam, O.; Cabunagan, R.C.; Chancellor, T. Methods for Evaluating Resistance to Rice Tungro Disease; International Rice Research Institute (IRRI): Manila, Philippines, 2000. [Google Scholar]
- Shim, J.; Torollo, G.; Angeles-Shim, R.B.; Cabunagan, R.C.; Choi, I.-R.; Yeo, U.-S.; Ha, W.-G. Rice tungro spherical virus resistance into photoperiod-insensitive japonica rice by marker-assisted selection. Breed. Sci. 2015, 65, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Bigirimana, V.d.P.; Hua, G.K.H.; Nyamangyoku, O.I.; Höfte, M. Rice Sheath Rot: An Emerging Ubiquitous Destructive Disease Complex. Front. Plant Sci. 2015, 6, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Meilin, A. Hama dan Penyakit Pada Tanaman Cabai Serta Pengendaliannya; Balai Pengkajian Teknologi Pertanian: Jambi, Indonesia, 2014. [Google Scholar]
- Blas, N.T.; Addawe, J.M.; David, G. A Mathematical Model of Transmission of Rice Tungro Disease by Nephotettix Virescens. Am. Inst. Phys. 2016, 1787, 080015. [Google Scholar]
- Blas, N.; David, G. Dynamical roguing model for controlling the spread of tungro virus via Nephotettix Virescens in a rice field. J. Phys. Conf. Ser. 2017, 893, 1–5. [Google Scholar] [CrossRef]
- Anggriani, N.; Yusuf, M.; Supriatna, A.K. The Effect of Insecticide on the Vector of Rice Tungro Disease: Insight from a Mathematical Model. Int. Interdiscip. J. 2017, 20, 6197–6206. [Google Scholar]
- Suryaningrat, W.; Anggriani, N.; Supriatna, A.K.; Istifadah, N. The Optimal Control of Rice Tungro Disease with Insecticide and Biological Agent. AIP Conf. Proc. 2020, 2264, 040002. [Google Scholar]
- Suryaningrat, W.; Anggriani, N.; Supriatna, A.K. Mathematical analysis and numerical simulation of spatial-temporal model for rice tungro disease spread. Commun. Math. Biol. Neurosci. 2022, 2022, 44. [Google Scholar]
- Maryati, A.; Anggriani, N.; Carnia, E. Stability Analysis of Tungro Disease Spread Model in Rice Plant Using Matrix Metho. Barekeng 2022, 16, 217–228. [Google Scholar] [CrossRef]
- Bokil, V.A.; Allen, L.J.S.; Jeger, M.J.; Lenhart, S. Optimal control of a vectored plant disease model for a crop with continuous replanting. J. Biol. Dyn. 2019, 13, 325–353. [Google Scholar] [CrossRef]
- Bi, K.; Chen, Y.; Wu, C.; Ben-Arieh, D. A memetic algorithm for solving optimal control problems of Zika virus epidemic with equilibriums and backward bifurcation analysis. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105176. [Google Scholar] [CrossRef]
- Bi, K.; Chen, Y.; Zhao, S.; Ben-Arieh, D.; Wu, C. A new zoonotic visceral leishmaniasis dynamic transmission model with age-structure. Chaos Solitons Fractals 2020, 133, 109622. [Google Scholar] [CrossRef]
- Bi, K.; Chen, Y.; Wu, C.; Ben-Arieh, D. Learning-based impulse control with event-triggered conditions for an epidemic dynamic system. Commun. Nonlinear Sci. Numer. Simul. 2021, 108, 106204. [Google Scholar] [CrossRef]
- Zhao, S.; Kuang, Y.; Wu, C.; Ben-Arieh, D.; Ramalho-Ortigao, M.; Bi, K. Zoonotic visceral leishmaniasis transmission: Modeling, backward bifurcation, and optimal control. J. Math. Biol. 2016, 73, 1525–1560. [Google Scholar] [CrossRef] [PubMed]
- Onah, I.S.; Aniaku, S.E.; Ezugorie, O.M. Analysis and optimal control measures of diseases in cassava population. Optim. Control Appl. Meth. 2022, 43, 1450–1478. [Google Scholar] [CrossRef]
- Hugo, A.; Lusekelo, E.M.; Kitengeso, R. Optimal Control and Cost Effectiveness Analysis of Tomato Yellow Leaf Curl Virus Disease Epidemic Model. Appl. Math. 2019, 9, 82–88. [Google Scholar]
- Matofali, A.X. Modelling and Optimal Control of Insect Transmitted Plant Disease. J. Math. Appl. 2020, 8, 1. [Google Scholar]
- Liao, Z.; Gao, S.; Yan, S.; Zhou, G. Transmission dynamics and optimal control of a Huanglongbing model with time delay. Math. Biosci. Eng. 2021, 18, 4162–4192. [Google Scholar] [CrossRef]
- Amelia, R.; Anggriani, N.; Supriatna, A.K.; Istifadah, N. Mathematical Model for Analyzing the Dynamics of Tungro Virus Disease in Rice: A Systematic Literature Review. Mathematics 2022, 10, 2944. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Agusto, F.; Khan, M. Optimal Control Strategies for Dengue Transmission in Pakistan. Math. Biosci. 2018, 305, 102–121. [Google Scholar] [CrossRef] [PubMed]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]




| Variable/ Parameter | Description |
|---|---|
| Susceptible green leafhoppers | |
| Green leafhopper infected with RTSV | |
| Green leafhopper infected with RTBV | |
| Green leafhopper infected with RTSV + RTBV | |
| Susceptible rice plants | |
| RTSV-Infected Rice Plants | |
| RTBV-Infected Rice Plants | |
| RTSV + RTBV-Infected Rice Plants | |
| Transmission rate of RTSV + RTBV by green leafhoppers infected with RTSV + RTBV in susceptible rice plants | |
| RTSV transmission rate by green leafhoppers infected with RTSV in susceptible rice plants | |
| Transmission rate of RTSV by green leafhoppers infected with RTSV + RTBV in susceptible rice plants | |
| Transmission rate of RTBV by green leafhoppers infected with RTBV in susceptible rice plants | |
| Transmission rate of RTBV by green leafhoppers infected with RTSV + RTBV in susceptible rice plants | |
| Transmission rate of RTSV + RTBV by green leafhoppers infected with RTSV + RTBV on rice plants infected with RTSV + RTBV | |
| Transmission rate of RTSV + RTBV by green leafhoppers infected with RTSV + RTBV on RTBV-infected rice plants | |
| The acquisition rate of RTSV + RTBV-infected rice plants by susceptible vectors to RTSV + RTBV-infected green leafhoppers. | |
| The acquisition rate of RTSV-infected rice plants by susceptible vectors to RTSV-infected green leafhoppers. | |
| The rate of acquisition of RTBV-infected rice plants by RTSV-infected green leafhoppers to RTSV + RTBV-infected green leafhoppers | |
| Roguing effectiveness rate |
| Initial Value/ Parameter | Value | Unit | Citation | Initial Value/ Parameter | Value | Unit | Citation |
|---|---|---|---|---|---|---|---|
| 0 | Vector | [23] | 0.996 | [22] | |||
| 0 | Vector | [23] | 0.996 | [22] | |||
| 0 | Vector | [23] | 0.5 | [22] | |||
| 4,000 | Vector | [23] | 0.33 | [22] | |||
| 20,000 | Plant | [23] | 0.996 | [22] | |||
| 0 | Plant | [23] | 0.008 | [22] | |||
| 0 | Plant | [23] | 0.009 | [22] | |||
| 0 | Plant | [23] | 0.0125 | [22] | |||
| 0.035 | [22] | 0.0125 | [22] | ||||
| 0.09 | [22] | 0.001 | [22] | ||||
| 0.01 | [22] | 0.033 | [22] | ||||
| 0.08 | [22] | 100,000 | Vector | [22] | |||
| 0.06 | [22] | 30,000 | Plant | Assumption | |||
| 0.07 | [22] | 0.03 | [22] | ||||
| 0.40 | [22] | 0.033 | [22] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amelia, R.; Anggriani, N.; Supriatna, A.K.; Istifadah, N. Analysis and Optimal Control of the Tungro Virus Disease Spread Model in Rice Plants by Considering the Characteristics of the Virus, Roguing, and Pesticides. Mathematics 2023, 11, 1151. https://doi.org/10.3390/math11051151
Amelia R, Anggriani N, Supriatna AK, Istifadah N. Analysis and Optimal Control of the Tungro Virus Disease Spread Model in Rice Plants by Considering the Characteristics of the Virus, Roguing, and Pesticides. Mathematics. 2023; 11(5):1151. https://doi.org/10.3390/math11051151
Chicago/Turabian StyleAmelia, Rika, Nursanti Anggriani, Asep K. Supriatna, and Noor Istifadah. 2023. "Analysis and Optimal Control of the Tungro Virus Disease Spread Model in Rice Plants by Considering the Characteristics of the Virus, Roguing, and Pesticides" Mathematics 11, no. 5: 1151. https://doi.org/10.3390/math11051151
APA StyleAmelia, R., Anggriani, N., Supriatna, A. K., & Istifadah, N. (2023). Analysis and Optimal Control of the Tungro Virus Disease Spread Model in Rice Plants by Considering the Characteristics of the Virus, Roguing, and Pesticides. Mathematics, 11(5), 1151. https://doi.org/10.3390/math11051151






