Abstract
Monkeypox (mpox) is a zoonotic viral disease that has caused recurring outbreaks in West Africa. The current global mpox virus (mpoxv) epidemic in endemic and non-endemic areas has seriously threatened public health. In this study, we design an SEIR-based deterministic model that considers prodromal stage, differential infectivity, and hospitalisation to investigate the transmission behaviour of mpoxv, which could help enhance control interventions. The model is theoretically analyzed by computing essential epidemiological quantities/dynamics, such as the basic reproduction number, which estimates the number of secondary infections caused by a typical primary case in an entirely susceptible community. Stability of the model’s equilibrium states is examined to evaluate the transmission potential of the mpoxv. Furthermore, partial rank correlation coefficient was adopted for sensitivity analysis to determine the top-rank model’s parameters for controlling the spread of mpoxv. Moreover, numerical simulations and model predictions are performed and are used to evaluate the influence of some crucial model parameters that help in strengthening the prevention and control of mpoxv infection.
Keywords:
monkeypox virus; epidemic; infectious diseases; mathematical modelling; stability analysis MSC:
34A08; 34A55; 65L09; 92D25; 92D30
1. Introduction
Public health and the economy continue to face a serious worldwide threat from emerging diseases [1]. A contagious disease known as monkeypox (mpox) is caused by the monkeypox virus (mpoxv) [2]. It is a viral infection that can spread from animals to humans (also known as viral zoonosis) [2]. Other zoonotic diseases causing serious concerns to public health include Lassa fever [3] and query fever [4]. In 1970, the first human cases were found in the Democratic Republic of the Congo, Liberia, and Sierra Leone [2]. The unexpected large outbreaks of mpoxv in both endemic and non-endemic nations, as well as the prevalence of sexual transmission routes, have recently raised severe concerns globally [2,5,6].
Even though mpox is a zoonotic viral infection found primarily in the tropical rainforests of Central and West Africa, it is occasionally exported to non-endemic areas. Contact with an infected individual, animal, or material can transmit mpoxv to humans [2]. In Nigeria, the primary mpoxv transmission routes are zoonotic and human-to-human. Potential symptoms comprise swollen lymph nodes, fever, lymphadenopathy, headache, and a rash that develops blisters and then encrusts the entire body [2]. The incubation period lasts 5 to 21 days, and 9.8 (95% CI: 5.9–21.4) days is the estimated mean serial interval (i.e., the interval between an infected person’s symptoms and those of a subsequently infected person) [2,7,8,9].
Over 83,000 people were affected by the virus between 10 May and 29 December 2022 in 110 locations with >98% of those locations with no previous infection [10,11]. Additionally, a significant proportion has been linked to males, especially those who identify as gay or bisexual [2,6,12]. There is no evidence that the virus might spread via sexual contact. However, transmission via close contact, particularly sexual contact, has been reported [13,14].
Smallpox vaccines are also effective against mpoxv infection [2]. However, the vaccine’s inadequacy is a serious problem and might make the situation more contagious. Thus, it is essential to put greater effort into non-pharmaceutical intervention control strategies for prompt mpoxv control. On 21 July 2022, the World Health Organization (WHO) declared the virus a Public Health Emergency of International Concern (PHEIC) due to the recent rise in mpoxv in non-endemic countries linked to an epidemic in the United Kingdom [2,15]. The basic reproduction number (, or the typical number of secondary mpoxv cases produced by a single case throughout the infectious period in a community without immunity or any intervention) of the mpoxv was predicted by early models to be >1 in populations of men who have sex with men (MSM) and ≤1 in other settings [2,7,16,17]. As a result, investigating the effectiveness of non-pharmaceutical intervention options to aid in transmission halt is critical.
To comprehend mpoxv transmission, considerable epidemiological models have been developed and employed, for instance, [5,12,18,19,20,21,22] and the references therein. In order to study the mpoxv transmission patterns and control strategy, Yuan et al. [5] developed a model taking into account the zoonotic transmission route. They discovered that effectively quarantining contacts with mpoxv in high-risk populations by post-exposure vaccination greatly slows the transmission. Additionally, in their similar research, Yuan et al. [18] proposed a new model to scrutinise the efficiency of vaccination and other control means at large gatherings. Their research demonstrates that, in the absence of public health management measures, the risk of a mpoxv outbreak persists at high levels during mass gathering occasions. They recommended that stringent contact tracing, testing, case identification, and isolation, as well as awareness campaigns, are crucial tactics to stop the spread of the mpoxv outbreaks. Endo et al. [12] developed a transmission model and applied it to empirical sexual partnership data to show that the heavy-tailed sexual partnership distribution could explain the ongoing spread of mpoxv among MSM population. They estimated to be >1 in the MSM context, complicating outbreak containment. They proposed that enlightenment programs could facilitate the prevention and early detection of mpoxv among MSM communities.
Although clinically less severe than smallpox, the symptoms of the viral zoonosis mpox are comparable to those experienced by individuals with smallpox in the past. Mpox has taken over as the most significant orthopoxvirus for public health since smallpox was eradicated in 1980 and smallpox vaccinations were subsequently discontinued. Primarily affecting Central and West Africa, the virus has been spreading into cities and is frequently seen close to tropical rainforests. Numerous rodent species and non-human primates serve as hosts for animals. As a result, it is critical to investigate more information and validate facts about the so-called ailment mpox, which has inspired us to conduct this study, thereby establishing more facts about the ailment.
This study’s objective is to develop a novel dynamic model to simulate the spread of mpoxv as an emerging zoonosis. The model incorporates human-to-human and animal-to-human transmission to evaluate the impact of high- and low-risk populations, various infection stages, and isolation on overall transmission. The model is utilised to determine the most effective tactics for containing the mpoxv outbreak in Nigeria. The results would help with a more thorough investigation of the mechanisms of disease transmission within and between the animal reservoir and humans, which would help calculate the risk of outbreaks via various transmission pathways.
Our model distinguishes different phases of the infection, including asymptomatically infected (prodromal) and symptomatically infected (mild and severe) stages [2,11,23]. The mild stage is characterised by common signs and symptoms that can be treated if caught early, including fever, exhaustion, body pains, and very light rashes in some areas of the body. The severity of the infection, however, is dependent on the infected individual’s health and the method of exposure, with complex symptoms including extensive rashes that affect all parts of the body, including the face, mouth, eyes, soles of the feet, throat, and genital and anal areas.
This paper is summarised as follows. Following this introductory Section 1, the mpoxv model is formulated and theoretically analyzed in Section 2 and Section 3, respectively. Numerical simulations and sensitivity analysis are conducted in Section 4. We end the paper with concluding remarks in Section 5.
2. Methods
2.1. Mpox Outbreak Data
More often, we retrieved the epidemiological cases data for the mpoxv infection on a weekly basis for Nigeria issued by the Nigeria Center for Disease Control (NCDC) for the situation from January 1 through August 27 of 2022 [23] after laboratory confirmation and case characterisation of mpoxv from the NCDC. From the data, we derived the weekly cumulative incidence and examined the Nigerian mpoxv cases scenarios.
2.2. Mpoxv Model Description
The model developed in this study will describe epidemiologically the dynamics of mpoxv transmission by examining the mpoxv outbreak’s propagation patterns and prevention measures using a traditional SEIR-typed model. The proposed model accounts for high- and low-risk susceptible populations to investigate the transmission behaviour of the mpoxv. We specifically distinguished between the various infectious stages to evaluate the overall dynamics of mpoxv epidemic propagation. Hospitalisation is also taken into account by the model as an intervention strategy, which is vital for the prevention and management of mpoxv. Isolation is usually enforced to help curtail widespread disease outbreaks, where infected people are admitted to hospitals or isolation facilities [5,24,25]. The parameter designates the fraction of newly recruited people moving to a high-risk susceptible population, , while represents the fraction of people moving to a low-risk susceptible population, . The parameters and represent recruitment rates for humans and rodents, respectively. All other parameters are epidemiologically explained in Table 1. We separated the total population of humans at time t, denoted by , into high-risk susceptible, ; low-risk susceptible, ; exposed, ; prodromal (asymptomatically infected), ; mild infectious, ; severe infectious, ; hospitalisation, ; and recovered, . Hence,

Table 1.
Enunciation of variables and parameters of governing system (1).
Similarly, we separated the overall population of rodents at time t, indicated by , into , , , and , hence
In light of the aforementioned details, we illustrated the mpoxv model in Figure 1. The following systems of non-linear ordinary differential equations are satisfied by the state variables and model parameters listed in Table 1:
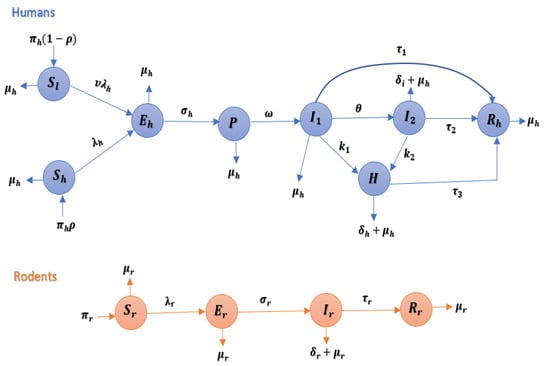
Figure 1.
Model (1) representation in a diagram. Transitions are indicated by solid arrows, and per capita flow rate between compartments is indicated by expressions adjacent to the arrows. Blue compartments represent the human population, and the orange compartments represent the rodent population.
The forces of infection for humans and rats are provided here by the model (1) variables, respectively.
where, , , and indicate human-to-human, rodent-to-human, and rodent-to-rodent transmission routes, respectively.
2.3. Fundamental Properties of the Mpoxv Model
As model (1) scrutinises the transmission of mpoxv in humans and rodents, all the parameters and variables of the model are taken to be strictly positive. To explore the fundamental qualitative properties of model (1), the rate of change of the overall populations of humans and rodents are firstly determined. Hence
and
2.3.1. Positivity of Model Solutions
To be epidemiologically significant, the mpoxv model (1) must show that all of the state variables are non-negative for all time . Alternatively, solutions of model system (1) with positive initial data will remain positive for all times .
Lemma 1.
Let the initial data , where . Then the solutions of model (1) are positive for all .
Proof.
Let Thus, . Since, it follows from the first equation of (1) that
Applying comparison theorem in conjunction with separation of variables method, we have
Hence, . Similarly, it can be shown that the remaining components of , i.e., are all non-negative for all . Hence, for all . □
2.3.2. Invariant Region
The following biological feasible region is considered,
To ensure that any system solutions that begin in the area remain in the area for all non-negative times t (i.e., ), the variables and given in Equations (3) and (4) have been simplified. Until now, the region has been positively invariant; thus, solutions only apply to this region are sufficient. Thus, model (1) satisfies the results for a normal existence, uniqueness, and continuation as per previous works [26,27,28,29].
3. Analytical Results
3.1. Disease-Free Equilibrium and Basic Reproduction Number
3.2. Basic Reproduction Number
The concept of the next-generation matrix (NGM) [30] is used to compute the basic reproduction number () for the governing model (1) [24,30,31,32]. The linear stability of is obtained by implementing NGM technique for model (1) [30,31], with F matrices, designating the infectious new terms, and V, designating the other transferring terms, with the general formula , where the in the relation characterises the spectral radius of the NGM.
Therefore, the is computed as follows.
As a result, the definitions of the mpoxv infection and transition matrices are respectively computed as:
where , , , , , , , , , , , and . Straightforward computation produces
and
Hence, the reproduction numbers for human and rodent populations are respectively obtained as:
So that the is now given as
where , , , , and .
By considering [30] and the local stability of the DFE of model (1), we state the following useful result. Similar results can be found in [33].
Theorem 1.
The DFE of model (1) is locally-asymptotically stable whenever and unstable if , with .
The epidemiological essence of the results above implies that a measly intake of mpoxv infection would not result in a substantial outbreak when . For the mpoxv containment measure, the prerequisite for making is suitable but unnecessary. As a result, when is decreased to less than 1, the disease eventually disappears, and when is increased to more than 1, the disease lingers. Hence, efficacious intervention strategies are mandated to mitigate the illness effectively [31].
3.3. Endemic Equilibrium and Its Stability
3.3.1. Endemic Equilibrium
Invasion of mpoxv indicates that at least one infected compartment is not empty. The vector field of (1) is set to zero, and we performed some algebraic calculations, which resulted in an endemic equilibrium (EE) state. Thus, the EE is calculated below.
Suppose the region at EE is given by
In forms of and , the EE becomes computed as follows.
Epidemiologically, the presence of EE demonstrates that the mpoxv circulates and prevails in the community by indicating that at least one of the infected classes in the model is not empty.
3.3.2. Global Stability Analysis of the Endemic Equilibrium
Herein, we examined the interior-of-the-feasible-region solutions for the governing model that converge to the unique EE provided by only if . At , the mpoxv will spread over the neighbourhood and endure. With the help of the Lyapunov function (LF) way, which can be possible by generating the LF from the governing system to confirm the general stability of the EE; see [26,27,34] and [34] for examples of other modelling assessments that have extensively employed this strategy.
Theorem 2.
The EE, , is globally-asymptotically stable (GAS) in the Ω region only if , and the condition (i) , (ii) , and (iii) , hold.
For the proof of the above Theorem 2, see below.
Proof.
Considering the technique as in [26,27,28,35,36] by constructing an LF as follows:
implies the derivative of the LF (11), along with the solutions of (1), are given by
Surmise that , implies, yields , and, if , implies . Thus for any [3,26,27,28,37].
Employing these definitions, with some algebra from (23) and the conditions above, yields
Similarly,
From Equation (23), we also have
Similarly,
Hence,
Equations (13)–(29) and conditions(i)–(iii) ensure that . Further, the equality holds only if , , , , , , , , and . Thus, the EE state (10) serves as the only invariant positive set to the governing model (1) contained entirely in . Note that and were not included in the GAS analysis since individuals in these classes have already recovered from the mpoxv and are not of much epidemiological interest in this regard. Hence, it follows from LaSalle’s invariance principle [34] that every solution to the Equation (1) with initial conditions in converge to EE points, , as . Thus, the positive EE is globally asymptotically stable. □
3.4. Bifurcation Analysis
The center manifold theory (CMT) is applied to examine the bifurcation analysis [38]. We look at the parameters in the model (1) that produce forward, or backward bifurcation [3,30,38]. The moment crosses unity from below, a small positive asymptotically stable equilibrium arises, and the DFE loses stability [38]. In the subsequent paragraph, we examine whether forward (exchange of DFE and EE stability at ) or backward bifurcation occurs in the current model (1). Thus, the results below follow.
Theorem 3.
Forward bifurcation occurs in the current mpoxv model (1) at only if the bifurcation coefficients, A and B, are negative and positive, respectively.
Proof.

The proof of the above theorem is based on the CMT [38,39]. Consider the expression , with representing the bifurcation parameter and f being continuously differentiable at least twice in both x and . The DFE () is the point and the local stability of the DFE changes at the point [30]. We now demonstrate that there exists a nontrivial equilibrium around the bifurcation point .
Surmise that is taken as a bifurcation parameter and taking from Equation (3) implies by Theorem A1.1, the DFE, , is locally stable only if and unstable when . Here, is a bifurcation value.
In a simpler way, let , , , , , , , , , , , and , so that and . Additionally, by using the identical vector notation with , the model (1) as where is as follows:
and each of the linked forces of infection is represented by
The Jacobian matrix of system (30), computed from the relation , where F and V are infections and transition matrices, respectively, evaluated at the DFE with , yields:
where , , , , , , , , , , , and .
The Jacobian matrix of the system (30) has a simple zero eigenvalue (other eigenvalues have negative real parts). Thus, the CMT [30,38] may be employed to scrutinise the dynamics of the model (30) located at [38] . The following computations are carried out using the notations in [38].
Eigenvectors of : When , one can observe that the has a right eigenvector (corresponding to the zero eigenvalues), given by , where
In similar way, the components of the left eigenvector of (corresponding to the zero eigenvalues), indicated by , are given by
Taking to account the free components (entry) are taken to be and respectively, where
and
so that (in line with [38]).
It can be demonstrated that the related bifurcation coefficients, A and B, are given, respectively, by computing the non-zero partial derivatives of :
where , , and .
Since , , , and , it implies that , and hence we have forward bifurcation if and only if (i.e., when and since ), else backward bifurcation (i.e., when ). To prove the above numerically, we used the parameter values given in Table 2 to verify that A () and B () are negative and positive, respectively.

Table 2.
Table summarizing model parameter values (1).
Hence, the mpoxv model (1) exhibits the phenomenon of forward bifurcation at . No EE appears if , and the DFE is the only local attractor, but if , then the EE exists. For this reason, there is a forward bifurcation because, in the neighbourhood of the bifurcation point, the disease prevalence is an increasing function of , which implies that the mpoxv model (1) has forward bifurcation property. □
4. Numerical Results
4.1. Model Prediction
We used the prior approach outlined in [35] to validate model (1) utilizing mpoxv surveillance data produced and released by the NCDC in [23]. Using the R statistical software, Pearson’s chi-square and the least square method are used for fitting the data using the R (version 4.2.1). The model is validated using actual mpoxv scenarios for cases from 1 January to 27 August 2022 (specifically for 35 epidemiological weeks). The model suited well to the mpoxv situation report in Nigeria using suitable biological parameters according to the results. This shows that the model can be used to understand the spread of mpoxv in the community. The total number of cases for 35 epidemiological weeks in the fitting findings of mpoxv confirmed cases are depicted in Figure 2.
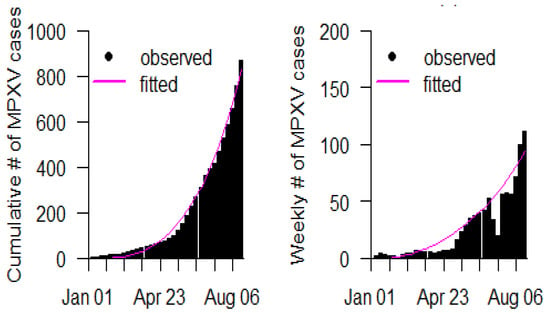
Figure 2.
The outcome of model fittings for the mpoxv outbreak in Nigeria. The black dots represent the real mpoxv scenario, and the purple curve represents the mpoxv model’s prediction.
We obtained demographic biological parameters for mpoxv in Nigeria from [40]. We also computed other related demographic parameters, including and . is evaluated as 8100 per day. Given that, as of last year, the predicted life expectancy in Nigeria was each year, indicating that = . Other than that, everything is set as in Table 2. It is crucial to comprehend that poor resource settings produced most of the mpoxv cases in Nigeria. Figure 2 shows the model-fitting result for 35 epidemiological weeks (i.e., from January through August 2022). The initial conditions employed are given: , , , , , , , , , , , . Moreover, from the prediction result, we observed that the mpoxv cases had reached an all-time peak since 2022, suggesting timely intervention to curtail the spread of the mpoxv outbreak in Nigeria.
4.2. Numerical Simulations
In this part, we analysed the model numerically to gain a profound understanding of the dynamic behaviour of the model. The classical model (1) is numerically simulated in this part using the biological parameters specified in Table 2. In order to solve the nonlinear model depicted in the model (1). The numerical findings are presented using first-order convergent numerical techniques. The numerical method used to solve differential equations of integer order is precise, conditionally stable, and convergent. Based on factors that are treated as variables, we were able to provide the graphical results.
We conducted numerical simulations to examine some key model parameters and evaluate the dynamics of each compartment. We examined the dynamics of the model compartments and found that several vital parameters substantially impact whether the mpoxv increases or decreases. These variables can also provide insight into how to lessen transmissions, such as by reducing the dangers to the most susceptible groups and the number of sick people. Additionally, understanding these quantities helps us better understand the contagiousness of a particular infection and how changes in the environment and certain interventions can affect it. In order to achieve this, the individual compartments’ dynamic features are represented in Figure 3. Simulation results showing the effect of the rate of infectiousness in humans moving from to are depicted in Figure 4a,b with some varying values, which shows increasing and decreasing patterns at some points. Moreover, the model was simulated to show the impact of hospitalisation rate parameters on and H, and on and H in Figure 4c–f, respectively. The transmission rates and probability are simulated with some varying values on the compartments , in Figure 4g–i, respectively. The behaviour of the rate at which mpoxv progresses, , from P to , is shown n the compartments P to in Figure 4i,j.
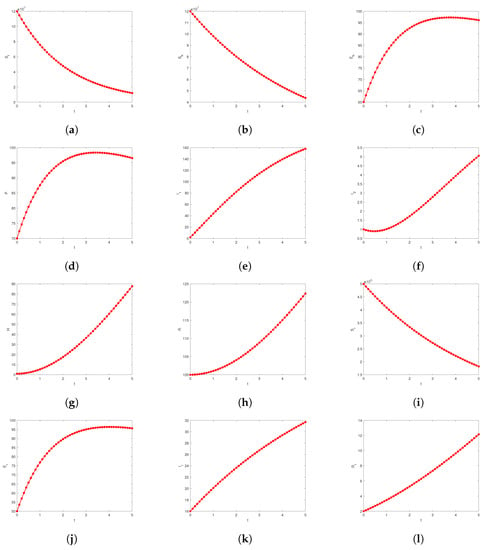
Figure 3.
Simulation results portraying the mpoxv dynamics of the individual compartments of the governing model (1).
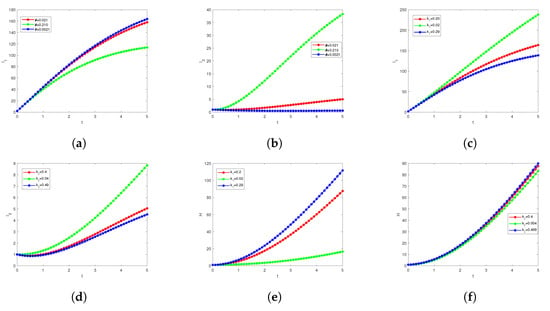
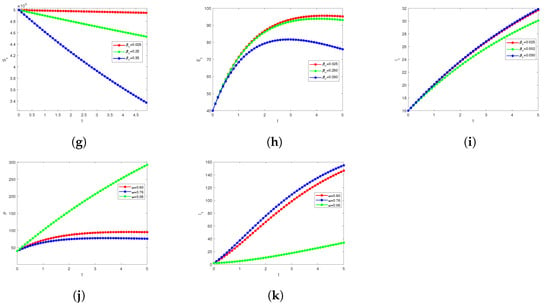
Figure 4.
Patterns of the model’s compartments based on varying some crucial parameters to show the overall transmission behaviour of mpoxv.
4.3. Sensitivity Analysis
In this subsection, sensitivity analysis is scrutinised to determine the powerful impact and influence of various parameters on mpoxv transmission in Nigeria. The sensitivity analysis of (1) with and infectious attack rate as response functions were revealed using the partial rank correlation coefficient (PRCC); see Figure 5. This technique has been widely used previously [46,47]. Our study outcomes imply and parameters are the most sensitive parameters of the model, necessitating close monitoring to reduce mpoxv transmission in Nigeria and other countries with similar settings. The diagrammatic representation of the PRCC in terms of and infectious attack rate is depicted in Figure 5. The parameter values in Table 1 are employed to perform the job.
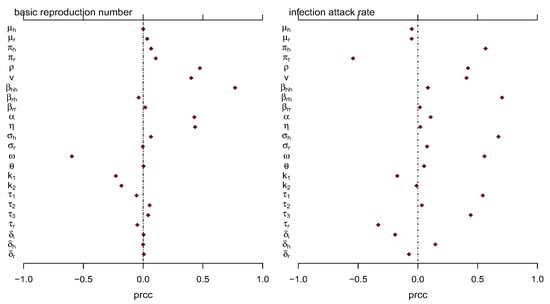
Figure 5.
The infectious attack rate in connection to model parameters and the partial rank correlation coefficient of . The bars show the 95% confidence interval, while the dots show the calculated correlation. Table 2 summarises the values of the parameters employed.
5. Concluding Remarks
The current spread of mpoxv in endemic and non-endemic countries appears to be strikingly different from previous epidemics, with a disproportionate number of cases in MSM [2,12]. Mpoxv is primarily transmitted from animals to humans in most endemic countries, such as Nigeria [2,11,23]. In this research, we proposed an epidemiological modelling approach to examine the transmission of mpoxv considering high-and low-risk susceptible populations. The model also considered the prodromal phase, mild and severe infection stages for mpoxv, as well as the role of hospitalisation to assess the prevailing mpoxv infection in Nigeria. The model fitted well to the Nigerian case scenarios to assess the current mpoxv situation, which would enhance mpoxv control, especially in West Africa, where the disease has been endemic for a long time.
We rigorously analysed the model mathematically and obtained some crucial threshold dynamics, such as the , which can be used to assess the effect of mpoxv control strategies. Subsequent theoretical analysis also revealed that the DFE of the model is GAS when is less than or equal to unity and unstable when it is greater than 1. We also found that the EE is GAS when is greater than 1, indicating the potential for mpoxv to spread in a community.
Moreover, the plausibility of the occurrence of bifurcation in the current model was investigated theoretically, and we found that forward bifurcation likely exists (see Section 3.4 for more detail). Consequently, forward bifurcation in the present model indicates the DFE and EE exchange stability at . That is, forward bifurcation exists in the current model at , and an endemic equilibrium exists (which is GAS under certain conditions as stated in Theorem 2) when . By epidemiological implication, the infection will persist in a community if the average number of newly infected individuals is greater than 1. Hence, we observed that the stability behavior of the current model changes (from stable to unstable) around the endemic equilibrium when the bifurcation parameter varies [48,49].
Results from our simulations suggest that the risk of a mpoxv outbreak remains high, especially in high-risk areas without intervention. This includes rural communities where the interaction of humans and rodents is more prevalent [7,17]. In particular, the broader populace could be at risk if transmission rates rise among high-risk groups. In the event of such a situation brought on by virus evolution, isolation of symptomatic cases may not be sufficient to stop the spread. Case detection and contact tracking in high-risk groups would become crucial techniques to avoid bridging from high-risk to low-risk groups. Additionally, areas with a higher percentage of MSM may face greater dangers and need stricter public health measures, such as contact tracing and isolation. Monitoring the prevalence of mpoxv in animals is essential to indicate the likelihood of mpoxv outbreaks since the virus’ transmission is tightly linked to seasonal fluctuations in animal host abundance and activity level [5].
We also investigated sensitivity analysis using the partial rank correlation coefficient to determine the powerful impact and influence of various model parameters on mpoxv transmission in Nigeria. Our sensitivity analysis results (with and infection attack rate as response functions) show that the parameters and are the most sensitive parameters. Indicating that reducing mpoxv transmission in Nigeria and other nations with similar settings requires constant monitoring as well as awareness campaigns, especially in poor resource areas.
Our findings also provided a deeper understanding of the trends and mechanisms that influence mpoxv spread in Nigeria. Environmental sanitisation, particularly in high-risk locations, is required since mpoxv is a zoonotic illness with humans living in low-resource settings being the most vulnerable. This will effectively minimise the morbidity and mortality of the disease. As the mpoxv transmission is presumably driven by ecological factors with rodents as the principal host; thus, we plan to investigate the effect of seasonality on the overall mpoxv transmission. We suggest that to earn sufficient mpoxv prevention and mitigation, extensive research on mpoxv, the supply of enough medical resources, and awareness programs are essential. Finally, our model can be extended to incorporate seasonality in order to investigate further the influence of seasonality and rodent-driven factors for the transmission of mpoxv in Nigeria.
Author Contributions
Methodology, S.S.M.; Software, S.S.M. and A.Y.; Validation, M.M.A.-S.; Formal analysis, M.M.A.-S., S.S.M. and A.Y.; Investigation, M.M.A.-S. and A.Y.; Data curation, S.S.M.; Writing—review & editing, A.Y.; Supervision, M.M.A.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 773-130-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data utilised in this study were obtained from public sites.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sherrard-Smith, E.; Hogan, A.B.; Hamlet, A.; Watson, O.J.; Whittaker, C.; Winskill, P.; Ali, F.; Mohammad, A.B.; Uhomoibhi, P.; Maikore, I.; et al. The potential public health consequences of COVID-19 on malaria in Africa. Nat. Med. 2020, 26, 1411–1416. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Monkeypox. Key Facts. 2022. Available online: https://www.who.int/news-room/fact-sheets/detail/monkeypox#:~:text=Monkeypox%20is%20usually%20a%20self,material%20contaminated%20with%20the%20virus (accessed on 12 October 2022).
- Musa, S.S.; Yusuf, A.; Bakare, E.A.; Abdullahi, Z.U.; Adamu, L.; Mustapha, U.T.; He, D. Unravelling the dynamics of Lassa fever transmission with differential infectivity: Modeling analysis and control strategies. Math. Biosci. Eng. 2022, 19, 13114–13136. [Google Scholar] [CrossRef] [PubMed]
- Asamoah, J.K.; Jin, Z.; Sun, G.Q. Non-seasonal and seasonal relapse model for Q fever disease with comprehen-sive cost-effectiveness analysis. Results Phys. 2021, 22, 103889. [Google Scholar] [CrossRef]
- Yuan, P.; Tan, Y.; Yang, L.; Aruffo, E.; Ogden, N.H.; Bélair, J.; Heffernan, J.; Arino, J.; Watmough, J.; Carabin, H.; et al. Assessing transmission risks and control strategy for monkeypox as an emerging zoonosis in a metropolitan area. J. Med. Virol. 2022, 95, e28137. [Google Scholar] [CrossRef]
- Kupferschmidt, K. Why monkeypox is mostly hitting men who have sex with men. Science 2022, 376, 1364–1365. [Google Scholar] [CrossRef]
- Du, Z.; Shao, Z.; Bai, Y.; Wang, L.; Herrera-Diestra, J.L.; Fox, S.J.; Ertem, Z.; Ertem, Z.; Lau, E.H.Y.; Cowling, B.J. Reproduction number of mon-keypox in the early stage of the 2022 multi-country outbreak. J. Trav. Med. 2022, 29, taac009. [Google Scholar] [CrossRef]
- Cowling, B.J.; Fang, V.J.; Riley, S.; Peiris, J.M.; Leung, G.M. Estimation of the serial interval of influenza. Epidemiology 2009, 20, 344. [Google Scholar] [CrossRef]
- Zhao, S. Estimating the time interval between transmission generations when negative values occur in the se-rial interval data: Using COVID-19 as an example. Math. Biosci. Eng. 2020, 17, 3512–3519. [Google Scholar] [CrossRef]
- Haider, N.; Guitian, J.; Simons, D.; Asogun, D.; Ansumana, R.; Honeyborne, I.; Velavan, T.P.; Ntoumi, F.; Valdoleiros, S.R.; Petersen, E.; et al. Increased outbreaks of monkeypox highlight gaps in actual disease burden in Sub-Saharan Africa and in animal reservoirs. Int. J. Infect. Dis. 2022, 122, 107–111. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. Monkeypox. 2022. Available online: https://www.cdc.gov/poxvirus/monkeypox/index.html (accessed on 29 November 2022).
- Endo, A.; Murayama, H.; Abbott, S.; Ratnayake, R.; Pearson, C.A.; Edmunds, W.J.; Fearon, E.; Funk, S. Heavy-tailed sexual con-tact networks and monkeypox epidemiology in the global outbreak. Science 2022, 2022, eadd4507. [Google Scholar]
- Akhmetzhanov, A.R.; Ponce, L.; Thompson, R.N. Emergence potential of monkeypox in the Western Pacific Region, July 2022. Int. J. Infect. Dis. 2022, 122, 829–831. [Google Scholar] [CrossRef] [PubMed]
- Antinori, A.; Mazzotta, V.; Vita, S.; Carletti, F.; Tacconi, D.; Lapini, L.E.; D’Abramo, A.; Cicalini, S.; Lapa, D.; Pittalis, S.; et al. Epidemiological, clinical and viro-logical characteristics of four cases of monkeypox support transmission through sexual contact, Italy, May 2022. Eurosurveillance 2022, 27, 2200421. [Google Scholar] [CrossRef] [PubMed]
- Najeeb, H.; Huda, Z. Monkeypox virus: A spreading threat for Pakistan? Ann. Med. Surg. 2022, 79, 103977. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zhao, S.; Sun, S.; He, D.; Chong, K.C.; Yeoh, E.K. Estimation of the serial interval of monkeypox during the early outbreak in 2022. J. Med. Virol. 2022, 95, e28248. [Google Scholar] [CrossRef] [PubMed]
- Musa, S.S.; Abdullahi, Z.U.; Zhao, S.; Bello, U.M.; Hussaini, N.; Habib, A.G.; He, D. Transmission Dynamics of Monkeypox Virus in Nigeria during the Current COVID-19 Pandemic and Estimation of Effective Repro-duction Number. Vaccines 2022, 10, 2153. [Google Scholar] [CrossRef] [PubMed]
- Yuan, P.; Tan, Y.; Yang, L.; Aruffo, E.; Ogden, N.H.; Belair, J.; Arino, J.; Heffernan, J.; Watmough, J.; Carabin, H.; et al. Modelling vaccination and control strategies of outbreaks of monkeypox at gatherings. medRxiv 2022. [Google Scholar] [CrossRef]
- Ogoina, D.; Iroezindu, M.; James, H.I.; Oladokun, R.; Yinka-Ogunleye, A.; Wakama, P.; Otike-Odibi, B.; Usman, L.M.; Obazee, E.; Aruna, O.; et al. Clinical course and outcome of human monkeypox in Nigeria. Clin. Infect. Dis. 2020, 71, e210–e214. [Google Scholar] [CrossRef]
- Ogoina, D.; Izibewule, J.H.; Ogunleye, A.; Ederiane, E.; Anebonam, U.; Neni, A.; Oyeyemi, A.; Etebu, E.N.; Ihekweazu, C. The 2017 human monkey-pox outbreak in Nigeria—Report of outbreak experience and response in the Niger Delta University Teaching Hospital, Bayelsa State, Nigeria. PLoS ONE 2019, 14, e0214229. [Google Scholar] [CrossRef]
- Happi, C.; Adetifa, I.; Mbala, P.; Njouom, R.; Nakoune, E.; Happi, A.; Ndodo, N.; Ayansola, O.; Mboowa, G.; Bed-ford, T.; et al. Urgent need for a non-discriminatory and non-stigmatizing nomenclature for monkeypox virus. PLoS Biol. 2022, 20, e3001769. [Google Scholar] [CrossRef]
- Peter, O.J.; Kumar, S.; Kumari, N.; Oguntolu, F.A.; Oshinubi, K.; Musa, R. Transmission dynamics of Monkeypox virus: A mathematical modelling approach. Model. Earth Syst. Environ. 2022, 8, 3423–3434. [Google Scholar] [CrossRef]
- Nigeria Centre for Disease Control. Disease Situation Report. 2022. Available online: https://ncdc.gov.ng/diseases/sitreps (accessed on 1 December 2022).
- Musa, S.S.; Zhao, S.; Gao, D.; Lin, Q.; Chowell, G.; He, D. Mechanistic modelling of the large-scale Lassa fever epidemics in Nigeria from 2016 to 2019. J. Theoret. Biol. 2020, 2020, 110209. [Google Scholar] [CrossRef] [PubMed]
- Safi, M.A.; Gumel, A.B. Qualitative study of a quarantine/isolation model with multiple disease stages. Appl. Math. Comput. 2011, 218, 1941–1961. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Wang, X.; Gao, D.; Wang, J. Impact of awareness programs on cholera dynamics: Two modeling ap-proaches. Bull. Math. Biol. 2017, 79, 2109–2131. [Google Scholar] [CrossRef] [PubMed]
- Roop, O.P.; Chinviriyasit, W.; Chinviriyasit, S. The effect of incidence function in backward bifurcation for malaria model with temporary immunity. Math. Biosci. 2015, 265, 47–64. [Google Scholar] [CrossRef]
- Musa, S.S.; Zhao, S.; Chan, H.S.; Jin, Z.; He, D.H. A mathematical model to study the 2014–2015 large-scale den-gue epidemics in Kaohsiung and Tainan cities in Taiwan, China. Math. Biosci. Eng. 2019, 16, 3841–3863. [Google Scholar] [CrossRef]
- Hussaini, N.; Okuneye, K.; Gumel, A.B. Mathematical analysis of a model for zoonotic visceral leishmaniasis. Infect. Dis. Model. 2017, 2, 455–474. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for com-partmental models of disease transmission. Math. Bosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef]
- Usman, S.; Adamu, I.I. Modeling the transmission dynamics of the monkeypox virus infection with treatment and vaccination interventions. J. Appl. Math. Phys. 2017, 5, 2335. [Google Scholar] [CrossRef]
- LaSalle, J.P. The Stability of Dynamical Systems, Regional Conference Series in Applied Mathematics; SIAM: Philadephia, PA, USA, 1976. [Google Scholar]
- Musa, S.S.; Hussaini, N.; Zhao, S.; Daihai, H. Dynamical analysis of chikungunya and dengue co-infection model. Disc. Cont. Dyn. Syst.-B 2019, 22, 1–27. [Google Scholar] [CrossRef]
- Shuai, Z.; Van den Driessche, P. Global stability of infectious disease models using Lyapunov functions. SIAM J. Appl. Math. 2013, 73, 1513–1532. [Google Scholar] [CrossRef]
- Musa, S.S.; Baba, I.A.; Yusuf, A.; Sulaiman, T.A.; Aliyu, A.I.; Zhao, S.; He, D. Transmission dynamics of SARS-CoV-2: A modeling analysis with high-and-moderate risk populations. Res. Phys. 2021, 26, 104290. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Chavez, C.; Song, B. Dynamical model of tuberculosis and their applications, Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef]
- Carr, J. Applications of Centre Manifold Theory; Springer: New York, NY, USA, 1981. [Google Scholar]
- Statista, Global No.1 Data Platform. 2022. Available online: https://www.statista.com/ (accessed on 6 December 2022).
- Sengupta, P. The laboratory rat: Relating its age with humans. Int. J. Prev. Med. 2013, 4, 624–630. [Google Scholar]
- World Bank, Data, Population Website. Available online: https://data.worldbank.org/indicator/SP.POP.TOTL?locations=NG (accessed on 6 December 2022).
- Ojo, M.M.; Gbadamosi, B.; Benson, T.O.; Adebimpe, O.; Georgina, A.L. Modeling the dynamics of Lassa fever in Nigeria. J. Egyptian Math. Soc. 2021, 29, 1185. [Google Scholar] [CrossRef]
- Bankuru, S.V.; Kossol, S.; Hou, W.; Mahmoudi, P.; Rychtář, J.; Taylor, D. A game-theoretic model of Monkeypox to assess vaccination strategies. PeerJ 2020, 8, e9272. [Google Scholar] [CrossRef]
- Khan, A.; Naveed, M.; Dur-e-Ahmad, M.; Imran, M. Estimating the basic reproductive ratio for the Ebola out-break in Liberia and Sierra Leone. Infect. Dis. Pov. 2015, 4, 1–8. [Google Scholar]
- Gao, D.; Lou, Y.; He, D.; Porco, T.C.; Kuang, Y.; Chowell, G.; Ruan, S. Prevention and control of Zika as a mosqui-to-borne and sexually transmitted disease: A mathematical modeling analysis. Sci Rep. 2016, 6, 28070. [Google Scholar] [CrossRef]
- Zhao, S.; Stone, L.; Gao, D.; He, D. Modelling the large-scale yellow fever outbreak in Luanda, Angola, and the impact of vaccination. PLoS. Neglect. Trop. Dis. 2018, 12, e0006158. [Google Scholar] [CrossRef]
- Ghosh, I.; Tiwari, P.K.; Chattopadhyay, J. Effect of active case finding on dengue control: Implications from a mathematical model. J. Theor. Biol. 2019, 464, 50–62. [Google Scholar] [CrossRef] [PubMed]
- Dubey, B.; Dubey, P.; Dubey, U.S. Dynamics of an SIR model with nonlinear incidence and treatment rate. Appl. Appl. Math. Int. J. (AAM) 2015, 10, 5. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).