Exploring the Impact of Nonlinearities in Police Recruitment and Criminal Capture Rates: A Population Dynamics Approach
Abstract
1. Introduction
2. Mathematical Model
- The population size of the community which is subject to criminal activity is large. This allows us to assume that there are no population size constraints on the dynamical interaction between criminal activity and policing effort.
- In the absence of any policing effort, the growth of criminal activity can be described by the logistic equation with intrinsic growth rate r and environmental carrying capacity K (which corresponds to the amount of criminal activity that could potentially occur in a given location);
- Policing effort is analogous to a Holling type II [34] predation rate in which the amount of criminal activity stopped is described by a saturating function with maximum removal rate and half-saturation constant ;
- In the absence of criminal activity, policing effort is maintained at a baseline level and, following any perturbation will return to that level at a rate ;
- Policing effort may be influenced by the amount of criminal activity [24]. We represent that as a bounded positive influence such that for some positive constant M.
2.1. Criminal Influence on Police Recruitment
2.2. Non-Dimensionalisation
- measures the amount of criminal activity stopped per unit policing effort over the time it takes to initiate new criminal activity when policing effort is most responsive to the amount of criminal activity (i.e., when u is small). This is labelled policing efficiency;
- a measures how quickly policing effort responds to increases in criminal activity such that small values of a correspond to a more rapid response.This is labelled responsiveness of policing effort. Since the domain is restricted to , when nonlinearity of the effect of policing effort on reducing criminal activity will NOT be observed in the dynamics. This is entirely feasible because it means that policing effectiveness is broadly proportional to the amount of criminal activity in the region. This feature is useful to recall below in Section 3 when we come to observe structural differences in the system depending on whether a is less than or greater than 1. For completeness, note that if , nonlinearity in policing control will be observed in the dynamical system. This corresponds to the case where increases in criminal activity cannot be matched by policing control;
- b measures the increase in policing effort per criminal activity relative to the baseline over the average time associated with police recruitment and turnover rates. Indirect feedback of criminal activity on that activity due to the criminal-policing interaction. This is labelled criminal-induced policing impact;
- c measures the effect or influence of the carrying capacity of criminal activity on the growth of policing effort.
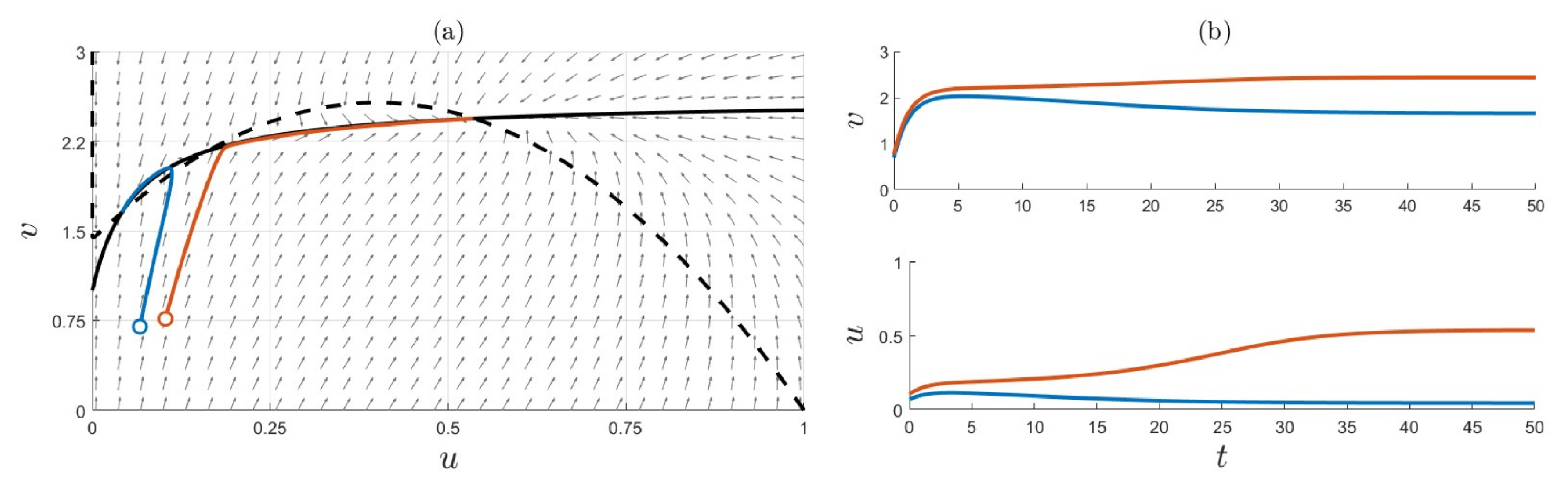
3. Model Analysis
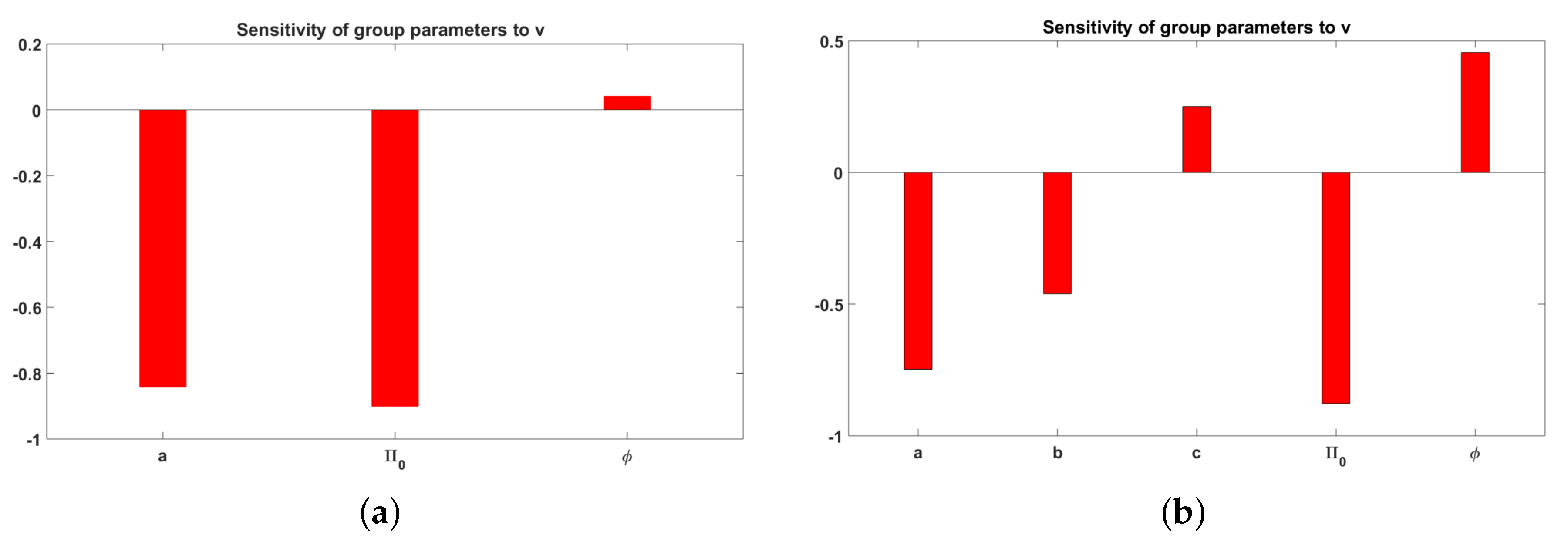
3.1. Sensitivity Analysis
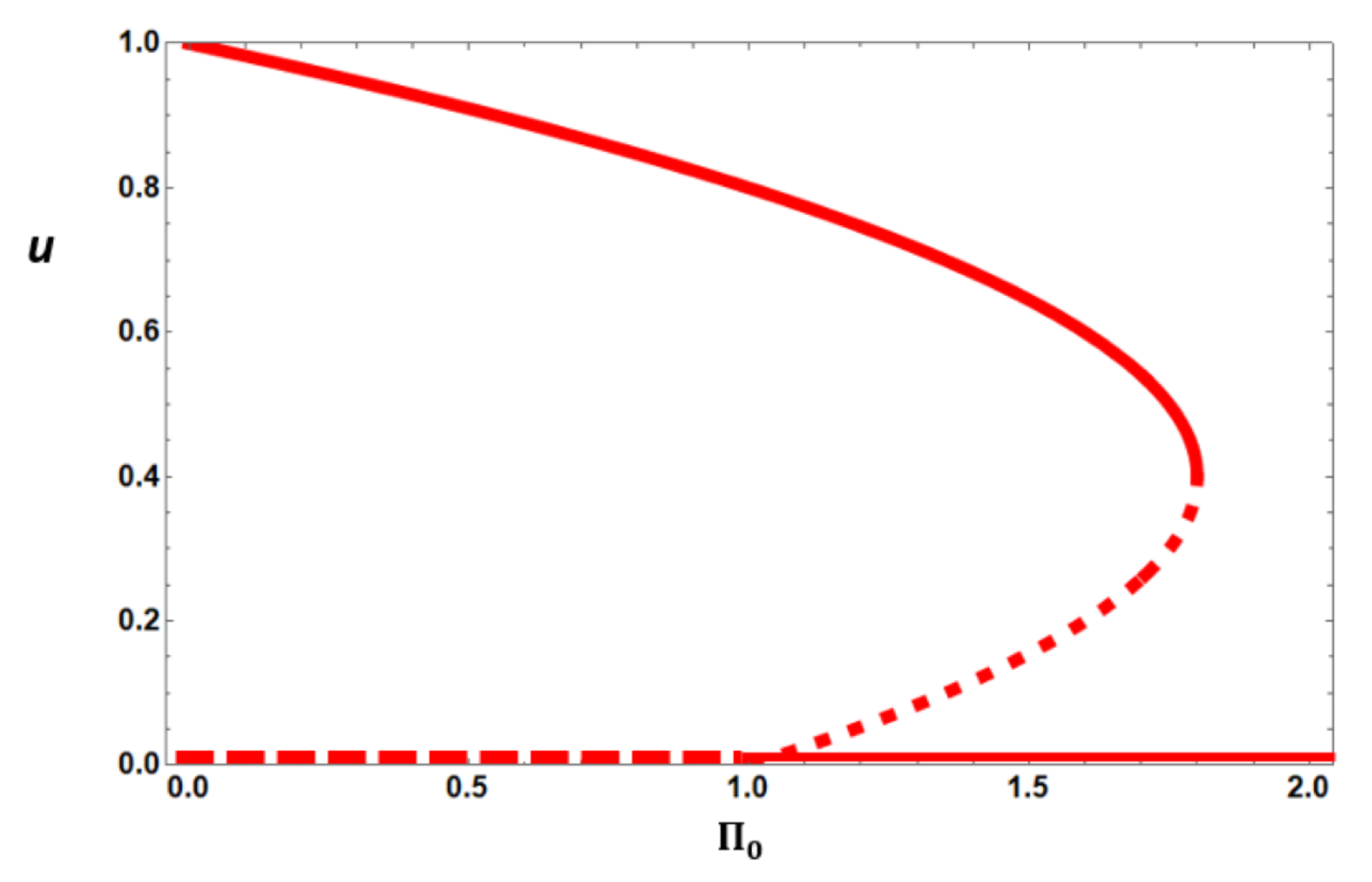
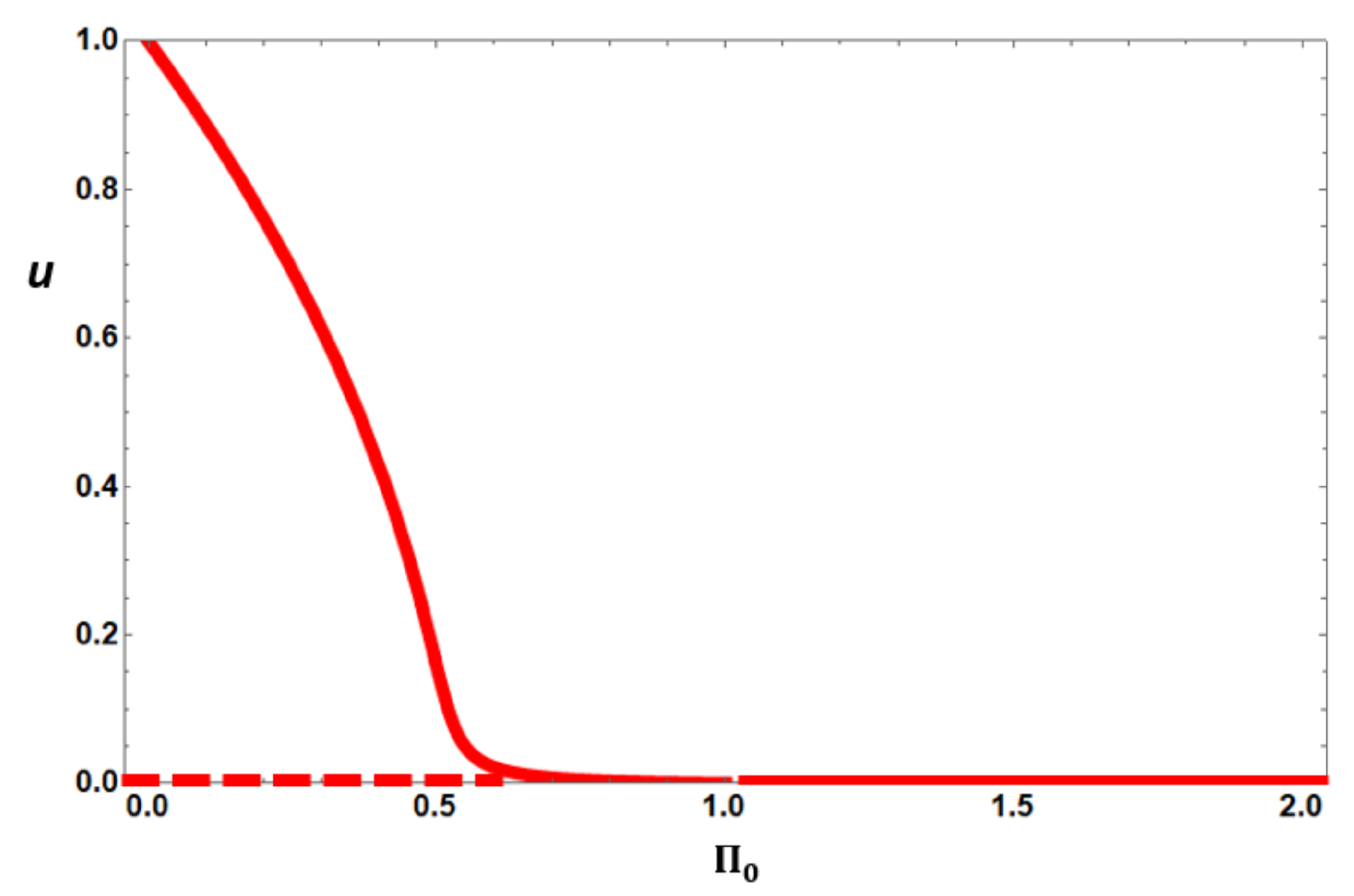
3.2. Steady State Analysis
- Solutions of (7) will only be real if (note that this is always satisfied if );
- If , there is a single positive steady state solution (the other solution is negative);
- If , then there will be two positive solutions provided that and no positive solutions if
- For :
- −
- There is a single non-trivial stable steady state if ;
- −
- For there are two non-trivial steady states the smaller of which is unstable and the larger of which is locally stable;
- −
- For , there is no non-trivial steady state.
- For , the following results are obtained:
- −
- For there is a single stable non-trivial steady state.
- −
- For there is no non-trivial steady state.
- For :
- −
- For there is no positive nontrivial steady state if whilst there are two nontrivial positive steady states if .
- −
- For there is a single positive nontrivial steady state ifand there will be three positive nontrivial steady states if
It is worth noting that this final condition giving rise to three positive nontrivial steady states is once again a condition on police responsiveness a falling below a threshold (which in this case is ). - For :
- −
- When there is no positive nontrivial steady state;
- −
- When there is a single positive nontrivial steady state.
Other Observations
- Increasing the value of (the ratio of baseline rates of increase in policing effort to criminal activity) reduces the potential to exhibit oscillatory dynamics as the steady state changes from a stable focus to a stable node.
- Increasing b (criminal-induced policing effort) increases the amplitude of the transient oscillatory dynamics by increasing the value of the determinant of the Jacobian which affects the size of this oscillation.
- Increasing c (corresponding to a reduction in the size of the environmental carrying capacity for criminal activity) reduces the number of non-trivial steady states that would be observed in the system. In relation to the model structures, the increase lowers the threshold for police responsiveness () which produces the bistable behaviours that we observe.
4. Linking the Model to Data
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saaty, T.L.; Alexander, J.M. Thinking with Models: Mathematical Models in the Physical, Biological, and Social Sciences; RWS Publications: Pittsburgh, PA, USA, 1981; Volume 2. [Google Scholar]
- Zimmermann, H.J. Testability and meaning of mathematical models in social sciences. Math. Model. 1980, 1, 123–139. [Google Scholar] [CrossRef]
- Weidlich, W. Sociodynamics: A Systematic Approach to Mathematical Modelling in the Social Sciences; Courier Corporation: North Chelmsford, MA, USA, 2006. [Google Scholar]
- Bertozzi, A. Mathematics of Crime—Mathematical Modelling of Complex Systems; University of Oxford: Oxford, UK, 2016; p. 4. [Google Scholar]
- Sooknanan, J.; Bhatt, B.; Comissiong, D. Catching a gang—A matematical model of the spread of gangs in a population treated as an infectious disease. Int. J. Pure Appl. Math. 2013, 83, 25–43. [Google Scholar] [CrossRef]
- Bertozzi, A.; Johnson, S.; Ward, M. Mathematical modelling of crime and security. Eur. J. Appl. Math. 2016, 27, 311–316. [Google Scholar] [CrossRef]
- Primicerio, M. The role of mathematical modelling in modern criminology Comment on “Statistical physics of crime: A review” by MR D’Orsogna and M. Perc. Phys. Life Rev. 2015, 12, 34–35. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.K.; Chen, Y.M.; Wu, D.; Chi, C.L. A game theory approach for assessment of risk and deployment of police patrols in response to criminal activity in San Francisco. Risk Anal. 2020, 40, 534–549. [Google Scholar] [CrossRef]
- Zhang, C.; Gholami, S.; Kar, D.; Sinha, A.; Jain, M.; Goyal, R.; Tambe, M. Keeping pace with criminals: An extended study of designing patrol allocation against adaptive opportunistic criminals. Games 2016, 7, 15. [Google Scholar] [CrossRef]
- Short, M.; Brantingham, P.; D’Orsogna, M. Cooperation and punishment in an adversarial game: How defectors pave the way to a peaceful society. Phys. Rev. E 2010, 82, 66–114. [Google Scholar] [CrossRef]
- De Mesquita, B.B.; Cohen, L.E. Self-interest, equity and crime control—A game-theoretic analysis of criminal decision making. Criminology 1995, 33, 483–518. [Google Scholar] [CrossRef]
- Short, M.; D’Orsogna, M.; Pasour, V.; Tita, G.; Brabtingham, P.; Bertozzi, A.; Chayes, L. A statistical model of criminal behaviour. Math. Model. Methods Appl. Sci. 2008, 18, 1249–1267. [Google Scholar] [CrossRef]
- Baloian, N.; Bassaletti, C.E.; Fernández, M.; Figueroa, O.; Fuentes, P.; Manasevich, R.; Orchard, M.; Peñafiel, S.; Pino, J.A.; Vergara, M. Crime prediction using patterns and context. In Proceedings of the 2017 IEEE 21st International Conference on Computer Supported Cooperative Work in Design (CSCWD), Wellington, New Zealand, 26–28 April 2017; pp. 2–9. [Google Scholar]
- Wang, D.; Ding, W.; Lo, H.; Morabito, M.; Chen, P.; Salazar, J.; Stepinski, T. Understanding the spatial distribution of crime based on its related variables using geospatial discriminative patterns. Comput. Environ. Urban Syst. 2013, 39, 93–106. [Google Scholar] [CrossRef]
- Manasevich, R.; Phan, Q.H.; Souplet, P. Global existence of solutions for a chemotaxis-type system arising in crime modelling. Eur. J. Appl. Math. 2013, 24, 273–296. [Google Scholar] [CrossRef]
- González-Parra, G.; Chen-Charpentier, B.; Kojouharov, H.V. Mathematical modeling of crime as a social epidemic. J. Interdiscip. Math. 2018, 21, 623–643. [Google Scholar] [CrossRef]
- Perc, M.; Donnay, K.; Helbing, D. Understanding recurrent crime as system-immanent collective behavior. PLoS ONE 2013, 8, e76063. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Van Hentenryck, P.; Cebrian, M. Competitive dynamics between criminals and law enforcement explains the super-linear scaling of crime in cities. Palgrave Commun. 2015, 1, 15022. [Google Scholar] [CrossRef]
- Brantingham, P.J.; Tita, G. Offender mobility and crime pattern formation from first principles. In Artificial Crime Analysis Systems: Using Computer Simulations and Geographic Information Systems; IGI Global: Hershey, PA, USA, 2008; pp. 193–208. [Google Scholar]
- Cracolici, M.F.; Uberti, T.E. Geographical distribution of crime in Italian provinces: A spatial econometric analysis. Jahrb. Reg. 2009, 29, 1–28. [Google Scholar] [CrossRef]
- Brown, M.A. Modelling the spatial distribution of suburban crime. Econ. Geogr. 1982, 58, 247–261. [Google Scholar] [CrossRef]
- Short, M.B.; Bertozzi, A.L.; Brantingham, P.J. Nonlinear patterns in urban crime: Hotspots, bifurcations, and suppression. SIAM J. Appl. Dyn. Syst. 2010, 9, 462–483. [Google Scholar] [CrossRef]
- Lloyd, D.J.; O’Farrell, H. On localised hotspots of an urban crime model. Phys. D Nonlinear Phenom. 2013, 253, 23–39. [Google Scholar] [CrossRef]
- McCabe, J. An Analysis of Police Department Staffing: How Many Officers do You Really Need? 2019. Available online: https://icma.org/sites/default/files/305747_Analysis%20of%20Police%20Department%20Staffing%20_%20McCabe.pdf (accessed on 27 July 2021).
- Misra, A. Modeling the effect of police deterrence on the prevalence of crime in the society. Appl. Math. Comput. 2014, 237, 531–545. [Google Scholar] [CrossRef]
- Lacey, A.; Tsardakas, M. A mathematical model of serious and minor criminal activity. Eur. J. Appl. Math. 2016, 27, 403–421. [Google Scholar] [CrossRef]
- Pitcher, A.B. Adding police to a mathematical model of burglary. Eur. J. Appl. Math. 2010, 21, 401–419. [Google Scholar] [CrossRef]
- Short, M.B.; Brantingham, P.J.; Bertozzi, A.L.; Tita, G.E. Dissipation and displacement of hotspots in reaction-diffusion models of crime. Proc. Natl. Acad. Sci. USA 2010, 107, 3961–3965. [Google Scholar] [CrossRef]
- Moses, L.B.; Chan, J. Algorithmic prediction in policing: Assumptions, evaluation, and accountability. Polic. Soc. 2018, 28, 806–822. [Google Scholar] [CrossRef]
- Jones, P.A.; Brantingham, J.; Chayes, L.R. Statistical models of criminal behaviour: The effects of law enforcement actions. Math. Model. Methods Appl. Sci. 2010, 20, 1397–1423. [Google Scholar] [CrossRef]
- Coclite, G.M.; Garavello, M.; Spinolo, L. A mathematical model for piracy control through police response. Nonlinear Differ. Equ. Appl. 2017, 24, 48. [Google Scholar] [CrossRef]
- Jane White, K.; Campillo-Funollet, E.; Nyabadza, F.; Cusseddu, D.; Kasumo, C.; Imbusi, N.M.; Juma, V.O.; Meir, A.; Marijani, T. Towards understanding crime dynamics in a heterogeneous environment: A mathematical approach. J. Interdiscip. Math. 2021, 24, 2139–2159. [Google Scholar] [CrossRef]
- Walsh, D. Occam’s Razor: A Principle of Intellectual Elegance. Am. Philos. Q. 1979, 16, 241–244. [Google Scholar]
- Holling, C.S. Some characteristics of simple types of predation and parasitism. Can. Entomol. 1959, 91, 385–398. [Google Scholar] [CrossRef]
- Boloye, G. Latin Hypercube Sampling and Partial Rank Correlation Coefficient Analysis Applied to an Optimal Control Problem. Available online: https://trace.tennessee.edu/utk_gradthes/1278 (accessed on 20 August 2022).
- Wu, J.; Dhingra, R.; Gambhir, M.; Remais, J.V. Sensitivity analysis of infectious disease models: Methods, advances and their application. J. R. Soc. Interface 2013, 10, 20121018. [Google Scholar] [CrossRef] [PubMed]
- Khanghahi, M.J.; Ghaziani, R.K. Bifurcation Analysis of a Modified May–Holling–Tanner Predator–Prey Model with Allee Effect. Bull. Iran. Math. Soc. 2022, 48, 3405–3437. [Google Scholar] [CrossRef]
- Official Statistics Police Officer Uplift, England and Wales, Quarterly Update to 31 March 2022. Available online: https://www.gov.uk/government/statistics/police-officer-uplift-quarterly-update-to-march-2022/police-officer-uplift-england-and-wales-quarterly-update-to-31-march-2022 (accessed on 27 August 2022).
- Data Downloads. Available online: https://data.police.uk/data/ (accessed on 27 August 2022).
- Roberts, M.; Andreasen, V.L.A.; Pellis, L. Nine challenges for deterministic epidemic models. Epidemics 2015, 10, 49–53. [Google Scholar] [CrossRef] [PubMed]
- Tewa, J.; Djeumen, V.; Bowong, S. Predator–Prey model with Holling response function of type II and SIS infectious disease. Appl. Math. Model. 2012, 37, 4825–4841. [Google Scholar] [CrossRef]


| Condition | Max # +ve st.st. | ||||
|---|---|---|---|---|---|
| , | + | + | + | + | Zero |
| , | + | + | + () | − | One |
| + | + | − () | − | One | |
| , | + | − () | + | + | Two |
| + | + () | + | + | Zero | |
| , | + | − () | + () | − | Three |
| + | Either +/− | − () | − | One |
| Year | Frontline Police Numbers | Number Crimes Reported | Number Crimes per Police per Year |
|---|---|---|---|
| 2013 | 2565 | N/A | N/A |
| 2014 | 2394 | N/A | N/A |
| 2015 | 2449 | N/A | N/A |
| 2016 | 2475 | N/A | N/A |
| 2017 | 2449 | N/A | N/A |
| 2018 | 2319 | N/A | N/A |
| 2019 | 2277 | N/A | N/A |
| 2020 | 2380 | 128,860 | 54 |
| 2021 | 2498 | 132,455 | 53 |
| 2022 | 2611 | 140,619 | 54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chikore, T.; Nyabadza, F.; White, K.A.J. Exploring the Impact of Nonlinearities in Police Recruitment and Criminal Capture Rates: A Population Dynamics Approach. Mathematics 2023, 11, 1669. https://doi.org/10.3390/math11071669
Chikore T, Nyabadza F, White KAJ. Exploring the Impact of Nonlinearities in Police Recruitment and Criminal Capture Rates: A Population Dynamics Approach. Mathematics. 2023; 11(7):1669. https://doi.org/10.3390/math11071669
Chicago/Turabian StyleChikore, Tichaona, Farai Nyabadza, and K. A. Jane White. 2023. "Exploring the Impact of Nonlinearities in Police Recruitment and Criminal Capture Rates: A Population Dynamics Approach" Mathematics 11, no. 7: 1669. https://doi.org/10.3390/math11071669
APA StyleChikore, T., Nyabadza, F., & White, K. A. J. (2023). Exploring the Impact of Nonlinearities in Police Recruitment and Criminal Capture Rates: A Population Dynamics Approach. Mathematics, 11(7), 1669. https://doi.org/10.3390/math11071669






