Enhancing the Heat Transfer Due to Hybrid Nanofluid Flow Induced by a Porous Rotary Disk with Hall and Heat Generation Effects

Abstract

A study of hybrid-nanofluid flow induced by the uniform rotation of a circular porous disk is presented for the purpose of facilitating the heat transfer rate. The Hall and Ohmic heating effects resulting from an applied magnetic field and the source of heat generation/absorption are also considered to see their impact on flow behavior and enhancing the heat transfer rate. The physical problem under the given configuration is reduced to a set of nonlinear partial differential equations using the conservation laws. Similarity transformations are adopted to obtain a system of ordinary differential equations which are further solved using the Shooting Method. Results are presented via graphs and tables thereby analyzing the heat transfer mechanism against different variations of physical parameters. Outcomes indicate that the wall suction plays a vital role in determining the behavior of different parameters on the velocity components. It is notable that the wall suction results in a considerable reduction in all the velocity components. The enhanced Hartman number yields a growth in the radial velocity and a decay in the axial velocity. Moreover, consequences of all parametric effects on the temperature largely depend upon the heat generation/absorption.

1. Introduction

The poor thermal characteristics of orthodox fluids have been a concern for engineers for a long time. Different methods were proposed and tested to enhance the performance of orthodox heat transfer fluids. During the last decade of the 20th century, Choi and Eastman [1] came up with the novel idea of suspending nanometer-sized metallic particles in the convectional fluids to enhance thermal performance of such fluids. This novelty proved to be more than helpful in a number of ways and the solutions resulting from the inclusion of nanoparticles in base fluids were termed as ‘nanofluids’. The nanofluids caught the attention of researchers from all over the globe due to their unique thermophysical and chemical properties, hence their wide-spread applications are found in different domains of engineering. To name a few, they include biomedical engineering, domestic and industrial cooling/heating systems, the IT and automobile industry, modern drug delivery systems, etc., that find several applications for nanofluids. Such diverse properties and wide-spread applications are the reasons behind the extensive research that is being carried out on nanofluids. Some analytical and numerical studies on fluid/nanofluid flows are shown through references [2,3,4,5,6,7,8].

Hybrid nanofluids are an advanced type of nanofluid obtained by mixing at least two types of nanoparticles in a single fluid. Such mixing helps to attain unique thermal/chemical properties which are difficult to obtain otherwise. Recently, the flow of hybrid nanofluids is being studied by many motivated researchers. Lund et al. [9] performed a stability analysis of hybrid nanofluids consisting of copper-alumina nanoparticles flowing over a shrinking surface. Sindhu et al. [10] analyzed the flow of hybrid nanofluids through a micro channel by incorporating the shape factors of the nanoparticles. Natural convection for hybrid nanofluids flowing through a porous medium has been investigated by Izadi et al. [11]. Abbasi et al. [12] performed a thermodynamic analysis of the electro-osmotic flow of hybrid nanofluids.

Flows produced by rotary disks are important due to their applications in many industrial processes as most industrial appliances are constituted of rotating parts submerged in fluids. Pioneering analysis presenting the modelling and analysis of such flows came from a classical study by Von Kármán [13]. In this study, he proved that the velocity components as well as pressure depend only upon the axial coordinate and hence similarity transformations were used to obtain the solutions. A similar methodology was used by several researchers to examine such flows under different flow configurations. Another comprehensive study presenting an insight into flow over rotating disks is presented by Brady and Durlofsky [14]. Andersson and Korte [15] studied the MHD flow of power-law fluid whereas Turkyilmazoglu [16] and Rashidi et al. [17] analyzed the flow and the entropy generation, respectively, of nanofluids while considering the rotary disks. Abdel-Wahed and Emam [18] examined MHD flow considering a rotating disk with Hall effects. The flow of nanofluids generated by a rotating porous disk was studied by Uddin et al. [19]. In another study, Turkyilmazoglu [20] analyzed the heat transfer and fluid flow due to rotating as well as vertically moving disks. Some recent studies in this regard can be seen through references [21,22].

Low thermal productivity of fluids is a main cause for several heat-transport mechanisms in engineering applications including engines, transformers, microwave tubes, heat exchangers, oils and lubricants, etc. It is well known that the materials that have high thermal conductivity (for example, copper, graphene, aluminum, etc.) are considered speedy exchangers of heat. Animasaun et al. [23] presented a detailed analysis of numerous self-similar flows emphasizing the dynamics of nanofluids, thereby listing the nanomaterials with high thermal conductivity for their more effective use in energy transfer. Asim and Siddiqui [24] analyzed a comprehensive perspective on properties of fundamental hydrothermal and heat and mass transfer of hybrid nanofluids. Heat transfer in rotating flows is an interesting area of research where there are enormous applications in the manufacturing of crystal growth, computer storage devices, thermal power generation and gas turbine motors. The literature review suggests that not much has been said about the hybrid nanofluid flow generated by a rotating porous disk despite having multiple applications in engineering and medical sciences. This study aims to fill that gap. It is well established that the contribution of hybrid nanofluids expedites the heat transfer rate, as is evident from the literature [25,26,27,28] whereas suction/injection facilitates keeping the temperature under control despite the heat generation. Thus, the novelty of the underlying problem lies in the fact that it analyzes heat transfer rate from fluid to the wall and vice versa due to the concentration of hybrid nanoparticles, suction/injection and heat generation and absorption for assisting the heat transportation. The nanoparticles consist of copper and titanium dioxide suspended in water, whereas the Lorentz force generated by a uniform magnetic field and its effects, i.e., the Hall and Ohmic heating is also assumed. Heat generation/absorption is also accounted for to present a detailed insight into the heat transfer phenomenon. Similarity transformations are adopted to reduce the nonlinear system of PDEs to a system of ODEs. Solutions are obtained using the numerical shooting method and results are presented in graphical and tabular form for analysis. For validation purposes, a comparison of the reduced case of the present study with previously available results is presented and a good agreement was noted.

The underlying article is arranged in the following prospects: Section 2 details the mathematical equations related to flow geometry with dimensional and non-dimensional settings whereas Section 3 briefly explains the adopted methodology for obtaining the flow parameters. The results and discussions are in Section 4 whilst key findings are provided in Section 5.

2. Governing Equations

Consider the steady flow of a hybrid-nanofluid induced by a uniformly rotating disk as shown by Figure 1. The disk is considered porous and rotating with a uniform angular velocity $\omega$. The cylindrical coordinate system $‘\left(r,\Theta , z\right)’$ has been adopted in a way that the disk rotates in $z=0$ plane and a hybrid nanofluid fills the space $z\ge 0$. The hybrid-nanofluid is composed of copper and titanium dioxide nanoparticles suspended in water. The disk and ambient are held at constant temperatures $T_w$ and $T_{\infty }$, respectively.

Rotation of the disk generates a 3D flow governed by the velocity field $‘\overline{V}={\left[u\left(r,\Theta ,z\right),v\left(r,\Theta ,z\right),w\left(r,\Theta ,z\right)\right]}^{’}$. Because of the radial symmetry, the variations in flow are considered independent of $\Theta$. Mathematical forms of conservation of mass, momentum and energy for present flow configuration are given as:

$$\frac{1}{r}\frac{\partial }{\partial r}\left(ur\right)+\frac{\partial w}{\partial z}=0,$$

(1)

$${\rho }_{hnf}\left(u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{v^2}{r}\right)=-\frac{\partial p}{\partial r}+{\mu }_{hnf}\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{{\partial }^{2}u}{\partial z^2}-\frac{u}{r^2}\right)+F_r,$$

(2)

$${\rho }_{hnf}\left(u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{uv}{r}\right)={\mu }_{hnf}\left(\frac{{\partial }^{2}v}{\partial r^2}+\frac{1}{r}\frac{\partial v}{\partial r}+\frac{{\partial }^{2}v}{\partial z^2}-\frac{v}{r^2}\right)+F_{\Theta },$$

(3)

$${\rho }_{hnf}\left(u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial p}{\partial z}+{\mu }_{hnf}\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{{\partial }^{2}w}{\partial z^2}\right)+F_z,$$

(4)

$${\left(\rho C_p\right)}_{hnf}\left(u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\right)=k_{hnf}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial z^2}\right)+\frac{1}{{\sigma }_{hnf}} \overline{J}.\overline{J}+\delta .$$

(5)

Here the subscript ‘$hnf$’ stands for hybrid nanofluid and $\rho , p,\mu , C_p, k,\sigma \left(=\frac{J}{E}\right), \delta \mathrm{and} \overline{J}$ denote the density, pressure, viscosity, specific heat, thermal conductivity and electric conductivity denoting the rate of charge flow, dimensional heat generation/absorption and current density, respectively. Effective quantities for hybrid nanofluid are given as follows [10,11,12]:

$$\{\begin{array}{c}{\rho }_{hnf}={\rho }_{Ti{O}_2}{\varphi }_{Ti{O}_2}+(1+\left(-{\varphi }_{Cu}-{\varphi }_{Ti{O}_2}\right)){\rho }_f+{\rho }_{Cu}{\varphi }_{Cu},\\ \frac{{\mu }_{hnf}}{{\mu }_f}={(1-\left({\varphi }_{Cu}+{\varphi }_{Ti{O}_2}\right))}^{-2.5},\\ {\left(\rho C_p\right)}_{hnf}={\left(\rho C_p\right)}_{Cu}{\varphi }_{Cu}+(1+\left(-{\varphi }_{Cu}-{\varphi }_{Ti{O}_2}\right)){\left(\rho C_p\right)}_f+{\left(\rho C_p\right)}_{Ti{O}_2}{\varphi }_{Ti{O}_2},\\ \frac{k_{hnf}}{k_f}=\frac{\left(\frac{{\varphi }_{Cu}{k}_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2}}{{\varphi }_{Cu}+{\varphi }_{Ti{O}_2}}\right)-2({\varphi }_{Cu}+{\varphi }_{Ti{O}_2})k_f+2k_f+2({\varphi }_{Cu}{k}_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2})}{\left(\frac{k_{Cu}{\varphi }_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2}}{{\varphi }_{Cu}+{\varphi }_{Ti{O}_2}}\right)-({\varphi }_{Cu}{k}_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2})+k_f\left(2+({\varphi }_{Cu}+{\varphi }_{Ti{O}_2})\right)}.\end{array}$$

(6)

Here the subscript ‘f’ stands for the base fluid, water in this case. The thermophysical parametric values for the nanoparticles and the base fluids considered herein are provided by

Table 1. Thermo-physical properties of nanoparticles and water.

Material	$\mathit{\rho }$	$\mathit{k}$	${\mathit{C}}_{\mathit{p}}$	$\mathit{\sigma }$
Copper	8933	401	385.0	$5.96\times {10}^7$
Water	997.1	0.613	4179	0.05
Titanium dioxide	4250	8.9538	686.2	$1.0\times {10}^{-12}$

[4,16] whereas units of $\rho$, $k$, $C_p$, and $\sigma$ are ${\mathrm{kgm}}^{-3}$, ${\mathrm{Wm}}^{-1}{\mathrm{k}}^{-1}$, ${\mathrm{Jkg}}^{-1}{\mathrm{K}}^{-1}$, and ${\mathrm{Sm}}^{-1}$, respectively.

The Lorentz force $(\overline{F}=\left[F_r, F_{\theta }, F_z\right]=\overline{J}\times \overline{B})$ generated due to a magnetic field of the form $\overline{B}=\left[0,0,B_0\right]$ is computed using the generalized Ohms law as follows:

$$\overline{J}={\sigma }_{hnf}\left[\overline{E}+\overline{V}\times \overline{B}-\frac{\left(\overline{J}\times \overline{B}\right)}{e{n}_e}\right].$$

(7)

Here $e \mathrm{and} n_e$ denote ‘charge of electron’ and ‘number density of free electrons’. It is relevant to mention that the free electron density determines the electrical conductivity of metal which is inserted via Ohm’s law. This also refers to the whole solution considering the nanofluids in general. The source of number density is a modified Ohm’s law for Hall effects. However, an explicit expression of number density is not used here because it is considered to be a part of a generalized Ohm’s law which is further non-dimensionalized. The comprehensive details of the set of formulae for various materials can be seen in [29].

Moreover, $\overline{E}$ is applied to an electric field which in the present scenario is considered zero. In the absence of an electric field, for the velocity and magnetic field under consideration, the Lorentz force takes the form:

$$\overline{F}=\left[\frac{A_1{B}_0{}^2}{A_1{}^2{m}^2+1}\left(-u+m{A}_{1}v\right){\sigma }_f,-\frac{{\sigma }_f{B}_0{}^2}{A_1{}^2{m}^2+1}\left(m{A}_{1}u+v\right),0\right].$$

(8)

Here $m=\frac{B_0{\sigma }_f}{n_e.e}$ is the Hall parameter and the form of $A_1$ having the electric conductivity for hybrid nanofluid consisting of copper and titanium dioxide nanoparticles suspended in water is given as:

$$A_1=1+\frac{3\left(\frac{{\sigma }_{Ti{O}_2}{\varphi }_{Ti{O}_2}+{\sigma }_{Cu}{\varphi }_{Cu}}{{\sigma }_f}\right)-3\left({\varphi }_{Ti{O}_2}+{\varphi }_{Cu}\right)}{\left(\frac{{\sigma }_{Ti{O}_2}{\varphi }_{Ti{O}_2}+{\sigma }_{Cu}{\varphi }_{Cu}}{{\sigma }_f\left({\varphi }_{Ti{O}_2}+{\varphi }_{Cu}\right)}+2\right)-\left(\frac{{\sigma }_{Ti{O}_2}{\varphi }_{Ti{O}_2}+{\sigma }_{Cu}{\varphi }_{Cu}}{{\sigma }_f}\right)-\left({\varphi }_{Ti{O}_2}+{\varphi }_{Cu}\right)}.$$

Here $\varphi$ indicates the ‘volume fraction of nanoparticles’ and subscripts $f, cu$ and $Ti{O}_2$ represent fluid (water), copper and titanium oxide, respectively.

Equations (1)–(5) subject to Equations (7) and (8) take the following form:

$$\frac{1}{r}\frac{\partial }{\partial r}\left(ur\right)+\frac{\partial w}{\partial z}=0,$$

(9)

$$\begin{gathered} {\rho }_{hnf}\left(u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{v^2}{r}\right)=-\frac{\partial p}{\partial r}+{\mu }_{hnf}\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{{\partial }^{2}u}{\partial z^2}-\frac{u}{r^2}\right) \\ -\frac{A_1{\sigma }_f{B}_0{}^2}{A_1{}^2{m}^2+1}\left(u-m{A}_{1}v\right), \end{gathered}$$

(10)

$$\begin{gathered} {\rho }_{hnf}\left(u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{uv}{r}\right)={\mu }_{hnf}\left(\frac{{\partial }^{2}v}{\partial r^2}+\frac{1}{r}\frac{\partial v}{\partial r}+\frac{{\partial }^{2}v}{\partial z^2}-\frac{v}{r^2}\right) \\ -\frac{{\sigma }_f{B}_0{}^2}{A_1{}^2{m}^2+1}\left(m{A}_{1}u+v\right), \end{gathered}$$

(11)

$${\rho }_{hnf}\left(u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial p}{\partial z}+{\mu }_{hnf}\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{{\partial }^{2}w}{\partial z^2}\right),$$

(12)

$$\begin{gathered} {\left(\rho C_p\right)}_{hnf}\left(u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\right)=k_{hnf}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial z^2}\right) \\ +\frac{{\sigma }_f{B}_0{}^2}{A_1{}^2{m}^2+1}\{{\left(u-m{A}_{1}v\right)}^2+{\left(m{A}_{1}u+v\right)}^2\}+\delta . \end{gathered}$$

(13)

The boundary conditions for present flow with ‘suction/injection’ at the face of the porous rotating disk are stated as below:

$$u=0, v=r\omega , w={\overline{v}}_w, T=T_w, at z=0,$$

(14)

$$u=0, v=0, w=0, T=0, as z\to \infty .$$

(15)

Here $v_w$ is the constant value of axial velocity at the boundary of the porous disk. Following the deductions of Kármán, and considering the velocity components to be dependent upon ‘$z$’, the following similarity transformations are considered [12,14,16]:

$$\begin{gathered} \eta =z{\left(\frac{\omega }{{\nu }_f }\right)}^{\frac{1}{2}}, \left(u,v,w\right)=\left(r\omega F\left(\eta \right),r\omega G\left(\eta \right),{\left(\omega {\nu }_f\right)}^{\frac{1}{2}} H\left(\eta \right)\right), \\ \left(p,T\right)=(p_{\infty }-\omega {\mu }_{f}p\left(\eta \right), T_{\infty }+\left(T_w-T_{\infty }\right)\theta \left(\eta \right)). \end{gathered}$$

(16)

Here $\eta$ is introduced as a dimensionless variable and $F\left(\eta \right), G\left(\eta \right)$ and $H\left(\eta \right)$ are dimensionless functions of $\eta$ considered in radial, azimuthal and axial directions, respectively. As quoted, the use of similarity transformations reduces our governing equations to a system of ODEs as follows:

$$H^{\prime }\left(\eta \right)+2F\left(\eta \right)=0$$

(17)

$$A_2{F}^{″}\left(\eta \right)=\frac{A_{1}M}{A_1{}^2{m}^2+1}(F\left(\eta \right)-m{A}_{1}G\left(\eta \right))+A_3(F^2\left(\eta \right)+H\left(\eta \right)F^{\prime }\left(\eta \right)-G^2\left(\eta \right))$$

(18)

$$A_2{G}^{″}\left(\eta \right)-\frac{A_{1}M}{A_1{}^2{m}^2+1}(G\left(\eta \right)+m{A}_{1}F\left(\eta \right))-A_3(2F\left(\eta \right)G\left(\eta \right)+H\left(\eta \right)G^{\prime }\left(\eta \right))=0,$$

(19)

$$H^{″}\left(\eta \right)-P^{\prime }\left(\eta \right)-H\left(\eta \right)H^{\prime }\left(\eta \right)=0,$$

(20)

$$A_4{\theta }^{″}\left(\eta \right)+\frac{PrEc{A}_{1}M}{A_1{}^2{m}^2+1}\left\{{(F\left(\eta \right)-m{A}_{1}G\left(\eta \right))}^2+{(G\left(\eta \right)+m{A}_{1}F\left(\eta \right))}^2\right\}-Pr{A}_{5}H\left(\eta \right){\theta }^{\prime }\left(\eta \right)+Prϵ=0.$$

(21)

$M, Pr, Ec and ϵ$, respectively, denote the Hartman number, the Prandtl number, the Eckert number, and dimensionless heat generation/absorption, given as:

$$M=\frac{{\sigma }_f{B}_0^2}{{\rho }_f\omega }, Pr=\frac{{\nu }_f{\left(\rho C_p\right)}_f}{K_f}, Ec=\frac{{\rho }_f{r}^2{\omega }^2}{{\left(\rho C_p\right)}_f\left(T_w-T_{\infty }\right)},ϵ=\frac{\delta }{\omega {\nu }_f}.$$

(22)

and the $A_{i}s$ appearing are given as:

$$\begin{array}{c}{A}_2={(1-\left({\varphi }_{Cu}+{\varphi }_{Ti{O}_2}\right))}^{-2.5}, \\ A_3={\rho }_{Ti{O}_2}{\varphi }_{Ti{O}_2}+(1+\left(-{\varphi }_{Cu}-{\varphi }_{Ti{O}_2}\right)){\rho }_f+{\rho }_{Cu}{\varphi }_{Cu},\\ A_4=\frac{\left(\frac{{\varphi }_{Cu}{k}_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2}}{{\varphi }_{Cu}+{\varphi }_{Ti{O}_2}}\right)-2\left({\varphi }_{Cu}+{\varphi }_{Ti{O}_2}\right)k_f+2k_f+2\left({\varphi }_{Cu}{k}_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2}\right)}{\left(\frac{k_{Cu}{\varphi }_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2}}{{\varphi }_{Cu}+{\varphi }_{Ti{O}_2}}\right)-\left({\varphi }_{Cu}{k}_{Cu}+{\varphi }_{Ti{O}_2}{k}_{Ti{O}_2}\right)+k_f(2+\left({\varphi }_{Cu}+{\varphi }_{Ti{O}_2}\right))},\\ A_5={\left(\rho C_p\right)}_{hnf}={\left(\rho Cp\right)}_{Cu}{\varphi }_{Cu}+(1+\left(-{\varphi }_{Cu}-{\varphi }_{Ti{O}_2}\right)).\end{array}$$

(23)

In view of such considerations, the dimensionless boundary conditions for current flow pattern are assumed as follows:

$$F\left(\eta \right)=0, H\left(\eta \right)=v_w, G\left(\eta \right)=1, \theta \left(\eta \right)=1 at \eta =0,$$

(24)

and

$$F\left(\eta \right)=G\left(\eta \right)=\theta \left(\eta \right)=0 as \eta \to \infty$$

(25)

The ‘local skin friction coefficients’ ($C_i$, where $i=F, G, H$ denotes skin friction coefficient for that specific component of velocity) and ‘heat transfer rate at the wall’ $(A_4{\theta }^{\prime }\left(0\right))$ are important quantities of interest and hence are included in the analysis.

3. Shooting Method

The nonlinear-coupled system of Equations (17)–(21) subject to boundary conditions (24) and (25) are difficult to solve exactly. Hence, the shooting method is adopted to obtain the solutions of said system of equations in Mathematica. The shooting method is usually employed by considering the boundary conditions as a multivariate function of initial conditions at some point. Therefore, as a first step, the boundary value problem is transformed to finding the initial conditions via an initial guess that offers a solution to the problem in a convenient manner. In the next step, the Runge–Kutta method is employed to target the other boundary and then the results are matched for the first initial guess. This process is continued until the acceptable solution with minimum error is achieved. Here, the step size is effectively taken to be 0.01 for all numerical computations. Numerical solutions are compiled in the form of graphical illustrations and are presented for physical analysis of the results in the subsequent section.

4. Results and Discussions

This section aims to analyze the obtained results via graphical and tabular illustrations. Plots of velocity components and temperature profile for variations in embedded parameters are presented and analyzed. To avoid repetition, only graphs of effective quantities of interest are included. Moreover, values of thermophysical quantities are taken as provided via Table 1, whereas $‘Pr=6.2, M=1, m=0.5, Ec=0.5,ϵ=0.5, \mathrm{and} v_w=-1’$ unless stated otherwise. It is important to note that the flow behavior is discussed in detail for pertinent parameters as stated, since the flow parameters in dimensional and non-dimensional settings are related to each other through Equations (6), (16), (22) and (24). A variation in flow behavior due to varying physical parameters can be viewed through graphical and tabular analysis to be explained subsequently. Further reasoning and justification can be extracted through parametric relations stated via Equations (6), (16), (22) and (24).

To verify the validation of present results, a comparison of the reduced case of the present study is provided with previously available studies via

Table 2. Comparison with previously reported results [17,19].

$\mathit{ϵ}$	${\mathit{v}}_{\mathit{w}}$	Rashidi et al. [17]	Uddin et al. [19]	${\mathit{F}}^{\prime }\left(0\right)$ for Present Study
0	0	0.309237	0.309236	0.309254
	−1	0.251039	0.251038	0.256351
	−2	0.188718	0.188715	0.197141

. It is noted that present results are in excellent agreement with previous results reported by Rashidi et al. [17] and Uddin et al. [19] in qualitative manner. Quantitatively, a difference of up to ${10}^{-2}$ is noted in the results, which is mainly due to the consideration of different viscosity models considered herein.

4.1. Analysis of Dimensionless Velocity

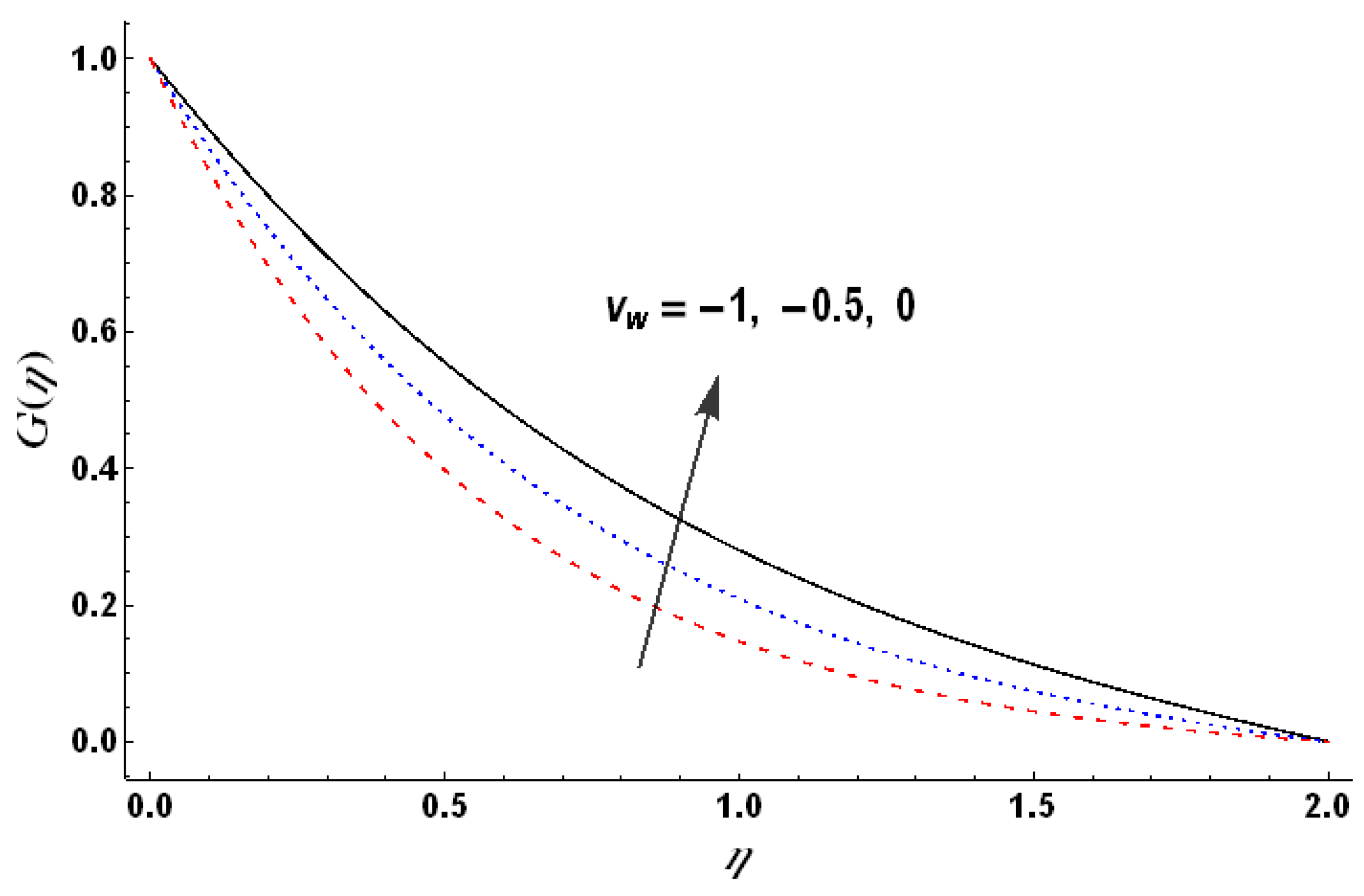
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 are plotted to examine the effects of variations in wall suction, the Hartman number, the Hall parameter and the nanoparticles’ volume fraction of both nanoparticles on the radial, azimuthal and axial velocity components. Figure 2 indicates that the radial velocity decreases with an increase in wall suction. This figure also highlights the fact that flows induced by a rigid rotating disk possess larger axial velocities compared to a porous disk. The azimuthal velocity tends to decrease with increasing wall suction parameters (see Figure 3). Such a decrease is less significant when compared with that of radial velocity. Notable and uniform reduction in the axial velocity is observed for enhanced wall suction (see Figure 4).

An increased Hartman number tends to enhance the radial velocity (see Figure 5) and such an increase is significant near the porous disk. Figure 6 and Figure 7 show that the azimuthal as well as axial velocity components decrease with an increase in the Hartman number ($M$). Such a decrease in $H\left(\eta \right)$ becomes larger as the distance from the disk increases. The effects of the Hall parameter ($m$) on the velocity components are analyzed through Figure 8, Figure 9 and Figure 10. It is noted via these figures that both the radial and azimuthal velocities show an increasing trend for an increase in $m$. Such an increase is large for the radial velocity and small in the case of the azimuthal velocity. The axial velocity on the other hand decreases significantly for an increase in $m$. The effects of the volume fractions of copper and titanium dioxide nanoparticles on the velocity components are studied via Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. These figures demonstrate that the radial velocity increases with an increase in the nanoparticles’ volume fraction of both types of nanoparticles. Such an increase is noted to be uniform for an increase in titanium dioxide nanoparticles. The axial velocity is noted to decrease with an increase in the nanoparticles’ volume fraction of both types of nanoparticles and again such a decrease is noted to be uniform for the titanium dioxide nanoparticles. The azimuthal velocity, on the other hand, demonstrates the opposite behavior for the two types of nanoparticles.

4.2. Analysis of Dimensionless Temperature

Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23 have been plotted to study the behavior of dimensionless temperature $\left(\theta \right)$ for variations in different embedded parameters. It is worth noting that the heat generation/absorption plays a key role on the impact of all parameters. Even a small value of heat generation parameters becomes influential due to the Prandtl number (say $ϵ=0.2$). 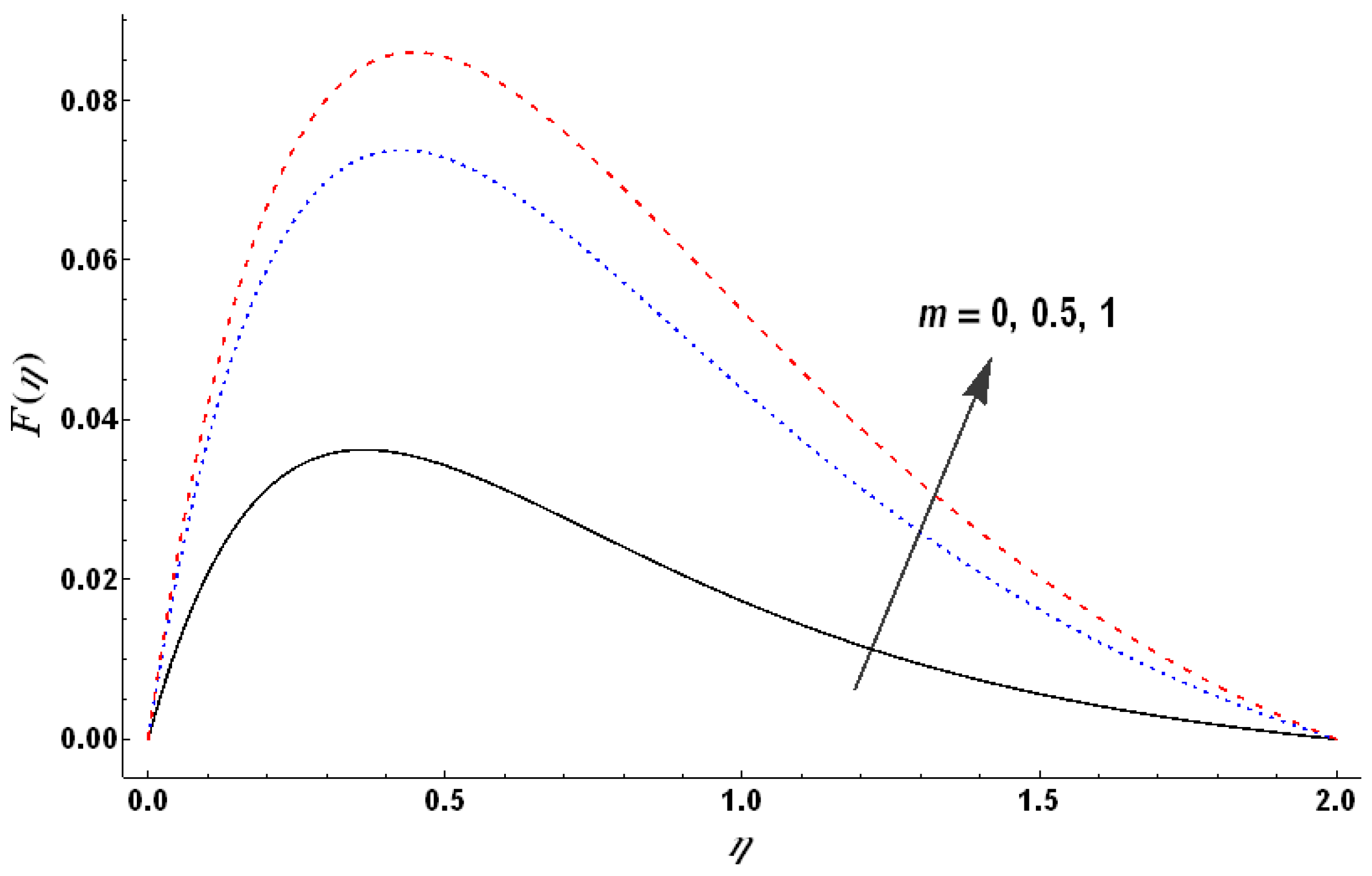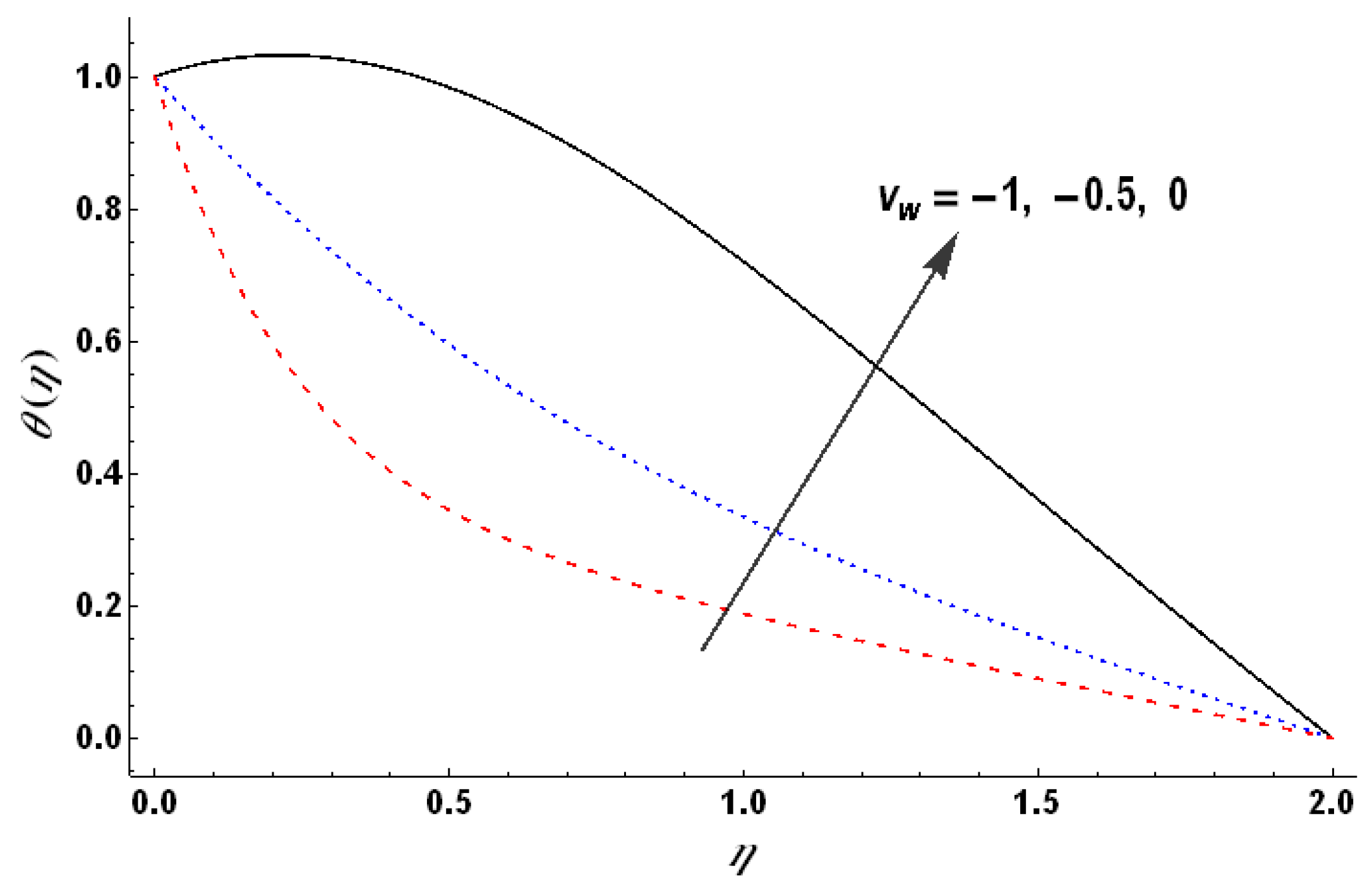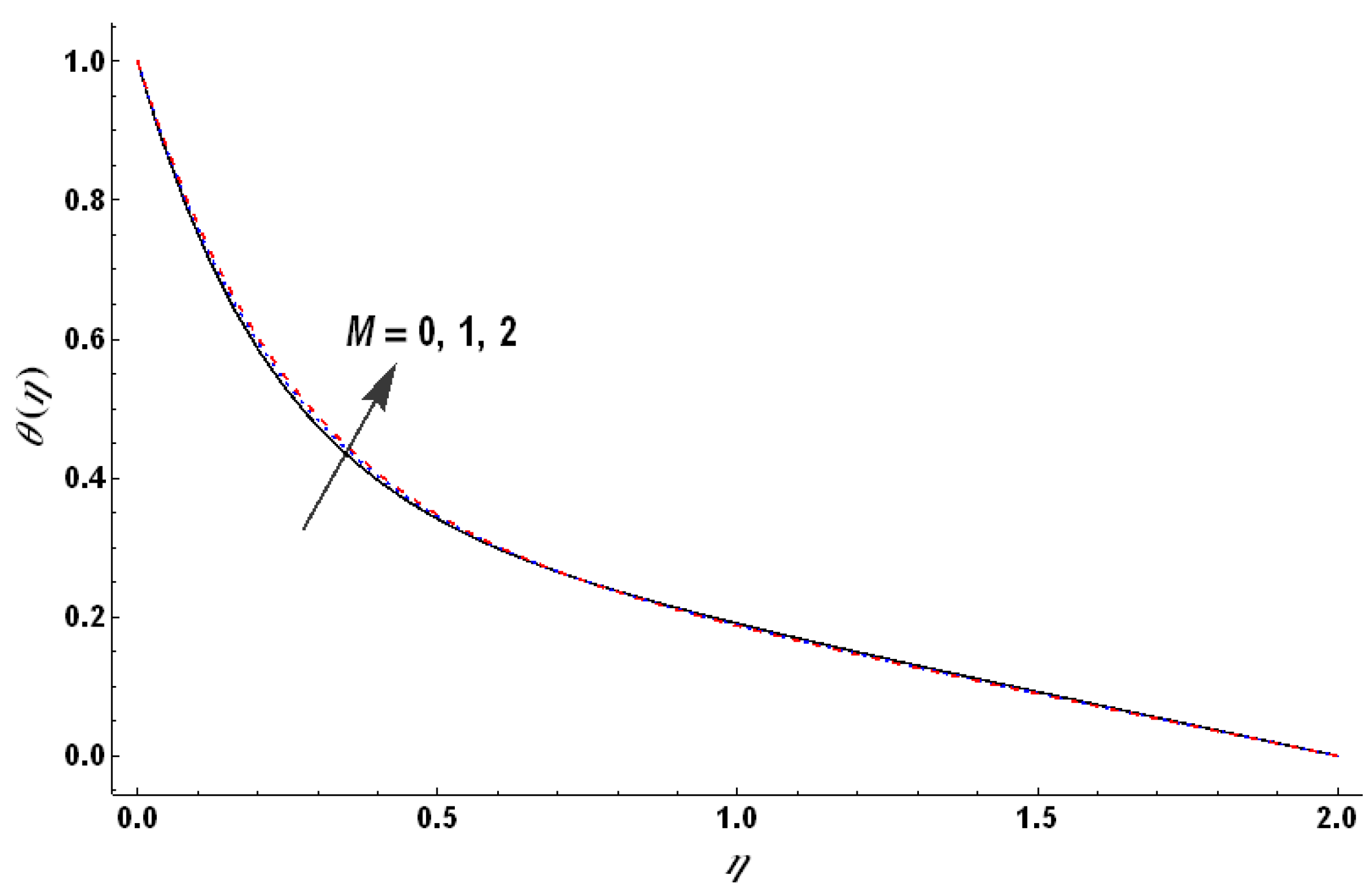Figure 17 shows that the temperature decreases with an increase in wall suction for the case of heat generation. This fact indicates that wall suction facilitates the cooling down of the rotating fluid and can help in keeping the temperature under control despite the heat generation. An increase in the value of the Hartman number increases the temperature which is mainly due to the consideration of Ohmic heating (see Figure 18). On the other hand, an increase in the values of the Hall parameter reduces the temperature. 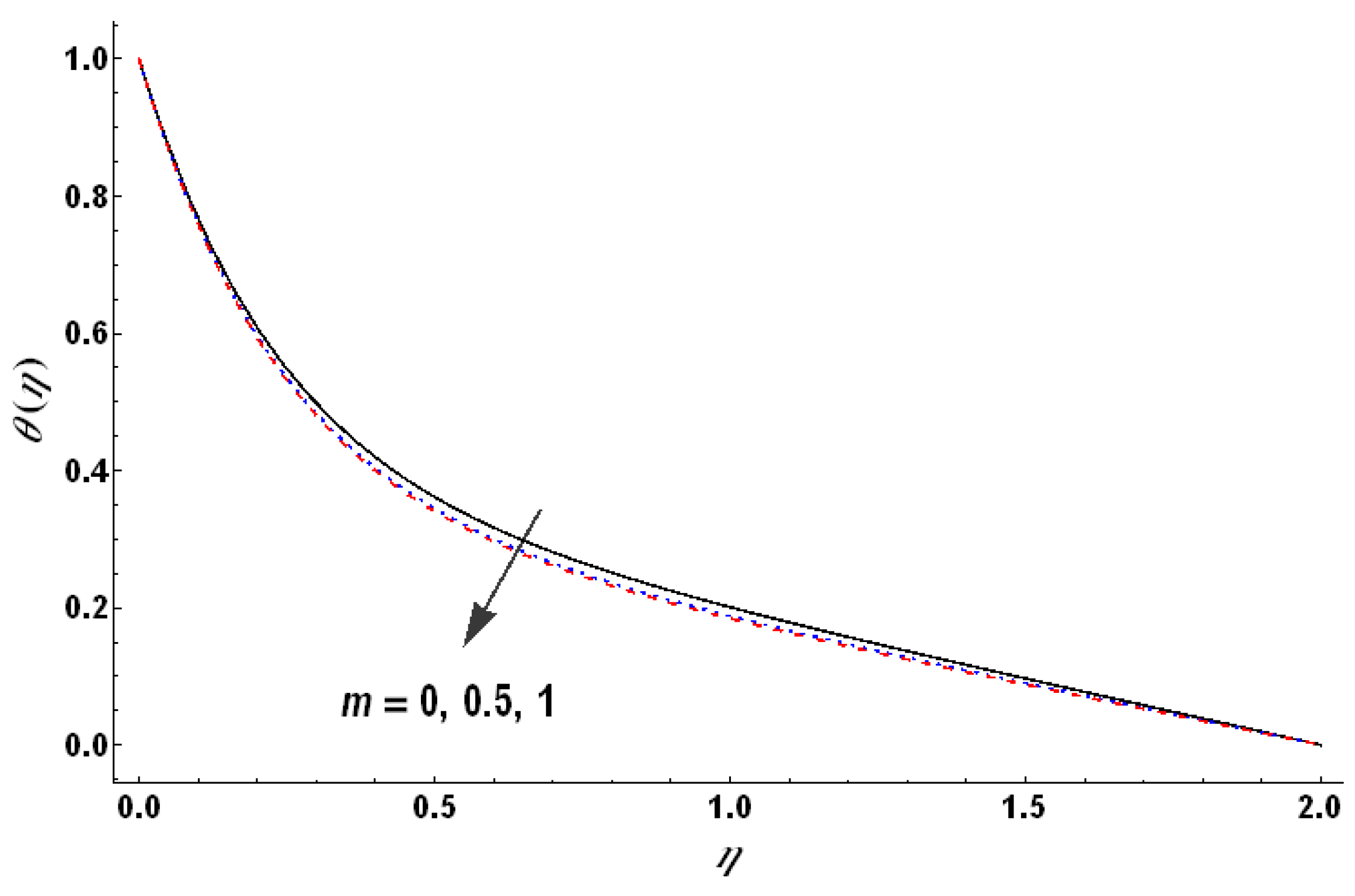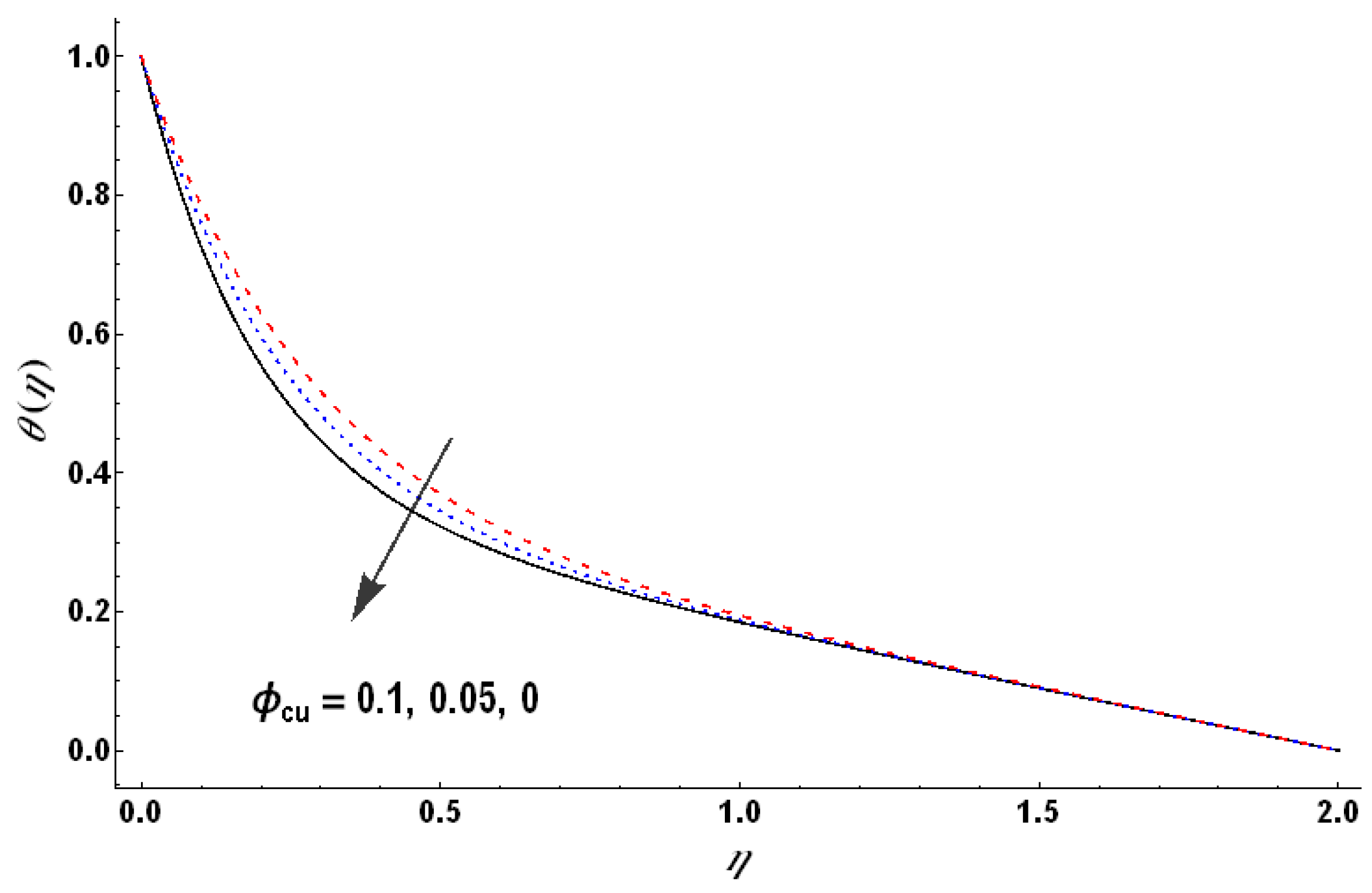Figure 20 and Figure 21 indicate that the dimensionless temperature of hybrid nanofluid increases with an increase in the volume fraction of both type of nanoparticles for the case of heat absorption as well as for minute heat generation ($ϵ=0.2-0.4$). 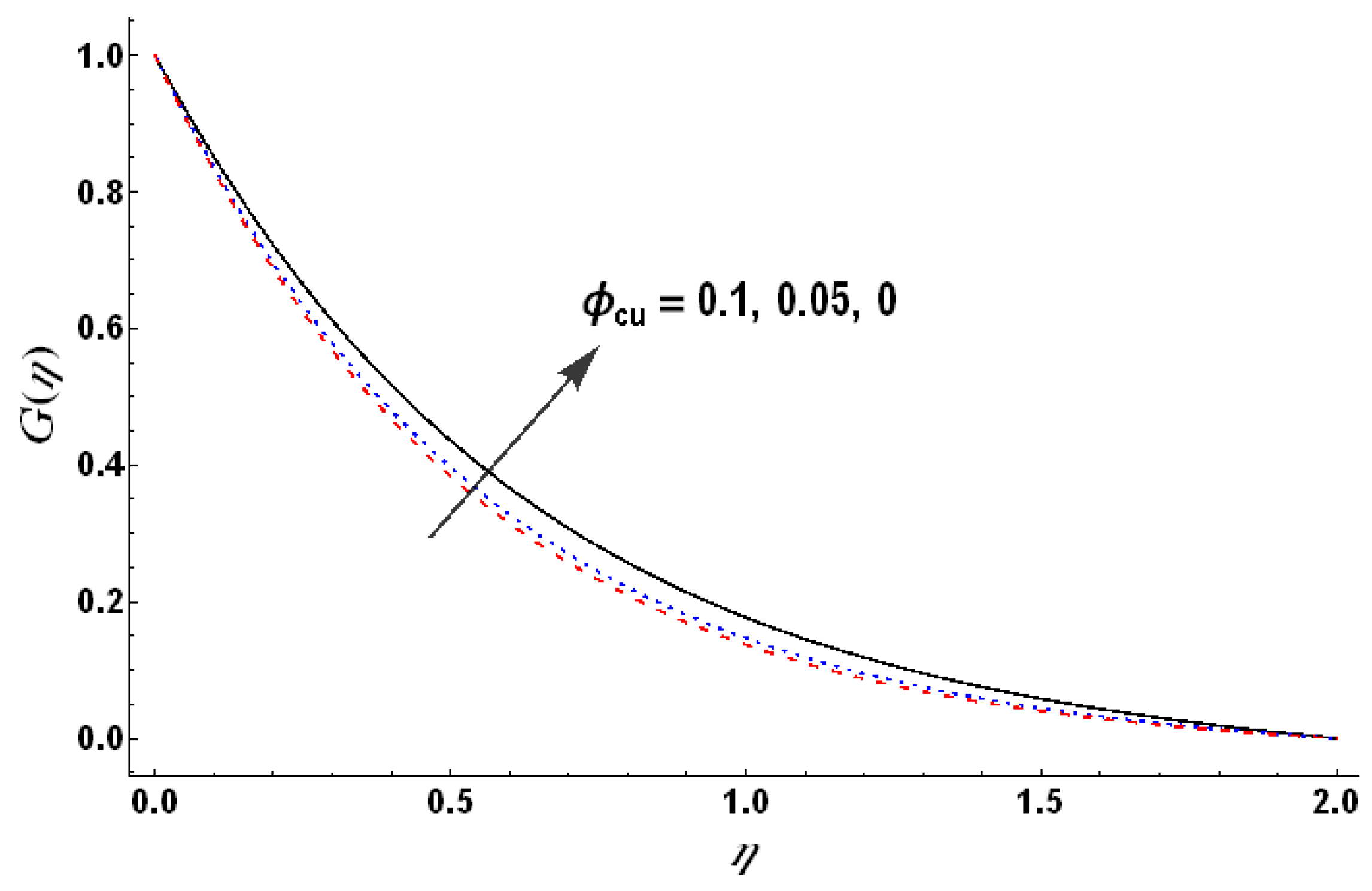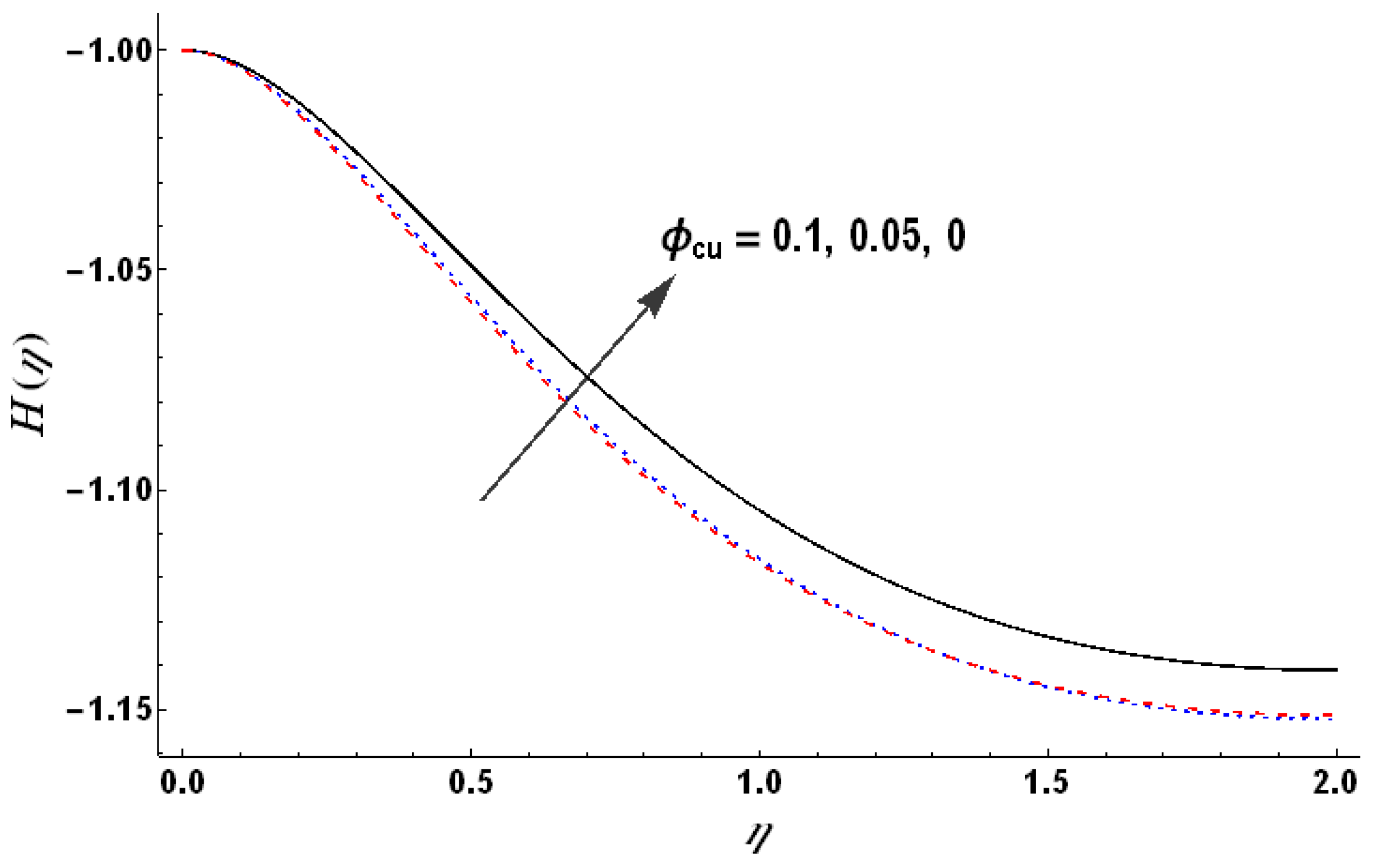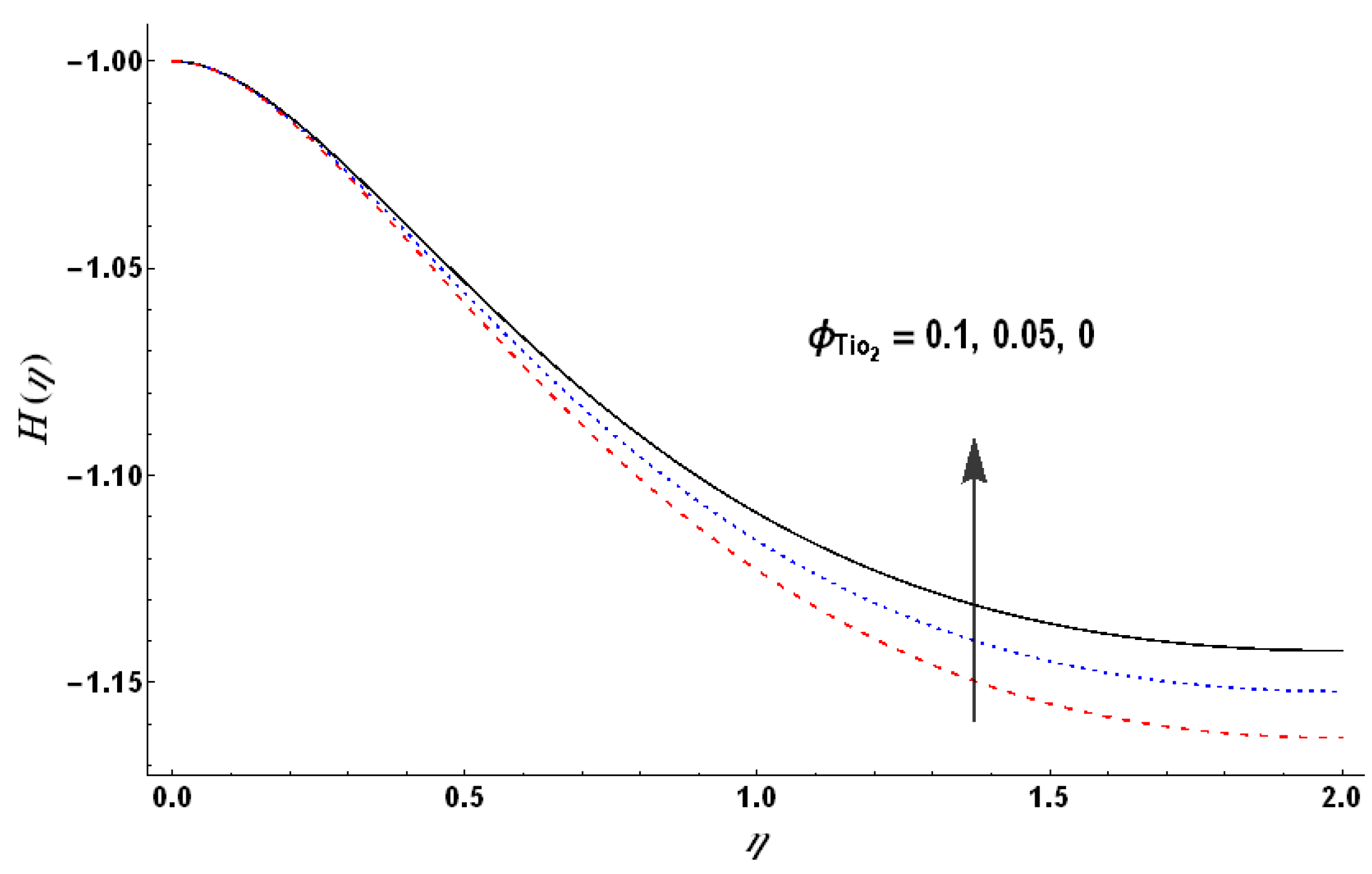This role of nanoparticles is reversed for larger heat generation with the fluid, i.e., an increase in the nanoparticles’ volume fraction reduces the dimensionless temperature (see Figure 22). This observation highlights the role of nanoparticles in facilitating the heat transfer from fluid to the wall and vice versa. 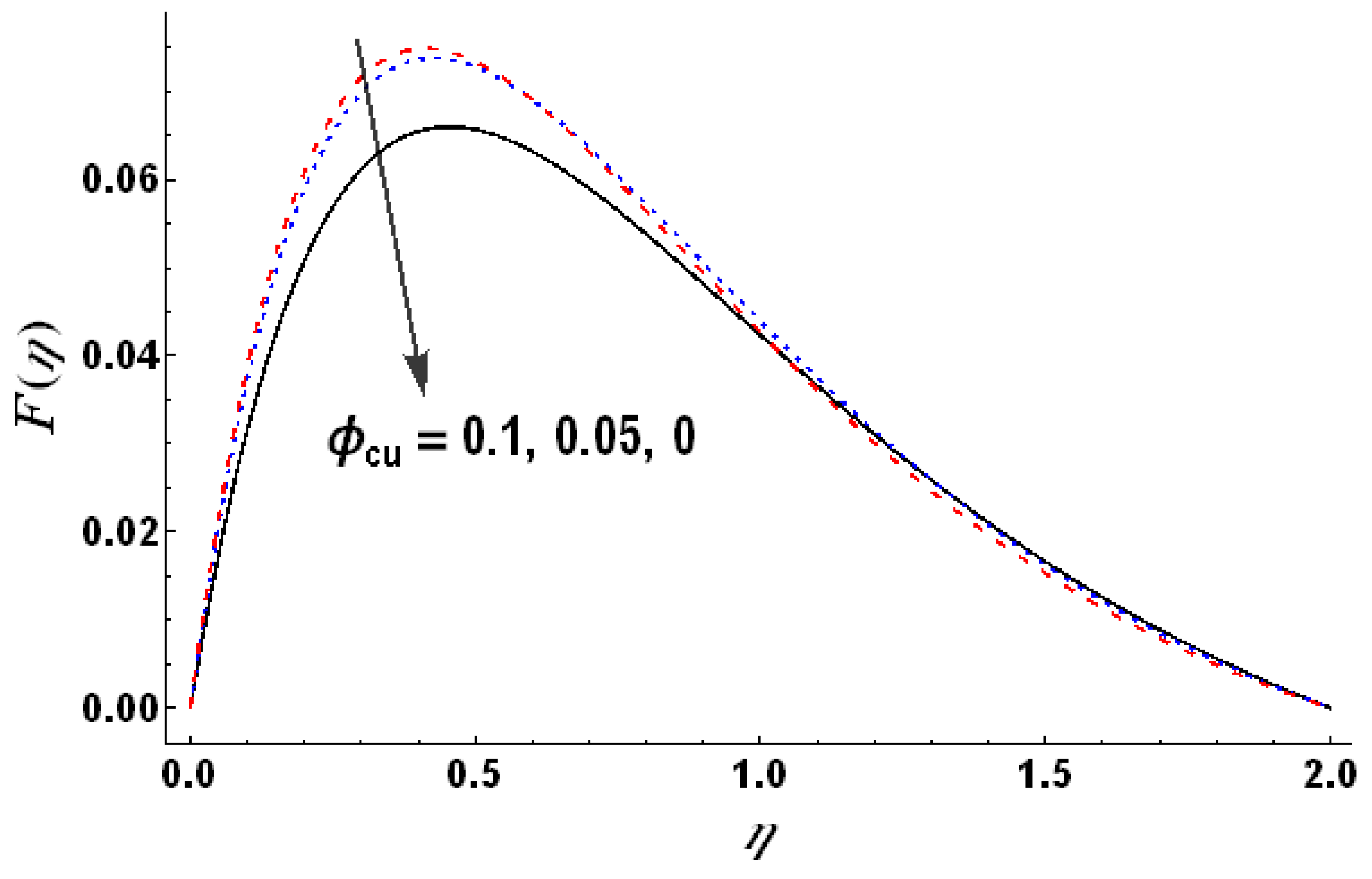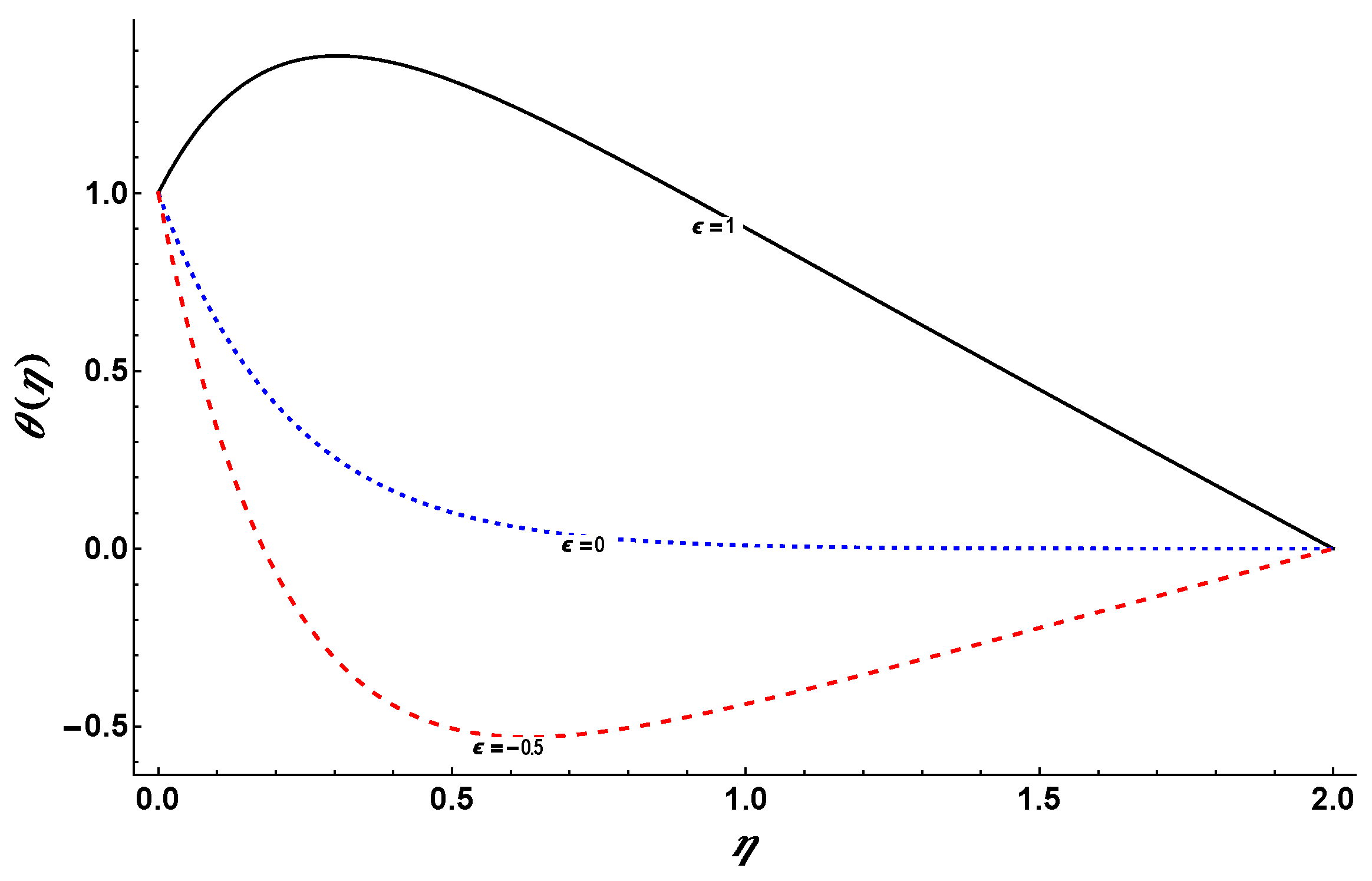Figure 23 depicts the dimensionless temperature for the cases of heat generation, no heat generation/absorption and heat absorption. This figure shows that temperature profile changes significantly for changes in $ϵ$.

The numerical values of local skin friction and the rate of heat transfer at the boundary for variations in the nanoparticles’ volume fraction of both types of nanoparticles and wall suction are given via

Table 3. Local skin friction coefficients for variations in different parameters.

${\mathit{\varphi }}_{\mathit{c}\mathit{u}}$	${\mathit{\varphi }}_{\mathit{T}\mathit{i}{\mathit{O}}_2}$	${\mathit{v}}_{\mathit{w}}$	${\mathit{A}}_2{\mathit{F}}^{\prime }\left(0\right)$	$-{\mathit{A}}_2{\mathit{G}}^{\prime }\left(0\right)$
0.0	0.05	−1	0.448061	1.82267
0.05			0.614161	2.31676
0.1			0.745451	2.76917
0.05	0.0		0.521083	2.06778
	0.05		0.614161	2.31676
	0.1		0.721574	2.57965
	0.05	0.5	0.731593	1.07797
		0.0	0.721085	1.4041
		−0.5	0.679381	1.81585

and

Table 4. Local heat transfer coefficient for variations in different parameters.

${\mathit{\varphi }}_{\mathit{c}\mathit{u}}$	${\mathit{\varphi }}_{\mathit{T}\mathit{i}{\mathit{O}}_2}$	${\mathit{v}}_{\mathit{w}}$	$\mathit{ϵ}$	$-{\mathit{A}}_4{\mathit{\theta }}^{\prime }\left(0\right)$
0.0	0.05	−1	0.5	0.749743
0.05				0.781668
0.1				0.800912
0.05	0.0			0.795555
	0.05			0.781668
	0.1			0.771571
	0.05	0.5		−1.48757
		0.0		−2.18461
		−0.05		−1.33788
		−1.0	0.5	0.781668
			0.0	5.94662
			−0.5	11.1116

. It is noted via these tables that an increase in the volume fraction of nanoparticles results in an increase in the skin friction coefficients. It is a noteworthy fact that the impact of copper nanoparticles on such increase is large compared to that of titanium dioxide nanoparticles. On the other hand, such an increase is relatively uniform for the case of $Ti{O}_2$ nanoparticles. The skin friction coefficient in the radial direction decreases whereas it increases with a decrease in the value of $v_w$ along the azimuthal direction. Here the positive value of $v_w$ indicates the case of minute injection.

The amount of heat transfer at the wall boosts with the rise in nanoparticles’ volume fraction of both nanoparticles for positive values of $ϵ$. Variation in the values of heat transfer at the wall depends on the heat generation/absorption as nanoparticles only facilitate the heat transfer. The amount of heat transfer at the boundary increases as one moves from the case of heat generation to heat absorption.

5. Conclusions

The heat transfer analysis for flow of hybrid nanofluid composed of copper and titanium dioxide nanoparticles suspended in water induced by the uniform rotation of a circular porous disk has been analyzed. The Hall and Ohmic heating effects along with heat generation/absorption have been considered. The main outcomes of this study are summarized below:

• Wall suction results in a considerable reduction in all the velocity components.
• An increase in the values of the Hartman number result in an increase in the radial and a reduction in the axial velocity.
• An increase in the values of the Hall parameter result in a slight increase in the azimuthal velocity. The effects of titanium dioxide nanoparticles on the velocity components are uniform compared to that of the copper nanoparticles.
• The consequences of physical parameters versus the dimensionless temperature largely depend upon the heat generation/absorption.

To see further aspects of this study, various experimental analyses report different empirical relationships for the apparent viscosity and thermal conductivity of nanofluids. Therefore, it will be useful to analyze the flow of nanofluids due to the rotating disk using different models for the apparent viscosity and thermal conductivity. Furthermore, in various engineering phenomena, the flux on a rotating disk is influenced by the impact of external magnetic flux. Thus, analyzing the response of base fluid with the concentration of various types of nanoparticle nanofluids under the influence of a magnetic field can also be considered.