Multidigraph Autocatalytic Set for Modelling Complex Systems
Abstract
1. Introduction
2. Preliminaries
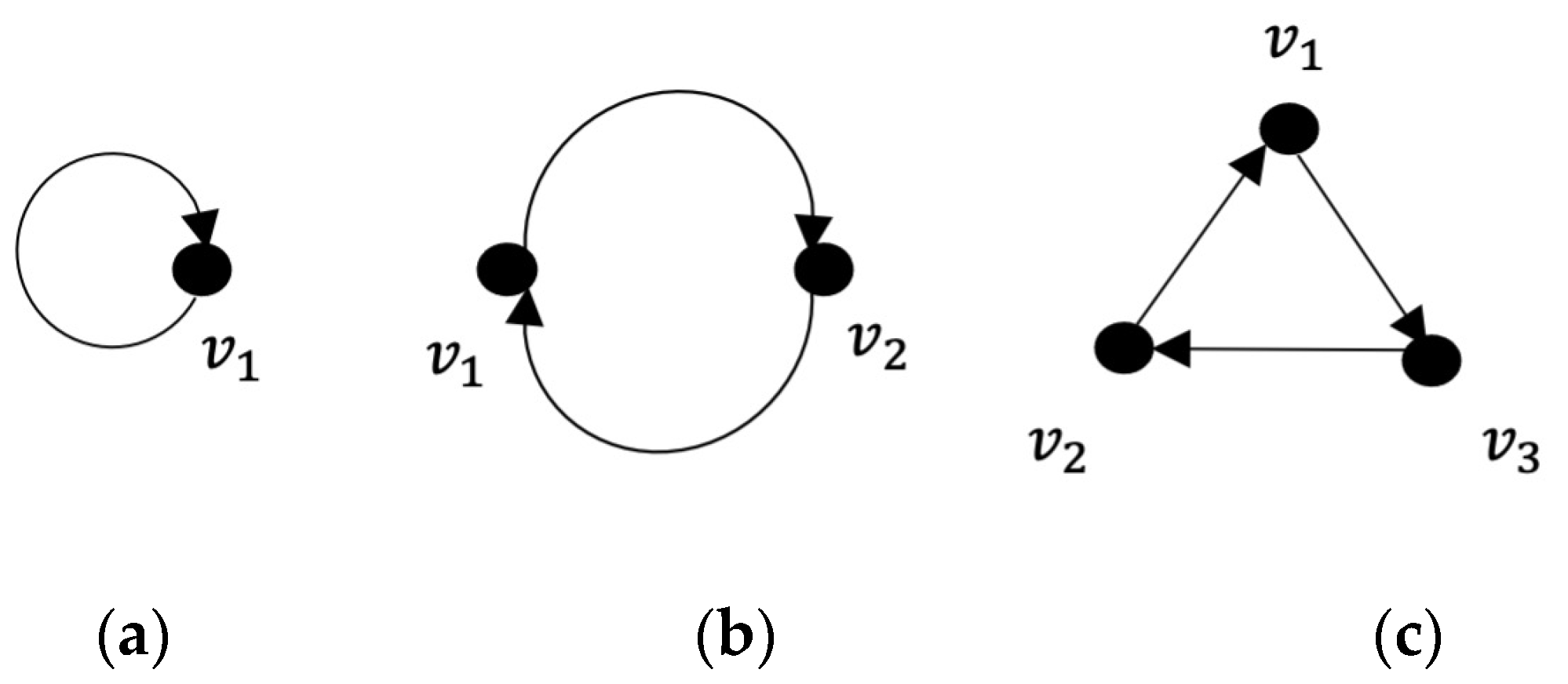
2.1. Autocatalytic Set
| (a) | (b) | (c) |
- if a graph has an ACS.
- if a graph has no ACS.
2.2. Fuzzy Autocatalytic Set
3. Materials and Methods
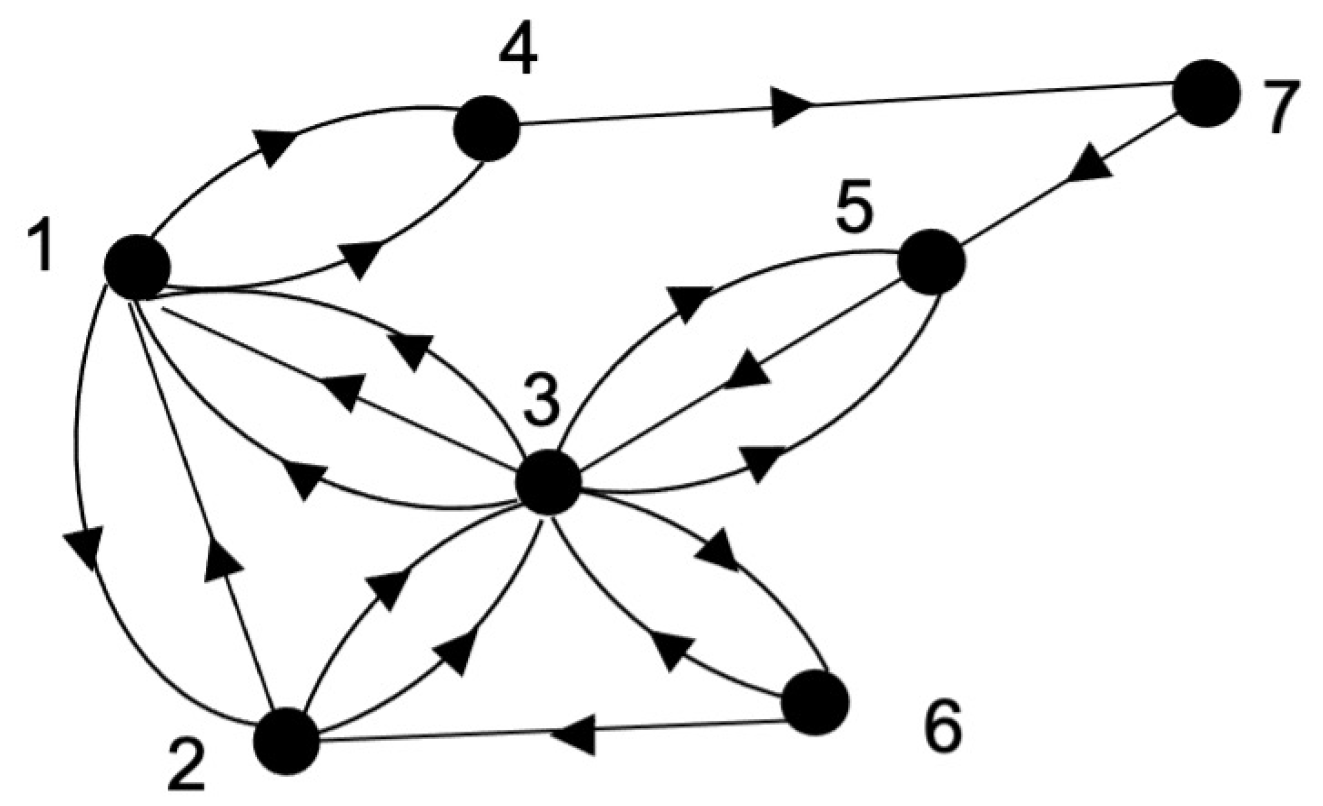
3.1. Multidigraph Autocatalytic Set (MACS)
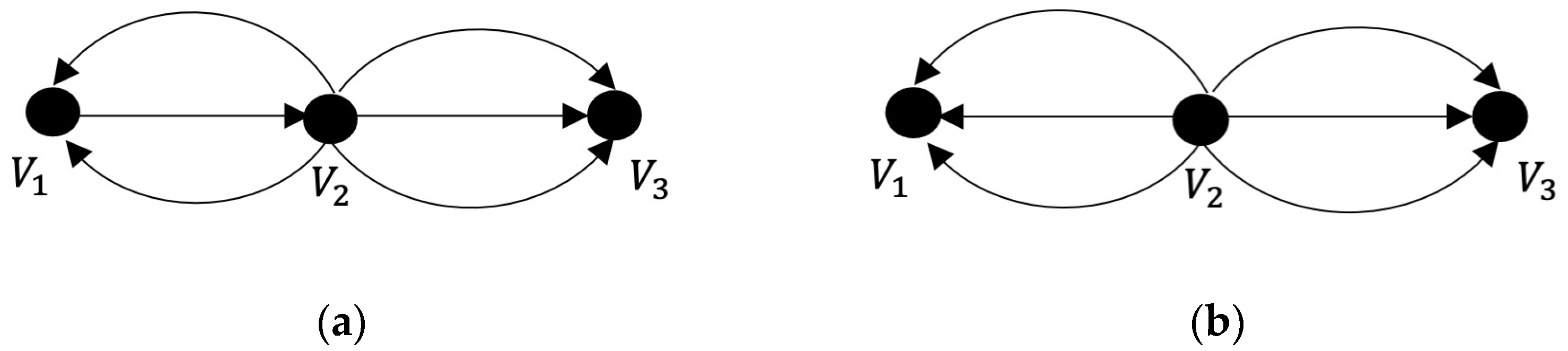
3.2. MACS’s Adjacency Matrix
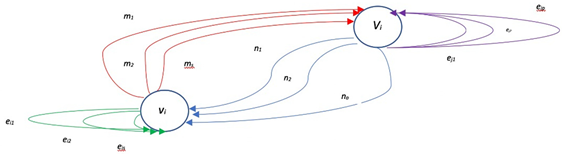
3.3. MACS and Perron–Frobenius Theorem
- (i)
- Both matrices A andpossess the strong Perron–Frobenius property.
- (ii)
- There exists an integersuch thatfor alland for the eigenvalues of A hold.
- (i)
- This immediately implies
- (ii)
- Furthermore, by Theorem 9.
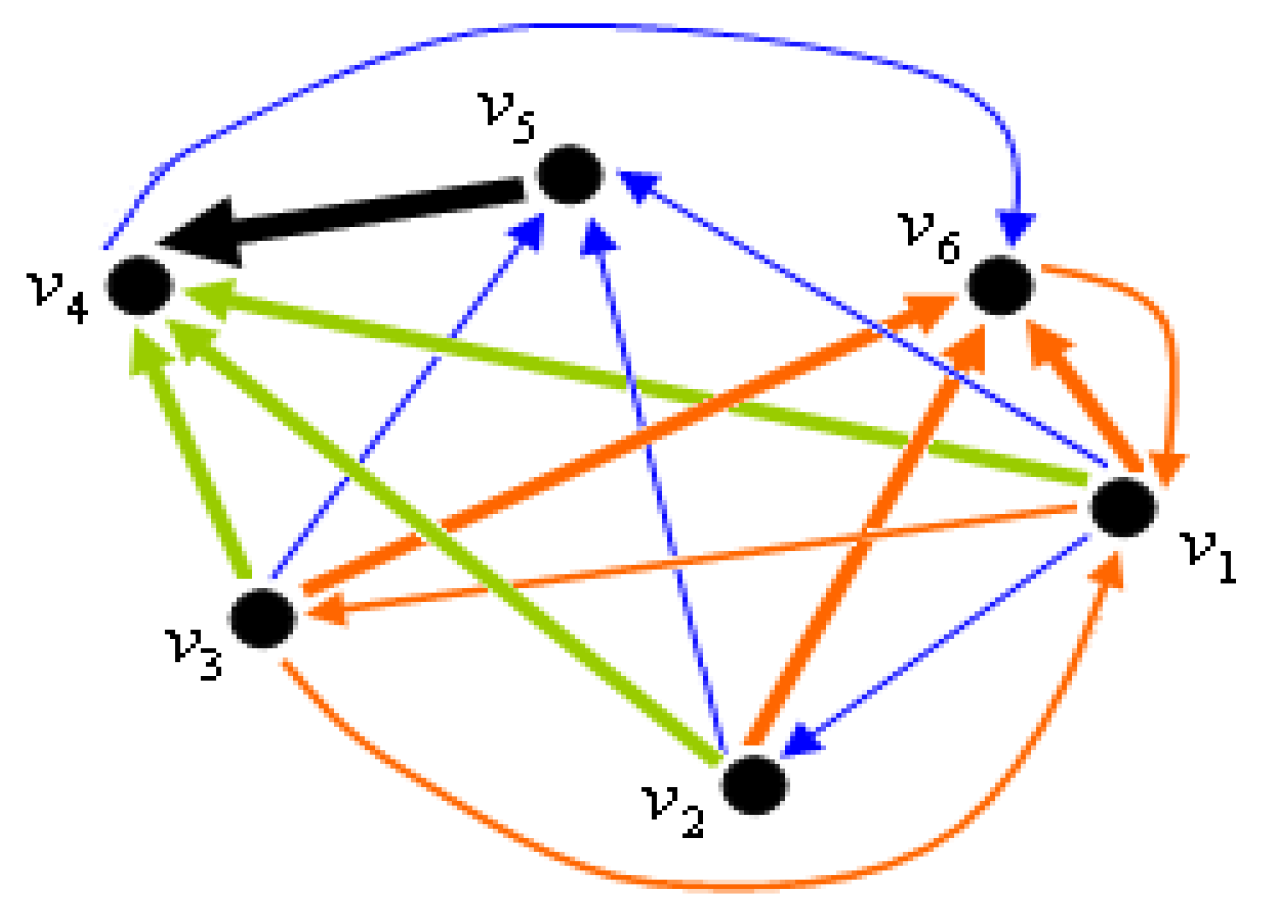
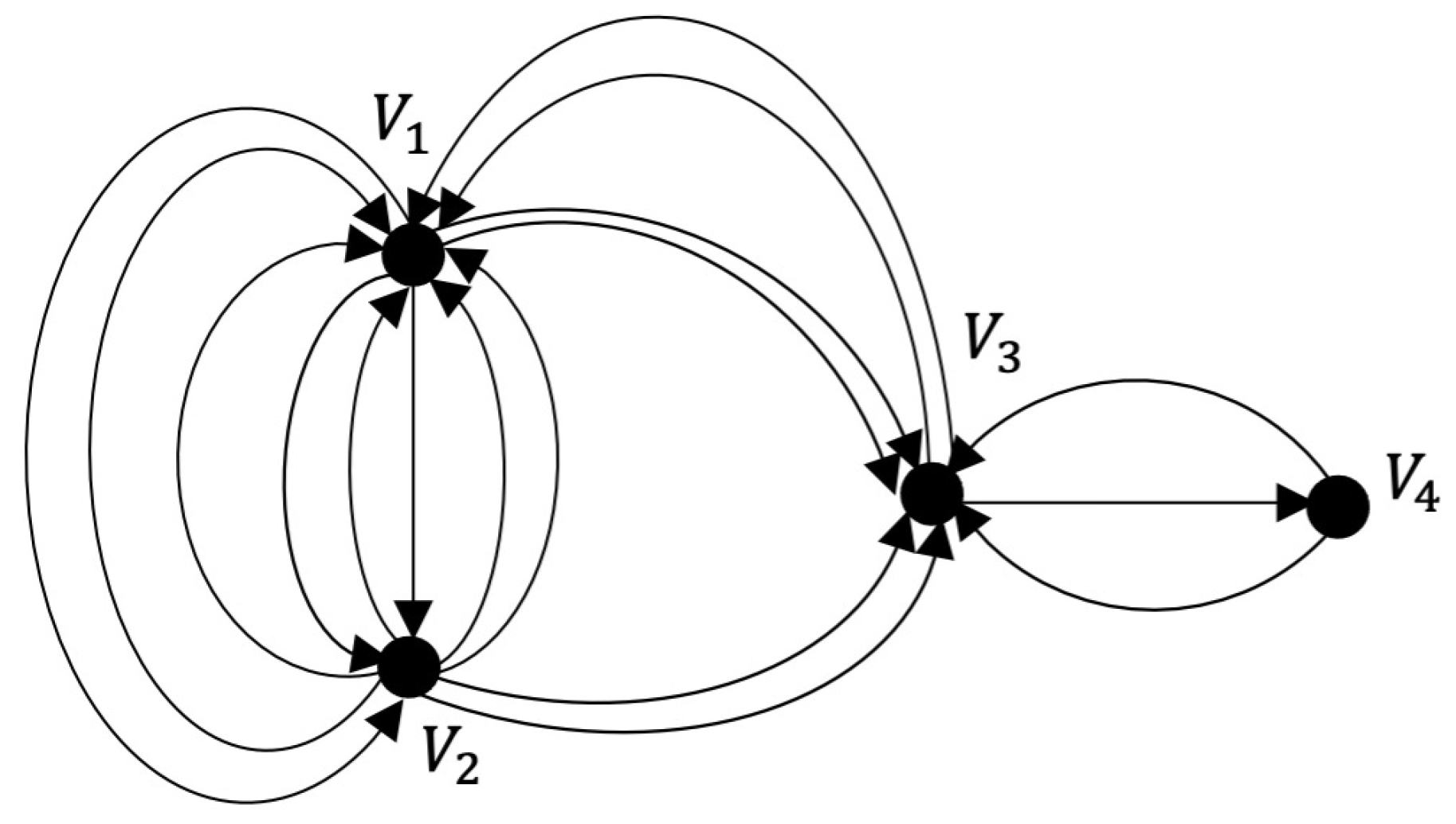
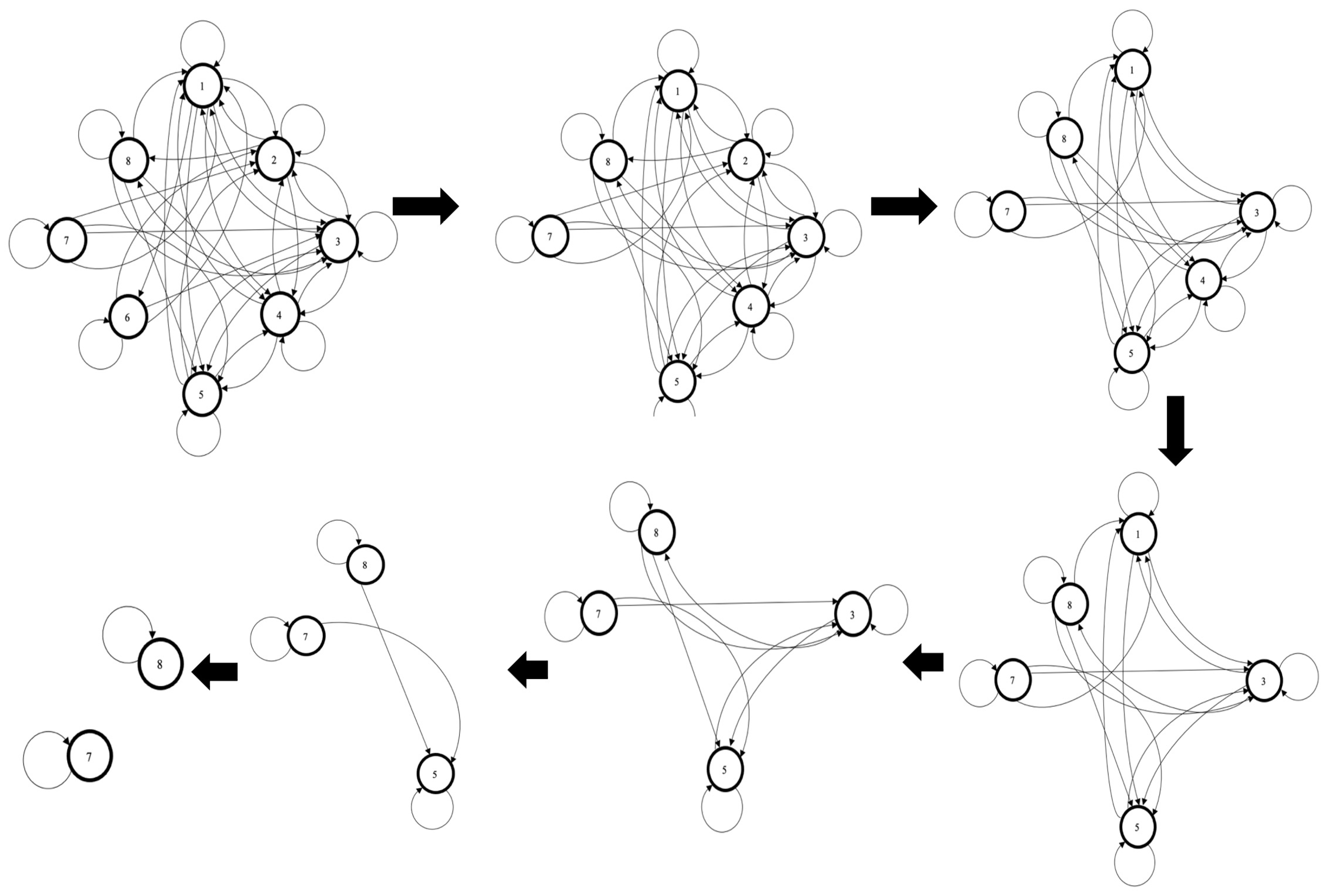
3.4. MACS Graph Algorithm (MACSGA)
| Algorithm 1: The MACS graph algorithm (MACSGA) | |
| 1. | Identify a given system as a multidigraph autocatalytic set, and determine its set of vertices for and its set of multiple directed edges, for . |
| 2. | Determine the complex adjacency matrix of the as defined by (1) in Definition 9. |
| 3. | Calculate the dynamic concentration for each variable, . Variable is evolved with time . The variable is large enough to get close to the Perron–Frobenius eigenvector, as denoted by . |
| (At this stage possesses the strong complex Perron–Frobenius property guaranteed by Theorem 11). | |
| 4. | Determine the lowest value of for Perron–Frobenius eigenvector (PFE) from; . The vertex that has the lowest PFE value is removed from graph . Hence, the resultant graph contains vertices. |
| 5. | Determine the new adjacency matrix for the updated graph . |
| 6. | Repeat Step 4 and Step 5 for the new multidigraph until a matrix with dimension is produced. |
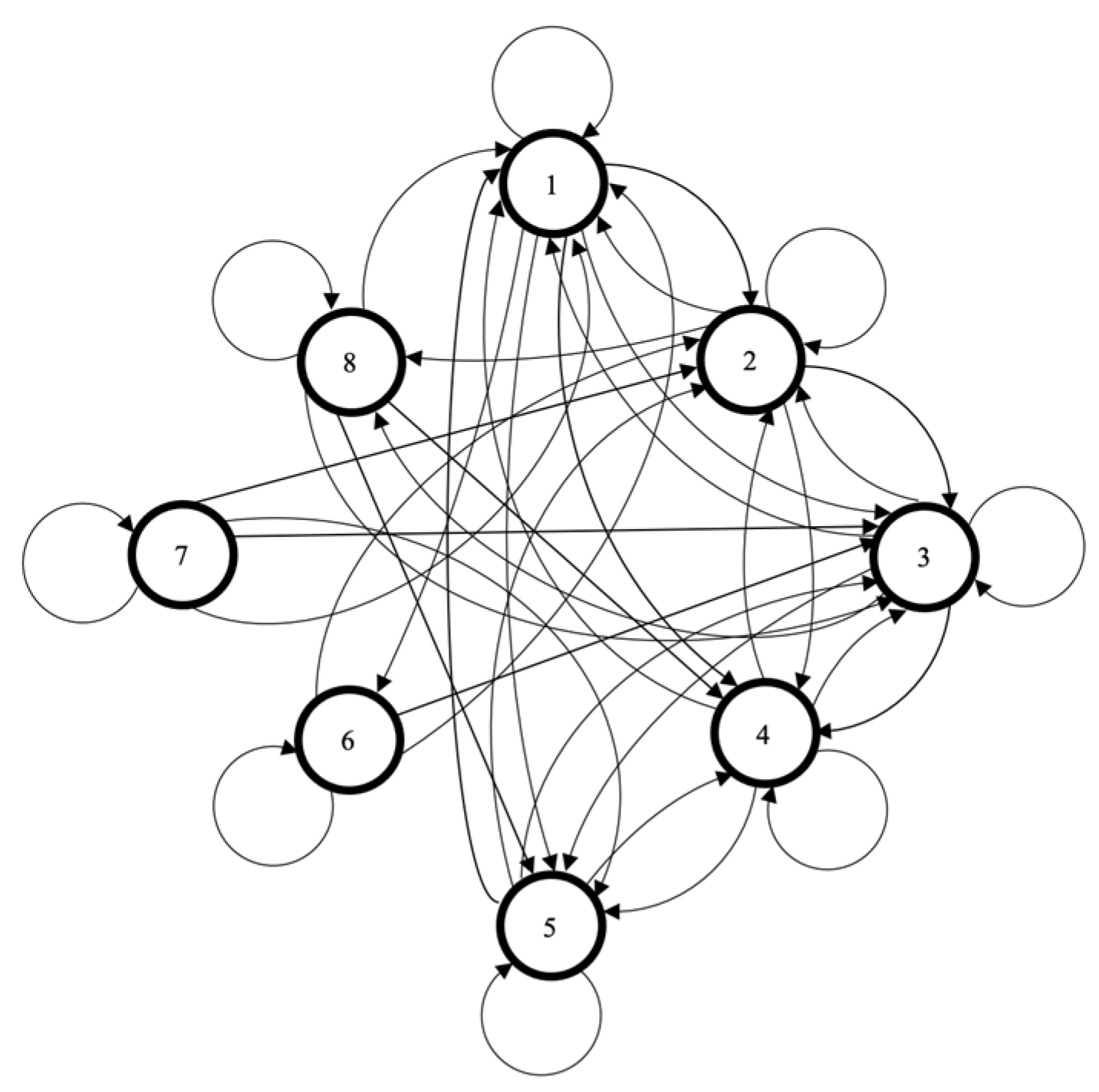
3.5. MACS’s Implementation and Results
4. Conclusions and Future Work
- It can model complex systems that possess multi parameters and relations.
- It requires less data, mainly for verification only.
- It is efficient and requires less computing time.
- No governing equation is needed.
- It can be used for any types of modelling, static or dynamic.
- ➢
- Most of the recent studies on complex systems have focused on what has come to be termed “connectivity”[31]. Connectivity is a description of the relationship between distinct parameters in the system [32]. The more complicated the system, the more complex the level of connectedness within it for example number and relation between its components increase, then the amount of data required and governing equations increase too. The MACS is able to simplify the connectivity in the system and act as a network representation of a complex system to gain a better understanding of how a system function and evolve.
- ➢
- Emergent behaviour is a crucial concept in complex system theory. It is the behaviour of a system that is determined by its interactions rather than its individual pieces. As a result, examining a system’s separate parts cannot anticipate emergent behaviour. It can only be predicted, managed, or controlled if the pieces and their relationships are understood. It is important to identify the relevant structure of the system and its most important parts. In any complex problem, if we cannot model the system accurately, we cannot solve the problem. The MACS can depict the structure of a complicated system, especially when the system has significant interrelationships.
- ➢
- For example, implement MACS in social network analysis. The discovery and identification of influencers and decision-makers are two of the most important jobs in social network analysis. Ensuring the continued engagement of these influencers can lead to increased overall network engagement or specific communities built around such people. MACS can be used for identifying the most influential users and identifying relationships between specific components. While data becomes more complex and interconnected, the application of MACS is essential for timely and effective data processing and analysis.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boccara, N. Modeling Complex Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Preiser, R. Identifying general trends and patterns in complex systems research: An overview of theoretical and practical implications. Syst. Res. Behav. Sci. 2019, 36, 706–714. [Google Scholar] [CrossRef]
- Fedriani, E.M.; Moyano, R. A Computational Measure of Heterogeneity on Mathematical Skills; Department of Economics, Quantitative Methods and Economic History: St. Ann Arbor, MI, USA, 2010. [Google Scholar]
- Zhang, H.; Chen, J. Bipartite Consensus of Linear Multi-Agent Systems Over Signed Digraphs: An Output Feedback Control Approach. IFAC Proc. Vol. 2014, 47, 4681–4686. [Google Scholar] [CrossRef]
- Iggidr, A.; Sallet, G.; Souza, M.O. On the dynamics of a class of multi-group models for vector-borne diseases. J. Math. Anal. Appl. 2016, 441, 723–743. [Google Scholar] [CrossRef]
- Lin, D.; Wu, J.; Yuan, Q.; Zheng, Z. T-EDGE: Temporal WEighted MultiDiGraph Embedding for Ethereum Transaction Network Analysis. Front. Phys. 2020, 8, 204. [Google Scholar] [CrossRef]
- Kauffman, S.A. Cellular Homeostasis, Epigenesis and Replication in Randomly Aggregated Macromolecular Systems. J. Cybern. 1971, 1, 71–96. [Google Scholar] [CrossRef]
- Rössler, O.E. A System Theoretic Model of Biogenesis. Z. Nat. B 1971, 26, 741–746. [Google Scholar] [CrossRef]
- Jain, S.; Krishna, S. Autocatalytic Sets and the Growth of Complexity in an Evolutionary Model. Phys. Rev. Lett. 1998, 81, 5684–5687. [Google Scholar] [CrossRef]
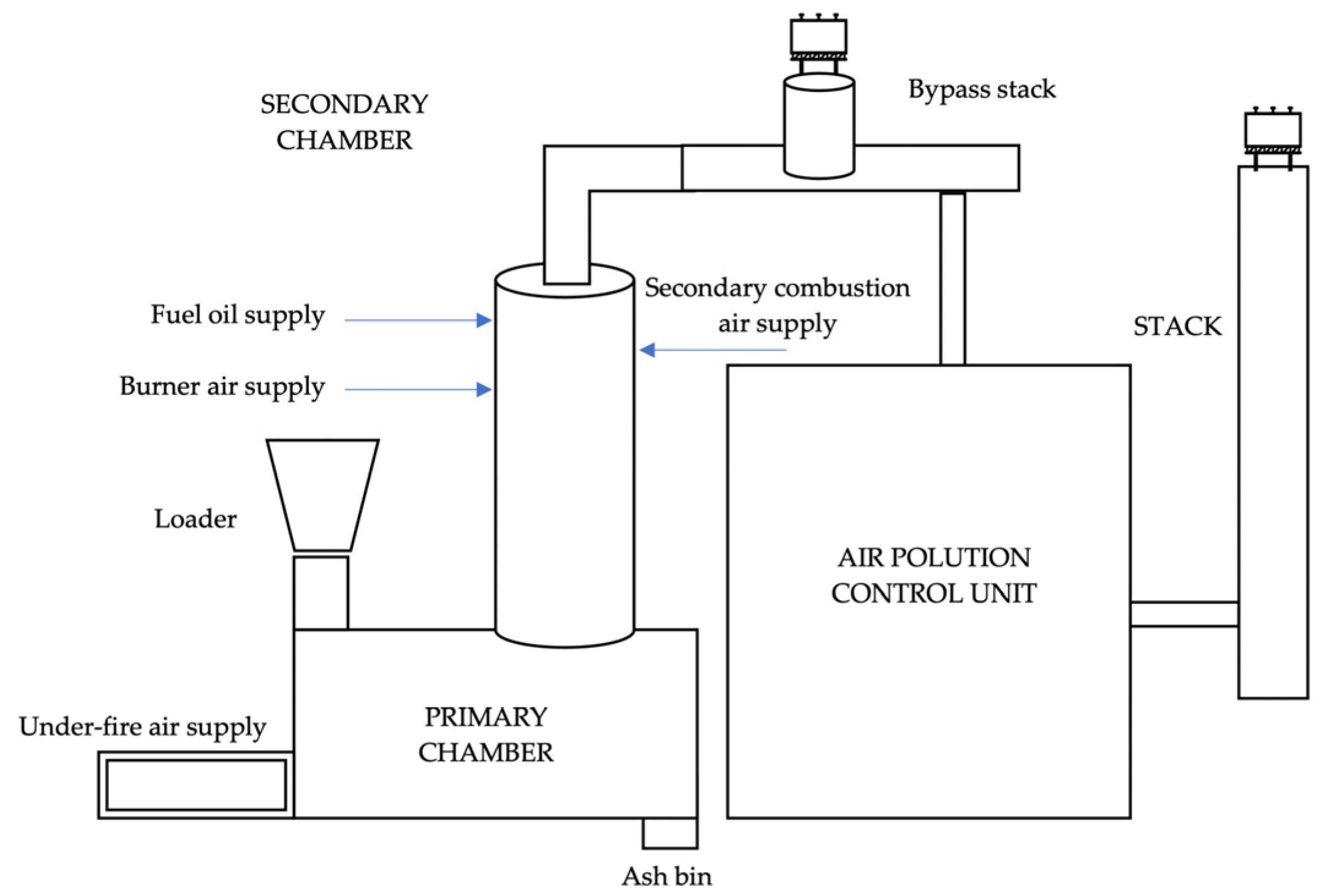
- Ahmad, T.; Baharun, S.; Arshad, K.A. Modeling a clinical incineration process using fuzzy autocatalytic set. J. Math. Chem. 2010, 47, 1263–1273. [Google Scholar] [CrossRef]
- Rosenfeld, A. Fuzzy Graphs. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes, Proceedings of the US–Japan Seminar on Fuzzy Sets and their Applications, Held at the University of California, Berkeley, CA, USA, 1–4 July 1974; Elsevier: Amsterdam, The Netherlands, 1975; pp. 77–95. [Google Scholar] [CrossRef]
- Ashaari, A.; Ahmad, T.; Shamsuddin, M.; Mohamad, W.M.W.; Omar, N. Graph representation for secondary system of pressurized water reactor with autocatalytic set approach. J. Math. Stat. 2016, 11, 107–112. [Google Scholar] [CrossRef]
- Ahmad, T.; Bakar, S.A.; Baharun, S.; Binjadhnan, F.A.M. Coordinated transformation for fuzzy autocatalytic set of fuzzy graph type-3. J. Math. Stat. 2016, 11, 119–127. [Google Scholar] [CrossRef]
- Hassan, N.; Ahmad, T.; Zain, N.M.; Awang, S.R. A fuzzy graph based chemometrics method for gelatin authentication. Mathematics 2020, 8, 1969. [Google Scholar] [CrossRef]
- Hordijk, W. A History of Autocatalytic Sets. Biol. Theory 2019, 14, 224–246. [Google Scholar] [CrossRef]
- Jain, S.; Krishna, S. Graph Theory and the Evolution of Autocatalytic Networks. 2002. Available online: https://www.researchgate.net/publication/2145591 (accessed on 15 December 2022).
- Harary, F. Graph Theory; Addison Wesley Publishing Company: Boston, MA, USA, 1969. [Google Scholar]
- Celik, F.; Cangul, I.N. On The Spectra of Cycles and Paths. 2019. Available online: https://acikerisim.isikun.edu.tr/xmlui/bitstream/handle/11729/2745/vol.9.no.3-17.pdf?sequence=1&isAllowed=y (accessed on 15 December 2022).
- Sameena, K. Clustering Using Strong Arcs in Fuzzy Graphs. 2015. Available online: https://www.emis.de/journals/GMN/yahoo_site_admin/assets/docs/6_GMN-6312-V30N1.301103206.pdfwww.i-csrs.orgAvailablefreeonlineathttp://www.geman.in (accessed on 15 December 2022).
- Yeh, R.T.; Bang, S.Y. Fuzzy Relations, Fuzzy Graphs, and Their Applications to Clustering Analysis. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes, Proceedings of the US–Japan Seminar on Fuzzy Sets and their Applications, Held at the University of California, Berkeley, CA, USA, 1–4 July 1974; Elsevier: Amsterdam, The Netherlands, 1975; pp. 125–149. [Google Scholar] [CrossRef]
- Liew, S.; Ahmad, T. Deduction of Fuzzy Autocatalytic Set to Omega Algebra and Transformation Semigroup. World Acad. Sci. Eng. Technol. 2010. [Google Scholar] [CrossRef]
- Liew, S.Y.; Ahmad, T. Category of Fuzzy Graph and Its Relation to Morphism. Mat. Malays. J. Ind. Appl. Math. 2011, 27, 11–20. [Google Scholar]
- Obaid, U.Q.; Ahmad, T. Novel Structures of Normed Spaces with Fuzzy Autocatalytic Set (FACS) of Fuzzy Graph Type-3. Res. J. Appl. Sci. Eng. Technol. 2016, 12, 562–573. [Google Scholar] [CrossRef]
- Mamat, S.S.; Awang, S.R.; Ahmad, T. Preference Graph of Potential Method as a Fuzzy Graph. Adv. Fuzzy Syst. 2020, 2020, 8697890. [Google Scholar] [CrossRef]
- Ashaari, A.; Ahmad, T.; Awang, S.; Shukor, N. A graph-based dynamic modeling for palm oil refining process. Processes 2021, 9, 523. [Google Scholar] [CrossRef]
- Chartrand, G.; Lesniak, L.; Zhang, P. Graphs & Digraphs; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Barik, S.; Sahoo, G. A new matrix representation of multidigraphs. AKCE Int. J. Graphs Comb. 2020, 17, 466–479. [Google Scholar] [CrossRef]
- Noutsos, D.; Varga, R.S. On the Perron-Frobenius Theory for Complex Matrices Dimitrios Noutsos Perron Frobenius Theory. 2010. Available online: http://ala2010.pmf.uns.ac.rs/presentations/4g1120dn.pdf (accessed on 15 December 2022).
- Noutsos, D.; Varga, R.S. On the Perron–Frobenius Theory for Complex Matrices. Linear Algebra Appl. 2012, 437, 1071–1088. [Google Scholar] [CrossRef]
- Iggidr, A.; Koiller, J.; Penna, M.; Sallet, G.; Silva, M.; Souza, M. Vector borne diseases on an urban environment: The effects of heterogeneity and human circulation. Ecol. Complex. 2017, 30, 76–90. [Google Scholar] [CrossRef]
- Turnbull, L.; Hütt, M.-T.; Ioannides, A.A.; Kininmonth, S.; Poeppl, R.; Tockner, K.; Bracken, L.J.; Keesstra, S.; Liu, L.; Masselink, R.; et al. Connectivity and complex systems: Learning from a multi-disciplinary perspective. Appl. Netw. Sci. 2018, 3, 11. [Google Scholar] [CrossRef] [PubMed]
- Kool, J.T.; Moilanen, A.; Treml, E.A. Population connectivity: Recent advances and new perspectives. Landsc. Ecol. 2013, 28, 165–185. [Google Scholar] [CrossRef]


| Researchers | Year | Contribution |
|---|---|---|
| Kauffman, 1971 [1] | 1971 | The concept of ACS as a possible tool to model the catalytic interaction of chemical compounds is introduced. |
| Rosenfeld, 1975 [2] | 1975 | Fuzzy graph theory was defined. |
| Jain and Krishna, 1998 [3] | 1998 | Introduction of ACS as a graph. |
| Ahmad et al., 2010 [4] | 2010 | A fuzzy autocatalytic set (FACS) was introduced. Each edge of an ACS carries its respective fuzzy membership value. |
| Liew and Ahmad, 2010 [5] | 2010 | Algebraic structure FACS (Ω-FACS) was generated. |
| Liew and Ahmad, 2011 [6] | 2011 | Category FACS was presented. |
| Ashaari et al., 2016 [7] | 2016 | Modelling Pressurized Water Reactor (PWR) system using a dynamic graph of FACS. |
| Bakar et al., 2016 [8] | 2016 | Coordinated FACS is introduced. |
| Qasim and Ahmad, 2016 [9] | 2016 | Proved FACS as a normed space of fuzzy graph Type-3. |
| Mamat et al., 2019 [10] | 2019 | Weak autocatalytic set (WACS) and fuzzy weak autocatalytic set (FWACS) were introduced. |
| Hassan et al., 2020 [11] | 2020 | Chemometrics FACS (c-FACS) was developed for gelatin authentication purposes. |
| Ashaari et al., 2021 [12] | 2021 | Modelling of palm oil refining process using FACS. |
| District | Basic Reproduction Number |
|---|---|
| Centro | 0.948 |
| Sul | 0.760 |
| Norte | 0.681 |
| Oeste | 0.487 |
| Baixada | 0.616 |
| Niteroi | 1.149 |
| Mage | 2.618 |
| Itaguaii | 1.991 |
| Parameter | PFE | Description |
|---|---|---|
| Niteroi is removed. | ||
| Sul is removed. | ||
| Oeste is removed. | ||
| Centro is removed. | ||
| Norte is removed | ||
| Baixada is removed | ||
| Mage and Itaguai are identified as the two culprit districts that caused the outbreak. | ||
| MACSGA | Bailey-Dietz Model | |
|---|---|---|
| District that caused the endemic. | Mage, Itaguai | Mage, Itaguai, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasmin, N.K.; Ahmad, T.; Idris, A.; Awang, S.R.; Abdullahi, M. Multidigraph Autocatalytic Set for Modelling Complex Systems. Mathematics 2023, 11, 912. https://doi.org/10.3390/math11040912
Kasmin NK, Ahmad T, Idris A, Awang SR, Abdullahi M. Multidigraph Autocatalytic Set for Modelling Complex Systems. Mathematics. 2023; 11(4):912. https://doi.org/10.3390/math11040912
Chicago/Turabian StyleKasmin, Nor Kamariah, Tahir Ahmad, Amidora Idris, Siti Rahmah Awang, and Mujahid Abdullahi. 2023. "Multidigraph Autocatalytic Set for Modelling Complex Systems" Mathematics 11, no. 4: 912. https://doi.org/10.3390/math11040912
APA StyleKasmin, N. K., Ahmad, T., Idris, A., Awang, S. R., & Abdullahi, M. (2023). Multidigraph Autocatalytic Set for Modelling Complex Systems. Mathematics, 11(4), 912. https://doi.org/10.3390/math11040912








