Abstract
The act of accessing the exact location, or position, of a node in a network is known as the localization of a network. In this methodology, the precise location of each node within a network can be made in the terms of certain chosen nodes in a subset. This subset is known as the locating set and its minimum cardinality is called the locating number of a network. The generalized hexagonal cellular network is a novel structure for the planning and analysis of a network. In this work, we considered conducting the localization of a generalized hexagonal cellular network. Moreover, we determined and proved the exact locating number for this network. Furthermore, in this technique, each node of a generalized hexagonal cellular network can be accessed uniquely. Lastly, we also discussed the generalized version of the locating set and locating number.
Keywords:
locating set; locating number; generalized hexagonal cellular network; fault-tolerant locating set; resolving set MSC:
05C90; 05C10; 68R01; 68R05; 68R10; 68R12; 68R15; 94C15
1. Introduction
The localization of a network is a methodology by which to access the exact location or position of a vertex (or a node). A compelling prototype is found in determining the precise location of a vertex in a network. When a computer sends a printing instruction in a workplace, localization will assist in: finding the nearest printer; a malfunctioning node; a network intruder; damaged equipment; illegal or misused connections; as well as the location of a roving robot [1]. The localization of a network is a strenuous, exorbitant costly, tedious, and laborious process. Multiple nodes or vertices are chosen in such a manner that the location of the required vertex can be determined by its distinct representation (alternatively, we can say that this is either the labeling, orientation, or location) with the help of chosen nodes. We have to pick the smallest amount of vertices possible to make this method efficient. The most important object in this procedure is the locating set, also known as the metric basis (in pure theoretical form), which is the set of chosen vertices. The cardinality of the smallest feasible set of the chosen vertices (also known as the metric dimension) is called a locating number. The task of identifying a graph’s locating number is a non-deterministic polynomial-time hard problem (NP); in addition, the algorithmic challenge is, as of yet, unknown [2,3,4,5].
The researcher in [6] put forward the idea of a locating set. This study was the first research work on the idea of determining the locating number of a graph, specifically conducted from the definition of a locating set. The locating number has the least cardinality of a locating set. The LORAN and sonar stations were the motivation for developing the idea of locating the set. After this, many researchers used this idea and renamed it in many other different ways. In the research work of [7] the concept of a locating set was renamed to a metric dimension. While understood in this pure theoretical way, the researchers in [8,9] renamed the same concept as the metric basis or resolving set. In the recent decade, a one-step advanced definition of the locating set was developed, in which the concept of one node faultiness from the locating set was discussed [10]. The concept is known as a fault-tolerant locating set and we can say it is a generalized version of a locating set. In the generalized view of the locating set, many ideas and implementations have since evolved. In the broader view, this idea is used in [11,12,13,14].
In the broader view, this idea is used in: pharmaceutical chemistry [5]; image processing [6]; some complex games or robotic roving [15]; combinatorial optimization [16]; and complex networks [11,12]. Furthermore, a technique to investigate various polyphenyl structures, particularly with respect to the polymer industry [13], and a recent advancement shows the implementation of a locating set (and its generalizations) in electronics [14].
Due to its vast variations and implementations in numerous fields, metric dimension (i.e., the locating set) has an extensive literature. However, we will only discuss the recent and most generalized results in this study. In [17], a generic graph of a kayak paddle and a few more graphs pertaining to cycles are discussed. Authors of [18] researched a cellulose network and calculated some upper boundaries for the structure. In [19], a graph metric that resembles a coronoid shape is restored. With the idea of locating numbers, a hydrocarbon-based class of structure was investigated in [20] and some other versions were also found. With the help of the definition of the locating set [21], the generalized class of the Harary family was investigated. In addition, the authors of [22] discussed multi-graphs and generalized Peterson graphs along with the idea of a metric basis. The academics that explored this concept on the Cayley graph and determined the locating number for such a generalized class are cited in [23]. Moreover, some recent study and the literature is available at [24,25,26].
There is a variety of literature on this subject: for example, one can check some current studies on this term found in [27,28,29,30,31]. In [32], the internet graph and its fault-tolerant topology are covered. In [33], the notion of a fault-tolerant locating number is used to study a quartz structure, ref. [34] as well as the studies networks of connections associated to computers. In [35], convex polytopes were studied in relation to a fault-tolerant locating set, and their precise fault-tolerant locating numbers were thus discovered.
Hexagonal tessellation is an arrangement of shapes, specifically of polygons without any gaps. It is in infinite geometric shape patterns specifically that the hexagonal arrangements are obtained, as proposed in [36]. After its discovery, it has become available in different fields, such as in the form of networks, the recent advancement found in [1], and with respect to cellular networks [37]. The hexagonal cellular network is widely used in different fields in a broader sense, such as in the planning and analysis of a network. Furthermore, its usage, planning, and analysis in terms of academia are available in the book [38]. For industrial usage, the study is available at [39,40,41,42]; moreover, detail on the topology of the hexagonal cellular network is the main point of discussion of [43].
We will now first start by introducing some fundamental concepts that will be used below in the development of our results.
Definition 1
([1]). Suppose a graph G is connected and that it has the vertex set . The distance between a pair of vertices and in is defined as the length of the shortest path between them. This distance is signified by .
Definition 2
([44]). Define for some vertex as an ordered simple subset. The location (or position, representation) of a with respect to is defined as the i-tuple distances . For any two vertices of G, if they have different locations with respect to the chosen subset then is said to be a locating set for G.
Definition 3
([44]). We define the cardinality of a minimal locating set as the locating number of the graph. This is denoted by .
Definition 4
([44]). A locating set is called a fault-tolerant locating set if it satisfies the following condition: for every vertex and if it remains a locating set.
Definition 5
([44]). The cardinality of a minimal fault-tolerant locating set is called the fault-tolerant locating number of the graph. This is denoted by .
2. Certain Important Results
Certain important results were very useful in regard to computing our main work.
Theorem 1
([6,8,45]). If G is a simple, undirected and connected graph, then
(1) iff
(2) iff
(3) iff
(4) iff
(5) if
(6) if
(7) Let T be a tree that is not a path and define to be the number of leaves (nodes of degree 1) in Further, define as the number of exterior major vertices in . Specifically, that is vertices with a degree of at least 3, which are also connected to at least one leaf by an edge or a path of vertices that are of degree 2. Then, the metric dimension of T is
Theorem 2
([19,46]). If and are the locating number and fault-tolerant locating number of a graph G respectively, then
In this work, localizing a generalized hexagonal cellular network will be taken into consideration. Moreover, we will identify and validate the precise network locating number. This method allows for the unique access to every node in a generalized hexagonal cellular network. We will also discuss the locating set and locating number in their generalized form. Moreover, we will also discuss the generalization of localization in this work, which is called a fault-tolerant localization, for this chosen hexagonal cellular network.
3. Construction
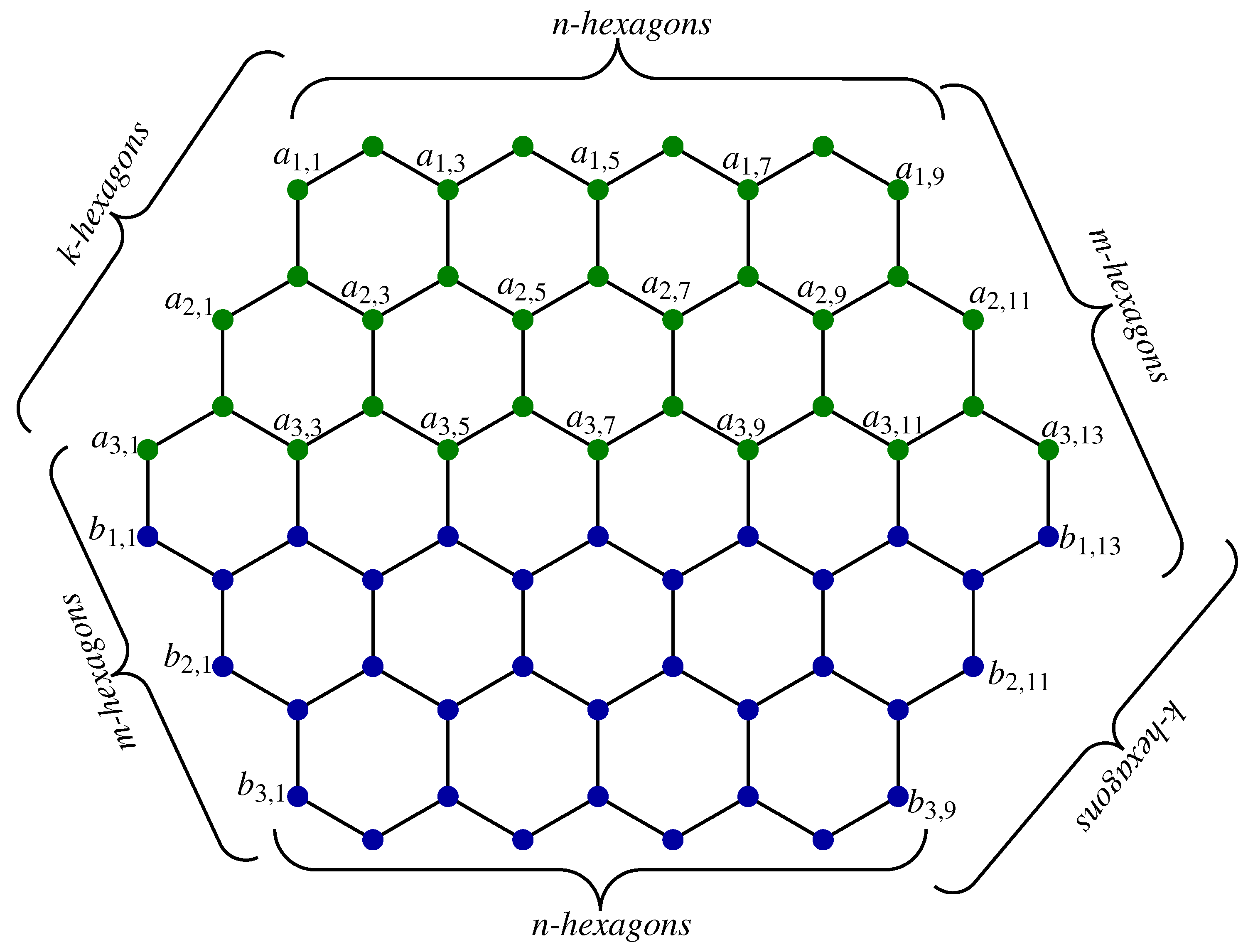
The network shown in Figure 1, is a generalized hexagonal cellular network. It contains three variables or parameters for its six-dimensional shape. As we named the network the parameters were set as These three parameters can be entirely different or the same, as well. Furthermore, we labeled the nodes and edges of this network for the proofs of our main result, as shown below.
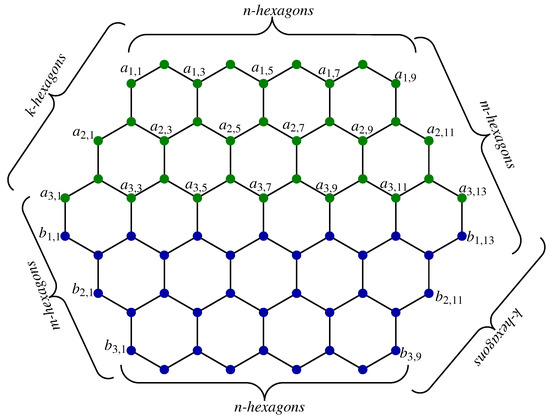
Figure 1.
Generalized Hexagonal Cellular Network with .
The order and size of this network is summarized as:
Figure 1 is with its particular values regarding the parameters These labels are used in the proofs of the theorems. Further, they can be generalized for all natural values of parameters by focusing on the Figure 1 labels, as well as the presented edge and vertex sets.
There is a relevant survey on network design [47]. Moreover, there are some localization techniques apart from this method that are presented in this study, as detailed in [48,49]. Moreover, there are some results on the metrics of a network with the shortest path technique, such as the method presented here, which are also elaborated in [50,51]. Furthermore, the same structure is also considered a peri-condensed benzenoid system with the formal name, in chemistry, of hexagonal-shaped graphene flakes [52].
In the next part of this section, we will discuss some of the main results regarding the locating set and locating number of the generalized hexagonal cellular network for all the possible natural values of the three parameters .
Lemma 1.
Let be a graph of the generalized hexagonal cellular network. Then, the locating number of is two.
Proof.


In order to prove this lemma, we need to follow Definition 2, to be able to choose an appropriate locating set. Let , which is a pertinent candidate for a locating set of , or for the particular values of a generalized hexagonal cellular network’s parameters. In order to prove our claim that the chosen subset is actually a locating set of we will follow Definition 1 in order to calculate the shortest paths of all nodes towards Then, we will use these paths in the actual definition of a location, as presented in Definition 2, which are shown in Table 1 and Table 2.

Table 1.
Locations of the nodes of .

Table 2.
Locations of the nodes of .
By looking at the Tables furnished in the locations of the nodes of which are all unique and distinct, we now check Definition 3. which concludes the proof. □
Lemma 2.
Let be a graph of the generalized hexagonal cellular network. Then, the locating number of is two.
Proof.


In order to prove this lemma, we need to follow Definition 2, which will allow us to choose an appropriate locating set. Let which is a pertinent candidate for a locating set of , or for the particular values of a generalized hexagonal cellular network’s parameters. In order to prove our claim that the chosen subset is actually a locating set of we will follow Definition 1 in order to calculate the shortest paths of all nodes toward Then, we will proceed by using these paths in the actual definition of the location presented in Definition 2, which are shown in Table 3 and Table 4.

Table 3.
Locations of the nodes of .

Table 4.
Locations of the nodes of .
By looking at the Tables furnished in the locations of the nodes of which are all unique and distinct, we now check Definition 3, which concludes the proof. □
Lemma 3.
Let be a graph of the generalized hexagonal cellular network. Then, the locating number of is two.
Proof.


In order to prove this lemma, we need to follow Definition 2, which will allow us to choose an appropriate locating set. Let . Then, this will be a pertinent candidate for a locating set of or for the particular values of generalized hexagonal cellular network’s parameters. In order to prove our claim that the chosen subset is actually a locating set of we will follow Definition 1 in order to calculate the shortest paths of all nodes toward Then, we will proceed by using these paths in the actual definition of the location presented in Definition 2, which are shown in Table 5 and Table 6.

Table 5.
Locations of the nodes of .

Table 6.
Locations of the nodes of .
By looking at the Tables furnished in the locations of the nodes of which are all unique and distinct, we now check Definition 3, which concludes the proof. □
Theorem 3.
Let with be a graph of the generalized hexagonal cellular network. Then, the locating number of is three.
Proof.
In order to prove this theorem with equality, we will check both inequalities. In order to check we need to follow Definition 2, such that we are able to choose an appropriate locating set. Let be a pertinent candidate for a locating set of , or for the particular values of the generalized hexagonal cellular network’s parameters with the condition In order o prove our claim that the chosen subset is actually a locating set of we will follow Definition 1 in order to calculate the shortest paths of all nodes toward Then, we will proceed by using these paths in the actual definition of the location presented in Definition 2, which are shown below.
For and the locations for the vertex subset are elaborated in the following manner:
For , with a condition on the parameters that are either with or with the locations for the vertex subset are elaborated in the following manner:
For , with a condition on parameters that are either with or with the locations for the vertex subset are elaborated in the following manner:
For and the locations for the vertex subset are elaborated in the following manner:
By looking at the furnished location of the nodes of which are given in Equations (1)–(4) and are all unique and distinct, we now check Definition 3, .
Now, we will check the reverse inequality, which is By taking negation, we can say or In order to prove the assertion given below, some possible cases are required in order to contradict the negation equality.
Sample 1: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 2: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 3: If and comprised only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 4: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 5: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 6: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 7: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 8: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 9: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 10: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 11: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 12: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 13: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 14: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
Sample 15: If and comprises only two members, then the chosen sample contradicts our supposition with the same locations of at least two vertices, which are along with .
All the Samples 1–15 discussed above contradicted with our suppositions. This discussion concluded that , as well as further implied that This, thus, completes the proof. □
Theorem 4.
Let with be a graph of the generalized hexagonal cellular network. Then, the locating number of is three.
Proof.
In order to prove this theorem with equality, we checked both inequalities. In order to check we needed to follow Definition 2, such that we are able to choose an appropriate locating set. Let be a pertinent candidate for a locating set of , or for the particular values of generalized hexagonal cellular network’s parameters with the condition In order to prove our claim that the chosen subset is actually a locating set of we will follow Definition 1, such that we are able to calculate the shortest paths of all nodes toward Then, we will proceed by using these paths in the actual definition of the location presented in Definition 2, which are shown below.
For and the locations for the vertex subset are elaborated in the following manner:
For , with a condition that the parameters are either with or with the locations for the vertex subset are elaborated in the following manner:
For , with a condition that the parameters are either with or with the locations for the vertex subset are elaborated in the following manner:
For and the locations for the vertex subset are elaborated in the following manner:
By looking at the furnished location of the nodes of , which are given in Equations (5)–(8) and are all unique and distinct, we are now able to check Definition 3, .
Then, we will check the reverse inequality, which is By taking negation, we can say or However, in order to prove this assertion we will to have already inspected the possible samples shown in the second part of the proof of Theorem 2. As shown above, all the chosen samples for fall into contradiction and thus it is concluded that This further shows that is the case, which completes the proof. □
Theorem 5.
Let with be a graph of the generalized hexagonal cellular network. Then, the fault-tolerant locating number of is four.
Proof.
In order to prove this theorem with equality, we will check both inequalities. In order to check we will need to follow Definition 4, such that we are able to choose an appropriate fault-tolerant locating set. Let be a pertinent candidate for a fault-tolerant locating set of , or for the particular values of the generalized hexagonal cellular network’s parameters with the condition In order to prove our claim that the chosen subset is actually a fault-tolerant locating set of we will follow the Definition 1 to calculate the shortest paths of all nodes towards Then, we will proceed by using these paths in the actual definition of the location presented in Definition 4, which are shown below.
For and the locations for the vertex subset are elaborated in the following manner:
For with a condition on the parameters that are either with or with the locations for the vertex subset are elaborated in the following manner:
For with a condition on the parameters that are either with or with the locations for the vertex subset are elaborated in the following manner:
For and the locations for the vertex subset are elaborated in the following manner:
By looking at the furnished location of the nodes of given in Equations (9)–(12), which are all unique and distinct, we can then check by eliminating any node from the subset . Indeed, this still provides the unique and distinct positions of the entire vertex set of This then allows us to check Definition 5, .
Next, we will check the reverse inequality, which is By taking negation, we can say or However, in order to prove this assertion we will follow Theorem 2. This, thus, concludes that is not possible. As such, it is finally deduced that □
Theorem 6.
Let with be a graph of the generalized hexagonal cellular network. Then, the fault-tolerant locating number of is four.
Proof.
In order to prove this theorem with equality, we will check both inequalities. In order to check we need to follow Definition 4, which will allow us to choose an appropriate fault-tolerant locating set. Let be a pertinent candidate for a fault-tolerant locating set of , or for the particular values of the generalized hexagonal cellular network’s parameters with the condition In order to prove our claim that the chosen subset is actually a fault-tolerant locating set of we will follow Definition 1, such that we are able to calculate the shortest paths of all nodes toward Then, we will proceed by using these paths in the actual definition of the location presented in Definition 4, which are shown below.
For and the locations for the vertex subset are elaborated in the following manner:
For , with a condition on the parameters that are either with or with the locations for the vertex subset are elaborated in the following manner:
For , with a condition on the parameters that are either with or with the locations for the vertex subset are elaborated in the following manner:
For and the locations for the vertex subset are elaborated in the following manner:
By looking at the furnished location of the nodes of which are given in the Equations (13)–(16) and are all unique and distinct, we can thus check by eliminating any node from the subset . By performing this, the unique and distinct positions of the entire vertex set of are still provided. This, thus, allows us to check the Definition 5, .
Next, we will check the reverse inequality, which is By taking negation, we can say or In order to prove this assertion we will then follow the Theorem 2. By so doing this, we can conclude that is not possible. Finally, it is deduced that □
4. Conclusions and Comparison with the Existing Research Work
We discussed the localization of generalized hexagonal cellular networks in this research work. We determined the exact locating number of the generalized hexagonal cellular network and proved that the locating number of such a network is independent of the order and size of the network. Although the locating number of the entire structure does not depend on the order and size network, it does change with the variation of all three parameters Moreover, we also discussed the generalized concept of the locating set for a generalized hexagonal cellular network. Furthermore, the summary of the results were elaborated upon in Table 7 and Table 8.

Table 7.
Locating sets of .

Table 8.
Locating numbers of .
In [53], a particular type of hexagonal networks were discussed. In that study, the researches determined the minimum metric bases for hexagonal networks. The hexagonal network they discussed was with only a single parameter and also increased with only one parameter. In our work, we tried to develop the structure with three parameters , which, in turn, is the generalization of work by [53]. In our obtained results, the chosen structures have only two metric dimensions, but our generalized structure possesses two and three metric dimensions. As such, this must be an advantage with respect to generalizing the structure, as well as in regard to then studying the hexagonal network in terms of metric dimension. Moreover, we also studied the fault-tolerant parameter of the metric dimension with a generalized structure. In addition, in [54], another study found the hexagonal structure, which is similar to our chosen network but with the same limitations found in [53]. With respect to the aforementioned, they conducted the research work for single parameter only.
The representation of v with respect to the above is defined as the k-vector for an ordered k-partition of and a vertex v of If the distinct vertices of G have distinct representations with respect to then the partition is known as a resolving partition for Furthermore, the partition dimension of G is the lowest k for which there is a resolving k-partition of Lastly, a minimal resolving partition is a resolving partition of that contains elements [55].
Problem 1.

The open problem, or future research direction for this particular chosen network, can be found in the Table 9.

Table 9.
Partition dimension of .
Author Contributions
Investigation, M.A., M.K.J. and Y.S.; writing—original draft preparation, M.A.; writing—review and editing, M.A., M.K.J. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nadeem, M.F.; Azeem, M.; Khalil, A. The locating number of hexagonal Möbius ladder network. J. Appl. Math. Comput. 2020, 66, 149–165. [Google Scholar] [CrossRef]
- Hauptmann, M.; Schmied, R.; Viehmann, C. Approximation complexity of metric dimension problem. J. Discret. Algorithms 2012, 14, 214–222. [Google Scholar] [CrossRef]
- Lewis, H.; Garey, M.; Johnson, D. Computers and intractability. A guide to the theory of NP-completeness. J. Symb. Log. 1983, 48, 498–500. [Google Scholar] [CrossRef]
- Johnson, M.A. Browsable Structure-Activity Datasets, Advances in Molecular Similarity; JAI Press: Greenwich, CT, USA, 1998; pp. 153–170. [Google Scholar]
- Johnson, M.A. Structure-activity maps for visualizing the graph variables arising in drug design. J. Biopharm. Stat. 1993, 3, 203–236. [Google Scholar] [CrossRef] [PubMed]
- Slater, P. Leaves of trees. In Proceeding of the 6th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Congressus Numerantium, Boca Raton, FL, USA, 17–20 February 1975; Volume 14, pp. 549–559. [Google Scholar]
- Harary, F.; Melter, R.A. On the metric dimension of a graph. Ars Comb. 1976, 2, 191–195. [Google Scholar]
- Chartrand, G.; Salehi, E.; Zhang, P. The partition dimension of graph. Aequationes Math. 2000, 59, 45–54. [Google Scholar] [CrossRef]
- Chartrand, G.; Eroh, L.; Johnson, M.A.O.; Ortrud, R. Resolvability in graphs and the metric dimension of a graph. Discret. Appl. Math. 2000, 105, 99–113. [Google Scholar] [CrossRef]
- Hernando, C.; Mora, M.; Slater, P.; Wood, D. Fault-tolerant metric dimension of graphs. Convexity Discret. Struct. 2008, 5, 81–85. [Google Scholar]
- Shang, Y. Local natural connectivity in complex networks. Chin. Phys. Lett. 2011, 28, 068903. [Google Scholar] [CrossRef]
- Shang, Y. Localized recovery of complex networks against failure. Sci. Rep. 2016, 6, 30521. [Google Scholar]
- Nadeem, M.F.; Hassan, M.; Azeem, M.; Khan, S.U.D.; Shaik, M.R.; Sharaf, M.A.F.; Abdelgawad, A.; Awwad, E.M. Application of Resolvability Technique to Investigate the Different Polyphenyl Structures for Polymer Industry. J. Chem. 2021, 2021, 6633227. [Google Scholar] [CrossRef]
- Ahmad, A.; Koam, A.N.; Siddiqui, M.; Azeem, M. Resolvability of the starphene structure and applications in electronics. Ain Shams Eng. J. 2021, 13, 101587. [Google Scholar] [CrossRef]
- Khuller, S.; Raghavachari, B.; Rosenfeld, A. Landmarks in graphs. Discret. Appl. Math. 1996, 70, 217–229. [Google Scholar] [CrossRef]
- Sebö, A.; Tannier, E. On metric generators of graphs. Math. Oper. Res. 2004, 29, 383–393. [Google Scholar] [CrossRef]
- Ahmad, A.; Bača, M.; Sultan, S. Computing the metric dimension of Kayak Paddles graph and Cycles with chord. Proyecc. J. Math. 2020, 39, 287–300. [Google Scholar] [CrossRef]
- Imran, S.; Siddiqui, M.K.; Hussain, M. Computing the upper bounds for the metric dimension Of cellulose network. Appl. Math. E-Notes 2019, 19, 585–605. [Google Scholar]
- Koam, A.N.A.; Ahmad, A.; Abdelhag, M.E.; Azeem, M. Metric and Fault-Tolerant Metric Dimension of Hollow Coronoid. IEEE Access 2021, 9, 81527–81534. [Google Scholar] [CrossRef]
- Azeem, M.; Nadeem, M.F. Metric-based resolvability of polycyclic aromatic hydrocarbons. Eur. Phys. J. Plus 2021, 136, 395. [Google Scholar] [CrossRef]
- Ahmad, A.; Baca, M.; Sultan, S. On Metric Dimension and Minimal doubly resolving sets of Harary graph. Acta Math. Univ. Comen. 2020, 89, 123–129. [Google Scholar]
- Imran, M.; Siddiqui, M.K.; Naeem, R. On the Metric Dimension of Generalized Petersen Multigraphs. IEEE Access 2018, 6, 74328–74338. [Google Scholar] [CrossRef]
- Ahmad, A.; Imran, M.; Al-Mushayt, O.; Bokhary, S.A.H. On the metric dimension of barcycentric subdivision of Cayley graphs Cay(Zn⊕Zm). Miskolc Math. Notes 2015, 16, 637–646. [Google Scholar]
- Azeem, M.; Imran, M.; Nadeem, M.F. Sharp bounds on partition dimension of hexagonal Möbius ladder. J. King Saud Univ.-Sci. 2022, 34, 101779. [Google Scholar] [CrossRef]
- Bukhari, S.; Jamil, M.K.; Azeem, M.; Swaray, S. Patched Network and its Vertex-Edge Metric-Based Dimension. IEEE Access 2023, 11, 4478–4485. [Google Scholar] [CrossRef]
- Koam, A.N.A.; Ahmad, A. Barycentric subdivision of Cayley graphs with constant edge metric dimension. IEEE Access 2020, 8, 80624–80628. [Google Scholar] [CrossRef]
- Ahmad, Z.; Chaudhary, M.A.; Baig, A.Q.; Zahid, M.A. Fault-tolerant metric dimension of P(n, 2) graph. J. Discret. Math. Sci. Cryptogr. 2021, 24, 647–656. [Google Scholar] [CrossRef]
- Vietz, D.; Wanke, E. The Fault-Tolerant Metric Dimension of Cographs. In Fundamentals of Computation Theory; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 350–364. [Google Scholar] [CrossRef]
- Sharma, S.K.; Bhat, V.K. Fault-tolerant metric dimension of two-fold heptagonal-nonagonal circular ladder. Discret. Math. Algorithms Appl. 2021, 14, 2150132. [Google Scholar] [CrossRef]
- Saha, L.; Lama, R.; Tiwary, K.; Das, K.; Shang, Y. Fault-tolerant metric dimension of circulant graphs. Mathematics 2022, 10, 124. [Google Scholar] [CrossRef]
- Nadeem, M.F.; Ali, W.; Siddiqui, H.M.A. Locating Number of Biswapped Networks. Int. J. Found. Comput. Sci. 2022, 33, 667–690. [Google Scholar] [CrossRef]
- Deng, W.; Karaliopoulos, M.; Mühlbauer, W.; Zhu, P.; Lu, X.; Plattner, B. k-Fault tolerance of the Internet AS graph. Comput. Netw. 2011, 55, 2492–2503. [Google Scholar] [CrossRef]
- Imran, M.; Ahmad, A.; Azeem, M.; Elahi, K. Metric-Based Resolvability of Quartz Structure. Comput. Mater. Contin. 2021, 71, 2053–2071. [Google Scholar]
- Raza, H.; Hayat, S.; Pan, X.F. On the fault-tolerant metric dimension of certain interconnection networks. J. Appl. Math. Comput. 2019, 60, 517–535. [Google Scholar] [CrossRef]
- Raza, H.; Hayat, S.; Pan, X.F. On the fault-tolerant metric dimension of convex polytopes. Appl. Math. Comput. 2018, 339, 172–185. [Google Scholar] [CrossRef]
- Donald, V.H.M. Advanced Mobile Phone Service: The Cellular Concept. Bell Syst. Tech. J. 1979, 58, 15–41. [Google Scholar] [CrossRef]
- Yang, X.; Fapojuwo, A.O. Performance analysis of hexagonal cellular networks in fading channels. Wirel. Commun. Mob. Comput. 2015, 16, 850–867. [Google Scholar] [CrossRef]
- Garg, V. Wireless Communications and Networking; Elsevier Inc.: Boston, MA, USA, 2007; pp. 47–147. [Google Scholar]
- Jacks, E.; Schumacher, G. NGMN Alliance Performance Evaluation Methodology; NGMN Technical Working Group Steering Committee (TWG-SC): Frankfurt, Germany, 2007; pp. 1–36. [Google Scholar]
- 3GPP TR 36.814 V9.0.0. Further Advancements for E-UTRA Physical Layer Aspect. 2010. Available online: https://www.scirp.org/(S(lz5mqp453edsnp55rrgjct55))/reference/ReferencesPapers.aspx?ReferenceID=996975 (accessed on 3 January 2023).
- Saquib, N.; Hossain, E.; Le, L.B.; Kim, D.I. Interference management in OFDMA femtocell networks: Issues and approaches. IEEE Wirel. Commun. 2012, 19, 86–95. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, G.; Jafar, S.A. Topological Interference Management for Hexagonal Cellular Networks. IEEE Trans. Wirel. Commun. 2015, 14, 2368–2376. [Google Scholar] [CrossRef]
- Alqahtani, Y.; Jamil, M.K.; Alshehri, H.; Ahmad, A.; Azeem, M. Vertex metric resolvability of COVID antiviral drug structures. J. Intell. Fuzzy Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Melter, R.A.; Tomescu, I. Metric bases in digital geometry. Comput. Vis. Graph. Image Process. 1984, 25, 113–121. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Javaid, I.; Salman, M. Fault-Tolerant metric and partition dimension of graphs. Utliltas Math. 2010, 83, 187–199. [Google Scholar]
- Abd-El-Barr, M. Topological network design: A survey. J. Netw. Comput. 2009, 32, 501–509. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, L.; Li, X. A novel hybrid localization scheme for deep mine based on wheel graph and chicken swarm optimization. Comput. Netw. 2019, 154, 73–78. [Google Scholar] [CrossRef]
- Aksu, H.; Aksoy, D.; Korpeoglu, I. A study of localization metrics: Evaluation of position errors in wireless sensor networks. Comput. Netw. 2011, 55, 3562–3577. [Google Scholar] [CrossRef]
- Ward, C.B.; Wiegand, N.M. Complexity results on labeled shortest path problems from wireless routing metrics. Comput. Netw. 2010, 54, 208–217. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, X.; Bie, R.; Song, H. Discovering time-dependent shortest path on traffic graph for drivers towards green driving. J. Netw. Comput. 2017, 83, 204–212. [Google Scholar] [CrossRef]
- Chou, C.P.; Li, Y.; Witek, H.A. Zhang–Zhang Polynomials of Various Classes of Benzenoid Systems. MATCH Commun. Math. Comput. Chem. 2012, 68, 31–64. [Google Scholar]
- Manuel, P.; Bharati, R.; Rajasingh, I.; M, C.M. On minimum metric dimension of honeycomb networks. J. Discret. Algorithms 2008, 6, 20–27. [Google Scholar] [CrossRef]
- Shreedhar, K.; Sooryanarayana, B.; Hegde, C.; Kumar, V. Metric dimension of a hexagonal cellular network. Int. J. Math. Sci. Eng. Appl. 2010, 4, 133–148. [Google Scholar]
- Huang, Q.; Khalil, A.; Ali, D.A.; Ahmad, A.; Luo, R.; Azeem, M. Breast cancer chemical structures and their partition resolvability. Math. Biosci. Eng. 2022, 20, 3838–3853. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).