Robust Statistic Estimation in Constrained Optimal Control Problems of Pollution Accumulation (Part II: Markovian Switchings)

Abstract

This piece is a follow-up of the research started by the authors on the constrained optimal control problem applied to pollution accumulation. We consider a dynamic system governed by a diffusion process with multiple modes that depends on an unknown parameter. We will study the components of the model and their restrictions and propose a scheme to solve the problem in which it is possible to determine (adaptive) policies that maximize a suitable discounted reward criterion using standard dynamic programming techniques in combination with discrete estimation methods for the unknown parameter. Finally, we develop a numerical example to illustrate our results with a particular case of the method of minimum least square error approximation.

1. Introduction

Pollution control in large cities is a problem of great interest worldwide, and that is why various organizations are continually seeking strategies to mitigate it. As for scientists, they have begun to analyze models that describe the stock of pollution through ordinary and stochastic differential equations. In particular, optimal control theory has been applied for the optimal management of pollution in economic sciences. This theory considers an economy that consumes some good and, as a by-product of that consumption, generates pollution. The hypotheses in our model are as follows:

• The contamination stock is only gradually dissolved by the environment;
• The growth rate of the pollution is constant or random;  
• The flow of pollution is constrained so that it satisfies some mandatory global standards in order to promote sustainable development (see, for instance, ref. [1]).

Social welfare is defined by the net utility from the consumption of some good vis à vis the disutility caused by pollution. Our objective is to find an optimal consumption policy for society. That is, we seek to maximize the difference between the utility function of consumption vs. the disutility caused by the polluting stock (see [2,3]).

This paper represents the second part of a project related to the constrained optimal control problem of pollution accumulation with an unknown parameter. To be in context, we begin by briefly summarizing the results obtained in Robust statistic estimation in constrained optimal control problems of pollution accumulation (Part I) (see [4]).

The first part considers the scenery where the dynamic system is given by a diffusion process and depends on an unknown parameter, say $\theta$. First, assuming the parameter $\theta$ as known, an approach with restrictions and one without them is proposed. The respective optimal value functions are $V_{\theta }^{\ast }$ and $V_{\theta ,\lambda }^{\ast }$. Then, estimation techniques for the parameter $\theta$ are applied and later combined with the characterizations and results previously analyzed. Roughly speaking, one of the results considers a sequence of estimated parameters (${\theta }_m$:m = 1, …) such that ${\theta }_m\to \theta$, then the value functions converge (in some sense), that is

$$V_{{\theta }_n}^{\ast }\to V_{\theta }^{\ast }\mathrm{and}{V}_{{\theta }_m,\lambda }^{\ast }\to V_{\theta ,\lambda }^{\ast }.$$

Another result states the existence of optimal policies such that ${\pi }_{{\theta }_m}\to {\pi }_{\theta }$. Furthermore, the relationship between the value functions $V_{\theta }^{\ast }$ and $V_{\theta ,\lambda }^{\ast }$ is shown.

In this piece, we obtain similar results considering the case where the dynamics of the stock of pollution evolves as a diffusion process with Markovian switching whose drift function, as well as the reward function, depends on the unknown parameter $\theta$. In addition, we impose some natural constraints on the performance index.

To avoid confusion, we try to preserve the notation of Part I in this work. First, a constrained control problem is proposed. Subsequently, assuming $\theta$ is the real parameter, we study a standard control problem under the discounted criterion, where it is possible to apply standard techniques and dynamic programming tools to determine optimal policies. Then a (discrete) procedure to estimate the unknown parameter $\theta$ is applied in combination with the standard results formerly mentioned to obtain the so-called adaptive policies that maximize a discounted reward criterion with constraints.

The idea is to estimate the parameter $\theta$, and then solve the optimal control problem when such an estimated value is replaced in the problem. In the literature, this approach is known as the Principle of Estimation and Control. This problem has been studied in several contexts. For instance, refs. [5,6,7,8] and the references therein are about stochastic control systems evolving in discrete time. On the other hand, adaptive optimal control for continuous time is studied in [9,10,11]. The estimation for diffusion processes using discrete observations has been studied in the works [12,13,14,15,16].

Dynamic optimization has been used to study the problem of pollution accumulation in the past; for example, the papers [17,18] use a linear quadratic model to explain this phenomenon, the article [2] deals with the average payoff in a deterministic framework, while [3,19] extend the former’s approach to a stochastic context, and [20] uses a robust stochastic differential game to model the situation. The study [21] is a statistical analysis of the impact of air pollution on public health. In order to develop adaptive policies that are almost surely optimal for the restricted optimization problem under the discounted reward on an infinite horizon with Markovian switchings, we use a statistical estimation approach to determine the unknown parameter $\theta$. These adaptive policies are created by replacing the estimates into optimal stationary controls (that is, the use of the PEC); for more information, see the works of Kurano and Mandl (cf. [7,8]). The statistic estimation method we use for the unknown parameter $\theta$ is the so-called least square estimator for stochastic differential equations based on many discrete observations. This resembles existing robust estimation techniques, such as the $H_{\infty }$ method, in the fact that in the applications, the dynamic systems are linear. However, the computational complexity of these techniques is greater. Indeed, with our least square estimator, only the inverse of a matrix must be calculated to obtain the estimator, while there are way more computations to be performed in the other algorithms (see [22,23]). Most risk analysts will not be as familiar with our methods as they are with, for example, the model predictive control, MATLAB’s robust control toolbox, or the polynomial chaos expansion method, which have been used in the literature to address similar issues. Since we review a constructive method for robust and adaptive control under deep uncertainty, our findings are similar to those reported in the article [24]. Moreover, our methods also resemble the adaptive moving mesh method for optimal control problems in viscous incompressible fluid used in [25].

This piece can be also be considered an extension of [26,27,28,29], who also study adaptive constrained optimal control methods. In fact, ref. [28] studies a constrained optimal control problem, but unlike our case, there, all the parameters are known, while [26] does the same but in the context of pollution accumulation. The references [27,29] study an unconstrained adaptive optimal control problem. Finally, it is important to highlight the numerical estimation technique that illustrates the results of this article.

The rest of the paper is organized as follows. We present the elements of our model and assumptions in Section 2. Next, Section 3 introduces our optimality criterion and the main results; an interesting numerical example illustrating our results is given in Section 4. We give our conclusions in Section 5, and finally, we included the proof of the important (but rather distracting) Theorem A1 on the convergence of the HJB equation under the topology of relaxed controls in Appendix A.

Notation and Terminology

For vectors $x=(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^n$ and matrices $A=\left(A_{k,p}\right)\in {\mathbb{M}}_n\left(\mathbb{R}\right)$, we denote by $|·|$ the Euclidean norm, that is,

$${\left|x\right|}^2:=\sum _{k=1}^n{x}_k^2\mathrm{and}{\left|A\right|}^2:=\mathrm{T}\mathrm{r}\left(A{A}^{\top }\right)=\sum _{k,p=1}^n{A}_{k,p}^2,$$

where $A^{\top }$ and $\mathrm{T}\mathrm{r}(·)$ denote the transpose and the trace of matrix, respectively. As an abbreviation, we write ${\partial }_i$ and ${\partial }_{ij}^2$ to refer to $:=\frac{\partial }{\partial x_i}$, and $\frac{{\partial }^2}{\partial x_i\partial x_j}$, respectively.

Given a Borel set B, we denote by $\mathcal{B}\left(B\right)$ its natural $\sigma$-algebra. As usual, $\mathcal{C}\left(\mathcal{O}\right)$, stands for the space of continuous functions whose domain is $\mathcal{O}$ and

$$\mathcal{C}(\mathcal{O}\times E):=\{\nu :\mathcal{O}\times E\to {\mathbb{R}}^n:\nu (·,i)\in \mathcal{C}(\mathcal{O}\times \mathcal{E})\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} i\in E\}.$$

Consequently we denote ${\mathcal{C}}_b(\mathcal{O}\times E)$ as the subspace of $\mathcal{C}(\mathcal{O}\times E)$ composed by bounded functions. The set ${\mathcal{C}}^{\kappa }(\mathcal{O}\times E):=\{\nu :\mathcal{O}\times E\to {\mathbb{R}}^n:\nu (·,i)\in {\mathcal{C}}^{\kappa }(\mathcal{O}\times \mathcal{E})\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} i\in E\}$, where ${\mathcal{C}}^{\kappa }(\mathcal{O}\times \mathcal{E})$ is the space of all real-valued continuous functions f on the bounded, open and connected subset $\mathcal{O}\subset {\mathbb{R}}^n$ with continuous derivatives up to order $\kappa \in \mathbb{N}$.

Fix $p\ge 1$ and a measure space $(\Omega ,\mathcal{F},\mu )$, we denote ${\mathcal{L}}^p(\Omega \times E)$ as the Lebesgue space of functions g on $\Omega \times E$ such that ${\int }_{\Omega }{\left|g(x,i)\right|}^p\mu \left(\mathrm{d}x\right)<\infty$ for $i\in E$.

Let X and Y be Borel spaces. A stochastic kernel $Q(·|·)$ on X given Y is a function such that $Q(·|y)$ is a probability measure on X for each $y\in Y$ and $Q\left(B\right|·)$ is a measurable function on Y for each $B\in \mathcal{B}\left(X\right)$.

Finally, the set $\mathcal{P}\left(B\right)$ denotes the family of probability measures on B endowed with the topology of weak convergence.

2. Model Formulation and Assumptions

Taking as reference the problem analyzed in Part I, we consider the scenery where the dynamics of the pollution stock is modeled as an n-dimensional controlled stochastic differential equation (SDE) with Markovian switching. Specifically, such a dynamic takes the form

$$\mathrm{d}x\left(t\right)=b(x\left(t\right),\psi \left(t\right),u\left(t\right),\theta )\mathrm{d}t+\sigma (x\left(t\right),\psi \left(t\right))\mathrm{d}W\left(t\right),(x\left(0\right),\psi \left(0\right))=(x_0,{\psi }_0),t\ge 0,$$

(1)

where $E=\{1,2,\cdots ,N\}$, $b:{\mathbb{R}}^n\times E\times U\times \Theta \to {\mathbb{R}}^n$ and $\sigma :{\mathbb{R}}^n\times E\to {\mathbb{R}}^{n\times d}$ are given functions, $W(·)$ is an ${\mathcal{F}}_t$-adapted d-dimensional Wiener process such that $W\left(t\right)-W\left(s\right)$ and ${\mathcal{F}}_s$ are pairwise independent, $W(·)$ is independent of $\psi (·)$, and the evolution of the Markov chain $\psi$ has intensity $Q={\left(q_{ij}\right)}_{i,j\in E}$ and transition rule given by

$$\mathbb{P}(\psi (t+\Delta t)=j|\psi \left(t\right)=i,(x\left(s\right),\psi \left(s\right)),s\le t)=\left\{\begin{array}{cc}{q}_{ij}\Delta t+o(\Delta t),\hfill & \mathrm{if} i\ne j,\hfill \\ 1+q_{ii}\Delta t+o(\Delta t),\hfill & \mathrm{if} i=j,\hfill \end{array}\right.$$

(2)

for $t\ge 0$ and ${\sum }_{j=1}^N{q}_{ij}=0$. The compact set $U\subset {\mathbb{R}}^{n_1}$ is called the control set. In the context of our problem, $u\left(t\right)$ is a stochastic process on U such that, at time t, it represents the flow of consumption which, in turn, is considered bounded to reflect the policies and rules imposed by governments or social entities.

It is important to remark that throughout this work, we assume that $\theta$ is an unknown parameter taking values on a compact set $\Theta \subset {\mathbb{R}}^m$, which is called the parameter set. Note that in the context of pollution problems, $\theta$ can be seen as the pollution decay rate.

Now we define the so-called randomized policies, also known as relaxed controls, or just policies.

Definition 1.

A policy is a family $\pi :={\left({\pi }_t(·|·,·)\right)}_{t\ge 0}$ of stochastic kernels on $\mathcal{B}\left(U\right)\times {\mathbb{R}}^n\times E$ (see Section 1). We denote by Π the set of stationary policies. In particular, a randomized policy is said to be stationary if there is a probability measure $\pi (·|x,i)\in \mathcal{P}(U)$ such that ${\pi }_t(·|x,i)=\pi (·|x,i)$ for all $t\ge 0$ and $(x,i)\in {\mathbb{R}}^n\times E$. Let $\mathbb{F}$ be the set of measurable functions f from ${\mathbb{R}}^n\times E$ to U. We denote the set of stationary Markov policies as ${\mathbb{F}}_1:=\{f:{\mathbb{R}}^n\times E\to U:for each i\in E,f(·,i)\in \mathbb{F}\}$.

For each randomized policy $\pi \in \Pi$ and a function whose domain is contained to U, say $v:{\mathbb{R}}^n\times E\times U\times \Theta \to \mathbb{R}$, we use the abbreviated notation

$$v(x,i,\pi ,\theta ):={\int }_{U}v(x,i,u,\theta )\pi \left(\mathrm{d}u\right|x,i).$$

(3)

A suitable adjustment should be made for functions with a different domain.

We endow $\Pi$ with a topology (see [30]) determined by the convergence criterion defined below (see [31,32], Lemma 3.2 in [30,33].

Definition 2.

A sequence ${\left({\pi }_m\right)}_{m\in \mathbb{N}}$ in Π converges to $\pi \in \Pi$ if

$${\int }_{{\mathbb{R}}^n}g(x,i)h(x,i,{\pi }_m)\mathrm{d}x\to {\int }_{{\mathbb{R}}^n}g(x,i)h(x,i,\pi )\mathrm{d}x.$$

for all $g\in {\mathcal{L}}^1({\mathbb{R}}^n\times E)$, and $h\in {\mathcal{C}}_b({\mathbb{R}}^n\times E\times U)$ (see (3)). Since this mode of convergence was introduced by Warga (cf. [30]), we denote it as ${\pi }_m\stackrel{W}{\to }\pi$.

For $\nu (·,·,\theta )\in {\mathcal{C}}^2({\mathbb{R}}^n\times E)$, $u\in U$ and $\theta \in \Theta$, the infinitesimal generator associated with the process $\left(x\right(·),\psi (·\left)\right)$ is

$${\mathbb{L}}^{u,\theta }\nu (x,i,\theta ):=\sum _{k=1}^n{b}_k(x,i,u,\theta ){\partial }_k\nu (x,\theta ,i)+\frac{1}{2}\sum _{k,\ell =1}^n{a}^{k,\ell }(x,i){\partial }_{k,\ell }^2\nu (x,i,\theta )+\sum _{j=1}^N{q}_{ij}\nu (x,i,\theta ),$$

where $b_k$ is the k-th component of the drift function b, and $a^{k,\ell }$ is the $(k,\ell )$ component of the matrix $a(·,·):=\sigma (·,·)\sigma {(·,·)}^{\top }$. As in (3), for each policy $\pi \in \Pi$, we write

$${\mathbb{L}}^{\pi ,\theta }\nu (x,i,\theta ):={\int }_U{\mathbb{L}}^{u,\theta }\nu (x,i,\theta )\pi \left(\mathrm{d}u\right|x,i).$$

The following set of assumptions and conditions ensures the existence and uniqueness of a strong solution as well as stability of the dynamic system (1) and (2) (see [31,33,34,35]).

Assumption 1.

(a)

The random process (1) belongs to a complete probability space $\left(\Omega ,\mathcal{F},{\mathbb{P}}^{u,\theta }\right)$. Here, ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ is a filtration on $(\Omega ,\mathcal{F})$ such that each ${\mathcal{F}}_t$ is complete relative to $\mathcal{F}$, and ${\mathbb{P}}^{u,\theta }$ is the law of the state process $x(·)$ given the parameter $\theta \in \Theta$ and the control $u(·)$.

(b)

The drift function $b(·,·,·,·)$ in (1) is continuous and satisfies that for each $R>0$, there exist non-negative constants $K_{\theta }\left(R\right)$ and $D\left(R\right)$ such that, for all $u\in U$, all $|{\theta }_1|,|{\theta }_2|\le R$ and $\left|x\right|,\left|y\right|\le R$,

$$|b(x,i,u,\theta )-b(y,i,u,\theta )|\le K_{\theta }\left(R\right)|x-y|,$$

$$|b(x,i,u,{\theta }_1)-b(x,i,u,{\theta }_2)|\le D\left(R\right)|{\theta }_1-{\theta }_2|,$$

Moreover, the function $u\mapsto b(x,i,u,\theta )$ is continuous on U.

(c)

The diffusion coefficient σ satisfies a local Lipschitz condition; that is, for each $R>0$, there exists a constant $K_1\left(R\right)>0$ such that, for all $\left|x\right|,\left|y\right|$ less than R,

$$|\sigma (x,i)-\sigma (y,i)|\le K_1\left(R\right)|x-y|.$$

(d)

A global linear growth condition is satisfied

$$\underset{(u,\theta )\in U\times \Theta }{sup}{\left|b\left(x,i,u,\theta \right)\right|}^2+{\left|\sigma (x,i)\right|}^2\le \tilde{K}{(1+|x|}^2)for all x\in {\mathbb{R}}^n,$$

where $\tilde{K}$ > 0 is a constant.

(e)

The matrix $a(x,i):=\sigma (x,i)\sigma {(x,i)}^{\top }$ satisfies that, for some constant $K_2>0$,

$$x^{\top }a(y,i)x\ge K_2{\left|x\right|}^{2}for all x,y\in {\mathbb{R}}^n.$$

Remark 1.

(i)

Properties such as continuity or Lipschitz continuity given in Assumption 1 are inherited to the drift function $b(x,i,\pi ,\theta )$.

(ii)

Under Assumption 1, once a policy $\pi \in \Pi$ and a parameter $\theta \in \Theta$ are fixed, the references [31] and [33] guarantee the existence of a probability space $\left(\Omega ,\mathcal{F},{\mathbb{P}}^{\pi ,\theta }\right)$ in which there exists a unique process $x^{\pi ,\theta }(·)$ with the Markov–Feller property which, in turn, is an almost surely strong solution.

The next hypothesis is known as the Lyapunov stability condition.

Assumption 2.

There exists a function $w\in {\mathcal{C}}^2({\mathbb{R}}^n\times E)$, $w(·,·)\ge 1$ and constants $d\ge \beta >0$ such that

(a)

${lim}_{\left|x\right|\to \infty }w(x,i)=\infty$ uniformly in $i\in E$.

(b)

${\mathbb{L}}^{\pi ,\theta }w(x,i)\le -\beta w(x,i)+d$ for all $\pi \in \Pi$, $\theta \in \Theta$ and $(x,i)\in {\mathbb{R}}^n\times E$.

Assumption 2 essentially asks for a twice-continuously differentiable function to solve the problem at hand. This hypothesis is equivalent to requiring positive-definite matrices in the context of linear matrix inequalities (see [36] and pages 113–135 in [37]). The existence of a function w with the conditions in Assumption 2 implies that the rate functions involved in our model can be unbounded (see Assumption 3). As in the first part, we define next an adequate space for these functions.

Definition 3.

Let v be a function from ${\mathbb{R}}^n\times E$ to $\mathbf{R}$, we define its w-norm as

$${∥v∥}_w:=\underset{(x,i)\in {\mathbb{R}}^n\times E}{sup}\frac{\left|v\right(x,i\left)\right|}{w(x,i)}<\infty .$$

Even more, let ${\mathcal{B}}_w({\mathbb{R}}^n\times E)$ be the Banach space of real-valued measurable functions with finite w-norm.

Let r and c be measurable functions from ${\mathbb{R}}^n\times E\times U\times \Theta$ to $\mathbb{R}$ identified as reward (social welfare) rate and the cost rate, respectively, and let $\eta$ from ${\mathbb{R}}^n\times E\times \Theta$ to $\mathbb{R}$ be another measurable function that models the constraint rate. In the context of pollution accumulation, in some situations, such a restriction is due to each country’s legal framework, and the cost of cleaning the environment must be bounded for some given quantity.

Assumption 3.

For each $i\in E$ fixed, the payoff rate $r(·,i,·,·)$, the cost rate $c(·,i,·,·)$ and the constraint rate $\eta (·,i,·)$ are continuous on ${\mathbb{R}}^n\times U\times \Theta$. Moreover, they are locally Lipschitz on ${\mathbb{R}}^n$, uniformly on E, U and Θ. That is, for each $R>0$, there are positive constants $K\left(R\right)$ and $K_2\left(R\right)$ such that for all $\left|x\right|,\left|y\right|\le R$,

$$\begin{array}{ccc}\hfill \underset{(i,u,\theta )\in E\times U\times \Theta }{sup}|r(x,i,u,\theta )-r(y,i,u,\theta )|+\underset{(i,u,\theta )\in E\times U\times \Theta }{sup}|c(x,i,u,\theta )-c(y,i,u,\theta )|& \le & K\left(R\right)|x-y|,\hfill \\ \hfill \underset{(i,\theta )\in E\times \Theta }{sup}|\eta (x,i,\theta )-\eta (y,i,\theta )|& \le & K_2\left(R\right)|x-y|.\hfill \end{array}$$

Even more, the rate functions belong to ${\mathcal{B}}_w({\mathbb{R}}^n\times E)$ and there exists $M>0$ such that for all $(x,i)\in {\mathbb{R}}^n\times E$,

$$\underset{(u,\theta )\in U\times \Theta }{sup}\left|\eta (x,i,\theta )\right|+\underset{(u,\theta )\in U\times \Theta }{sup}\left|r(x,i,u,\theta )\right|+\underset{(u,\theta )\in U\times \Theta }{sup}\left|c(x,i,u,\theta )\right|\le Mw(x,i).$$

3. Discounted Optimality Problems and Main Results

Through this section, we establish the contamination problem of our interest in terms of the terminology of optimal control. To this end, we will introduce the functions that evaluate the behavior of the system throughout the process associated with payments, costs, and restrictions.

In order to avoid confusion, we will preserve the notation and the ordering in the presentation of the results from the first part of the project.

3.1. Discounted Optimality Criterion

Definition 4.

Given the initial state $(x,i)\in {\mathbb{R}}^n\times E$, a parameter value $\theta \in \Theta$ and a discount rate $\alpha >0$, we define the total expected α-discounted reward, cost and constraint when the controller uses a policy π in Π as

$$\begin{array}{ccc}\hfill V(x,i,\pi ,r,\theta )& :=& {\mathbb{E}}_{x,i}^{\pi ,\theta }\left[{\int }_0^{\infty }{\mathrm{e}}^{-\alpha t}r\left(x\left(t\right),\psi \left(t\right),\pi ,\theta \right)\mathrm{d}t\right],\hfill \\ \hfill V(x,i,\pi ,c,\theta )& :=& {\mathbb{E}}_{x,i}^{\pi ,\theta }\left[{\int }_0^{\infty }{\mathrm{e}}^{-\alpha t}c\left(x\left(t\right),\psi \left(t\right),\pi ,\theta \right)\mathrm{d}t\right]and\hfill \end{array}$$

$$\overline{\eta }(x,i,\pi ,\theta ):=\alpha {\mathbb{E}}_{x,i}^{\pi ,\theta }\left[{\int }_0^{\infty }{\mathrm{e}}^{-\alpha t}\eta \left(x\left(t\right),\psi \left(t\right),\theta \right)\mathrm{d}t\right].$$

respectively, and ${\mathbb{E}}_{x,i}^{\pi ,\theta }[·]$ is the expectation of · taken with respect to the probability measure ${\mathbb{P}}^{\pi ,\theta }$ when $\left(x\right(t),\psi (t\left)\right)$ starts at $(x,i)$.

Proposition 1.

If Assumptions 1–3 hold, the functions $V\left(·,·,\pi ,r,\theta \right)$ and $V\left(·,·,\pi ,c,\theta \right)$ belong to ${\mathcal{B}}_w({\mathbb{R}}^n\times E)$ for each π in Π; in fact, for each $(x,i)\in {\mathbb{R}}^n\times E$ and $\theta \in \Theta$ we have

$$\underset{\pi \in \Pi }{sup}\left|V\left(x,i,\pi ,r,\theta \right)\right|+\underset{\pi \in \Pi }{sup}\left|V\left(x,i,\pi ,c,\theta \right)\right|\le 2M\left(\alpha \right)w(x,i)$$

where $M\left(\alpha \right):=M\frac{\alpha +d}{\alpha \beta }$, the constants c and d are as in Assumption 2, and M is as in Assumption 3 (b).

Proposition 1 can be obtained directly using the following inequality, which is an application of Dynkin’s formula to the function $v(t,x,i):={\mathrm{e}}^{\beta t}w(x,i)$, and Assumption 2 (b) yield that, for all $\pi \in \Pi$, $\theta \in \Theta$, $(x,i)\in {\mathbb{R}}^n\times E$ and $t\ge 0$,

$${\mathbb{E}}_{x,i}^{\pi ,\theta }\left[w\left(x\left(t\right),\psi \left(t\right)\right)\right]\le {\mathrm{e}}^{-\beta t}w(x,i)+\frac{d}{\beta }\left(1-{\mathrm{e}}^{-\beta t}\right).$$

(4)

Remark 2.

The function $\overline{\eta }(·,·,\pi ,\theta )$ is in ${\mathcal{B}}_w({\mathbb{R}}^n\times E)$ for each $\pi \in \Pi$. Moreover, for each $(x,i)\in {\mathbb{R}}^n\times E$, we have

$$\underset{\pi \in \Pi }{sup}\left|\overline{\eta }(x,i,\pi ,\theta )\right|\le {\parallel \eta \parallel }_w\frac{\alpha +d}{\beta }w(x,i).$$

Let $\theta \in \Theta$ be fixed, and again apply Dynkin’s formula to the function V (see Theorem 1.45 in p. 48 in [34] or Theorem 1 (iii) in [38]) to yield the following result.

Proposition 2.

Let Assumptions 1, 2 hold, and let v be a measurable function on ${\mathbb{R}}^n\times E\times U\times \Theta$ satisfying Assumption 3. Then, for $\pi \in \Pi$, the associated expected α-discounted reward $V(·,·,·,\pi ,\theta )$ belongs to ${\mathcal{W}}^{2,p}({\mathbb{R}}^n\times E)\cap {\mathcal{B}}_w({\mathbb{R}}^n\times E)$, and satisfies

$$\alpha V(x,i,\pi ,v,\theta )=V(x,i,\pi ,v,\theta )+{\mathbb{L}}^{\pi ,\theta }V(x,i,\pi ,v,\theta )for all(x,i)\in {\mathbb{R}}^n\times E and \theta \in \Theta .$$

(5)

Conversely, if some function $\phi (·,·,\theta )$ in ${\mathcal{W}}^{2,p}({\mathbb{R}}^n\times E)\cap {\mathcal{B}}_w({\mathbb{R}}^n\times E)$ satisfies Equation (5), then

$$\phi (x,i,\theta )=V(x,i,\pi ,v,\theta )for all (x,i)\in {\mathbb{R}}^n\times E and \theta \in \Theta .$$

(6)

Even more, if relation (5) is an inequality, then (6) holds with the respective inequality.

Consider that ${\mathcal{W}}^{\ell ,p}({\mathbb{R}}^n\times E)$ is the Sobolev space of real-valued measurable functions on ${\mathbb{R}}^n\times E$ whose derivatives up to order $\ell \ge 0$ are in ${\mathcal{L}}^p({\mathbb{R}}^n\times E)$ for $p\ge 1$.

Given the initial conditions $(x,i)\in {\mathbb{R}}^n\times E$ a parameter $\theta \in \Theta$, and a constraint function $\eta$ satisfying Assumption 3, we define the set of policies

$${\mathcal{F}}_{\theta }^{x,i}:=\left\{\pi \in \Pi |V(x,i,\pi ,c,\theta )\le \overline{\eta }(x,i,\pi ,\theta )\right\}.$$

(7)

We assume, for the moment, that the set defined in (7) is nonempty. Up to this point, we are in a position to formulate the discounted problem with constraints (DPC), which is defined below.

Definition 5.

Given the initial condition $(x,i)\in {\mathbb{R}}^n\times E$ and the parameter $\theta \in \Theta$ we say that policy ${\pi }^{\ast }\in \Pi$ is optimal for the DPC if ${\pi }^{\ast }\in {\mathcal{F}}_{\theta }^{x,i}$ and

$$V\left(x,i,{\pi }^{\ast },r,\theta \right)=\underset{\pi \in {\mathcal{F}}_{\theta }^{x,i}}{sup}V\left(x,i,\pi ,r,\theta \right).$$

Furthermore, the function $V^{\ast }(x,i,r,\theta ):=V\left(x,i,{\pi }^{\ast },r,\theta \right)$ is known as the $\alpha —$discount optimal reward for the DPC.

3.2. Unconstrained Discounted Optimality

The objective of this part is to transform the original DPC (presented above) into an unconstrained problem, and thus, to be able to propose results and techniques known in the literature. To this end, we will apply the Lagrange multipliers technique used in [26]. Take $\lambda \le 0$ and consider the function

$$r^{\lambda }(x,i,u,\theta ):=r(x,i,u,\theta )+\lambda (c(x,i,u,\theta )-\alpha \eta (x,i,\theta )).$$

(8)

For our purpose, $r^{\lambda }$ represents the new reward rate. Now recalling (3), we write (8) as

$$r^{\lambda }(x,i,\pi ,\theta ):=r(x,i,\pi ,\theta )+\lambda (c(x,i,\pi ,\theta )-\alpha \eta (x,i,\theta )),\pi \in \Pi ,\theta \in \Theta .$$

Remark 3.

For each $\alpha >0$ and $\lambda <0$, by direct calculations, it is possible to show that $r^{\lambda }(·,·,\pi ,\theta )\in {\mathcal{B}}_w({\mathbb{R}}^n\times E)$ uniformly in $\pi \in \Pi$ and $\theta \in \Theta$. Even more, by Assumption 3, this new reward rate is a Lipschitz function.

In the same way as in Definition (4), for all $(x,i)\in {\mathbb{R}}^n\times E$ and $\theta \in \Theta$, we define the function

$$V(x,i,\pi ,r^{\lambda },\theta ):={\mathbb{E}}_{x,i}^{\pi ,\theta }\left[{\int }_0^{\infty }{\mathrm{e}}^{-\alpha t}{r}^{\lambda }\left(x\left(t\right),\psi \left(t\right),\pi ,\theta \right)\mathrm{d}t\right].$$

So, the discounted unconstrained problem is defined as follows.

Definition 6

(The adaptive $\theta$-control problem with Markovian switching). A policy ${\pi }^{\ast }\in \Pi$ is said to be α-discount optimal for the λ-DUP given that θ is the true parameter value, if 

$$V^{\ast }(x,i,r^{\lambda },\theta ):=V(x,i,{\pi }^{\ast },r^{\lambda },\theta )=\underset{\pi \in \Pi }{sup}V(x,i,\pi ,r^{\lambda },\theta )$$

(9)

for all $(x,i)\in {\mathbb{R}}^n\times E$. The function $V^{\ast }$ will be called the value function of the adaptive θ-control problem with Markovian switching.

Let $v:{\mathbb{R}}^n\times E\times U\times \Theta \to \mathbb{R}$ be a measurable function satisfying the conditions given in Assumption 3. The following result (obtained from [33]) shows that the function $V^{\ast }(·,·,v,\theta )$ is the unique solution of (10), and also proves the existence of stationary optimal policies.

Proposition 3.

Suppose that Assumptions 1–3 hold. Then we have the following:

(i)

The α-optimal discount reward $V^{\ast }(·,·,v,\theta )$ belongs to ${\mathcal{W}}^{2,p}({\mathbb{R}}^n\times E)\cap {\mathcal{B}}_w({\mathbb{R}}^n\times E)$ and it verifies the discounted reward HJB equation. That is, for all $(x,i)\in {\mathbb{R}}^n\times E$ and $\theta \in \Theta ,$

$$\begin{array}{ccc}\hfill \alpha V^{\ast }(x,i,v,\theta )& =& \underset{u\in U}{sup}\{r(x,i,u,\theta )+{\mathbb{L}}^{u,\theta }{V}^{\ast }(x,i,v,\theta )\}.\hfill \end{array}$$

(10)

Conversely, if a function ${\phi }_{\theta }\in {\mathcal{W}}^{2,p}({\mathbb{R}}^n\times E)\cap {\mathcal{B}}_w({\mathbb{R}}^n\times E)$ satisfies (10), then ${\phi }_{\theta }(x,i)=V^{\ast }(x,i,v,\theta )$ for all $(x,i)\in {\mathbb{R}}^n\times E$.

(ii)

There exists a stationary policy $f_{\theta }^{\ast }\in \mathbb{F}$ that maximizes the right-hand side of (10). That is,

$$\alpha V^{\ast }(x,i,v,\theta )=r(x,i,f_{\theta }^{\ast },\theta )+{\mathbb{L}}^{f_{\theta }^{\ast },\theta }{V}^{\ast }(x,i,v,\theta )for all (x,i)\in {\mathbb{R}}^n\times E,$$

and $f_{\theta }^{\ast }$ is α-discount optimal given that θ is the true parameter value.

Remark 4.

(a)

Notice that $V(x,i,\pi ,r^{\lambda },\theta )=V(x,i,\pi ,r,\theta )+\lambda \left[V(x,i,\pi ,c,\theta )-\overline{\eta }(x,i,\pi ,\theta )\right],$ and by Definition 4, $V(x,i,\pi ,c,\theta )-\overline{\eta }(x,i,\pi ,\theta )=V(x,i,\pi ,c-\alpha \eta ,\theta )$,

(b)

Remark 3 and Proposition 1 yield that ${sup}_{\pi \in \Pi }\left|V(x,i,\pi ,r^{\lambda },\theta )\right|\le M_{\alpha }^{\lambda }w(x,i),$ with $M_{\alpha }^{\lambda }:=N^{\lambda }\frac{\alpha +d}{\alpha \beta }$ and $N^{\lambda }$ is a bound of $\parallel r^{\lambda }{\parallel }_w$, implying in turn that $V(·,·,\pi ,r^{\lambda },\theta )\in {\mathcal{B}}_w({\mathbb{R}}^n\times E)$.

(c)

If Assumptions 1, 2 and 3 hold, then by Proposition 3.4 in [28], the mappings $\pi \to V(x,i,\pi ,v,\theta )$, $\pi \to V(x,i,\pi ,c-\alpha \eta ,\theta )$ and $\pi \to V(x,i,\pi ,r^{\lambda },\theta )$ are continuous on Π for each $(x,i)\in {\mathbb{R}}^n\times E$ and $\theta \in \Theta .$

3.3. Convergence of Value Functions and Estimation Methods

Finally, in this part, we will present one of the main results of this work, which combines optimality and the statistical approximation scheme (in a discrete way) of our unknown parameter. To do this, we define the concept of consistent estimator and the approximation technique that will be used for it.

Definition 7.

A sequence ${\left({\theta }_m\right)}_{m\in \mathbb{N}}$ of measurable functions ${\theta }_m:\Omega \to \Theta$ is said to be a sequence of uniformly strongly consistent (USC) estimators of $\theta \in \Theta$ if, as $m\to \infty$,

$${\theta }_m\left(\omega \right)\to \theta {\mathbb{P}}^{\pi ,\theta }-a.s.for all \pi \in \Pi .$$

For ease of notation, we write ${\theta }_m:={\theta }_m\left(\omega \right)\in \Theta$. Let $v:{\mathbb{R}}^n\times U\times \Theta \to \mathbb{R}$ be a measurable function satisfying similar conditions as those given in Assumption 3. The following observations and estimation procedure are an adaptation to what was done in the first part and show us that our set of hypotheses and procedures are consistent.

Remark 5.

(a)

Let ${\left({\theta }_m\right)}_{m\in \mathbb{N}}$ be a sequence of USC estimators of $\theta \in \Theta$ and let $v:{\mathbb{R}}^n\times E\times \Pi \times \Theta \to \mathbb{R}$ be a function that satisfies the Assumptions 1–3. Theorem 4.5 in [29], guarantees that every sequence ${\left(V\left(x,i,\pi ,v,{\theta }_m\right)\right)}_{m\in \mathbb{N}}$ converges to $V\left(x,i,\pi ,v,\theta \right)$, ${\mathbb{P}}^{\pi ,\theta }$ almost surely.

(b)

Let ${\left({\pi }_m\right)}_{m\in \mathbb{N}}$ be a sequence in Π. Since Π is a compact set, there exists a subsequence ${\left({\pi }_{m_k}\right)}_{k\in \mathbb{N}}\subset {\left({\pi }_m\right)}_{m\in \mathbb{N}}$ such that ${\pi }_{m_k}\stackrel{W}{\to }\pi \in \Pi$, and thus, combining Remark 4 (a) and Remark 4 (c), and applying a suitable triangular inequality, it is possible to deduce that for every measurable function v satisfying Assumption 3,

$$\begin{array}{c}\hfill V(x,i,{\pi }_{m_k},v,{\theta }_{m_k})\to V(x,i,\pi ,v,\theta ){\mathbb{P}}^{\pi ,\theta }-a.s.as k\to \infty .\end{array}$$

(c)

By Proposition 3, and taking into account that $r^{\lambda }$ in (8), the function $V^{\ast }(·,·,r^{\lambda },\theta )$ verifies (10). In addition, the second part of Proposition 3 ensures the existence of stationary policy $f_{\theta }^{\lambda }\in {\mathbb{F}}_1$.

(d)

For each $\lambda \le 0$, $\theta \in \Theta$ and $\alpha >0$, we define the set

$${\Pi }^{\lambda ,\theta }:=\left\{\pi \in \Pi :\alpha V^{\ast }(x,i,r^{\lambda },\theta )=r^{\lambda }(x,i,\pi ,\theta )+{\mathbb{L}}^{\pi ,\theta }{V}^{\ast }(x,i,r^{\lambda },\theta )\forall (x,i)\in {\mathbb{R}}^n\times E\right\}.$$

(11)

Since ${\mathbb{F}}_1$ can be seen as an embedding of Π, Proposition 3 (ii) guarantees that ${\Pi }^{\lambda ,\theta }$ is a nonempty set.

(e)

As in [4], the set of hypotheses considered in this paper and Lemma 3.15 in [28] ensures that for each $\theta \in \Theta$ fixed and any sequence ${\left({\lambda }_m\right)}_{m\in \mathbb{N}}$, converging to λ (with $\lambda ,{\lambda }_m\le 0$); if there exists a sequence of policies ${\left({\pi }^{{\lambda }_m,\theta }\right)}_{m\in \mathbb{N}}\in {\Pi }^{{\lambda }_m,\theta }$ such that ${\pi }^{{\lambda }_m,\theta }\stackrel{W}{\to }\pi$, then $\pi \in {\Pi }^{\lambda ,\theta }$.

(f)

Lemma 3.16 in [28] ensures that the mapping $\lambda \mapsto V^{\ast }(x,i,r^{\lambda },\theta )$ is differentiable on $(-\infty ,0)$. In fact, for each $\lambda <0$ and $\theta \in \Theta$

$$\frac{\partial V^{\ast }(x,i,r^{\lambda },\theta )}{\partial \lambda }=V(x,i,{\pi }^{\lambda },c,\theta )-\overline{\eta }(x,i,{\pi }^{\lambda },\theta ).$$

(12)

The unknown parameter $\theta$ will be estimated as Pedersen [39] describes. That is, the functions $h_m:\Omega \times \Theta \to \mathbb{R},\mathrm{for} m=1,\cdots$ will measure how likely the different values of $\theta$ are. If for each $\omega \in \Omega$ fixed, the function $h_m(\omega ,\theta )$ has a unique maximum point ${\theta }_m\left(\omega \right)\in \Theta$, then $\theta$ is estimated by ${\theta }_m\left(\omega \right)$.

Under the assumption that, for $m\in \mathbb{N}$ and $\theta \in \Theta$, $h_m(·,\theta )$ is a measurable function of $\omega$ and that it is also twice continuously differentiable in $\theta$ for all ${\mathbb{P}}^{\pi ,\theta }-$almost all $\omega \in \Omega$, it is proven that the function $\theta \to h_m(\omega ,\theta )$ is continuous and has a unique maximum point ${\theta }_m\left(\omega \right)$ for each $\omega \in \Omega$ fixed. The number $m\in \mathbb{N}$ is the index of a sequence of random experiments on the measurable space $(\Omega ,\mathcal{F})$. This method is known as the approximate maximum likelihood estimator.

In our scenery, given a partition of times $\{0=t_0<t_1<t_m:=T\}$ from $[0,T]$, the outcomes of the random experiments will be represented by a sequence $X_T:=\left(x_{t_i}:i=0,\dots ,m\right)$ of a trajectory $x^{u,\theta }\left(t\right)$ up to time T on $(\Omega ,\mathcal{F}):=\left(\mathcal{C}\right([0,\infty )),\mathcal{B}(\mathcal{C}\left(\right[0,\infty \left)\right))$ and the function $h_m$ will be called the least square function (LSE), i.e., $h_m(w,\theta ):=LSE(w,\theta ).$

It is evident that $x^{u,\theta }\left(t\right)$ in (1) is observed up to a finite time, say T, for which we define

$$LSE(X_T,\theta ):=\sum _{i=1}^m{\left(x_{t_i}-x_{t_{i-1}}-b(x_{t_{i-1}},\psi \left(t_{i-1}\right),u_{t_{i-1}},\theta )(t_i-t_{i-1})\right)}^2,$$

(13)

with the drift function b as in (1). The above function generates the least square estimator until time T with m observations:

$${\theta }_{LSE}\equiv {\theta }_{LSE}\left(X_T\right):=arg\underset{\theta \in \Theta }{min}LSE(X_T,\theta ).$$

(14)

Remark 6.

The fact that $x^{u,\theta }\left(t\right)$ in (1) can only be observed in a finite horizon is one of the hypotheses of the so-called model predictive control. However, at least from a theoretical point of view, our version of the PEC makes no such assumption, but still chooses T as large as practically possible and thus defines (13) and (14). In this sense, there is a connection between these two perspectives.

In [12,16,39], the consistency and asymptotic normality of ${\theta }_{LSE}$ are studied. In particular, Shoji (see [16]) shows that the optimization based on the LSE function is equivalent to the optimization based on the discrete approximate likelihood ratio function in the one-dimensional stochastic differential equation case and with a constant diffusion coefficient considered:

$$\begin{array}{cc}\hfill & MLR(X_T,\theta ):=\sum _{i=1}^{m}b(y_{t_{i-1}},u_{t_{i-1}},\theta ){\left[\sigma \left(y_{t_{i-1}}\right)\sigma {\left(y_{t_{i-1}}\right)}^{\top }\right]}^{-1}(x_{t_i}-x_{t_{i-1}})\hfill \\ \hfill & -\frac{1}{2}\sum _{i=1}^m\left\{b{(y_{t_{i-1}},u_{t_{i-1}},\theta )}^{\top }{\left[\sigma \left(y_{t_{i-1}}\right)\sigma {\left(y_{t_{i-1}}\right)}^T\right]}^{-1}·b(y_{t_{i-1}},u_{t_{i-1}},\theta )(t_i-t_{i-1})\right\},\hfill \end{array}$$

with $y_{t_{i-1}}:=(x_{t_{i-1}},\psi \left(t_{i-1}\right)),and$b and $\sigma$ as in (1). The MLR function generates the discrete approximate likelihood ratio estimator:

$${\theta }_{LR}\equiv {\theta }_{LR}\left(X_T\right):=arg\underset{\theta \in \Theta }{max}MLR(X_T,\theta ).$$

Now, we will establish our main result.

Theorem 1.

Let ${\left({\theta }_m\right)}_{m\in \mathbb{N}}$ be a sequence of USC estimators of $\theta \in \Theta$. For each m, let ${\pi }_m$ be a α-discount optimal policy. Then there exists a subsequence ${\left(m_k\right)}_k$ of ${\left(m\right)}_m$ and a policy ${\pi }^{\ast }$ such that ${\pi }_{m_k}\stackrel{W}{\to }{\pi }^{\ast }$. Moreover, if Assumptions 1–3 hold, as $k\to \infty$,

$$V^{\ast }(x,i,{\theta }_{m_k})\to V^{\ast }(x,i,\theta ){\mathbb{P}}^{{\pi }^{\ast },\theta }-a.s.for each x\in {\mathbb{R}}^{n}andi\in E,$$

and ${\pi }^{\ast }$ is α-discount optimal for the θ-control problem ${\mathbb{P}}^{{\pi }^{\ast },\theta }$ almost surely.

Proof. 

Consider a sequence of USC estimators ${\left({\theta }_m\right)}_{m\in \mathbb{N}}$ such that ${\theta }_m\to \theta$ as $m\to \infty$. Let $R>0$, and take the open ball $B_R\times E:=\{(x,i)\in {\mathbb{R}}^n\times E\left|\right|x|<R,i\in E\}$. For $(x,i)\in B_R\times E$, let ${\left({\pi }_m\right)}_{m\in \mathbb{N}}\subset \Pi$ be a sequence of $\alpha$-discounted optimal policies. Since $\Pi$ is a compact set, there exists a subsequence ${\left({\pi }_{m_k}\right)}_{k\in \mathbb{N}}\subset {\left({\pi }_m\right)}_{m\in \mathbb{N}}$ such that ${\pi }_{m_k}$ converges to ${\pi }^{\ast }\in \Pi$ in the topology of relaxed controls given in Definition 2.

Let us first fix an arbitrary $m_k\in \mathbb{N}$. Then, Theorem 6.1 in [33] ensures that the value function $V^{\ast }(x,i,{\theta }_{m_k})$ in (9) is the unique solution of the HJB Equation (10), i.e., it satisfies

$$\begin{array}{ccc}\hfill \alpha V^{\ast }(x,i,{\theta }_{m_k})& =& r(x,i,{\pi }_{m_k},{\theta }_{m_k})+{\mathbb{L}}^{{\pi }_{m_k},{\theta }_{m_k}}{V}^{\ast }(x,i,{\theta }_{m_k}),\hfill \end{array}$$

(15)

and by Theorem 9.11 in [40], there exists a constant $C_0$ (depending on R) such that, for fixed ${\theta }_{m_k}$ and $p>n$, we have

$$\begin{array}{ccc}\hfill |V^{\ast }(x,i,{\theta }_{m_k}){|}_{{\mathcal{W}}^{2,p}(B_{2R}\times E)}& \le & C_0({∥V^{\ast }(x,i,{\theta }_{m_k})∥}_{{\mathcal{L}}^p(B_{2R}\times E)}+{∥r(x,i,{\pi }_{m_k},{\theta }_{m_k})∥}_{{\mathcal{L}}^p(B_{2R}\times E)}\hfill \\ & \le & (M+M\left(\alpha \right))|B_{2R}{|}^{1/p}{\displaystyle \underset{(x,i)\in B_{2R}\times E}{max}}w(x,i)<\infty ,\hfill \end{array}$$

(16)

where $|{\overline{B}}_{2R}|$ represents the volume of the closed ball with radius $2R$, and M and $M\left(\alpha \right)$ are the constants in Assumption 3 (b) and Proposition 1, respectively.

Now, observe that conditions (a)–(e) of Theorem A1 hold. In fact, for each ${\pi }_{m_k}$, (15) can be written in terms of the operator (A2) as ${\mathbb{L}}^{{\pi }_{m_k},\theta }{V}^{\ast }(x,i,{\theta }_{m_k})=0$ with the functions $v_2$, $\lambda$, $\rho$ equal to zero, $v_1\equiv r$ and $h_{m_k}(x,i)\equiv V^{\ast }(x,i,{\theta }_{m_k})$. So, taking ${\xi }_{m_k}\equiv 0$, $\lambda \equiv 0$, conditions (a),(c) and (d) hold. In addition, by (16), condition (b) is verified as well.

Then, by Theorem A1, we claim the existence of a function $h(·,·,\theta )\in {\mathcal{W}}^{2,p}({\mathbb{R}}^n\times E)$, together with a subsequence $\left(m_k:k=1,\cdots \right)$ such that $V^{\ast }(·,·,{\theta }_{m_k})\to h(·,·,\theta )$ uniformly in $B_R\times E$, and pointwise on ${\mathbb{R}}^n\times E$ as $k\to \infty$ and ${\pi }_{m_k}\stackrel{W}{\to }{\pi }^{\ast }$. Furthermore, $h(·,·,\theta )$ satisfies

$$\alpha h(x,i,\theta )=r(x,i,{\pi }^{\ast })+{\mathbb{L}}^{{\pi }^{\ast },\theta }h(x,i,\theta ){\mathbb{P}}^{{\pi }^{\ast },\theta }-\mathrm{a}.\mathrm{s}.,$$

(17)

with $h(·,·,\theta )\in {\mathcal{W}}^{2,p}(B_R\times E)$. Since the radius $R>0$ is arbitrary, we can extend our analysis to all of $(x,i)\in {\mathbb{R}}^n\times E$.

Thus, as $V^{\ast }(x,i,\theta )$ is the unique solution of the HJB equation (17), we can deduce that $h(x,i,\theta )$ coincides with $V^{\ast }(x,i,\theta )$. So, by (15) and (17), as $k\to \infty$,

$$V^{\ast }(x,i,{\theta }_{m_k})\to V^{\ast }(x,i,\theta ){\mathbb{P}}^{{\pi }^{\ast },\theta }-\mathrm{a}.\mathrm{s}.,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{h} x\in {\mathbb{R}}^n\mathrm{and} i\in E.$$

On the other hand, by Proposition 3, for each $i\in E$ and ${\theta }_{m_k}\in \Theta$ fixed, we have

$$\begin{array}{ccc}\hfill \alpha V^{\ast }(x,i,{\theta }_{m_k})& \ge & r(x,i,\pi ,{\theta }_{m_k})+{\mathbb{L}}^{\pi ,{\theta }_{m_k}}{V}^{\ast }(x,i,{\theta }_{m_k})\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} \pi \in \Pi .\hfill \end{array}$$

(18)

Hence, letting $k\to \infty$ and using Theorem A1 from appendix again, we obtain that (18) converges to

$$\begin{array}{ccc}\hfill \alpha V^{\ast }(x,i,\theta )& \ge & r(x,i,\pi ,\theta )+{\mathbb{L}}^{\pi ,\theta }{V}^{\ast }(x,i,\theta )\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} \pi \in \Pi .\hfill \end{array}$$

(19)

Thus, by (17) and (19), we obtain

$$\begin{array}{ccc}\hfill \alpha V^{\ast }(x,i,\theta )& =& {\displaystyle \underset{\pi \in \Pi }{sup}}\{r(x,i,\pi ,\theta )+{\mathbb{L}}^{\pi ,\theta }{V}^{\ast }(x,i,\theta )\}.\hfill \end{array}$$

implying that ${\pi }^{\ast }$ is $\alpha$-optimal for the $\theta$-control problem with Markovian switching.    □

In the following section, we present a numerical example to illustrate our results. To this end, we implement Algorithm 1. In it, first we introduce the number of iterations in our process and define the variables we need to simulate the dynamic system $x\left(t\right)$ and the Markov chain $\psi \left(t\right)$. Such simulations are inspired by the algorithm proposed in [41], and allow us to obtain the discrete observations $\{x_k:k=1,2,\dots \}$ needed to feed (13) and (14) and thus approximate the real value of $\theta$.

Algorithm 1: Method of LSE to find $\theta$

Remark 7.

Now we list some limitations of our approach.

1.

Approximation of the derivative. In our case, we use central differences, but in each application, the approximation type to be used must be analyzed.

2.

Least squares approximation. The most common restrictions are the amount of data, the regularity of the samples, and the size of the subintervals.

3.

Euler–Maruyama method. The most common restrictions in this method occur if the differential equation presents stiffness, inappropriate step size, or sudden growth. In our application, the Euler–Maruyama method converges with strong order 1/2 to the true solution. See Theorem 10.2.2 in [42].

4. Numerical Example

This application complements the one we used in [38]. We represent the stock of pollution as the controlled diffusion process with Markovian switchings of the form

$$\mathrm{d}x\left(t\right)=\left[u\right(t,\psi \left(t\right))-\theta x(t\left)\right]\mathrm{d}t+\sigma \mathrm{d}W\left(t\right),x\left(0\right)=x>0,\psi \left(0\right)=i,$$

(20)

where $\psi \left(t\right)$ is a Markov chain with generator

$$Q=\left(\begin{array}{cc}-{\lambda }_0& {\lambda }_0\\ {\lambda }_1& -{\lambda }_1\end{array}\right).$$

$\psi \left(t\right)$ stands for the perception of society toward the current level of pollution at each time. It takes values from the set $E:=\{1,2\}$. So, if the Markov chain is initially in state $\psi \left(0\right)=1$, then before its first jump from state 1 to state 2 at its first random jump time ${\tau }_1$, the stock of pollution obeys the following SDE

$$\mathrm{d}x\left(t\right)=\left[u\right(t,\psi \left(1\right))-\theta x(t\left)\right]\mathrm{d}t+\sigma \mathrm{d}W\left(t\right),$$

(21)

with initial state $x\left(0\right)=0$. At time ${\tau }_1$, the Markov chain jumps to 2, where it will stay until the next jump, at time ${\tau }_2$. During the period $[{\tau }_1,{\tau }_2]$, the stock of pollution is driven by the SDE

$$\mathrm{d}x\left(t\right)=\left[u\right(t,\psi \left(2\right))-\theta x(t\left)\right]\mathrm{d}t+\sigma \mathrm{d}W\left(t\right),$$

(22)

with initial value $x\left({\tau }_1\right)$ at time ${\tau }_1$, and the stock of pollution switches to (22) from (21). The stock of pollution will continue to alternate between these two states ad infinitum.

We also consider the pollution flow to be constrained. This means that our controller variable $u\left(t\right)$ will be taking values in

$$\begin{array}{cc}[0,\eta ]& \mathrm{if} \psi \left(t\right)=1,\mathrm{or} \mathrm{in}\hfill \\ \left[\eta ,\gamma \right]& \mathrm{if} \psi \left(t\right)=2.\hfill \end{array}$$

for a constant $0\le \eta \le \gamma .$ So, $u\left(t\right):=u(t,\psi (t\left)\right)$. We introduce the reward rate function $r:[0,\infty )\times E\times U\to \mathbb{R}$, that represents the social welfare defined by

$$r(x,i,u):=\sqrt{u}-a\left(i\right)x,\mathrm{for} \mathrm{all} (x,i,u)\in [0,\infty )\times E\times U,$$

whereas the cost and constraint rates are

$$\begin{array}{ccc}\hfill c(x,i,u)& =& c_1\left(i\right)x+c_2\left(i\right)u\mathrm{for} \mathrm{all} (x,i,u)\in [0,\infty )\times E\times U,\hfill \\ \hfill \eta (x,i,\theta )& :=& \frac{c_1\left(i\right)x}{\alpha +\theta }+q,\hfill \end{array}$$

where q is a positive constant. Clearly, (20) satisfies Assumption 1. The infinitesimal generator for a function $v\in {\mathcal{C}}^2(\mathbb{R}\times E)$ is

$${\mathbb{L}}^{u,\theta }v(x,i)=[u-\theta x]\frac{\partial v(x,i)}{\partial x}+\frac{1}{2}{\sigma }^2\frac{{\partial }^{2}v(x,i)}{\partial x^2}+\sum _{j=0}^1{q}_{ij}v(x,j),\mathrm{for} x>0\mathrm{and} i\in E.$$

We use $w(x,i):=x^{2}i+1$. It is easy to verify that ${\mathbb{L}}^{u,\theta }w(x,i)\le -b_{1}w(x,i)+g(x,i,u,\theta )$, with $0<b_1<2\theta -q_{1i}$, where $g(x,i,u,\theta ):=b_{1}w(x,i)+(2ux-2\theta x^2+{\sigma }^2)i+q_{i1}{x}^2$.

Take $b_1$ such that $b_1-2\theta +q_{i1}<0$, and note that for every $(x,i)\in \mathbb{R}\times E$, $(u,\theta )\to g(x,i,u,\theta )$ is continuous on the compact sets U and $\Theta$; therefore, there exists a constant $d_1$ such that $g(x,i,u,\theta )\le d_1$ for all $(x,i)\in \mathbb{R}\times E$, $u\in U$ and $\theta \in \Theta$. So, Assumption 2 is satisfied.

In this problem, the payoff rate is $r^{\lambda }(x,i,u):=r(x,i,u)-\lambda c(x,i,u)$ where $\lambda$ is the Lagrange multiplier, the $\alpha —$discounted expected payoff is

$$V(x,i,\pi ,r_1,\theta ):={\mathbb{E}}_{x,i}^{\pi ,\theta }\left[{\int }_0^{\infty }{\mathrm{e}}^{-\alpha t}{r}^{\lambda }\left(x\left(t\right),\psi \left(t\right),\pi \right)\mathrm{d}t\right],$$

and the value function is

$$V^{\ast }(x,i,\theta )=\underset{\pi \in \Pi }{sup}V(x,i,\pi ,r_1,\theta ).$$

(23)

In order to find the optimal control and the value function $V^{\ast }(x,i,\theta )$ given in (23), we need to solve (10) for each $i\in E$. The HJB equations associated with this example are

$$\begin{array}{cc}\hfill \alpha \phi (x,1)=& \underset{0\le u\le \eta }{sup}\{\sqrt{u}-a\left(0\right)x+\lambda \left[c_1\left(1\right)x+c_2\left(1\right)u-\alpha \left(\frac{c_1\left(1\right)x}{\alpha +\theta }+q\right)\right]\hfill \\ \hfill & +(u-\theta x)\frac{\partial \phi (x,1)}{\partial x}+\frac{1}{2}{\sigma }^2\frac{{\partial }^2\phi (x,1)}{\partial x^2}+\sum _{j=1}^2{q}_{1j}\phi (x,j)\}\mathrm{for} \mathrm{all} x>0.\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \alpha \phi (x,2)=& \underset{0\le u\le \gamma }{sup}\{\sqrt{u}-a\left(2\right)x+\lambda \left[c_1\left(2\right)x+c_2\left(2\right)u-\alpha \left(\frac{c_1\left(2\right)x}{\alpha +\theta }+q\right)\right]\hfill \\ \hfill & +(u-\theta x)\frac{\partial \phi (x,2)}{\partial x}+\frac{1}{2}{\sigma }^2\frac{{\partial }^2\phi (x,2)}{\partial x^2}+\sum _{j=1}^2{q}_{2j}\phi (x,j)\}\mathrm{for} \mathrm{all} x>0.\hfill \end{array}$$

(25)

Assuming that a solution to (24) and (25) has the form $\phi (x,i)=k_1\left(i\right)x+k_2\left(i\right)$ with $k_1,k_2:E\to \mathbb{R}$ measurable functions, we get $\frac{\partial \phi (x,i)}{\partial x}=k_1\left(i\right)$ and $\frac{{\partial }^2\phi (x,i)}{\partial x^2}=0.$ Replacing the derivatives of $\phi (x,i)$ into (24) and (25), we obtain

$$\begin{array}{ccc}\hfill k_1\left(i\right)& =& \frac{\lambda \theta c_1\left(i\right)-(\alpha +\theta )a\left(i\right)}{{(\alpha +\theta )}^2}+\frac{{\sum }_{j=1}^2{q}_{ij}{k}_1\left(j\right)}{\alpha +\theta },\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \alpha k_2\left(1\right)& =& {\displaystyle \underset{0\le u\le \eta }{sup}}\left(\sqrt{u}-a_{\lambda ,\theta ,1}u\right)-\lambda \alpha q+{\displaystyle \sum _{j=1}^2}{q}_{1j}{k}_2\left(j\right),\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill \alpha k_2\left(2\right)& =& \underset{\eta \le u\le \gamma }{sup}\left(\sqrt{u}-a_{\lambda ,\theta ,1}u\right)-\lambda \alpha q+\sum _{j=1}^2{q}_{2j}{k}_2\left(j\right),\hfill \end{array}$$

(27)

with

$$a_{\lambda ,\theta ,i}:=\frac{(\alpha +\theta )a\left(i\right)-\lambda [\theta c_1\left(i\right)+{(\alpha +\theta )}^2{c}_2\left(i\right)]}{{(\alpha +\theta )}^2}+\frac{{\sum }_{j=1}^2{q}_{ij}{k}_1\left(j\right)}{\alpha +\theta }>0,$$

Notice that the suprema in (26) and (27) are attained at

$$f_{\theta }^{\lambda }\left(1\right)=\left\{\begin{array}{cc}\frac{1}{4{\left(a_{\lambda ,\theta ,0}\right)}^2}\hfill & \mathrm{if}\frac{1}{2\sqrt{\eta }}<a_{\lambda ,\theta ,0},\hfill \\ \hfill & \\ \eta \hfill & \mathrm{if}\frac{1}{2\sqrt{\eta }}\ge a_{\lambda ,\theta ,0},\hfill \end{array}\right.$$

(28)

$$f_{\theta }^{\lambda }\left(2\right)=\left\{\begin{array}{cc}\frac{1}{4{\left(a_{\lambda ,\theta ,1}\right)}^2}\hfill & \mathrm{if}\frac{1}{2\sqrt{\gamma }}<a_{\lambda ,\theta ,1},\hfill \\ \hfill & \\ \gamma \hfill & \mathrm{if}\frac{1}{2\sqrt{\gamma }}\ge a_{\lambda ,\theta ,1}.\hfill \end{array}\right.$$

(29)

Thus, $k_2(·)$ can be written as

$$k_2\left(i\right)=\frac{\sqrt{f_{\theta }^{\lambda }\left(i\right)}-a_{\lambda ,\theta ,i}{f}_{\theta }^{\lambda }\left(i\right)}{\alpha }-\lambda q+\frac{1}{\alpha }\sum _{j=0}^1{q}_{ij}{k}_2\left(j\right).$$

By Proposition 3, the optimal control is (28) and (29), and the value function is $\phi (x,i)$, i.e.,

$$\begin{array}{cc}\hfill \phi (x,i)=V^{\ast }(x,i,\theta ,r)=& \left[\frac{\lambda \theta c_1\left(i\right)-(\alpha +\theta )a\left(i\right)}{{(\alpha +\theta )}^2}+\frac{{\sum }_{j=0}^1{q}_{ij}{k}_1\left(j\right)}{\alpha +\theta }\right]x\hfill \\ \hfill +& \frac{\sqrt{f_{\theta }^{\lambda }\left(i\right)}-a_{\lambda ,\theta ,i}{f}_{\theta }^{\lambda }\left(i\right)}{\alpha }-\lambda q+\frac{1}{\alpha }\sum _{j=0}^1{q}_{ij}{k}_2\left(j\right).\hfill \end{array}$$

(30)

For the numerical experiment, we consider the particular form of (1) given by (20) to test Algorithm 1 with $Q=\left(\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right)$ as the generator of the continuous-time Markov chain $\psi \left(t\right)$ embedded within (20). Also, let $x\left(0\right)=0$, $T=5$, $\mathrm{d}t={10}^{-4}$, $u(t,1)=0.5$, $u(t,2)=1.5$, $\sigma =\sqrt{{10}^{-10}}$, and $\theta =2.5$ as the true parameter value of the pollution decay rate. 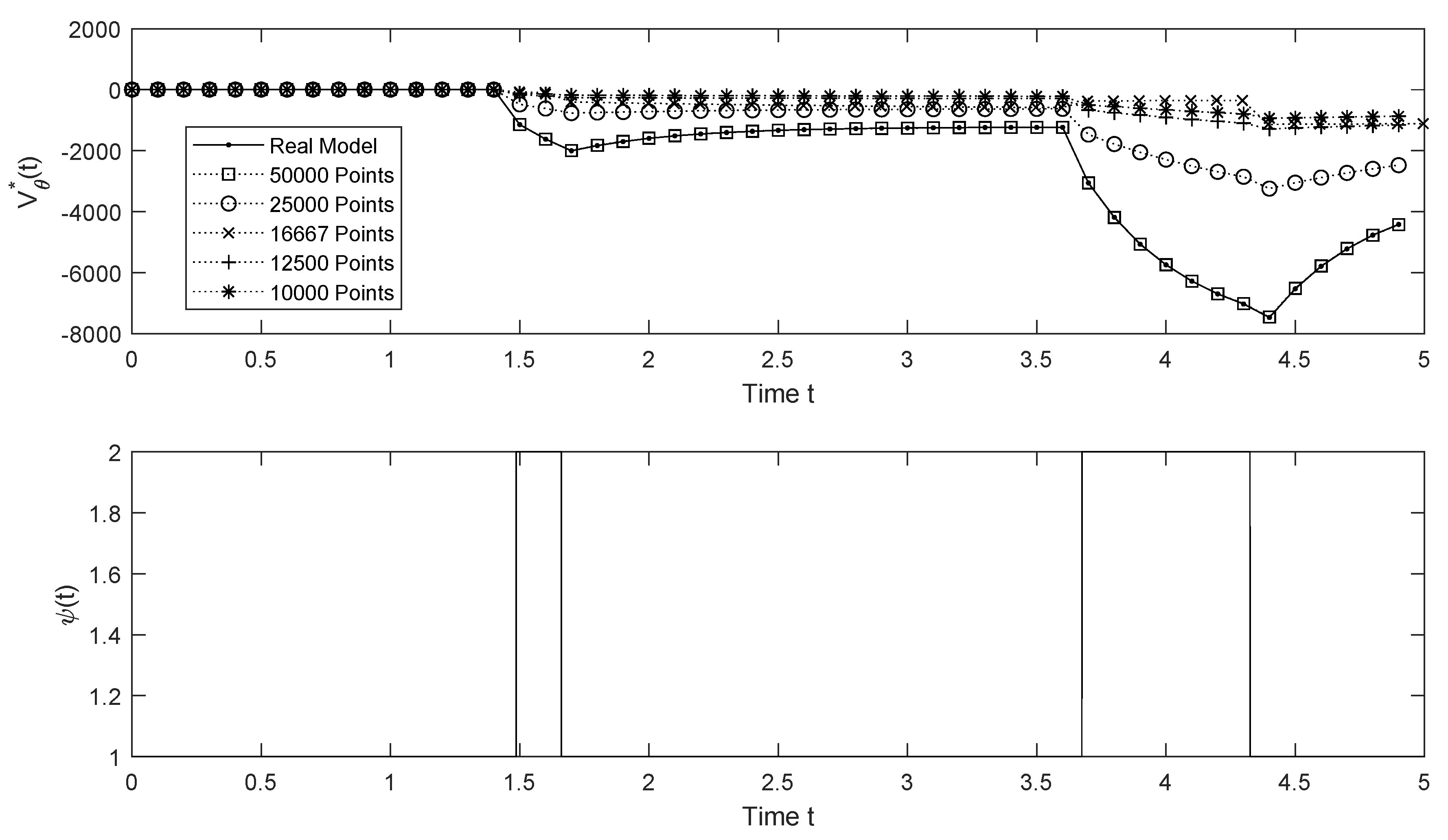These last data allow us to simulate (20) in the interval $[0,5]$, and, for the sake of comparison, it will be considered as the real model (see Figure 1). Based on this information, $m=50,000$ discrete observations were obtained. Now, we suppose that $\theta$ is the unknown parameter and we estimate it by means of the least square function LSE in (13) and (14). Substituting $b(x,i,u,\theta )=u(t,i)-\theta x\left(t\right)$ in (13), we obtain the following estimator for each state $i\in E=\{1,2\}$.

$$\theta {\left(i\right)}_{LS{E}_m}=\frac{{\displaystyle \sum _{k=2}^{m-1}u{x}_k-x_k\mathrm{d}{x}_k}}{{\displaystyle \sum _{i=2}^{m-1}{x}_k^2}},$$

(31)

where $\mathrm{d}{x}_k:=\frac{1}{2}\frac{x_{k+1}-x_{k-1}}{t_{k+1}-t_k}.$ Given that the dynamic system for $x\left(t\right)$ is governed by a stochastic differential equation with Markovian switching, it is not possible to have a single value for $\theta$, but rather a set of values (the number of these values strictly depends on the number of jumps that occur in the interval $[0,T]$), which we will denote as in (31). These approximations allow us to simulate the stochastic differential equation with Markovian switching again with the same jumps. The outputs of the approximate stochastic differential equation with Markovian switching $x^{{\theta }_m^j}\left(t\right)$ and the one with the real value for $\theta$, $x^{\theta }\left(t\right)$ are displayed in

Table 1. Estimated processes using ${\theta }_{LS{E}_m}$ and the real processes ($\theta =2.5$).

m	RMSE	RMSE	RMSE	RMSE
	$(\mathbf{\theta }-{\mathbf{\theta }}_{{\mathit{LSE}}_{\mathit{m}}})$	$({\mathit{x}}^{\mathbf{\theta }}-{\mathit{x}}^{{\mathbf{\theta }}_{{\mathit{LSE}}_{\mathit{m}}}})$	$({\mathit{f}}_{\mathbf{\theta }}^{\mathbf{\lambda }}\left(\mathit{i}\right)-{\mathit{f}}_{{\mathbf{\theta }}_{{\mathit{LSE}}_{\mathit{m}}}}^{\mathbf{\lambda }}\left(\mathit{i}\right))$	$({\mathit{V}}_{\mathbf{\theta }}^{\ast }({\mathit{x}}^{\mathbf{\theta }},\mathit{i})-{\mathit{V}}_{{\mathbf{\theta }}_{\mathit{LSE}\mathit{m}}}^{\ast }{(}^{{\mathbf{\theta }}_{{\mathit{LSE}}_{\mathit{m}}}},\mathit{i}))$
50,000	0.00496364	0.00059318	$5.72448\times {10}^{-5}$	5.09465
25,000	0.00497008	0.0423565	$5.72228\times {10}^{-5}$	1707.61
16,667	3.23512	0.112074	0.00174892	2648.67
12,500	0.0049845	0.0873181	$5.72787\times {10}^{-5}$	2518.47
10,000	0.00498072	0.10305	$5.72684\times {10}^{-5}$	2669.93

.

To graph the value function $V_{\theta }^{\ast }(x,i):=V^{\ast }(x,i,\theta ,r)$ given in (30) we take $\eta =3,$ $\gamma =3,$ $a\left(1\right)=1.25$, $a\left(2\right)=2$, $c_1\left(1\right)=100$, $c_1\left(2\right)=150$, $c_2\left(1\right)=10$, $c_1\left(2\right)=1.5$, $\alpha =0.2$, and $q=60$, and $\theta {\left(i\right)}_{LS{E}_m}$ with $m=10,000,12,500,16,667,25,000$ and 5000, see Figure 2.

The symbol $\left(x{\left(t\right)}^{{\theta }_{LS{E}_m}},f_{{\theta }_{LS{E}_m}}^{\lambda }\left(i\right),V_{{\theta }_{LS{E}_m}}^{\ast }(x,i)\right)$ denotes the value estimates of the dynamic system $x\left(t\right)$, the optimal control $f_{\theta }^{\lambda }$ and of the value function $V_{\theta }^{\ast }$ when we take ${\theta }_{LS{E}_m}$ instead of $\theta$.

We obtained $m=50,000$ discrete observations of (20) on $[0,5]$. Given that the Markov chain is known, the vector of jump times $({\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,{\tau }_5)$ is known as well. The estimator used in each interval $[{\tau }_k,{\tau }_{k+1}]$ with $k=0,1,2,3,4$ and ${\tau }_0=0$ is ${\theta }_{LS{E}_m}$ given in (31). Figure 1 and Figure 2, together with Table 1 show that, as m increases, the estimator approaches the true parameter value $\theta =2.5$, and the RMSE between the estimations $\left(x{\left(t\right)}^{{\theta }_{LS{E}_m}},f_{{\theta }_{LS{E}_m}}^{\lambda }\left(i\right),V_{{\theta }_{LS{E}_m}}^{\ast }(x,i)\right)$ and the actual values of $\left(x{\left(t\right)}^{\theta },f_{\theta }^{\lambda }\left(i\right),V_{\theta }^{\ast }(x,i)\right)$ decreases, thus implying a good fit.

Theorem 5.5 in [28] ensures that for a fixed point $z>0$ such that

$$q<\frac{\eta c_1\left(i\right)z}{{(\alpha +\theta )}^2}+\frac{[\theta c_1\left(i\right)+{(\alpha +\theta )}^2{c}_2\left(i\right)]\gamma }{\alpha {(\alpha +\theta )}^2}\mathrm{for} \mathrm{all} i=1,2$$

if the inequality $\frac{1}{2\sqrt{\left(\frac{\alpha {(\alpha +\theta )}^{2}q-\alpha \theta c_1\left(i\right)z}{\theta c_1\left(i\right)+{(\alpha +\theta )}^2{c}_2\left(i\right)}\right)}}>\frac{a\left(i\right)}{\alpha +\theta }$ holds, then the mapping $\lambda ⟼V^{\ast }(z,i,\theta ,r^{\lambda })$ admits a critical point ${\lambda }_{z,\theta }^{\ast }\equiv {\lambda }_{z,\theta }^{\ast }(\alpha ,z)<0$ satisfying

$$a_{{\lambda }_{z,\theta }^{\ast },\theta }\left(i\right)=\frac{(\alpha +\theta )a\left(i\right)-{\lambda }_{z,\theta }^{\ast }[\theta c_1\left(i\right)+{(\alpha +\theta )}^2{c}_2\left(i\right)]}{{(\alpha +\theta )}^2}=\frac{1}{2\sqrt{\left(\frac{\alpha {(\alpha +\theta )}^{2}q-\alpha \theta c_1\left(i\right)z}{\theta c_1\left(i\right)+{(\alpha +\theta )}^2{c}_2}\right)}}.$$

Therefore, every ${\pi }^{{\lambda }_{z,\theta }^{\ast }}\in {\Pi }^{{\lambda }_{z,\theta }^{\ast }}$ is $\alpha$-optimal for the DPC and $V(z,i,{\pi }^{{\lambda }_{z,i,\theta }^{\ast }},c,\theta )=\overline{\eta }(z,i,{\pi }^{{\lambda }_{z,\theta }^{\ast }},\theta )$; in particular, the $\alpha$-optimal policy for the DPC is $f_{\theta }^{{\lambda }_{z,\theta }^{\ast }}\in \mathbb{F}\cap {\Pi }^{{\lambda }_{z,\theta }^{\ast }}$ of the form

$$f_{\theta }^{{\lambda }_{z,\theta }^{\ast }}\left(i\right)=\frac{\alpha {(\alpha +\theta )}^{2}q-\alpha \theta c_1\left(i\right)z}{\theta c_1\left(i\right)+{(\alpha +\theta )}^2{c}_2\left(i\right)},$$

(32)

and the $\alpha$-optimal value for the DPC is given by

$$\begin{array}{cc}\hfill & V^{\ast }(z,i,\theta ,r^{{\lambda }_{z,\theta }^{\ast }})=V^{\ast }(z,{\pi }^{{\lambda }_{z,i,\theta }^{\ast }},\theta ,r)\hfill \\ \hfill & =-\frac{a\left(i\right)z}{\alpha +\theta }+\frac{1}{\alpha }\sqrt{\left(\frac{\alpha {(\alpha +\theta )}^{2}q-\alpha \theta c_1\left(i\right)z}{\theta c_{(}{i)+(\alpha +\theta )}^2{c}_2\left(i\right)}\right)}-\frac{a\left(i\right)}{\alpha +\theta }\left[\frac{{(\alpha +\theta )}^{2}q-\theta c_1\left(i\right)z}{\theta c_1\left(i\right)+{(\alpha +\theta )}^2{c}_2\left(i\right)}\right].\hfill \end{array}$$

(33)

5. Conclusions

We studied controlled stochastic differential equations with Markovian switching of the form (1), where the drift coefficient depends on an unknown parameter $\theta \in \Theta$.

Two problems were analyzed, each one under a corresponding reward criterion: the discounted unconstrained problems (DUP) and the discounted problem with constraints (DPC) with optimal value functions $V_{\theta }^{\ast }(x,i,r)$ and $V_{\theta }^{\ast }(x,i,r^{\lambda })$, respectively. Once a suitable procedure estimation of $\theta$ is obtained, it generates a sequence of estimators ${\left({\theta }_m\right)}_{m\in \mathbb{N}}$ such that ${\theta }_m\to \theta$ as $m\to \infty$, and the results obtained guarantee the following:

• For each initial state and parameter ${\theta }_m$, $V_{{\theta }_m}^{\ast }\to V_{\theta }^{\ast }$ almost surely for both problems.
• For each estimation ${\theta }_m$ and problem (DUP or PDC), there are optimal policies ${\pi }_{{\theta }_m}$.
• There is a subsequence of policies ${({\pi }_{{\theta }_{m_k}})}_{k\in \mathbb{N}}$ and a policy ${\pi }_{\theta }^{\ast }\in \Pi$ such that ${\pi }_{{\theta }_{m_k}}\stackrel{W}{\to }{\pi }_{\theta }^{\ast }$, and, moreover, ${\pi }_{\theta }^{\ast }$ is optimal for the $\theta$-OCP.
• Similar to the previous point, for the DUP, there is a subsequence of policies and a policy ${\pi }_{\theta }^{\ast }\in {\Pi }^{\lambda ,\theta }$ such that ${\pi }^{{\lambda }_{m_k},{\theta }_{m_k}}\stackrel{W}{\to }{\pi }_{\theta }^{\ast }$, and ${\pi }_{\theta }^{\ast }$ is optimal for the $\theta$-DUP. Moreover, if ${\lambda }_{m_k}<0$ is a critical point of $V_{{\theta }_{m_k}}^{\ast }(x,r^{\lambda })$, then ${\pi }_{\theta }^{\ast }$ is optimal for the $\theta$-DCP.

The numerical part is one of the strengths of this work. Indeed, it aims at solving an estimation problem and a control problem. This task requires knowledge and storage of the optimal policies ${\pi }_{\theta }$ for all the values of $\theta$, which may take considerable offline execution time. In addition, we propose and implement an algorithm to approximate $\theta$.

Finally, the idea of modeling the dynamic $x\left(t\right)$ as a controlled diffusion process with Markovian switchings allows us to consider extra factors or elements that affect the pollution stock. Such factors could be seen, in particular, as multiple pollution sources. An interesting task or challenge would be to pose this scenario as a multi-objective problem, where both sources of contamination and the stock require to be minimized under certain restrictions. This could be done by adapting and defining a suitable multi-objective linear program (convex program) and guaranteeing the existence of a saddle-point—or Pareto optimal policy—as studied in [43,44]. Another technique, called the multi-objective evolutionary algorithm, combines multi-objective problems with statistical techniques to approximate the Pareto optimal as in [45]. In both cases, it is still necessary to apply extra techniques due to the unknown parameter $\theta$.