Phase-Space Modeling and Control of Robots in the Screw Theory Framework Using Geometric Algebra
Abstract
1. Introduction
2. Geometric Algebra
3. Mathematical Development
3.1. Screws
Lie Algebra Elements
3.2. Velocity Kinematics
3.3. Co-Screws
3.4. Lagrangian Formulation of Dynamics Using Screw Theory
3.5. Hamilton’s Equations
4. Hamilton Control Using Screw Theory
5. Examples
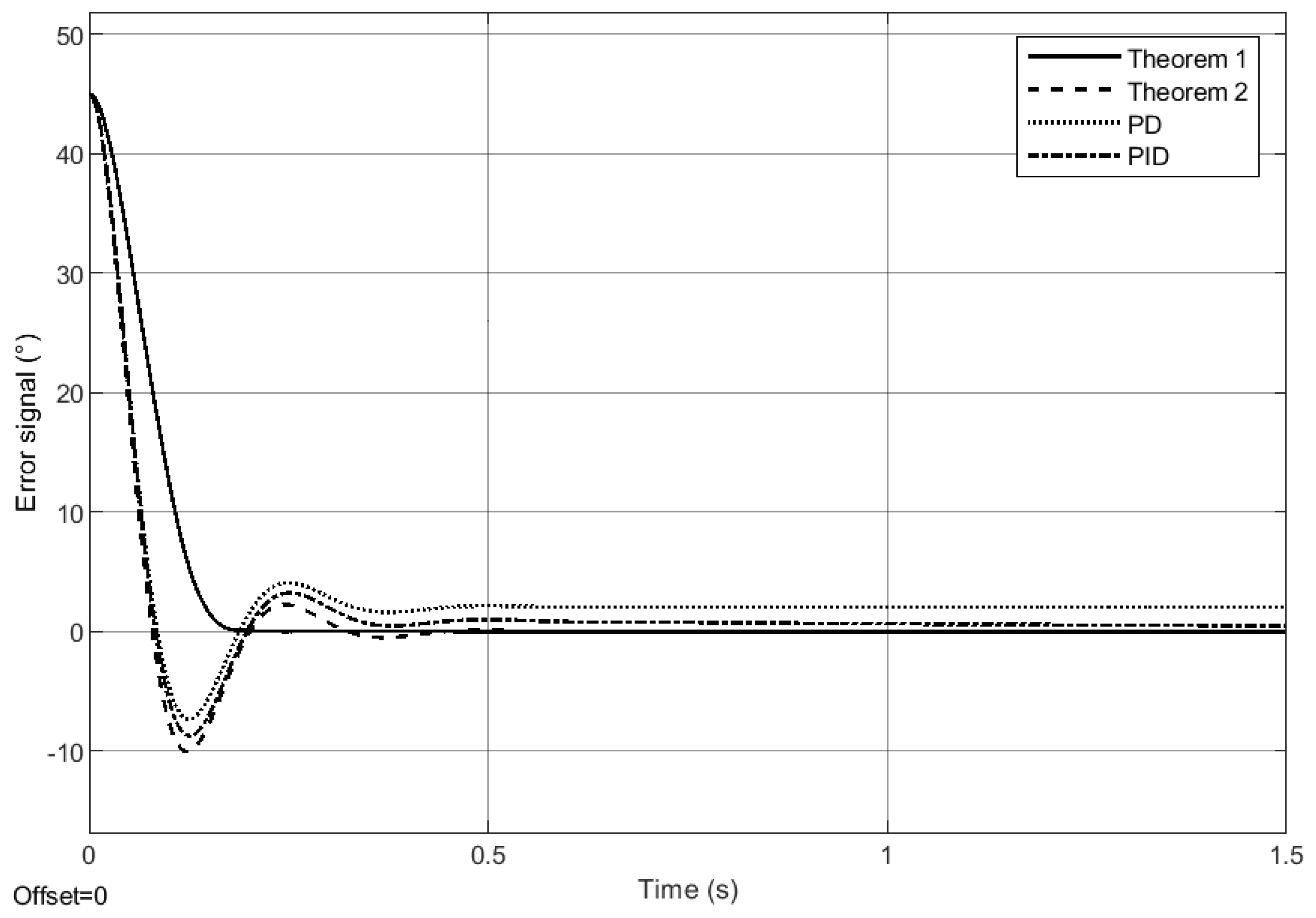
5.1. Single Degree-of-Freedom Robot
Comparison with Other Techniques
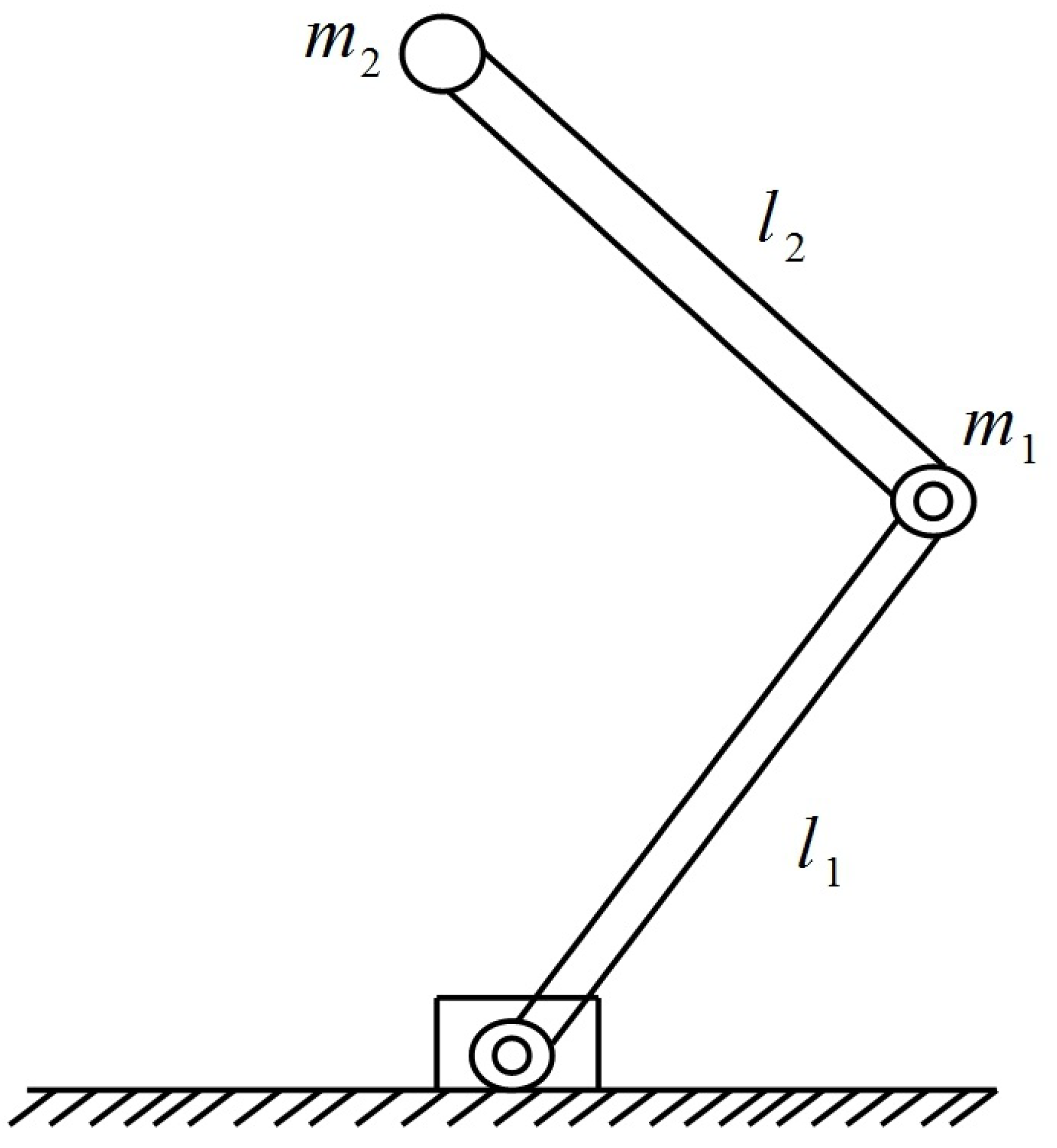
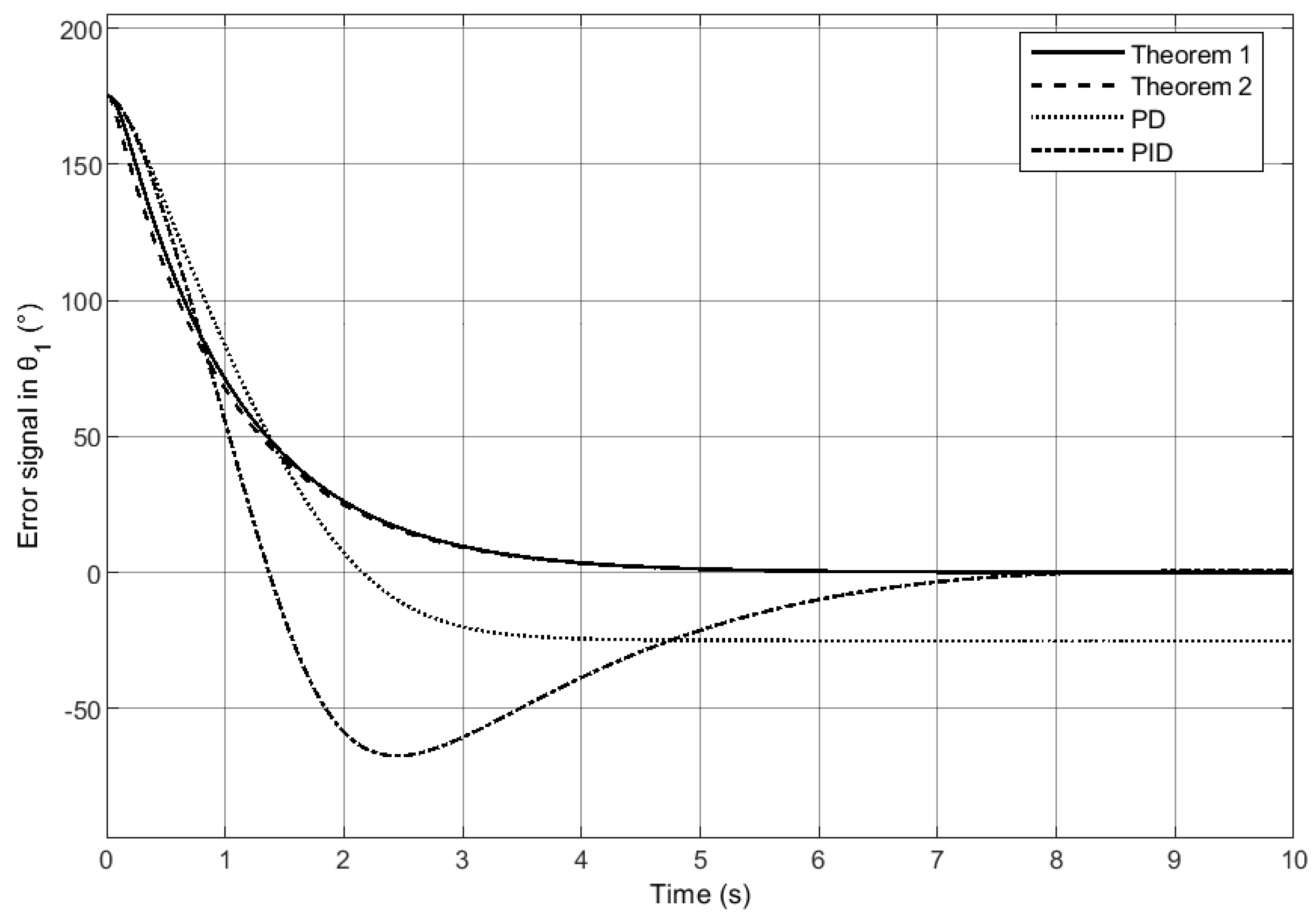
5.2. Two Degrees-of-Freedom Robot
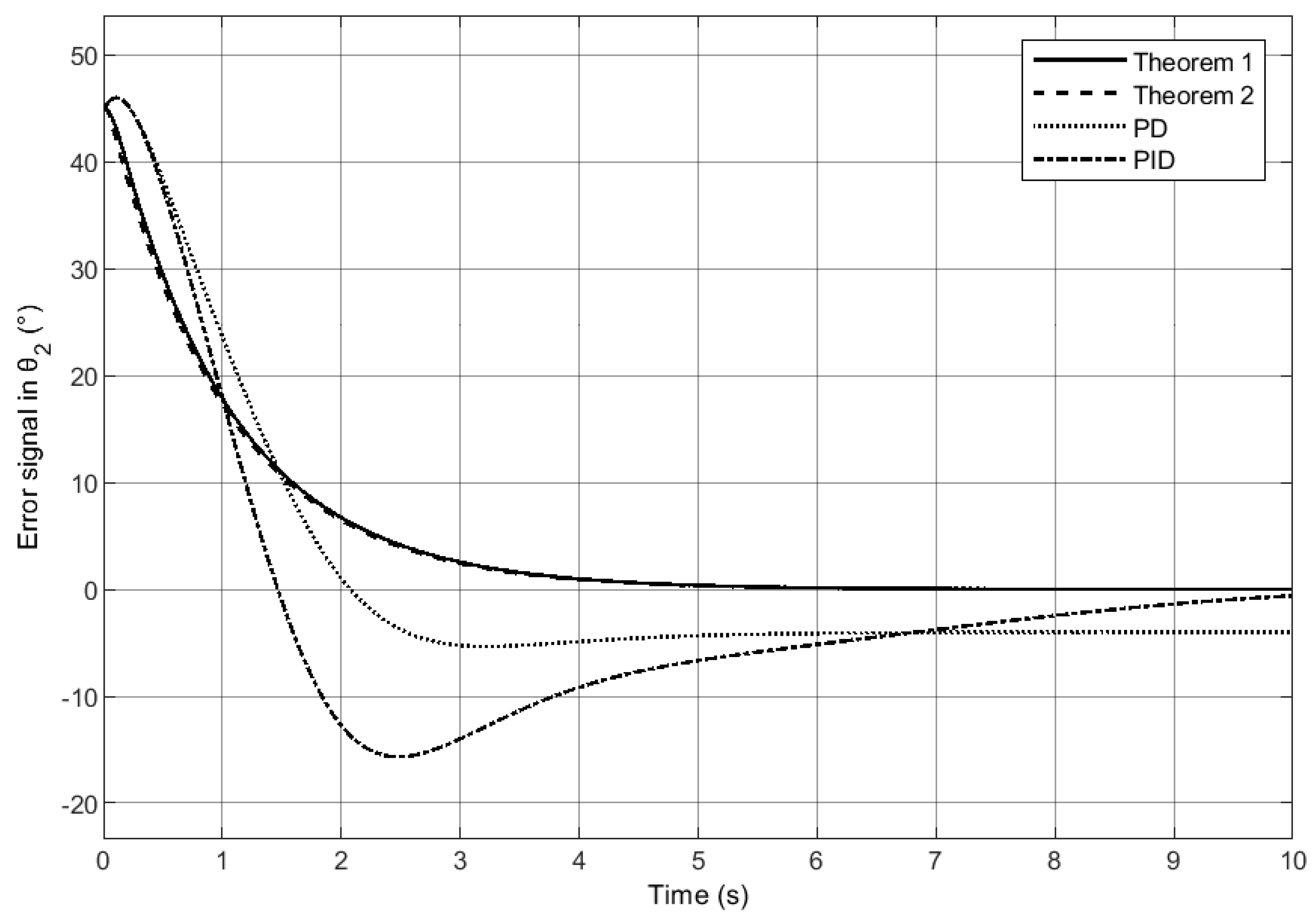
Comparison
6. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Robot Dynamics Using Screw Theory
Appendix A.2. Hamilton’s Equations Using Screw Theory
References
- Goldstein, H. Classical Mechanics; Addison-Wesley: Boston, MA, USA, 1980. [Google Scholar]
- Taylor, J. Classical Mechanics; G—Reference, Information and Interdisciplinary Subjects Series; University Science Books: Melville, NY, USA, 2005. [Google Scholar]
- Peymani, E.; Fossen, T.I. A Lagrangian framework to incorporate positional and velocity constraints to achieve path-following control. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 3940–3945. [Google Scholar] [CrossRef]
- Arimoto, S. Control Theory of Non-Linear Mechanical Systems: A Passivity-Based and Circuit-Theoretic Approach; Oxford Engineering Science Series; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Záda, V.; Belda, K. Mathematical modeling of industrial robots based on Hamiltonian mechanics. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 29 May–1 June 2016; pp. 813–818. [Google Scholar] [CrossRef]
- Chi, J.; Yu, H.; Yu, J. Hybrid Tracking Control of 2-DOF SCARA Robot via Port-Controlled Hamiltonian and Backstepping. IEEE Access 2018, 6, 17354–17360. [Google Scholar] [CrossRef]
- Záda, V. Exponentially stable tracking control in terms of Hamiltonian mechanics. In Proceedings of the 2017 18th International Carpathian Control Conference (ICCC), Sinaia, Romania, 28–31 May 2017; pp. 483–487. [Google Scholar] [CrossRef]
- Hestenes, D. Hamiltonian Mechanics with Geometric Calculus. In Proceedings of the Spinors, Twistors, Clifford Algebras and Quantum Deformations; Oziewicz, Z., Jancewicz, B., Borowiec, A., Eds.; Springer: Dordrecht, The Netherlands, 1993; pp. 203–214. [Google Scholar]
- Bayro-Corrochano, E.; Zamora-Esquivel, J. Differential and inverse kinematics of robot devices using conformal geometric algebra. Robotica 2007, 25, 43–61. [Google Scholar] [CrossRef]
- Dahab, E.A.E. A formulation of Hamiltonian mechanics using geometric algebra. Adv. Appl. Clifford Algebr. 2000, 10, 217–223. [Google Scholar] [CrossRef]
- Bayro-Corrochano, E.; Medrano-Hermosillo, J.; Osuna-González, G.; Uriostegui-Legorreta, U. Newton–Euler modeling and Hamiltonians for robot control in the geometric algebra. Robotica 2022, 40, 4031–4055. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Q.; Ding, H. Basics of Screw Theory; Springer: Berlin, Germany, 2013; pp. 1–16. [Google Scholar] [CrossRef]
- Müller, A. Screw Theory–A forgotten Tool in Multibody Dynamics. PAMM 2017, 17, 809–810. [Google Scholar] [CrossRef]
- Ball, R. A Treatise on the Theory of Screws; Cambridge Mathematical Library; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Toscano, G.S.; Simas, H.; Castelan, E.B.; Martins, D. A new kinetostatic model for humanoid robots using screw theory. Robotica 2018, 36, 570–587. [Google Scholar] [CrossRef]
- Hunt, K.H. Special configurations of robot-arms via screw theory. Robotica 1986, 4, 171–179. [Google Scholar] [CrossRef]
- Selig, J.M. Geometric Fundamentals of Robotics (Monographs in Computer Science); Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Lynch, K.; Park, F. Modern Robotics: Mechanics, Planning, and Control; Cambridge Univeristy Press: Cambridge, UK, 2017. [Google Scholar]
- Yi, B.J.; Kim, W.K. Screw-Based Kinematic Modeling and Geometric Analysis of Planar Mobile Robots. In Proceedings of the 2007 International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007; pp. 1734–1739. [Google Scholar] [CrossRef]
- Medrano-Hermosillo, J.A.; Lozoya-Ponce, R.; Ramírez-Quintana, J.; Baray-Arana, R. Forward Kinematics Analysis of 6-DoF Articulated Robot using Screw Theory and Geometric Algebra. In Proceedings of the 2022 XXIV Robotics Mexican Congress (COMRob), Mineral de la Reforma/State of Hidalgo, Mexico, 9–11 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, A.; Zhang, Q.; Zhang, B.; Wu, X.; Qin, T. Design and Experimental Research of 3-RRS Parallel Ankle Rehabilitation Robot. Micromachines 2022, 13, 950. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Lian, B.; Yang, S.; Song, Y. Kinematic Calibration of Serial and Parallel Robots Based on Finite and Instantaneous Screw Theory. IEEE Trans. Robot. 2020, 36, 816–834. [Google Scholar] [CrossRef]
- Liang, Z.; Meng, S.; Changkun, D. Accuracy analysis of SCARA industrial robot based on screw theory. In Proceedings of the 2011 IEEE International Conference on Computer Science and Automation Engineering, Shanghai, China, 10–12 June 2011; Volume 3, pp. 40–46. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, Q.; Wei, S.; Guo, L. Research on Dynamics of a Bicycle Robot with Front-Wheel Drive by Using Kane Equations Based on Screw Theory. In Proceedings of the 2010 International Conference on Artificial Intelligence and Computational Intelligence, Sanya, China, 23–24 October 2010; Volume 1, pp. 546–551. [Google Scholar] [CrossRef]
- Selig, J.M.; McAree, P.R. Constrained robot dynamics I: Serial robots with end-effector constraints. J. Robot. Syst. 1999, 16, 471–486. [Google Scholar] [CrossRef]
- Cheng, J.; Bi, S.; Yuan, C.; Cai, Y.; Yao, Y.; Zhang, L. Dynamic Modeling Method of Multibody System of 6-DOF Robot Based on Screw Theory. Machines 2022, 10, 499. [Google Scholar] [CrossRef]
- Qin, Q.; Gao, G. Screw Dynamic Modeling and Novel Composite Error-Based Second-order Sliding Mode Dynamic Control for a Bilaterally Symmetrical Hybrid Robot. Robotica 2021, 39, 1264–1280. [Google Scholar] [CrossRef]
- Abaunza, H.; Chandra, R.; Özgür, E.; Ramón, J.A.C.; Mezouar, Y. Kinematic screws and dual quaternion based motion controllers. Control Eng. Pract. 2022, 128, 105325. [Google Scholar] [CrossRef]
- Bayro-Corrochano, E. Geometric Algebra Applications Vol. I: Computer Vision, Graphics and Neurocomputing; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Bayro-Corrochano, E. A Survey on Quaternion Algebra and Geometric Algebra Applications in Engineering and Computer Science 1995–2020. IEEE Access 2021, 9, 104326–104355. [Google Scholar] [CrossRef]
- Ji, P.; Li, C.; Ma, F. Sliding Mode Control of Manipulator Based on Improved Reaching Law and Sliding Surface. Mathematics 2022, 10, 1935. [Google Scholar] [CrossRef]
- Hestenes, D.; Sobczyk, G. Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics; Fundamental Theories of Physics; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Perwass, C. Geometric Algebra with Applications in Engineering; Springer: Berlin, Germany, 2009; Volume 4. [Google Scholar] [CrossRef]
- Lee, J. Velocity workspace analysis for multiple arm robot systems. Robotica 2001, 19, 581–591. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 2010. [Google Scholar]
- Craig, J. Introduction to Robotics, Global Edition; Pearson Education Limited: London, UK, 2021. [Google Scholar]
- Selig, J.; Ding, X. A screw theory of static beams. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 312–317. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Khalil, H. Nonlinear Systems; Pearson Education; Prentice Hall: Kent, OH, USA, 2002. [Google Scholar]
- Kelly, R. A tuning procedure for stable PID control of robot manipulators. Robotica 1995, 13, 141–148. [Google Scholar] [CrossRef]
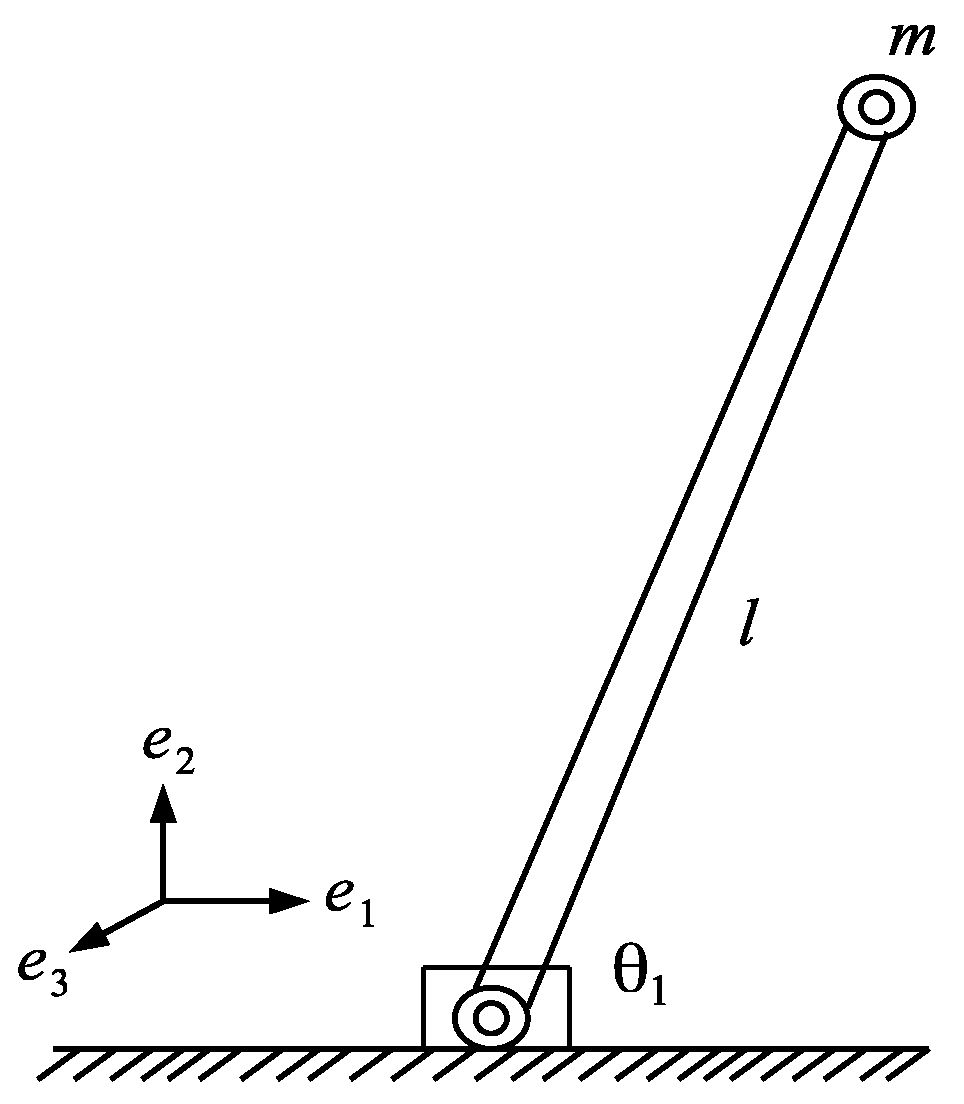
| Parameter | Value | Unit |
|---|---|---|
| m | 0.25 | kg |
| l | 0.5 | m |
| g | 9.81 |
| Law of Control | Law of Control | Gains |
|---|---|---|
| Theorem 1 | See Equation (49) | |
| Theorem 2 | See Equation (55) | |
| PD | ||
| PID |
| Parameter | Value | Unit |
|---|---|---|
| 0.25 | kg | |
| 2 | m | |
| g | 9.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medrano-Hermosillo, J.A.; Lozoya-Ponce, R.; Rodriguez-Mata, A.E.; Baray-Arana, R. Phase-Space Modeling and Control of Robots in the Screw Theory Framework Using Geometric Algebra. Mathematics 2023, 11, 572. https://doi.org/10.3390/math11030572
Medrano-Hermosillo JA, Lozoya-Ponce R, Rodriguez-Mata AE, Baray-Arana R. Phase-Space Modeling and Control of Robots in the Screw Theory Framework Using Geometric Algebra. Mathematics. 2023; 11(3):572. https://doi.org/10.3390/math11030572
Chicago/Turabian StyleMedrano-Hermosillo, Jesús Alfonso, Ricardo Lozoya-Ponce, Abraham Efraím Rodriguez-Mata, and Rogelio Baray-Arana. 2023. "Phase-Space Modeling and Control of Robots in the Screw Theory Framework Using Geometric Algebra" Mathematics 11, no. 3: 572. https://doi.org/10.3390/math11030572
APA StyleMedrano-Hermosillo, J. A., Lozoya-Ponce, R., Rodriguez-Mata, A. E., & Baray-Arana, R. (2023). Phase-Space Modeling and Control of Robots in the Screw Theory Framework Using Geometric Algebra. Mathematics, 11(3), 572. https://doi.org/10.3390/math11030572








