Abstract
In the longitudinal data analysis we integrate flexible linear predictor link function and high-correlated predictor variables. Our approach uses B-splines for non-parametric part in the linear predictor component. A generalized estimation equation is used to estimate the parameters of the proposed model. We assess the performance of our proposed model using simulations and an application to an analysis of acquired immunodeficiency syndrome data set.
Keywords:
generalized estimating equations; longitudinal data; multicollinearity; partially generalized linear models; ridge regression MSC:
62J07; 62H12; 32H30
1. Introduction
Generalized linear models (GLMs) [1], which have a link function connecting the predictors linearly, are now part of regression models toolbox. Assuming a linear predictor link function could be very restrictive as the true relationship could be non-linear. Generalized partial linear models (GPLMs) accommodates both parametric and nonparametric connections. For example, in modelling longitudinal data, the GPLMs have proved useful as the model account for possible dependencies in the data [2,3,4,5,6].
One of the basic assumptions in the regression analysis is that all the explanatory variables are linearly independent. However two or more of the explanatory variables could be correlated with one another, resulting into a multicollinearity problem. Thus, it becomes harder to distinguish between effects of the independent variables on the outcome variable. It also results in the inflation of the variance of the regression parameter estimates. Ridge regression is widely used in regression model analyses with a large number of highly correlated independent variables [7,8,9,10,11,12,13,14,15,16,17]. While ridge regression techniques have widely been used in modelling cross-section data, there have been very few studies and applications in longitdinal data [18,19,20,21,22].
In this paper, we consider two typical problems name: of multicollinearity among predictor variables and linear predictor link function in the analysis of longitudinal non-normal data. For the former, we employ ridge regression and for the later we adopt the use of B-splines for nonparametric component of the linear predictor in an integrated approach. We concentrate on the estimation of population averaged model parameters. For this, we have the marginal mean model specification and account for the possible dependencies in the longitudinal data in a nonparametric manner through a convenient working within-subject covariance and employ the generalised estimation equations (GEE) for estimating the parameters.
In Section 2, we specify the underlying longitudinal model with the nonparametric part using splines. The estimation and asymptotic properties of the model parameters are also presented in Section 2. Simulation studies and an application to acquired immunodeficiency syndrome data set are in Section 3. We conclude the paper in Section 4.
2. Model and Estimation Procedure
2.1. GPLMs for Longitudinal Data
Suppose we have n subjects and subject i has observations denoted by () for a total of observations. Also, be a vector of time-varying covariate. Thus, the total observed data set for the analysis is . Further let and , where is a scale parameter and is a known variance function. We model the longitudinal data with a GPLM, and specify a marginal model on the first two moments of . Especially, the marginal mean is modeled as
where g(.) is a link function for the GLM, is the regression coefficient vector with dimension p, and is an unknown smooth function. We also assume independency between observations from different subjects. Finally, we assume are all scaled into the interval .
Similar to [3,23,24], we approximate the unspecified smooth function by the following polynomial spline
where d is the degree of the polynomial component, is the number of interior knots (rate of will be specified in Remark 1), are knots of the ith subject, is a vector of basis functions, is the number of basis functions used to approximate , , , and is the spline coefficients vector of dimension . The nonparametric part in the linear prediction part is set as the basis functions with pseudo-design variables. In this way, the regression model problem in (1) could be linearised
is a design matrix, which combines both the fixed and spline effects for the jth outcome of the ith subject. The combined regression coeffieicnts has dimension . Let , , where , and . By the linear form of the GPLM in (1), using the spline approach, any computational algorithm developed for the GLM can be used for the GPLM.
Remark 1.
In spline smoothing, it is important to select the knots efficiently. Concentrating on the estimation of β, Ref. [3] noticed that knot selection is more important for estimating rather than β. Because in most of the studies, the focus is on β and providing sufficient statistical inference, and one only needs some basic information about . Therefore they particularly used the sample quantiles of as knots. For instance, with three internal knots, we take three quartiles of the observed . Considering splines of order 4, they applied cubic splines with the integer part of , the number of internal knots, where M is the number of distinct values in . Another study, Ref. [25], proposed that the number of distinct knots should increase with sample size to achieve asymptotic consistency. One must note that having too many knots increases the variance of estimators. Thus, the number of knots must be appropriately selected. When n goes to ∞, the number of knots should increase at . Thus, here, we use with integer value m as the number of internal knots. We fix , and choose , for asymptotic consistency. However, it is mainly based on practical experience and a desire for simplicity and is not an optimal choice. We considered a similar procedure in simulation and real data.
2.2. Ridge Generalized Estimating Equation (RGEE)
In most applications of GPLMs, the primary research interest is to make statistical inferences on the regression coefficient , along with and understanding of basic features of . For the ridge GEE procedure for , we briefly review the GEE method. For the estimating equation of , we have
where is a covariance matrix of . For most applications, the actual intracluster covariance is regularly unknown. We take the working correlation matrix as , with the finite-dimensional parameter . Some commonly used working correlation structures include independence, autocorrelation (AR)-1, equally correlated (also called compound symmetry), or unstructured correlation. For a given working correlation structure, can be estimated using the residual-based moment method. Here, similar to [26], the marginal density of follows a canonical exponential family. Consequently, and , where , for a differentiable function and a scaling constant . Assume is the estimated working correlation matrix. Then, (3) simplifies to
We formally define the GEE estimator as the solution of the above-estimating equations. For ease of exposition, we assume in the rest of the article.
To account for multicollinearity in longitudinal data, we use the ridge GEE in the GPLM in (1) for parameter estimation. We do this by adding a shrinkage term to the objective function for handling correlated predictors. The ridge GEE has form
where
are the estimating functions defining the GEE. Here, is the tuning parameter that determines the shrinkage amount. The RGEE estimator is the solution to . We use the Newton–Raphson algorithm along with (6) to get the following iterative algorithm
Here, , . Further, and represent a vector of 1 with dimension p, and a zero vector of dimension , respectively. The suggested estimation approach can be implemented step by step, and the detailed computation procedure can be summarized in Algorithm 1, describing the combination of ridge regression into the Newton–Raphson iterative algorithm of GEE. With prespecified and initial value , the above algorithm is repeated to update untill convergence.
| Algorithm 1: Monte Carlo Newton–Raphson (MCNR) algorithm |
|
It is critical to choose a suitable value of tuning parameter to achieve satisfactory performance of the selection procedure. Many authors have introduced many methods for choosing an optimal tuning parameter within a given set of candidates. Traditional model selection criteria, such as AIC and BIC, have several limitations. The generalized cross validation (GCV) suggested by [27], later [28] proposed a Bayesian information criterion (BIC). How to choose for high-dimensional data discussed by [29]. They proposed a modified BIC. Further [30] extended the BIC information criterion. For the selection of the tuning parameter , here, we apply the suggested GCV of [27], given by
where
is the residual sum of squares, and effective number is equal to
The optimal parameter denoted by is the minimizer of the . In practical implementation, one can use PGEE package of R software, where function CVfit computes cross-validated tuning parameter value for longitudinal data. In numerical studies of the current paper, we used R codes similarly to compute .
2.3. Asymptotics
We now discuss the asymptotic properties of the estimators and for the ridge GEE. Assuming (A.1)–(A.4) in Appendix A, the following theorems state the large sample property for and , respectively. For the proofs, refer to Appendix A.
Theorem 1.
For we have
where and .
Theorem 2.
Under the named regularity Conditions (A.1)–(A.4), has the asymptotic p-variate normal distribution with the zero-vector mean and covariate matrix , where
3. Numerical Analyses
3.1. Simulations
Here, we assess the performance of the GEE compared to its counterpart, the ridge GEE, for multiple correlated predictor variables. We generate the explanatory variables using
where are assumed to be independent and generated from a normal distribution with zero mean and unit variance. The parameter reflects the correlation such that any two explanatory variables correlate equally to . We generality, we consider . The nonparametric part of (1) has form . In the entire process, for each subject i and use the following GPLM for simulation
We set the true as . We generate from the uniform distribution over . The is generated from a normal distribution with zero mean, a common marginal variance . Moreover, the correlation structure is , i.e., for , . Each simulated data set is fitted separately by the GEE approach of [26] and our ridge GEE using Algorithm 1. Then, 200 replications are run for each combination of and .
To assess the behavior of both estimators encountering misspecified correlation structures, we conduct a comparison between and . We test the exchangeable working correlation structure (GEE-I) or (RGEE-I) when the true correlation structure is AR(1), (GEE-C), or (RGEE-C). For each of the estimators, we measure the accuracy in estimation using the mean squared error (MSE) given by . We recall the tuning parameter was obtained using the GCV, where was the minimizer of the . Alternatively, one can use the ridge trace to find . Figure 1 illustrates the ridge trace for the first generated random sample. As can be seen, the minimizer occurs at , which is the same value as the minimizer of GCV. The simulation results for MSE are presented in the latest column of Table 1. Table 1 reports the empirical biases and standard deviations (SDs) of the estimated from the GEE and RGEE methods. We can take the following observations: Our proposed RGEE has a superior performance in the MSE criterion. For misspecified correlation structures, the RGEE outperforms. However, it has more bias and offers a smaller SD in most cases compared to the GEE. By increasing the correlation among predictors, the increase in RGEE MSE is lesser than the GEE for all considered criteria. The conclusion is evident at the extreme level of correlation .
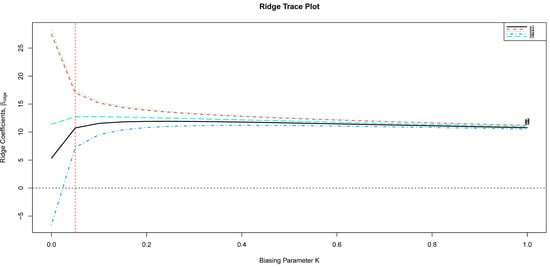
Figure 1.
The ridge trace plot, for the first simulated data.

Table 1.
Estimated regression coefficients for the important variables; bias (SD) based on 200 replications.
3.2. AIDS Data Analysis
For illustration, in this section, the proposed model is used to analyze the CD4 cell data. From the number of 369 patients, 2376 CD4 measurements are recorded. The population’s average time course of CD4 decay is regressed on the following covariates: packs per day for an indication of smoking; binary variable recreational drug use; SEXP as an indication of the number of sexual partners; and depression symptoms as measured by the CESD scale (larger values indicate increased depressive symptoms). Similar to most literature, we take the square root of CD4 numbers. For the reason of the latter transformation, the reader is referred to [31,32]. For the correlation structure, we follow the approach of [31] and fit the compound symmetry covariance, where . We then used our proposed RGEE compared with the GEE for parameter estimation. We computed the standard errors (SDs) calculated using the bootstrap method. Table 2 provides the parameter estimates. From the result of this table, our proposed RGEE gives effectively smaller SD values compared to the GEE.

Table 2.
Regression coefficient estimates (SD) in the analysis of the CD4 data.
4. Concluding Remarks and Discussion
We considered a generalized partially linear model (GPLM) and ridge regression to tackle the problems of multicollinearity and non-linearity in the relationship between the mean response and covariates in the longitudinal data analysis. The generalized estimation Equation (GEE) methods were used to estimate parameters in our proposed model. Using simulation studies, our methods resulted in smaller biases for estimating parameters than could have been obtained in a standard GEE. The performance of our proposed method decreased with increased dependencies between the model predictors. We also applied our model to a specific data set on AIDS data analysis.
Author Contributions
Conceptualization, M.T., M.A. and S.M.; Funding acquisition, M.A. and S.M.; Methodology, M.T. and M.A.; Software, M.T.; Supervision, M.A. and S.M.; Visualization, M.T., M.A. and S.M.; Formal analysis, M.T. and M.A.; Writing—original draft preparation, M.T.; Writing—review and editing, M.T., M.A. and S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was based upon research supported in part by the National Research Foundation (NRF) of South Africa, SARChI Research Chair UID: 71199, the South African DST-NRF-MRC SARChI Research Chair in Biostatistics (Grant No. 114613) and STATOMET at the Department of Statistics at the University of Pretoria, South Africa. The opinions expressed and conclusions arrived at are those of the authors and are not necessarily to be attributed to the NRF.
Data Availability Statement
The data is publicly available.
Acknowledgments
We sincerely thank two anonymous reviewers for their constructive comments that significantly improved the presentation and led to putting many details in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
To study the asymptotic properties of RGEE estimators, the following regularity conditions are required.
- (A.1)
- Number of observations over time () is a bounded sequence of positive integers, and the distinct values of form a quasi-uniform sequence that grows dense on , and the kth derivative of is bounded for some ;
- (A.2)
- The covariates , , are uniformly bounded;
- (A.3)
- The unknown parameter belongs to a compact subset , the true parameter value lies in the interior of ;
- (A.4)
- There exist two positive constants, and , such thatwhere (resp. ) denotes the minimum (resp. maximum) eigenvalue of a matrix.
To verify Theorem 1, we need the following lemma.
Lemma A1.
Under Condition (A.1), there exists a constant C depending only on such that
The proof of this lemma follows readily from Theorem 12.7 of Schumaker [33].
Proof of Theorem 1.
By Lemma A1, we approximate by , then by choosing we have
which proves Theorem 1. □
Proof of Theorem 2.
To proof Theorem 2 define the linear operator . It is straightforward to calculate that the ridge estimator can be expressed as where is ordinary GEE estimator. The expectation of the ridge estimator can be expressed as
Clearly, for any . Hence, the ridge estimator is biased with . The variance of the RGEE estimator is straightforwardly obtained when exploiting its linearly relation with the GEE estimator. Then,
where . Combining the expectation and variance terms, the proof is complete. □
References
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman and Hall: London, UK, 1989. [Google Scholar]
- He, X.; Zhu, Z.Y.; Fung, W.K. Estimation in a Semiparametric model for longitudinal data with unspecified dependence structure. Biometrika 2002, 89, 579–590. [Google Scholar] [CrossRef]
- He, X.M.; Fung, W.K.; Zhu, Z.Y. Robust estimation in a generalized partially linear model for cluster data. J. Am. Stat. Assoc. 2005, 100, 1176–1184. [Google Scholar] [CrossRef]
- Qin, G.; Bai, Y.; Zhu, Z. Robust empirical likelihood inference for generalized partial linear models with longitudinal data. J. Multivar. Anal. 2012, 105, 32–44. [Google Scholar] [CrossRef]
- Chen, B.; Zhou, X.H. Generalized partially linear models for incomplete longitudinal data in the presence of population-Level information. Biometrics 2013, 69, 386–395. [Google Scholar] [CrossRef]
- Zhang, J.; Xue, L. Empirical likelihood inference for generalized partially linear models with longitudinal data. Open J. Stat. 2020, 10, 188–202. [Google Scholar] [CrossRef]
- Hoerl, A.; Kennard, R. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Hoerl, A.; Kennard, R. Ridge regression: Application to nonorthogonal problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Theobald, C.M. Generalization of mean squer error applied to ridge regresion. J. R. Stat. Soc. 1974, 36, 103–106. [Google Scholar]
- Tikhonov, A. On the stability of inverse problems. Proc. USSR Acad. Sci. 1943, 39, 267–288. [Google Scholar]
- Saleh, A.K.M.; Kibria, B.M.G. Performances of some new preliminary test ridge regression estimators and their properties. Commun. Stat.—Theory Methods 1993, 22, 2747–2764. [Google Scholar] [CrossRef]
- Kibria, B.M.G.; Saleh, A.K.M.E. Effect of W,LR and LM tests on the performance of preliminary test ridge regression estimators. J. Jpn. Stat. Soc. 2003, 33, 119–136. [Google Scholar] [CrossRef]
- Kibria, B.M.G.; Saleh, A.K.M.E. Preliminary test ridge regression estimators with student’s /errors and conflicting test-statistics. Metrika 2004, 59, 105–124. [Google Scholar] [CrossRef]
- Arashi, M.; Tabatabaey, S.M.M.; Iranmanesh, A. Improved estimation in stochastic linear models under elliptical symmetry. J. Appl. Probab. Stat. 2010, 5, 145–160. [Google Scholar]
- Bashtian, H.M.; Arashi, M.; Tabatabaey, S.M.M. Using improved estimation strategies to combat multicollinearity. J. Stat. Comput. Simul. 2011, 81, 1773–1797. [Google Scholar] [CrossRef]
- Bashtian, H.M.; Arashi, M.; Tabatabaey, S.M.M. Ridge estimation under the stochastic restriction. Commun. Stat.—Theory Methods 2011, 40, 3711–3747. [Google Scholar] [CrossRef]
- Arashi, M.; Tabatabaey, S.M.M.; Soleimani, H. Simple regression in view of elliptical models. Linear Algebra Its Appl. 2012, 437, 1675–1691. [Google Scholar] [CrossRef]
- Zhang, B.; Horvath, S. Ridge regression based hybrid genetic algorithms for multi-locus quantitative trait mapping. Bioinform. Res. Appl. 2006, 1, 261–272. [Google Scholar] [CrossRef]
- Malo, N.; Libiger, O.; Schork, N. Accommodating linkage disequilibrium in genetic-association analyses via ridge regression. Am. J. Hum. Genet. 2008, 82, 375–385. [Google Scholar] [CrossRef]
- Eliot, M.; Ferguson, J.; Reilly, M.P.; Foulkes, A.S. Ridge regression for longitudinal biomarker data. Int. J. Biostat. 2011, 7, 37. [Google Scholar] [CrossRef]
- Rahmani, M.; Arashi, M.; Mamode Khan, N.; Sunecher, Y. Improved mixed model for longitudinal data analysis using shrinkage method. Math. Sci. 2018, 12, 305–312. [Google Scholar] [CrossRef]
- Taavoni, M.; Arashi, M. Semiparametric ridge regression for longitudinal data. In Proceedings of the 14th Iranian Statistics Conference, Shahrood University of Technology, Shahrood, Iran, 25–27 August 2018. [Google Scholar]
- Qin, G.Y.; Zhu, Z.Y. Robustified maximum likelihood estimation in generalized partial linear mixed model for longitudinal data. Biometrics 2009, 65, 52–59. [Google Scholar] [CrossRef] [PubMed]
- Taavoni, M.; Arashi, M. High-dimensional generalized semiparametric model for longitudinal data. Statistics 2021, 55, 831–850. [Google Scholar] [CrossRef]
- Qin, G.Y.; Zhu, Z.Y. Robust estimation in generalized semiparametric mixed models for longitudinal data. J. Multivar. Anal. 2007, 98, 1658–1683. [Google Scholar] [CrossRef]
- Liang, K.Y.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
- Fan, J.Q.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Wang, H.S.; Li, R.Z.; Tcai, C.L. Tuning parameter selectors for the smoothly clipped absolute deviation method. Biometrika 2007, 94, 553–568. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.S.; Li, B.; Leng, C.L. Shrinkage tuning parameter selection with a diverging number of parameters. J. R. Stat. Soc. Ser. B 2009, 71, 671–683. [Google Scholar] [CrossRef]
- Li, G.R.; Peng, H.; Zhu, L.X. Nonconcave penalized M-estimation with a diverging number of parameters. Stat. Sin. 2011, 21, 391–419. [Google Scholar]
- Zeger, S.L.; Diggle, P.J. Semi-parametric models for longitudinal data with application to CD4 cell numbers in HIV seroconverters. Biometrics 1994, 50, 689–699. [Google Scholar] [CrossRef]
- Wang, N.; Carroll, R.; Lin, X.H. Efficient semiparametric marginal estimation for longitudinal/clustered data. J. Am. Stat. Assoc. 2005, 100, 147–157. [Google Scholar] [CrossRef]
- Schumaker, L.L. Spline Functions; Wiley: New York, NY, USA, 1981. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).