Scale Mixture of Maxwell-Boltzmann Distribution

Abstract

This paper presents a new distribution, the product of the mixture between Maxwell-Boltzmann and a particular case of the generalized gamma distributions. The resulting distribution, called the Scale Mixture Maxwell-Boltzmann, presents greater kurtosis than the recently introduced slash Maxwell-Boltzmann distribution. We obtained closed-form expressions for its probability density and cumulative distribution functions. We studied some of its properties and moments, as well as its skewness and kurtosis coefficients. Parameters were estimated by the moments and maximum likelihood methods, via the Expectation-Maximization algorithm for the latter case. A simulation study was performed to illustrate the parameter recovery. The results of an application to a real data set indicate that the new model performs very well in the presence of outliers compared with other alternatives in the literature.

1. Introduction

The Maxwell-Boltzmann (MB) distribution was introduced by Maxwell [1] to describe the distribution of speeds of molecules at thermal equilibrium and nowadays is widely applied in many fields such as statistical physics, statistical mechanics and accounting theory, among others. The MB distribution has been discussed in many works in the literature, for example, Tyagi and Bhattacharya [2] and Bekker and Roux [3].

Some recent extensions of the MB distribution are discussed, for example, in Sharma et al. [4], Vivekanand et al. [5], Iriarte et al. [6], Dey et al. [7], Sharma et al. [8] and Segovia et al. [9]. Product distributions or independent random variable quotients are of great interest; for example, Shakil et al. [10] studied the $XY$ and $X/Y$ distribution, where X and Y are independent random variables that have MB and Rayleigh distributions respectively.

A random variable V follows the MB distribution with scale parameter $\beta$, denoted as $V\sim MB\left(\beta \right)$, if its probability density function (pdf) and cumulative distribution function (cdf) are given by

$$f_V(v;\beta )=\frac{4{\beta }^{3/2}}{\sqrt{\pi }}{v}^2{e}^{-\beta v^2}\mathrm{a}\mathrm{n}\mathrm{d}{F}_V(v;\beta )=\frac{2}{\sqrt{\pi }}\gamma \left(\frac{3}{2},\beta v^2\right),$$

(1)

respectively, where $v,\beta >0$ and $\gamma (a,v)={\int }_0^v{t}^{a-1}{e}^{-t}dt$ is the incomplete gamma function.

An extension of the MB distribution, called slash Maxwell-Boltzmann (SMB), was proposed by Acitas et al. [11]. The SMB distribution, denoted as $SMB(\beta ,q)$, is defined as

$$Z=\frac{V}{U^{1/q}},q>0,$$

where V and U are independent random variables with MB($\beta$) and $U(0,1)$ distributions, respectively, and $q>0$. As $\beta$ in the MB distribution is a scale parameter, the motivation to define Z is the introduction of a shape parameter q, which makes this distribution more flexible. Note also that the model is parsimonious, being an alternative to traditional models such as the Weibull or gamma distributions, for example. The pdf of Z is

$$f_z(z;\beta ,q)={\displaystyle \frac{2q}{\Gamma (1/2)\beta }}\Gamma \left(\frac{q+3}{2}\right){\left(\frac{z}{\beta }\right)}^{-(1+q)}G\left(z^2;\frac{q+3}{2};{\beta }^2\right),z,\beta ,q>0,$$

where $\Gamma (·)$ denotes the gamma function and G$(·;a;b)$ the cdf of a gamma distribution with shape and scale parameters a and b, respectively.

The main object of this article is to study an extension of the MB distribution with a greater range of the kurtosis coefficient, in order to use this new distribution to model datasets with atypical observations. We employ the slash methodology, as in the SMB version proposed by Acitas et al. [11]. Other authors have successfully applied the slash methodology. To name a few, Reyes et al. [12] obtained a generalization of the Birnbaum-Saunders (BS) distribution and Astorga et al. [13] introduced an extension on the power Muth distribution. In this work, we will show that the new distribution has heavier tails than the SMB distribution. Furthermore, this new distribution can be represented as a mixture of scales that allows us to perform simulation studies and obtain maximum likelihood (ML) estimators by means of the Expectation-Maximization (EM) algorithm.

The paper is organized as follows. Section 2 contains the representation of this model, and we generate the density of the new distribution. We present the scale mixture property, and the closed expressions for pdf, cdf, moments and coefficients of skewness and kurtosis, hazard and survival functions, and the Rényi entropy. Section 3 contains the inference, where we obtain the moments and ML estimators, and the implementation of the EM algorithm. In Section 4 we carry out a simulation study to assess the performance of the ML estimators in finite samples. Section 5 presents an application, comparing the fit of the scale mixture Maxwell–Boltzmann (SMMB) with the SMB, Weibull (W) and BS distributions to a real data set. Finally, Section 6 presents some conclusions.

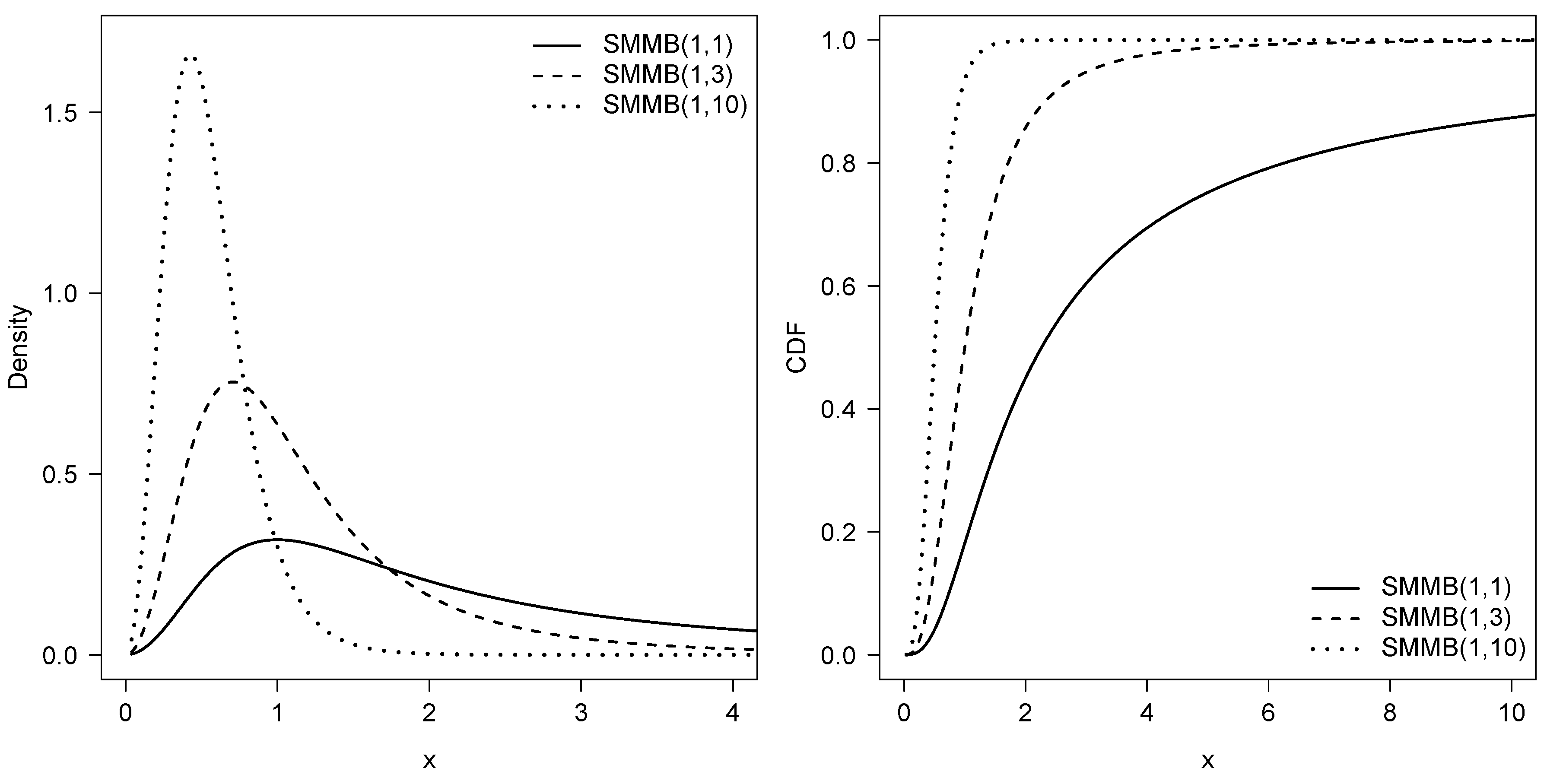
2. Definition and Properties

Our proposal is based on the generalized gamma (GG) distribution introduced by Stacy [14]. The pdf for this model is given in Definition 1.

Definition 1.

A random variable Z follows the three-parameter GG distribution, denoted by $Z\sim GG(a,d,p)$, if its pdf is

$$f_Z(z;a,d,p)=\frac{p{a}^d}{\Gamma \left(\frac{d}{p}\right)}{z}^{d-1}{e}^{-{\left(az\right)}^p},$$

with $a>0$, $d>0$, $p>0$ and $z>0$.

Definition 2.

A random variable X follows a SMMB distribution with scale parameter $\beta >0$ and shape parameter $q>0$, denoted by $X\sim SMMB(\beta ,q)$, if X can be expressed as the ratio

$$X={\displaystyle \frac{V}{W}},$$

(2)

where $V\sim MB\left(\beta \right)$ and $W\sim GG(1,q,2)$, both independent.

The following Proposition presents the pdf for the SMMB model.

Proposition 1.

Let $X\sim SMMB(\beta ,q)$ with $\beta >0$ and $q>0$. Then the pdf of X is

$$\begin{array}{c}\hfill f_X(x;\beta ,q)={\displaystyle \frac{2{\beta }^{3/2}{x}^2}{B\left(\frac{q}{2},\frac{3}{2}\right){\left(1+\beta x^2\right)}^{\frac{q+3}{2}}}},\end{array}$$

where $x>0$ and $B(·,·)$ denotes the beta function.

Proof. 

Using the representation given in (2) and computing the Jacobian transformation, we have that:

$$\left.\begin{array}{cc}X={\displaystyle \frac{V}{W}}& \\ Z=W\end{array}\right\}\Rightarrow \left.\begin{array}{cc}V=XZ& \\ W=Z\end{array}\right\}\Rightarrow J=\left|\begin{array}{cc}{\displaystyle \frac{\partial v}{\partial x}}& {\displaystyle \frac{\partial v}{\partial z}}\\ & \\ {\displaystyle \frac{\partial w}{\partial x}}& {\displaystyle \frac{\partial w}{\partial z}}\end{array}\right|=\left|\begin{array}{cc}z& x\\ 0& 1\end{array}\right|=z.$$

Then,

$$f_{X,Z}(x,z)=\left|J\right|f_{V,W}(xz,z)={\displaystyle \frac{8{\beta }^{3/2}{x}^2}{\sqrt{\pi }\Gamma (q/2)}}{z}^{q+2}\exp \left\{-z(1+\beta x^2)\right\},x>0,z>0.$$

The marginal pdf of X is:

$$f_X(x;\beta ,q)={\displaystyle \frac{8{\beta }^{3/2}{x}^2}{\sqrt{\pi }\Gamma (q/2)}}{\int }_0^{\infty }{z}^{(q+3)-1}\exp \left\{-z(1+\beta x^2)\right\}dz,x>0.$$

(3)

Note that the integrand in (3) is related to the pdf of a GG$\left({(1+\beta x^2)}^{1/2},q+3,2\right)$ distribution. Therefore, the desired result follows.    □

The following proposition presents the cdf of the SMMB model, which is an expression involving the hypergeometric function that is defined by the power series:

$${}_2{F}_1(a,b,c;x)=\sum _{n=0}^{\infty }\frac{{\left(a\right)}_n{\left(b\right)}_n}{{\left(c\right)}_n}\frac{x^n}{n!},$$

where ${\left(a\right)}_n=\left\{\begin{array}{cc}1,\hfill & n=0;\hfill \\ a(a+1)\cdots (a+n-1),\hfill & n>0.\hfill \end{array}\right.$ For more details we refer the reader to Abramowitz and Stegun [15].

Proposition 2.

Let $X\sim SMMB(\beta ,q)$. Then the cdf of X is given by

$$F_X(x;\beta ,q)={\displaystyle \frac{2{\beta }^{3/2}{x}^3}{3B\left(\frac{q}{2},\frac{3}{2}\right)}}{}_2{F}_1\left({\displaystyle \frac{q+3}{2}},{\displaystyle \frac{3}{2}},{\displaystyle \frac{5}{2}};-\beta x^2\right),$$

where $x>0$, $\beta >0$ and $q>0$.

Proof. 

We can write

$$F_X(x;\beta ,q)={\int }_0^x{\displaystyle \frac{2{\beta }^{3/2}{t}^2}{B\left(\frac{q}{2},\frac{3}{2}\right){(1+\beta t^2)}^{\frac{q+3}{2}}}}dt={\displaystyle \frac{2{\beta }^{3/2}}{B\left(\frac{q}{2},\frac{3}{2}\right)}}{\int }_0^x{t}^2{(1+\beta t^2)}^{-\frac{q+3}{2}}dt.$$

Hence, we make the following change of variable $u=t^2$, to obtain

$$F_X(x;\beta ,q)={\displaystyle \frac{{\beta }^{3/2}}{B\left(\frac{q}{2},\frac{3}{2}\right)}}{\int }_0^{x^2}{u}^{\frac{1}{2}}{(1+\beta u)}^{-\frac{q+3}{2}}du.$$

(4)

Using the following result presented by Singh [16] (page 5)

$${\int }_0^t{u}^a{(1+\beta u)}^{b}du={\displaystyle \frac{t^{a+1}}{a+1}}{}_2{F}_1\left(-b,a+1,a+2;-\beta t\right),$$

in Equation (4), the result is shown.    □

Figure 1 shows the pdf and cdf for the SMMB$(\beta =1,q)$, for different values of q.

Remark 1.

For $W\sim GG(1,q,2)$, it is possible to check that $U=W^2\sim G(q/2,1)$, i.e., the traditional gamma distribution with shape parameter $q/2$ and rate 1. It therefore follows, from the properties of the inverse gamma model, that

$$E\left(U^{-1}\right)=\frac{1}{q/2-1}andV\left(U^{-1}\right)=\frac{1}{{(q/2-1)}^2(q/2-2)},ifq>4.$$

Provided that $E\left(U^{-1}\right)\to 0$ and $E\left(V^{-1}\right)\to 0$, as $q\to \infty$, it follows that

$$U^{-1}=\frac{1}{W^2}\stackrel{\mathrm{P}}{\to }0,asq\to \infty ,$$

where $\stackrel{\mathrm{P}}{\to }$ denotes convergence in probability. Equivalently,

$$\frac{1}{W}\stackrel{\mathrm{P}}{\to }0,as q\to \infty .$$

Based on the stochastic representation for the SMMB distribution in Equation (2), it follows that SMMB$(\beta ,q)\stackrel{\mathrm{P}}{\to }0$, as $q\to \infty$.

2.1. Lifetime Analysis

As the SMMB distribution is related to a non-negative and asymmetric variable, it can be used to model survival time data. In this section, the main features of interest in this field are studied. The survival and hazard functions for a SMMB model are provided in Corollaries 1 and 2.

Corollary 1.

Let $X\sim SMMB(\beta ,q)$. Then, the survival function of the X ($R_X$) is given by

$$R_X(x;\beta ,q)={\displaystyle \frac{3B\left(\frac{q}{2},\frac{3}{2}\right)-2{\beta }^{3/2}{x}^3{}_2{F}_1\left(\frac{q+3}{2},\frac{3}{2};\frac{5}{2};-\beta x^2\right)}{3B\left(\frac{q}{2},\frac{3}{2}\right)}},x,\beta ,q>0.$$

Corollary 2.

Let $X\sim SMMB(\beta ,q)$. Then, the hazard function of the X ($h_X$) is given by

$$h_X(x;\beta ,q)={\displaystyle \frac{6{\beta }^{3/2}{x}^2}{B\left(\frac{q}{2},\frac{3}{2}\right){(1+\beta x^2)}^{\frac{q+3}{2}}\left[3B\left(\frac{q}{2},\frac{3}{2}\right)-2{\beta }^{3/2}{x}^3{}_2{F}_1\left(\frac{q+3}{2},\frac{3}{2};\frac{5}{2};-\beta x^2\right)\right]}}.$$

Figure 2 shows the survival and hazard functions. Additionally, we can see that the curve related to the hazard function is unimodal, and that as q grows, the curve has longer tails and extends over a greater range.

Note that considering $\eta \left(t\right):=\frac{f_X^{\prime }\left(t\right)}{f_X\left(t\right)}=\frac{\beta (q+3)t}{1+\beta t^2}-\frac{2}{t}$ for $t>0$, we have ${\eta }^{\prime }\left(t\right)=\frac{-{\beta }^2(q+1)t^4+\beta (q+7)t^2+2}{t^2{(1+\beta t^2)}^2}$. From this we obtain that

$$t^2{(1+\beta t^2)}^2{\eta }^{\prime }\left(t\right)=-{\beta }^2(q+1)t^4+\beta (q+7)t^2+2,$$

which implies that the zeros and signs of the ${\eta }^{\prime }$ are same as those of the polynomial $p\left(t\right):=-{\beta }^2(q+1)t^4+\beta (q+7)t^2+2$.

We note that $t=\sqrt{\frac{q+7}{2\beta (q+1)}}$ is a positive zero of the $p^{\prime }\left(t\right)=2\beta t(-2\beta (q+1)t^2+q+7)$, and $p^{″}\left(\sqrt{\frac{q+7}{2\beta (q+1)}}\right)=-12{\beta }^2(q+1)\frac{q+7}{2\beta (q+1)}+2\beta (q+7)=-4\beta (q+7)<0$. Therefore, at $t=\sqrt{\frac{q+7}{2\beta (q+1)}}$ a maximum is reached, with value: $p\left(\sqrt{\frac{q+7}{2\beta (q+1)}}\right)=\frac{{(q+7)}^2}{4(q+1)}+2>2=p\left(0\right).$ As $t_0=\sqrt{\frac{q+7+\sqrt{q^2+22q+57}}{2\beta (q+1)}}$ is a zero of $p\left(t\right)$, we can conclude that

$${\eta }^{\prime }\left(t\right)>0fort\in (0,t_0)and{\eta }^{\prime }\left(t\right)<0fort\in (t_0,\infty ).$$

On the other hand, if we consider $g^{\prime }\left(t\right)$ defined as in Glaser [17], in our case we have that

$$g^{\prime }\left(t\right)=\frac{(\beta (q+1)t^2-2){(1+\beta t^2)}^{\frac{q+1}{2}}}{t^3}\left[\frac{\sqrt{\pi }\Gamma (q/2)}{4{\beta }^{3/2}\Gamma ((q+3)/2)}-\frac{1}{3}{t}^3{}_2{F}_1(\frac{3}{2},\frac{q+3}{2};\frac{5}{2};-\beta t^2)\right]-1,$$

(5)

where ${}_2{F}_1$ is the hypergeometric function. We note that $g^{\prime }\left(t\right)$ tends to $-\infty$ as t tends to $0^{+}$; and taking $x=\sqrt{\beta }t$, $g^{\prime }\left(t\right)$ it can be rewritten as

$$fq\left(x\right)=\frac{((q+1)x^2-2){(1+x^2)}^{\frac{q+1}{2}}}{x^3}\left[\frac{\sqrt{\pi }\Gamma (q/2)}{4\Gamma \left(\right(q+3)/2)}-\frac{1}{3}{x}^3{}_2{F}_1(\frac{3}{2},\frac{q+3}{2};\frac{5}{2};-x^2)\right]-1,$$

so the number of positive zeros of $g^{\prime }\left(t\right)$ is equal to that of $fq\left(x\right)$. In

Table 1. Specific values of ${}_2{F}_1(\frac{3}{2},\frac{q+3}{2};\frac{5}{2};-\beta t^2)$ for different q values.

q	${}_2{F}_1(\frac{3}{2},\frac{q+3}{2};\frac{5}{2};-\beta t^2)$	q	${}_2{F}_1(\frac{3}{2},\frac{q+3}{2};\frac{5}{2};-\beta t^2)$
1	$\frac{3}{2{\beta }^{3/2}{t}^3}\left[{\tan }^{-1}\left(\sqrt{\beta }t\right)-\frac{\sqrt{\beta }t}{1+\beta t^2}\right]$	5	$\frac{1}{16{\beta }^{3/2}{t}^3}\left[3{\tan }^{-1}\left(\sqrt{\beta }t\right)+\frac{\sqrt{\beta }t(\beta t^2+3)(3\beta t^2-1)}{{(1+\beta t^2)}^3}\right]$
2	$1/{(1+\beta t^2)}^{3/2}$	6	$\frac{4\beta t^2(2\beta t^2+7)+35}{35{(1+\beta t^2)}^{7/2}}$
3	$\frac{3}{8{\beta }^{3/2}{t}^3}\left[{\tan }^{-1}\left(\sqrt{\beta }t\right)+\frac{\sqrt{\beta }t(\beta t^2-1)}{{(1+\beta t^2)}^2}\right]$	7	$\frac{1}{128{\beta }^{3/2}{t}^3}\left[\frac{\sqrt{\beta }t(\beta t^2(5\beta t^2(3\beta t^2-11)+73)-15)}{{(1+\beta t^2)}^4}+15{\tan }^{-1}\left(\sqrt{\beta }t\right)\right]$
4	$\frac{5+2\beta t^2}{5{(1+\beta t^2)}^{5/2}}$	8	$\frac{105+2\beta t^2(4\beta t^2(2\beta t^2+9)+63)}{105{(1+\beta t^2)}^{9/2}}$

, the hypergeometric function ${}_2{F}_1(\frac{3}{2},\frac{q+3}{2};\frac{5}{2};-\beta t^2)$ is shown for different values of q (see Weisstein [18]).

Based on $g^{\prime }\left(t\right)$ graphs of the function defined in (5) for different q values shown in Figure 3, and using Theorem (d) part (i) in Glaser [17], we obtain that failure time density has an inverted bathtub shape.

The following proposition presents the scale mixture property for the SMMB distribution.

Proposition 3.

If $X|V=v\sim MB(v^2\beta )$ and $V\sim GG(1,q,2)$, is obtained $X\sim SMMB(\beta ,q)$.

Proof. 

We have that the joint function of $(X,V)$ is $f_{X,V}(x,v)=f_{X|V}\left(x\right|v)f_V\left(v\right)$, therefore, $f_X\left(x\right)$ is given by

$$f_X(x;\beta ,q)={\int }_0^{\infty }{f}_{X,V}(x,v)dv=\frac{8{\beta }^{\frac{3}{2}}{x}^2}{\sqrt{\pi }\Gamma \left(\frac{q}{2}\right)}{\int }_0^{\infty }{v}^{(q+3)-1}\exp \left\{{\left[-v{(1+\beta x^2)}^{\frac{1}{2}}\right]}^2\right\}dx.$$

Note that this function corresponds to the pdf of a random variable with GG$({(1+\beta x^2)}^{\frac{1}{2}},q+3,2)$ distribution. Then the integral is equal to 1, consequently we have that

$$f_X(x;\beta ,q)={\displaystyle \frac{2{\beta }^{3/2}{x}^2}{B\left(\frac{q}{2},\frac{3}{2}\right){\left(1+\beta x^2\right)}^{\frac{q+3}{2}}}},$$

where $x>0$ and B is the beta function, also $X\sim SMMB(\beta ,q).$    □

Remark 2.

Proposition 1 shows that the SMMB pdf has a closed expression, as occurs with its respective cdf given in Proposition 2. Proposition 3 shows that a SMMB distribution can also be obtained as a scale mixture of a MB and a GG distribution. This property is very important for generating random numbers and the implementation of the EM algorithm.

2.2. Moments

In this subsection, the following proposition shows the computation of the moments of a random variable with SMMB$(\beta ,q)$ distribution. Hence, it also displays the coefficients of skewness and kurtosis. For this, the following lemma will be useful.

Lemma 1.

Let $W\sim GG(1,q,2)$ with $q>0$. For $r>0$ and $r<q$, then the r-th moment of $W^{-r}$ is given by

$$E\left(W^{-r}\right)={\displaystyle \frac{\Gamma \left(\frac{q-r}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}}.$$

(6)

Proof. 

By definition,

$$E\left(W^{-r}\right)={\displaystyle \frac{2}{\Gamma (q/2)}}{\int }_0^{\infty }{w}^{-r-q-1}{e}^{-w^2}dw,$$

and hence the result follows making the variable transformation $u=w^2$.    □

In the next proposition, the moments of a SMMB model are given:

Proposition 4.

Let $X\sim SMMB(\beta ,q)$. Then the r-th moment of X is given by

$${\mu }_r=E\left(X^r\right)={\displaystyle \frac{2}{\sqrt{\pi }{\beta }^{r/2}}}\Gamma \left({\displaystyle \frac{r+3}{2}}\right){\displaystyle \frac{\Gamma \left({\displaystyle \frac{q-r}{2}}\right)}{\Gamma \left({\displaystyle \frac{q}{2}}\right)}}.$$

In particular,

$${\mu }_1={\displaystyle \frac{2}{\sqrt{\pi \beta }}}{\displaystyle \frac{\Gamma \left(\frac{q-1}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}},q>1,{\mu }_2={\displaystyle \frac{3}{2\beta }}{\displaystyle \frac{\Gamma \left(\frac{q-2}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}},q>2,$$

$${\mu }_3={\displaystyle \frac{4}{\sqrt{\pi }{\beta }^{3/2}}}{\displaystyle \frac{\Gamma \left(\frac{q-3}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}},q>3,{\mu }_4={\displaystyle \frac{15}{4{\beta }^2}}{\displaystyle \frac{\Gamma \left(\frac{q-4}{2}\right)}{\Gamma \left(\frac{q}{2}\right)}},q>4,$$

$$V\left(X\right)={\displaystyle \frac{3\pi \Gamma \left(\frac{q-2}{2}\right)\Gamma \left(\frac{q}{2}\right)-8{\left[\Gamma \left(\frac{q-2}{2}\right)\right]}^2}{2\pi \beta {\left[\Gamma \left(\frac{q}{2}\right)\right]}^2}},q>2.$$

Proof. 

Using the stochastic representation for the distribution given in (2), we have that

$$E\left(X^r\right)=E\left[{\left({\displaystyle \frac{V}{W}}\right)}^r\right]=E\left(V^r\right)E\left(W^{-r}\right)={\displaystyle \frac{2}{\sqrt{\pi }{\beta }^{r/2}}}\Gamma \left({\displaystyle \frac{r+3}{2}}\right){\displaystyle \frac{\Gamma \left({\displaystyle \frac{q-r}{2}}\right)}{\Gamma \left({\displaystyle \frac{q}{2}}\right)}},$$

where $E\left(V^r\right)={\displaystyle \frac{2}{\sqrt{\pi }{\beta }^{r/2}}}\Gamma \left({\displaystyle \frac{r+3}{2}}\right)$ is the r-th moment of a MB$\left(\beta \right)$ distribution and $E\left(W^{-r}\right)$ was given in (6).    □

The asymmetry and kurtosis coefficients of the SMMB model are presented in the following proposition.

Proposition 5.

Let $X\sim SMMB(\beta ,q)$ with $\beta >0$. Then the asymmetry and kurtosis coefficients of X are

$$\begin{array}{cc}\hfill \sqrt{{\beta }_1}& ={\displaystyle \frac{2\sqrt{2}\left[4\pi a_{31}{a}_{02}-9\pi a_{12}{a}_{21}{a}_{01}+16a_{13}\right]}{{\left[27{\pi }^3{a}_{23}{a}_{03}-216{\pi }^2{a}_{22}{a}_{02}{a}_{12}+576\pi a_{21}{a}_{01}{a}_{14}-512a_{16}\right]}^{1/2}}},for q>3and\hfill \\ \hfill {\beta }_2& ={\displaystyle \frac{\left[15{\pi }^2{a}_{41}{a}_{03}-128\pi a_{11}{a}_{31}{a}_{02}+136\pi a_{12}{a}_{21}{a}_{01}-192a_{14}\right]}{\left[9{\pi }^2{a}_{22}{a}_{02}-48\pi a_{21}{a}_{01}{a}_{12}+64a_{14}\right]}},for q>4,\hfill \end{array}$$

respectively, where $a_{ij}={\left[\Gamma \left({\displaystyle \frac{q-i}{2}}\right)\right]}^j$.

Proof. 

Recall that by definition

$$\begin{array}{c}\hfill \sqrt{{\beta }_1}=\frac{E\left[{(X-E\left(X\right))}^3\right]}{{\left(V\left(X\right)\right)}^{3/2}}=\frac{{\mu }_3-3{\mu }_1{\mu }_2+2{\mu }_1^3}{{\left({\mu }_2-{\mu }_1^2\right)}^{3/2}},and\\ \hfill {\beta }_2=\frac{E\left[{(X-E\left(X\right))}^4\right]}{{\left(V\left(X\right)\right)}^2}=\frac{{\mu }_4-4{\mu }_1{\mu }_3+6{\mu }_1^2{\mu }_2-3{\mu }_1^4}{{\left({\mu }_2-{\mu }_1^2\right)}^2},\end{array}$$

where ${\mu }_1$, ${\mu }_2$, ${\mu }_3$ and ${\mu }_4$ were given in Proposition 4. The result follows replacing the corresponding terms.    □

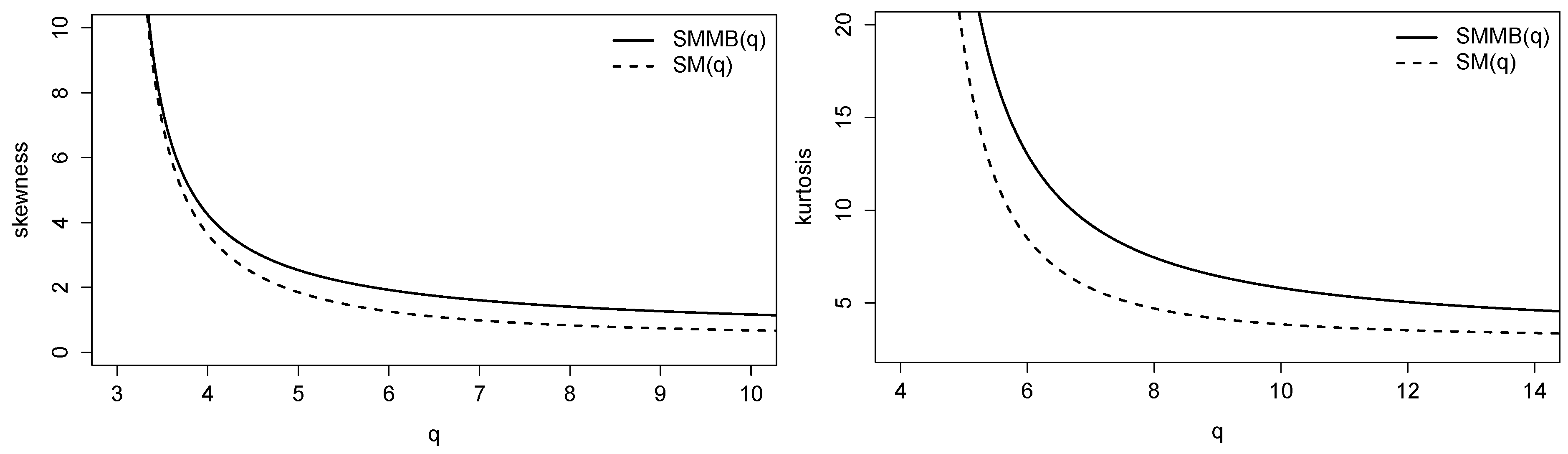
Figure 4 shows the skewness and kurtosis coefficients for the SMMB and SMB distributions in terms of the shape parameter q. Note that both the skewness and kurtosis coefficients become smaller as q increases.

2.3. Order Statistics

Given a random sample of size n of $X\sim$ SMMB$(\beta ,q)$ and denoting by $X_{\left(j\right)}$ the j-th order statistics, $j\in \{1,\cdots ,n\}$. The following proposition presents the pdf for order statistics from the SMMB model.

Proposition 6.

The pdf of $X_{\left(j\right)}$ is

$$\begin{array}{c}\hfill f_{X_{\left(j\right)}}\left(x\right)={\displaystyle \frac{3n!}{(j-1)!(n-j)!x{(1-\beta x^2)}^{\frac{q+3}{2}}}}{\left[{\displaystyle \frac{2{\beta }^{3/2}{x}^3}{3B\left(\frac{q}{2},\frac{3}{2}\right)}}\right]}^j{}_2{F}_1^{j-1}\left({\displaystyle \frac{q+3}{2}},{\displaystyle \frac{3}{2}};{\displaystyle \frac{5}{2}};-\beta x^2\right)\\ \hfill \times {\left[1-{\displaystyle \frac{2{\beta }^{3/2}{x}^3}{3B\left(\frac{q}{2},\frac{3}{2}\right)}}{}_2{F}_1\left({\displaystyle \frac{q+3}{2}},{\displaystyle \frac{3}{2}};{\displaystyle \frac{5}{2}};-\beta x^2\right)\right]}^{n-j}.\end{array}$$

In particular, the pdf of the minimum, $X_{\left(1\right)}$, is

$$f_{X_{\left(1\right)}}\left(x\right)={\displaystyle \frac{2n{\beta }^{3/2}{x}^2}{{(1-\beta x^2)}^{\frac{q+3}{2}}B\left(\frac{q}{2},\frac{3}{2}\right)}}{\left[1-{\displaystyle \frac{2{\beta }^{3/2}{x}^3}{3B\left(\frac{q}{2},\frac{3}{2}\right)}}{}_2{F}_1\left({\displaystyle \frac{q+3}{2}},{\displaystyle \frac{3}{2}};{\displaystyle \frac{5}{2}};-\beta x^2\right)\right]}^{n-1},$$

and the pdf of the maximum, $X_{\left(n\right)}$, is

$$f_{X_{\left(n\right)}}\left(x\right)={\displaystyle \frac{3n}{x{(1-\beta x^2)}^{\frac{q+3}{2}}}}{\left[{\displaystyle \frac{2{\beta }^{3/2}{x}^3}{3B\left(\frac{q}{2},\frac{3}{2}\right)}}\right]}^n{}_2{F}_1^{n-1}\left({\displaystyle \frac{q+3}{2}},{\displaystyle \frac{3}{2}};{\displaystyle \frac{5}{2}};-\beta x^2\right).$$

Proof. 

Since we are dealing with an absolutely continuous model, the pdf of the j-th order statistics is obtained by applying

$$f_{X_{\left(j\right)}}\left(x\right)={\displaystyle \frac{n!}{(j-1)!(n-j)!}}f\left(x\right){\left[F\left(x\right)\right]}^{j-1}{\left[1-F\left(x\right)\right]}^{n-j},$$

where F and f are the cdf and pdf of the SMMB distribution.    □

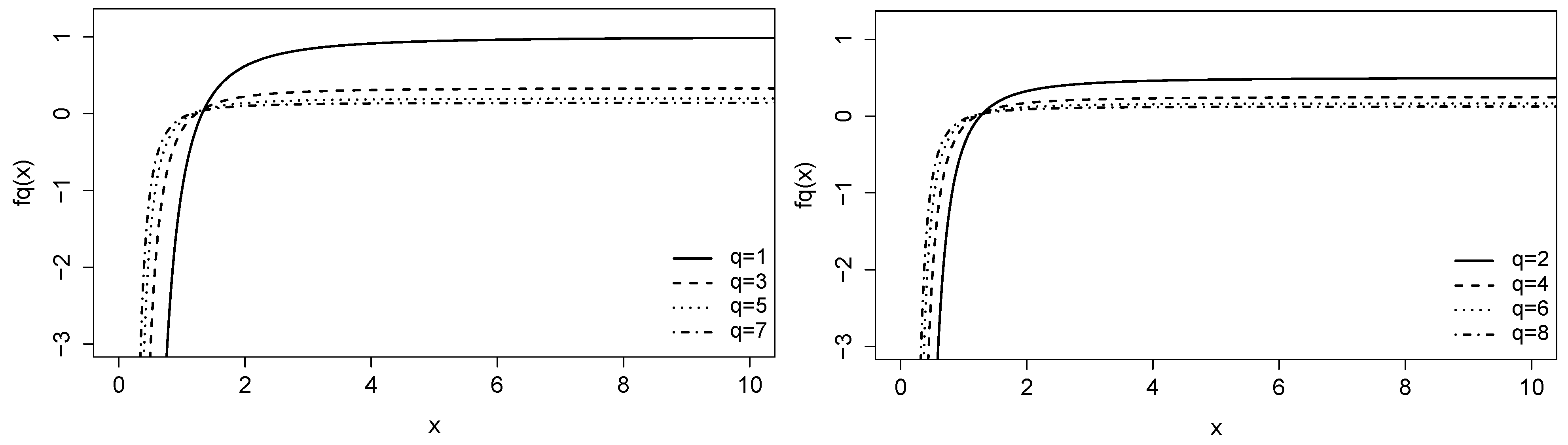
2.4. Entropy

The following results show the Rényi and Shannon entropy of a random variable $X\sim$ SMMB$(\beta ,q)$. Such results are commonly related with a state of disorder or uncertainty, and are used in different fields such as thermodynamics, statistical physics and information theory.

Proposition 7.

The Rényi ($R_{\gamma }$) entropy for a random variable $X\sim SMMB(\beta ,q)$ and values of $\gamma >0$ and $\gamma \ne 1$ is as follows

$$R_{\gamma }\left(X\right)=\frac{1}{1-\gamma }\left[(\gamma -1)\log \left(2\sqrt{\beta }\right)+\psi \left(\frac{2\gamma +1}{2}\right)+\psi \left(\frac{\gamma q+\gamma -1}{2}\right)+\gamma \kappa \left(q\right)-\psi \left(\gamma {\rho }_3\right)\right],$$

where ${\rho }_i=\frac{q+i}{2}$, with $i=0,3$, $\psi (·)$ is the digamma function and $\kappa \left(q\right)=\psi \left({\rho }_3\right)-\psi \left({\rho }_0\right)-\psi \left(1.5\right)$.

Proof. 

Calculating the Rényi entropy by its definition we have:

$$R_{\gamma }\left(X\right)=\frac{1}{1-\gamma }\log \left[{\int }_0^{\infty }{f}_X{(x;\beta ,q)}^{\gamma }dx\right]=\frac{1}{1-\gamma }\log \left[{\displaystyle {\int }_0^{\infty }{\displaystyle \frac{2^{\gamma }{\beta }^{3\gamma /2}{x}^{2\gamma }}{B^{\gamma }\left(\frac{q}{2},\frac{3}{2}\right){\left(1+\beta x^2\right)}^{\frac{\gamma (q+3)}{2}}}}dx}\right],$$

then considering the change of variable $u=\beta x^2$, we obtain the result.    □

Corollary 3.

Let $X\sim SMMB(\beta ,q)$, the Shannon (S) entropy for random variable X is given by

$$S\left(X\right)={\rho }_3{\psi }^{\prime }\left({\rho }_3\right)-{\rho }_1{\psi }^{\prime }\left({\rho }_0\right)+\psi \left({\rho }_0\right)+\psi \left(1.5\right)-\psi \left({\rho }_3\right)-{\psi }^{\prime }\left(1.5\right)-\log \left(2\sqrt{\beta }\right),$$

(7)

where ${\rho }_i=\frac{q+i}{2}$, with $i=0,1,3.$

Proof. 

The Shannon entropy is obtained for the limit case $\gamma \to 1$ in the definition for the Renyi entropy $R_{\gamma }\left(X\right)$. Therefore, applying L’Hopital’s rule, ${\displaystyle \underset{\gamma \to 1}{\lim }{R}_{\gamma }\left(X\right)}$, the result is obtained.    □

3. Inference

In this section, we present the estimators for the parameters $\beta$ and q of the SMMB distribution obtained by the moments and maximum likelihood methods.

3.1. Moments Estimators

The following proposition presents the moment estimators for the SMMB distribution.

Proposition 8.

Let $X_1,\cdots ,X_n$ be a random sample from $X\sim SMMB(\beta ,q)$. Then the moments estimators $({\widehat{\beta }}_M,{\widehat{q}}_M)$ of $(\beta ,q)$ for $q>2$ are as follows

$${\widehat{\beta }}_M={\left({\displaystyle \frac{2\Gamma \left(\frac{{\widehat{q}}_M-1}{2}\right)}{\sqrt{\pi }\overline{X}\Gamma \left(\frac{{\widehat{q}}_M}{2}\right)}}\right)}^2,$$

(8)

$$8\overline{X^2}{\Gamma }^2\left(\frac{{\widehat{q}}_M-1}{2}\right)-3\pi {\overline{X}}^2\Gamma \left(\frac{{\widehat{q}}_M}{2}\right)\Gamma \left(\frac{{\widehat{q}}_M-2}{2}\right)=0,$$

(9)

where (9) is solved for ${\widehat{q}}_M$ numerically, then the value of ${\widehat{q}}_M$ found is replaced in (8) and ${\widehat{\beta }}_M$ is obtained.

Proof. 

From Proposition 4 and using the first two equations, and following the moments method, we have

$$\overline{X}={\displaystyle \frac{2\Gamma \left(\frac{q-1}{2}\right)}{\sqrt{\pi \beta }\Gamma \left(\frac{q}{2}\right)}},\overline{X^2}={\displaystyle \frac{3\Gamma \left(\frac{q-2}{2}\right)}{2\beta \Gamma \left(\frac{q}{2}\right)}}.$$

Solving the first equation above for $\beta$ we obtain ${\widehat{\beta }}_M$ given in (8). Substituting ${\widehat{\beta }}_M$ in the second equation above, we obtain the result given in (9).    □

3.2. Maximum Likelihood Estimator

Let $X_1,...,X_n$ be a random sample from $X\sim$ SMMB$(\beta ,q)$. Then the log-likelihood function is

$$\ell (\beta ,q)=n\log \left(2\sqrt{{\beta }^3}\right)+2\sum _{i=1}^n\log x_i-n\log B\left(\frac{q}{2},\frac{3}{2}\right)-\left(\frac{q+3}{2}\right)\sum _{i=1}^n\log \left(1+\beta x_i^2\right).$$

(10)

The score equations are given by

$$\begin{array}{c}\hfill \beta (q+3)\sum _{i=1}^n\frac{x_i^2}{1+\beta x_i^2}=3n,\end{array}$$

(11)

$$\begin{array}{c}\hfill n\psi \left(\frac{q}{2}\right)+\sum _{i=1}^n\log (1+\beta x_i^2)=n\psi \left(\frac{q+3}{2}\right).\end{array}$$

(12)

Solutions for Equations (11) and (12) can be obtained by using numerical procedures such as the Newton-Raphson algorithm. An alternative to obtain the ML estimates is by maximizing (10) using the optim subroutine in the R software package [19].

3.3. EM-Algorithm

Employing the stochastic representation of the SMMB model given in Proposition 2, we can apply an iterative method to find maximum likelihood estimators based on the EM algorithm (see Dempster [20]). This will greatly simplify the estimation process, since the steps of the algorithm that we will develop will both have a closed form (both E and M steps). We next present Lemma 2, which will be useful in the application of the EM algorithm.

Lemma 2.

Let $X\sim Gamma(k,\sigma )$ with $k>0$ shape parameter and $\sigma >0$ rate parameter, where density function is $f_X\left(x\right)=\frac{1}{\Gamma \left(k\right)}{\sigma }^k{x}^{k-1}{e}^{-\sigma x}$, $x>0$. Then

1 .

$X^k\sim GG\left({\sigma }^m,\frac{k}{m},\frac{1}{m}\right)$, $m>0$ with pdf given in (1).

2 .

$E\left[\log \right(X\left)\right]=\psi \left(k\right)-\log \sigma$.

In this context, the SMMB distribution can also be written employing the hierarchical representation defined in Proposition 3:

$$X_i\mid Z_i=z_i\sim MB\left(z_i^2\beta \right)and{Z}_i\sim GG(1,q,2),i=1,\dots ,n.$$

In this scenario, we have that joint pdf $X_i$ and $Z_i$ is

$$f_{X_i,Z_i}(x_i,z_i\mid \mathbf{\theta })=f_{X_i\mid Z_i}(x_i\mid z_i,\mathbf{\theta })·f_{Z_i}(z_i\mid \mathbf{\theta })={\displaystyle \frac{8{\beta }^{3/2}{x}_i^2{z}_i^{q+2}}{\sqrt{\pi }\Gamma \left(\frac{q}{2}\right)}}\exp \{-z_i^2(1+\beta x_i^2)\},$$

(13)

where $\mathbf{\theta }={(\beta ,q)}^{\top }$ is the vector of parameters. We have that $\mathit{x}={(x_1,\dots ,x_n)}^{\top }$ and $\mathit{z}={(z_1,\dots ,z_n)}^{\top }$ represent the observed and unobserved data, respectively. The complete data are given by ${\mathit{x}}_c={({\mathit{x}}^{\top },{\mathit{z}}^{\top })}^{\top }$. Furthermore, we denote ${\ell }_c(\mathbf{\theta }\mid {\mathit{x}}_c)$ and $Q(\mathbf{\theta }\mid \widehat{\mathbf{\theta }})=\mathbb{E}[{\ell }_c\left(\mathbf{\theta }\right|{\mathit{x}}_c)\mid \mathit{x},\widehat{\mathbf{\theta }}]$ as the log-likelihood complete function and its expected conditional value over the observed data. From (13), we see directly that the complete log-likelihood function is given by

$$\begin{array}{cc}\hfill {\ell }_c(\mathbf{\theta }\mid {\mathit{x}}_c)& =\sum _{i=1}^n\log f(x_i,z_i|\theta )\hfill \\ \hfill & =(q+2)\sum _{i=1}^n\log z_i+{\displaystyle \frac{3n}{2}}\log \beta -n\log \Gamma \left(\frac{q}{2}\right)-\sum _{i=1}^n{z}_i^2(1+\beta x_i^2)+C,\hfill \end{array}$$

where C is a constant that does not depend on $\mathbf{\theta }$. To obtain $Q(\mathbf{\theta }\mid \widehat{\mathbf{\theta }})$, we need to calculate $\mathbb{E}[z_i^2\mid x_i,\mathbf{\theta }]$ and $\mathbb{E}[\log \left(z_i\right)\mid x_i,\mathbf{\theta }]$. From Equation (13), it is direct that

$$f(z_i\mid x_i,\mathbf{\theta })\propto z_i^{q+2}\exp \{-z_i^2(1+\beta x_i^2)\}\propto z_i^{(q+3)-1}\exp \{-{\left[z_i{(1+\beta x_i^2)}^{1/2}\right]}^2\}.$$

(14)

Therefore, we conclude that $Z_i|x_i,\mathbf{\theta }\sim GG\left({(1+\beta x_i^2)}^{1/2},q+3,2\right)$. Then, using Lemma 2 it follows

$$\begin{array}{cc}\hfill \mathbb{E}[Z_i^2\mid x_i,\mathbf{\theta }]& ={\left[{\left(1+\beta x_i^2\right)}^{-1/2}\right]}^2{\displaystyle \frac{\Gamma \left(\frac{(q+3)+2}{2}\right)}{\Gamma \left(\frac{q+3}{2}\right)}}={\displaystyle \frac{q+3}{2(1+\beta x_i^2)}},\mathrm{and}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \mathbb{E}\left[\log \left(Z_i\right)\right|x_i,\mathbf{\theta }]& ={\displaystyle \frac{1}{2}}\psi \left({\displaystyle \frac{q+3}{2}}\right)-{\displaystyle \frac{1}{2}}\log (1+\beta x_i^2).\hfill \end{array}$$

(16)

Thus,

$$Q(\mathbf{\theta }\mid \widehat{\mathbf{\theta }})=(q+2)\sum _{i=1}^n\widehat{\log \left(z_i\right)}+{\displaystyle \frac{3n}{2}}\log \beta -n\log \Gamma \left(\frac{q}{2}\right)-\sum _{i=1}^n\widehat{z_i^2}(1+\beta x_i^2),$$

(17)

where $\widehat{z_i^2}=\mathbb{E}[Z_i^2\mid x_i,\mathbf{\theta }=\widehat{\mathbf{\theta }}]$ and $\widehat{\log \left(z_i\right)}=\mathbb{E}[\log \left(Z_i\right)\mid x_i,\mathbf{\theta }=\widehat{\mathbf{\theta }}]$ are given in (15) and (16), respectively. Hence, partially differentiating with respect to $\beta$ and q and equalising to zero, we obtain the following expressions:

$$\begin{array}{c}\hfill \widehat{\beta }={\displaystyle \frac{3n}{2{\sum }_{i=1}^n\widehat{z_i^2}{x}_i^2}}\mathrm{and}\widehat{q}=2{\psi }^{-1}\left(2·\overline{\widehat{\log \left(z\right)}}\right),\end{array}$$

where $\overline{\widehat{\log \left(z\right)}}$ is the mean of ${\widehat{\log \left(z_i\right)}}^{\prime }s$ and ${\psi }^{-1}(·)$ is the inverse of the digamma function. It is possible to check that $\partial Q\left(\mathbf{\theta }\right|\widehat{\mathbf{\theta })}/\partial \beta$ and $\partial Q\left(\mathbf{\theta }\right|\widehat{\mathbf{\theta })}/\partial q$ are increasing functions in $\beta$ and q, respectively. This guarantees that $\widehat{\beta }$ and $\widehat{q}$ are the unique maximum for this function. Thus, the EM algorithm is reduced to the following steps:

• Step-E: For $i=1,\dots ,n$ compute

  $${\widehat{z_i^2}}^{(k+1)}={\displaystyle \frac{q^{\left(k\right)}+3}{2\left(1+{\beta }^{\left(k\right)}{x}_i^2\right)}}\mathrm{a}\mathrm{n}\mathrm{d}{\widehat{\log \left(z_i\right)}}^{(k+1)}={\displaystyle \frac{1}{2}}\left[\psi \left({\displaystyle \frac{q^{\left(k\right)}+3}{2}}\right)-\log \left(1+{\beta }^{\left(k\right)}{x}_i^2\right)\right].$$
• Step-M: Update the parameters as

  $${\widehat{\beta }}^{(k+1)}={\displaystyle \frac{3n}{2{\sum }_{i=1}^n{\widehat{z_i^2}}^{(k+1)}{x}_i^2}}\mathrm{a}\mathrm{n}\mathrm{d}{\widehat{q}}^{(k+1)}=2{\psi }^{-1}\left(2·\overline{{\widehat{\log \left(z\right)}}^{(k+1)}}\right).$$

Steps E and M are repeated until we reach a defined convergence criterion. For instance, we specify that the difference between the successively obtained values should be inferior to a pre-established value, i.e.,

$$max\left(\left|{\beta }^{\left(k\right)}-{\beta }^{(k-1)}\right|,\left|q^{\left(k\right)}-q^{(k-1)}\right|\right)<ϵ,withϵ={10}^{-4}.$$

3.4. Fisher’s Information Matrix

Let us now consider $X\sim SMMB(\beta ,q)$. For a single observation x of X, the log-likelihood function for $\mathbf{\theta }={(\beta ,q)}^{\top }$ is given by

$$\ell \left(\mathbf{\theta }\right)=\log \left(2\right)+\frac{3}{2}\log \left(\beta \right)+2\log \left(x\right)-\log \left(B\left(\frac{q}{2},\frac{3}{2}\right)\right)-\left(\frac{q+3}{2}\right)\log (1+\beta x^2).$$

The corresponding first and second partial derivatives of the log-likelihood function are derived in Appendix A. It can be shown that the Fisher’s information matrix, denoted by $I_F(·)$, for the $SMMB$ distribution is provided by

$$I_F\left(\mathbf{\theta }\right)=\left(\begin{array}{cc}\frac{3q}{2{\beta }^2(q+5)}& \frac{3}{2\beta (q+3)}\\ \frac{3}{2\beta (q+3)}& \frac{1}{4}\left({\psi }^{\prime }\left(\frac{q+3}{2}\right)-{\psi }^{\prime }\left(\frac{q}{2}\right)\right)\end{array}\right),$$

where ${\psi }^{\prime }(·)$ is the trigamma function. Hence, for large samples, the ML estimator, $\widehat{\mathbf{\theta }}$, of $\mathbf{\theta }$ is asymptotically normal bivariate, i.e.,

$$\sqrt{n}\left(\widehat{\mathbf{\theta }}-\mathbf{\theta }\right)\stackrel{\mathcal{D}}{⟶}{N}_2(\mathbf{0},{\left[I_F\left(\mathbf{\theta }\right)\right]}^{-1}),\mathrm{a}\mathrm{s} n\to +\infty .$$

As a result, the asymptotic covariance matrix of the ML estimators $\widehat{\mathbf{\theta }}$ is the inverse of Fisher’s information matrix $I_F\left(\mathbf{\theta }\right)$. Since the parameters are unknown, the observed information matrix is usually considered, where the unknown parameters are estimated by ML. Note that asymptotic confidence intervals for $\beta$ and q with confidence level $100(1-\alpha )\%$ should be constructed as

$$\begin{array}{cc}\hfill CI\left(\beta ,100(1-\alpha )\%\right)& =\widehat{\beta }\mp z_{\alpha /2}\times \widehat{se}\left(\widehat{\beta }\right)\mathrm{a}\mathrm{n}\mathrm{d}\hfill \\ \hfill CI\left(q,100(1-\alpha )\%\right)& =\widehat{q}\mp z_{\alpha /2}\times \widehat{se}\left(\widehat{q}\right),\hfill \end{array}$$

where $\widehat{se}\left(\widehat{\beta }\right)$ and $\widehat{se}\left(\widehat{q}\right)$ are the root of the first and second element of the diagonal of ${\left[I_F\left(\mathbf{\theta }\right)\right]}^{-1}$, respectively, and $z_{\alpha /2}$ satisfies $P(Z>z_{\alpha /2})=\alpha /2$, with Z a random variable with standard normal distribution.

4. Simulation Study

In this section, we present a simulation study to assess the performance of the EM algorithm for the estimators of $\beta$ and q in the SMMB model. We consider 1000 replicates of three sample sizes generated using the SMMB model: $n=50$, 100 and 200. By using the stochastic representation given in Equation (2), it is possible to generate random numbers for the SMMB($\beta ,q$) distribution, which leads to the following algorithm:

1.

Generate $P_i\sim {\chi }_3^2$ (chi squared with 3 degrees of freedom), $i=1,\cdots ,n.$

2.

Compute $V_i=\sqrt{{\displaystyle \frac{P_i}{2\beta }}}$, $i=1,\cdots ,n.$

3.

Generate $W_i\sim GG(1,q,2)$, $i=1,\cdots ,n.$

4.

Compute $X_i={\displaystyle \frac{V_i}{W_i}}$$i=1,\cdots ,n.$

It then follows that $X\sim SMMB(\beta ,q)$.

For each sample generated, ML estimates were calculated using the EM algorithm. In

Table 2. Simulation study for different combinations of parameters for the SMMB($\beta ,q$) model.

True Value			$\mathit{n}=50$				$\mathit{n}=100$				$\mathit{n}=200$
$\mathbf{\beta }$	$\mathit{q}$	Estim.	Bias	SE	RMSE	CP	Bias	SE	RMSE	CP	Bias	SE	RMSE	CP
3	1	$\widehat{\beta }$	0.113	1.294	1.334	90.1	0.074	0.897	0.925	92.1	0.027	0.623	0.661	92.2
		$\widehat{q}$	0.057	0.216	0.232	96.5	0.024	0.145	0.153	95.0	0.016	0.102	0.111	94.1
	2	$\widehat{\beta }$	0.065	1.290	1.335	90.1	0.039	0.896	0.921	92.5	0.019	0.628	0.665	91.8
		$\widehat{q}$	0.211	0.613	0.709	95.9	0.090	0.388	0.426	95.5	0.052	0.265	0.296	94.9
	3	$\widehat{\beta }$	0.040	1.396	1.444	89.6	0.015	0.966	0.996	92.1	0.009	0.679	0.709	92.0
		$\widehat{q}$	0.524	1.329	1.625	95.7	0.226	0.758	0.892	95.1	0.115	0.495	0.558	95.2
5	1	$\widehat{\beta }$	0.188	2.155	2.222	90.1	0.122	1.495	1.541	92.1	0.044	1.038	1.102	92.2
		$\widehat{q}$	0.057	0.216	0.232	96.5	0.024	0.145	0.153	95.1	0.016	0.102	0.111	94.1
	2	$\widehat{\beta }$	0.106	2.149	2.224	90.1	0.064	1.493	1.534	92.5	0.030	1.046	1.108	91.8
		$\widehat{q}$	0.211	0.613	0.709	95.9	0.091	0.388	0.426	95.5	0.053	0.265	0.296	94.9
	3	$\widehat{\beta }$	0.061	2.324	2.410	89.5	0.024	1.610	1.659	92.1	0.014	1.132	1.182	92.0
		$\widehat{q}$	0.567	1.478	2.120	95.7	0.227	0.758	0.892	95.1	0.116	0.495	0.558	95.2
7	1	$\widehat{\beta }$	0.262	3.017	3.111	90.1	0.169	2.093	2.157	92.1	0.061	1.453	1.542	92.2
		$\widehat{q}$	0.057	0.216	0.232	96.5	0.024	0.145	0.153	95.1	0.016	0.102	0.111	94.1
	2	$\widehat{\beta }$	0.148	3.008	3.113	90.1	0.088	2.090	2.148	92.5	0.041	1.464	1.550	91.8
		$\widehat{q}$	0.211	0.613	0.709	95.9	0.091	0.388	0.426	95.5	0.053	0.265	0.296	94.9
	3	$\widehat{\beta }$	0.078	3.251	3.378	89.4	0.033	2.254	2.322	92.1	0.019	1.585	1.655	92.0
		$\widehat{q}$	0.610	1.566	2.519	95.7	0.227	0.758	0.892	95.1	0.116	0.495	0.559	95.2

the empirical bias (Bias), the mean of the standard errors (SE), the root of the empirical mean squared error (RMSE) and the 95% coverage probability (CP) based on the asymptotic distribution for ML estimators are given for the parameter estimators. We conclude that the ML estimates have desirable properties. Bias is reasonable and decreases as the sample size increases. As expected, SE and RMSE terms are closer when the sample size increases, which suggests that the SE estimates are well estimated.

5. Application

In this section, we present an illustration using a real dataset in order to compare the fit of the SMMB model with those of the SMB, W and BS distributions. These models are compared using the Akaike Information Criterion (AIC) (see Akaike [21]), and the Bayesian Information Criterion (BIC), introduced in Schwarz [22]. The data set is related to zinc (Zn) concentrations in 86 soil samples obtained from the Mining Department, Universidad de Atacama, Chile; it is available in Reyes et al. [23].

Table 3. Descriptive statistics for zinc data set.

n	$\overline{\mathit{x}}$	s	${\mathit{b}}_1$	${\mathit{b}}_2$
86	96.721	148.434	5.088	32.342

provides the descriptive summary for the data, including the sample asymmetry coefficient $b_1$ and sample kurtosis coefficient $b_2$.

Figure 5 and Table 3 show the type of situation in which the SMMB distribution is appropriate: distribution with a very heavy tail (see the typical boxplot), and high sample kurtosis coefficient ($b_2=32.3421$).

Table 4. Estimates, SE in parenthesis, log-likelihood, AIC and BIC values for zinc concentration data.

Parameters	BS	W	SMB	SMMB
$\alpha$	1.3038 (0.0995)	0.0125 (0.0047)	3.4666 (0.1226)	-
$\beta$	50.8841 (5.8694)	0.9632 (0.0701)	-	0.0007 (0.0002)
q	-	-	0.4077 (0.1827)	1.6506 (0.3079)
log-likelihood	−484.7785	−479.0418	−471.7718	−469.5580
AIC	973.557	962.084	947.544	943.1161
BIC	978.466	966.992	952.452	948.0248

shows the results for the fit of the BS, W, SMB and SMMB models. Note that the SMMB model provides a better fit than the others since its AIC and BIC values are less than the rest of models. Finally, Figure 6 shows the qq-plot comparing the quantiles for the zinc dataset with the quantiles for the fitted SMMB model, and the empirical cdf for the zinc data compared with the estimated cdf for the fitted SMMB, SMB, BS and W distributions. The first plot suggests that the SMMB model is appropriated for this data and the second confirms that the SMMB model provides a better fit for this data than the other models considered.

6. Conclusions

In this paper, we introduce a new model with a greater kurtosis than the SMB distribution. To estimate the parameters, we use the EM algorithm, obtaining acceptable results for the ML estimators. In the application to a real data set, it shows a better fit than other known models. Some additional characteristics are:

• SMMB distribution has a more flexible kurtosis coefficient than the SMB distribution, as is clearly shown in Figure 4 (Right panel)
• Closed expressions are given for its main characteristics: pdf, cdf, moments and coefficients of skewness and kurtosis.
• We discuss the hazard and survival functions, which are in terms of the hypergeometric function and the order statistics of the SMMB model.
• Employing the scale mixture representation, the EM algorithm was implemented to calculate the ML estimators.
• The results of a simulation study indicate that, with a reasonable sample size, an acceptable bias is obtained.
• An illustration with real data shows that the SMMB model achieves a better fit in terms of the AIC and BIC criteria.

In future research, we plan to extend the proposed model to create a multivariate scale mixture of the Maxwell–Boltzmann model [24] to handle multivariate/clustered and positive data in order to explore other estimation methods for the model [25].