Abstract
By using stochastic modeling, the investigation of the energy and wave characteristics of novel structures that develop in the sea and ocean currents becomes one of the most important advancements in the generation of sustainable and renewable energy. Theoretical examinations of random nonlinear Kundu–Mukherjee–Naskar (RNKMN) structures have become recommended in a random mode. The two-dimensional RNKMN equation permits exact and solved solutions that give rise to solitonic structures with adaptable properties. The obtained stochastic waves, under the influence of random water currents, represent a dynamically controlled system. It has been demonstrated that the stochastic parameter modulates wave forcing and produces energy wave collapse accompanied by medium turbulence. The fundamental wave characteristics establish an exact pattern for describing sea and ocean waves.
Keywords:
stochastic modeling; stochastic waves; mathematical solver; spatio-temporal modeling; stochastic solutions; wave collapsing; sea and ocean wave applications MSC:
35C05; 35R60; 60H30; 35Q55
1. Introduction
Different types of nonlinear partial differential equations (NPDEs) can be used to describe a variety of complex nonlinear physical processes [1,2,3]. In fact, NPDEs have been the most extensively researched objects in various fields of applied science, such as molecular biology, optical fiber communications, chemical engineering, superfluids, solid-state physics, plasma physics, and many others [4,5,6]. The topic of optical solitons is critical for the exploration of soliton propagation via nonlinear fiber. One of the most well-known governing equations for the dynamics of optical solitons is the nonlinear Schrödinger equation (NLSE), which plays a crucial role in the dynamics of nonlinear effects in fiber optic communications. The NLSEs, which disclose solitary-type solutions, have become the primary representative method for defining wave behaviors in numerous vital applications [7,8,9,10].
Stochastic nonlinear partial differential equations (SNPDEs) are foundational models of physical systems with unpredictable inputs, interactions, or environments. Indeed, SNPDEs perform an important role in various fields of natural sciences [11,12,13,14]. Therefore, finding solutions to SNPDEs is a prominent research topic. Brownian motion (Wiener process) is a classic stochastic process that is both a martingale and a Markov process [15]. In dispersive environments, Brownian motion is frequently employed as a stochastic process. It is used in biology, kinematics, new physics, engineering, and the study of flower pollen in water [16,17,18]. Indeed, there is a vital link between stochastic processes and partial differential equations. There are numerous processes that depend on particles moving stochastically in random potentials. As previously discovered, noise can be incorporated directly into the equation when examining wave propagation using stochastic nonlinear dispersive equations.
In this work, we demonstrate how the newly extended NLSE can be understood in terms of Brownian motion. Specifically, we investigate the newly extended stochastic NLSE (SNLSE) with Kerr law nonlinearity, which is also known as the stochastic nonlinear Kundu–Mukherjee–Naskar (SKMN) equation [19,20,21,22]:
where represents the nonlinear wave envelope and * refers to the complex conjugate. The first and second terms represent, respectively, the temporal evolution of the wave and the disturbance of the dispersion. The parameter is distinct from conventional Kerr law nonlinearity. The noise is a Brownian time derivative of , and denotes the noise amplitude [23]. Hole waves, oceanic rogue waves, bending of light beams, and erbium atoms are all described by Equation (1) [21,22].
This paper investigates certain aspects of the influence of noise, in the Itô sense, on the SKMN equation. This is an enormously broad and fascinating field, with active study in a variety of directions. This topic’s ability to mix methods from both classical and stochastic analyses is one of its most intriguing aspects [24]. We employ a robust solver [25] to reveal some new stochastic solutions for the SKMN equation. These solutions demonstrate various important physics related to hole waves, oceanic rogue waves, bending of light beams and erbium atoms, and many others.
The organization of this article is as follows. Section 2 presents the SKMN in the Itô sense and its corresponding potential. Section 3 presents the closed form of solutions to the SKMN equation using a powerful solver. Section 4 provides a physical interpretation of the solution to the SKMN equation. The results are then summarized in Section 5.
2. The New Stochastic Solutions
The traveling wave solution [21] in Equation (1) is used as follows:
Here, and represent the soliton frequencies in the x- and y-directions, is the phase constant of the soliton, and represents the wave number. and denote the inverse width of the soliton along the x- and y-directions, and denotes the soliton velocity. Equation (1) is reduced to two equations in the form of
for real and imaginary parts:
In order to formulate the system of equations (real and imaginary), one can take the expectation on both sides of Equation (3), yielding
Indeed, , and then Equation (5) becomes
By solving Equation (4), the dispersion-constrained equation for Equation (6) reads:
To find exact solutions to Equation (6), we integrate it, and after some algebraic steps, it is transformed into an energy equation with the potential
By solving Equation (8), an exact solution to Equation (5) is expressed as:
3. Closed-Form Solutions
4. Physical Interpretation
In this work, we study the system of the Kundu–Mukherjee–Naskar model, which is a powerful nonlinear model that exhibits the characteristics of the dynamics of hole and oceanic waves. Namely, we consider this model via the Brownian motion process. This process is defined as a stochastic process, which is continuous in time. For more properties of the Brownian motion process , see [15].
In order to obtain some unique stochastic solutions to this model with multiplicative noise in the Itô sense, we use the unified solver approach. This theoretical solver process has been applied to identify some new and brief random solutions to the RNKMN model with multiplicative random parameters, resulting in Solutions (9), (11), (13), and (15), which exhibited a diversity of solitonic and dissipative structures. The obtained results account for a number of intriguing wave phenomena with applications in water wave physics and engineering. In fact, the provided solutions included blow-up and shock structure solutions to the nonlinear system, in addition to bright, rational explosive, breather, shock-like, explosively dissipated, and dark solitons.
The model with the noise term and random function reduces to Equation (6). The expectation of (3) with transforms the equation into a probability density function that is solved to yield several important solutions. Using Matlab Release 18 [26], we plot 2D, 3D, and contour graphs to explain the wave structures for some chosen solutions to Equation (6) with appropriate parametric values, i.e., .
Solution (9) expresses a set of random solitonic depictions, as shown in Figure 1. Figure 1a,b present the effect of the intensive randomness coefficient on the structure, amplitude, bandwidth, and energy. Figure 1b shows that with increasing time t, the influence of randomness increases along with the rate of wave collapse. It was noted that near-complete collapse occurs at . By increasing , we found that both wave amplitude and width decreased and the wave began to collapse, as shown in Figure 1c.
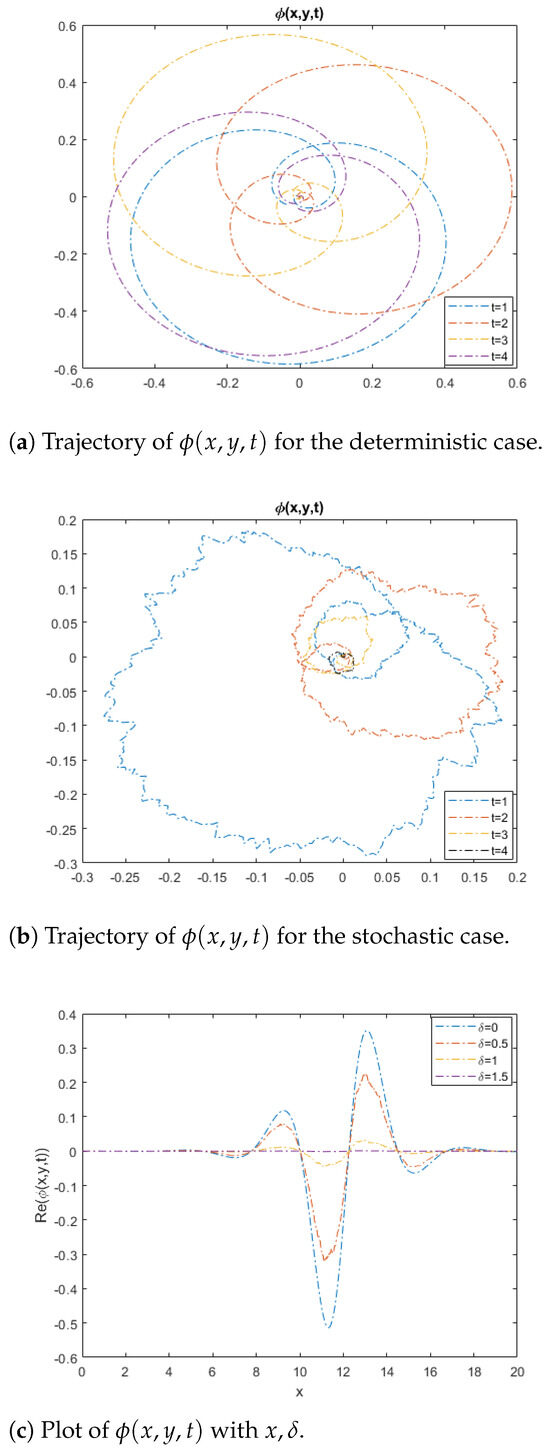
Figure 1.
A set of random solitonic depictions of .
In the same context, it was found that the dark solution (15), which exhibits a dissipative wave, is affected by time t and the random coefficient , as shown in Figure 2. By increasing t, the rate of collapse of the dissipative wave increased, as shown in Figure 2b. Also, the parameter caused the wave to collapse and transform into a superwave with a small amplitude, as shown in Figure 2c. In the absence of random effects, the studied solutions are of great importance due to their different solitary characteristics, some of which we aim to highlight. For example, Solution (9) yielded breather waves and both localized and super solitons, as shown in Figure 3. Solution (13) formed two types of applicable waves: the first was a shock-like soliton and the second was a winged soliton, as shown in Figure 4. Figure 4a,b depicts the overlap between the solitonic and dissipative waves, which is dependent on the system parameters.
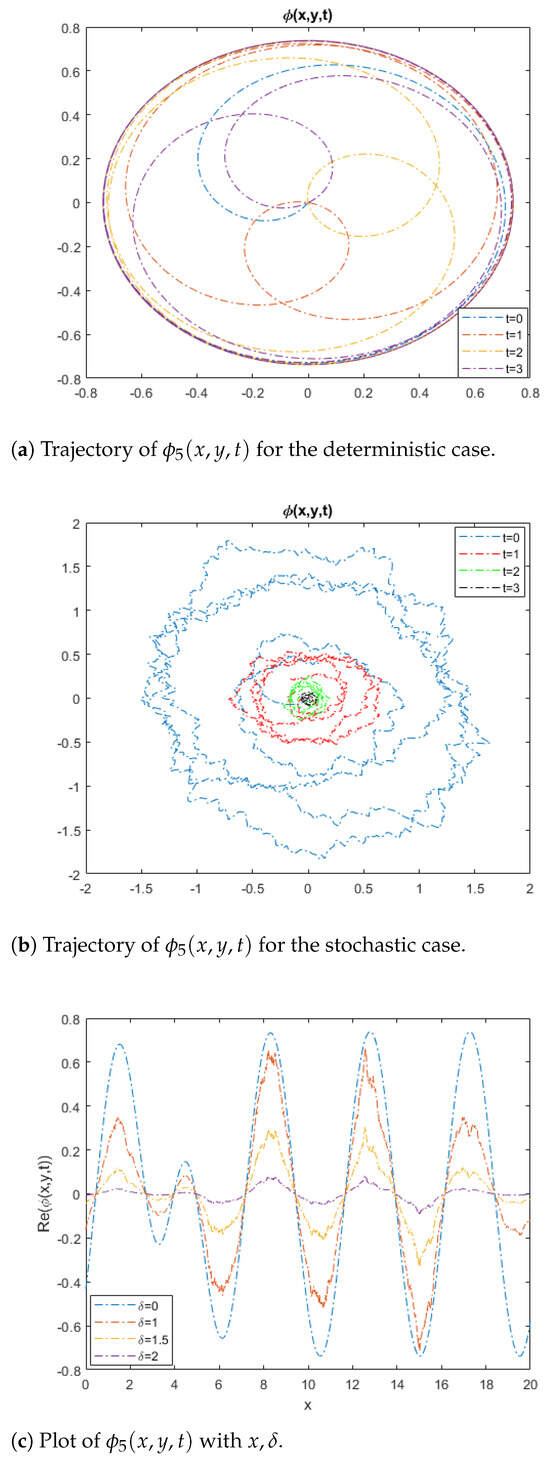
Figure 2.
A set of random solitonic depictions of .
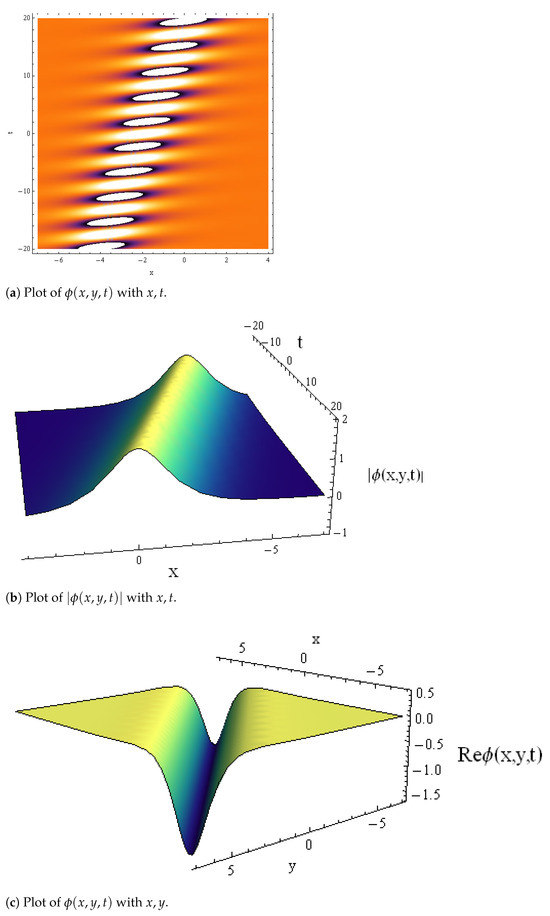
Figure 3.
A set of solitonic depictions of .
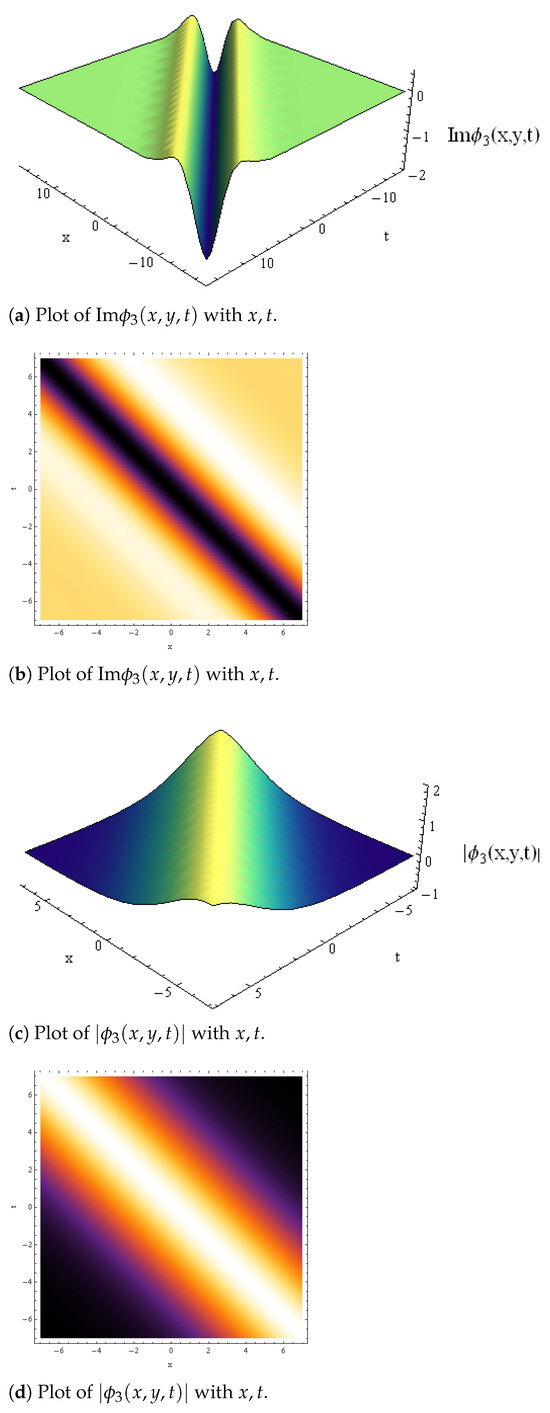
Figure 4.
A set of solitonic depictions of .
On the other hand, Solution (15) is considered one of the most useful physical applications in the study of dissipative and explosive waves. Figure 5a,b show the formation of the dissipated oscillatory waves with time. By varying x, the oscillatory form turned into a rational explosive structure with high energy. Finally, Figure 6a,b depict a dissipative blow-up wave.
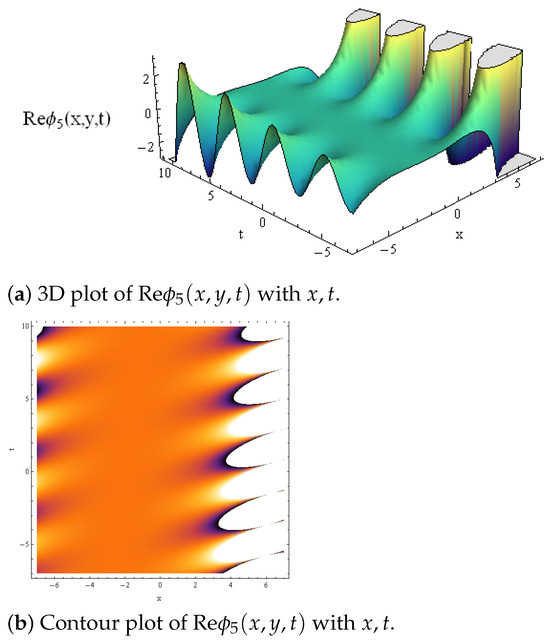
Figure 5.
A set of solitonic structural of .
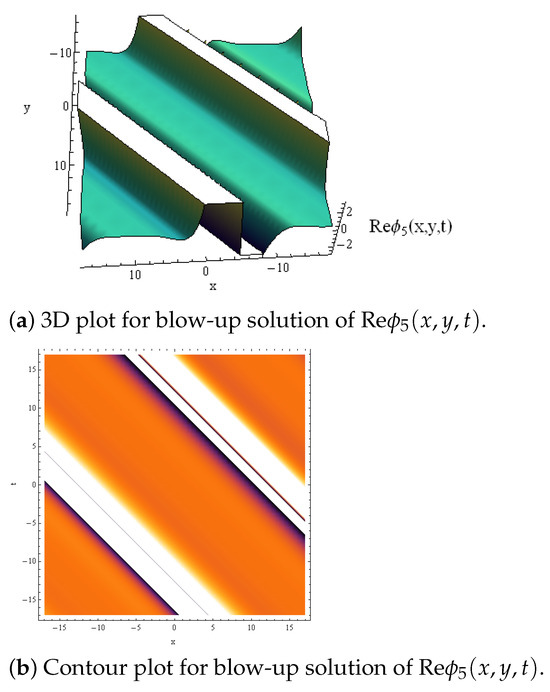
Figure 6.
Plot of Re with .
In fact, the results of random waves exhibiting the properties of stochastic pulses obtained in this work represent great progress in explaining physical phenomena with decaying and damping characteristics that can cause a sharp decrease in wave amplitude and dissipation coefficients. They are consistent with many of the observations made in various fields, such as electrostatic waves in fiber optics, space plasma, and deep ocean water waves propagating in random environments [20,27,28,29]. If the stochastic properties of the random pulse are neglected, our results are consistent with previous work on solitonic and shock solutions [19,20,21]. We also provided a precise description of the explosive, explosive-shock, and dissipative solutions of shock-like solitons, in addition to the winged soliton solutions. This highlights the accuracy and importance of the method used in this work [18,29,30,31].
In summary, the merits of the stochastic structures of the RNKMN model with the noise term inspired the dynamical energy properties of the obtained solitary and dissipative waves.
5. Conclusions
We implemented a unified solver to solve the RNKMN equation. Significant wave characteristics for exact solitary, oscillatory shock, breather, and super soliton waves were examined in the RNKMN equation. The modulations of stochastic parameters on the obtained solution amplitude and energy were investigated. It was noted that the stochastic effects can demonstrate some amendments in collapsing dissipative and explosive water waves. This theoretical investigation could be used in sea and ocean wave applications. Our goal is to expand this approach to include decaying and damped characteristic dispersion and dissipation nonlinear equations in future work. It is also necessary to investigate the explosive, explosive-shock, and dissipative solutions of our model under fractal random environmental conditions.
Author Contributions
E.K.E.-S.: Conceptualization, Software, Formal analysis, Writing—review and editing. N.F.A.: Conceptualization, Data curation, Writing—original draft. M.A.E.A.: Conceptualization, Software, Formal analysis, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The Deputyship for Research & Innovation, Ministry of Education, Saudi Arabia, funded this research work under project number 445-9-428.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education, Saudi Arabia, for funding this research work through project number 445-9-428.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Malik, H.K.; Srivastava, R.; Kumar, S.; Singh, D. Small amplitude dust acoustic solitary wave in magnetized two ion temperature plasma. J. Taibah Univ. Sci. 2020, 14, 417–422. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Kaur, L. Optical solitons for nonlinear Schrödinger equation in the normal dispersive regimes. Optik 2019, 184, 428–435. [Google Scholar] [CrossRef]
- Younis, M.; Ali, S.; Mahmood, S.A. Solitons for compound KdV Burgers equation with variable coefficients and power law nonlinearity. Nonlinear Dyn. 2015, 81, 1191–1196. [Google Scholar] [CrossRef]
- Abdelwahed, H.G.; Abdelrahman, M.A.E. New nonlinear periodic, solitonic, dissipative waveforms for modified-Kadomstev-Petviashvili-equation in nonthermal positron plasma. Results Phys. 2020, 19, 103393. [Google Scholar] [CrossRef]
- Singh, S.V.; Lakhina, G.S. Ion-acoustic supersolitons in the presence of non-thermal electrons. Commun. Nonlinear Sci. Numer. Simul. 2015, 23, 274–281. [Google Scholar] [CrossRef]
- Abdelwahed, H.G. Nonlinearity contributions on critical MKP equation. J. Taibah Univ. Sci. 2020, 14, 777–782. [Google Scholar] [CrossRef]
- Nakkeeran, K. Bright and dark optical solitons in fiber media with higher-order effects. Chaos Solitons Fractals 2002, 13, 673–679. [Google Scholar] [CrossRef]
- Triki, H.; Bensalem, C.; Biswas, A.; Khan, S.; Zhou, Q.; Adesanya, S.; Moshokoa, S.P.; Belic, M. Self-similar optical solitons with continuous-wave background in a quadratic-cubic non-centrosymmetric waveguide. Opt. Commun. 2019, 437, 392–398. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Triki, H. Soliton solutions of the cubic-quintic nonlinear Schrödinger equation with variable coefficients. Rom. J. Phys. 2016, 61, 360–366. [Google Scholar]
- Wazwaz, A.M. Bright and dark optical solitons for (2+1)-dimensional Schrödinger (NLS) equations in the anomalous dispersion regimes and the normal dispersive regimes. Optik 2019, 192, 162948. [Google Scholar] [CrossRef]
- ⌀ksendal, B. Stochastic Differential Equations: An Introduction with Applications, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Macías-Díaz, J.E.; Raza, A.; Ahmed, N.; Rafiq, M. Analysis of a nonstandard computer method to simulate a nonlinear stochastic epidemiological model of coronavirus-like diseases. Comput. Methods Programs Biomed. 2021, 204, 106054. [Google Scholar] [CrossRef] [PubMed]
- Mirzaee, F.; Rezaei, S.; Samadyar, N. Numerical solution of two-dimensional stochastic time-fractional sine-Gordon equation on non-rectangular domains using finite difference and meshfree methods. Eng. Anal. Bound. Elem. 2021, 127, 53–63. [Google Scholar] [CrossRef]
- Rafiq, M.; Ahmadian, A.; Raza, A.; Baleanu, D.; Ahsan, M.S.; Abdul Sathar, M.H. Numerical control measures of stochastic malaria epidemic model. Comput. Mater. Contin. 2020, 65, 33–51. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S.E. Brownian Motion and Stochastic Calculus, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Pishro-Nik, H. Introduction to Probability, Statistics and Random Processes; Kappa Research, LLC: Sunderland, MA, USA, 2014. [Google Scholar]
- Raza, A.; Arif, M.S.; Rafiq, M. A reliable numerical analysis for stochastic gonorrhea epidemic model with treatment effect. Int. J. Biomath. 2019, 12, 1950072. [Google Scholar] [CrossRef]
- Raza, A.; Arif, M.S.; Rafiq, M. A reliable numerical analysis for stochastic dengue epidemic model with incubation period of virus. Adv. Differ. Equ. 2019, 2019, 32. [Google Scholar] [CrossRef]
- Kundu, A.; Mukherjee, A.; Naskar, T. Modelling rogue waves through exact dynamical lump soliton controlled by ocean currents. Proc. R. Soc. A 2014, 470, 20130576. [Google Scholar] [CrossRef]
- Wen, X. Higher-order rational solutions for the (2+1)-dimensional KMN equation. Proc. Rom. Acad. Ser. A 2017, 18, 191–198. [Google Scholar]
- Ekici, M.; Sonmezoglua, A.; Biswas, A.; Belic, M.R. Optical solitons in (2+1)-Dimensions with Kundu-Mukherjee-Naskar equation by extended trial function scheme. Chin. J. Phys. 2019, 57, 72–77. [Google Scholar] [CrossRef]
- Biswas, A.; Yildirim, Y.; Yasar, E.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with quadraticcubic nonlinearity using a couple of strategic algorithms. Chin. J. Phys. 2018, 56, 1990–1998. [Google Scholar] [CrossRef]
- Alkhidhr, H.A.; Abdelwahed, H.G.; Abdelrahman, M.A.E.; Alghanim, S. Some solutions for a stochastic NLSE in the unstable and higher order dispersive environments. Results Phys. 2022, 34, 105242. [Google Scholar] [CrossRef]
- Fedrizzi, E. Partial Differential Equation and Noise. Ph.D. Thesis, Université Paris Diderot, Paris, France, 2012. [Google Scholar]
- Alomair, R.A.; Hassan, S.Z.; Abdelrahman, M.A.E. A new structure of solutions to the coupled nonlinear Maccari’s systems in plasma physics. AIMS Math. 2022, 7, 8588–8606. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/support/search.html?q=plots&page=1 (accessed on 4 November 2023).
- Almutairi, A.; El-Shewy, E.K.; Amin, A.H.; Abdelrahman, M.A.E. New solitary electrostatic structures for Zakharov model in subsonic limit for solar-wind. Results Phys. 2022, 37, 105521. [Google Scholar] [CrossRef]
- Abdelwahed, H.G.; El-Shewy, E.K.; Alghanim, S.; Abdelrahman, M.A.E. On the physical fractional modulations on Langmuir plasma structures. Fractal Fract. 2022, 6, 430. [Google Scholar] [CrossRef]
- Biondini, G.; El, G.A.; Hoefer, M.A.; Miller, P.D. Dispersive hydrodynamics: Preface. Phys. D 2016, 333, 1–5. [Google Scholar] [CrossRef]
- Chang, J.J.; Engels, P.; Hoefer, M.A. Formation of dispersive shock waves by merging and splitting Bose-Einstein condensates. Phys. Rev. Lett. 2008, 101, 170404. [Google Scholar] [CrossRef]
- Guan, W.Y.; Li, B.Q. New observation on the breather for a generalized nonlinear Schrödinger system with two higher-order dispersion operators in inhomogeneous optical fiber. Optik 2019, 181, 853–861. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).