On Fixed-Point Equations Involving Geraghty-Type Contractions with Solution to Integral Equation

Abstract

In this study, the authors verify fixed-point results for Geraghty contractions with a restricted co-domain of the auxiliary function in the context of generalized metric structure, namely the $S_b$-metric space. This new idea of defining Geraghty contraction for self-operators generalizes a large number of previously published, closely related works on the presence and uniqueness of a fixed point in $S_b$-metric space. Also, the outcomes are achieved by removing the continuity constraint of self-operators. We also provide examples to elaborate on the obtained results and an application to the integral equation to illustrate the significance in the literature.

1. Introduction

The development of other sciences depends heavily on mathematics, and the natural sciences are intimately interconnected. As a result, mathematicians are constantly attempting to create methods and systems that will enable other fields to advance. When it comes to helping mathematicians solve models in partial and ordinary differential equations developed by physicists, engineers, or chemists, one of the most effective tools at their disposal is the fixed-point methodology in metric spaces having a symmetric property. Additionally, the fixed-point theory is still regarded as a vital tool in the advancement of research in numerous fields and disciplines, including dynamical systems (and chaos), functional analysis, economics, logic programming, artificial intelligence, differential equations, topology, and game theory.

It is important to remember that the first mathematical discovery to focus on fixed points (FPs) for mapping under particular kinds of contraction conditions was Banach’s contraction theorem (BCT) [1]. Mathematicians started extending the Banach contraction theorem in a variety of ways because of the significance of fixed points. Some generalized the Banach contraction condition in numerous ways, while others extended metric spaces to new spaces and expanded the Banach contraction theory to new forms. For example, the concept of metric space is generalized to b-metric space [2], S-metric space [3] and these two generalizations of metric space are combined to introduce the concept of $S_b$-metric space [4,5,6]. Furthermore, in order to provide novel fixed-point results, others have introduced more generic contraction conditions.

Utilizing an auxiliary function $g:[0,\infty )\to [0,1)$ with the condition $\underset{n\to \infty }{lim}g\left(t_n\right)=1$ gives $\underset{n\to \infty }{lim}{t}_n=0$. Geraghty [7] introduced the Geraghty contraction, an intriguing contraction condition, in 1973 and illustrated certain FPs under this condition by extending BCT into a complete metric space (CMS). Numerous authors have dedicated a great deal of attention to Geraghty’s results. In metric-like space, Aydi et al. [8] examined FP theorems for a new type of Geraghty contractions, Karapinar et al. [9] expanded the theory in generalized metric structure, namely b-metric-like-space, Wang et al. [10] presented intriguing results pertaining to FP consequences through the notion of Geraghty contraction-type maps in $G_b$—metric spaces, and very recently, Alam et al. [11] solved a two-point boundary value problem introducing rational-type Geraghty contraction.

Wang et al. [10] obtained the following result by generalizing the result obtained by Karapinar et al. [9].

Theorem 1

([10]). Let T be a mapping defined on X, where $(X,G_b)$ is a complete $G_b$-metric space. Let $g:[0,\infty )⟶[0,\frac{1}{b}),b\ge 1$ be such that

$$G_b(Tu,Tv,Tv)\le g\left(M(u,v)\right)M(u,v),$$

for all $u,v\in X$, where $M(u,v)=G_b(u,v,v)+|G_b(u,Tu,Tu)-G_b(v,Tv,Tv)|$ and g satisfies $\underset{n\to \infty }{lim}g\left(p_n\right)=\frac{1}{b}\Rightarrow \underset{n\to \infty }{lim}{p}_n=0$. Then, T has a distinct fixed point $x\in X$.

Following Geraghty [7] and Wang et al. [10], we explored new Geraghty types of contractions in the context of $S_b$-metric space. The auxiliary function, which is used to define the first contraction, has a restricted co-domain and a limiting condition that is different from the limiting condition of Geraghty. We demonstrate that the self-operators that fulfill this contraction need to have only one fixed point within the framework of $S_b$-metric spaces. Additionally, examples are provided that explain the obtained outcomes, and a utilization of the integral equation demonstrates how significant they are in the literature. The primary goal of this work includes assisting young researchers by providing a framework for Geraghty-type outcomes in $S_b$-metric space and demonstrating that there is still an opportunity for many more researchers to explore this intriguing area with its vast potential for applications.

2. Preliminaries

We now look over several definitions, illustrations, and results that are pertinent to understanding this work.

Definition 1

([6]). Suppose X is a nonempty set. Let $b\in \mathbb{R}$ and $b\ge 1$. Let $S_b:X^3⟶[0,+\infty )$ be a mapping satisfying the properties listed below:

(i)

$S_b(p,q,r)>0$, for all $p,q,r\in X$ with $p\ne q\ne r$;

(ii)

$S_b(p,q,r)=0$, if and only if $p=q=r$;

(iii)

$S_b(p,q,r)\le b[S_b(p,p,t)+S_b(q,q,t)+S_b(r,r,t)]$, for all $p,q,r,t\in X$.

Then, the mapping $S_b$ is called an $S_b$-metric and the pair $(X,S_b)$ is called an $S_b$-metric space for $b\ge 1$.

Definition 2

([4]). An $S_b$-metric $S_b$ for $b\ge 1$ is called symmetric if

$$S_b(p,p,q)=S_b(q,q,p),forallp,q\in X.$$

Lemma 1

([6]). In any $S_b$-metric space $(X,S_b)$ for $b\ge 1$, we have

$$S_b(p,p,q)\le b{S}_b(q,q,p)and{S}_b(q,q,p)\le b{S}_b(p,p,q),forallp,q\in X.$$

Lemma 2

([6]). In any $S_b$-metric space $(X,S_b)$ for $b\ge 1$, we have

$$S_b(p,p,q)\le 2b{S}_b(p,p,r)+b^2{S}_b(r,r,q),forallp,q,r\in X.$$

Definition 3

([6]). In an $S_b$-metric space $(X,S_b)$ for $b\ge 1$, the sequence $\left\{p_n\right\}$ in X is said to be:

(i)

Convergent to the point $p\in X$, if for any given $\epsilon >0$, there exists $n_0\in \mathbb{N}$ such that $S(p_n,p_n,p)<\epsilon$ or $S(p,p,p_n)<\epsilon$, for all $n\ge n_0$, and it is denoted by $\underset{n\to \infty }{lim}{p}_n=p$.

(ii)

A Cauchy sequence if, for some given $\epsilon >0$, we can find some $n_0\in \mathbb{N}$ such that $S(p_n,p_n,p_m)<\epsilon$, for each $m,n\ge n_0$.

Definition 4

([6]). A complete $S_b$-metric space $(X,S_b)$ for $b\ge 1$ is that space in which every Cauchy sequence in X is convergent in X.

Now, we recall the following collections of functions with examples. Let $\mathcal{G}=\left\{g:[0,\infty )\to [0,1)\right\}$ be the set of all those functions g with the condition $\underset{n\to \infty }{lim}g\left(p_n\right)=1$⇒$\underset{n\to \infty }{lim}{p}_n=0$ and $\mathfrak{G}=\left\{g:[0,\infty )\to [0,\frac{1}{b^2})\right\}$ be the set of all those functions g with the condition $li{m}_{n\to \infty }g\left(p_n\right)=\frac{1}{b^2}$⇒$\underset{n\to \infty }{lim}{p}_n=0$, where $b\ge 1$.

Example 1.

Let

$$g\left(t\right)=\left\{\begin{array}{cc}\frac{1}{1+2t},\hfill & t>0;\hfill \\ \frac{1}{3},\hfill & t=0.\hfill \end{array}\right.$$

Then, $g\in \mathcal{G}$.

Example 2.

Let

$$g\left(t\right)=\left\{\begin{array}{cc}\frac{1}{b^2}{e}^{-t},\hfill & t>0;\hfill \\ \frac{1}{b^2+1},\hfill & t=0.\hfill \end{array}\right.$$

Then, $g\in \mathfrak{G}$.

3. Main Results

We begin our main outcome with the following theorem.

Theorem 2.

Let A be a self-mapping in a complete $S_b$-metric space $(W,S_b)$ for $b\ge 1$ such that $g\in \mathfrak{G}$ satisfies

$$S_b(A\mu ,A\mu ,Av)\le g\left(\mathrm{\Gamma }(\mu ,v)\right)\mathrm{\Gamma }(\mu ,v),$$

(1)

for all $\mu ,v\in W$, where

$$\mathrm{\Gamma }(\mu ,v)=S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|.$$

(2)

Then, the mapping A fixes a unique point $u\in W$.

Proof. 

Suppose ${\mu }_0$ is an element of W. For $n\in \mathbb{N}$, let us construct a sequence $\left\{{\mu }_n\right\}$ in W as ${\mu }_{n+1}=A{\mu }_n=A^{n+1}{\mu }_0$. For some $n_0$, if $S_b({\mu }_{n_0},{\mu }_{n_0},{\mu }_{n_0+1})=0$, then we know that ${\mu }_{n_0}$ is a fixed point of A. In this case, the proof is completed. Thus, let $S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})\ne 0$, for all $n\in \mathbb{N}$. From (1), we have

$$\begin{array}{ccc}\hfill 0<S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})& =& S_b(A{\mu }_{n-1},A{\mu }_{n-1},A{\mu }_n)\hfill \\ & \le & g\left(\mathrm{\Gamma }({\mu }_{n-1},{\mu }_n)\right)\mathrm{\Gamma }({\mu }_{n-1},{\mu }_n),n\ge 1,\hfill \end{array}$$

(3)

where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }({\mu }_{n-1},{\mu }_n)& =& S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n)\hfill \\ & & +|S_b({\mu }_{n-1},{\mu }_{n-1},A{\mu }_{n-1})-S_b({\mu }_n,{\mu }_n,A{\mu }_n)|\hfill \\ & =& S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n)+|S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n)-S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})|.\hfill \end{array}$$

(4)

Take

$$S_{b\left(n\right)}=S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n).$$

(5)

From (3)

$$0<S_{b(n+1)}\le g(S_{b\left(n\right)}+|S_{b\left(n\right)}-S_{b(n+1)}\left|\right)(S_{b\left(n\right)}+|S_{b\left(n\right)}-S_{b(n+1)}\left|\right).$$

(6)

Let $n_0>0$ such that $S_{b\left(n_0\right)}\le S_{b(n_0+1)}$. Then, by (6), we have

$$S_{b(n_0+1)}\le g\left(S_{b(n_0+1)}\right)S_{b(n_0+1)}<\frac{1}{b^2}{S}_{b(n_0+1)},b\ge 1,$$

(7)

which is a contradiction. Therefore, $S_{b\left(n\right)}>S_{b(n+1)}$, for all $n>0$. From (6), we have

$$0<S_{b(n+1)}\le g(2S_{b\left(n\right)}-S_{b(n+1)})(2S_{b\left(n\right)}-S_{b(n+1)}).$$

(8)

That is, the sequence of real $\left\{S_{b\left(n\right)}\right\}$ is decreasing. Suppose there exists $\gamma \ge 0$ such that $\underset{n\to \infty }{lim}{S}_{b\left(n\right)}=\gamma$. Let $\gamma >0$. Letting $n⟶\infty$ in (8), we have

$$\begin{array}{ccc}\hfill \gamma & =& \underset{n\to \infty }{lim}{S}_{b(n+1)}\hfill \\ & \le & \underset{n\to \infty }{lim}\left[g(2S_{b\left(n\right)}-S_{b(n+1)})(2S_{b\left(n\right)}-S_{b(n+1)})\right].\hfill \end{array}$$

(9)

Now, we have two cases.

Case I: If $b=1$, then (9) becomes

$$\begin{array}{ccc}\hfill \gamma & =& \underset{n\to \infty }{lim}{S}_{b(n+1)}\hfill \\ & \le & \underset{n\to \infty }{lim}\left[g(2S_{b\left(n\right)}-S_{b(n+1)})(2S_{b\left(n\right)}-S_{b(n+1)})\right]\hfill \\ & \le & \frac{1}{b^2}\underset{n\to \infty }{lim}(2S_{b\left(n\right)}-S_{b(n+1)})\hfill \\ & =& \frac{1}{b^2}\gamma =\gamma .\hfill \end{array}$$

(10)

We have

$$\underset{n\to \infty }{lim}g(2S_{b\left(n\right)}-S_{b(n+1)})=\frac{1}{b^2}.$$

(11)

Since $g\in \mathfrak{G}$,

$$\gamma =\underset{n\to \infty }{lim}(2S_{b\left(n\right)}-S_{b(n+1)})=0,$$

(12)

which is in conflict.

Case II: If $b>1$, according to (9), we have

$$\begin{array}{ccc}\hfill \gamma & =& \underset{n\to \infty }{lim}{S}_{b(n+1)}\hfill \\ & \le & \underset{n\to \infty }{lim}\left[g(2S_{b\left(n\right)}-S_{b(n+1)})(2S_{b\left(n\right)}-S_{b(n+1)})\right]\hfill \\ & \le & \frac{1}{b^2}\underset{n\to \infty }{lim}(2S_{b\left(n\right)}-S_{b(n+1)})=\frac{1}{b^2}\gamma ,b>1,\hfill \end{array}$$

(13)

which is in conflict.

From the above two cases, we assume $\gamma =0$, that is,

$$\underset{n\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,{\mu }_{n+1})=0.$$

(14)

Utilizing the properties of $S_b$-metric space, we have

$$\begin{array}{ccc}\hfill S_b({\mu }_{n+1},{\mu }_{n+1},{\mu }_n)& \le & b[S_b({\mu }_{n+1},{\mu }_{n+1},{\mu }_{n+1})+S_b({\mu }_{n+1},{\mu }_{n+1},{\mu }_{n+1})+S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})]\hfill \\ \hfill & \le & b{S}_b({\mu }_n,{\mu }_n,{\mu }_{n+1}).\hfill \end{array}$$

(15)

Thus, we obtain

$$\underset{n\to \infty }{lim}{S}_b({\mu }_{n+1},{\mu }_{n+1},{\mu }_n)=0.$$

(16)

We shall prove the sequence $\left\{{\mu }_n\right\}$ in $(W,S_b)$ is a Cauchy sequence; i.e.,

$$\underset{n,m\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,{\mu }_m)=0,m>n,$$

(17)

will be proved.

Let us assume (17) is not true, so there exists some $\epsilon >0$ for which we can find two subsequences $\left\{{\mu }_{m_k}\right\}$ and $\left\{{\mu }_{n_k}\right\}$ of $\left\{{\mu }_n\right\}$ with $m_k>n_k>k$ such that

$$S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})\ge \epsilon$$

(18)

and

$$S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})<\epsilon .$$

(19)

By inequalities (18), (19) and Lemma 2, we have

$$\begin{array}{ccc}\hfill \epsilon & \le & S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})\hfill \\ & \le & [2b{S}_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{n_k+1})+b^2{S}_b({\mu }_{n_k+1},{\mu }_{n_k+1},{\mu }_{m_k})].\hfill \end{array}$$

(20)

Taking $k\to \infty$ in (20) and using (14), we obtain

$$\begin{array}{ccc}\hfill \epsilon & \le & \underset{k\to \infty }{lim}inf{S}_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})\hfill \\ & \le & b^2\underset{k\to \infty }{lim}inf{S}_b({\mu }_{n_k+1},{\mu }_{n_k+1},{\mu }_{m_k}).\hfill \end{array}$$

(21)

From (1), we have

$$\begin{array}{ccc}\hfill S_b({\mu }_{n_k+1},{\mu }_{n_k+1},{\mu }_{m_k})& =& S_b(A{\mu }_{n_k},A{\mu }_{n_k},A{\mu }_{m_k-1})\hfill \\ & \le & g\left(\mathrm{\Gamma }({\mu }_{n_k},{\mu }_{m_k-1})\right).\mathrm{\Gamma }({\mu }_{n_k},{\mu }_{m_k-1})\hfill \\ & =& g(S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})+|S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{n_k+1})\hfill \\ & & -S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{m_k})\left|\right).(S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})\hfill \\ & & +|S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{n_k+1})-S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{m_k})\left|\right).\hfill \end{array}$$

(22)

Let $M=S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})+|S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{n_k+1})-S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{m_k})|$ and taking $k\to \infty$ in the above equation and using (14) and (19), we obtain

$$\underset{k\to \infty }{lim}inf{S}_b({\mu }_{n_k+1},{\mu }_{n_k+1},{\mu }_{m_k})\le \epsilon \underset{k\to \infty }{lim}infg\left(M\right).$$

(23)

Thus,

$$\frac{1}{\epsilon }\underset{k\to \infty }{lim}inf{S}_b({\mu }_{n_k+1},{\mu }_{n_k+1},{\mu }_{m_k})\le \underset{k\to \infty }{lim}infg\left(M\right).$$

(24)

From (21) and (24), we have

$$\begin{array}{ccc}\hfill \frac{1}{b^2}& =& \frac{1}{\epsilon }\frac{\epsilon }{b^2}\le \frac{1}{\epsilon }\underset{k\to \infty }{lim}inf{S}_b({\mu }_{n_k+1},{\mu }_{n_k+1},{\mu }_{m_k})\hfill \\ & \le & \underset{k\to \infty }{lim}infg\left(M\right)\le \underset{k\to \infty }{lim}supg\left(M\right)\le \frac{1}{b^2}.\hfill \end{array}$$

(25)

Hence,

$$\underset{k\to \infty }{lim}g\left(M\right)=\frac{1}{b^2}.$$

(26)

Since $g\in \mathfrak{G}$, utilizing (14) and (16), we have

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim}M& =& \underset{k\to \infty }{lim}(S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})\hfill \\ & & +|S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{n_k+1})-S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{m_k})|)\hfill \\ & =& \underset{k\to \infty }{lim}{S}_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})\hfill \\ & =& 0.\hfill \end{array}$$

(27)

From (14) and (27), we have

$$\begin{array}{ccc}\hfill \epsilon & \le & S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})\hfill \\ & \le & |2b{S}_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})+b^2{S}_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{m_k})|\to 0ask\to \infty ,\hfill \end{array}$$

(28)

a contradiction. Thus,

$$\underset{n,m\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,{\mu }_m)=0.$$

(29)

This shows that $\left\{{\mu }_n\right\}$ is a Cauchy sequence in $(W,S_b)$. So, there exists $u\in W$, such that

$$\underset{n\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,u)=0.$$

(30)

From Lemma 1 and (30), we obtain

$$\underset{n\to \infty }{lim}{S}_b(u,u,{\mu }_n)=0.$$

(31)

Now, we need to prove that $u\in A$ is some fixed point of A. Suppose $u\ne Au$, then $S_b(u,u,Au)>0$. From (1) and (2), we have

$$\begin{array}{ccc}\hfill S_b({\mu }_{n+1},{\mu }_{n+1},Au)& =& S_b(A{\mu }_n,A{\mu }_n,Au)\hfill \\ & \le & g\left(\mathrm{\Gamma }({\mu }_n,u)\right)\mathrm{\Gamma }({\mu }_n,u)\hfill \\ & \le & \frac{1}{b^2}\mathrm{\Gamma }({\mu }_n,u),\hfill \end{array}$$

(32)

where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }({\mu }_n,u)& =& S_b({\mu }_n,{\mu }_n,u)\hfill \\ & & +|S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})-S_b(u,u,Au)|.\hfill \end{array}$$

(33)

We also have

$$\begin{array}{ccc}\hfill S_b(u,u,Au)& \le & \{2b{S}_b(u,u,A{\mu }_n)+b^2{S}_b(A{\mu }_n,A{\mu }_n,Au)\}\hfill \\ & =& 2b{S}_b(u,u,{\mu }_{n+1})+b^2{S}_b({\mu }_{n+1},{\mu }_{n+1},Au)\hfill \\ & \le & 2b{S}_b(u,u,{\mu }_{n+1})+b^{2}g\left(\mathrm{\Gamma }({\mu }_n,u)\right)\mathrm{\Gamma }({\mu }_n,u)\hfill \\ & <& 2b{S}_b(u,u,{\mu }_{n+1})+\mathrm{\Gamma }({\mu }_n,u).\hfill \end{array}$$

(34)

Taking $n\to \infty$ and utilizing (30), (31), and (33), we obtain

$$\begin{array}{ccc}\hfill S_b(u,u,Au)& \le & 2b\underset{n\to \infty }{lim}{S}_b(u,u,{\mu }_{n+1})\hfill \\ & & +b^2\underset{n\to \infty }{lim}\left[g\left(\mathrm{\Gamma }({\mu }_n,u)\right)\mathrm{\Gamma }({\mu }_n,u)\right]\hfill \\ & \le & 2b\underset{n\to \infty }{lim}{S}_b(u,u,{\mu }_{n+1})+\underset{n\to \infty }{lim}\mathrm{\Gamma }({\mu }_n,u)\hfill \\ & \le & 0+\underset{n\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,u)\hfill \\ & & +|\underset{n\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,{\mu }_{n+1})-\underset{n\to \infty }{lim}{S}_b(u,u,Au)|\hfill \\ & \le & S_b(u,u,Au).\hfill \end{array}$$

(35)

Therefore,

$$\underset{n\to \infty }{lim}{b}^{2}g\left(\mathrm{\Gamma }({\mu }_n,u)\right)=1.$$

(36)

Since $g\in \mathfrak{G}$, then

$$\underset{n\to \infty }{lim}\mathrm{\Gamma }({\mu }_n,u)=0,$$

(37)

which is a contradiction. So, $S_b(u,u,Au)=0$ and so $u=Au$. Consequently, A fixes the point u.

To prove the distinctness of this fixed point, let $v\ne u$ be another fixed point of A; that is, $v=Av$ and $S_b(v,v,Av)=0$. Now,

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(u,v)& =& S_b(u,u,v)+|S_b(u,u,u)-S_b(v,v,v)|\hfill \\ & =& S_b(u,u,v),\hfill \end{array}$$

(38)

and by (1),

$$\begin{array}{ccc}\hfill 0& <& S_b(u,u,v)=S_b(Au,Au,Av)\hfill \\ & \le & g\left(\mathrm{\Gamma }\right(u,v\left)\right)\mathrm{\Gamma }(u,v)\hfill \\ & =& g\left(S_b(u,u,v)\right)S_b(u,u,v)\hfill \\ & <& \frac{1}{b^2}{S}_b(u,u,v).\hfill \end{array}$$

(39)

which is a contradiction. So, A fixes a unique point. □

The example below illustrates the above result.

Example 3.

Let $W=\{0,1,2\}$ be endowed with the $S_b$-metric $S_b$ for $b\ge 1$, given by

$$\begin{array}{ccc}\hfill S_b(0,0,0)=S_b(1,1,1)=S_b(2,2,2)& =& 0,\hfill \\ \hfill S_b(0,0,1)=S_b(1,1,0)=S_b(0,0,2)=S_b(2,2,0)& =& 1,\hfill \\ \hfill S_b(1,1,2)=S_b(2,2,1)& =& 2,\hfill \\ \hfill S_b(0,1,2)& =& 6.\hfill \end{array}$$

Consider $A:W⟶W$ as $A0=A1=0$ and $A2=1$. Take

$$\begin{array}{ccc}\hfill g\left(t\right)& =& \{\begin{array}{cc}\frac{1}{1+\frac{5}{11}t},& ift>0,\\ \frac{1}{3},& ift=0.\end{array}\hfill \end{array}$$

For $(\mu ,\mu ,\upsilon )=(0,0,2)$.

$$\begin{array}{ccc}\hfill Since\mathrm{\Gamma }(0,2)& =& S_b(0,0,2)+|S_b(0,0,A0)-S_b(2,2,A2)|\hfill \\ & =& 1+|S_b(0,0,0)-S_b(2,2,1)|\hfill \\ & =& 1+|0-2|=1+2=3,\hfill \\ \hfill S_b(A0,A0,A2)& =& S_b(0,0,1)=1,\hfill \\ \hfill g\left(\mathrm{\Gamma }\right(0,2\left)\right)& =& g\left(3\right)=\frac{1}{1+\frac{5}{11}\times 3}=\frac{11}{11+15}=\frac{11}{26}.\hfill \\ \hfill \therefore S_b(A0,A0,A2)& =& 1\le \frac{11}{26}\times 3=g\left(\mathrm{\Gamma }(0,2)\right)\mathrm{\Gamma }(0,2).\hfill \end{array}$$

For, $(\mu ,\mu ,\upsilon )=(1,1,2)$

$$\begin{array}{ccc}\hfill Since\mathrm{\Gamma }(1,2)& =& S_b(1,1,2)+|S_b(1,1,A1)-S_b(2,2,A2)|\hfill \\ & =& 2+|S_b(1,1,0)-S_b(2,2,1)|\hfill \\ & =& 2+|1-2|=3,\hfill \\ \hfill S_b(A1,A1,A2)& =& S_b(0,0,1)=1.\hfill \\ \hfill \therefore S_b(A1,A1,A2)& \le & g\left(\mathrm{\Gamma }\right(1,2\left)\right)\mathrm{\Gamma }(1,2).\hfill \end{array}$$

For $(\mu ,\mu ,\upsilon )=(0,0,1)$

$$\begin{array}{ccc}\hfill Since\mathrm{\Gamma }(0,1)& =& S_b(0,0,1)+|S_b(0,0,A0)-S_b(1,1,A1)|\hfill \\ & =& 1+|0-1|=2,\hfill \\ \hfill S_b(A0,A0,A1)& =& S_b(0,0,0)=0.\hfill \\ \hfill \therefore S_b(A0,A0,A1)& \le & g\left(\mathrm{\Gamma }\right(0,1\left)\right)\mathrm{\Gamma }(0,1).\hfill \end{array}$$

Thus, (1) holds for all $\mu ,\upsilon \in W$; that is, all hypotheses of Theorem 2 are satisfied, so A must fix a unique point. Clearly $u=0$ is such point with $S_b(0,0,0)=0$.

Next, we prove the following theorem.

Theorem 3.

Let $A:W⟶W$ be defined in a complete $S_b$-metric space $(W,S_b)$ for $b\ge 1$ and $g\in \mathcal{G}$ such that

$$S_b(A\mu ,A\mu ,Av)\le g\left(\mathrm{\Gamma }(\mu ,v)\right)\mathrm{\Gamma }(\mu ,v),$$

(40)

for all $v,\mu \in W$, where

$$\mathrm{\Gamma }(\mu ,v)=\frac{1}{b^3}(S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|).$$

(41)

Then, the mapping A fixes a unique point $u^{*}\in W$.

Proof. 

Suppose ${\mu }_0$ is an element of the space W. For $n\in \mathbb{N}$, let us construct a sequence $\left\{{\mu }_n\right\}$ in W as ${\mu }_{n+1}=A{\mu }_n=A^{n+1}{\mu }_0$. For some $n_0$, if $S_b({\mu }_{n_0},{\mu }_{n_0},{\mu }_{n_0+1})=0$, then we know that ${\mu }_{n_0}$ is one of the fixed points of A. In this case, the proof is complete. Thus, let $S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})\ne 0$ for all $n\in \mathbb{N}$. Using (40), we have

$$\begin{array}{ccc}\hfill 0& <& S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})=S_b(A{\mu }_{n-1},A{\mu }_{n-1},A{\mu }_n)\hfill \\ & \le & g\left(\mathrm{\Gamma }({\mu }_{n-1},{\mu }_n)\right)\mathrm{\Gamma }({\mu }_{n-1},{\mu }_n),\hfill \end{array}$$

(42)

where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }({\mu }_{n-1},{\mu }_n)& =& \frac{1}{b^3}(S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n)\hfill \\ & & +|S_b({\mu }_{n-1},{\mu }_{n-1},A{\mu }_{n-1})-S_b({\mu }_n,{\mu }_n,A{\mu }_n)\left|\right)\hfill \\ & =& \frac{1}{b^3}(S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n)\hfill \\ & & +|S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n)-S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})\left|\right).\hfill \end{array}$$

(43)

Take

$$S_{b\left(n\right)}^{*}=S_b({\mu }_{n-1},{\mu }_{n-1},{\mu }_n).$$

(44)

From (42), we obtain

$$S_{b(n+1)}^{*}\le g\left(\frac{1}{b^3}(S_{b\left(n\right)}^{*}+|S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*}|)\right)\left(\frac{1}{b^3}(S_{b\left(n\right)}^{*}+|S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*}|)\right).$$

(45)

Let $n_0>0$ be such that $S_{b\left(n_0\right)}^{*}\le S_{b(n_0+1)}^{*}$. Then, from (45), we obtain

$$\begin{array}{ccc}\hfill S_{b(n_0+1)}^{*}& =& g\left(\frac{1}{b^3}{S}_{b(n_0+1)}^{*}\right).\left(\frac{1}{b^3}{S}_{b(n_0+1)}^{*}\right)\hfill \\ & <& \frac{1}{b^3}{S}_{b(n_0+1)}^{*},\hfill \end{array}$$

(46)

which is not possible, as $b\ge 1$. Thus, for all $n>0$, $S_{b\left(n\right)}^{*}>S_{b(n+1)}^{*}$. So, $\left\{S_{b\left(n\right)}^{*}\right\}$ is a decreasing sequence. Consequently, $\underset{n\to \infty }{lim}{S}_{b\left(n\right)}^{*}=\delta$, for some $\delta \ge 0$. Next, we prove that

$$\delta =0.$$

(47)

From (45), we have

$$\begin{array}{ccc}\hfill S_{b(n+1)}^{*}& \le & g\left(\frac{1}{b^3}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})\right).\frac{1}{b^3}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})\hfill \\ & \le & g\left(\frac{1}{b^3}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})\right).(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})\hfill \\ & <& 2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*}.\hfill \end{array}$$

(48)

Taking $n\to \infty$ in (48), we have

$$\begin{array}{ccc}\hfill \delta & =& \underset{n\to \infty }{lim}{S}_{b(n+1)}^{*}\hfill \\ & \le & \underset{n\to \infty }{lim}g\left(\frac{1}{b^3}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})\right).\underset{n\to \infty }{lim}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})\hfill \\ & \le & \underset{n\to \infty }{lim}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})=\delta .\hfill \end{array}$$

(49)

We obtain

$$\underset{n\to \infty }{lim}g\left(\frac{1}{b^3}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})\right)=1.$$

(50)

Since $g\in \mathcal{G}$,

$$\underset{n\to \infty }{lim}\frac{1}{b^3}(2S_{b\left(n\right)}^{*}-S_{b(n+1)}^{*})=\frac{1}{b^3}\delta =0.$$

(51)

Therefore,

$$\delta =0.$$

(52)

Thus, we have

$$\underset{n\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,{\mu }_{n+1})=0.$$

(53)

From Lemma 1 and (53), we obtain

$$\underset{n\to \infty }{lim}{S}_b({\mu }_{n+1},{\mu }_{n+1},{\mu }_n)=0.$$

(54)

Next, we want to show that $\left\{{\mu }_n\right\}\in W$ is a Cauchy sequence, i.e., to prove

$$\underset{n,m\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,{\mu }_m)=0,m>n.$$

(55)

On the contrary, we assume that (55) is not true. So, there exists some $\epsilon >0$ depending on which we can find the subsequences $\left\{{\mu }_{m_k}\right\}$ and $\left\{{\mu }_{n_k}\right\}$ of $\left\{{\mu }_n\right\}$ with $m_k>n_k>k$ such that

$$S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})\ge \epsilon$$

(56)

and

$$S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})<\epsilon .$$

(57)

By (40) and (56), we obtain

$$\begin{array}{ccc}\hfill \epsilon & \le & S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})=S_b(A{\mu }_{n_k-1},A{\mu }_{n_k-1},A{\mu }_{m_k-1})\hfill \\ & \le & g(\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1}).\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})\hfill \\ & <& \mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1}),\hfill \end{array}$$

(58)

where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})& =& \frac{1}{b^3}(S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})\hfill \\ & & +|S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{n_k})-S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{m_k})\left|\right).\hfill \end{array}$$

(59)

Utilizing (58) and (59) in (53), we obtain

$$\begin{array}{ccc}\hfill \epsilon & \le & \underset{k\to \infty }{lim}inf\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})\hfill \\ & =& \frac{1}{b^3}\underset{k\to \infty }{lim}inf{S}_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1}).\hfill \end{array}$$

(60)

On the other hand, using (57), we obtain

$$\begin{array}{ccc}\hfill & & S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})\hfill \\ & & \le 2b{S}_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{n_k})+b^2{S}_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})\hfill \\ & & <2b{S}_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{n_k})+b^2\epsilon .\hfill \end{array}$$

(61)

Taking $k\to \infty$, we have

$$\underset{k\to \infty }{lim}sup{S}_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})\le b^2\epsilon .$$

(62)

By (60) and (62), we obtain

$$\begin{array}{ccc}\hfill \epsilon & \le & \frac{1}{b^3}\underset{k\to \infty }{lim}inf{S}_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})\hfill \\ & \le & \frac{1}{b^3}\underset{k\to \infty }{lim}sup{S}_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})\le \frac{1}{b^3}.b^2\epsilon =\frac{\epsilon }{b},\hfill \end{array}$$

(63)

which is a contradiction with $b>1$.

Next, we look at the case for $b=1$. If $b=1$, then from Lemma 1, we obtain

$$S_b(x,x,y)=S_b(y,y,x),$$

for all $x,y\in W$.

By (56) and (57), we obtain

$$\begin{array}{ccc}\hfill \epsilon & \le & S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})\hfill \\ & =& S_b({\mu }_{m_k},{\mu }_{m_k},{\mu }_{n_k})\hfill \\ & \le & 2S_b({\mu }_{m_k},{\mu }_{m_k},{\mu }_{m_k-1})+S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k-1})\hfill \\ & <& 2S_b({\mu }_{m_k},{\mu }_{m_k},{\mu }_{m_k-1})+\epsilon .\hfill \end{array}$$

(64)

Taking $k\to \infty$ in (64) and using (54), we obtain

$$\underset{k\to \infty }{lim}{S}_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})=\epsilon .$$

(65)

Also,

$$\begin{array}{ccc}\hfill & & |S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})-S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})|\hfill \\ & & =|S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})-S_b({\mu }_{m_k},{\mu }_{m_k},{\mu }_{n_k})|\hfill \\ & & \le |2S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{n_k})+S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{n_k})\hfill \\ & & -2S_b({\mu }_{m_k},{\mu }_{m_k},{\mu }_{m_k-1})-S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{n_k})|\hfill \\ & & =|2S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{n_k})-2S_b({\mu }_{m_k},{\mu }_{m_k},{\mu }_{m_k-1})|.\hfill \end{array}$$

(66)

Taking $k\to \infty$ and by (53), we can obtain

$$\underset{k\to \infty }{lim}{S}_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})=\epsilon .$$

(67)

From (40), we have

$$\begin{array}{ccc}\hfill \epsilon & \le & S_b({\mu }_{n_k},{\mu }_{n_k},{\mu }_{m_k})=S_b(A{\mu }_{n_k-1},A{\mu }_{n_k-1},A{\mu }_{m_k-1})\hfill \\ & \le & g(\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})\hfill \\ & <& \mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1}),\hfill \end{array}$$

(68)

where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})& =& S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{m_k-1})\hfill \\ & & +|S_b({\mu }_{n_k-1},{\mu }_{n_k-1},{\mu }_{n_k})-S_b({\mu }_{m_k-1},{\mu }_{m_k-1},{\mu }_{m_k})|.\hfill \end{array}$$

(69)

Using (53), we get

$$\underset{k\to \infty }{lim}\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})=\epsilon .$$

(70)

Taking $k\to \infty$ in (68), we can obtain

$$\underset{k\to \infty }{lim}g\left(\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})\right)=1.$$

(71)

Since $g\in \mathcal{G}$,

$$\underset{k\to \infty }{lim}\mathrm{\Gamma }({\mu }_{n_k-1},{\mu }_{m_k-1})=0,$$

(72)

a contradiction. From the above two situations, the sequence $\left\{{\mu }_n\right\}\in W$ is a Cauchy sequence in $(W,S_b)$. Therefore, there must exists $u^{*}\in W$ satisfying

$$\underset{n\to \infty }{lim}{S}_b({\mu }_n,{\mu }_n,u^{*})=0.$$

(73)

We now confirm $S_b(u^{*},u^{*},A{u}^{*})=0$. In fact, if $S_b(u^{*},u^{*},A{u}^{*})\ne 0$, then by (40) and (41), we have

$$\begin{array}{ccc}\hfill S_b({\mu }_{n+1},{\mu }_{n+1},A{u}^{*})& =& S_b(A{\mu }_n,A{\mu }_n,A{u}^{*})\hfill \\ & \le & g\left(\mathrm{\Gamma }({\mu }_n,u^{*})\right).\mathrm{\Gamma }({\mu }_n,u^{*})\hfill \\ & <& \mathrm{\Gamma }({\mu }_n,u^{*}),\hfill \end{array}$$

(74)

where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }({\mu }_n,u^{*})& =& \frac{1}{b^3}(S_b({\mu }_n,{\mu }_n,u^{*})\hfill \\ & & +|S_b({\mu }_n,{\mu }_n,A{\mu }_n)-S_b(u^{*},u^{*},A{u}^{*})\left|\right)\hfill \\ & =& \frac{1}{b^3}(S_b({\mu }_n,{\mu }_n,u^{*})\hfill \\ & & +|S_b({\mu }_n,{\mu }_n,{\mu }_{n+1})-S_b(u^{*},u^{*},A{u}^{*})\left|\right)\hfill \\ & \to & \frac{1}{b^3}{S}_b(u^{*},u^{*},A{u}^{*})whenn\to \infty .\hfill \end{array}$$

(75)

Also,

$$\begin{array}{ccc}\hfill S_b(u^{*},u^{*},A{u}^{*})& \le & 2b{S}_b(u^{*},u^{*},A{\mu }_n)+b^2{S}_b(A{\mu }_n,A{\mu }_n,A{u}^{*})\hfill \\ & \le & 2b{S}_b(u^{*},u^{*},{\mu }_{n+1})+b^{2}g\left(\mathrm{\Gamma }({\mu }_n,u^{*})\right)\mathrm{\Gamma }({\mu }_n,u^{*})\hfill \\ & <& 2b{S}_b(u^{*},u^{*},{\mu }_{n+1})+b^2\mathrm{\Gamma }({\mu }_n,u^{*}).\hfill \end{array}$$

(76)

Taking $n\to \infty$ and by (73), we obtain

$$\begin{array}{ccc}\hfill S_b(u^{*},u^{*},A{u}^{*})& \le & 2b\underset{n\to \infty }{lim}{S}_b(u^{*},u^{*},{\mu }_{n+1})\hfill \\ & & +b^2\underset{n\to \infty }{lim}g\left(\mathrm{\Gamma }({\mu }_n,u^{*})\right)\mathrm{\Gamma }({\mu }_n,u^{*})\hfill \\ & \le & b^2\underset{n\to \infty }{lim}\mathrm{\Gamma }({\mu }_n,u^{*})\hfill \\ & =& \frac{1}{b}{S}_b(u^{*},u^{*},A{u}^{*}).\hfill \end{array}$$

(77)

When $b=1$, we obtain

$$\underset{n\to \infty }{lim}g\left(\mathrm{\Gamma }({\mu }_n,u^{*})\right)=1.$$

(78)

Since $g\in \mathcal{G}$,

$$\underset{n\to \infty }{lim}\mathrm{\Gamma }({\mu }_n,u^{*})=S_b(u^{*},u^{*},A{u}^{*})=0,$$

(79)

which is a contradictory result.

If $b>1$, from (77) we obtain a contradiction. Thus, from the above two cases $S_b(u^{*},u^{*},A{u}^{*})=0$, that is, $A{u}^{*}=u^{*}$. Therefore, A fixes the point $u^{*}$. Next, we want to prove that such $u^{*}$ is unique in A. On the contrary, let there exist $v^{*}\in W$ and $v^{*}\ne u^{*}$ such that $v^{*}=A{v}^{*}$. Then,

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(u^{*},v^{*})& =& \frac{1}{b^3}(S_b(u^{*},u^{*},v^{*})+|S_b(u^{*},u^{*},u^{*})-S_b(v^{*},v^{*},v^{*})|)\hfill \\ & =& \frac{1}{b^3}{S}_b(u^{*},u^{*},v^{*})\hfill \end{array}$$

(80)

and by (40)

$$\begin{array}{ccc}\hfill 0& <& S_b(u^{*},u^{*},v^{*})=S_b(A{u}^{*},A{u}^{*},A{v}^{*})\hfill \\ & \le & g\left(\mathrm{\Gamma }(u^{*},v^{*})\right)\mathrm{\Gamma }(u^{*},v^{*})\hfill \\ & =& g\left(\frac{1}{b^3}{S}_b(u^{*},u^{*},v^{*})\right)\frac{1}{b^3}{S}_b(u^{*},u^{*},v^{*})\hfill \\ & <& \frac{1}{b^3}{S}_b(u^{*},u^{*},v^{*}),\hfill \end{array}$$

a contradiction. Thus, the self-mapping A in W fixes a unique $u^{*}\in W$. □

The example below illustrates the above result.

Example 4.

Let $W=[0.03,4]$ be endowed with the $S_b$-metric $S_b$ given by

$$\begin{array}{ccc}\hfill S_b(u,v,w)& =& {\left(\right|u+w-2v|+|v-w\left|\right)}^2,\forall u,v,w\in [0,\infty )\mathrm{for}b=4.\hfill \end{array}$$

Consider $A:[0.03,4]⟶[0.03,4]$ as

$$Au=\left\{\begin{array}{c}\frac{3}{17u+20},0.03\le u\le 2\hfill \\ \frac{u}{17},u>2.\hfill \end{array}\right.$$

Take

$$\begin{array}{ccc}\hfill g\left(t\right)& =& \{\begin{array}{cc}\frac{1}{16}{e}^{-t},& ift>0,\\ \frac{1}{17},& ift=0.\end{array}\hfill \end{array}$$

When $Au=\frac{3}{17u+20},0.03\le u\le 2$, the terms of inequality (40) are

$$\begin{array}{ccc}\hfill S_b(A\mu ,A\mu ,Av)& =& 4|\frac{3}{17v+20}-\frac{3}{17\mu +20}{|}^2,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(\mu ,v)& =& \frac{1}{64}\left[{4|v-\mu |}^2+\left|4\right|\frac{3}{17\mu +20}-\mu {|}^2+4|\frac{3}{17v+20}-v{|}^2|\right]\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill g\left(\mathrm{\Gamma }\right(\mu ,v\left)\right)& =& \frac{1}{16}{e}^{-\frac{1}{64}\left[{4|v-\mu |}^2+\left|4\right|\frac{3}{17\mu +20}-\mu {|}^2+4|\frac{3}{17v+20}-v{|}^2|\right]}.\hfill \end{array}$$

When $Au=\frac{u}{17},2<u\le 4$, the terms of inequality (40) are

$$\begin{array}{ccc}\hfill S_b(A\mu ,A\mu ,Av)& =& 4|\frac{v}{17}-\frac{\mu }{17}{|}^2,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(\mu ,v)& =& \frac{1}{64}\left[{4|v-\mu |}^2+\left|4\right|\frac{\mu }{17}-\mu {|}^2+4|\frac{v}{17}-v{|}^2|\right]\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill g\left(\mathrm{\Gamma }\right(\mu ,v\left)\right)& =& \frac{1}{16}{e}^{-\frac{1}{64}\left[{4|v-\mu |}^2+\left|4\right|\frac{\mu }{17}-\mu {|}^2+4|\frac{v}{17}-v{|}^2|\right]}.\hfill \end{array}$$

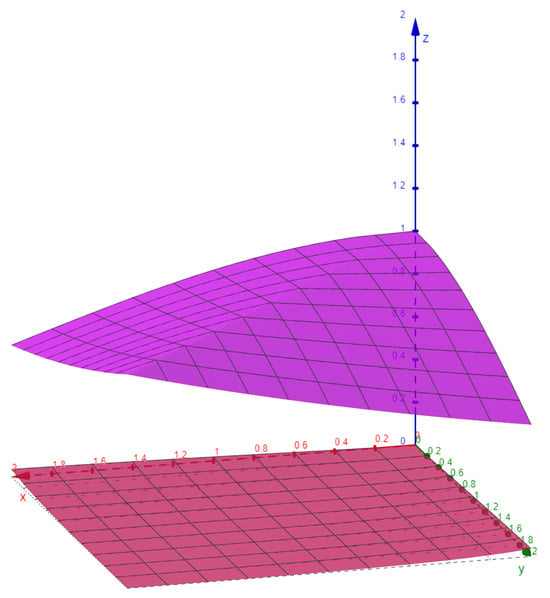
Now, we draw surfaces for the terms $S_b(A\mu ,A\mu ,Av)$ and $g\left(\mathrm{\Gamma }\right(\mu ,v\left)\right)\mathrm{\Gamma }(\mu ,v)$ in one figure when $Au=\frac{3}{17u+20},0.03\le u\le 2$ and in another figure when $Au=\frac{u}{17},2<u\le 4$.

Then, from Figure 1, we see the inequality (40) satisfies in the interval $[0.03,2]\times [0.03,2]$, and from Figure 2, we see the inequality (40) satisfies in the interval $[2,4]\times [2,4]$.

Thus, (40) holds for all $\mu ,\upsilon \in W$. That is, all hypotheses of Theorem 3 are satisfied, so A must fix a unique point. Clearly, $u=0.135$ is such point with $S_b(0.135,0.135,0.135)=0$.

The following remark will distinguish the Theorem 2 and 3.

Figure 1. When $Au=\frac{3}{17u+20},0.03\le u\le 2$, the graph showing that the surface of left side term of inequality (40) is always below the surface of right side term of inequality (40).

Figure 2. When $Au=\frac{u}{17},2<u\le 4$, the graph showing that the surface of left side term of inequality (40) is always below the surface of right side term of inequality (40).

Remark 1.

The inequality (40) in Theorem 3 will imply the inequality (1) in Theorem 2 only when either $g\in \mathcal{G}$ or $g\in \mathfrak{G}$ in both cases. But we used the function g from different collection for both the theorems, where the collections $\mathcal{G}=\left\{g:[0,\infty )\to [0,1)\right\}$ is the set of all those functions g with the condition $\underset{n\to \infty }{lim}g\left(p_n\right)=1$⇒$\underset{n\to \infty }{lim}{p}_n=0$ and $\mathfrak{G}=\left\{g:[0,\infty )\to [0,\frac{1}{b^2})\right\}$ is the set of all those functions g with the condition $li{m}_{n\to \infty }g\left(p_n\right)=\frac{1}{b^2}$⇒$\underset{n\to \infty }{lim}{p}_n=0$, for $b\ge 1$, are completely different. So, we cannot compare the inequalities. Also, the term $\mathrm{\Gamma }(\mu ,v)$ is different in both the theorems.

We now present some consequent results.

Corollary 1.

Let A be a self-mapping in a complete $S_b$-metric space $(W,S_b)$ for $b\ge 1$ such that $g\in \mathfrak{G}$ satisfies

$$S_b(A\mu ,A\mu ,Av)\le g\left(\mathrm{\Gamma }(\mu ,v)\right)\mathrm{\Gamma }(\mu ,v),$$

(81)

for all $\mu ,v\in W$, where

$$\mathrm{\Gamma }(\mu ,v)=max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)\left|\right\}.$$

(82)

Then, the mapping A fixes a unique point $u\in W$.

Proof. 

For the defined sequence in Theorem 2, if $\mu ={\mu }_{n-1},v={\mu }_n$, then

$$\begin{gathered} max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)\left|\right\} \\ =S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|. \end{gathered}$$

Consequently, the result follows Theorem 2. □

Corollary 2.

Let A be a self-mapping in a complete $S_b$-metric space $(W,S_b)$ for $b\ge 1$ such that $g\in \mathcal{G}$ satisfies

$$S_b(A\mu ,A\mu ,Av)\le g\left(\mathrm{\Gamma }(\mu ,v)\right)\mathrm{\Gamma }(\mu ,v),$$

(83)

for all $\mu ,v\in W$, where

$$\mathrm{\Gamma }(\mu ,v)=\frac{1}{b^3}max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)\left|\right\}.$$

(84)

Then, the mapping A fixes a unique point $u\in W$.

Proof. 

For the defined sequence in Theorem 3, if $\mu ={\mu }_{n-1},v={\mu }_n$, then

$\frac{1}{b^3}max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)\left|\right\}$

$$\begin{array}{ccc}& =& \frac{1}{b^3}(S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|).\hfill \end{array}$$

Consequently, the result follows Theorem 3. □

Corollary 3.

Let A be a self-mapping in a complete $S_b$-metric space $(W,S_b)$ for $b\ge 1$ such that $g\in \mathfrak{G}$ satisfies

$$S_b(A\mu ,A\mu ,Av)\le g\left(\mathrm{\Gamma }(\mu ,v)\right)\mathrm{\Gamma }(\mu ,v),$$

(85)

for all $\mu ,v\in W$, where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(\mu ,v)& =& max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|,\hfill \\ & & \frac{S_b(\mu ,\mu ,Av),S_b(v,v,A\mu )}{S_b(\mu ,\mu ,v)}\}.\hfill \end{array}$$

Then, the mapping A fixes a unique point $u\in W$.

Proof. 

For the defined sequence in Theorem 2, if $\mu ={\mu }_{n-1},v={\mu }_n$, then

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(\mu ,v)& =& max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|,\hfill \\ & & \frac{S_b(\mu ,\mu ,Av),S_b(v,v,A\mu )}{S_b(\mu ,\mu ,v)}\}\hfill \\ & =& S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|.\hfill \end{array}$$

Consequently, the result follows Theorem 2. □

Corollary 4.

Let A be a self-mapping in a complete $S_b$-metric space $(W,S_b)$ for $b\ge 1$ such that $g\in \mathcal{G}$ satisfies

$$S_b(A\mu ,A\mu ,Av)\le g\left(\mathrm{\Gamma }(\mu ,v)\right)\mathrm{\Gamma }(\mu ,v),$$

(86)

for all $\mu ,v\in W$, where

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(\mu ,v)& =& \frac{1}{b^3}max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|,\hfill \\ & & \frac{S_b(\mu ,\mu ,Av),S_b(v,v,A\mu )}{S_b(\mu ,\mu ,v)}\}.\hfill \end{array}$$

Then, the mapping A fixes a unique point $u\in W$.

Proof. 

For the defined sequence in Theorem 3, if $\mu ={\mu }_{n-1},v={\mu }_n$, then

$$\begin{array}{ccc}\hfill \mathrm{\Gamma }(\mu ,v)& =& \frac{1}{b^3}max\{S_b(\mu ,\mu ,A\mu ),S_b(v,v,A\mu ),S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|,\hfill \\ & & \frac{S_b(\mu ,\mu ,Av),S_b(v,v,A\mu )}{S_b(\mu ,\mu ,v)}\}\hfill \\ & =& \frac{1}{b^3}(S_b(\mu ,\mu ,v)+|S_b(\mu ,\mu ,A\mu )-S_b(v,v,Av)|).\hfill \end{array}$$

Consequently, the result follows Theorem 3. □

4. Application

When it comes to solving differential equations in mathematics, integral equations are usually crucial. FP methods have been utilized by numerous authors to solve integral problems. Within this framework of inquiry, we utilize Theorem 2 to determine whether the integral equation below has a solution. Consider the following integral equation

$$w\left(s\right)=q\left(s\right)+{\int }_0^{1}F(s,u)h(u,w\left(u\right))du,s\in [0,1],$$

(87)

where $h:[0,1]\times \mathbb{R}\to \mathbb{R}$ and $q:[0,1]\to \mathbb{R}$ are continuous, $F:[0,1]\times [0,1]\to [0,\infty )$ is a function, and $F(s,·)\in L^1\left([0,1]\right)$ for all $s\in [0,1]$ (see, [12,13]).

Let $W=C([0,1],\mathbb{R})=\left\{w:[0,1]⟶\mathbb{R},becontinuous\right\}$ and $S_b:W\times W\times W\to [0,\infty )$ be $S_b$-metric given by

$$S_b(w,v,z)=(\underset{s\in [0,1]}{sup}|w\left(s\right)-z\left(s\right)|+\underset{s\in [0,1]}{sup}{|v\left(s\right)-z\left(s\right)|)}^2,$$

(88)

for all $w,v,z\in W$. Then, $(W,S_b)$ is an $S_b$-metric space with regard to the parameter $b\ge 1$.

Let $A:W\to W$ be given by

$$A\left(w\left(s\right)\right)=q\left(s\right)+{\int }_0^{1}F(s,u)h(u,w\left(u\right))du,s\in [0,1].$$

(89)

Now, we present a result for existence of a solution of (87).

Theorem 4.

Let the following conditions be met:

(1)

there exists $\eta :W\times W\to [0,\infty )$ for all $u\in [0,1]$

$$\begin{array}{ccc}\hfill 0& \le & \left|h\right(w,w\left(u\right))-h(w,v\left(u\right)\left)\right|\hfill \\ & \le & \eta (w,v)\left|w\right(u)-v(u\left)\right|,forallw,v\in W.\hfill \end{array}$$

(2)

there exists $g:[0,\infty )\to [0,\frac{1}{b^2})$ with

$$\begin{array}{ccc}& & {\displaystyle \underset{x\in [0,1]}{sup}}{\int }_0^{1}F(x,u)\eta (w,v)dx\hfill \\ & & \le \sqrt{g\left((2\underset{x\in [0,1]}{sup}{\left|L\right|)}^2+\left|\right(2\underset{x\in [0,1]}{sup}{\left|M\right|)}^2-(2\underset{x\in [0,1]}{sup}{\left|N\right|)}^2\right)},\hfill \end{array}$$

(90)

where

$$\begin{array}{ccc}\hfill L& =& w-v,\hfill \\ \hfill M& =& w-Aw,\hfill \\ \hfill N& =& v-Av.\hfill \end{array}$$

(91)

Then, the integral equation given in (87) has a unique solution.

Proof. 

We know that a fixed point of A corresponds to a solution of (87). By (1) and (2), we have

$$\begin{array}{c}{S}_b(A\left(w\left(x\right)\right),A\left(w\left(x\right)\right),A\left(v\left(x\right)\right))\hfill \\ ={\left(2\underset{x\in [0,1]}{sup}|A\left(w\left(x\right)\right)-A\left(v\left(x\right)\right)|\right)}^2\hfill \\ ={\left(2\underset{x\in [0,1]}{sup}|{\int }_0^{1}F(x,u)h(u,w\left(u\right))du-{\int }_0^{1}F(x,u)h(u,v\left(u\right))du|\right)}^2\hfill \end{array}$$

$$\begin{array}{ccc}& =& {\left(2\underset{x\in [0,1]}{sup}|{\int }_0^{1}F(x,u)[h(u,w\left(u\right))-h(u,v\left(u\right))]du)|\right)}^2\hfill \\ & \le & {\left(2\underset{x\in [0,1]}{sup}{\int }_0^{1}F(x,u)\eta (w,v)|w\left(u\right)-v\left(u\right)|du\right)}^2\hfill \\ & =& {\left(2\underset{x\in [0,1]}{sup}{\int }_0^{1}F(x,u)\eta (x,y).\frac{1}{2}((2|w\left(u\right)-{v\left(u\right)\left|\right)}^2{)}^{\frac{1}{2}}du\right)}^2\hfill \\ & \le & \mathrm{\Gamma }(w,v).{\left(\underset{x\in [0,1]}{sup}{\int }_0^{1}F(x,u)\eta (w,v)\right)}^2\hfill \\ & \le & \mathrm{\Gamma }(w,v).g\left(\mathrm{\Gamma }\right(w,v\left)\right),\hfill \end{array}$$

where

$$\mathrm{\Gamma }(w,v)={(2\underset{x\in [0,1]}{sup}\left|L\right|)}^2+|{(2\underset{x\in [0,1]}{sup}\left|M\right|)}^2-{(2\underset{x\in [0,1]}{sup}\left|N\right|)}^2|$$

with

$$\begin{array}{ccc}\hfill L& =& w-v,\hfill \\ \hfill M& =& w-Aw,\hfill \\ \hfill N& =& v-Av.\hfill \end{array}$$

Thus,

$$S_b(Aw,Aw,Av)\le g\left(\mathrm{\Gamma }(w,v)\right)\mathrm{\Gamma }(w,v),$$

for all $u,v\in W.$ This shows that A satisfies Theorem 2. Therefore, A fixes a unique point $W=C\left(\right[0,1],\mathbb{R})$; that is, the integral Equation (87) has a unique solution. □

5. Conclusions

In conclusion, following Geraghty [7] and Wang et al. [10] we presented a new type of Geraghty contraction and studied fixed point results within the framework of $S_b$-metric space for these contractions which includes auxiliary functions with a restricted co-domain. This new idea of defining Geraghty contraction for self operators generalized a large number of previously published and closely related works for the presence and uniqueness of a fixed point in $S_b$-metric space. We demonstrated that the self-operators that fulfill this contraction need to have only one fixed point. Additionally, we offer examples that explain on the obtained outcomes, and a utilization of the integral equation demonstrates how significant they are in the literature.