Abstract
A multivariate folded normal distribution is a distribution of the absolute value of a Gaussian random vector. In this paper, we provide the marginal and conditional distributions of the multivariate folded normal distribution, and also prove that independence and non-correlation are equivalent for it. In addition, we provide a numerical approach using the R language to fit a multivariate folded normal distribution. The accuracy of the estimated mean and variance parameters is then examined. Finally, a real data application to body mass index data are presented.
Keywords:
multivariate folded normal distribution; marginal and conditional density functions; maximum likelihood estimation MSC:
62F10
1. Introduction
Let be a normal random variable with a mean and a variance . The normal distribution has been widely used in various applications. However, as pointed out by Leone et al. and Johnson [1,2], in many situations, the algebraic sign of measurements is irretrievably lost. Consequently, the concept of a folded normal random variable arises to describe the absolute value of a normal random variable. It is denoted by , where and are parameters.
In recent decades, the folded normal distribution has been extensively discussed in various applications. Applications include, but are not limited to, principal arc analysis on direct product manifolds [3], asymmetric multivariate stochastic volatility models [4], ongoing clinical trials while the randomized treatment codes remain blinded [5], fitting insurance loss data [6], the determination of reliability density function when the failure rate is a folded random variable [7], the detrended fluctuation analysis of EEG in detecting cross-modal plasticity in the brain from blind and blindfolded normal individuals [8], electromagnetic transport components and sheared flows in drift–Alfven turbulence [9], and DNA interactions visualized using electron microscopy [10].
In addition to the widespread applications of the folded normal distribution, properties including the characteristic and moment-generating functions, characteristics of stochastic ordering, and the parameter estimations of and have also been discussed in [3,11,12,13,14,15,16,17].
Several studies have investigated the multivariate folded normal distribution. For instance, Psarakis and Panaretos [18] generalized the folded normal distribution to the bivariate case, where they proved that the marginal distributions of the bivariate folded standard normal distribution are folded standard normal distributions. Recently, Chakraborty and Chatterjee [19] introduced the multivariate folded normal distribution, where the mean vector, dispersion matrix, and the moment-generating function of the multivariate folded normal distribution were derived and corrected later in Murthy [20]. To our knowledge, neither the marginal and conditional distributions nor the parameter estimation of the multivariate folded normal distribution has been provided. In this paper, we will fill in these gaps.
The rest of the paper is organized as follows. In Section 2, the properties of the multivariate folded normal distribution are discussed. Specifically, we provide the marginal and conditional distributions of the multivariate folded normal distribution and also prove that independence and non-correlation are equivalent for the multivariate folded normal distribution. In Section 3, the parameter estimations of the multivariate folded normal distribution are investigated.
2. Properties of a Multivariate Folded Normal Distribution
In this section, the properties of a multivariate folded normal distribution are discussed. Specifically, we provide the marginal and conditional distributions of the multivariate folded normal distribution and also prove that independence and non-correlation are equivalent for the multivariate folded normal distribution.
First, let us recall the definition of the n-dimensional folded normal random vector. More details can be found in [19].
Definition 1.
A random vector is said to have a multivariate folded normal distribution with a real vector and a symmetric positive definite matrix , if its probability density function is given by
where
represents a possible sign vector, and the diagonal sign matrix is . We further denote for simplicity.
The parameters and in the above definition are the mean vector and variance matrix of the corresponding n-dimensional random vector with multivariate normal distribution . Without loss of generality, we assume the variance matrix is positive and definite. Otherwise, is singular, and the corresponding multivariate folded normal distribution is degenerate.
Then, we derive the marginal and conditional density functions of a multivariate folded normal distribution as follows.
Proposition 1.
Let . If , Σ and are partitioned as follows,
where , , , . . In addition, with
Then
- (1)
- and
- (2)
- , where
Proof.
(1) Let be a multivariate normal random vector satisfying
Then, we denote
According to the properties of the multivariate normal distribution, we have and . Thus,
(2) For with , we have
It is well known that the submatrix if is positive definite. Since the inverse of the block matrix is
we have
where
Furthermore, the determinant of the block matrix is
For with , we have
Therefore, the conclusion follows. □
In general, random variables may be uncorrelated but statistically dependent. However, when random variables are distributed with a multivariate normal distribution, being uncorrelated is equivalent to being independent. The equivalence of independence and non-correlation is demonstrated in Proposition 2 for the multivariate folded normal distribution.
Proposition 2.
Let . If , Σ and are partitioned as follows:
where , , , . and with
then and are independent if and only if .
Proof.
The necessity is trivial because independent random vectors are uncorrelated. We only prove the sufficiency. If , according to Proposition 1, we have . Therefore, and are independent. This completes the proof of the proposition. □
3. Parameter Estimation
Suppose that we have an independently and identically distributed data set sampled from a multivariate folded normal distribution . This section discusses the parameter estimations of and via maximum likelihood.
First, of all, the log-likelihood function is the logarithm of the product of m multivariate folded normal density functions in the following.
Taking the derivative with respect to matrices and separately, we can derive Equation (1) as follows.
Unfortunately, no analytical solutions exist for Equation (1) even for the univariate folded normal distribution when setting them to zero. As a result, numerical solutions are necessary to approximate the solutions. Various algorithms have been developed for the univariate case, such as the EM algorithm proposed by Jung et al. [3,21] in Matlab, and Newton-type optimization algorithms introduced by Tsagris et al. and MacDonald [11,13,14] in the R language [22]. However, to the best of our knowledge, no algorithm has been provided to solve the maximum likelihood estimators (MLEs) of a multivariate folded normal distribution.
Motivated by the Newton-type optimization algorithms in Tsagris et al. and MacDonald [11,13,14], we employ the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm, which is a popular quasi-Newton optimization method, to fit a multivariate folded normal distribution.
Theoretically, we assume that the covariance matrix is positive definite. However, this assumption may not always hold in numerical realization during the parameter estimation process, leading to meaningless estimations. To address this issue, we apply reparameterization using Cholesky decomposition on to ensure that remains positive definite. Specifically, we express as , where is a lower triangular matrix. Since is equivalent to and , we assume in the numerical realization that to ensure the positive definiteness of . By substituting for , the estimation equations follow as shown in (2).
Our algorithm to derive the MLEs of a multivariate folded normal distribution is written in R language [22] and is available at https://github.com/yfyang86/rfnorm/(accessed date 6 October 2023).
3.1. Simulation Studies
Numerical simulations are conducted to demonstrate the value and the accuracy of estimated parameters of a multivariate folded normal distribution.
3.1.1. An Example of Estimating Parameters
We began by generating 100 samples from a bivariate folded normal distribution with mean parameters and the covariance matrix given by:
Next, we computed the sample means and performed Cholesky decomposition on the sample covariance matrix to obtain the lower triangular matrix as the initial values. Using our algorithm, we obtained the maximum likelihood estimators (MLEs) for the bivariate folded normal distribution as follows:
Estimated means:
Estimated covariance matrix: = .
These results highlight the accuracy of our estimation method in capturing the underlying parameters of the bivariate folded normal distribution based on the given samples.
3.1.2. Accuracy of Estimated Parameters
Additional simulations are performed to assess the accuracy of the estimated parameter values through confidence intervals for both bivariate and four-dimensional folded normal distributions. In this context, the term “accuracy” refers to the estimated coverage probability of the confidence intervals for the parameters. Following the approach of Tsagris et al. [11], confidence intervals are calculated using the normal approximation, where the variance matrix is estimated using the inverse of the Hessian matrix.
In each scenario of the following simulations, we conducted 1000 repeated experiments, varying the sample sizes from 20 to 100. The ratios of mean to standard deviation are denoted by , where . Here, represents the bivariate case, while corresponds to the four-dimensional case.
The results of the simulations for the bivariate case are summarized in Table 1. These tables provide a comprehensive overview of the various simulation scenarios and the corresponding accuracy of the estimated parameter values based on the confidence intervals.

Table 1.
A summary of simulations .
As shown in Table 1, considering a bivariate case, four scenarios are simulated in total. The first scenario is a baseline in our simulations for a bivariate case, which is compared with each of the remaining three simulated scenarios. In the first scenario, we set and thus . The values of range from 0.5 to 2.5, and the covariance matrix is fixed to
Table 2 shows the coverage of the confidence intervals for the mean parameters at different pairs of sample sizes and ratios for the bivariate folded normal distribution. The rows correspond to the sample size, whereas the columns correspond to the ratio vectors .

Table 2.
Estimated coverage probability of the confidence intervals of the mean parameters.
Table 3 shows the coverage of the confidence intervals for the variance parameters at different pairs of sample sizes and ratios for the bivariate folded normal distribution, where . The rows correspond to the sample size, whereas the columns correspond to the ratio vectors .

Table 3.
Estimated coverage probability of the 95% confidence intervals of the variance parameters.
Table 2 and Table 3 show that the accuracy of estimated mean and variance parameters slightly increases when sample size increases, while it dramatically increases and reaches the desired nominal when the ratios of the mean to standard deviation increase.
We also derive similar Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6 (in Appendix A) for the remaining three scenarios. Fixing the variances while increasing the and in the second scenario, the accuracy of the estimated and dramatically increases, especially when is less than 1 (Table A1 and Table A2). Fixing the while increasing and in the third scenario, the accuracy of estimated mean and variance parameters are almost equal to that in the first scenario (Table A3 and Table A4). Our algorithm works when is nearly singular in the fourth scenario. The accuracy of estimated mean parameters is similar to that of the first scenario. However, the accuracy of the estimated variance parameters dramatically decreases, which can increase when the sample size increases (Table A5 and Table A6). The above findings are summarized in the following table (Table 4).

Table 4.
A summary of findings in simulations .
Like the bivariate case, the settings in the four-dimensional case are as follows. The ratios of mean to standard deviation range from 0.5 to 2.5, with . Table 5 and Table 6 show the coverage of the confidence intervals for mean parameters and the variance parameters at different pairs of sample size and ratios for the four-dimensional folded normal distribution. The rows correspond to the sample size, whereas the columns correspond to the ratio vectors . The variance parameters are , where the th element of is . Here, .

Table 5.
Estimated coverage probability of the 95% confidence intervals of the mean parameters.

Table 6.
Estimated coverage probability of the 95% confidence intervals of the variance parameters.
As indicated in Table 5 and Table 6, similar to the findings in the bivariate case, the accuracy of the estimated mean, and variance parameters exhibit a slight improvement as the sample size increases. However, a dramatically improvement is observed when the ratios of the mean to standard deviation increase, eventually reaching the desired nominal coverage probability. These results highlight the impact of both sample size and the ratios of mean to standard deviation on the accuracy of parameter estimation in the multivariate folded normal distributions.
In addition to Table 5 and Table 6, we obtained similar Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 (in Appendix A) from simulated scenarios 6–8. The findings are summarized as follows (Table 7).

Table 7.
A summary of findings in simulations .
3.2. Real Data Application
We applied our algorithm to fit a bivariate folded normal distribution on real data. The real data contains 700 observations of body mass index and age of New Zealand adults, which can be accessed through the R package VGAM [23], as introduced by Tsagris et al. [11]. These observations were sampled from the Fletcher Challenge/Auckland Heart and Health survey. Further details regarding the real data can be found in [24]. Figure 1 presents two panels of perspective plots that visualize the three-dimensional density of the observations. The left panel displays the parametric density, specifically the folded normal density, while the right panel showcases the non-parametric density based on the kernel density estimation of the observations. These plots provide a visual representation of the distribution of the real data in both the parametric and non-parametric contexts.
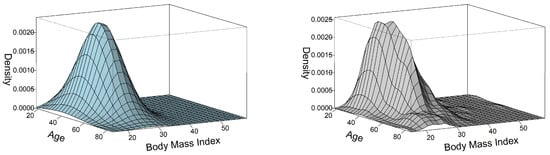
Figure 1.
The perspective plot on the left shows the fitted folded normal density, and the perspective plot on the right shows the kernel density of the observations.
Applying our algorithm to fit the real data, we obtained the estimated mean of age and BMI of 43.74 and 26.69, respectively. The estimate of the corresponding covariance matrix is .
4. Conclusions
In this paper, we have established the marginal and conditional distributions of the multivariate folded normal distribution, which serves as a fundamental probability property for further investigations and applications involving this distribution. Notably, we have demonstrated an interesting result that independence and non-correlation are equivalent concepts within the multivariate folded normal distribution framework.
Furthermore, we have presented a numerical approach implemented in the R language, utilizing the BFGS algorithm, to fit a multivariate folded normal distribution. To assess the accuracy of parameter estimation, we have employed simulation studies to obtain confidence intervals based on asymptotic theory. Through the simulations, we evaluated the coverage of these confidence intervals for the mean and variance parameters across eight different scenarios. We observed that in cases with small sample sizes or when the ratio of the mean to the standard deviation was lower than 1, the coverage of the confidence intervals was lower than the desired nominal level.
Additionally, we have showcased a real data application of the bivariate folded normal distribution to body mass index data. This application serves as empirical evidence supporting the efficient utilization of the multivariate folded normal distribution for fitting non-negative data.
Overall, this paper contributes to the understanding and practical implementation of the multivariate folded normal distribution, highlighting its potential applications and providing insights into parameter estimation and inference. Further research can focus on developing robust estimation methods and improving the accuracy of confidence intervals, particularly in cases with small sample sizes or challenging data characteristics.
Author Contributions
X.L. and Y.J. drafted the proofs, X.L. and Y.Y. prepared the MLE algorithm and simulations. X.P. led the study and drafted the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data was generated in this study.
Acknowledgments
We sincerely appreciate editor and reviewers for their insightful comments and suggestions, which significantly improved and clarified the presentation of our paper.
Conflicts of Interest
Author Yifan Yang was employed by Transwarp Technology (Shanghai) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
This section reports the tables of the accuracy of estimated mean and variance parameters in simulated scenarios 2–4 and 6–8, respectively.
In the second scenario, we set , and thus . The values of range from 0.5 to 2.5, and the covariance matrix is fixed to The accuracy of estimated mean and variance parameters are in Table A1 and Table A2.

Table A1.
Estimated coverage probability of the confidence intervals of the mean parameters (Scenario 2).
Table A1.
Estimated coverage probability of the confidence intervals of the mean parameters (Scenario 2).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 2.5) | (1, 2.5) | (1.5, 2.5) | (2, 2.5) | (2.5, 2.5) |
| 20 | (0.72, 0.94) | (0.90, 0.94) | (0.94, 0.94) | (0.94, 0.94) | (0.94, 0.94) |
| 30 | (0.73, 0.95) | (0.88, 0.95) | (0.93, 0.95) | (0.94, 0.95) | (0.93, 0.95) |
| 40 | (0.79, 0.94) | (0.93, 0.94) | (0.95, 0.94) | (0.93, 0.94) | (0.93, 0.94) |
| 50 | (0.78, 0.94) | (0.91, 0.93) | (0.96, 0.93) | (0.94, 0.93) | (0.94, 0.93) |
| 60 | (0.77, 0.94) | (0.90, 0.94) | (0.95, 0.94) | (0.95, 0.94) | (0.95, 0.94) |
| 70 | (0.77, 0.94) | (0.90, 0.94) | (0.95, 0.94) | (0.94, 0.94) | (0.94, 0.94) |
| 80 | (0.78, 0.94) | (0.91, 0.94) | (0.96, 0.94) | (0.94, 0.94) | (0.94, 0.94) |
| 90 | (0.78, 0.96) | (0.93, 0.96) | (0.96, 0.96) | (0.96, 0.96) | (0.95, 0.96) |
| 100 | (0.78, 0.95) | (0.93, 0.95) | (0.95, 0.95) | (0.94, 0.95) | (0.94, 0.95) |

Table A2.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 2).
Table A2.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 2).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 2.5) | (1, 2.5) | (1.5, 2.5) | (2, 2.5) | (2.5, 2.5) |
| 20 | (0.74, 0.84, 0.87) | (0.83, 0.91, 0.87) | (0.86, 0.94, 0.87) | (0.87, 0.94, 0.87) | (0.88, 0.94, 0.87) |
| 30 | (0.76, 0.86, 0.88) | (0.83, 0.90, 0.88) | (0.87, 0.94, 0.88) | (0.89, 0.96, 0.88) | (0.90, 0.96, 0.88) |
| 40 | (0.80, 0.87, 0.91) | (0.84, 0.90, 0.91) | (0.90, 0.93, 0.91) | (0.91, 0.94, 0.91) | (0.91, 0.94, 0.91) |
| 50 | (0.81, 0.87, 0.92) | (0.85, 0.93, 0.92) | (0.91, 0.96, 0.92) | (0.93, 0.96, 0.92) | (0.93, 0.96, 0.92) |
| 60 | (0.81, 0.86, 0.92) | (0.84, 0.92, 0.92) | (0.89, 0.94, 0.92) | (0.91, 0.95, 0.92) | (0.91, 0.95, 0.92) |
| 70 | (0.81, 0.85, 0.91) | (0.84, 0.91, 0.91) | (0.91, 0.95, 0.91) | (0.92, 0.95, 0.91) | (0.92, 0.96, 0.91) |
| 80 | (0.82, 0.87, 0.92) | (0.86, 0.92, 0.92) | (0.93, 0.94, 0.92) | (0.94, 0.94, 0.92) | (0.92, 0.94, 0.92) |
| 90 | (0.82, 0.86, 0.93) | (0.87, 0.92, 0.93) | (0.93, 0.96, 0.93) | (0.94, 0.95, 0.93) | (0.94, 0.95, 0.93) |
| 100 | (0.82, 0.87, 0.93) | (0.86, 0.93, 0.93) | (0.93, 0.96, 0.93) | (0.94, 0.96, 0.93) | (0.93, 0.96, 0.93) |
In the third scenario, we set , and . The values of range from 0.5 to 2.5, and the covariance matrix is fixed to The accuracy of estimated mean and variance parameters are in Table A3 and Table A4.

Table A3.
Estimated coverage probability of the confidence intervals of the mean parameters (Scenario 3).
Table A3.
Estimated coverage probability of the confidence intervals of the mean parameters (Scenario 3).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5) | (1, 1) | (1.5, 1.5) | (2, 2) | (2.5, 2.5) |
| 20 | (0.66, 0.70) | (0.89, 0.90) | (0.94, 0.94) | (0.94, 0.95) | (0.94, 0.95) |
| 30 | (0.66, 0.66) | (0.87, 0.89) | (0.94, 0.95) | (0.93, 0.94) | (0.93, 0.94) |
| 40 | (0.71, 0.72) | (0.91, 0.90) | (0.96, 0.95) | (0.94, 0.94) | (0.93, 0.94) |
| 50 | (0.71, 0.69) | (0.89, 0.90) | (0.95, 0.95) | (0.93, 0.94) | (0.93, 0.94) |
| 60 | (0.67, 0.73) | (0.90, 0.92) | (0.96, 0.95) | (0.95, 0.94) | (0.94, 0.94) |
| 70 | (0.70, 0.72) | (0.89, 0.91) | (0.95, 0.95) | (0.95, 0.95) | (0.95, 0.94) |
| 80 | (0.71, 0.74) | (0.91, 0.91) | (0.95, 0.94) | (0.94, 0.94) | (0.94, 0.94) |
| 90 | (0.72, 0.73) | (0.92, 0.90) | (0.97, 0.96) | (0.96, 0.96) | (0.96, 0.96) |
| 100 | (0.71, 0.72) | (0.90, 0.92) | (0.94, 0.96) | (0.94, 0.96) | (0.93, 0.95) |

Table A4.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 3).
Table A4.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 3).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5) | (1, 1) | (1.5, 1.5) | (2, 2) | (2.5, 2.5) |
| 20 | (0.70, 0.78, 0.70) | (0.81, 0.87, 0.81) | (0.86, 0.93, 0.85) | (0.87, 0.95, 0.87) | (0.87, 0.95, 0.86) |
| 30 | (0.72, 0.77, 0.70) | (0.82, 0.86, 0.82) | (0.88, 0.94, 0.87) | (0.89, 0.96, 0.88) | (0.89, 0.95, 0.89) |
| 40 | (0.77, 0.80, 0.76) | (0.82, 0.89, 0.84) | (0.88, 0.95, 0.89) | (0.90, 0.95, 0.90) | (0.91, 0.96, 0.90) |
| 50 | (0.78, 0.77, 0.76) | (0.84, 0.91, 0.85) | (0.90, 0.96, 0.91) | (0.92, 0.96, 0.92) | (0.92, 0.95, 0.92) |
| 60 | (0.75, 0.77, 0.78) | (0.85, 0.90, 0.87) | (0.90, 0.94, 0.91) | (0.92, 0.95, 0.92) | (0.92, 0.95, 0.92) |
| 70 | (0.78, 0.79, 0.79) | (0.84, 0.88, 0.84) | (0.92, 0.94, 0.90) | (0.93, 0.94, 0.91) | (0.94, 0.94, 0.91) |
| 80 | (0.80, 0.79, 0.80) | (0.87, 0.91, 0.86) | (0.93, 0.94, 0.91) | (0.94, 0.95, 0.90) | (0.94, 0.95, 0.91) |
| 90 | (0.79, 0.79, 0.78) | (0.86, 0.90, 0.87) | (0.93, 0.95, 0.93) | (0.93, 0.95, 0.93) | (0.92, 0.94, 0.94) |
| 100 | (0.78, 0.78, 0.78) | (0.86, 0.92, 0.87) | (0.93, 0.97, 0.93) | (0.93, 0.97, 0.93) | (0.93, 0.97, 0.93) |
In the fourth scenario, we consider a near singular scenario. The values of range from 0.5 to 2.5, and the covariance matrix is fixed to The accuracy of estimated mean and variance parameters are in Table A5 and Table A6.

Table A5.
Estimated coverage probability of the confidence intervals of the mean parameters (Scenario 4).
Table A5.
Estimated coverage probability of the confidence intervals of the mean parameters (Scenario 4).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5) | (1, 1) | (1.5, 1.5) | (2, 2) | (2.5, 2.5) |
| 20 | (0.73, 0.74) | (0.91, 0.91) | (0.94, 0.94) | (0.95, 0.95) | (0.95, 0.94) |
| 30 | (0.71, 0.71) | (0.91, 0.91) | (0.94, 0.94) | (0.94, 0.94) | (0.94, 0.94) |
| 40 | (0.74, 0.73) | (0.92, 0.92) | (0.94, 0.94) | (0.94, 0.94) | (0.94, 0.94) |
| 50 | (0.71, 0.72) | (0.92, 0.92) | (0.94, 0.94) | (0.93, 0.94) | (0.93, 0.93) |
| 60 | (0.76, 0.76) | (0.91, 0.91) | (0.95, 0.95) | (0.94, 0.94) | (0.94, 0.94) |
| 70 | (0.73, 0.73) | (0.92, 0.92) | (0.94, 0.94) | (0.94, 0.94) | (0.94, 0.94) |
| 80 | (0.76, 0.76) | (0.93, 0.92) | (0.95, 0.95) | (0.95, 0.95) | (0.95, 0.95) |
| 90 | (0.75, 0.76) | (0.92, 0.92) | (0.96, 0.96) | (0.95, 0.96) | (0.96, 0.96) |
| 100 | (0.71, 0.71) | (0.92, 0.92) | (0.95, 0.95) | (0.94, 0.94) | (0.95, 0.94) |

Table A6.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 4).
Table A6.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 4).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5) | (1, 1) | (1.5, 1.5) | (2, 2) | (2.5, 2.5) |
| 20 | (0.58, 0.58, 0.59) | (0.74, 0.75, 0.74) | (0.82, 0.82, 0.82) | (0.84, 0.84, 0.84) | (0.85, 0.84, 0.84) |
| 30 | (0.62, 0.61, 0.61) | (0.78, 0.79, 0.78) | (0.85, 0.85, 0.85) | (0.88, 0.87, 0.87) | (0.87, 0.88, 0.88) |
| 40 | (0.69, 0.69, 0.69) | (0.84, 0.83, 0.83) | (0.88, 0.88, 0.88) | (0.89, 0.89, 0.89) | (0.89, 0.89, 0.89) |
| 50 | (0.69, 0.69, 0.70) | (0.84, 0.84, 0.84) | (0.90, 0.90, 0.90) | (0.92, 0.92, 0.92) | (0.93, 0.92, 0.92) |
| 60 | (0.72, 0.73, 0.73) | (0.86, 0.86, 0.85) | (0.89, 0.90, 0.90) | (0.91, 0.91, 0.91) | (0.92, 0.92, 0.92) |
| 70 | (0.72, 0.72, 0.72) | (0.85, 0.86, 0.85) | (0.88, 0.88, 0.88) | (0.90, 0.90, 0.90) | (0.90, 0.91, 0.91) |
| 80 | (0.72, 0.72, 0.72) | (0.86, 0.86, 0.86) | (0.89, 0.90, 0.89) | (0.90, 0.90, 0.90) | (0.90, 0.90, 0.90) |
| 90 | (0.73, 0.73, 0.73) | (0.85, 0.86, 0.86) | (0.91, 0.91, 0.91) | (0.92, 0.92, 0.93) | (0.94, 0.94, 0.94) |
| 100 | (0.74, 0.74, 0.73) | (0.87, 0.87, 0.86) | (0.92, 0.92, 0.93) | (0.94, 0.94, 0.94) | (0.95, 0.94, 0.94) |
In the sixth scenario, we consider , . The values of range from 0.5 to 2.5, and the covariance matrix is fixed to The accuracy of estimated mean and variance parameters are in Table A7 and Table A8.

Table A7.
Estimated coverage probability of the 95% confidence intervals of the mean parameters (Scenario 6).
Table A7.
Estimated coverage probability of the 95% confidence intervals of the mean parameters (Scenario 6).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5, 0.5, 2.5) | (1, 1, 1, 2.5) | (1.5, 1.5, 1.5, 2.5) | (2, 2, 2, 2.5) | (2.5, 2.5, 2.5, 2.5) |
| 20 | (0.70, 0.71, 0.70, 0.93) | (0.82, 0.84, 0.84, 0.94) | (0.90, 0.93, 0.91, 0.94) | (0.92, 0.94, 0.93, 0.94) | (0.93, 0.94, 0.93, 0.93) |
| 30 | (0.65, 0.68, 0.66, 0.94) | (0.82, 0.84, 0.84, 0.94) | (0.93, 0.92, 0.93, 0.94) | (0.94, 0.93, 0.93, 0.94) | (0.94, 0.93, 0.93, 0.94) |
| 40 | (0.67, 0.67, 0.70, 0.94) | (0.85, 0.82, 0.84, 0.94) | (0.93, 0.93, 0.93, 0.94) | (0.94, 0.93, 0.93, 0.94) | (0.94, 0.94, 0.92, 0.94) |
| 50 | (0.67, 0.68, 0.70, 0.94) | (0.85, 0.84, 0.85, 0.94) | (0.94, 0.94, 0.94, 0.94) | (0.95, 0.94, 0.94, 0.94) | (0.95, 0.94, 0.94, 0.94) |
| 60 | (0.68, 0.69, 0.67, 0.95) | (0.86, 0.86, 0.86, 0.95) | (0.94, 0.94, 0.94, 0.95) | (0.94, 0.94, 0.94, 0.95) | (0.94, 0.94, 0.94, 0.95) |
| 70 | (0.70, 0.68, 0.69, 0.95) | (0.88, 0.87, 0.85, 0.95) | (0.94, 0.96, 0.94, 0.95) | (0.94, 0.96, 0.93, 0.95) | (0.93, 0.96, 0.94, 0.95) |
| 80 | (0.72, 0.68, 0.69, 0.95) | (0.88, 0.86, 0.89, 0.95) | (0.95, 0.95, 0.95, 0.95) | (0.95, 0.94, 0.94, 0.95) | (0.94, 0.95, 0.94, 0.95) |
| 90 | (0.70, 0.70, 0.72, 0.95) | (0.89, 0.87, 0.88, 0.95) | (0.95, 0.95, 0.96, 0.95) | (0.95, 0.95, 0.96, 0.95) | (0.95, 0.95, 0.95, 0.95) |
| 100 | (0.70, 0.70, 0.70, 0.96) | (0.90, 0.90, 0.88, 0.96) | (0.95, 0.96, 0.93, 0.96) | (0.95, 0.95, 0.94, 0.96) | (0.95, 0.95, 0.94, 0.96) |

Table A8.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 6).
Table A8.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 6).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5, 0.5, 2.5) | (1, 1, 1, 2.5) | (1.5, 1.5, 1.5, 2.5) | (2, 2, 2, 2.5) | (2.5, 2.5, 2.5, 2.5) |
| 20 | |||||
| 50 | |||||
| 100 |
In the seventh scenario, we consider , and . The values of range from 0.5 to 2.5, and the covariance matrix is fixed to The accuracy of estimated mean and variance parameters are in Table A9 and Table A10.

Table A9.
Estimated coverage probability of the 95% confidence intervals of the mean parameters (Scenario 7).
Table A9.
Estimated coverage probability of the 95% confidence intervals of the mean parameters (Scenario 7).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5, 0.5, 0.5) | (1, 1, 1, 1) | (1.5, 1.5, 1.5, 1.5) | (2, 2, 2, 2) | (2.5, 2.5, 2.5, 2.5) |
| 20 | (0.68, 0.68, 0.68, 0.71) | (0.82, 0.82, 0.83, 0.83) | (0.91, 0.91, 0.90, 0.92) | (0.93, 0.93, 0.93, 0.93) | (0.93, 0.94, 0.93, 0.93) |
| 30 | (0.64, 0.60, 0.64, 0.67) | (0.84, 0.81, 0.82, 0.83) | (0.92, 0.91, 0.93, 0.92) | (0.94, 0.94, 0.94, 0.94) | (0.93, 0.93, 0.93, 0.94) |
| 40 | (0.62, 0.61, 0.63, 0.64) | (0.84, 0.82, 0.83, 0.82) | (0.94, 0.93, 0.94, 0.93) | (0.95, 0.93, 0.95, 0.93) | (0.95, 0.93, 0.95, 0.93) |
| 50 | (0.60, 0.63, 0.65, 0.64) | (0.82, 0.82, 0.83, 0.84) | (0.93, 0.94, 0.94, 0.94) | (0.93, 0.94, 0.95, 0.94) | (0.93, 0.94, 0.95, 0.94) |
| 60 | (0.62, 0.65, 0.62, 0.63) | (0.85, 0.85, 0.82, 0.86) | (0.94, 0.94, 0.93, 0.95) | (0.95, 0.94, 0.94, 0.95) | (0.94, 0.94, 0.93, 0.94) |
| 70 | (0.60, 0.59, 0.59, 0.63) | (0.84, 0.83, 0.85, 0.85) | (0.95, 0.94, 0.94, 0.95) | (0.96, 0.94, 0.93, 0.96) | (0.96, 0.94, 0.93, 0.96) |
| 80 | (0.62, 0.64, 0.60, 0.64) | (0.84, 0.86, 0.86, 0.86) | (0.95, 0.95, 0.96, 0.96) | (0.95, 0.94, 0.95, 0.94) | (0.95, 0.94, 0.94, 0.94) |
| 90 | (0.63, 0.59, 0.59, 0.65) | (0.88, 0.85, 0.88, 0.87) | (0.95, 0.95, 0.95, 0.95) | (0.95, 0.95, 0.95, 0.95) | (0.95, 0.94, 0.95, 0.95) |
| 100 | (0.63, 0.65, 0.63, 0.64) | (0.87, 0.88, 0.89, 0.87) | (0.95, 0.95, 0.95, 0.95) | (0.95, 0.94, 0.95, 0.94) | (0.95, 0.94, 0.95, 0.94) |

Table A10.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 7).
Table A10.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 7).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5, 0.5, 0.5) | (1, 1, 1, 1) | (1.5, 1.5, 1.5, 1.5) | (2, 2, 2, 2) | (2.5, 2.5, 2.5, 2.5) |
| 20 | |||||
| 50 | |||||
| 100 |
In the eighth scenario, we consider a near singular scenario. The values of range from 0.5 to 2.5, and the covariance matrix is fixed to The accuracy of estimated mean and variance parameters are in Table A11 and Table A12.

Table A11.
Estimated coverage probability of the 95% confidence intervals of the mean parameters (Scenario 8).
Table A11.
Estimated coverage probability of the 95% confidence intervals of the mean parameters (Scenario 8).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5, 0.5, 0.5) | (1, 1, 1, 1) | (1.5, 1.5, 1.5, 1.5) | (2, 2, 2, 2) | (2.5, 2.5, 2.5, 2.5) |
| 20 | (0.84, 0.84, 0.83, 0.84) | (0.88, 0.87, 0.88, 0.87) | (0.90, 0.90, 0.90, 0.90) | (0.92, 0.92, 0.92, 0.92) | (0.93, 0.93, 0.93, 0.92) |
| 30 | (0.79, 0.79, 0.78, 0.79) | (0.89, 0.89, 0.89, 0.89) | (0.92, 0.92, 0.92, 0.92) | (0.93, 0.93, 0.93, 0.93) | (0.93, 0.93, 0.93, 0.93) |
| 40 | (0.78, 0.77, 0.78, 0.78) | (0.87, 0.86, 0.86, 0.87) | (0.93, 0.92, 0.93, 0.92) | (0.94, 0.93, 0.93, 0.93) | (0.94, 0.93, 0.94, 0.93) |
| 50 | (0.74, 0.72, 0.74, 0.73) | (0.88, 0.88, 0.88, 0.88) | (0.93, 0.93, 0.93, 0.93) | (0.93, 0.93, 0.94, 0.94) | (0.93, 0.93, 0.94, 0.94) |
| 60 | (0.73, 0.72, 0.73, 0.72) | (0.90, 0.89, 0.89, 0.90) | (0.93, 0.93, 0.93, 0.93) | (0.94, 0.94, 0.94, 0.94) | (0.94, 0.94, 0.94, 0.94) |
| 70 | (0.72, 0.72, 0.72, 0.72) | (0.89, 0.89, 0.89, 0.89) | (0.95, 0.94, 0.95, 0.95) | (0.95, 0.95, 0.95, 0.95) | (0.96, 0.96, 0.95, 0.96) |
| 80 | (0.73, 0.73, 0.74, 0.73) | (0.89, 0.89, 0.88, 0.89) | (0.94, 0.94, 0.94, 0.94) | (0.94, 0.94, 0.94, 0.94) | (0.94, 0.95, 0.94, 0.94) |
| 90 | (0.74, 0.74, 0.74, 0.74) | (0.91, 0.90, 0.90, 0.91) | (0.94, 0.94, 0.94, 0.94) | (0.94, 0.95, 0.94, 0.94) | (0.95, 0.95, 0.95, 0.95) |
| 100 | (0.70, 0.70, 0.69, 0.70) | (0.88, 0.88, 0.88, 0.88) | (0.93, 0.93, 0.93, 0.93) | (0.95, 0.94, 0.94, 0.95) | (0.95, 0.95, 0.95, 0.95) |

Table A12.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 8).
Table A12.
Estimated coverage probability of the 95% confidence intervals of the variance parameters (Scenario 8).
| Values | of | () | |||
|---|---|---|---|---|---|
| Sample Size | (0.5, 0.5, 0.5, 0.5) | (1, 1, 1, 1) | (1.5, 1.5, 1.5, 1.5) | (2, 2, 2, 2) | (2.5, 2.5, 2.5, 2.5) |
| 20 | |||||
| 50 | |||||
| 100 |
References
- Johnson, N.L. Cumulative sum control charts for the folded normal distribution. Technometrics 1963, 5, 451–458. [Google Scholar] [CrossRef]
- Leone, F.C.; Nottingham, R.B.; Nelson, L.S. The folded normal distribution. Technometrics 1961, 3, 543–550. [Google Scholar] [CrossRef]
- Jung, S.; Foskey, M.; Marron, J.S. Principal arc analysis on direct product manifolds. Ann. Appl. Stat. 2011, 5, 578–603. [Google Scholar] [CrossRef]
- Asai, M.; McAleer, M. Asymmetric multivariate stochastic volatility. Econom. Rev. 2006, 25, 453–473. [Google Scholar] [CrossRef]
- Chen, M.; Kianifard, F. Estimation of treatment difference and standard deviationwith blinded data in clinical trials. Biom. J. 2003, 45, 135–142. [Google Scholar] [CrossRef]
- Brazauskas, V.; Kleefeld, A. Folded and log-folded-t distributions as models for insurance loss data. Scand. Actuar. J. 2011, 59–74. [Google Scholar] [CrossRef]
- Yadavalli, V.S.S.; Singh, N. Determination of reliability density function when the failure rate is a random variable. Microelectron. Reliab. 1995, 35, 699–701. [Google Scholar] [CrossRef]
- Kalaivani, M.; Ravindran, G. Detrended fluctuation analysis of EEG in detecting cross-modal plasticity in brain for blind. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 3441–3444. [Google Scholar]
- Naulin, V. Electromagnetic transport components and sheared flows in drift-Alfven turbulence. Phys. Plasmas 2003, 10, 4016–4028. [Google Scholar] [CrossRef]
- Cherny, D.I.; Striker, G.; Subramaniam, V.; Jett, S.D.; Palecek, E.; Jovin, T.M. DNA bending due to specific p53 and p53 core domain-DNA interactions visualized by electron microscopy. J. Mol. Biol. 1999, 294, 1015–1026. [Google Scholar] [CrossRef]
- Tsagris, M.; Beneki, C.; Hassani, H. On the folded normal distribution. Mathematics 2014, 2, 12–28. [Google Scholar] [CrossRef]
- Elandt, R.C. The folded normal distribution: Two methods of estimating parameters from moments. Technometrics 1961, 3, 551–562. [Google Scholar] [CrossRef]
- Macdonald, I.L. Letter to the editor: Fitting a folded normal distribution without EM. Ann. Appl. Stat. 2020, 14, 2096–2098. [Google Scholar] [CrossRef]
- MacDonald, I.L. Rejoinder: Fitting a folded normal distribution without EM. Ann. Appl. Stat. 2020, 14, 2101. [Google Scholar] [CrossRef]
- Horn, P.S. On the Stochastic Ordering of Absolute Univariate Gaussian Random Variables. Ann. Stat. 1988, 16, 1327–1329. [Google Scholar] [CrossRef]
- Wang, B.; Wang, M. Stochastic ordering of folded normal random variables. Stat. Probab. Lett. 2011, 81, 524–528. [Google Scholar] [CrossRef]
- Yao, J.; Lou, B.; Pan, X. Characterizations of stochastic ordering for non-negative random variables. Stat. Probab. Lett. 2023, 203, 109919. [Google Scholar] [CrossRef]
- Psarakis, S.; Panaretos, J. On some bivariate extensions of the folded normal and the folded T distributions. J. Appl. Stat. Sci. 2001, 10, 119–136. [Google Scholar]
- Chakraborty, A.K.; Chatterjee, M. On multivariate folded normal distribution. Sankhya B 2013, 75, 1–15. [Google Scholar] [CrossRef]
- Murthy, G.S.R. A Note on Multivariate Folded Normal Distribution. Sankhyā Indian J. Stat. Ser. B (2008-) 2015, 77, 108–113. [Google Scholar] [CrossRef]
- Jung, S.; Foskey, M.; Marron, J.S. Response to ‘Fitting a folded normal distribution without EM’. Ann. Appl. Stat. 2020, 14, 2099–2100. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computingr; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Yee, T.W. The VGAM package for categorical data analysis. J. Stat. Softw. 2010, 32, 1–34. [Google Scholar] [CrossRef]
- MacMahon, S.; Norton, R.; Jackson, R.; Mackie, M.J.; Cheng, A.; Vander Hoorn, S.; Milne, A.; McCulloch, A. Fletcher challenge-university of Auckland heart and health study: Design and baseline findings. N. Z. Med. J. 1995, 108, 499–502. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).