Unsupervised Classification under Uncertainty: The Distance-Based Algorithm

Abstract

This paper presents a method for unsupervised classification of entities by a group of agents with unknown domains and levels of expertise. In contrast to the existing methods based on majority voting (“wisdom of the crowd”) and their extensions by expectation-maximization procedures, the suggested method first determines the levels of the agents’ expertise and then weights their opinions by their expertise level. In particular, we assume that agents will have relatively closer classifications in their field of expertise. Therefore, the expert agents are recognized by using a weighted Hamming distance between their classifications, and then the final classification of the group is determined from the agents’ classifications by expectation-maximization techniques, with preference to the recognized experts. The algorithm was verified and tested on simulated and real-world datasets and benchmarked against known existing algorithms. We show that such a method reduces incorrect classifications and effectively solves the problem of unsupervised collaborative classification under uncertainty, while outperforming other known methods.

1. Introduction

Classification under uncertainty by a group of agents is a common task that appears in different fields. In some applications it is formulated as a labeling process of similar entities (also called “instances”), while in others it is formulated as clustering procedures. For example, consider a group of physicians analyzing the medical records of a patient. Each physician analyzes the symptoms of the patient and diagnoses possible diseases, thus classifying or tagging the case with the disease name. The final diagnosis of the group is made based on the collective classifications provided by the group members. Naturally, with prior knowledge of the expertise of each physician, a larger weight can be given to those physicians who are experts in the specific disease. Note, however, that the challenge of reaching a collective decision is further enhanced when there is no prior knowledge on the agents’ expertise. This can be the case when ad hoc classifications are obtained by online surveys and questionnaires based on anonymous users with different yet unknown expertise levels.

One of the most popular methods to reach a collective classification based on a group of agents’ answers is known as the “wisdom of the crowd” (WOC). According to this approach, a decision can be reached based on the aggregated opinion of the agents, including both the experts and non-experts [1]. WOC is usually based on a majority (or plurality) vote, meaning that an opinion preferred by most of the agents is considered to be a correct answer. The WOC’s main assumption is that the expertise level of the agents is distributed somewhat symmetrically around the unknown true answer. Therefore, it makes sense to apply a majority vote procedure to obtain better accuracy (i.e., relying on the law of large numbers). Numerically, the majority vote is represented by the median statistics, and for a relatively large number of non-skewed agents, it effectively solves the group classification problem. Another setting where a majority vote is effective is when agents who make classifications have high and homogeneous levels of expertise in the considered field.

Nonetheless, in various settings, the WOC assumption does not hold. For example, in online questionnaires over the internet in specific fields, only a few of the users are real experts in the field, while most of the users are non-experts, and considering their opinions can seriously reduce the collective classification accuracy.

In this paper, we focus on ad hoc classification by a group of agents with unknown different levels of expertise. The suggested algorithm includes two stages:

-

Classification of the agents according to the levels of their expertise;

-

Classification of the entities with respect to the agents’ levels of expertise.

In other words, in the first stage, the algorithm recognizes the experts in the fields of the presented entities, and in the second stage it classifies the entities, preferring the opinions of these experts (for example, using some weighting scheme or expectation-maximization scheme).

In the classification of the agents, we assume that the agents with the same fields of expertise have relatively close or even the same opinions in their field of expertise, while the non-experts’ opinions (if they are not biased) are more scattered over other possible classifications. Accordingly, if the agents propose similar classes for the same entities, then these agents are considered to be experts in these classes. Consequently, a lower level of expertise can be associated with agents who are inconsistent in their opinions and create classes that differ from the classes proposed by the other agents. Certainly, if the levels of the agents’ expertise are known, then this stage can be omitted, and the problem can be reduced to the majority or plurality votes and further optimization procedures.

In the classification of the entities, one can utilize conventional methods such as combination of the weighted agents’ classifications. We follow the expectation-maximization (EM) approach as suggested by Dawid and Skene [2]. In the expectation (E) step, the algorithm estimates correct choices according to the agent’s expertise, and in the maximization (M) step, it maximizes the likelihood of the agent’s expertise with respect to the distances from the correct choices. To measure the distances between the agents’ classifications, we use the weighted Hamming distance, which is a normalized metric over the set of partitions that represent the agents’ classifications.

The suggested algorithm was validated and tested using simulated and real-world datasets [3,4]. The obtained classifications were compared against several approaches: (i) classifications obtained by a brute-force likelihood-maximization (LM) algorithm (see Section 4), (ii) majority vote (see Section 6.2.1), (iii) the recently developed fast Dawid–Skene (FDS) algorithm [5], and (iv) the widely known GLAD classification algorithm [6]. It was found that the proposed algorithm considerably outperforms these popular methods due to its higher accuracy and lower computation time.

The rest of this paper is organized as follows: In Section 2, we briefly overview the related methods that form a basis for the suggested techniques. Section 3 includes a formal description of the considered problem. In Section 4, we outline and clarify the brute-force likelihood-maximization algorithm, which is used for comparisons of the classifications of small datasets. Section 5 presents the suggested distance-based collaborative classification (DBCC) algorithm. Section 6 includes the results of the numerical simulations and the comparisons of the proposed DBCC algorithm with other classification techniques. Section 7 concludes the discourse.

2. Related Work

In terms of the classification problems, aggregation of the agents’ opinions is often treated as a proper application of crowdsourcing techniques. Chiu et al. [7] considered decision-making processes with crowdsourcing and outlined three potential roles of the crowd: intelligence (problem identification), design (alternative solutions), and choice (evaluation of alternatives). Each of these problems can be considered by different methods and, in particular, by recognition of the crowd’s preferences and choices of the alternatives based on these preferences, or in contrast, by as many alternating opinions as possible and further aggregation of these opinions into the unified one.

Crowd opinion aggregation is conducted by several methods and depends on the problem set. For example, Ma et al. [8] (2014) developed an algorithm for gradual aggregation based on measuring the distances between opinions at three similarity levels. In the above-considered problems, following the “wisdom of the crowd” (WOC) approach, the most commonly used aggregation technique was expectation maximization (EM) [9], which was also implemented in the well-known Dawid–Skene (DS) algorithm [2]. First, this algorithm was applied to analyze the error rate, and then it was extended to different problems that required an aggregation of opinions. In particular, Zhang et al. [10] proposed a two-stage version of the algorithm and justified its performance using spectral methods. Shah et al. [11] considered a permutation-based model and introduced a new error metric that compares different estimators in the DS algorithm. Finally, Sinha et al. [5] suggested a fast-executable version of the DS algorithm (termed the FDS algorithm), and at the estimation step (E-step) the dataset is estimated based on the current values of the parameters. Moreover, while at the maximization step (M-step), the values of the parameters are chosen such that the likelihood of the dataset is maximized. Starting from the initial estimates, the algorithm alternates between the M-step and the E-step until the estimates converge to a unified decision.

In parallel to the development of the DS method, other studies have focused on the data analysis phase of the problem, as well as on the possible extensions of the method to multilabel classifications. Following this direction, Duan et al. [12] proposed three statistical quality control models based on the DS algorithm. The authors incorporated label dependency to estimate the multiple true labels given crowdsourced multilabel agents for each instance (entity). Another approach based on the Bayesian models was suggested by Wei et al. [13], who considered the agent’s reliability and the dependency of the classes.

The EM-based methods were also enriched by learning methods to obtain a better classification. In particular, the techniques of multiple Gaussian processes enabled us to learn from the agents and estimate the reliability of the individual agents from the data without any prior knowledge. Groot et al. [14] and Rodrigues and Pereira [15] introduced different models based on standard Gaussian classifiers and presented a precise handling of multiple agents with different levels of expertise.

Other suggested methods for estimating the agents’ expertise levels were based on probabilistic methods. Using such an approach, Whitehill et al. [6] proposed a procedure for determining the agents’ expertise (called the GLAD algorithm), while Raykar et al. [16] suggested a method for estimating the classes’ true labels. Bachrach et al. [17] proposed a probabilistic graphical model that considered the entities, the agents’ expertise, and the true labels of the entities. Finally, since the considered problem could be deemed a framework of unsupervised learning, Rodrigues and Pereira [15] addressed it as a problem of deep learning using crowd opinions in neural networks. Moayedikia et al. [18] proposed an unsupervised approach based on optimization methods using the “harmony search” over different agent combinations.

Following the work of Chiu et al. [7], the present paper focuses on the evaluation of classification alternatives, where the crowd preferences are identified and analyzed ad hoc for further support of the decision-making process. This study presents a novel heuristic that follows the direction outlined in the DS algorithm and its faster FDS (fast DS) version. This study addresses the problem of unsupervised classification for a relatively small number of entities and varying levels of the agents’ expertise. The performance of the suggested heuristic is compared with several known approaches and, especially, with the performance of the popular majority voting method and the FDS algorithm.

3. Problem Setup

Let $X=\{x_1,x_2,\dots ,x_n\}$ be a set of $n$ entities that represent certain characteristics of some phenomenon, and let $j=1,2,\dots ,l$ be the labels by which the set of entities can be divided into $l$ classes $C_j\subset X$, such that ${\bigcup }_{j=1}^l{C}_j=X$ and $C_i\cap C_j=\varnothing$ while $i\ne j$. The set of the correct classes $C_j$ forms an ordered partition $\gamma =\{C_1,C_2,\dots ,C_l\}$, where the order of the classes is defined by the order of the labels in the sense that if the labels $i$ and $j$ holds $i<j$, then class $C_i$ precedes class $C_j$ in $\gamma$.

We assume that the classification of the entities is conducted by $m$ agents. Consequently, each $k$th agent, $k=1,2,\dots ,m$, generates a partition ${\alpha }_k=\{C_1^k,C_2^k,\dots ,C_l^k\}$ of the set $X$ by labeling the entities, and this partition represents the agent’s opinion on the considered phenomenon. Similar to the partition $\gamma$, the order in the agents’ partitions ${\alpha }_k$, $k=1,2,\dots ,m,$ is defined by the order of the labels $j=1,2,\dots ,l$. It is assumed that the agents are independent in their opinions. However, different agents, $u$ and $v$, $u\ne v$, can generate equivalent classifications ${\alpha }_u={\alpha }_v$, where $C_j^u=C_j^v$, $j=1,2,\dots ,l$. In addition, it is assumed that for each class, $C_j\subset X$, $j=1,2,\dots ,l$, there exists at least one agent $u$ who is an expert in this class. This assumption implies that if the correct classification $\gamma =\{C_1,C_2,\dots ,C_l\}$ is available, class $C_j^u$ from the agent’s classification ${\alpha }_u$ is equivalent to class $C_j$ from the correct classification $\gamma$.

The considered problem is formulated as follows: given the set $X=\{x_1,x_2,{\dots ,x}_n\}$ of entities and the set $\mathcal{A}=\left\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m\right\}$ of classifications created by $m$ experts using $l$ labels, find a classification ${\gamma }^{*}=\{C_1^{*},C_2^{*},\dots ,C_l^{*}\}$, $l\le n$, which is as close as possible to the unknown correct classification $\gamma =\{C_1,C_2,\dots ,C_l\}$.

To clarify the problem, let us consider a toy example of the dataset presented in Table 1. The dataset consists of $n=12$ entities classified by $m=6$ agents with $l=4$ classes. The unknown correct classification is denoted by $\gamma$. In addition, we use ${\gamma }_M$ to denote the classification obtained by the majority vote.

Table 1. Example of the simulated data with the correct classification and the majority vote for $m=6$ agents classifying $n=12$ entities by $l=4$ classes.

	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$	${\mathit{a}}_6$	$\mathit{\gamma }$	${\mathit{\gamma }}_{\mathit{M}}$
$1$	2	2	2	4	3	1	2	2
$2$	1	3	1	4	3	1	1	1
$3$	3	2	2	1	1	1	2	1
$4$	4	4	4	3	1	3	3	4
$5$	4	4	4	3	2	3	3	4
$6$	1	3	1	1	2	2	1	1
$7$	4	3	3	1	4	4	4	4
$8$	1	3	1	2	2	2	1	2
$9$	3	3	4	2	4	4	4	4
$10$	3	2	2	1	1	1	2	1
$11$	4	3	4	3	2	3	3	3
$12$	3	3	3	1	4	4	4	3
Accuracy	42%	33%	58%	33%	25%	58%	−	50%

The columns in the table are denoted by ${\left(r_{\mathrm{1,1}},r_{\mathrm{2,1}},\dots ,r_{\mathrm{12,1}}\right)}^T$, …, ${\left(r_{\mathrm{1,6}},r_{\mathrm{2,6}},\dots ,r_{\mathrm{12,6}}\right)}^T$, where the table entry $r_{i,k}$ represents the classification of element $x_{\mathrm{i}}$ by agent $a_k$ to one of the classes $C_1$, $C_2$, $C_3$, and $C_4$. The actual table entries are the tags of the corresponding class, namely, $1$, $2$, $3,$ and $4$.

In this example, we assume that the first agent, $k=1,$ is an expert in class $C_1$, the second agent, $k=2$, is an expert in class $C_2$, the third agent, $k=3$, is an expert in classes $C_1$ and $C_2$, the fourth agent, $k=4,$ is an expert in class $C_3$, the fifth agent, $k=5,$ is an expert in class $C_4$, and finally, the sixth agent, $k=6$, is an expert in the last classes $C_3$ and $C_4$. The data are summarized in Table 1.

The results of the comparison of the agents’ classifications $a_k$ with the correct classification $\gamma$ appear in the eighth column of Table 1. It can be seen that each agent $k=1,2,\dots ,6$ provides the classification $a_k$ which is rather far from the correct classification, $\gamma$. Similarly, the classification ${\gamma }_M$, in the last column of Table 1, generated by the majority vote is also far from the correct classification (with an accuracy level of $50\%$). Thus, majority voting does not work well in this case, since the agents’ classifications are not symmetrically distributed around the correct class. Note, however, that classification of the proposed algorithm that is presented in Section 5, and denoted by ${\gamma }^{*}$, which classifies the entities by the agent’s expertise (which is unknown a priori), is equivalent to the correct classification $\gamma$, i.e., it results in a $100\%$ accurate classification, where for

-

Expert $k=1$, class $C_1=\left\{x_2,x_6,x_8\right\}$;

-

Expert $k=2$, class $C_2=\left\{x_1,x_3,x_{10}\right\}$;

-

Expert $k=3$, classes $C_1=\left\{x_2,x_6,x_8\right\}$ and $C_2=\left\{x_1,x_3,x_{10}\right\}$;

-

Expert $k=4$, class $C_3=\left\{x_4,x_5,x_{11}\right\}$;

-

Expert $k=5$, class $C_4=\left\{x_7,x_9,x_{12}\right\}$;

-

Expert $k=6$, classes $C_3=\left\{x_4,x_5,x_{12}\right\}$ and $C_4=\left\{x_7,x_9,x_{12}\right\}$.

Thus, by identifying the expert agents, a correct classification can be achieved (see the implementation of the proposed algorithm to Table 1 at the end of Section 5).

Note, again, that in the considered setup both the correct classification and the agents’ levels and fields of expertise are unknown, and this information should be estimated only from the agents’ classifications. As seen later, the recognition of the expert agents is based on the assumption that experts in the same field of expertise provide closer answers than the answers of the non-expert agents.

4. Local Search by Likelihood Maximization

Inspired by the considered example, where the best classification is provided by considering the opinions of the experts, we start with an algorithm that provides an exact solution by maximization of the expected likelihood between the agents’ classifications. This algorithm follows the brute force approach and, because of its high computational complexity, it can be applied only to small datasets.

Let $X=\{x_1,x_2,{\dots ,x}_n\}$ be a set of entities and $\mathcal{A}=\left\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m\right\}$ be the set of agents’ classifications ${\alpha }_k=\{C_1^k,C_2^k,\dots ,C_l^k\}$, $k=1,2,\dots ,m$, while the correct classification $\gamma =\left\{C_1,C_2,\dots ,C_l\right\}$ is unknown to the agents.

Let $r_{ik}\in \left\{1,\dots ,l\right\}$ be the tag by which the $k$th agent-labeled entity is $x_i$ (see the columns in Table 1); in other words, the values $r_{ik}$ are the opinions of the agents about that entity, and $r_{ik}=j$ denotes that in the classification of an agent ${\alpha }_k$, entity $x_i$ is in class $C_j^k$.

Assume that in the correct classification $\gamma$ an entity $x_i\in X$ belongs to class $C_j$. Since $\gamma$ is unknown, we consider the probability $p_{j{j}^{\prime }}^k=Pr\left\{r_{ik}=j^{\prime }|x_i\in C_j\right\}$ that the $k$th agent classifies an entity $x_i$ as a member of the class $C_{j^{\prime }}$ while the correct class is $C_j$, and $P_k={‖p_{j{j}^{\prime }}^k‖}_{l\times l}$ denotes the probability matrix that includes the opinions $p_{j{j}^{\prime }}^k$ of the $k$th agent, $k=1,2,\dots ,m$, on the membership of the entity $x_i$, $i=1,2,\dots ,n$ to the classes $C_j$, $j=1,2,\dots ,l$. If agent $k$ is completely reliable, then $P_k$ is a unit matrix. In general, the agent is considered to be an expert in class $C_j$ if $p_{j{j}^{\prime }}^k$ is close to one, while $p_{j{j}^{\prime }}^k$ and $p_{j^{\prime }j}^k$ are close to zero for all $j\ne j^{\prime }$.

Finally, we denote by $p_C=Pr\left\{C\ne \varnothing \right\}$ the probability that class $C\subset X$ includes at least one entity. Then, if $\tilde{C}\left(i\right)$ is an estimated class for the entity $x_i$, then $p_{\tilde{C}\left(i\right)}$ is the probability that entity $x_i$ will be classified to class $\tilde{C}\left(i\right)$. Additionally, we denote by ${\tilde{c}}_i\le l$ the label associated with class $\tilde{C}\left(i\right)$. Similarly, $C\left(i\right)$ denotes the correct class; for the $i$th entity $x_i$, the value $p_{C\left(i\right)}$ is the probability that the entity $x_i$ will be correctly included in the class $C\left(i\right)$.

Using these terms, the classification problem can be formulated as a problem of finding the classes $\tilde{C}\left(i\right)$, $i=1,2,\dots ,n$, the matrices $P_k$, $k=1,2,\dots ,m$, and the probabilities $p_{{\tilde{c}}_i,r_{ik}}^k$ that maximize the likelihood function

$$L\left(\tilde{C},p_{\tilde{C}},P_1,P_2,\dots ,P_m\right)={\prod }_{i=1}^n\left(p_{\tilde{C}\left(i\right)}{\prod }_{j=1}^m{p}_{{\tilde{c}}_i,r_{ik}}^k\right).$$

In the other words, it is required to maximize the value of the likelihood function

$$L\left(\tilde{C},p_{\tilde{C}},P_1,P_2,\dots ,P_m\right)\to max$$

(1)

with respect to its arguments and subject to the relevant conditions:

$${\sum }_{j\prime =1}^l{p}_{jj\prime }^k=1, p_{jj\prime }^k\ge 0, k=1,2,\dots ,m, j,j^{\prime }=1,2,\dots ,l.$$

$${\sum }_{j=1}^l{p}_{\tilde{C}\left(i\right)}=1, {\tilde{c}}_i\in \left\{1,2,\dots ,l\right\}, p_{\tilde{C}\left(i\right)}\ge 0, i=1,2,\dots ,n.$$

An approximated solution of this problem can be defined as follows:

$$p_{C\left(i\right)}={\sum }_{i=1}^n\mathbb{I}\left(\tilde{C}\left(i\right)=C\left(i\right)\right)/n,$$

$$p_{c_i,j}^k={\sum }_{i=1}^n\mathbb{I}\left(\tilde{C}\left(i\right)=C\left(i\right)\wedge r_{ik}=j\right)/{\sum }_{i=1}^n\mathbb{I}\left(\tilde{C}\left(i\right)=C\left(i\right)\right),$$

where $\mathbb{I}$ is an indicator function that is $\mathbb{I}\left(a=b\right)=1$ if $a=b$ and $\mathbb{I}\left(a=b\right)=0$ otherwise. The approximated solution can be obtained, for example, by majority vote (see Section 6.2.1), which can also be used as an initial solution in the considered optimization algorithm.

The proposed algorithm, which aims to solve optimization problem (1) by local search. is outlined as follows (Algorithm 1).

Algorithm 1: Likelihood Maximization

Given the set $X$ of $n$ items $x_i$, $i=1,2,\dots ,n$, and the set of the agents’ classifications ${\alpha }_k$, $k=1,2,\dots ,m$, do: Create the agents’ opinions matrix $r=‖r_{ik}‖$, $i=1,2,\dots ,n$, $k=1,2,\dots ,m$. Start with the solution given by the approximate formulae or by majority vote. Solve optimization problem (1). While no improvements to the current solution (which is the set of classes $\tilde{C}\left(i\right)$, $i=1,2,\dots ,n$) in its entire neighborhood are found, do: Define the neighbors of the solution as the classifications that can be obtained from the solution by changing the estimated class $\tilde{C}\left(i\right)$ for a single entity $x_i$; Calculate the likelihood for the set of neighboring classifications; Exclude the neighbors with a small likelihood; Solve optimization problem (1); End while. Return the obtained solution.

Following the outlined algorithm, an initial solution is refined iteratively until reaching the maximal expected likelihood. Such a method can provide an optimal solution to the problem; however, it requires high computation power and can be implemented only for relatively small problems. The time complexity of the Algorithm 1 is $\mathcal{O}\left(\upsilon nm{l}^3\right)$, where $n$ is the number of entities, $m$ is the number of agents, $l$ is the number of classes, and $\upsilon$ is the number of iterations until algorithm convergence. Here, $\upsilon$ is the number of repetitions of lines 5–8 in the while loop, where a maximum of $l$ classes are defined for each entity of a maximum of $n$ entities, and the optimization problem is solved by $m{l}^2$ steps. Since the number of classes $l$ is at most equal to the number of items $n$, the complexity of the Algorithm 1 in the worst case is $\mathcal{O}\left(\upsilon m{n}^4\right)$.

Having said that, the above Algorithm 1 can be used to prove the existence of a solution to the problem under the indicated assumption. Moreover, in the simulations shown below, we use this algorithm for analysis and comparison of the optimal classifications against the classifications generated by the heuristic method that is suggested next.

5. Suggested Algorithm: Distance-Based Collaborative Classification

The suggested algorithm, called the distance-based collaborative classification (DBCC) algorithm, consists of two stages: in the first stage, based on the presented opinions, the agents are tagged as experts and non-experts for each of the different classes, and in the second stage, the classification of the entities is conducted with respect to the agents’ levels of expertise.

Classification of the agents according to their expertise levels is based on the assumption that agents with similar fields of expertise produce similar classifications of the related entities. On the other hand, the classifications of non-expert agents are distributed over a relatively larger range of classes. Consequently, the tagging of the agents as experts and non-experts is conducted by clustering the agents’ classifications ${\alpha }_k$, $k=1,2,\dots ,m$, with respect to the different classes.

Let $sim\left({\alpha }_u,{\alpha }_v|C\right)$ be a certain measure of similarity between two classifications ${\alpha }_u$ and ${\alpha }_v$ with respect to the class $C\subset X$, $u,v=1,2,\dots ,m$. Then, over all of the agents’ classifications ${\alpha }_k$, $k=1,2,\dots ,m$, a central classification $\xi \left(C\right)$ with respect to class $C$ can be defined as follows:

$$\xi \left(C\right)=\underset{u=1,2,\dots ,m}{\mathrm{argmin}}{\sum }_{v=1}^{m}sim\left({\alpha }_u,{\alpha }_v|C\right).$$

(2)

The assumption about the closeness of the classifications produced by experts in a certain class implies that the values $sim\left({\alpha }_k,\xi |C\right)$ of similarities between the agents’ classifications ${\alpha }_k$, $k=1,2,\dots ,m$, and some central classification $\xi \left(C\right)$ are distributed according to the mixture of two distributions: the first represents the distribution of the experts in class $C$, and the second represents the distribution of the non-experts in this class.

The similarity between the classifications can be measured by several methods, for example, by the Rokhlin or Ornstein distances, or by the symmetric version of the Kullback–Leibler divergence (for the use of such metrics, refer, e.g., to [19]). However, to avoid additional specification of probabilistic measures over the entities, in the suggested algorithm, we use a normalized version of the well-known Hamming distance. This distance is defined as follows:

Let ${\alpha }_u=\{C_1^u,C_2^u,\dots ,C_l^u\}$ and ${\alpha }_v=\{C_1^v,C_2^v,\dots ,C_l^v\}$ be two classifications of the set $X=\{x_1,x_2,{\dots ,x}_n\}$ entities. Consider the classes $C_j^u\in {\alpha }_u$ and $C_j^v\in {\alpha }_v$, $j=1,2,\dots ,l$, and let $\mathfrak{n}\left({\alpha }_u|j\right)=\#C_j^u$ denote the cardinality of the class $C_j^u$, while $\mathfrak{n}\left({\alpha }_v|j\right)=\#C_j^v$ denotes the cardinality of the class $C_j^v$. The values $\mathfrak{n}\left({\alpha }_u|j\right)$ and $\mathfrak{n}\left({\alpha }_v|j\right)$ are the numbers of entities that are included in the $j$th class or, similarly, are tagged with the label $j$ by agents $u$ and $v$, respectively. In other words, $\mathfrak{n}\left({\alpha }_u|j\right)$ and $\mathfrak{n}\left({\alpha }_v|j\right)$ represent the independent opinions of agents $u$ and $v$ about the $j$th class.

In addition, let $\mathfrak{n}\left({\alpha }_u,{\alpha }_v|j\right)=\#\left(\left(C_j^u\cup C_j^v\right)\backslash \left(C_j^u\cap C_j^v\right)\right)$ denote the cardinality of the symmetric difference between the classes $C_j^u$ and $C_j^v$. The number $\mathfrak{n}\left({\alpha }_u,{\alpha }_v|j\right)$ represents the disagreement of the agents about the $j$th class. The normalized Hamming distance between the classifications ${\alpha }_u$ and ${\alpha }_v$ is defined as the following ratio:

$$d_{norHam}\left({\alpha }_u,{\alpha }_v|j\right)=\mathfrak{n}\left({\alpha }_u,{\alpha }_v|j\right)/\left(\mathfrak{n}\left({\alpha }_u|j\right)+\mathfrak{n}\left({\alpha }_v|j\right)\right).$$

(3)

For each $j$, the defined distance $d_{NorHam}\left({\alpha }_u,{\alpha }_v|j\right)$ is a metric such that $0\le d_{norHam}\left({\alpha }_u,{\alpha }_v|j\right)\le 1$. This represents the disagreements between the agents with respect to different classes and, consequently, enables the definition of experts and non-experts per class.

Additionally, using this distance, the set of classifications ${\alpha }_k$ and, consequently, the set of $m$ agents can be considered as a metric space that allows for the application of conventional clustering algorithms. In the suggested DBCC algorithm, we apply Gaussian mixture clustering and the expectation-maximization algorithm [20].

As a result of the clustering, the agents are tagged according to their level of expertise with respect to each class $C\subset X$. These levels are represented by the weights $w_k\left(C\right)$ associated with the agents and are used at the classification stage of the entities.

Classification of the entities $x_i\in X$, $i=1,2,\dots ,n$, based on the agents’ opinions ${\alpha }_k$, $k=1,2,\dots ,m$, with respect to their expertise levels $w_k\left(C\right)$, $C\subset X$, is conducted using conventional voting techniques; in the suggested DBCC algorithm, we use the relative majority vote.

In general, the suggested algorithm acts as follows: In the first stage, for each class, the differences (in terms of the normalized Hamming distance) between the agents’ classifications are defined. Using these distances, the agents are divided into two groups: experts and non-experts. At this stage, an assumption is made that the experts in their area of expertise provide similar classifications of the related instances, unlike the non-experts, whose classifications are more diverse. Accordingly, the opinions of the experts gain higher weights with respect to the non-experts when all of the opinions are aggregated.

In the second stage, the entities are classified by majority vote with respect to the weighted opinions of the agents. Then, the obtained solution is corrected following the stages of the EM algorithms; the resulting classification of the entities is considered as an estimated classification obtained at the M-step and is used at the E-step for the definition of more precise levels of the agents’ expertise.

The DBCC algorithm is outlined as follows (Algorithm 2):

Algorithm 2: Distance-Based Collaborative Classification (DBCC) Algorithm

Given the set $X$ of $n$ items $x_i$, $i=1,2,\dots ,n$, the enumeration $j=1,2,\dots ,l$ of possible classes and the set of the agents’ classifications ${\alpha }_k$, $k=1,2,\dots ,m$, do: Initialization Initialize distance matrices ${‖d‖}_{m\times m}$, distance arrays ${‖a‖}_m$, and weight arrays ${‖w‖}_m$. Initialize expertise map ${‖E‖}_{n\times m}$. Classification of the agents and definition of the expertise levels 3. For each class $C_j$, $j=1,\dots ,l$, do: 4. For each agent $u=1,2,\dots ,m$, do: 5. For each agent $v=1,2,\dots ,m$, do: 6. Set distance $d_{uv}=d_{norHam}\left({\alpha }_u,{\alpha }_v|j\right)$ between the classifications ${\alpha }_u$ and ${\alpha }_v$ with respect to class $C_j$ into the distance matrix ${‖d‖}_{m\times m}$. 7. End 8. End 9. Find central classification ${\xi }_j=\underset{u=1,2,\dots ,m}{\mathrm{Argmin}}{\sum }_{v=1}^m{d}_{uv}$. 10. For each agent $k=1,2,\dots ,m$, do: 11. Set distance $d_k=d_{norHam}\left({\xi }_j,{\alpha }_k|j\right)$ from agent’s classification ${\alpha }_k$ to the central classification ${\xi }_j$ into the distance array ${‖a‖}_m$. 12. End 13. Cluster the agents into two groups (experts and non-experts) with respect to distance array ${‖a‖}_m$. 14. For each agent $k=1,2,\dots ,m$, do: 15. Set weight $w_k$ into the weights array: the agent with the closest to the center vector obtains the weight 1, and more distant agents obtain the weight 0. 16. End 17. For each agent in the group of expert agents, do: 18. Add class $C_j$ to the expertise map $E_{jk}$ of the $k$th agent with the weight $w_u$. 19. End 20. End Classification of the entities with respect to the agents’ expertise 21. For each entity $x_i$, $i=1,\dots ,n$, do: 22. For each class $C_j$, $j=1,2,\dots ,l$, do: 23. Initialize the score of $C_j$ by zero. 24. End 25. For each agent $k=1,2,\dots ,m$, do: 26. If class $C_j$ is in the agent’s expertise map $E_{jk}$, then add a score to this class. 27. End 28. Set a label for entity $x_i$ as an index $j$ of the class with the highest score. 29. End Correction of the classification by repeating the expectation maximization steps 30. Repeat until convergence (expectation maximization): 31. M-step: from the estimated correct classification, obtain normalized Hamming distances for all agents. 32. E-step: estimate the correct classification by running steps 4–17 over the obtained distances. 33. End

The suggested DBCC algorithm is a heuristic procedure utilized the EM techniques. At the M-step, it maximizes the likelihood of agents’ expertise by using the distances from the estimated correct classifications. The latter is obtained at the E-step with respect to the agents’ expertise at the previous iteration. The process converges in the sense that the difference between the classifications obtained in two sequential steps tends to be zero. In practice, the process can be terminated when the difference between two sequential classifications decreases more than a certain predefined value of order $n\times {10}^{-3}$.

The time complexity of the suggested Algorithm 2 is $\mathcal{O}\left(\upsilon \left(l{m}^2+(l+m)n\right)\right)$, where $n$ is the number of entities, $m$ is the number of agents, $l$ is the number of classes, and $\upsilon$ is the number of iterations up to the convergence of the EM part of the algorithm. Here, $\upsilon$ defines the number of iterations of the algorithm (see Line 32); in the term $l{m}^2$, $l$ is the number of iterations the for loop (Lines 3–20), and $m^2$ is the number of iterations for the loops (lines 4–8) and the number of steps in the operation in Line 9 (the other loops require $m$ steps), and the term $(l+m)n$ represents the number of iterations for the loop in Lines 21–29 and two internal for loops (Lines 22–24 and 25–27). Since the number of classes $l$ is at most equal to the number of items $n$, the complexity of the algorithm in the worst case is $\mathcal{O}\left(\upsilon \left(m^{2}n+n^2\right)\right)$.

To clarify the main advantage of the algorithm that aims to find experts and non-experts for further classification, let us refer back to the dataset presented in Table 1.

Consider the classifications $a_1$ and $a_2$ provided by the first and the second agents with respect to class $C_1$. Following Equation (3), the distance between the classifications $a_1$ and $a_2$ is a ratio between the number of disagreements of the agents about the membership of the entity to a certain class. For the first and the second agents with respect to $C_1$, one obtains $\mathfrak{n}\left({\alpha }_1,{\alpha }_2|1\right)=3$, which represents the disagreement regarding three entities $x_2$, $x_6$, and $x_8$ that were classified by the first agent to the class $C_1$ ($\mathfrak{n}\left({\alpha }_1|1\right)=3$); however, they were classified to other classes by the second agent ($\mathfrak{n}\left({\alpha }_2|1\right)=0)$. Thus, the distance $d_{NorHam}\left({\alpha }_1,{\alpha }_2|1\right)=3/\left(3+0\right)=1$ is the maximal possible distance between these classifications.

Similarly, the distance between the classifications $a_3$ and $a_4$ with respect to the class $C_1$ is as follows: The number of disagreements between the agents is $\mathfrak{n}\left({\alpha }_3,{\alpha }_4|1\right)=6$ (entities $x_2$, $x_3$, $x_7$, $x_8$, $x_{10}$ and $x_{12}$), while regarding entity $x_6$, the agents agree with one another. The numbers of independent classifications of the third and fourth agents about class $C_1$ are $\mathfrak{n}\left({\alpha }_3|1\right)=3$ (entities $x_2$, $x_6$ and $x_8$) and $\mathfrak{n}\left({\alpha }_4|1\right)=5$ (entities $x_3$, $x_6$, $x_7$, $x_{10}$ and $x_{12}$), respectively. Thus, $d_{NorHam}\left({\alpha }_3,{\alpha }_4|1\right)=6/\left(3+5\right)=0.75$.

Calculation of the distances among the agents with respect to all four classes $C_j$, $j=1,\dots ,4,$ results in the following tables (zero distances are shown in bold font):

$\mathbf{Class}{\mathit{C}}_{\mathbf{1}}$	${\mathit{\alpha }}_{\mathbf{1}}$	${\mathit{\alpha }}_{\mathbf{2}}$	${\mathit{\alpha }}_{\mathbf{3}}$	${\mathit{\alpha }}_{\mathbf{4}}$	${\mathit{\alpha }}_{\mathbf{5}}$	${\mathit{\alpha }}_{\mathbf{6}}$
${\alpha }_{\mathbf{1}}$	$-$	$1.0$	$\mathbf{0}$	$0.75$	$1.0$	$0.71$
${\alpha }_2$	$1.0$	$-$	$1.0$	$1.0$	$1.0$	$1.0$
${\alpha }_3$	$\mathbf{0}$	$1.0$	$-$	$0.75$	$1.0$	$0.71$
${\alpha }_4$	$0.75$	$1.0$	$0.75$	$-$	$0.5$	$0.56$
${\alpha }_5$	$1.0$	$1.0$	$1.0$	$0.5$	$-$	$0.43$
${\alpha }_6$	$0.71$	$1.0$	$0.71$	$0.56$	$0.43$	$-$

$\mathbf{Class}{\mathit{C}}_{\mathbf{2}}$	${\mathit{\alpha }}_{\mathbf{1}}$	${\mathit{\alpha }}_{\mathbf{2}}$	${\mathit{\alpha }}_{\mathbf{3}}$	${\mathit{\alpha }}_{\mathbf{4}}$	${\mathit{\alpha }}_{\mathbf{5}}$	${\mathit{\alpha }}_{\mathbf{6}}$
${\alpha }_1$	$-$	$0.5$	$0.5$	$1.0$	$1.0$	$1.0$
${\alpha }_2$	$0.5$	$-$	$\mathbf{0}$	$1.0$	$1.0$	$1.0$
${\alpha }_3$	$0.5$	$\mathbf{0}$	$-$	$1.0$	$1.0$	$1.0$
${\alpha }_4$	$1.0$	$1.0$	$1.0$	$-$	$0.67$	$0.5$
${\alpha }_5$	$1.0$	$1.0$	$1.0$	$0.67$	$-$	$0.33$
${\alpha }_6$	$1.0$	$1.0$	$1.0$	$0.5$	$0.33$	$-$

$\mathbf{Class}{\mathit{C}}_{\mathbf{3}}$	${\mathit{\alpha }}_{\mathbf{1}}$	${\mathit{\alpha }}_{\mathbf{2}}$	${\mathit{\alpha }}_{\mathbf{3}}$	${\mathit{\alpha }}_{\mathbf{4}}$	${\mathit{\alpha }}_{\mathbf{5}}$	${\mathit{\alpha }}_{\mathbf{6}}$
${\alpha }_1$	$-$	$0.64$	0$.67$	$1.0$	$1.0$	$1.0$
${\alpha }_2$	$0.64$	$-$	$0.56$	$0.8$	$0.78$	$0.8$
${\alpha }_3$	$0.67$	$0.56$	$-$	$1.0$	$1.0$	$1.0$
${\alpha }_4$	$1.0$	$0.8$	$1.0$	$-$	$1.0$	$\mathbf{0}$
${\alpha }_5$	$1.0$	$0.78$	$1.0$	$1.0$	$-$	$1.0$
${\alpha }_6$	$1.0$	$0.8$	$1.0$	$\mathbf{0}$	$1.0$	$-$

$\mathbf{Class}{\mathit{C}}_{\mathbf{4}}$	${\mathit{\alpha }}_{\mathbf{1}}$	${\mathit{\alpha }}_{\mathbf{2}}$	${\mathit{\alpha }}_{\mathbf{3}}$	${\mathit{\alpha }}_{\mathbf{4}}$	${\mathit{\alpha }}_{\mathbf{5}}$	${\mathit{\alpha }}_{\mathbf{6}}$
${\alpha }_1$	$-$	$0.33$	0$.25$	$1.0$	$071$	$0.71$
${\alpha }_2$	$0.33$	$-$	$0.33$	$1.0$	$1.0$	$1.0$
${\alpha }_3$	$0.25$	$0.33$	$-$	$1.0$	$0.71$	$0.71$
${\alpha }_4$	$1.0$	$1.0$	$1.0$	$-$	$0.5$	$0.56$
${\alpha }_5$	$0.71$	$1.0$	$0.71$	$1.0$	$-$	$\mathbf{0}$
${\alpha }_6$	$0.71$	$1.0$	$0.71$	$1.0$	$\mathbf{0}$	$-$

Note that, for each class, the minimal distance between the classifications is zero, and the experts can be defined with respect to this distance. For class $C_1$, a zero distance $d_{NorHam}\left({\alpha }_1,{\alpha }_3|1\right)=0$ is obtained between classifications ${\alpha }_1$ and ${\alpha }_3$, i.e., the first and third agents are considered to be experts with respect to class $C_1$. Similarly, for class $C_2,$, zero distances are obtained for $d_{NorHam}\left({\alpha }_2,{\alpha }_3|2\right)=0$ and, thus, the second and third agents are considered to be experts with respect to class $C_2$; $d_{NorHam}\left({\alpha }_4,{\alpha }_6|3\right)=0$, so the fourth and sixth agents are experts in class $C_3$; and $d_{NorHam}\left({\alpha }_5,{\alpha }_6|4\right)=0$, so the fifth and sixth agents are considered to be experts with respect to class $C_4$.

Following these distance calculations, the “experts” in each class obtain a weight of $1$, while the other nonexpert agents obtain zero weights. Thus, in this weighting scheme, only expert classifications are considered. Finally, in the considered dataset (see Table 1), according to the opinions of the experts (the first and third agents), the first class is $C_1^{*}=\left\{x_2,x_6,x_8\right\}$; according to the opinions of the experts (the second and third agents), the second class is $C_2^{*}=\left\{x_1,x_3,x_{10}\right\}$; according to the opinions of the experts (the fourth and sixth agents), the third class is $C_3^{*}=\left\{x_4,x_5,x_{11}\right\}$; and according to the opinions of the experts (the fifth and sixth agents), the fourth class is $C_4^{*}=\left\{x_7,x_9,x_{12}\right\}$.

Then, the resulting partitioning of the dataset is as follows:

$${\gamma }^{*}=\left\{C_1^{*},C_2^{*},C_3^{*},C_4^{*}\right\}=\left\{\left\{x_2,x_6,x_8\right\},\left\{x_1,x_3,x_{10}\right\},\left\{x_4,x_5,x_{11}\right\},\left\{x_7,x_9,x_{12}\right\}\right\}.$$

Note that this straightforward, illustrative example does not require (and does not demonstrate) the complicated clustering and correction steps by the E-M algorithm, which plays an important role in the real-world datasets, where the division of the agents into experts and non-experts is not binary.

6. Numerical Simulations and Comparisons

The suggested algorithm was studied using two data settings: simulated data with known characteristics, which enabled the analysis of the effectiveness and robustness of the DBCC algorithm, and real-world data obtained from a dedicated questionnaire.

Classifications obtained by the suggested Algorithm 2 were compared with the results provided by the optimal likelihood-maximization brute-force algorithm, the majority vote, the most accurate heuristic FDS algorithm, and the fastest GLAD algorithm.

The algorithms were implemented in the Python programming language and run on a standard Lenovo ThinkPad T480 PC with an Intel^® Core™ i7-8550U Processor (8M Cache, 4.00 GHz) and 32 GB memory (DDR4 4267 MHz).

6.1. Data

To analyze the proposed method, it was applied to different datasets: (i) simulated data, (ii) real-world data with simulated classes and, finally, (iii) an entirely real-world questionnaire dataset. In the first case, for a given $n$ entity $x_i$, $i=1,2,\dots ,n$, we simulated both the classes $C_j$, $j=1,2,\dots ,l$, and the agents’ classifications ${\alpha }_k$, $k=1,2,\dots ,m$; in the second case, we used real-world data with simulated labeled datasets; and in the third case, we created and analyzed an online questionnaire that measures the levels of expertise of users regarding famous paintings and painters (the questionnaire is available via the link Famous painters (google.com); see the Appendix A).

6.1.1. Simulated Data

In the simulated data, we used $m\in \left\{4,10,16,20,24,32\right\}$ agents in the trials, while their classifications ${\alpha }_k$, $k=1,2,\dots ,m$, were randomly generated. The probability of obtaining correct classifications for expert agents was specified as $p_e\in \left[0.6,1.0\right]$, and for non-expert agents as $p_n\in \left[0.2,0.6\right]$. The number of entities in the trials was $n\in \left\{50,200,300,500,1000,2000\right\}$, and the number of classes was $l\in \left\{2,3,4,6,8,10,12,16\right\}$.

6.1.2. Real-World Data with Simulated Classes

In the case of real-world data with simulated classes, we considered the real-world data from different databases, where to define multiple agents with different expertise, we used simulated labeling of the data. The agents were simulated by using different classifiers (e.g., random forests), and their expertise over different classes was simulated by scrambling the features in the dataset. In a comparative analysis, we used seven known datasets from Kaggle [3], as follows: Iris, Abalone Age, Glass Type, Students’ Results, User Activity, Robots Conversation, and Wine Quality.

For example, in the Iris dataset, the agents’ expertise was defined as follows: Agent 1 and Agent 2 are experts in the class “Iris-setosa”, Agent 2 is an expert in the class “Iris-versicolor”, and Agent 4 is an expert in the class “Iris-verginica”. Recall that according to this definition, the probability that these agents provide correct classification of the entities of these classes is higher.

In addition, we used the Wi-Fi localization database from the Machine Learning Repository [21]. The datasets have different numbers of entities $150<n<4000$ and different numbers of classes $l\in \left\{3,4,5,6\right\}$; per the different numbers of classes, different numbers of agents $10<m<20$ are simulated with various levels of expertise.

6.1.3. Real-World Data

To obtain real-world data, we designed and distributed an online questionnaire that contains questions on painters and paintings based on common knowledge. In particular, the questionnaire contains 40 paintings created by eight famous painters. The agents were asked to indicate the painter of each painting. Thus, in terms of classification, the agents were required to classify $n=40$ entities into $l=8$ classes. The questionnaire was offered to $m=90$ volunteers in the university, including both students and professors, without any specific educational background in the arts. An example of the paintings and questionnaire that was used are presented in the Appendix A.

6.2. Algorithms for Comparisons

The results obtained by the suggested algorithm were compared with the results obtained by four baseline methods: (i) the widely used majority voting algorithm; (ii) the brute-force maximum-likelihood optimization; (iii) the FDS algorithm, which was recently proposed as an effective heuristic to establish an expert-based classification; and (iv) the GLAD algorithm.

6.2.1. Majority Vote

A majority vote is a simple and popular rule that is often used in different tasks of social choices. The algorithm based on this rule acts as follows:

Let $X=\{x_1,x_2,{\dots ,x}_n\}$ be a set of entities that should be classified by $m$ experts to $l\le n$ possible number of classes. Then, the entity $x_i$, $i=1,2,\dots ,n$, is classified to class $C_j$, $j=1,2,\dots ,l$, if the majority of the agents classified it to this class (thus, labeling it by the $j$th label); ties are broken randomly.

As indicated above, despite its simplicity, in crowdsourcing tasks, the majority vote rule provides good results when the number of agents is relatively large and with similar levels and fields of expertise.

6.2.2. Likelihood Maximization

The likelihood-optimization procedure—the Algorithm 1 presented in Section 4, is an optimal brute-force algorithm that is used to obtain an optimal solution in relatively small problems.

In the numerical simulations, optimization problem (1) has been solved by using a local search heuristic that is feasible for considered cases with a small number of agents.

6.2.3. Fast Dawid–Skene Algorithm

As indicated above, the fast Dawid–Skene (FDS) algorithm [5] is a modification of the original DS aggregation algorithm proposed by Dawid and Skene [2].

The FDS algorithm follows the EM approach, such that at the E-step, the data are classified using the current parameter values, and at the M-step, these values are corrected to maximize the likelihood of the data. The algorithm starts with some initial classification. It then alternates between the E-step and the M-step up to convergence, such that the difference between the current and the previously obtained classifications is less than the predefined small value.

The unsupervised classification algorithm follows the same approach with the above-indicated differences in the classifications conducted at the E-step and in the used parameters.

6.2.4. GLAG Algorithm

The generative model for labels, abilities, and difficulties (GLAD) [6] is a probabilistic algorithm that simultaneously infers the expertise of each agent, the context of the entity, and the most likely class for each entity.

Similar to the other indicated methods, this algorithm follows the EM approach, namely, given the agents’ classifications and initial expertise. At the E-step, it computes the posterior probability for every entity, and at the M-step it maximizes the expectation of the log-likelihood of the observed and hidden parameters using gradient descent.

6.3. Simulation Results

The suggested algorithm was implemented over different datasets, as indicated above, with different groups of agents, and compared with the four outlined algorithms.

6.3.1. Likelihood Maximization vs. Majority Voting

The comparison of the algorithm based on majority voting (Section 6.2.1) and the likelihood-maximization Algorithm 1 (Section 6.2.2) was conducted using the simulated settings, with $m=8$ and $m=12$ agents. In both cases, the number of entities was $n=400$, and the number of classes was $l=4$. Such a relatively small dataset enables the application of the optimal likelihood-maximization Algorithm 1 and its timely execution. The results of the simulations are summarized in Table 2.

Table 2. Simulation results of majority voting and likelihood maximization for $m=8$ and $m=12$ agents classifying $n=400$ entities by $l=4$ classes.

$\mathit{m}=8$ Agents			$\mathit{m}=12$ Agents
Hit Rate		CPU Time (s)	Hit Rate		CPU Time (s)
Majority Rule	Suggested Rule		Majority Rule	Suggested Rule
$0.815$	$0.958$	$54.1$	$0.818$	$0.990$	$49.3$
$0.807$	$0.938$	$54.3$	$0.860$	$0.988$	$49.2$
$0.802$	$0.948$	$39.2$	$0.823$	$0.993$	$29.7$
$0.802$	$0.958$	$38.7$	$0.850$	$0.988$	$49.0$
$0.787$	$0.963$	$31.2$	$0.833$	$0.973$	$29.4$
$0.772$	$0.960$	$38.9$	$0.840$	$0.995$	$29.5$
$0.830$	$0.963$	$31.1$	$0.838$	$0.995$	$29.5$
$0.812$	$0.973$	$38.9$	$0.828$	$0.983$	$29.4$
$0.810$	$0.963$	$54.5$	$0.843$	$0.985$	$59.3$
$0.785$	$0.950$	$23.6$	$0.865$	$0.995$	$39.9$

In the considered settings, the likelihood-maximization Algorithm 1 outperformed majority voting both for $m=8$ and for $m=12$ agents and provided a higher accuracy hit rate within similar computation times.

6.3.2. Suggested Algorithm vs. Majority Voting

In the next simulations, the proposed DBCC algorithm was compared with the majority voting rule. In the simulations, agents of different levels of expertise were selected, such that their classifications ${\alpha }_k$, $k=1,2,\dots ,m$ would follow a correct classification with probabilities $p_n\in \left[0.2,0.6\right]$ for non-expert agents, and with probabilities (reliability) $p_e\in \left[0.6,1.0\right]$ for expert agents. Since the probabilities $p_n$ and $p_e$ are, in essence, measures of the agents’ levels of expertise in certain fields, we refer to these probabilities as the reliabilities of the agents.

The trials were executed for $m=32$ experts classifying $n=500$ entities into $l=8$ classes. The probabilities of correct classifications (considered as the reliabilities of the agents) were $p_e\in \left[0.6,1.0\right]$. The percentage of times where the proposed DBCC algorithm outperformed the majority vote method with respect to the ratio of expert and non-expert reliability is given in Figure 1.

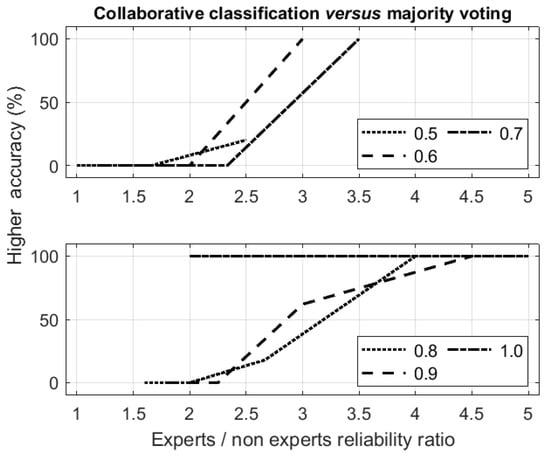
Figure 1. Percentage of cases in which the suggested algorithm outperformed the majority voting method in terms of accuracy (y-axis) with respect to the ratio of expert reliability to non-expert reliability (x-axis). Different dashed lines correspond to different levels of the agents’ reliability, which represent the levels of the agents’ expertise.

As expected, for homogeneous groups that included agents with close levels of expertise, majority voting outperformed the suggested algorithm. However, for heterogeneous groups of agents with different levels of expertise, the suggested DBCC algorithm outperformed the majority voting method.

These results demonstrate once again that the suggested algorithm is preferable over a majority vote for practical tasks where the group of agents includes both experts and non-experts with respect to different fields.

Figure 2 demonstrates the percentage of times when the proposed DBCC algorithm outperformed the majority voting method in a classification of $n$ entities. In these simulations, the probability that the experts would provide correct classifications was $p_e=0.7$, and the probability that the non-experts would provide correct classifications was $p_n=0.2$.

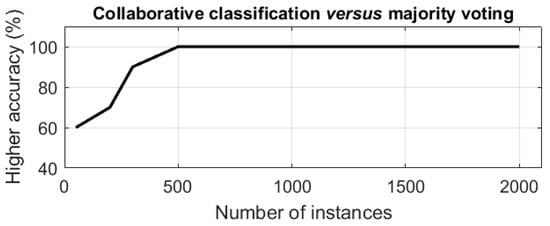
Figure 2. Percentage of cases where the suggested algorithm obtained more accurate classifications than the majority voting method (y-axis) with respect to the number of entities $n$ (x-axis).

It can be seen that for a heterogeneous group of agents that includes both experts and non-experts, the suggested algorithm substantially outperforms the majority voting method, and its effectiveness increases with the size of the group.

In both settings, that group of agents included experts and non-experts of different levels of expertise. For these agents, the suggested DBCC algorithm outperformed the majority voting method. At the same time, the effectiveness of the suggested algorithm decreased with the decrease in expertise levels, and when the group of agents included only non-experts, it became less effective than majority voting.

The obtained results demonstrate that the suggested algorithm is preferable in tasks where a small number m of agents classifies a large number n of entities. In contrast, if the number $n$ of entities is small and the number $m$ of agents is large, it is preferred to use a majority vote.

6.3.3. Accuracy Analysis

The accuracy of the suggested algorithm was compared against the accuracy of the majority voting (see Section 6.2.1), the likelihood-maximization Algorithm 1 (see Section 6.2.2), and the FDS algorithm (see Section 6.2.3). In addition, we also present the results of the GLAD algorithm [6]. The results of the simulations are shown in Figure 3.

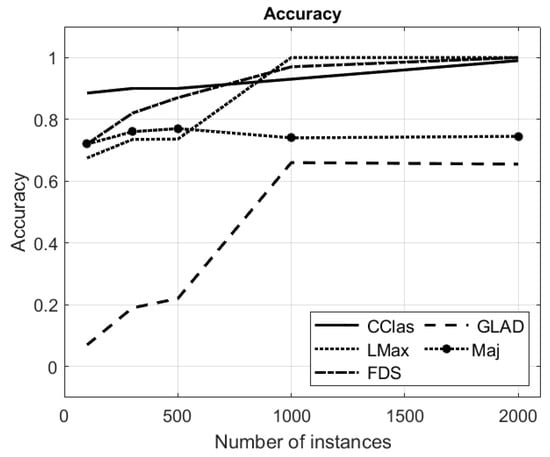
Figure 3. Accuracy of the suggested DBCC algorithm and the benchmark algorithms (y-axis) with respect to the number $n$ of entities (x-axis). In the figure, the algorithms are denoted as follows: CClas—the suggested DBCC algorithm, LMax—the likelihood-maximization algorithm, FDS—fast Dawid–Skene algorithm, GLAD—GLAD algorithm, Maj—majority voting method.

It can be seen that for a relatively small number of entities ($n<750$), the suggested DBCC algorithm outperforms the benchmark algorithms. For a larger number of entities, the DBCC is close to the FDS and the likelihood-maximization algorithms. The other two methods, majority voting and GLAD, result in lower accuracy.

For many entities (n > 1000), the confusion matrices in the likelihood-maximization become more accurate and very close to optimal, which affects the algorithm’s accuracy until it becomes closer to the optimal solution, obtaining 100% accuracy.

In the next simulations, the algorithms were applied to the real-world data [3,21] with simulated labeling, as indicated in Section 6.1.2. The results of the simulations are shown in Figure 4.

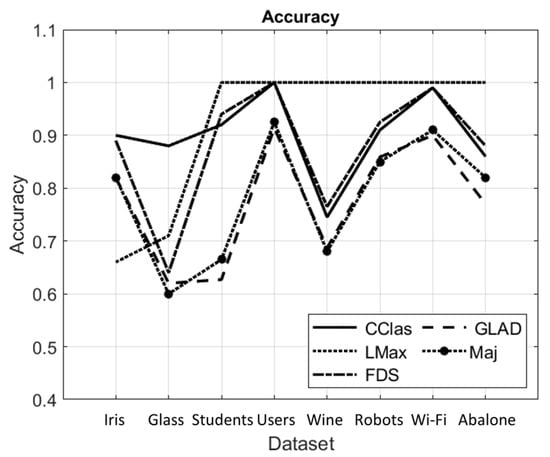
Figure 4. Accuracy of the suggested and benchmark algorithms applied to real-world data with simulated labeling. In the figure, the algorithms are denoted as follows: CClas—suggested DBCC algorithm, LMax—the likelihood-maximization algorithm, FDS—fast Dawid–Skene algorithm, GLAD—GLAD algorithm, Maj—majority voting method. The number $n$ of entities in the datasets is as follows: Iris—$150$, Glass—$215$, Students—$1000$, User—$1000$, Wine—$1000$, Robots—$2000$, Wi-Fi—$2000$, and Abalone—$4000$.

The DBCC algorithm and the FDS algorithm outperformed the majority voting in all of the datasets. Additionally, it should be noted that since the likelihood-maximization Algorithm 1 utilizes the probabilities that the agents provide correct classification and depends on the correctness of these probabilities, it results in lower accuracy on the datasets with a relatively small number of entities than the other algorithms. In contrast, the datasets with large numbers of entities demonstrate optimal accuracy. This observation illustrates the well-known difference between statistical probabilities estimated by relatively small samples vs. theoretical probabilities that are defined over infinite populations.

6.3.4. Run Time until convergence

In the last simulations, the run time until convergence of the suggested algorithm was studied. We compared it with the benchmark methods: the likelihood-maximization Algorithm 1 (see Section 6.2.2), the FDS algorithm (see Section 6.2.3), and the previously mentioned GLAD algorithm (see Section 6.2.2). Since the majority voting method is not an iterated process, we did not consider it in these simulations. The graphs of the run time with respect to the number $n$ of entities are shown in Figure 5.

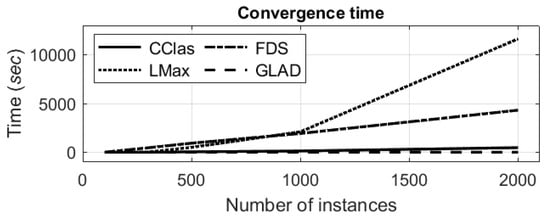
Figure 5. Run time of the suggested and known algorithms with respect to the number $n$ of entities. In the figure, the algorithms are denoted as follows: CClas—the proposed DBCC algorithm, LMax—the likelihood-maximization algorithm, FDS—fast Dawid–Skene algorithm, GLAD—GLAD algorithm.

It can be seen that the run time of the suggested algorithm is very close to the run time of the fastest GLAD algorithm and, as in the GLAD algorithm, it linearly depends on the number of entities.

The likelihood-maximization Algorithm 1 is the slowest algorithm, since it checks all of the possibilities to find the maximum likelihood according to the given confusion matrices. The number of such possibilities increases exponentially with the number of entities.

The FDS algorithm is faster than the likelihood-maximization Algorithm 1, but it is still slower than the suggested algorithm since, in contrast to the suggested algorithm, it calculates the maximum likelihood of every class for every entity in the E-step.

Thus, from the run time point of view, the suggested algorithm acts similarly to the fastest algorithm and results in classifications that are close in accuracy to the classifications created by the most accurate algorithms.

7. Conclusions

In this paper, we present a novel algorithm for unsupervised collaborative classification of a set of arbitrary entities. In contrast to the existing methods, the suggested algorithm starts with the classification of the agents to experts and non-experts in each domain, and then it generates classification of the entities by preferring the opinions of the expert agents.

Classification of the agents is based on the assumption that the experts have similar opinions in their field of expertise, while the non-experts often tend to disagree and adopt different opinions in fields in which they are not experts.

Classification of the entities is based on the conventional expectation-maximization method initialized by majority vote and using the agents’ levels of expertise, as defined at the stage of the agents’ classification.

To verify the activity of the algorithm, we also formalized the considered task in the form of an optimization problem and suggested the likelihood-maximization algorithm (LMax) that uses brute force and provides the accurate solution.

Numerical simulations of the suggested DBCC algorithm and its comparisons with the known methods, such as majority vote, the FDS algorithm, and the GLAD algorithm, demonstrated that the run time of the suggested Algorithm 2 depends linearly on the number of entities, and it is close in run time to the fastest GLAD algorithm.

The accuracy of the suggested Algorithm 2 depends on the expertise levels of the agents. For the heterogeneous group that includes both experts and non-experts, the suggested Algorithm 2 resulted in a higher accuracy than the known heuristic algorithms and, especially, outperformed them in the scenarios where a small group of the agents considered a dataset with many entities.