Abstract
This study delves into the heightened efficiency and accuracy of 11 deep learning models classifying 11 dynamograph classes in the oil production sector. Introducing a novel framework with the Grad–CAM method, we address the “black box” issue, providing transparency in the models’ decision-making processes. Our analysis includes a comparative study with human experts, revealing a comprehensive understanding of both machine and human interpretive strategies. Results highlight the notable speed and precision of machine learning models, marking a significant advancement in rapid, reliable dynamograph classification for oil production decision-making. Additionally, nuanced findings in the model’s diagnostic accuracy reveal limitations in situations featuring the simultaneous occurrence of multiple pump issues. This underscores the need for additional features and domain-specific logic to enhance discernment and diagnostic precision in complex scenarios. The exploration of qualitative aspects distinguishes interpretive approaches, highlighting strengths and limitations. Machines, driven by algorithmic patterns and data processing, excel in rapid identification, albeit with occasional misclassifications. In contrast, human experts leverage experience and domain-specific knowledge for nuanced interpretation, providing a comprehensive understanding of both quantitative metrics and qualitative nuances. In conclusion, this study not only demonstrates the accelerated and enhanced accuracy of dynamograph classification by machine learning models compared to junior and medior domain experts, but also provides valuable insights into specific features and patterns guiding the decision-making process. This understanding allows continuous refinement, combining machine speed with human understanding for improved results in oil production. The potential for further studies and improvements in this domain is substantial.
MSC:
68t01
1. Introduction
In oil production, the initial phase often sees wells producing oil through a process known as natural lift. This phase relies on the inherent energy of the reservoir, which, when substantial enough, enables fluids to ascend to the surface at economically viable flow rates [1]. The reservoir’s inherent pressure diminishes gradually, proving insufficient to offset the cumulative pressure losses experienced during the fluid’s ascent to the surface storage tanks; hence, there arises a crucial requirement to enhance energy within the reservoir. This enhancement is accomplished through the application of artificial lift strategies [2].
Artificial lift methods, essential to the continued productivity of oil wells, are broadly classified into two fundamental categories: pneumatic methods, which use gas to lighten the fluid column or to inject under pressure, and pumping methods, which involve the use of mechanical pumps. A standout amongst these pumping methods is the sucker-rod pumping system, a tried and true technique with a history as rich as the oil industry itself [3].
Sucker-rod pumping systems are distinguished by their widespread adoption in the oil and gas industry, where they serve as the primary solution for extracting fluids from beneath the Earth’s surface when natural reservoir energy is insufficient. Accounting for an estimated 90% of artificial lift systems around the world, these systems are not only extensively used but are also celebrated for their dependability, operational efficiency, and adaptability across a myriad of applications [4,5]. Critical to the optimal operation and analysis of these systems is a diagnostic tool known as the dynamometer card (dynamographs or “dyna card”). These cards offer graphical portrayals of the polished rod’s load as a function of its position, serving as a revealing lens into the intricate dynamics of the entire pumping system and allowing engineers to make data-driven decisions to maintain system integrity and performance [6].
Leveraging the dyna card in beam pump diagnostics is complicated, as card shapes reflect the health of the pumping well and each has its own distinct signature. This makes manual diagnosis not only tedious and expertise-dependent [7] but also a lengthy process requiring specialized knowledge. With the modern oil industry inundated by various data streams (such as dynamometer cards, temperature readings, and pressure metrics), even seasoned experts grapple to stay afloat. The task of navigating this massive data deluge for accurate sucker-rod pump diagnosis is daunting, underscoring the need for innovative solutions [8].
Over the past few decades, the analysis of dynamographs using machine learning (ML) techniques has garnered significant attention, showcasing promising results in various studies [9,10,11,12]. These advanced methodologies have significantly enhanced accuracy and efficiency in dynamograph analysis.
In this study, we rigorously trained and evaluated 11 distinct deep learning models, comprising two vision transformer models and nine convolutional neural networks tailored for the classification of 11 unique dynamograph classes. Each model underwent a comprehensive assessment to measure its predictive accuracy and efficiency.
However, a recurring concern in these advancements is the “black box” nature of many ML models (especially deep learning models), which often leads to obscurity in their decision-making processes [13]. The implications of this opacity extend beyond mere academic curiosity; in real-world applications, the inability to interpret or understand why a model makes a particular decision can pose serious challenges, especially when the stakes are high [14].
Recognizing the criticality of this gap, this study ventures into new territories by introducing a novel framework built on deep learning techniques for computer vision [15,16]. Our approach does not merely predict or analyze: it elucidates. By presenting a mechanism to visualize which regions of the dynamograph the deep learning model predominantly focuses on during its deliberations, based on the Grad–CAM method [17], we peel back the layers of the conventional black box, offering a transparent and intuitive insight into the deep learning predictions.
In this study, we go beyond comparing our 11 deep learning models to each other: we also measure them against human experts in the field of dynamograph analysis. Our goal is to see how ML compares to human skills and knowledge. We take a close look at where our models are correct and where they miss the mark, shedding light on their strengths and weaknesses. This comparison gives us valuable insights into how both humans and machines interpret dynamographs, helping us understand the bigger picture.
To summarize, the contributions of this work are as follows:
- We developed and evaluated 11 customized deep learning models for classifying 11 unique dynamograph classes.
- We introduced a novel framework, utilizing Grad–CAM, that unveils the internal decision-making processes of these models, mitigating the ”black box” issue.
- We conducted an unprecedented comparative study measuring the models against human experts, offering insights into their relative strengths and weaknesses.
- We facilitated a more comprehensive understanding of dynamograph analysis, by blending machine precision and human interpretive insights.
The remainder of the paper is structured as follows. Section 2 delves into the background of dynamographs and their traditional evaluation. Section 3 highlights related work. The experimental setup and its results in real-world applications are detailed in Section 4 and Section 5, respectively. Finally, conclusions are presented in Section 6.
2. Background
2.1. Traditional Interpretation of Dyna Cards
To comprehend the fundamental patterns of surface dynamometer cards produced by traditional dynamometers, we first consider cards under basic conditions. The relationship between the polished rod’s load and its position is depicted as the parallelogram 1234 in Figure 1.
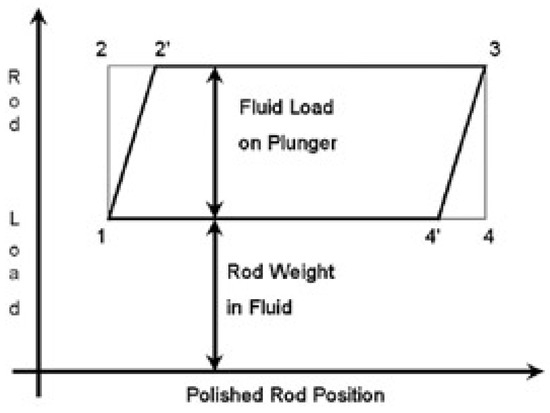
Figure 1.
Theoretical surface dynamometer card shapes.
At point 1, the upward motion initiates, leading to the instant closure of the traveling valve. The load on the polished rod, which matches the floating weight of the string at point 1, swiftly escalates to the value indicated by point 2 when the fluid load transitions from the standing valve to the traveling valve. The plunger, alongside the polished rod, proceeds in unison until point 3, maintaining a steady load throughout this phase. At point 3, the upward motion concludes, marking the onset of the downward motion, which corresponds with the prompt opening of the traveling valve. The rod’s load precipitously descends to point 4 as the fluid load is no longer sustained by the traveling valve. Between points D and A, with the traveling valve now open, the rod string descends amidst the well fluids, with the polished rod load mirroring the floating weight of the rod string. Point A marks the start of a subsequent cycle [18].
From a properly recorded dyna card, various loads can be ascertained. These are illustrated in the example card shown in Figure 2 [19].
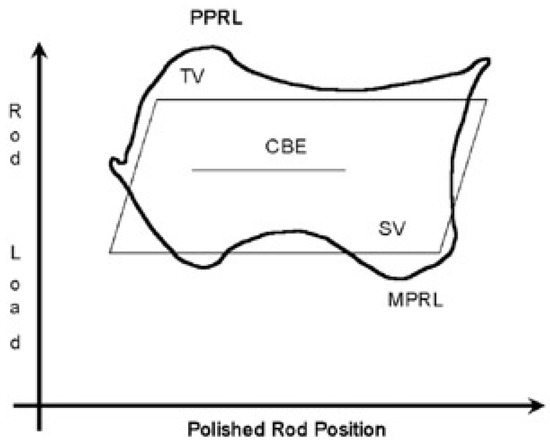
Figure 2.
Example of loads on a dyna card.
The zero load or baseline, serving as the reference point against which all other loads are measured.
The SV load, ascertained through a standing valve test. Ideally, in the absence of any standing valve leaks, the SV load aligns with the buoyant weight of the rod string.
The TV load, assessed during a traveling valve test. When both the plunger and the valves of the sucker-rod pump are in flawless condition, this load comprises the combined buoyant weight of the rod and the fluid load applied to the plunger.
The peak polished rod load (PPRL), outlined in Equation (1), signifies the maximum load encountered during the pumping cycle. It reflects the TV load along with the peak dynamic loads experienced during the upstroke:
The minimum polished rod load (MPRL), calculated using Equation (2), denotes the SV load subtracted by the maximum downstroke dynamic load. This value is identified on the dynamometer card as the minimum load observed during the pumping cycle:
where
—buoyant weight of the rod string (kg)
F1/Skr and F2/Skr—functions found from graphs in standard [20].
The CBE, signifying the force exerted on the polished rod, is determined by the maximum counterweight moment.
2.1.1. Fluid Load and Working Fluid Level
The fluid load (Fo) is obtained as the difference between the TV load and SV load checks [21], as
If the specific gravity of the produced fluid mixture in the tubing can be estimated, the depth to the working fluid level can be computed as
where
- —working or net fluid level from the surface (ft)
- —fluid load (lb)
- —specific gravity of the fluid produced
- —plunger area (inch2)
This depth should be similar to that obtained from a fluid level survey performed at the same time the dyna card is recorded.
2.1.2. Wellbore Pressures
Once the working fluid level is known, an estimate of the intake pressure to the pump can be computed from the measured casing head pressure [22], as
where
- —pump intake pressure (psi)
- D—pump setting depth (ft)
- —gas pressure above the working fluid level
- (psi)
- —surface casing pressure (psi)
The flowing bottomhole pressure (BHP) inside the wellbore is equal to if the pump is set at the perforation depth. If the pump is above the perforations, the BHP can be estimated using
where
- —flowing BHP inside the wellbore (psi)
- —depth of the perforations (ft)
The previous calculations assume that the gradient of the fluid columns has been estimated from the density of the produced liquids; they do not take into account the possible presence of free gas in the fluid mixture [23].
2.1.3. Normal Operations Dynamograph
In preceding sections, we outlined the characteristics of an optimal dynamograph and highlighted the typical variations that might arise during standard pump functioning. Figure 3 offers insights into the general shape of a dynamograph. As the polished rod concludes its downward movement, the plunger continues its descent due to a lag in transmitting stress within the string. Consequently, the traveling valve (TV) only engages after the polished rod initiates its upward motion. Once the traveling valve is activated, an elongation occurs in the rods, resulting in an uptick in the polished rod load until its maximum value is attained. As the upstroke nears its end, dynamic forces lead to the compression of the rod string, leading to a reduction in polished rod loads. Subsequently, a delay arises in the traveling valve’s operation, and it only disengages once the polished rod commences its downward trajectory. This results in the rods beginning to revert to their original form and impacts the polished rod loads [24].
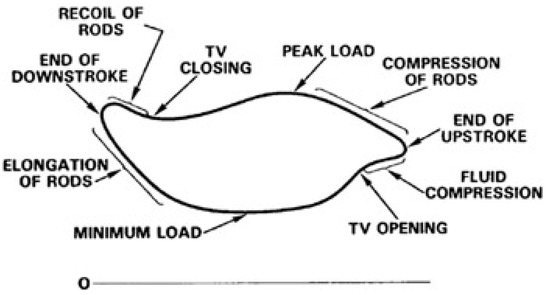
Figure 3.
Characteristic features of a general dynamometer card.
Evaluating operational conditions requires a periodic review of dynamometer cards. Originating from surface cards via the wave equation’s implementation, dynamographs provide an in-depth snapshot of well activities. Such dynamographs play a pivotal role in numerous operations, including determining well-flow velocities, pump conditions, and the forces applied on polished rods. Their pivotal role lies in predicting the state of equipment during active operations, a crucial step in maintaining optimal well operations and minimizing disruptions in the context of sucker-rod pump systems [25].
In the past, dynamograph interpretation predominantly depended on manual methodologies, necessitating profound knowledge and seasoned expertise. Professionals such as production engineers or analysts were responsible for scrutinizing these visual plots, spotting distinct configurations that mirror various pump system conditions. Given the myriad of interacting factors and the vast array of potential pump challenges, there is virtually no limit to the potential dynamograph designs, leading to the perception that evaluating surface dynamographs is more of an art than a precise discipline. A robust diagnostic assessment of the pumping mechanism largely leans on the proficiency of the analyst. A standard dynamograph configuration is principally dictated by the rate of pumping and the fluid’s weight on the plunger. However, other factors such as rod string composition, the slip of the primary driver, and more also play a role. This understanding was acknowledged by Sucker Rod Pumping Research Inc. when they innovated an analog computing system to mimic the pump’s activity. Their findings, subsequently integrated by the API into the RP 11L, paved the way to dynamographs for a plethora of hypothetical scenarios [26].
Before delving into the interpretation of problematic pump cards, it is essential to grasp the characteristics of cards obtained under optimal pumping conditions. The features of ideal conditions for a sucker-rod pump can be summarized as follows:
- The pump’s barrel and plunger are in impeccable condition.
- The standing and traveling valves exhibit no leaks.
- All friction forces along the rod string result from viscous damping.
- Only single-phase liquid enters the pump barrel.
- The barrel completely fills up during the upstroke.
Under such conditions, pump cards calculated from the solution of the wave equation show distinctively characteristic and straightforward shapes, facilitating the easy identification of the most crucial pumping parameters [27].
Takacs underscored the significance of seasoned knowledge and proficiency when it comes to deciphering these cards. He highlighted how distinct card configurations can shed light on a range of pump operation statuses, from peak performance to several inefficiencies and breakdowns. Additionally, he elaborated on the potential obstacles and constraints that professionals might face when analyzing these dynamographs, pointing out the interpretative nature of the evaluations and the substantial background needed for precise judgments [28].
2.1.4. Detailed Analysis and Pattern Recognition
Professionals within the industry undergo rigorous training to decipher the intricate patterns exhibited on dyna cards; each pattern serves as a visual language conveying the operational health of the sucker-rod pump system. A normative or “full pump” card, characterized by a smooth, elongated ellipse, serves as a benchmark, representing efficient and trouble-free operations within the system [29]. However, deviations from this norm manifest as distinctive and meaningful patterns, each indicative of potential issues within the downhole environment [29]. For instance, the appearance of a sharp corner on the dynamograph may be a telltale sign of gas interference, alerting operators to investigate and address this specific challenge promptly. Similarly, a wavy line in the card may signal fluid pound, prompting a targeted inspection and diagnosis. Meanwhile, a truncated or irregular shape might suggest worn pump components, necessitating a closer examination to pinpoint and rectify the source of wear.
The dynamographs, with their nuanced shapes and patterns, provide a visual language for diagnosing potential problems. In instances where erratic and inconsistent patterns emerge, these often point to mechanical friction within the system, alerting operators to the need for maintenance or intervention to optimize performance and prevent potential failures. To illustrate these concepts further, we have included examples of dyna cards for various downhole problems in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, drawing from industry-standard references [30]. These examples provide a visual reference guide for the diverse patterns associated with specific issues, offering a comprehensive resource for industry professionals to enhance their diagnostic capabilities and respond effectively to the unique challenges posed by different dynamograph shapes.
Figure 4.
Dynamometer card—gas interference.
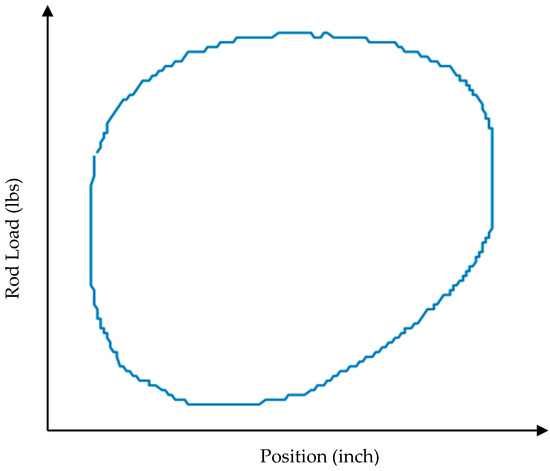
Figure 5.
Dynamometer card—high viscosity fluid.
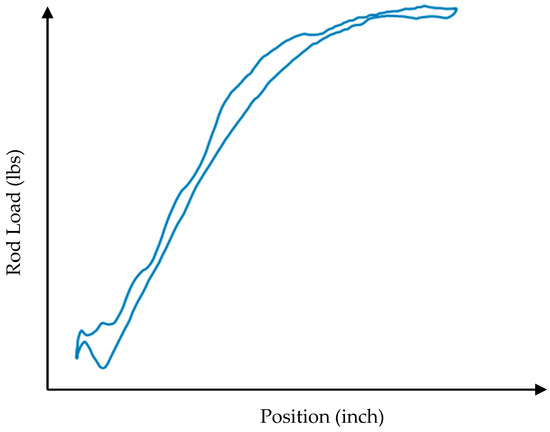
Figure 6.
Dynamometer card—gas lock.
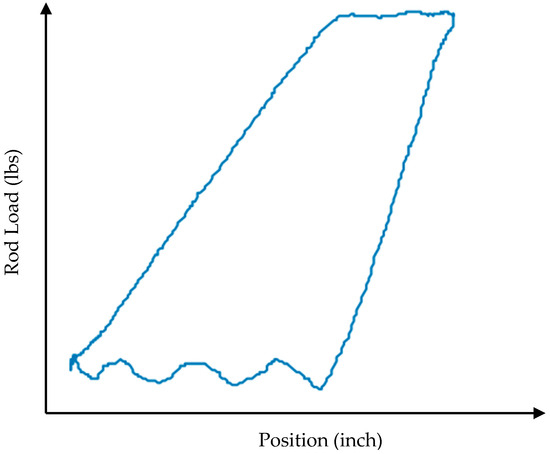
Figure 7.
Dynamometer card—pump wear.
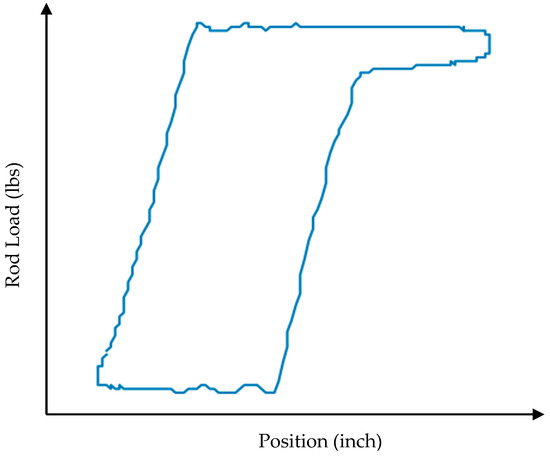
Figure 8.
Dynamometer card—fluid pound.
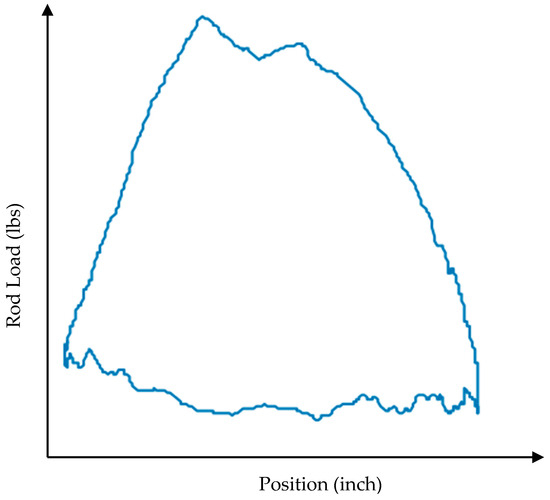
Figure 9.
Dynamometer card—TV leaking.
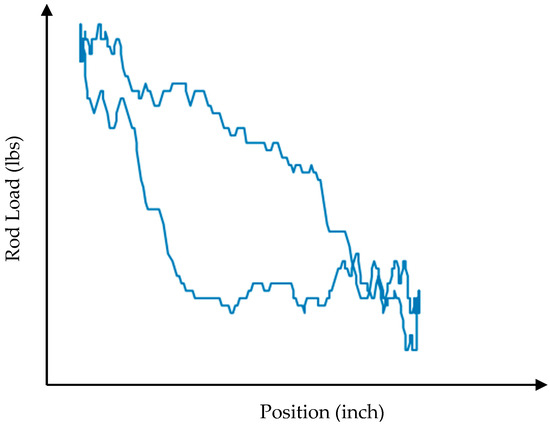
Figure 10.
Dynamometer card—flow through pump.
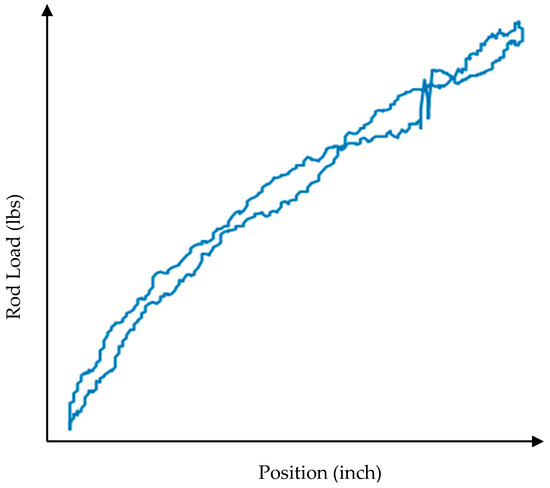
Figure 11.
Dynamometer card—stuck plunger.
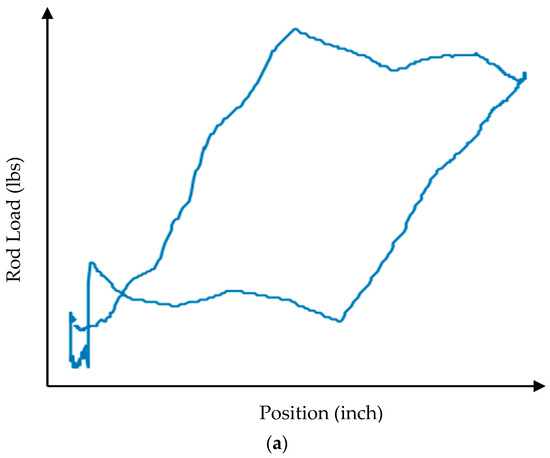
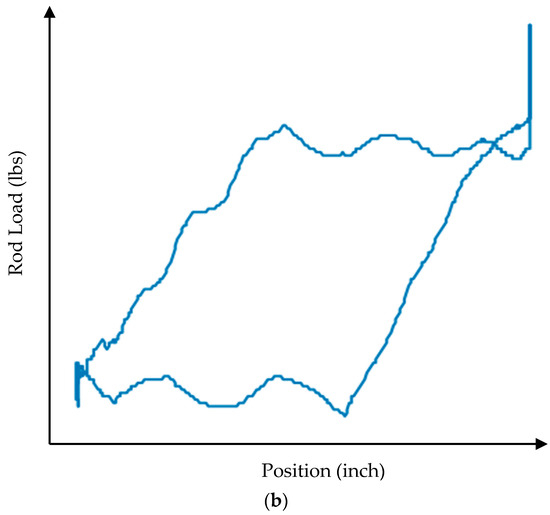
Figure 12.
(a) Dynamometer card—bottom tagging. (b) Dynamometer card—top tagging.
Gas Interference
The curve at the beginning of the pump card upstroke is caused by an expansion of the gas trapped in the barrel at the end of the downstroke. The downstroke produces the characteristic gas compression curve. A significant volume of gas is being compressed and is flowing through the pump, which reduces the tubing flow gradient. In Figure 4, a gas interference dynamometer card is presented.
Highly Viscous Fluid
In the context of sucker-rod pumps, the behavior of the traveling and standing valves can be notably affected when pumping highly viscous fluids. The fluid’s resistance might cause a delay in the opening and closing of these valves, potentially leading to the pump barrel not filling completely or not discharging the fluid entirely during its operational cycles. This behavior can be discerned on the dynamometer card, where the presence of viscous fluid might manifest as a stretched-out pattern, particularly evident during the upstroke. This indicates the pump’s increased effort to lift the viscous fluid. Additionally, the dynamometer card might display irregularities in its load pattern, hinting at potential valve operation issues stemming from the fluid’s viscosity [31]. In Figure 5, a high viscosity fluid dynamometer card is presented.
Gas Locking
When a pump is gas-locked and both its valves fail to open due to insufficient pressure, the dynamometer card will typically display a flat or nearly constant load line. This is because the pump is not taking in or discharging any fluid. The reduced load on the dynamograph indicates the pump’s decreased efficiency, as gas is less dense than liquid. Essentially, a consistent or flat load line on the dynamograph suggests that the pump is non-functional, not producing any fluid, and requires intervention. In Figure 6, a gas lock dynamometer card is presented.
When a pump experiences wear, its efficiency and performance can be compromised. In the context of the dynamograph, pump wear, especially wear in the plunger or the associated components, can lead to a delay in load uptake during the upstroke. This means that as the upstroke begins, the dynamograph will show a lag or delay in the increase of load, indicating that the plunger is not immediately taking on the expected load. This lag is a result of worn-out components failing to engage or seal properly, causing a delay before the plunger starts lifting the fluid. Essentially, a delayed load increase during the upstroke on the dynamograph can be a telltale sign of pump wear, signaling the need for maintenance or component replacement. In Figure 7, a dynamometer card showing pump wear is presented.
Fluid Pound
Fluid pound occurs when the inflow from the well is inadequate in comparison to the displacement of the downhole pump, resulting in incomplete filling of the barrel during the upstroke. The upper portion of the pump is empty. Since the traveling valve only opens when the plunger is in close proximity to the liquid level in the barrel, the plunger’s impact on the liquid may generate elevated compression loads in the rod string. Figure 8 illustrates a dynamometer card depicting fluid pound.
TV Leakage
The occurrence of any leakage in the traveling valve or between a worn pump barrel and plunger allows fluids to pass from above the traveling valve. This fluid leakage gradually raises the pressure in the space between the pump’s two valves, causing the standing valve to slowly close. Once closed, the fluid load is no longer borne by the plunger and the rod string; instead, it is entirely transferred to the standing valve and tubing. Figure 9 illustrates a dynamometer card depicting TV leaking.
Flow through the Pump
High pump intake pressures create pressure differences in the pump. The travelling valve and standing valves open as a result and fluid flows through the pump. There is no difference between minimum and maximum loads. In Figure 10, a dynamometer card showing flow through the pump is presented.
Stuck Plunger
Here, the loads at the polished rod and at the plunger increase and decrease linearly and exceed the normal peak loads for this rod string by a factor of two or three. The slope of the load versus the position matches the combined elastic constant of the rod string and tubing. This indicates that the plunger is stuck inside the barrel. In Figure 11, a stuck plunger dynamometer card is presented.
Tagging
In tagging, the plunger hits up or down because of improper spacing of the pump. This is a common characteristic of rod pumps implemented as a countermeasure against gas locking. On the dynamograph, one can observe a notable drop in load when components come into contact with the pump head. If not aligned correctly, the piston impacts the top, and a significant increase in load can be expected. This provides clarity on the tagging phenomenon. In Figure 12a,b, bottom and top tagging dynamometer cards are presented, respectively.
3. Related Work
This interpretative process relies heavily on the experience and intuition of the analyst. Seasoned engineers often can make accurate diagnoses just by glancing at a dyna cards, due to their extensive experience with similar patterns in the past. They also frequently rely on their intuition to make judgments when the card patterns are ambiguous or fall between known categories [32].
Interpreting dyna cards is a time-consuming task, and the accuracy can vary depending on the individual interpreting the cards. Different analysts may arrive at varying conclusions when examining the same card, leading to inconsistencies in diagnosis and subsequent actions. This subjectivity is one of the significant drawbacks of traditional dyna card interpretation [33].
Moreover, the traditional interpretation of dyna cards may not detect early-stage anomalies, which can result in delayed action and increased operational risks [34]. For example, subtle changes that may be indicative of a developing problem (such as a slowly wearing pump or gradually worsening gas interference) might not be noticeable until the issue becomes more pronounced.
Additionally, this traditional method is heavily dependent on the availability of skilled analysts. In regions or periods where experienced personnel are in short supply, the quality of the dyna card interpretation can suffer significantly. This dependency creates a vulnerability in operations, as timely and accurate interpretations are crucial for maintaining optimal production levels and equipment health.
The interpretation of dyna cards is also complicated by changes over time. A pumping system’s dyna card can evolve due to factors like equipment wear, changes in fluid properties, or variations in the reservoir conditions. Analysts must not only interpret a single card but often need to compare current cards with historical data to understand the evolving state of the well, adding another layer of complexity to the task.
Initial attempts to apply ML to dyna card diagnostics focused on simple classification tasks. For example, Sharaf [35] employed basic neural network models to classify dyna cards into categories indicating either normal or anomalous behavior. While these early models demonstrated the potential of ML [36,37], they were limited by the available computing power and data at the time. Further, these initial models often struggled with generalizing to new, unseen data and required substantial feature engineering and expert input to achieve useful accuracy [38]. Additionally, a wide variety of research papers have been published that are related to the application of artificial intelligence in upstream oil and gas problems [39,40,41].
More recent work has sought to employ advanced ML techniques for pattern recognition in dyna card data. Souza [42] applied convolutional neural networks (CNNs) to recognize specific patterns indicative of pump faults or inefficiencies. Their work showed that CNNs could outperform traditional methods in both speed and accuracy, highlighting the potential of deep learning techniques in this domain. They also noted the ability of CNNs to automatically learn relevant features from raw dyna card data, reducing the need for manual feature engineering [43].
An emerging area of research is the use of ML for anomaly detection and predictive maintenance. Serradilla [44] presented a model that uses unsupervised learning algorithms such as autoencoders to detect anomalous patterns in dyna card data, which might indicate a pending failure or suboptimal operation. Such approaches allow for early intervention, reducing the risk of costly equipment damage and downtime [45]. Additionally, integrating these anomaly-detection models with other data sources, such as equipment maintenance logs and sensor data, is a burgeoning field aiming to develop comprehensive predictive maintenance systems [46].
While ML approaches have shown significant promise in dyna card diagnostics, several challenges remain. Data quality and availability are consistent issues, as noted by Chicheng [47], with noisy or incomplete data potentially leading to inaccurate predictions.
Furthermore, the interpretability of ML models is a common concern in the industry, as engineers and decision-makers often require understandable and actionable insights [48]. The “black box” nature of some ML models, especially deep neural networks, can be a significant barrier to their adoption, as operators are traditionally cautious and want to understand the basis for the model’s predictions.
Additionally, the deployment and integration of ML models into existing workflows and systems present another set of challenges. Ensuring that ML models are reliable and robust enough for deployment in critical industrial environments, where mistakes can have severe consequences, is a non-trivial task that involves thorough validation and testing [49].
Moreover, keeping the ML models up-to-date and adapting to the changing conditions of the oilfield (e.g., new equipment, changing reservoir conditions, and different operational strategies) requires continuous monitoring and updating of the models, which could be resource-intensive [50].
In addressing the aforementioned challenges, we introduced deep learning models for enhanced dyna card diagnostics, coupled with Grad-CAM for interpretability. Our models were tested against human experts, blending machine accuracy with human insight. They are designed for adaptability, ensuring sustained relevance in changing oilfield conditions. This marks a key advancement in dyna card analysis.
4. Materials and Method
4.1. Dataset Description
The primary data for our research were sourced from a collection of dynamographs. These cards serve as a pivotal tool in our analysis, revealing nuanced details related to various issues observed. For the scope of this study, the dynamographs were obtained from a comprehensive database over the duration of the last 2 years from wells operating with sucker-rod pumps in the western Serbian region.
To guarantee consistency and precision in our investigation, each dynamograph card underwent systematic categorization based on the specific issue it represented. This process was not merely procedural but a critical step to foster structured and coherent analysis. As elucidated in the background section (Section 2) of our paper, our systematic categorization adheres to industry-accepted procedures. This methodological approach ensures that each labeled data point aligns with recognized standards, contributing to the reliability of our dataset. It is imperative to highlight that the systematic categorization was executed with great care and attention to detail. To fortify the accuracy of our data labeling, we engaged domain-side experts with profound expertise in pump dynamics. Their involvement not only added a layer of veracity to our dataset but also reinforced the quality and reliability of our labeled data. This meticulous process, as detailed in our background section, establishes a robust foundation for subsequent analyses and underlines our commitment to methodological rigor and data integrity.
In Table 1, we present the total number of instances along with their distribution for training, validation, and testing. The dataset is split in a 70/15/15 ratio, allocating 70% for training, 15% for validation, and 15% for testing purposes.

Table 1.
Overview of issues as reflected in the dynamograph dataset.
4.2. Models Description
In the rapidly evolving field of ML and computer vision, selecting an appropriate model is pivotal to the success of any task related to image classification or pattern recognition. Each model brings with it a unique set of capabilities, intricacies, and suitability for diverse scenarios. In the context of our research, we have utilized a range of renowned deep learning models to comprehensively tackle the complexities associated with dyna card diagnostics. Each model, from densely connected convolutional networks (DenseNet) and residual networks (ResNet) to the innovative Vision Transformer (ViT), has been meticulously chosen for their distinct advantages in feature extraction, computational efficiency, and performance accuracy.
DenseNets, or densely connected convolutional networks, are renowned for their densely connected layers, each receiving input from all preceding layers. This facilitates feature reuse and renders the network more efficient in terms of parameters. Different variants such as DenseNet121, DenseNet161, DenseNet169, and DenseNet201 are distinguished by their depths, which denote their layer complexities.
- DenseNet121 possesses 121 layers, ensuring comprehensive feature extraction and a complex representational capability.
- DenseNet161 escalates in complexity with 161 layers, enhancing the model’s capacity to discern intricate patterns.
- DenseNet169 offers a balanced performance with its 169 layers, standing as a middle ground in complexity.
- DenseNet201 tops the list with 201 layers, underlining an advanced capacity for the most detailed feature extraction.
ResNet, or residual networks, introduce the innovative concept of “skip connections”, allowing gradients to bypass layers during training. This architecture mitigates the vanishing gradient issue, enabling the training of deep networks. Models such as ResNet18, ResNet34, ResNet50, ResNet101, and ResNet152 vary based on their number of layers.
- ResNet18 is a fundamental model with 18 layers, ideal for simpler tasks and swift computations.
- ResNet34, with 34 layers, scales up in capacity, offering a more nuanced feature extraction.
- ResNet50 strikes a balance with 50 layers, aligning computational efficiency with enhanced performance.
- ResNet101, having 101 layers, is tailored for intricate tasks, ensuring in-depth pattern recognition.
- ResNet152 is the pinnacle, with 152 layers, engineered for the most intricate feature extraction and pattern recognition.
The Vision Transformer (ViT) model departs from conventional CNN architectures, introducing the transformer architecture initially designed for natural language processing to vision. ViT dissects an image into fixed-size patches, linearly embeds them, and processes them as a sequence. It is adept at handling long-range dependencies and demonstrates robust performance in image-classification tasks.
These models collectively present a diverse set of tools for handling a broad spectrum of visual recognition tasks, each exhibiting distinct advantages based on the task’s complexity and computational constraints.
4.3. Grad-CAM
Grad-CAM (gradient-weighted class activation mapping) serves as a pivotal tool in our approach, offering insights into the internal workings of deep learning models. The principal objective of employing Grad-CAM is to enhance the interpretability of these models, providing visual explanations for their predictions. It addresses the “black box” problem often associated with complex models, thereby fostering trust and visually highlighting the regions in the input image that are pivotal in driving the model’s predictions. It leverages the gradients of any target concept flowing into the final convolutional layer to produce a coarse localization map highlighting the important regions in the image for predicting the concept. In the context of our study, Grad-CAM aids in unveiling the specific features and patterns within the dyna cards that our models focus on during their decision-making processes. This not only enhances transparency but also facilitates a richer understanding of model behavior and prediction rationale, integral for validation and actionable insight extraction. The integration of Grad-CAM bridges the gap between the technical complexity of ML models and the intuitive interpretive insights desired in practical applications.
4.4. Hyperparameter Tuning
For the various models deployed in our study, uniform settings were employed to maintain consistency in evaluation and result interpretation. Adam was utilized across all models with a fixed learning rate of 1 × 10−5. Early stopping mechanisms were employed by monitoring the validation set to determine the optimal number of epochs for training. We leveraged pre-trained networks, a strategy that harnesses previously learned features and patterns from extensive datasets to enhance the model’s learning capability. These networks were then fine-tuned on our specific dataset to tailor the models to the unique characteristics and patterns inherent in dyna card diagnostics. Specific hyperparameters are optimized for both CNNs and vision transformers to enhance their performance. The number of layers in the fully connected network (FCN) at the output is denoted as ‘_h’. Each model was subjected to a maximum of 100 epochs for training, ensuring that they had ample opportunity to learn and adapt to the data. However, with the incorporation of early stopping, training could be halted within 5 epochs if no significant improvement in performance on the validation set was observed. This balanced approach ensures that the models are neither undertrained nor overfitted, optimizing their generalization capability and performance efficiency.
4.5. Framework for Dyna Card Type Prediction and Visual Interpretation of Model Decisions
Our framework provides a systematic approach to classifying and interpreting dyna cards utilizing advanced deep learning techniques. This sophisticated methodology ensures not only precise classification into various types but also offers visual interpretations for each decision made by the model, ensuring transparency and understandability. Dyna cards are extracted from a database and are then inputted to a deep learning model to be classified into 1 of 11 distinct types. Following the classification, the model’s output class and the deep learning model itself are introduced into the Grad-CAM method to produce an explanation. These explanations are illustrated as heat maps overlaid on the input images. Areas marked in red on the heat maps signify the regions that the model particularly focuses on during the classification process, while those marked in blue indicate regions considered irrelevant by the model. The framework for dyna card type prediction and the visual interpretation of model decisions is comprehensively presented in Figure 13.
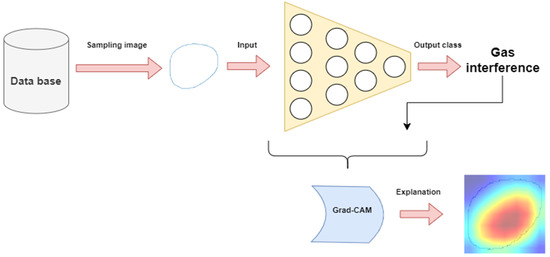
Figure 13.
Framework for dyna card type prediction and visual interpretation of model decisions.
5. Results and Discussion
In our pursuit to leverage ML for the diagnostics of sucker-rod pumps within the exploitation of oil wells, we rigorously evaluated a series of deep learning architectures, including DenseNet, ResNet, and ViT, on a comprehensive labeled dataset. Additionally, we presented the performance of these models against manual analyses conducted by human experts of varying expertise levels (senior, medior, and junior). In Table 2, the performances of various ML models are presented. Additionally, to further validate the generalizability of our results, we conducted extra tests by training our model on various random seeds for the separation of training, testing, and validation sets. These tests yielded results with remarkably consistent accuracy, exhibiting only a minimal average deviation of 0.001 from the results presented in Table 2. This consistency across different data splits reinforces our confidence in the stability and reliability of our model under varied conditions.

Table 2.
ML model performance.
Our results unequivocally highlight the potential of deep learning in this domain. Among the architectures evaluated, the ResNet models consistently outperformed both the DenseNet and ViT models. The ResNet34_h_2 variant emerged as a standout, registering the highest accuracy of 0.945. This robustness in identifying anomalies or failures in sucker-rod pumps underscores the efficacy of the ResNet architecture in capturing intricate patterns associated with equipment diagnostics. While the ViT_b_32_h_1 model also showed commendable performance, it was the ResNet models that consistently delivered top-tier results, emphasizing their superiority in this specific application.
In comparison, human experts exhibited varying performances based on their expertise levels, which can be observed in Table 3. A senior domain expert, with years of experience and deep domain knowledge, achieved perfect scores across all metrics, taking only 16 h for the analysis. A medior domain expert, who possesses a moderate level of experience and domain knowledge, achieved an accuracy of 0.925 within 16 h. The precision, recall, and F1 scores for the medior expert were 0.878, 0.877, and 0.877, respectively. On the other hand, a junior domain expert took 40 h and achieved an accuracy of 0.748, with precision, recall, and F1 scores of 0.678, 0.677, and 0.677, respectively. This difference in performance highlights the importance of experience and domain knowledge in manual diagnostics. However, it also underscores the efficiency and potential of ML models, which can achieve comparable or even superior performance whilst requiring only a fraction of the time taken by human experts.

Table 3.
Human expert analysis time & metrics.
However, this rapid analysis does not negate the value of human input. The senior engineer’s expertise, distilled through years of experience, is a rare commodity. Senior-level experts are not always readily available, and their time is typically a premium commodity, translating to higher costs for organizations. The medior engineer’s expertise, whilst not as extensive as the senior’s, still plays a crucial role in diagnostics. Medior-level experts might be more readily available than senior experts, offering a balance between cost and expertise for organizations. In comparison, while junior engineers might be even more accessible and less expensive, they might not provide the depth of insights that more experienced professionals would. Thus, ML models can serve as powerful tools for preliminary data processing, especially in large-scale datasets, freeing human experts to focus on more nuanced, intricate analytical tasks and driving cost-effectiveness.
A significant observation across several ML models was the discrepancy between micro and macro metrics, hinting at a potential class imbalance in our dataset. Addressing this imbalance is crucial, given the high stakes associated with oil well operations.
In terms of model architecture, it is fascinating to observe how different configurations can lead to varying results. For instance, the DenseNet architecture, known for its densely connected layers, can sometimes outperform or underperform compared to the ResNet architecture, which leverages residual connections. This is a testament to the fact that in ML, it is not always the complexity of the model that determines its effectiveness. Sometimes, simpler models such as ResNet18_h_1 can achieve comparable results to their more complex counterparts, emphasizing the importance of proper tuning and understanding the underlying data.
In summation, while the model ResNet34_h_2 stands out in its performance, its real value may lie in complementing human expertise, bridging the gap between computational speed and nuanced human interpretation and introducing a more cost-efficient and timelier analytical framework.
The confusion matrix in focus provides insights into the performance of a classification model adept at distinguishing between 11 classes, each representing different operational states and issues within a mechanical system. These classes are: “good dynamograph”, “stuck plunger”, “TV leaking”, “gas lock”, “pump wear”, “high viscosity”, “bottom tagging”, “fluid pound”, “gas interference”, “flow through pump”, and “polished rod tagging”. Upon careful scrutiny, the matrix indicates that the model is particularly proficient in classifying “good dynamograph”, “gas lock”, and “flow through pump” classes, as evidenced by the high number of true positives and minimal false negatives for these categories. The “pump wear” class also exhibits a promising true positive rate, with only a few misclassifications. The confusion matrices for ML model ResNet34_h_2 and medior and junior domain experts are presented in Figure 14, Figure 15 and Figure 16, respectively.
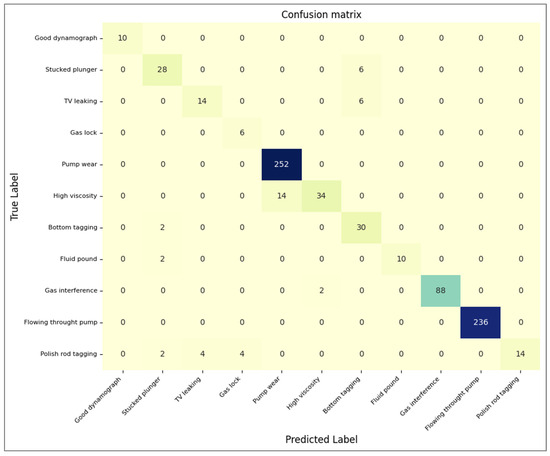
Figure 14.
Confusion matrix of ResNet34_h_2.
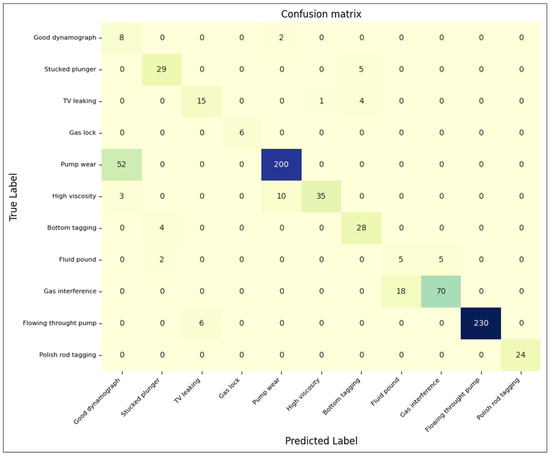
Figure 15.
Confusion matrix of medior domain expert.
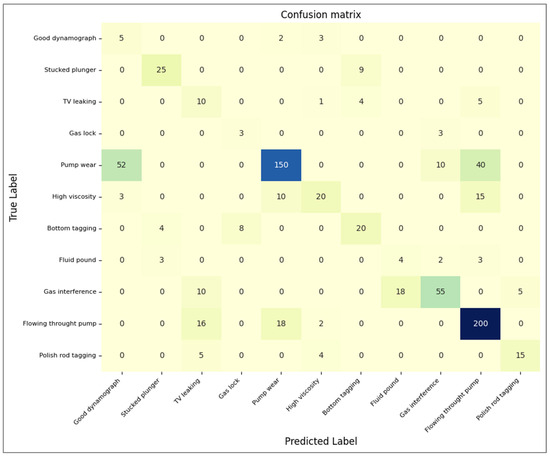
Figure 16.
Confusion matrix junior domain engineer.
The matrices of the ML models show areas warranting improvement. Notably, there is a tendency for the model to misclassify between “stuck plunger” and “bottom tagging”, albeit less frequently than previously observed. A slight misclassification is also noted between “TV leaking” and “bottom tagging”. These instances underline the model’s challenges in differentiating between these closely related classes, necessitating further refinement to bolster its predictive accuracy.
Furthermore, occasional confusion is observed between the “pump wear” and “high viscosity” classes, highlighting the need for a more in-depth examination of the features and classification boundaries pertinent to these categories. The “polished rod tagging” class is predominantly well-classified, with a minor misclassification observed as “gas interference”.
In conclusion, while the ML model demonstrates admirable accuracy for several classes, the confusion matrix illuminates areas where performance enhancement is feasible. The observed misclassifications between “stuck plunger”, “TV leaking”, and “bottom tagging”, as well as between “pump wear” and “high viscosity”, and the minor misclassification involving “polished rod tagging” and “gas interference”, underscore the necessity for further refinement to augment the model’s overall predictive accuracy and reliability.
The confusion matrix provided by the medior domain expert (Figure 14) illustrates the adept performance of a classification model in identifying 11 distinct operational states and issues within a mechanical system, including “good dynamograph”, “stuck plunger”, “TV leaking”, “gas lock”, “pump wear”, “high viscosity”, “bottom tagging”, “fluid pound”, “gas interference”, “flow through pump”, and “polished rod tagging”. The matrix shows promising accuracy in classifying these states, with noteworthy true positives in classes such as “pump wear” and “flow through pump”. However, there are areas for improvement, as evidenced by misclassifications in “stuck plunger” and “bottom tagging”, and between “gas interference” and “fluid pound”. Despite these, the overall trend indicates a high level of accuracy across most classes, highlighting the medior domain expert’s capability in effectively distinguishing between various operational states and issues. In conclusion, the matrix depicts a proficient medior domain expert with reliable accuracy in classifying diverse operational states and issues, making it a valuable asset for future applications and studies in the field.
The confusion matrix provided by the junior domain expert (Figure 15) delineates the classification model’s performance in identifying 11 distinct operational states and issues within a mechanical system: “good dynamograph”, “stuck plunger”, “TV leaking”, “gas lock”, “pump wear”, “high viscosity”, “bottom tagging”, “fluid pound”, “gas interference”, “flow through pump”, and “polished rod tagging”. The matrix reveals that the junior domain expert accurately classifies “gas lock” and “bottom tagging” but struggles with classes such as “pump wear” and “flow through pump”, with a significant number of misclassifications. For instance, “pump wear” is often confused with “good dynamograph” and “flow through pump”, while “flow through pump” is misclassified as “stuck plunger”, “TV leaking”, and “bottom tagging”. There are also misclassifications observed between “gas interference” and “fluid pound”. These errors indicate areas where the junior domain expert needs further refinement and training to improve classification accuracy. In conclusion, while the junior domain expert shows proficiency in classifying several operational states and issues, there is a need for improvement in distinguishing between closely related classes, to enhance overall reliability and accuracy in classification.
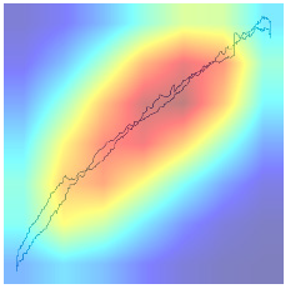
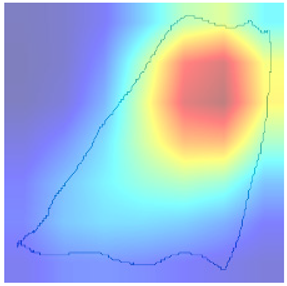
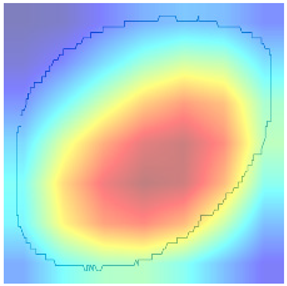
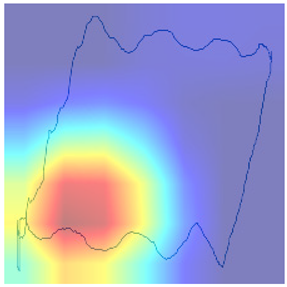
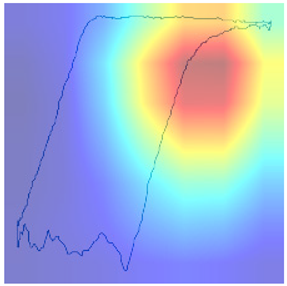
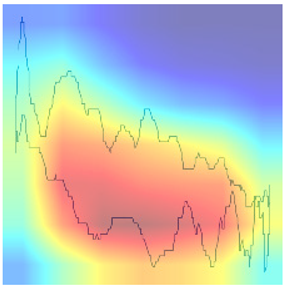
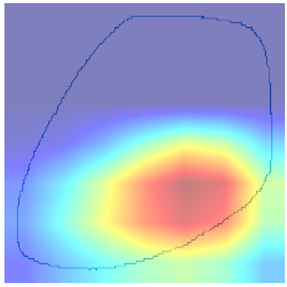
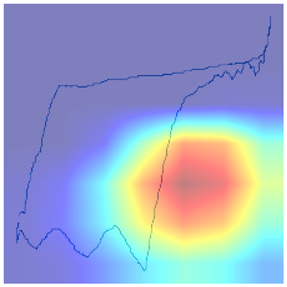
Following the initial analysis of the confusion matrices, the subsequent step in our research involves a meticulous examination of the misclassifications made by the selected model, ResNet34_h_2. To gain deeper insights into the reasons behind the model’s mistakes, domain experts conducted an in-depth review of the heatmaps generated from the model’s predictions (presented in Table 4 and Table 5). These heatmaps visually represent areas in the input data that the model focused on or “attended to” when making classification decisions. By presenting these heatmaps, experts can identify patterns or features in the data that may have led the model to misclassify certain instances. For example, the model may consistently focus on irrelevant or non-discriminative features when making incorrect predictions. Understanding these patterns is crucial, as it provides valuable information that can be used to refine and improve the model’s accuracy and reliability in classifying data points across the 12 classes under consideration.

Table 4.
True model result explanations.

Table 5.
False model result explanations.
In conclusion, the model’s diagnostic accuracy diminishes in situations characterized by the simultaneous occurrence of multiple pump issues. This limitation underscores the necessity of incorporating additional features and domain-specific logic into the model, to enhance its discernment and diagnostic precision in complex, multifaceted scenarios. By doing so, the model will be better equipped to navigate and accurately diagnose situations where multiple issues intersect, thereby providing a more comprehensive and reliable assessment of pump health and operational status.
In addition to the quantitative evaluation of our machine learning models and human experts, it is essential to delve into the qualitative aspects that distinguish their interpretative approaches. Machines, driven by algorithmic patterns and large-scale data processing capabilities, excel in rapid identification and consistent pattern recognition, as evidenced by the ResNet34_h_2 model’s commendable accuracy across various operational states. However, the model’s reliance on features and patterns inherent in the dataset can sometimes lead to misclassifications, particularly in cases of closely related dynamograph classes. On the contrary, human experts bring a nuanced understanding, leveraging years of experience and domain-specific knowledge to decipher intricate dynamograph patterns. The senior domain expert’s flawless performance is a testament to the depth of expertise, but the junior expert’s occasional misclassifications highlight the learning curve inherent in human interpretation. By scrutinizing both quantitative metrics and qualitative nuances, we gain a comprehensive understanding of the strengths and limitations of machine learning models and human experts in the intricate domain of sucker-rod pump dynamograph analysis.
6. Conclusions
In this study, we showed how deep learning models can be extremely helpful in quickly and accurately sorting dynamograph classes, an important task in the oil production field. We introduced 11 models and a new way of using the Grad-CAM method to make the decision-making process of these models clear and easy to understand. Our tests showed that these ML models work faster and with greater accuracy for classifying dynamographs. This is a big step towards making decisions faster and more reliable in oil production. By also showing how these models think and make decisions visually, we made it easier to understand and trust the results they give. We also compared how these models work against how human experts perform the same task. This helped us determine the strengths and weaknesses of both and gave us a clearer picture of how machines and humans understand dynamographs. In short, our work not only accelerates and enhances the accuracy of dynamograph classification compared to junior and medior domain experts but also provides valuable insights into the specific features and patterns that machine learning models focus on during the decision-making process. This understanding enables us to continually refine and improve the model for even greater effectiveness. We believe this combination of machine speed and human understanding will lead to much better results in oil production. Looking ahead, we propose further research into the potential of using dynamographs, in conjunction with measured tabular data from other measurement devices on sucker-rod pumps, to predict flow rates. Exploring this aspect could significantly broaden the application of our findings and contribute to more nuanced and data-driven decision-making in oil production. We believe that combining machine efficiency with human expertise will lead to substantially improved outcomes in this sector. The prospects for additional studies and advances in this domain are vast, offering exciting opportunities for future exploration and development.
Author Contributions
Conceptualization, B.M. and A.P.; methodology, A.P., B.M. and B.D.; software, M.B.; validation, B.M. and A.P.; formal analysis, B.M. and M.B.; investigation, B.M.; resources, B.M. and M.B.; data curation, D.D.; writing—original draft preparation, B.M.; writing—review and editing, A.P. and B.M.; visualization, M.B.; supervision, B.D.; project administration, B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alemi, M.; Jalalifar, H.; Kamali, G.R.; Kalbasi, M. A mathematical estimation for artificial lift systems selection based on ELECTRE model. J. Pet. Sci. Eng. 2011, 78, 193–200. [Google Scholar] [CrossRef]
- Golan, M.; Whitson, H.C. Well Performance, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Boomer, P.M.; Podio, A.L. The Beam Lift Handbook; PETEX: Austin, TX, USA, 2015. [Google Scholar]
- Zhang, A.; Gao, X. Fault diagnosis of sucker rod pumping systems based on Curvelet Transform and sparse multi-graph regularized extreme learning machine. Int. J. Comput. Intell. Syst. 2018, 11, 428–437. [Google Scholar] [CrossRef]
- Bello, O.; Dolberg, E.; Teodoriu, C.; Karami, H.; Devegowdva, D. Transformation of academic teaching and research: Development of a highly automated experimental sucker rod pumping unit. J. Pet. Sci. Eng. 2020, 190, 107087. [Google Scholar] [CrossRef]
- Gibbs, S.; Neely, A. Computer diagnosis of down-hole conditions in sucker rod pumping wells. J. Pet. Technol. 1966, 18, 91–98. [Google Scholar] [CrossRef]
- Ordonez, B.; Codas, A.; Moreno, U. Improving the Operational Conditions for the Sucker-rod Pumping System. In Proceedings of the 2009 IEEE Control Applications, (CCA) & Intelligent Control, (ISIC), St. Petersburg, Russia, 8–10 July 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1259–1264. [Google Scholar]
- Li, K.; Gao, X.-W.; Tian, Z.; Qiu, Z. Using the curve moment and the PSO-SVM method to diagnose downhole conditions of a sucker rod pumping unit. Pet. Sci. 2013, 10, 73–80. [Google Scholar] [CrossRef]
- Xu, P.; Xu, S.; Yin, H. Application of self-organizing competitive neural network in fault diagnosis of suck rod pumping system. J. Pet. Sci. Eng. 2007, 58, 43–48. [Google Scholar] [CrossRef]
- Cheng, H.; Yu, H.; Zeng, P.; Osipov, E.; Li, S.; Vyatkin, V. Automatic Recognition of Sucker-Rod Pumping System Working Conditions Using Dynamometer Cards with Transfer Learning and SVM. Sensors 2020, 20, 5659. [Google Scholar] [CrossRef]
- Bezerra, M.A.D.; Schnitman, L.; Baretto Filho, M.d.A.; de Souza, J.A.M.F. Pattern Recognition for Downhold Dynamometer Card in Oil Rod Pump System using Artificial Neural Networks. In Proceedings of the 11th International Conference on Enterprise Information Systems, Volume AIDSS, Milan, Italy, 6–10 May 2009; pp. 351–355. [Google Scholar]
- Zhao, H.; Wang, J.; Gao, P. A Deep Learning Approach for Condition-based Monitoring and Fault Diagnosis of Rod Pump. Serv. Trans. Internet Things (STIOT) 2017, 1, 32–42. [Google Scholar] [CrossRef]
- Ali, S.; Abuhmed, T.; El-Sappagh, S.; Muhammad, K.; Alonso-Moral, J.M.; Confalonieri, R.; Guidotti, R.; Del Ser, J.; Díaz-Rodríguez, N.; Herrera, F. Explainable artificial intelligence (XAI): What we know and what is left to attain trustworthy artificial intelligence. Inf. Fusion 2023, 99, 101805. [Google Scholar] [CrossRef]
- Brożek, B.; Furman, M.; Jakubiec, M.; Kucharzyk, B. The black box problem was revisited. Real and imaginary challenges for automated legal decision-making. Artif. Intell. Law 2023. [Google Scholar] [CrossRef]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef] [PubMed]
- O’Mahony, N.; Campbell, S.; Carvalho, A.; Harapanahalli, S.; Hernandez, G.V.; Krpalkova, L.; Walsh, J. Deep learning vs. traditional computer vision. In Advances in Computer Vision, Proceedings of the 2019 Computer Vision Conference (CVC), Las Vegas, NV, USA, 2–3 May 2019; Springer: Cham, Switzerland, 2020; Volume 1, pp. 128–144. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 618–626. [Google Scholar]
- Kemler, E. An Investigation of Experimental Methods of Determining Sucker-Rod Loads. Trans. AIME 1936, 118, 89–99. [Google Scholar] [CrossRef]
- Gipson, F.W.; Swaim, H.W. The beam pumping design chain. In Proceedings of the 31st Annual Southwestern Petroleum Short Course, Lubbock, TX, USA, 23–25 April 1984; Texas Tech University: Lubbock, TX, USA, 1984; pp. 296–376. [Google Scholar]
- American Petroleum Institute. API RP 11L Recommended Practice for Design Calculations for Sucker Rod Pumping Systems (Conventional Units), 4th ed.; American Petroleum Institute: Washington, DC, USA, 1988. [Google Scholar]
- Soza, R.L. Review of Downhole Dynamometer Testing. In Proceedings of the Permian Basin Oil and Gas Recovery Conference, Midland, TX, USA, 27–29 March 1998. [Google Scholar]
- Economides, M.J.; Hill, D.A.; Ehlig Economides, C. Petroleum Production Systems; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Russell, J.H., Jr. Interpretation of Dynamometer Cards. World Oil, July 1953. [Google Scholar]
- Fagg, L.W. Dynamometer charts and well weighing. Pet Trans AIME 1950, 189, 165–174. [Google Scholar] [CrossRef]
- Milovzorov, G.; Ilyin, A.; Shirobokov, P. Diagnostics of the condition of sucker-rod pumping units after the analysis of dynamogram cards. MATEC Web Conf. 2019, 298, 00137. [Google Scholar] [CrossRef]
- API. API Bul 11L2 Catalog of Analog Computer Dynamometer Cards, 1st ed.; American Petroleum Institute: Dallas, TX, USA, 1969. [Google Scholar]
- Podio, A.L.; McCoy, J.N.; Rowlan, O.L.; Becker, D. Dynamometer analysis plots improve ability to troubleshoot and analyze problems. In Proceedings of the 50th Annual Southwestern Petroleum Short Course, Lubbock, TX, USA, 16–17 April 2003; Texas Tech University: Lubbock, TX, USA, 2003; pp. 160–176. [Google Scholar]
- Takacs, G. Sucker-Rod Pumping Handbook: Production Engineering Fundamentals and Long-Stroke Rod Pumping; Elsevier Science: New York, NY, USA, 2015. [Google Scholar]
- Tripp, H. A review: Analyzing beam-pumped wells. J. Pet. Technol. 1989, 41, 457–458. [Google Scholar] [CrossRef]
- McCoy, J.N.; Rowlan, O.L.; Podio, A.L. Pump card analysis simplified and improved. In Proceedings of the 52nd Annual Southwestern Petroleum Short Course, Lubbock, TX, USA, 20–21 April 2005; Texas Tech University: Lubbock, TX, USA, 2005; pp. 154–164. [Google Scholar]
- Zhang, R.; Yin, Y.; Xiao, L.; Chen, D. Calculation Method for Inflow Performance Relationship in Sucker Rod Pump Wells Based on Real-Time Monitoring Dynamometer Card. Geofluids 2020, 2020, 8884988. [Google Scholar] [CrossRef]
- Derek, H.J.; Jennings, J.W.; Morgan, S.M. EXPROD: Expert Advisor Program for Rod Pumping. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27–30 September 1988. [Google Scholar]
- Takács, G. Use of Conventional Dynamometer Cards in the Analysis of Sucker-Rod Pumped Installations. Engineering 2001. [Google Scholar]
- Nascimento, J.; Maitelli, A.; Maitelli, C.; Cavalcanti, A. Diagnostic of Operation Conditions and Sensor Faults using Machine Learning in Sucker-Rod Pumping Wells. Sensors 2021, 21, 4546. [Google Scholar] [CrossRef]
- Sharaf, S.A.; Bangert, P.; Fardan, M.; Alqassab, K.; Abubakr, M.; Ahmed, M. Beam-Pump Dynamometer Card Classification Using Machine Learning. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 18–21 March 2019. [Google Scholar]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Xu, Y.; Qian, W.; Li, N.; Li, H. Typical advances of artificial intelligence in civil engineering. Adv. Struct. Eng. 2022, 25, 3405–3424. [Google Scholar] [CrossRef]
- Dreyfus, G. Neural Networks Methodology and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Koroteev, D.; Tekic, Z. Artificial intelligence in oil and gas upstream: Trends, challenges, and scenarios for the future. Energy AI 2021, 3, 100041. [Google Scholar] [CrossRef]
- Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of machine learning and artificial intelligence in oil and gas industry. Pet. Res. 2021, 6, 379–391. [Google Scholar] [CrossRef]
- Li, H.; Yu, H.; Cao, N.; Tian, H.; Cheng, S. Applications of artificial intelligence in oil and gas development. Arch. Comput. Methods Eng. 2021, 28, 937–949. [Google Scholar] [CrossRef]
- Souza, A.M.F.D.; Bezerra, M.A.D.; Filho, M.D.A.B.; Schnitman, L. Using artificial neural networks for pattern recognition of downhole dynamometer card in oil rod pump system. In Proceedings of the AIKED’09: Artificial Intelligence, Knowledge Engineering and Data Bases, Cambridge, UK, 21–23 February 2009. [Google Scholar]
- He, Y.; Liu, Y.; Shao, S.; Zhao, X.; Liu, G.; Kong, X.; Liu, L. Application of CNN-LSTM in Gradual Changing Fault Diagnosis of Rod Pumping System. Math. Probl. Eng. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Serradilla, O.; Zugasti, E.; Ramirez de Okariz, J.; Rodriguez, J.; Zurutuza, U. Adaptable and Explainable Predictive Maintenance: Semi-Supervised Deep Learning for Anomaly Detection and Diagnosis in Press Machine Data. Appl. Sci. 2021, 11, 7376. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y. How AI Affects the Future Predictive Maintenance: A Primer of Deep Learning. In Advanced Manufacturing and Automation VII; Springer: Singapore, 2018; pp. 1–9. [Google Scholar]
- Jimenez-Cortadi, A.; Irigoien, I.; Boto, F.; Sierra, B.; Rodriguez, G. Predictive Maintenance on the Machining Process and Machine Tool. Appl. Sci. 2020, 10, 224. [Google Scholar] [CrossRef]
- Xu, C.; Fu, L.; Lin, T.; Li, W.; Ma, S. Machine learning in petrophysics: Advantages and limitations. Artifical Intell. Geosci. 2022, 3, 157–161. [Google Scholar] [CrossRef]
- Hong, S.R.; Hullman, J.; Bertini, E. Human Factors in Model Interpretability: Industry Practices, Challenges, and Needs. Proc. ACM Hum.-Comput. Interact. 2020, 4, 1–26. [Google Scholar] [CrossRef]
- Teixeira, A.F.; Secchi, A.R. Machine learning models to support reservoir production optimization. IFAC-Pap. 2019, 52, 498–501. [Google Scholar] [CrossRef]
- Martyushev, D.A.; Ponomareva, I.N.; Zakharov, L.A.; Shadrov, T.A. Application of machine learning for forecasting formation pressure in oil field development. Izv. Tomsk. Politekh. Univ. Inz. Georesursov. 2021, 332, 140–149. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).