Insider Trading with Semi-Informed Traders and Information Sharing: The Stackelberg Game

Abstract

This paper presents a financial Stackelberg game model with two partially informed risk neutral insiders. Each insider receives a private signal about the stock value and competes with the other insider under a Stackelberg setting. Linear strategies for the game’s participants are considered and normal distributions for the fundamentals are assumed. Based on the Stackelberg game and the Backward Induction theory, the unique linear equilibrium is characterized. The findings reveal that the level of partial information might increase/decrease the insiders’ profits as well as the market parameter in the Stackelberg setting relative to the Cournot setting. Additionally, this paper considers the information sharing scenario between the two insiders competing in this Stackelberg game. The results show that multiple equilibria exist in contrast to the information sharing scenario in the Cournot game where the Nash equilibrium is unique.

1. Introduction

Asymmetric information refers to one party having more information than other market participants, leading to an imbalance in the market. In the case of insider trading, where insiders have access to material non-public information, asymmetric information can distort the efficient allocation of resources, where those may be allocated towards investments that are not necessarily the most productive or deserving, as prices may not accurately reflect the true value of the securities. In addition, investors lose confidence in the fairness and integrity of the market and are discouraged to trade, leading to reduced liquidity and potentially hindering market efficiency.

Owing to their position within the firm, corporate insiders, such as corporate executives or board members, are more informed than outsiders about any event involving the firm they work for and whose stock is publicly traded. They can use this information to make profitable trades at the expense of other market participants who do not have access to the same information. Typically, this private, price-sensitive information is expected to alter the behavior of the company’s stock and reduce market efficiency.

With the recurrence of insider trading scandals, academic research has consistently renewed its interest in this topic. The innovative work of [1] on insider trading is very famous in explaining how markets can incorporate private information. Ref. [1] studies the single auction model where three kinds of traders exchange one risky asset for a risk-less asset. The traders are a fully informed risk neutral insider who has access to private observation of the ex-post liquidation value of the risky asset of the firm, uninformed noise traders, and market makers who set prices conditional on the information they have about the quantities traded by others. Then, many other scholars extended the Kyle one-shot game model in several directions. One direction investigated the effect of risk attitudes of fully informed insiders on the equilibrium outcomes. For example, [2] studies the case of risk averse insiders. Ref. [3] consider the case of one risk averse and one risk neutral insiders. Ref. [4] studies the case of two insiders in which the first insider is risk-neutral while the second insider is overconfident.

A second direction extended the static Kyle model to the case in which signals are correlated. For example, in [5]’s model, the market maker observed correlated signals about the stock value. Ref. [6] studied the Kyle model in which the noise traders are able to correlate their trade with the true price.

A third extension of the Kyle model, studied the case of partially informed insiders (see [7,8]). Moreover [9] extended the Kyle model to incorporate a finite number of insiders, all knowing perfectly the value of the risky asset. Recently, ref. [10] investigated the case of two partially risk neutral informed traders.

A fourth extension of the Kyle model investigated the existence and/or uniqueness of equilibria in the Kyle-type model. For instance, ref. [11] provided conditions under which normality is necessary for the existence of a linear equilibrium (Ref. [12] characterized the distributions that imply existence of linear equilibria in the Kyle-model. Ref. [13] discussed the existence of equilibrium when the market maker is risk averse and does not set the price according to semi-strong form efficiency. Ref. [14] analyzed the closed form solution of the Kyle model. Ref. [15] allowed for a more complex environment of the information structure of the model).

A very interesting extension of the static Kyle model resides in the investigation of the effect of different market structures on the equilibrium outcomes. Indeed, there are different types of insiders in the firm, some without any managerial responsibilities (the president and the members of the board of directors, for example), with the objective of maximizing their profits from trading the stock of the firm whose inside information they possess. Therefore, competition among fully informed insiders is another form of competition that influences the amount of information disseminated in the stock price. Fully informed insiders could compete in a Cournot duopoly model or in a Stackelberg model in the financial market (see [16]).

This paper adds to the literature on insider trading in the spirit of [1] by modeling Stackelberg competition among two insiders who are partially informed. The owner acts as a Stackelberg leader in the financial market, and the manager acts as a Stackelberg-follower in the financial sector to the owner who knows his reaction function before making any decision. The Stackelberg structure in the financial market with the owner serving as the Stackelberg leader seems very realistic. Indeed, the owner designs the manager’s compensation mechanism and chooses a capable manager to serve his purpose; therefore, he should have information on the manager’s reaction. In addition, feedback from staff of various levels can tell the owner about any improper behavior of the manager, so the owner can frequently adjust his perception. The results show that in the presence of partial information, the follower makes more profits than the leader. Moreover, when the insiders’ signals have the same precision, the insiders’ profits are higher under Stackelberg setting than in Cournot setting.

Although insiders tend to compete in the financial markets, they also tend to share trading information. For instance, evidence suggests that mutual fund managers trade based on local word-of-mouth communication in the asset-management community. Sharing information reduces the informational advantage of the insider and therefore it is important to understand what benefit investors obtain from sharing information. Ref. [17] study information sharing between strategic investors who are informed about asset fundamentals. They show that a coarsely informed investor optimally chooses to share information if his counterpart investor is well informed. By doing so, the coarsely informed investor invites the other investor to trade against his information, thereby reducing his price impact. Paradoxically, the well-informed investor loses from receiving information because of the resulting worsened market liquidity and the more aggressive trading by the coarsely informed investor. Another contribution of the current paper is to investigate the effect of information sharing among partially informed insiders competing in a Stackelberg game on the dissemination of information. The results show that the follower has no incentive to share information, while the leader is indifferent between sharing and not sharing information, leading to multiple equilibria.

The paper is organized as follows: Section 2 contains to the literature review. Section 3 presents the model and methodology. Section 4 displays the results and analysis. Finally, Section 5 presents the discussion and conclusion.

2. Literature Review

The pioneering paper of [1] on insider trading is considered as the baseline model that explains how an insider uses his private information to take advantage of noise traders in a security market. A large body of the literature has since then been devoted to extend the Kyle one-shot game model. Ref. [18] extend Kyle’s model to the case where the insider may be subject to an additional trading penalty, increasing in the size of their trades, and characterize the set of insider trading penalties which are efficient from the point of view of a regulator who cares both about market liquidity and price informativeness.

Some papers extended the Kyle model to include different risk attitude traders. Ref. [2] shows that competition among multiple risk-averse traders using a dynamic setting, increases the information rapidly. Ref. [19] studies a continuous time version of [2] and shows that the market depth decreases with time. Ref. [20] shows that the information is revealed slowly under disclosure requirements. Recently, ref. [3] extend the Kyle model to the case of two insiders, one risk-neutral and one risk-averse. They find that the market depth depends crucially on the degree of risk aversion, and show that regardless of the degree of risk aversion, the stock price reveals more information than the stock price in [2]. Ref. [4] study the case of two insiders in which the first insider is risk-neutral while the second insider is overconfident. They show that the market depth parameter and price information revelation vary with the degree of overconfidence.

Another direction of the extension of [1] is in [5] who allow for the market maker to observe a second signal that is correlated with the order flow. They find that the stock price is more informative and that the insider’s profits are lower than in [1], when the market maker only observes the order flow.

Subsequent works have also studied the relationship between the financial decisions and real decisions of the firm in a static Kyle model. In [21]’s model, the insider is considered the manager of the firm that profits from a monopoly position on the real market. Therefore, the insider chooses both the amount of the real output to be produced and the amount of the stock of the firm to trade. In the model, the market maker observes two correlated signals: the total order flow and the market price of the real good. They show that the real output chosen by the insider/manager is greater than it would be in the absence of insider trading, and that the stock price reveals more information than in [1]. In an extension of this model, ref. [22] assume that the publicly-owned firm competes in the real market, like Cournot, with another privately-owned firm. Their findings highlight the effect Cournot duopoly in the real market on the stock price coefficients relative to the monopoly case, as well as the negative effect on the insider’s profits and his compensation scheme relative to monopoly, but do not show any effect on the amount of information incorporated in the stock price. Ref. [23] suggest a two-tier model where the production of the real good by the publicly-owned firm involves constant labor costs, in addition to the intermediary products produced by another privately-owned firm. Their findings highlight the influence of the insider on the market of the final good and the stock price coefficients. However, this two-tier market structure does not change the amount of information disseminated in the stock price relatively to [21,22]. Ref. [24] study the impact of product differentiation on the real and financial decisions of a publicly-owned firm, competing like Cournot with another privately-owned firm. They show that the degree of product differentiation alters the output of the publicly-owned firm and the stock price coefficients, in addition to having a detrimental effect on the insider/manager’s profits and compensation scheme.

As different types of insiders with different managerial responsibilities exist in the firms, another strand of the literature extended the Kyle model to investigate the effect of competition among two insiders (the owner and the manager) on the amount of information disseminated in the stock price. Refs. [25,26] extend, respectively, refs. [21,22] and model Cournot competition between insiders in the financial market. Their findings show that competition between insiders increases the amount of information disseminated in the stock price. Ref. [27]’s model incorporates Cournot competition in the real market, with Stackelberg competition in the financial market where the owner is considered as the Stackelberg leader. They find that the owner’s profits as well as the amount of information revealed in the stock price increase in comparison with [25]. Ref. [16] extend the Kyle-type model of [5] with two signals to include Cournot duopoly among insiders in the financial market and find that each insider loses market power and partially controls the stock price. Hence, the stock price reveals more information with respect to [5]. The unconditional profits of each insider also decrease. Ref. [16] also extend the model of [5] with two signals to investigate the effect Stackelberg competition in the financial market on information revelation. They assume that one of the insiders, the owner, is high in the organizational hierarchy and chooses the second insider, the manager, to serve his purpose. In other words, the owner is the leader and knows the reaction function of the manager. They show that with Stackelberg competition in the financial market, the manager trades less and hence earns less than in the Cournot case. However, the owner, due to their role as a leader, trades more than in the Cournot and earns more profits. In addition, the price reveals more information in the Stackelberg than in the Cournot structure. Ref. [28] develops a sequential fair Stackelberg auction model in the spirit of [1] in which each of the two risk-seeking insiders has an equal chance to be a leader or a follower at each auction stage. The authors establish the existence and uniqueness of sequential fair Stackelberg equilibria when both insiders adopt linear strategies, and find that, at the sequential equilibria, these two insiders compete aggressively and cause the liquidity of the market to drop, the information to be revealed, and the profit to go down very rapidly while the trading intensity becomes substantially high.

While the above-mentioned works study the behavior of fully informed insiders, the originality of the current paper stems from adding to the literature on the Kyle model by modeling Stackelberg competition among two partially informed insiders in the financial market. It also adds to the literature on information sharing [17] by investigating the effect of information sharing among partially informed insiders on the dissemination of information.

3. Model and Methodology

Let $(\Omega ,\mathcal{F},\mathbb{P})$ be a probability space, all the random variables are defined with respect to this probability space. This model is a modified version of [1] with two insiders, each of them being partially informed about the underlying value of the stock. Consider an economy with one financial asset, the stock of the firm. There are three types of agents trading in the financial market. First, there are two risk-neutral rational traders (the insiders), each of them is partially informed about the the realization z of $\tilde{z}$, the value of the stock. Specifically, it is assumed that the partially informed trader $i,(i=1,2)$ observes the signal ${\tilde{s}}_i=\tilde{z}+{\tilde{\epsilon }}_i$ correlated with $\tilde{z}$ where ${\tilde{\epsilon }}_i$ is normally distributed with zero mean and variance ${\sigma }_i^2$. Second, there are (non-rational) noise traders, representing small investors with no information on z. The aggregate noise trade is assumed to be a random variable $\tilde{u}$, which is normally distributed with mean zero and variance ${\sigma }_u^2$. Finally, there are $K(K\ge 2$) risk-neutral market makers who act like Bertrand competitors. Each of the variables $\tilde{z}$ and ${\tilde{\epsilon }}_i(i=1,2)$, is independent from $\tilde{u}$. (Random variables are denoted with a tilde. Realized values lack the tilde. The mean of the random variable is denoted with bar).

Following [1], the trading mechanism is organized in two steps. In step one, a linear pricing rule and optimal order rule are determined by the market makers and the insiders, respectively, as a Bayesian–Nash equilibrium. The market makers determine a (linear) pricing rule p, based on their a priori beliefs, where p is a measurable function $p:\mathbb{R}⟶\mathbb{R}$. Each insider $i=1,2$ chooses a stock trade function $\widetilde{x_i}$, where $x_i:\mathbb{R}⟶\mathbb{R}$ is a measurable function. In the second step, the insiders observe the realization of the signals, and submit their stock order to the market makers based on the equilibrium stock trade functions. The market makers also receive orders from the noise traders, all these orders arrive as a total order flow signal $\tilde{r}={\tilde{x}}_1+{\tilde{x}}_2+\tilde{u}$. The order flow signal is used by the market makers to set the price $\tilde{p}=p\left(\tilde{r}\right)$, based on the equilibrium price function, to clear the market. Each partially informed insider $i,i=1,2$ knows only the realization $s_i$ of ${\tilde{s}}_i$ and does not know the values of $\tilde{u},,\tilde{r},$ before the order flow decisions is made. Moreover, each market maker does not know neither the realization z of $\tilde{z}$ nor the realization $s_i$ of ${\tilde{s}}_i$ but only knows their distribution. Finally, the market makers cannot observe either $x_i$ or u.

In this model, Stackelberg competition is introduced among the two insiders in the financial market. Specifically, we assume that one of the insiders, the owner (insider 1), is high on the organizational hierarchy and acts as a Stackelberg leader in the financial market. The second insider (insider 2), the manager, is in the lower ladder of the organizational hierarchy and acts as a Stackelberg follower in the financial sector to the owner who knows his reaction function before making any decision (e.g., see [29]). The Stackelberg structure in the financial market with the owner serving as the Stackelberg leader seems very realistic. Indeed, the owner designs the manager’s compensation mechanism and chooses a capable manager to serve their purpose; therefore, they should have information on the manager’s reaction.

The theoretical methods of economic theory are used to characterize and analyze the main results of the model. Specifically, this is a game of incomplete information and we seek for a Bayesian–Nash equilibrium. A Bayesian–Nash equilibrium is a vector of three functions $[x_1(.),x_2(.),p(.)]$ such that:

(a)

Profit maximization of insider 1,

$$\begin{array}{c}\hfill E[\tilde{z}-p({\tilde{x}}_1+{\tilde{x}}_2+\tilde{u})){\tilde{x}}_1|{\tilde{s}}_1]\ge E[\tilde{z}-p{\tilde{x}}_1^{\prime }+{\tilde{x}}_2+\tilde{u})){\tilde{x}}_1^{\prime }\left|{\tilde{s}}_1\right]\end{array}$$

(1)

for any level of trading order ${\tilde{x}}_1^{\prime }$ decided by the insider;

(b)

Profit maximization of insider 2,

$$\begin{array}{c}\hfill E[\tilde{z}-p({\tilde{x}}_1+{\tilde{x}}_2+\tilde{u})){\tilde{x}}_1|{\tilde{x}}_1,{\tilde{s}}_2]\ge E[\tilde{z}-p({\tilde{x}}_1+{\tilde{x}}_2^{\prime }+\tilde{u})){\tilde{x}}_2^{\prime }|{\tilde{x}}_1,{\tilde{s}}_2]\end{array}$$

(2)

for any level of trading order ${\tilde{x}}_2^{\prime }$ decided by the insider;

(c)

Semi-strong market efficiency: The pricing rule $p(.)$ satisfies,

$$p\left(\tilde{r}\right)=E\left[\tilde{z}\right|\tilde{r}].$$

(3)

4. Results and Analysis

Before characterizing the equilibrium of the model, it should be pointed out to the reader that a linear linear Bayesian equilibrium is being sought. Formally, an equilibrium is linear if the insiders’ strategies are linear with respect to their observed signals and the pricing rule is linear with respect to the order flow signal. In other words, there are constants $a_0,a_1,b_0,b_1,b_2,\mu ,\lambda$ such that,

$$\begin{array}{c}\hfill x_1\left(s_1\right)=a_0+a_1{s}_1{x}_2(s_2,x_1)=b_0+b_1{x}_1+b_2{s}_2\end{array}$$

(4)

and

$$\begin{array}{c}\hfill \forall r,p\left(r\right)=\mu +\lambda r.\end{array}$$

(5)

Note that conditions (1) and (2) define the optimal strategies of the insiders while condition (3) guarantees the zero expected profits for the market makers. The stock price, set by the market makers, is equal to the conditional expectation of the asset given the available information. The study is restricted to linear equilibrium. The normal distributions of the exogenous random variables, together with the particular expressions of the insiders’ strategies and the market price, enable us to derive and to prove the existence of a unique linear equilibrium. In Proposition 1, the unique linear equilibrium outcomes of the model are characterized.

Proposition 1. 

In the Stackelberg model with two partially informed traders, a linear equilibrium exists and it is unique. It is characterized by,

$$\begin{array}{c}\hfill {\tilde{x}}_1\left({\tilde{s}}_1\right)=a_1({\tilde{s}}_1-{\overline{s}}_1)\mathrm{and}{\tilde{x}}_2(\widetilde{x_1},{\tilde{s}}_2)=b_1{\tilde{x}}_1+b_2({\tilde{s}}_2-{\overline{s}}_2)\end{array}$$

(6)

$$\begin{array}{c}\hfill a_1=\frac{h_1{h}_2}{2\lambda (1+h_1)(1+h_1+h_2)},b_1=-\frac{1}{2}+\frac{1+h_1}{h_2}\mathrm{and}{b}_2=\frac{h_2}{2\lambda (1+h_1+h_2)}\end{array}$$

(7)

$$\begin{array}{c}\hfill \lambda =\frac{\sqrt{(1+h_1)[4h_1{(1+h_1)}^2+4(1+h_1)(1+2h_1)h_2+(4+3h_1)h_2^2){\sigma }_z^2]{\sigma }_u^2}}{4(1+h_1)(1+h_1+h_2){\sigma }_u^2}\end{array}$$

(8)

$$\begin{array}{c}\hfill \mu =\overline{z},E\left[{\pi }_1\right]=a_1[\gamma (1-\lambda b_2)-\lambda a_1(1+b_1)]({\sigma }_z^2+{\sigma }_1^2)\mathrm{and}E\left[{\pi }_2\right]=\lambda E\left[{\tilde{x}}_2^2\right]\end{array}$$

(9)

where $h_1=\frac{{\sigma }_z^2}{{\sigma }_1^2}$, $h_2=\frac{{\sigma }_z^2}{{\sigma }_2^2}$ and $\gamma =\frac{{\sigma }_z^2}{{\sigma }_z^2+{\sigma }_1^2}$,

Proof. 

See Appendix A. □

Proposition 1 highlights the impact of market structure (the Stackelberg setting) and information asymmetry on the equilibrium outcomes. Hence, the relationship between this model and the existing literature should be clarified. First, this paper studies the impact of partial information on the equilibrium outcomes in alignment with [16,28] which both consider a Stackelberg structure of [1] with fully informed traders. Moreover, this model differs from [8,17] which study the case of a Cournot setting with partially informed traders, by studying the impact of the Stackelberg structure in the financial sector. Consequently, this paper will be able to show the effect of market structure and information asymmetry on the equilibrium outcomes.

The sequential structure of the players’ information and moves in the Stackelberg game has a direct effect on the equilibrium outcomes. Indeed, when the two insiders are fully informed, this paper reduces to the case studied by [16]. To achieve such result, a two-step procedure is implemented: in the first step, the equilibrium outcomes are characterized when the variance of the follower’s signal noise is replaced by zero (equivalently, the limit when $h_2$ goes to infinity is considered). In the second step, the variance of the leader’ signal noise is replaced by zero (equivalently, the limit when $h_1$ goes to infinity is considered) of the resulting outcomes. Specifically, the following result is as follows.

Lemma 1. 

When the two insiders are fully informed, this paper reduces to the case studied in [16]. (The superscript “D” refers to [16].) Indeed,

$$\begin{array}{c}\hfill {\tilde{x}}_1^D\left(\tilde{z}\right)=\underset{h_1\to \infty }{lim}(\underset{h_2\to \infty }{lim}\left(a_1({\tilde{s}}_1-{\overline{s}}_1)\right))=\frac{1}{2{\lambda }^D}(\tilde{z}-\overline{z})\end{array}$$

(10)

$$\begin{array}{c}\hfill {\tilde{x}}_2^D\left(\tilde{z}\right)=\underset{h_1\to \infty }{lim}(\underset{h_2\to \infty }{lim}(b_1{\tilde{x}}_1+b_2({\tilde{s}}_2-{\overline{s}}_2)))=\frac{1}{2{\lambda }^D}(\tilde{z}-\overline{z})\end{array}$$

(11)

$$\begin{array}{c}\hfill \mu =\overline{z}\mathrm{and}{\lambda }^D=\underset{h_1\to \infty }{lim}(\underset{h_2\to \infty }{lim}\lambda )=\frac{{\sigma }_z\sqrt{3}}{4{\sigma }_u}\end{array}$$

(12)

$$\begin{array}{c}\hfill E{\left[{\pi }_1\right]}^D=\underset{h_1\to \infty }{lim}(\underset{h_2\to \infty }{lim}\left(E\left[{\pi }_1\right]\right)=\frac{{\sigma }_z{\sigma }_u}{2\sqrt{3}}\end{array}$$

(13)

$$\begin{array}{c}\hfill E{\left[{\pi }_2\right]}^D=\underset{h_1\to \infty }{lim}(\underset{h_2\to \infty }{lim}\left(E\left[{\pi }_2\right]\right)=\frac{{\sigma }_z{\sigma }_u}{4\sqrt{3}}\end{array}$$

(14)

Note that this procedure is restrictive to the Stackelberg structure. Indeed. in the Cournot model with partially informed traders studied in [8,17], the equilibrium outcomes converge to the full information case when both $h_1$ and $h_2$ go simultaneously to infinity. Moreover, it should be noted that the information structure in the Stackelberg game imposes the order of convergence. In other words, the full information case is not obtained if first $h_1$ goes to infinity and then $h_2$ goes to infinity.

5. Discussion and Conclusions

This section discusses the impact of market structure on equilibrium outcomes. On the one hand, a comparative statics analysis of this model’s results is carried out with respect to the results of [8,17], and on the other hand, the impact of information sharing on the insiders’ decisions is studied.

The equilibrium outcomes of this model are first compared to the ones in [8,17]. Given the complexity of the expressions of the equilibrium outcomes, the analysis is restricted to the case when the two insiders observe the same signal. In this case, Proposition 1 becomes

Proposition 2. 

When the precision of the two signals are the same (${\sigma }_1^2={\sigma }_2^2$), the equilibrium is characterized by,

$$\begin{array}{c}\hfill {\tilde{x}}_1\left({\tilde{s}}_1\right)=a_1({\tilde{s}}_1-{\overline{s}}_1)\mathrm{and}{\tilde{x}}_2({\tilde{x}}_1,{\tilde{s}}_2)=b_1{\tilde{x}}_1+b_2({\tilde{s}}_2-{\overline{s}}_2)\end{array}$$

(15)

$$\begin{array}{c}\hfill a_1=\frac{h^2}{2\lambda (1+h)(1+2h)},b_1=\frac{1}{2}+\frac{1}{h}\mathrm{and}{b}_2=\frac{h}{2\lambda (1+2h)}\end{array}$$

(16)

$$\begin{array}{c}\hfill \mu =\overline{z}\mathrm{and}\lambda =\frac{{\sigma }_z\sqrt{h(1+h)(8+3h(8+5h\left)\right)}}{4{\sigma }_u(1+h)(1+2h)}\end{array}$$

(17)

$$\begin{array}{c}\hfill E\left[{\pi }_1\right]=\frac{h^2(2+3h){\sigma }_z{\sigma }_u}{2(1+2h)\sqrt{h(1+h)(8+3h(8+5h\left)\right)}}\end{array}$$

(18)

$$\begin{array}{c}\hfill E\left[{\pi }_2\right]=\frac{h{(4+3h)}^2{\sigma }_z{\sigma }_u}{4(1+2h)\sqrt{h(1+h)(8+3h(8+5h\left)\right)}}\end{array}$$

(19)

where $h=h_1=h_2$.

Lemma 2 shows graphically (see Figure 1) the impact of the Stackelberg structure when compared to the Cournot setting studied in [8,17].

Lemma 2. 

The relation between the Stackelberg and Cournot models when the signals’ errors have the same precision is given by

$$\begin{array}{c}\hfill {\lambda }^S>{\lambda }^C,{\pi }_1^S>{\pi }_1^C\mathrm{and}{\pi }_2^S>{\pi }_2^C\end{array}$$

(20)

First note that Stackelberg competition between the two insiders increases their unconditional profits when compared to the Cournot competition between the insiders. Second, the market depth parameter $\lambda$ is higher in this model than in the Cournot case. It should be pointed out that these results do not hold in the case when both insiders are fully informed about the stock value (see [16]). Consequently, in the presence of incomplete information, the insiders benefit more in the Stackelberg setting than in the Cournot setting.

To better understand the impact the information asymmetry between the insiders on the market structure, this paper considers the case when insider 2 is fully informed about the stock value (${\tilde{s}}_2=\tilde{z}$) while insider 1 is partially informed. In this case, Proposition 1 becomes

Proposition 3. 

When insider 2 is fully informed about the stock value (${\tilde{s}}_2=\tilde{z}$) and insider 1 is partially informed (${\tilde{s}}_1=\tilde{s}$ and $h_1=h$), the equilibrium is characterized by,

$$\begin{array}{c}\hfill {\tilde{x}}_1\left(\tilde{s}\right)=a_1({\tilde{s}}_1-\overline{s})\mathrm{and}{\tilde{x}}_2({\tilde{x}}_1,\tilde{z})=b_1{\tilde{x}}_1+b_2(\tilde{z}-\overline{z})\end{array}$$

(21)

$$\begin{array}{c}\hfill a_1=\frac{h}{2\lambda (1+h)},b_1=\frac{-1}{2}\mathrm{and}{b}_2=\frac{1}{2\lambda }\end{array}$$

(22)

$$\begin{array}{c}\hfill \mu =\overline{z}\mathrm{and}\lambda =\frac{{\sigma }_z\sqrt{(1+h)(3h+4)}}{4{\sigma }_u(1+h)}\end{array}$$

(23)

$$\begin{array}{c}\hfill E\left[{\pi }_1\right]=\frac{h{\sigma }_z{\sigma }_u}{2\sqrt{(1+h)(3h+4)}}\end{array}$$

(24)

$$\begin{array}{c}\hfill E\left[{\pi }_2\right]=\frac{(4+h){\sigma }_z{\sigma }_u}{4\sqrt{(1+h)(3h+4)}}\end{array}$$

(25)

Lemma 3 graphically shows (See Figure 2) the impact of the Stackelberg structure when compared to the Cournot setting studied in [8,17] when insider 2 is fully informed while insider 1 is partially informed.

Lemma 3. 

The relations between the Stackelberg and Cournot models when insider 2 is fully informed and insider 1 is partially informed, is given by

$$\begin{array}{c}\hfill {\lambda }^S<{\lambda }^C,{\pi }_1^S<{\pi }_1^C\mathrm{and}{\pi }_2^S<{\pi }_2^C\end{array}$$

(26)

Lemma 3 reveals that Cournot structure is more beneficial for both insiders when one of the two insiders in fully informed. Moreover, a quick comparison between insiders’ profits (see Equations (24) and (25)) shows that the unconditional profits of the leader (insider 1) are greater than the profits of the follower (insider 2) when the signal of insider 1 is less noisy.

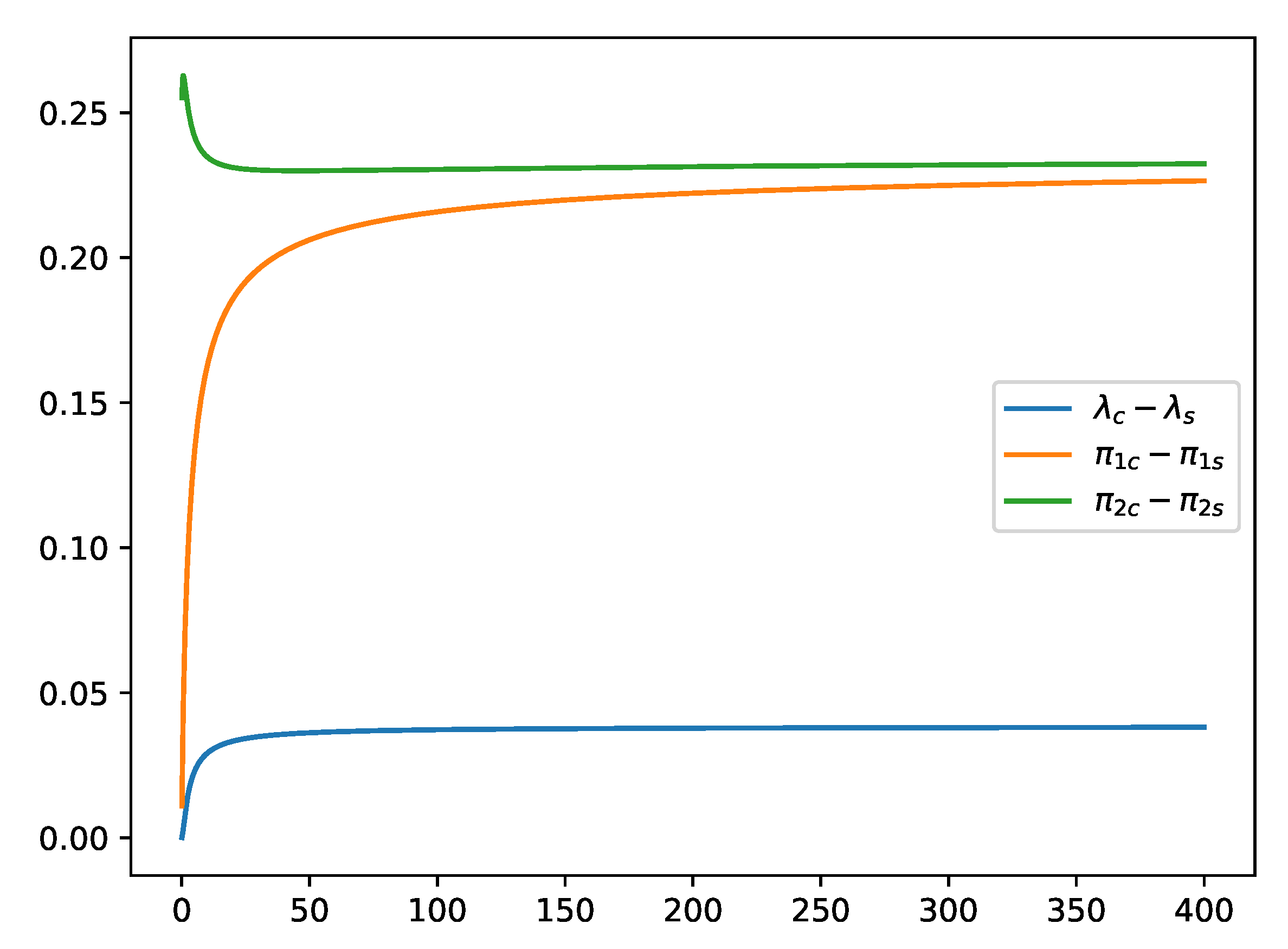
Finally, it is worth noticing that Proposition 1 sheds light on the impact of partial information on the equilibrium outcomes in a Stackelberg game structure. Indeed, Figure 3 shows that the profits of the follower (insider 2) are greater than the profits of the leader (insider 1).

The second part of this discussion studies the impact of information sharing on the insiders’ decisions. For comparison purposes, the same structure of [17] who study the impact of the information in the Cournot case is adopted. Specifically, it is assumed that insider 2 is fully informed about the asset value, i.e., Proposition 3 holds. Moreover, it is assumed as in [17], that $\overline{z}=0$ and ${\sigma }_z^2=1$. Following [17], the fully informed insider (insider 2 in this model) is denoted by H while the semi-informed insider (insider 1 in this model) by L. At $t=0$, H and L simultaneously decide whether to share their private information to maximize their respective expected trading profits. For investor $i\in H,L$, $A_i\in \{S,\varnothing \}$ is used to denote the information-sharing decisions, where $A_i=S$ means that the investor fully shares information with the other investor, whereas $A_i=\varnothing$ means that the investor keeps it secret. It is assumed that the date-0 information sharing decisions become common knowledge at the beginning of date 1, so that backward induction can be applied to compute the equilibrium of this economy.

Trading occurs on $t=1$. Conditional on the endowed private information, as well as the shared information (if any), investor $i\in H,L$ places market order to maximize the expected trading profit. Let ${\mathbb{F}}_i$ indicates investor i’s information set. For instance, if L shares information with H but H does not share information with L (i.e., $A_L=S$ and $A_H=\varnothing$), then the two investors’ information sets are, respectively, ${\mathbb{F}}_L=\left\{\tilde{s}\right\}$ and ${\mathbb{F}}_H=\{\tilde{z},\tilde{s}\}$ (see Figure 1 which describes the timeline of the economy).

Given the information-sharing decisions of the investors $A_L$ and $A_H$ on date 0, different trading subgames follow on date 1, depending on whether the investors share their respective private information or not. The investors’ expected profits evaluated on the date-1 subgame equilibrium will serve as their payoffs of the date-0 information-sharing game. We next discuss each subgame separately.

Subgame 1: Neither Investor Shares Information ($A_L=A_H=\varnothing$).

When neither investor shares information, we obtain the expression of the expected profits stated in Proposition 3.

Subgame 2: L Shares Information but H Does Not ($A_L=\left\{\tilde{s}\right\}$ and $A_H=\varnothing$).

Since H is the follower and plays at the second stage of the game, observing the signal of L, which is linearly dependent to his strategy, will not change the profits maximization problem of each of the two players. Hence, this case will coincide with subgame 1 and the expression of the expected profits is stated in Proposition 3.

Subgame 3: H Shares Information ($A_H=S$).

There are two subgames when H shares information, depending on whether L shares his information. Nonetheless, it turns out that the equilibrium in these two subgames is the same because H owns perfect information about the asset fundamental, and once he shares it with L, L no longer uses his own noisy signal $\tilde{s}$ in predicting the asset fundamental. Thus, regardless of L’s information-sharing decision, once H shares information, the trading game degenerates to the [16] with two perfectly-informed traders. Consequently, the expression of the expected profits stated in Lemma 1 is obtained.

Now, the insiders’ payoffs of the date-0 information sharing game is summarized in

Table 1. Insiders’ payoffs of the date-0 information sharing game.

		H
		Not Share	Share
L	$Notshare$	$\frac{h{\sigma }_u}{2\sqrt{(1+h)(3h+4)}},\frac{(4+h){\sigma }_u}{4\sqrt{(1+h)(3h+4)}}$	$\frac{{\sigma }_u}{2\sqrt{3}},\frac{{\sigma }_u}{4\sqrt{3}}$
	$Share$	$\frac{h{\sigma }_u}{2\sqrt{(1+h)(3h+4)}},\frac{(4+h){\sigma }_u}{4\sqrt{(1+h)(3h+4)}}$	$\frac{{\sigma }_u}{2\sqrt{3}},\frac{{\sigma }_u}{4\sqrt{3}}$

. It can be easily noticed that this game has 2 equilibria with the same players’ payoffs. Indeed, the strategy of player H, “Not share” is a dominant strategy. (Consider the function $f\left(h\right)=\frac{(4+h){\sigma }_u}{4\sqrt{(1+h)(3h+4)}}$. It is easy to check that this function is decreasing on $(0,\infty )$ and having a horizontal asymptote with equation $y=\frac{{\sigma }_u}{4\sqrt{3}}$.) Taking this information into account, player L is indifferent between “Share” or “Not share” since both strategies lead to the same payoff.

Finally, it should be noted that the result is quite different than the result found in [17] in which the equilibrium consists of player L sharing his information whereas player H does not. This difference is due to the fact that in the Stackelberg game, on the one hand, the fully informed player is the follower and on the other hand, it is also due to the sequential structure of the game timing.

In this paper, the authors generalize the Kyle model with two risk neutral insiders to the case where each insider is partially informed about the value of the stock and compete under a Stackelberg game setting in the financial market. Based on the backward induction theory, the linear Bayesian equilibrium is first characterized. Given the information structure of the signal of the two insiders which is realistic and well used in the field of market microstructure, this paper can provide important reference for market analysts and practitioners in the field of insider trading.

However, there are still some limitations in the paper. First, the current analysis illustrates the impact and the important role that Stackelberg structure has on the insiders’ decisions and the equilibrium variables. In particular, it is shown that the relation between the market depth parameters under Cournot and Stackelberg settings is quite ambiguous and depends crucially on the precision of the insiders’ signals. Therefore, understanding the role of partial information and its implications to the regulatory aspects of the world of insider trading should be examined more closely. Secondly, in the case of general correlated signals (see [10]), a linear equilibrium might not be necessarily unique. This is an open question for future research.