Modeling of Junior Servers Approaching a Senior Server in the Retrial Queuing-Inventory System
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Research Gap
1.4. Novelty and Contribution of the Model
- Innovative Service Configuration: This research introduces a unique stochastic retrial queuing-inventory system where junior servers provide service to the customers and receive consultation from the senior server as per the specific circumstances.
- Analysis of the System: The paper contributes by utilizing the Neuts and Rao truncation method to solve the level-dependent QBD and Neuts matrix geometric method to establish the stability condition and calculate the stationary probability vector.
- Comprehensive Performance Analysis: Through rigorous numerical analysis, the study delves into various critical aspects including the expected total cost, waiting time, and the workload of junior servers. This detailed investigation provides practical insights into the system’s operational efficiency under different modes of operation for junior servers.
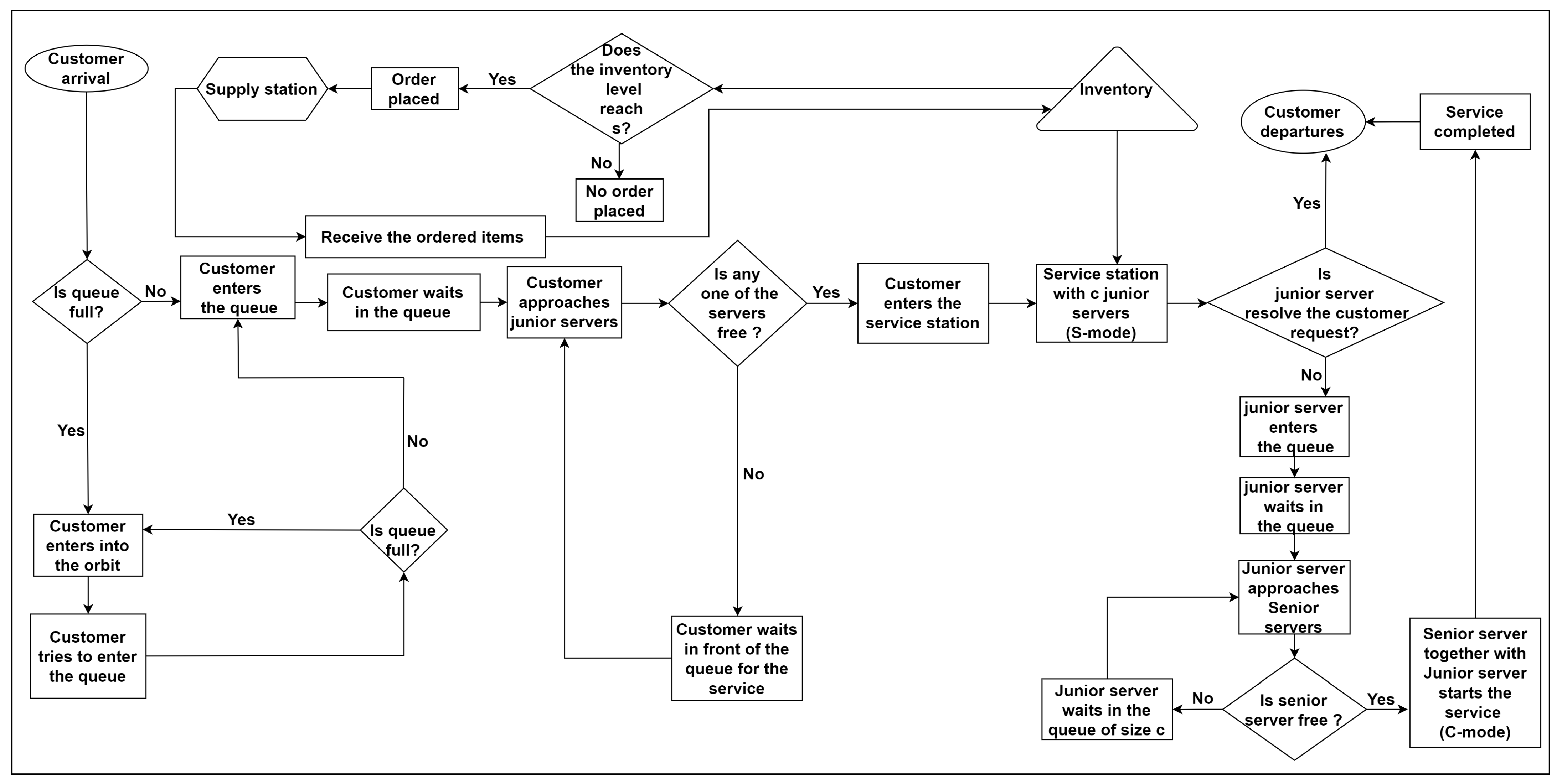
2. Model Description
- When the junior server takes on the duty of offering service to the customers in the waiting hall, he performs the role of a server, known as server mode (S-mode).
- When a junior server seeks assistance from the senior server in solving the encountered problem in S-mode, the junior server receives consultation from the senior server (Consultant), known as consultant mode (C-mode).
3. Mathematical Analysis
3.1. Neuts and Rao Matrix Geometric Approximation
3.2. Limiting Probability Distribution
4. Computation of Matrix
5. System Performance Measures
- Mean Inventory level:
- Mean Reorder Rate:
- Mean Number of Customers in Waiting Hall:
- Mean Number of Customers Enter into the Waiting Hall:
- Mean Waiting Time of Customers in Waiting Hall:
- Mean Number of Junior Servers in C-mode:
- Mean Number of Junior Servers Enter into C-mode:
- Mean Waiting Time of Junior Servers in C-mode:
- Mean Number of Busy Junior Servers in S-mode:
- Mean Number of Idle Junior Servers in S-mode:
- Mean Number of Customers in the Orbit:
- Mean Number of Customers Enter into Orbit:
- Mean Waiting Time of Customers in Orbit:
- Successful Rate of Retrial:
- Overall Rate of Retrial:
- Fraction of Successful Rate of Retrial:
The Expected Total Cost
- c1
- refers to the expense associated with holding each unit of an item.
- c2
- signifies the cost incurred for setting up each unit of an item.
- c3
- represents the cost accrued for each customer in the waiting hall per unit of time.
- c4
- denotes the cost incurred for each junior server in C-mode per unit of time.
- c5
- pertains to the cost accrued for each customer in orbit per unit of time.
- c6
- represents the expenditure linked to each engaged junior server.
- c7
- signifies the cost associated with each idle junior server.
6. Cost Analysis and Numerical Illustration
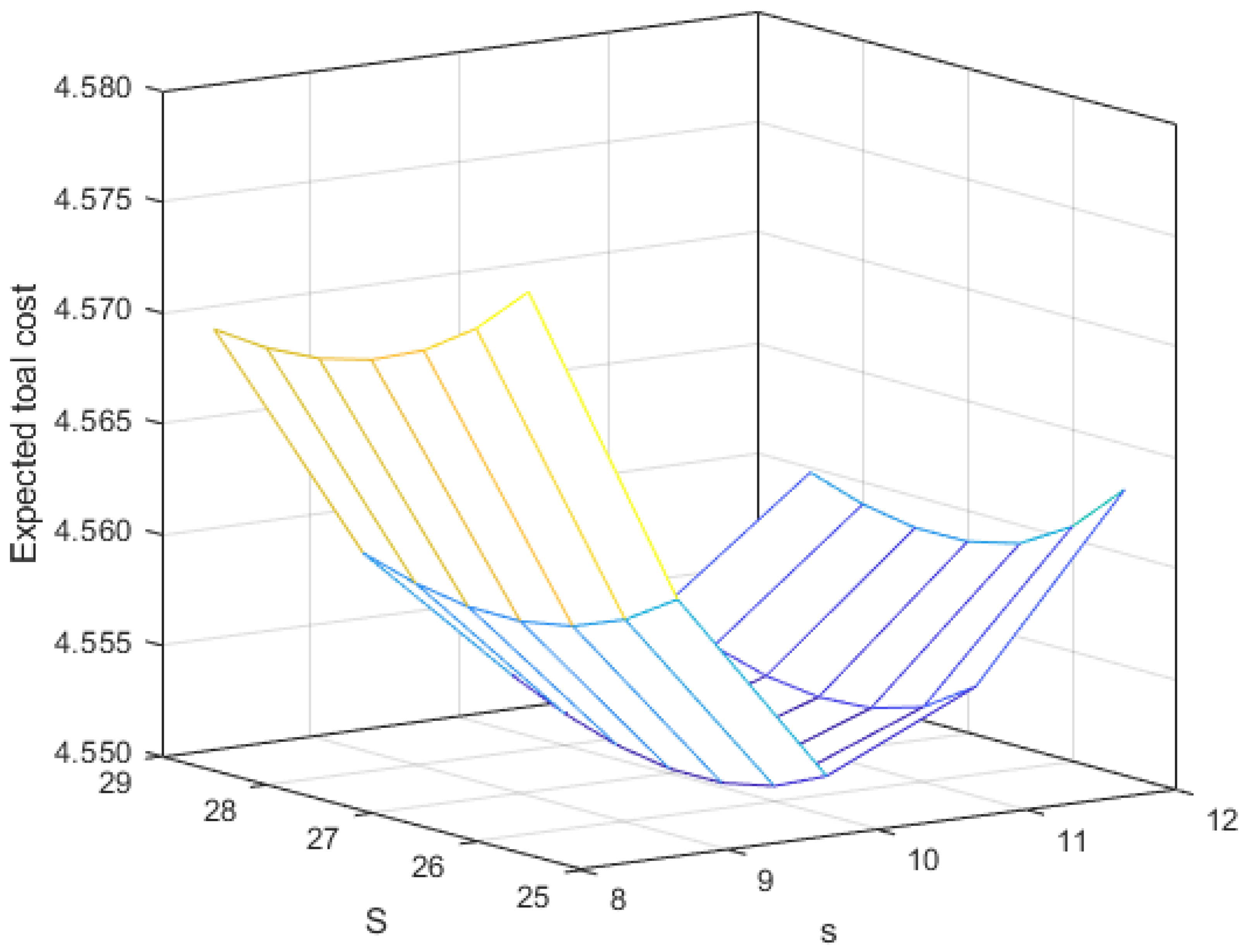
6.1. Analysis on the Expected Total Cost
- As the arrival rate rises, there is a notable upswing in due to the increased presence of customers inside the waiting hall.
- Elevating the probability value p hinders junior servers from approaching their senior counterparts. As a result, customers inside the waiting hall tend to depart promptly at the end of service in S-mode, resulting in a decrease in .
- With an increase in the retry rate , the anticipated orbit level diminishes as an increasing number of customers enter the waiting area. Since the expected orbit level correlates with the total cost, this leads to a reduction in .
- Higher service rates and lead to a drop in each customer’s mean service duration. Consequently, Z decreases, contributing to a decrease in .
- Raising the rate results in a decrease in the average lead time per order. Consequently, the expected total cost decreases.
- Altering the number of junior servers in the system incurs additional expenses. Hence, an increase in c leads to an increase in .
- An expansion in the waiting hall size corresponds to a rise in Z. As a result, the overall cost exhibits a positive correlation with the parameter N.
6.2. Analysis on Mean Waiting Time of Customers in the Waiting Hall
- As the waiting hall size N is enlarged, there is an observed rise in waiting time attributable to an increase in Z.
- Augmenting the service rates for both junior and senior servers reduces their average service period. Hence, customer’s waiting time decreases.
- An escalation in the arrival rate corresponds to an uptick in primary arrivals, leading to an increase in Z. Likewise, as the retry rate rises, orbiting customers transition into the waiting hall, influencing Z.
- It is a well-established fact that an augmentation in the number of servers generally leads to a decrease in waiting time. Accordingly, the parameter c is reflected in Z.
- Increasing the rate results in a reduction in the average lead time per order and Z diminishes.
6.3. Analysis of Mean Waiting Time for Customer in the Orbit
- By increasing N, the waiting hall offers more space, allowing orbital customers to transition into the waiting hall. As a result, their waiting time is reduced.
- Elevating the service rates for both junior and senior servers leads to a reduction in their average service time. Consequently, customers in the waiting hall tend to leave promptly, creating room for orbital customers to enter. This leads to a reduction in the waiting time for orbital customers.
- An increase in signifies a rise in primary arrivals, causing Z to also increase. This, in turn, results in an extended Z.
- Similarly, as the rate rises, orbital customers move into the waiting hall, decreasing Z.
- It is a well-established fact that augmenting the number of servers generally leads to a decrease in waiting time. Therefore, the parameter c contributes to optimizing Z.
- The rate of parameter is being increased. It is associated with a reduction in the lead time per order that minimizes Z.
6.4. Analysis on Mean Waiting Time of Junior Servers in C-Mode
- As the rate of customer arrival increases, there is a corresponding growth in the quantity of customers present in the waiting area. As a result, there is an increased probability of junior servers operating in C-mode, hence resulting in a corresponding rise in their waiting duration.
- Similarly, an increase in the retrial rate allows orbital customers to transition into the waiting hall, resulting in an increase in Z
- Increasing the value of c leads to a rise in the average number of busy junior servers. Additionally, the number of junior servers in C-mode also increases with an increase in c.
- An expansion in the capacity of the waiting area corresponds to a proportional increase in the number of busy servers in C-mode, as there is a rise in Z.
- The reduction in the number of servers in C-mode is seen when there is an increase in the service rate for the senior server. However, this relationship is reversed for junior servers.
- A reduction in the rate always leads to a decrease in lead time, consequently resulting in a decrease in Z.
- Upon observing the effects of varying the probability p, there is a notable reduction in the waiting time of junior servers in C-mode.
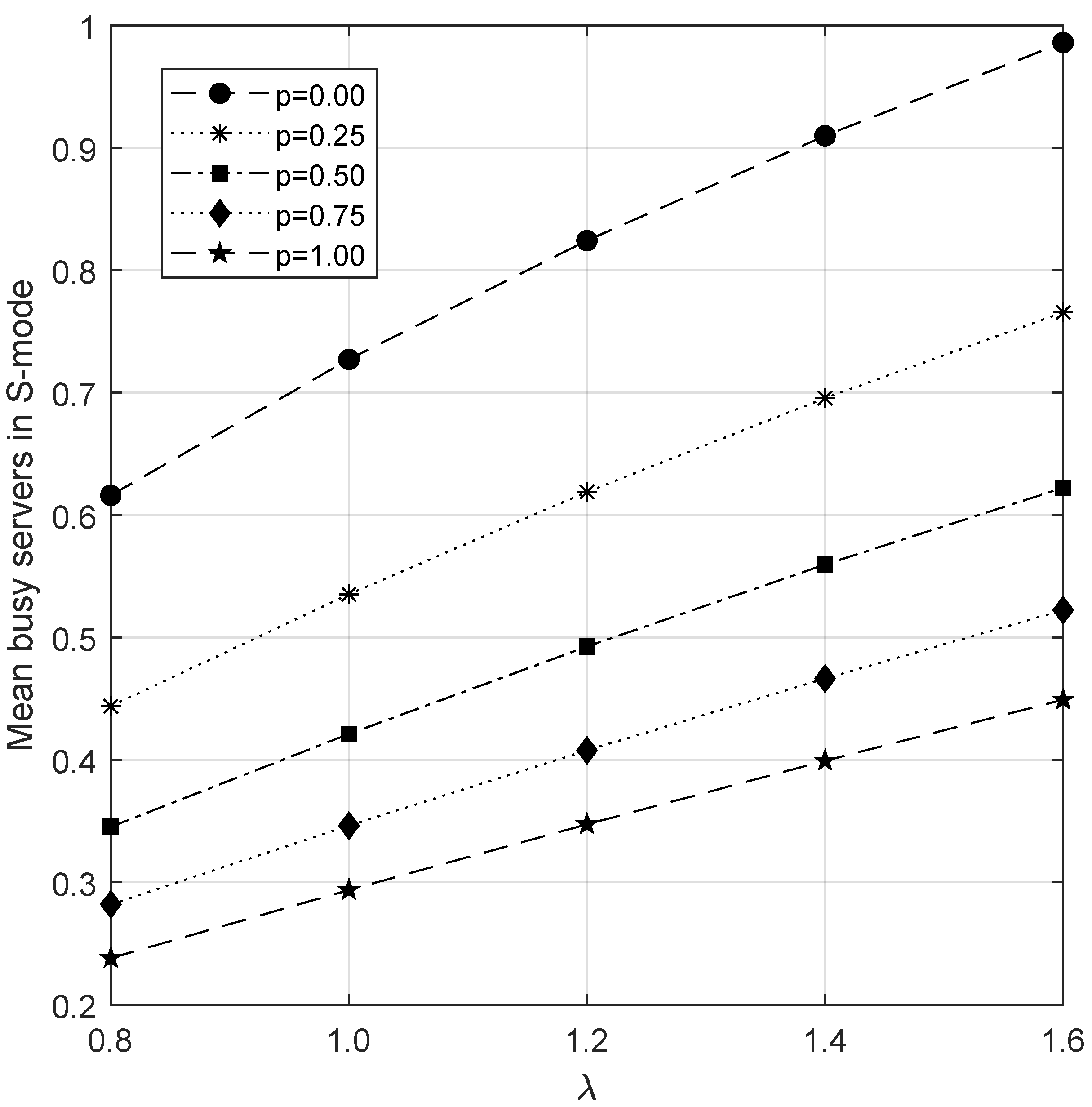
6.5. Analysis of Busy Junior Servers in S-Mode
- As arrivals increase, Z rises. This, in turn, raises the probability of junior servers being in S-mode.
- Similarly, when the retrial rate is raised, orbital customers have a higher chance of entering the waiting hall. Consequently, there is an uptick in the count of junior servers in S-mode.
- Increasing the value of c results in a higher average of occupied junior servers. Simultaneously, there is a rise in Z with an increase in c.
- Expanding the capacity of the waiting hall leads to a corresponding increase in the number of occupied servers in S-mode due to the upswing in the average number of servers in S-mode.
- With an increase in the service rates for both senior and junior servers, Z decreases due to the reduction in average service time per customer.
- An increase in the rate consistently leads to a reduction in lead time. Consequently, there is a decrease that can be seen in Z.
- An examination of the effect of varying the probability p in combination with each parameter consistently reveals a decrease in the number of junior servers in S-mode.
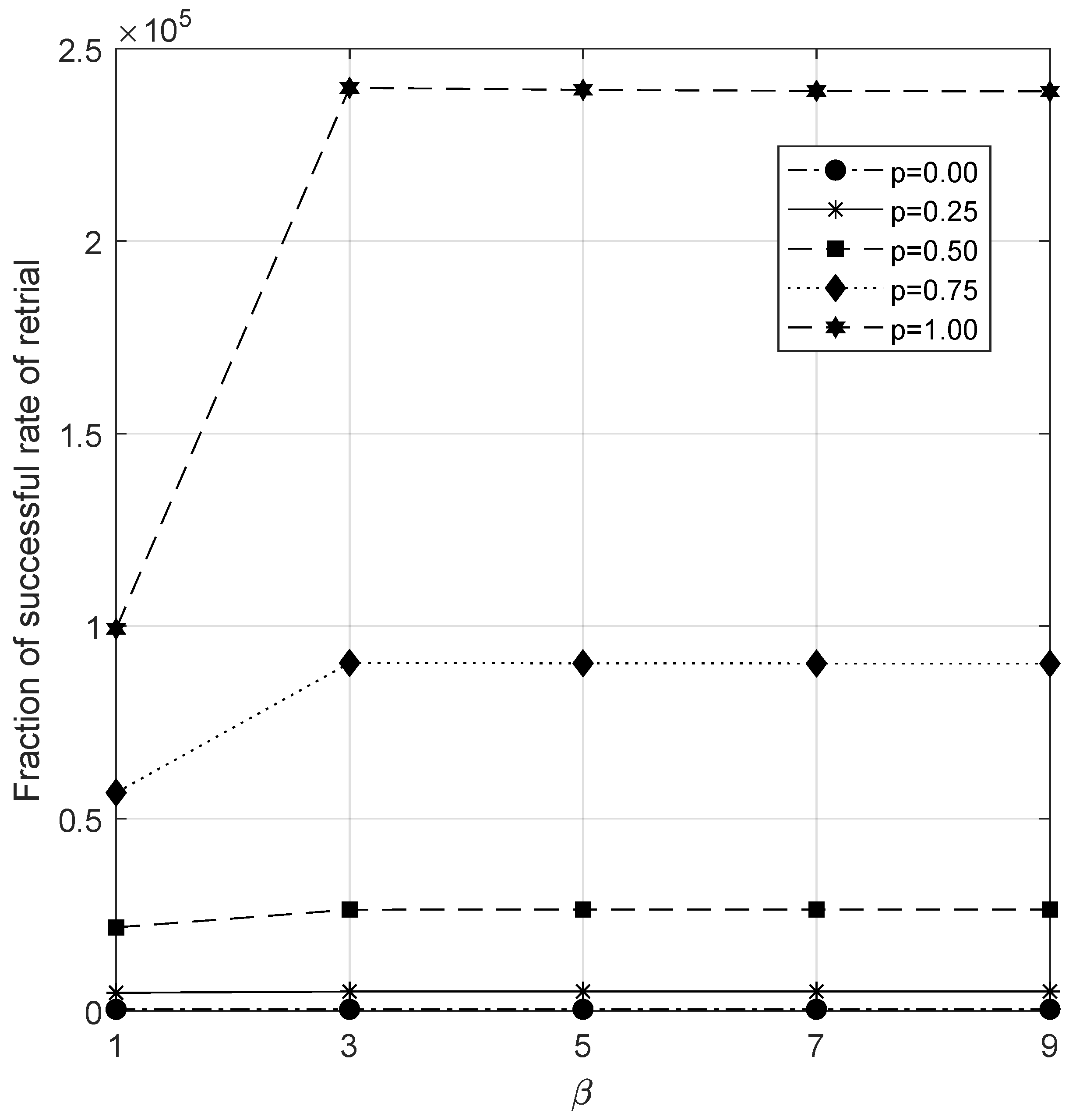
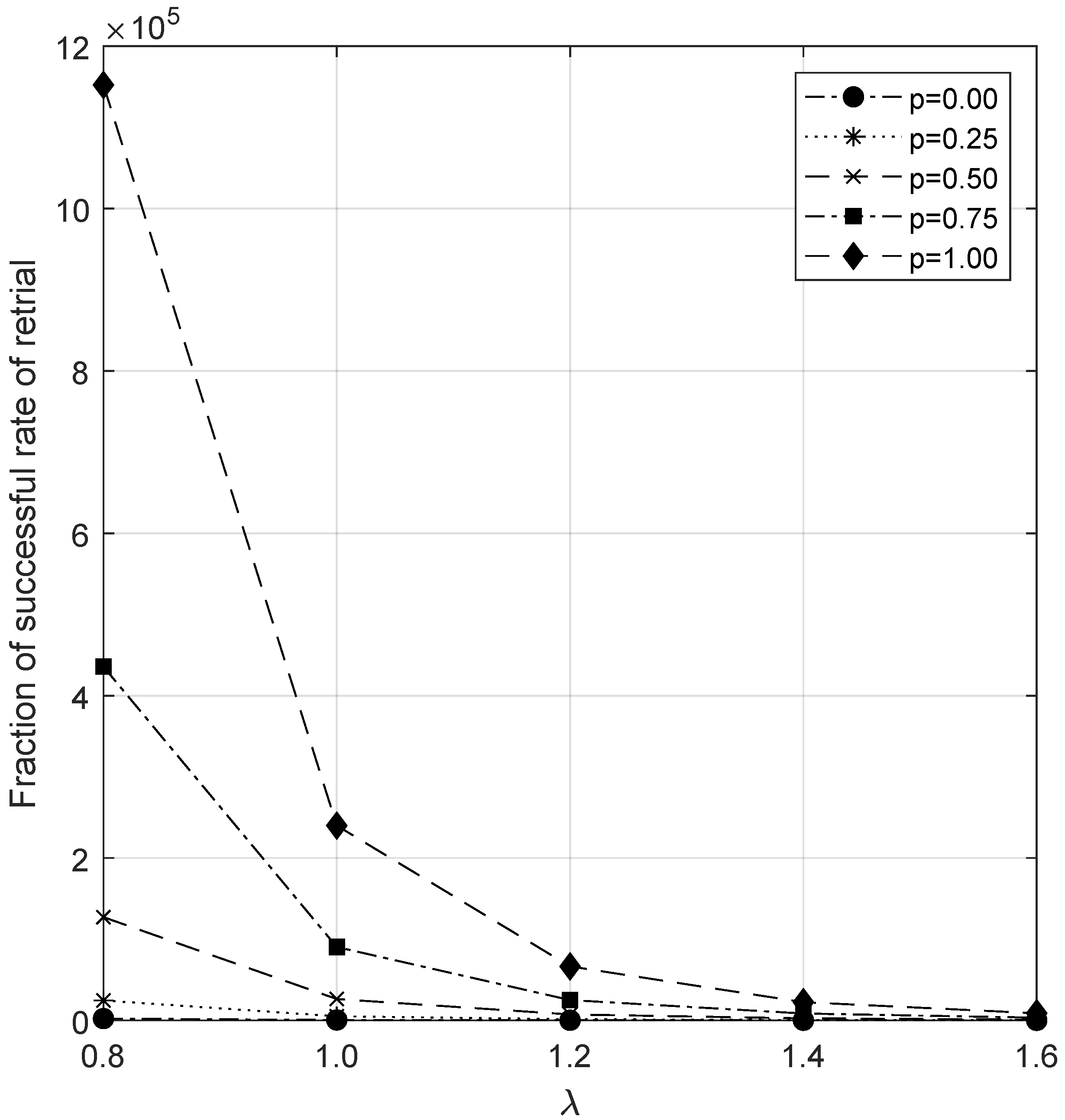
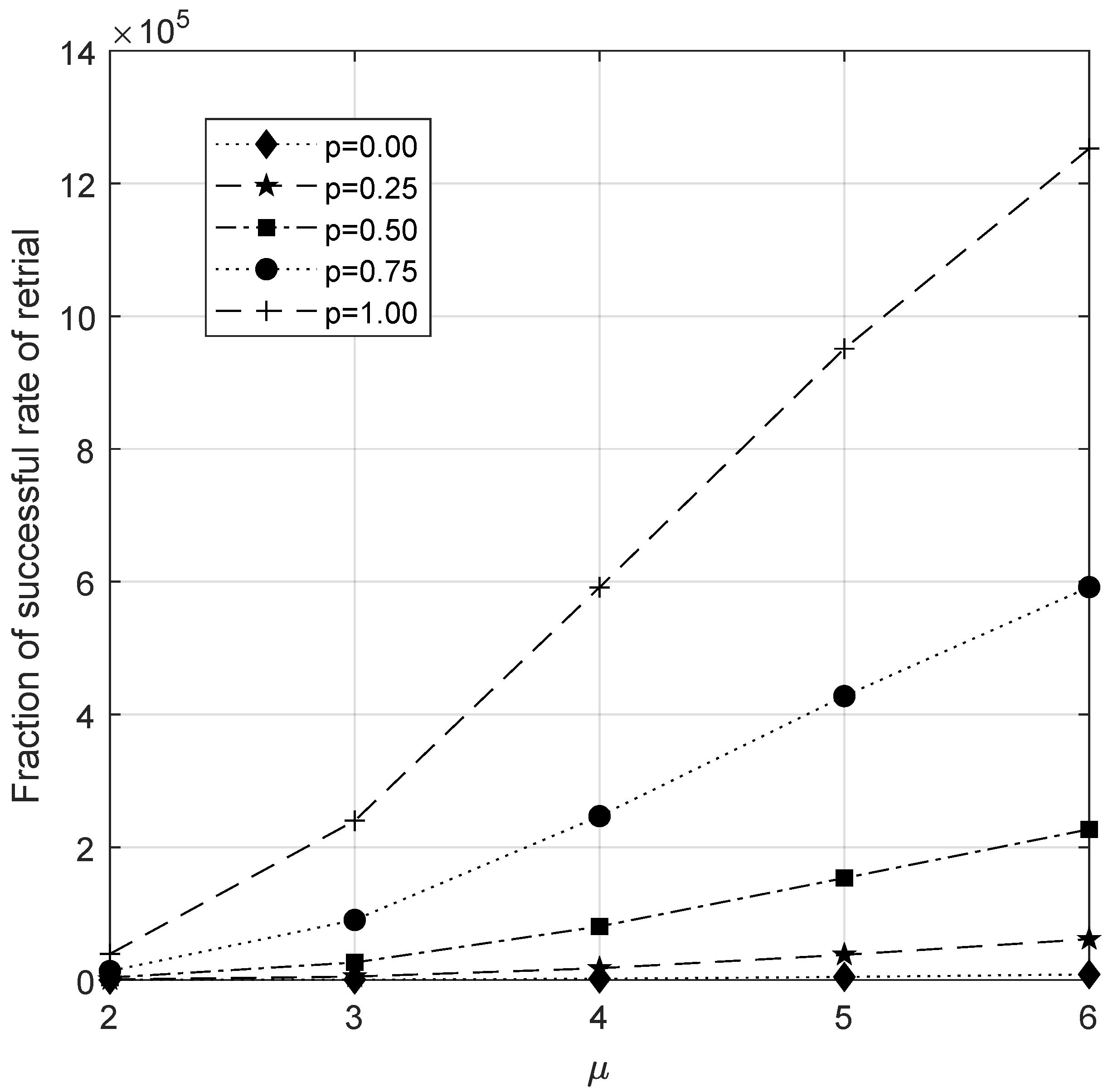
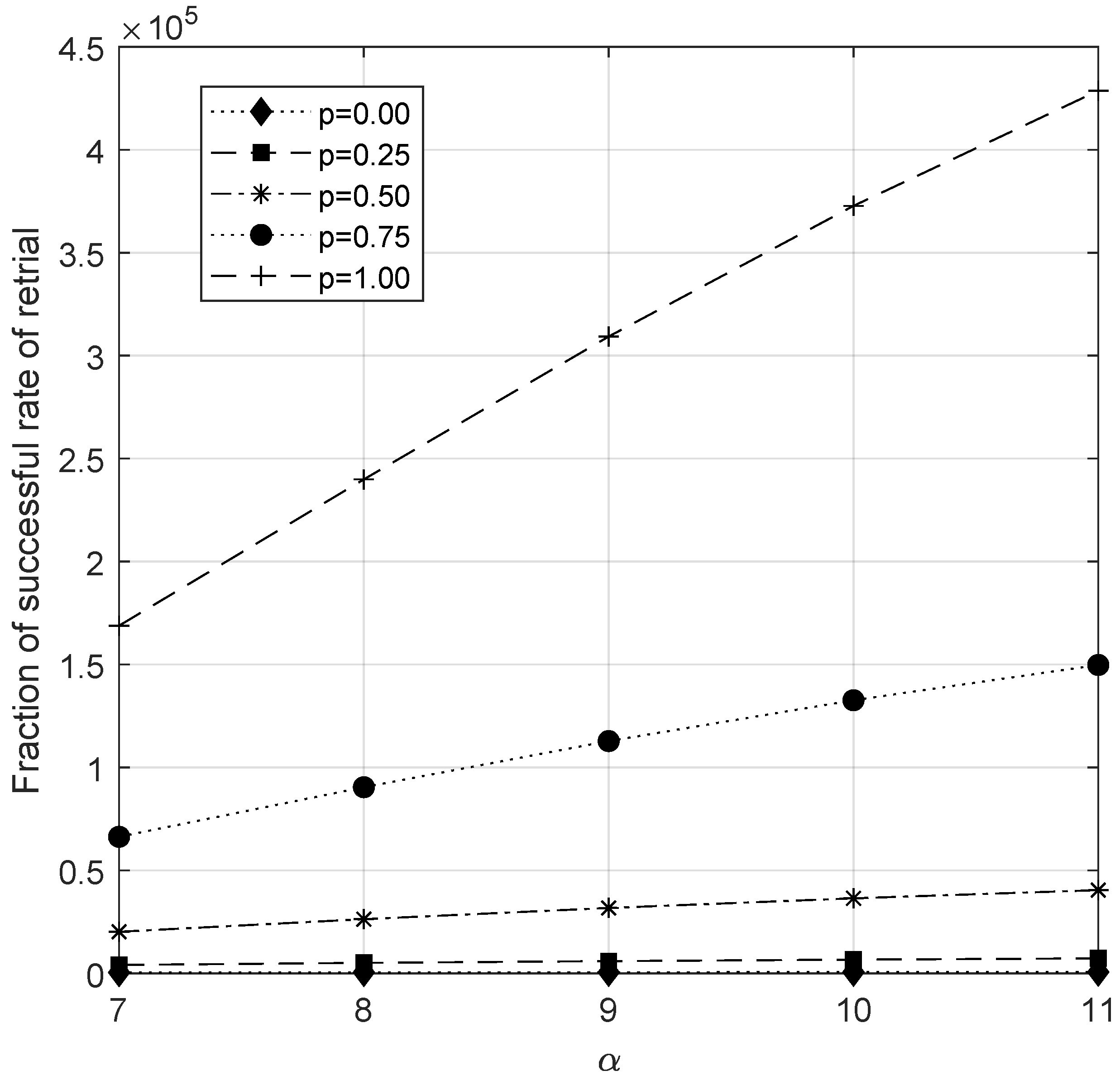
6.6. Analysis of Fraction of Successful Retrial Rate
- There is a gradual increase in Z while varying the parameter . However, after some point, the increase is not notably significant.
- An immediate response of increasing c can be observed in Z as it increases.
- The fraction of the successful retrial rate decreases when the arrival rate of the customer increases. After some values, it moves faster towards the value zero.
- An increase in the service rate directly decreases the service time per customer. It is suitable for the service rates of both junior and senior servers. As a result, they increase the rate of successful retrials.
- Increasing the capacity of the waiting hall increases the chance of a retrial’s success. Hence Z increases when we increase N.
- As similar to lambda, while increasing the rate , the waiting hall soon becomes full, which decreases the chance of a successful retrial.
6.7. Observations
- The obtained convexity of the total cost helps in identifying efficient configurations that minimize the overall costs.
- The parameters , and expose a favorable output for each analysis.
- Though the parameters N and c increase the total cost, they are actually helpful in increasing the fraction of successful retrials.
- When , the model turns out to be the standard QIS without consultation.
- The rate decreases the waiting time of customers in the orbit when it increases. But, in the case of customers in the waiting hall, it acts inversely.
- The rate increases the total cost, waiting time of customers, and number of junior servers in C and S mode.
- An increase in p means that the junior servers are developed as experienced servers.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations
| 0 | A matrix where all entries are zero |
| e | A column vector of appropriate dimensions, with each coordinate set to one |
| I | An identity matrix |
| Heaviside function | |
References
- Melikov, A.Z.; Molchanov, A.A. Stock optimization in transportation/storage systems. Cybern. Syst. Anal. 1992, 28, 484–487. [Google Scholar] [CrossRef]
- Sigman, K.; Simchi-Levi, D. Light traffic heuristic for an M/G/1 queue with limited inventory. Ann. Oper. Res. 1992, 40, 371–380. [Google Scholar] [CrossRef]
- Yadavalli, V.S.; Sivakumar, B.; Arivarignan, G.; Adetunji, O. A multi-server perishable inventory system with negative customer. Comput. Ind. Eng. 2011, 61, 254–273. [Google Scholar] [CrossRef]
- Yadavalli, V.S.; Sivakumar, B.; Arivarignan, G.; Adetunji, O. A finite source multi-server inventory system with service facility. Comput. Ind. Eng. 2012, 63, 739–753. [Google Scholar] [CrossRef]
- Nair, A.N.; Jacob, M.J.; Krishnamoorthy, A. The multi server M/M/(s,S) queueing inventory system. Ann. Oper. Res. 2015, 233, 321–333. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; an Manik, R.; Shajin, D. Analysis of a multiserver queueing-inventory system. Adv. Oper. Res. 2015, 2015, 747328. [Google Scholar] [CrossRef]
- Wang, F.F. Approximation and optimization of a multi-server impatient retrial inventory-queueing system with two demand classes. Qual. Technol. Quant. Manag. 2015, 12, 269–292. [Google Scholar] [CrossRef]
- Wang, F.F.; Bhagat, A.; Chang, T.M. Analysis of priority multi-server retrial queueing inventory systems with MAP arrivals and exponential services. Opsearch 2017, 54, 44–66. [Google Scholar] [CrossRef]
- Hanukov, G.; Avinadav, T.; Chernonog, T.; Yechiali, U. A multi-server queueing-inventory system with stock-dependent demand. IFAC PapersOnLine 2019, 52, 671–676. [Google Scholar] [CrossRef]
- Jeganathan, K.; Reiyas, M.A.; Lakshmi, K.P.; Saravanan, S. Two server Markovian inventory systems with server interruptions: Heterogeneous vs. homogeneous servers. Math. Comput. Simul. 2019, 155, 177–200. [Google Scholar] [CrossRef]
- Suganya, C.; Sivakumar, B. MAP/PH (1), PH (2)/2 finite retrial inventory system with service facility, multiple vacations for servers. Int. J. Math. Oper. Res. 2019, 15, 265–295. [Google Scholar] [CrossRef]
- Jose, K.P.; Beena, P. On a retrial production inventory system with vacation and multiple servers. Int. J. Appl. Comput. Math. 2020, 6, 108. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Rumyantsev, A. Analytical and simulation studies of queueing-inventory models with MAP demands in batches and positive phase-type services. Simul. Model. Pract. Theory 2020, 103, 102092. [Google Scholar] [CrossRef]
- Jeganathan, K.; Reiyas, M.A. Two parallel heterogeneous servers Markovian inventory system with modified and delayed working vacations. Math. Comput. Simul. 2020, 172, 273–304. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Shajin, D.; Krishnamoorthy, A. Infinite server queueing-inventory models. J. Indian Soc. Probab. Stat. 2020, 21, 43–68. [Google Scholar] [CrossRef]
- Hanukov, G.; Avinadav, T.; Chernonog, T.; Yechiali, U. A multi-server system with inventory of preliminary services and stock-dependent demand. Int. J. Prod. Res. 2021, 59, 4384–4402. [Google Scholar] [CrossRef]
- Jeganathan, K.; Harikrishnan, T.; Selvakumar, S.; Anbazhagan, N.; Amutha, S.; Acharya, S.; Rajendra, D.; Joshi, G.P. Analysis of interconnected arrivals on queueing-inventory system with two multi-server service channels and one retrial facility. Electronics 2021, 10, 576. [Google Scholar] [CrossRef]
- Rasmi, K.; Jacob, M.J.; Rumyantsev, A.S.; Krishnamoorthy, A. A multi-server heterogeneous queuing-inventory system with class-dependent inventory access. Mathematics 2021, 9, 1037. [Google Scholar] [CrossRef]
- Rasmi, K.; Jacob, M.J. Analysis of a multiserver queueing inventory model with self-service. Int. J. Math. Model. Numer. Optim. 2021, 11, 275–291. [Google Scholar] [CrossRef]
- Shajin, D.; Krishnamoorthy, A.; Melikov, A.Z.; Sztrik, J. Multi-server queuing production inventory system with emergency replenishment. Mathematics 2022, 10, 3839. [Google Scholar] [CrossRef]
- Jeganathan, K.; Selvakumar, S.; Saravanan, S.; Anbazhagan, N.; Amutha, S.; Cho, W.; Joshi, G.P.; Ryoo, J. Performance of stochastic inventory system with a fresh item, returned item, refurbished item, and multi-class customers. Mathematics 2022, 10, 1137. [Google Scholar] [CrossRef]
- Almaqbali, K.A.; Joshua, V.C.; Krishnamoorthy, A. Multi-class, multi-server queueing inventory system with batch service. Mathematics 2023, 11, 830. [Google Scholar] [CrossRef]
- Aghsami, A.; Samimi, Y.; Aghaie, A. A combined continuous-time Markov chain and queueing-inventory model for a blood transfusion network considering ABO/Rh substitution priority and unreliable screening laboratory. Expert Syst. Appl. 2023, 215, 119360. [Google Scholar] [CrossRef]
- Selvakumar, S.; Jeganathan, K.; Srinivasan, K.; Anbazhagan, N.; Lee, S.; Joshi, G.P.; Doo, I.C. An optimization of home delivery services in a stochastic modeling with self and compulsory vacation interruption. Mathematics 2023, 11, 2044. [Google Scholar] [CrossRef]
- Yue, D.; Ye, Z.; Yue, W. Analysis of a Queueing-Inventory System with Synchronous Vacation of Multiple Servers. Queueing Models Serv. Manag. 2023, 6, 1–26. [Google Scholar]
- Artalejo, J.R.; Krishnamoorthy, A.; Lopez-Herrero, M.J. Numerical analysis of (s,S) inventory systems with repeated attempts. Ann. Oper. Res. 2006, 141, 67–83. [Google Scholar] [CrossRef]
- Ushakumari, P.V. On (s,S) inventory system with random lead time and repeated demands. J. Appl. Math. Stoch. Anal. 2006, 2006, 81508. [Google Scholar] [CrossRef]
- Amirthakodi, M.; Sivakumar, B. An inventory system with service facility and feedback customers. Int. J. Ind. Syst. Eng. 2019, 33, 374–411. [Google Scholar] [CrossRef]
- Lopez-Herrero, M.J. Waiting time and other first-passage time measures in an (s,S) inventory system with repeated attempts and finite retrial group. Comput. Oper. Res. 2010, 37, 1256–1261. [Google Scholar] [CrossRef]
- Hanukov, G. A queueing-inventory system in which customers can orbit during the service. IFAC PapersOnLine 2022, 55, 619–624. [Google Scholar] [CrossRef]
- Sugapriya, C.; Nithya, M.; Jeganathan, K.; Anbazhagan, N.; Joshi, G.P.; Yang, E.; Seo, S. Analysis of stock-dependent arrival process in a retrial stochastic inventory system with server vacation. Processes 2022, 10, 176. [Google Scholar] [CrossRef]
- Melikov, A.; Aliyeva, S.; Nair, S.S.; Kumar, B.K. Retrial queuing-inventory systems with delayed feedback and instantaneous damaging of items. Axioms 2022, 11, 241. [Google Scholar] [CrossRef]
- Nithya, N.; Anbazhagan, N.; Amutha, S.; Jeganathan, K.; Park, G.-C.; Joshi, G.P.; Cho, W. Controlled arrivals on the retrial queueing–inventory system with an essential interruption and emergency vacationing server. Mathematics 2023, 11, 3560. [Google Scholar] [CrossRef]
- Reiyas, M.A.; Jeganathan, K. A classical retrial queueing inventory system with two component demand rate. Int. J. Oper. 2023, 47, 508–533. [Google Scholar] [CrossRef]
- Jain, M.; Kumar, I. Cost optimization of a queueing inventory system with two-level supply mode, retrial demands and multiple vacations using a genetic algorithm. Int. J. Appl. Comput. Math. 2023, 9, 51. [Google Scholar] [CrossRef]
- Jeganathan, K.; Koffer, V.A.; Sugapriya, C.; Nagarajan, D. A matrix-analytic method for the steady-state analysis of a Markovian queueing system with scrap items. Decis. Anal. J. 2023, 7, 100244. [Google Scholar] [CrossRef]
- Bazizi, L.; Rahmoune, F.; Lekadir, O.; Labadi, K. Modelling, performance evaluation and optimisation of (s,Q) retrial inventory system with partial backlogging demands: A gspn approach. Eur. J. Ind. Eng. 2023, 17, 529–569. [Google Scholar] [CrossRef]
- Jeganathan, K.; Harikrishnan, T.; Lakshmi, K.P.; Nagarajan, D. A multi-server retrial queueing-inventory system with asynchronous multiple vacations. Decis. Anal. J. 2023, 9, 100333. [Google Scholar] [CrossRef]
- Chakravarthy, S.R. A multi-server queueing model with server consultations. Eur. J. Oper. Res. 2014, 233, 625–639. [Google Scholar] [CrossRef]
- Hanukov, G. A service system where junior servers approach a senior server on behalf of customers. Int. J. Prod. Econ. 2022, 244, 108351. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Dudin, A.N.; Dudin, S.A.; Dudina, O.S. Queueing System with Potential for Recruiting Secondary Servers. Mathematics 2023, 11, 624. [Google Scholar] [CrossRef]
- Neuts, M.F.; Rao, B.M. Numerical investigation of a multiserver retrial model. Queueing Syst. 1990, 7, 169–189. [Google Scholar] [CrossRef]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; Courier Corporation: North Chelmsford, MA, USA, 1994. [Google Scholar]









| p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | ||
|---|---|---|---|---|---|---|---|
| 3 | 7 | 6.031736 | 5.065806 | 4.594173 | 4.313232 | 4.126693 | |
| 8 | 5.939920 | 5.006762 | 4.550207 | 4.278155 | 4.097510 | ||
| 9 | 5.870337 | 4.961519 | 4.516374 | 4.251100 | 4.074969 | ||
| 4 | 7 | 5.488890 | 4.714822 | 4.332903 | 4.105023 | 3.953676 | |
| 8 | 5.396855 | 4.655079 | 4.288480 | 4.069652 | 3.924297 | ||
| 9 | 5.326736 | 4.609159 | 4.254219 | 4.042323 | 3.901571 | ||
| 5 | 7 | 5.171290 | 4.506030 | 4.176982 | 3.980651 | 3.850284 | |
| 8 | 5.078740 | 4.445875 | 4.132323 | 3.945139 | 3.820815 | ||
| 9 | 5.008045 | 4.399572 | 4.097844 | 3.917677 | 3.798003 | ||
| p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | |||
|---|---|---|---|---|---|---|---|---|
| 1.0 | 0.1 | 2 | 5.941777 | 5.006924 | 4.550238 | 4.278163 | 4.097513 | |
| 3 | 5.935194 | 5.002773 | 4.547378 | 4.276104 | 4.095999 | |||
| 4 | 5.931683 | 5.000643 | 4.545962 | 4.275120 | 4.095300 | |||
| 0.5 | 2 | 5.940224 | 5.006786 | 4.550212 | 4.278156 | 4.097510 | ||
| 3 | 5.933647 | 5.002635 | 4.547351 | 4.276097 | 4.095996 | |||
| 4 | 5.930138 | 5.000505 | 4.545936 | 4.275112 | 4.095297 | |||
| 0.9 | 2 | 5.939920 | 5.006762 | 4.550207 | 4.278155 | 4.097510 | ||
| 3 | 5.933346 | 5.002612 | 4.547347 | 4.276096 | 4.095995 | |||
| 4 | 5.929838 | 5.000481 | 4.545932 | 4.275111 | 4.095297 | |||
| 1.5 | 0.1 | 2 | 7.539386 | 5.970785 | 5.263147 | 4.848807 | 4.575142 | |
| 3 | 7.524784 | 5.960969 | 5.255680 | 4.842871 | 4.570300 | |||
| 4 | 7.516844 | 5.955703 | 5.251778 | 4.839841 | 4.567878 | |||
| 0.5 | 2 | 7.514470 | 5.968412 | 5.262689 | 4.848674 | 4.575092 | ||
| 3 | 7.499993 | 5.958607 | 5.255224 | 4.842738 | 4.570250 | |||
| 4 | 7.492103 | 5.953344 | 5.251322 | 4.839708 | 4.567828 | |||
| 0.9 | 2 | 7.509099 | 5.967982 | 5.262613 | 4.848653 | 4.575084 | ||
| 3 | 7.494679 | 5.958184 | 5.255149 | 4.842718 | 4.570243 | |||
| 4 | 7.486809 | 5.952924 | 5.251248 | 4.839688 | 4.567821 | |||
| 2.0 | 0.1 | 2 | 9.652635 | 7.022696 | 6.000656 | 5.429878 | 5.058704 | |
| 3 | 9.623882 | 7.005369 | 5.987205 | 5.418726 | 5.049210 | |||
| 4 | 9.609102 | 6.996062 | 5.980050 | 5.412893 | 5.044321 | |||
| 0.5 | 2 | 9.563897 | 7.005378 | 5.997239 | 5.428880 | 5.058325 | ||
| 3 | 9.534545 | 6.988206 | 5.983825 | 5.417744 | 5.048842 | |||
| 4 | 9.519482 | 6.978943 | 5.976676 | 5.411911 | 5.043953 | |||
| 0.9 | 2 | 9.532591 | 7.002251 | 5.996667 | 5.428720 | 5.058266 | ||
| 3 | 9.503364 | 6.985142 | 5.983269 | 5.417590 | 5.048786 | |||
| 4 | 9.488287 | 6.975898 | 5.976124 | 5.411758 | 5.043898 | |||
| c | N | p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 |
|---|---|---|---|---|---|---|---|
| 3 | 6 | 5.939920 | 5.006762 | 4.550207 | 4.278155 | 4.097510 | |
| 7 | 5.943270 | 5.007606 | 4.550499 | 4.278280 | 4.097572 | ||
| 8 | 5.945190 | 5.008096 | 4.550672 | 4.278356 | 4.097610 | ||
| 4 | 6 | 7.328508 | 6.329089 | 5.816626 | 5.504202 | 5.293634 | |
| 7 | 7.328949 | 6.329197 | 5.816658 | 5.504214 | 5.293639 | ||
| 8 | 7.329114 | 6.329223 | 5.816665 | 5.504216 | 5.293640 | ||
| 5 | 6 | 8.678503 | 7.621454 | 7.063953 | 6.717419 | 6.480568 | |
| 7 | 8.678304 | 7.621446 | 7.063953 | 6.717419 | 6.480568 | ||
| 8 | 8.678374 | 7.621456 | 7.063955 | 6.717420 | 6.480568 | ||
| p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | ||
|---|---|---|---|---|---|---|---|
| 1 | 0.7 | 0.818034 | 0.676300 | 0.576869 | 0.503096 | 0.446129 | |
| 0.9 | 0.818077 | 0.676309 | 0.576872 | 0.503096 | 0.446130 | ||
| 1.1 | 0.818122 | 0.676322 | 0.576876 | 0.503098 | 0.446130 | ||
| 1.5 | 0.7 | 0.853010 | 0.693696 | 0.587304 | 0.510087 | 0.451152 | |
| 0.9 | 0.853583 | 0.693816 | 0.587331 | 0.510093 | 0.451153 | ||
| 1.1 | 0.854016 | 0.693942 | 0.587372 | 0.510108 | 0.451159 | ||
| 2 | 0.7 | 0.944325 | 0.730811 | 0.606190 | 0.521327 | 0.458600 | |
| 0.9 | 0.949729 | 0.731874 | 0.606448 | 0.521392 | 0.458614 | ||
| 1.1 | 0.952303 | 0.732582 | 0.606687 | 0.521479 | 0.458648 | ||
| c | p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 0.894707 | 0.718120 | 0.603122 | 0.521038 | 0.459102 | |
| 2 | 0.894216 | 0.717907 | 0.602988 | 0.520932 | 0.459009 | ||
| 3 | 0.894138 | 0.717889 | 0.602984 | 0.520932 | 0.459010 | ||
| 3 | 1 | 0.818223 | 0.676429 | 0.576976 | 0.503191 | 0.446218 | |
| 2 | 0.818040 | 0.676300 | 0.576870 | 0.503096 | 0.446129 | ||
| 3 | 0.818026 | 0.676296 | 0.576868 | 0.503095 | 0.446129 | ||
| 4 | 1 | 0.810804 | 0.672472 | 0.574604 | 0.501661 | 0.445179 | |
| 2 | 0.810654 | 0.672354 | 0.574502 | 0.501568 | 0.445092 | ||
| 3 | 0.810646 | 0.672351 | 0.574501 | 0.501567 | 0.445092 | ||
| N | p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | ||
|---|---|---|---|---|---|---|---|---|
| 5 | 2 | 7 | 1.203648 | 0.779707 | 0.579805 | 0.461953 | 0.384052 | |
| 8 | 1.178165 | 0.765030 | 0.569407 | 0.453902 | 0.377485 | |||
| 9 | 1.159069 | 0.753881 | 0.561460 | 0.447727 | 0.372437 | |||
| 3 | 7 | 0.841619 | 0.551896 | 0.411114 | 0.327681 | 0.272442 | ||
| 8 | 0.817536 | 0.537408 | 0.400787 | 0.319667 | 0.265897 | |||
| 9 | 0.799442 | 0.526400 | 0.392894 | 0.313520 | 0.260864 | |||
| 4 | 7 | 0.669833 | 0.439553 | 0.327314 | 0.260796 | 0.216771 | ||
| 8 | 0.645964 | 0.425118 | 0.317012 | 0.252796 | 0.210233 | |||
| 9 | 0.628029 | 0.414150 | 0.309138 | 0.246659 | 0.205206 | |||
| 6 | 2 | 7 | 1.208293 | 0.780137 | 0.579873 | 0.461968 | 0.384057 | |
| 8 | 1.182238 | 0.765400 | 0.569464 | 0.453914 | 0.377489 | |||
| 9 | 1.162759 | 0.754211 | 0.561510 | 0.447738 | 0.372440 | |||
| 3 | 7 | 0.842290 | 0.551948 | 0.411122 | 0.327683 | 0.272442 | ||
| 8 | 0.818072 | 0.537448 | 0.400793 | 0.319668 | 0.265897 | |||
| 9 | 0.799896 | 0.526432 | 0.392899 | 0.313521 | 0.260864 | |||
| 4 | 7 | 0.670011 | 0.439567 | 0.327317 | 0.260797 | 0.216771 | ||
| 8 | 0.646091 | 0.425128 | 0.317013 | 0.252796 | 0.210233 | |||
| 9 | 0.628128 | 0.414157 | 0.309139 | 0.246659 | 0.205207 | |||
| 7 | 2 | 7 | 1.223024 | 0.782166 | 0.580291 | 0.462086 | 0.384098 | |
| 8 | 1.195385 | 0.767176 | 0.569825 | 0.454015 | 0.377524 | |||
| 9 | 1.174808 | 0.755817 | 0.561834 | 0.447827 | 0.372471 | |||
| 3 | 7 | 0.845365 | 0.552284 | 0.411189 | 0.327701 | 0.272449 | ||
| 8 | 0.820602 | 0.537717 | 0.400845 | 0.319683 | 0.265902 | |||
| 9 | 0.802076 | 0.526660 | 0.392943 | 0.313533 | 0.260869 | |||
| 4 | 7 | 0.671008 | 0.439674 | 0.327338 | 0.260803 | 0.216773 | ||
| 8 | 0.646849 | 0.425206 | 0.317029 | 0.252800 | 0.210235 | |||
| 9 | 0.628743 | 0.414219 | 0.309151 | 0.246662 | 0.205208 | |||
| N | p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | ||
|---|---|---|---|---|---|---|---|---|
| 5 | 2 | 7 | 17.974591 | 16.126918 | 15.134281 | 14.557830 | 14.196432 | |
| 8 | 17.385102 | 15.680368 | 14.769172 | 14.246196 | 13.923038 | |||
| 9 | 16.951712 | 15.348465 | 14.494552 | 14.008187 | 13.709900 | |||
| 3 | 7 | 15.496179 | 14.688288 | 14.214487 | 13.819129 | 13.354706 | ||
| 8 | 15.039793 | 14.342994 | 13.940541 | 13.577170 | 13.084691 | |||
| 9 | 14.697968 | 14.073332 | 13.711969 | 13.357540 | 12.824969 | |||
| 4 | 7 | 14.823263 | 14.195999 | 13.603035 | 12.876039 | 11.961140 | ||
| 8 | 14.464449 | 13.938156 | 13.340046 | 12.460582 | 11.545646 | |||
| 9 | 14.175495 | 13.699796 | 13.059647 | 12.004922 | 11.494981 | |||
| 6 | 2 | 7 | 15.398444 | 13.833228 | 12.987423 | 12.502860 | 12.217659 | |
| 8 | 14.886138 | 13.443967 | 12.670814 | 12.235936 | 11.988846 | |||
| 9 | 14.509286 | 13.154461 | 12.432376 | 12.031705 | 11.810049 | |||
| 3 | 7 | 13.290115 | 12.611500 | 12.260900 | 12.051000 | 11.885700 | ||
| 8 | 12.899227 | 12.324800 | 12.051900 | 11.904900 | 11.787000 | |||
| 9 | 12.606572 | 12.101900 | 11.879100 | 11.771100 | 11.680400 | |||
| 4 | 7 | 12.721641 | 12.279487 | 11.983881 | 11.707888 | 11.390321 | ||
| 8 | 12.432918 | 12.114537 | 11.906196 | 11.672482 | 11.338833 | |||
| 9 | 12.205155 | 11.968338 | 11.815081 | 11.598996 | 11.229460 | |||
| 7 | 2 | 7 | 12.982237 | 11.655100 | 10.927200 | 10.508000 | 10.264500 | |
| 8 | 12.537662 | 11.316500 | 10.653400 | 10.279400 | 10.070800 | |||
| 9 | 12.210647 | 11.064900 | 10.447500 | 10.104900 | 9.920400 | |||
| 3 | 7 | 11.171236 | 10.580468 | 10.287446 | 10.142443 | 10.073247 | ||
| 8 | 10.836051 | 10.338327 | 10.114754 | 10.028237 | 10.010985 | |||
| 9 | 10.586480 | 10.152566 | 9.976379 | 9.929820 | 9.918257 | |||
| 4 | 7 | 10.654105 | 10.297545 | 10.115627 | 10.042687 | 10.05909 | ||
| 8 | 10.410305 | 10.163202 | 10.069510 | 10.034289 | 10.00849 | |||
| 9 | 10.224213 | 10.053975 | 9.024084 | 9.0077514 | 8.925115 | |||
| p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | ||
|---|---|---|---|---|---|---|---|
| 1 | 0.7 | 6.168542 | 4.411438 | 3.410960 | 2.348533 | 1.446406 | |
| 0.9 | 5.039675 | 3.494077 | 2.670702 | 1.839568 | 1.137603 | ||
| 1.1 | 4.338611 | 2.932733 | 2.217329 | 1.524989 | 0.944842 | ||
| 1.5 | 0.7 | 9.004800 | 7.463500 | 6.438000 | 4.978400 | 3.376200 | |
| 0.9 | 7.149300 | 5.759400 | 4.923600 | 3.820000 | 2.612900 | ||
| 1.1 | 6.016700 | 4.733400 | 4.010400 | 3.113900 | 2.141300 | ||
| 2 | 0.7 | 16.816769 | 15.988781 | 15.693862 | 14.625320 | 12.438549 | |
| 0.9 | 12.899227 | 11.969791 | 11.634857 | 10.840719 | 9.288518 | ||
| 1.1 | 10.564923 | 9.601746 | 9.246775 | 8.601285 | 7.401879 | ||
| c | p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 35.941785 | 29.674531 | 28.507375 | 28.603095 | 29.006031 | |
| 2 | 16.676209 | 13.582353 | 12.923631 | 12.734906 | 12.420229 | ||
| 3 | 4.417784 | 2.637320 | 1.175358 | 0.480075 | 0.234289 | ||
| 3 | 1 | 28.543326 | 27.075633 | 27.309766 | 27.759411 | 28.048548 | |
| 2 | 12.899227 | 11.969791 | 11.634857 | 10.840719 | 9.288518 | ||
| 3 | 2.656402 | 0.945474 | 0.300075 | 0.131414 | 0.080402 | ||
| 4 | 1 | 26.155253 | 25.882732 | 26.404486 | 26.976858 | 27.352461 | |
| 2 | 11.639618 | 11.124192 | 10.458458 | 8.803575 | 6.357663 | ||
| 3 | 1.770459 | 0.466486 | 0.145741 | 0.071584 | 0.049899 | ||
| N | p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | ||
|---|---|---|---|---|---|---|---|---|
| 5 | 2 | 7 | 0.214168 | 0.173785 | 0.153179 | 0.140672 | 0.132265 | |
| 8 | 0.205232 | 0.165357 | 0.144930 | 0.132515 | 0.124167 | |||
| 9 | 0.197841 | 0.158327 | 0.138030 | 0.125685 | 0.117382 | |||
| 3 | 7 | 0.311016 | 0.243614 | 0.208336 | 0.186755 | 0.172203 | ||
| 8 | 0.300123 | 0.233510 | 0.198503 | 0.177056 | 0.162586 | |||
| 9 | 0.291243 | 0.225200 | 0.190392 | 0.169047 | 0.154639 | |||
| 4 | 7 | 0.548656 | 0.420817 | 0.348025 | 0.302173 | 0.270858 | ||
| 8 | 0.534660 | 0.408228 | 0.335948 | 0.290339 | 0.259165 | |||
| 9 | 0.523450 | 0.398053 | 0.326153 | 0.280728 | 0.249662 | |||
| 6 | 2 | 7 | 0.214574 | 0.173874 | 0.153211 | 0.140687 | 0.132273 | |
| 8 | 0.205650 | 0.165451 | 0.144964 | 0.132532 | 0.124176 | |||
| 9 | 0.198264 | 0.158424 | 0.138066 | 0.125702 | 0.117391 | |||
| 3 | 7 | 0.312723 | 0.243974 | 0.208462 | 0.186813 | 0.172234 | ||
| 8 | 0.301814 | 0.233874 | 0.198631 | 0.177115 | 0.162617 | |||
| 9 | 0.292917 | 0.225563 | 0.190521 | 0.169106 | 0.154671 | |||
| 4 | 7 | 0.560953 | 0.423295 | 0.348857 | 0.302539 | 0.271048 | ||
| 8 | 0.546575 | 0.410671 | 0.336772 | 0.290703 | 0.259353 | |||
| 9 | 0.535072 | 0.400464 | 0.326969 | 0.281088 | 0.249849 | |||
| 7 | 2 | 7 | 0.215571 | 0.174074 | 0.153276 | 0.140714 | 0.132287 | |
| 8 | 0.206497 | 0.165628 | 0.145023 | 0.132557 | 0.124189 | |||
| 9 | 0.199010 | 0.158583 | 0.138120 | 0.125726 | 0.117403 | |||
| 3 | 7 | 0.315726 | 0.244621 | 0.208679 | 0.186906 | 0.172281 | ||
| 8 | 0.304383 | 0.234445 | 0.198826 | 0.177200 | 0.162661 | |||
| 9 | 0.295190 | 0.226081 | 0.190700 | 0.169185 | 0.154712 | |||
| 4 | 7 | 0.571828 | 0.426441 | 0.349984 | 0.303037 | 0.271302 | ||
| 8 | 0.555640 | 0.413467 | 0.337792 | 0.291157 | 0.259587 | |||
| 9 | 0.542875 | 0.403013 | 0.327913 | 0.281511 | 0.250067 | |||
| p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | ||
|---|---|---|---|---|---|---|---|
| 1 | 0.7 | 0.298673 | 0.230565 | 0.195358 | 0.173921 | 0.159507 | |
| 0.9 | 0.301814 | 0.233874 | 0.198631 | 0.177115 | 0.162617 | ||
| 1.1 | 0.302669 | 0.234794 | 0.199552 | 0.178019 | 0.163501 | ||
| 1.5 | 0.7 | 0.391362 | 0.295437 | 0.244605 | 0.213324 | 0.192213 | |
| 0.9 | 0.395540 | 0.300339 | 0.249639 | 0.218302 | 0.197071 | ||
| 1.1 | 0.396814 | 0.301838 | 0.251218 | 0.219896 | 0.198652 | ||
| 2 | 0.7 | 0.484258 | 0.357994 | 0.293037 | 0.252562 | 0.225074 | |
| 0.9 | 0.487276 | 0.363284 | 0.298753 | 0.258276 | 0.230623 | ||
| 1.1 | 0.488741 | 0.365234 | 0.300915 | 0.260522 | 0.232891 | ||
| c | p | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 0.200141 | 0.149298 | 0.123846 | 0.108641 | 0.098556 | |
| 2 | 0.200125 | 0.149298 | 0.123846 | 0.108641 | 0.098556 | ||
| 3 | 0.200117 | 0.149297 | 0.123845 | 0.108640 | 0.098555 | ||
| 3 | 1 | 0.301820 | 0.233874 | 0.198631 | 0.177115 | 0.162617 | |
| 2 | 0.301810 | 0.233873 | 0.198630 | 0.177114 | 0.162616 | ||
| 3 | 0.301818 | 0.233872 | 0.198629 | 0.177113 | 0.162615 | ||
| 4 | 1 | 0.315977 | 0.249250 | 0.212910 | 0.189968 | 0.174199 | |
| 2 | 0.315622 | 0.249228 | 0.212908 | 0.189967 | 0.174199 | ||
| 3 | 0.315402 | 0.249212 | 0.212905 | 0.189966 | 0.174198 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeganathan, K.; Harikrishnan, T.; Lakshmanan, K.; Melikov, A.; Sztrik, J. Modeling of Junior Servers Approaching a Senior Server in the Retrial Queuing-Inventory System. Mathematics 2023, 11, 4581. https://doi.org/10.3390/math11224581
Jeganathan K, Harikrishnan T, Lakshmanan K, Melikov A, Sztrik J. Modeling of Junior Servers Approaching a Senior Server in the Retrial Queuing-Inventory System. Mathematics. 2023; 11(22):4581. https://doi.org/10.3390/math11224581
Chicago/Turabian StyleJeganathan, Kathirvel, Thanushkodi Harikrishnan, Kumarasankaralingam Lakshmanan, Agassi Melikov, and Janos Sztrik. 2023. "Modeling of Junior Servers Approaching a Senior Server in the Retrial Queuing-Inventory System" Mathematics 11, no. 22: 4581. https://doi.org/10.3390/math11224581
APA StyleJeganathan, K., Harikrishnan, T., Lakshmanan, K., Melikov, A., & Sztrik, J. (2023). Modeling of Junior Servers Approaching a Senior Server in the Retrial Queuing-Inventory System. Mathematics, 11(22), 4581. https://doi.org/10.3390/math11224581








