Dynamic Game Analysis on Cooperative Advertising Strategy in a Manufacturer-Led Supply Chain with Risk Aversion
Abstract
1. Introduction
2. Literature Review
2.1. Cooperative Advertising in Supply Chain
2.2. Risk Aversion in Supply Chain
2.3. Complexity in Supply Chain Game
3. Supply Chain Model
3.1. Model Description
3.2. Model Assumption
- (1)
- The unit production cost of the manufacturer and unit handling cost of the retailer incurred in addition to purchasing cost are assumed to be equal to zero.
- (2)
- Cooperative advertising is divided into the manufacturer’s national advertising expenditure and the retailer’s local advertising Due to different formula editors, some formula formats are not uniform. We will adjust the format of this part in later stage of production. , which are decision variables for the supply chain participants.
- (3)
- In this model, the manufacturer and retailer are risk-averse, which revenues are represented by exponential utility functions and follow a normal distribution.
3.3. Model Construction
3.4. The Stability of the System
4. Dynamics Analysis and Numerical Simulation
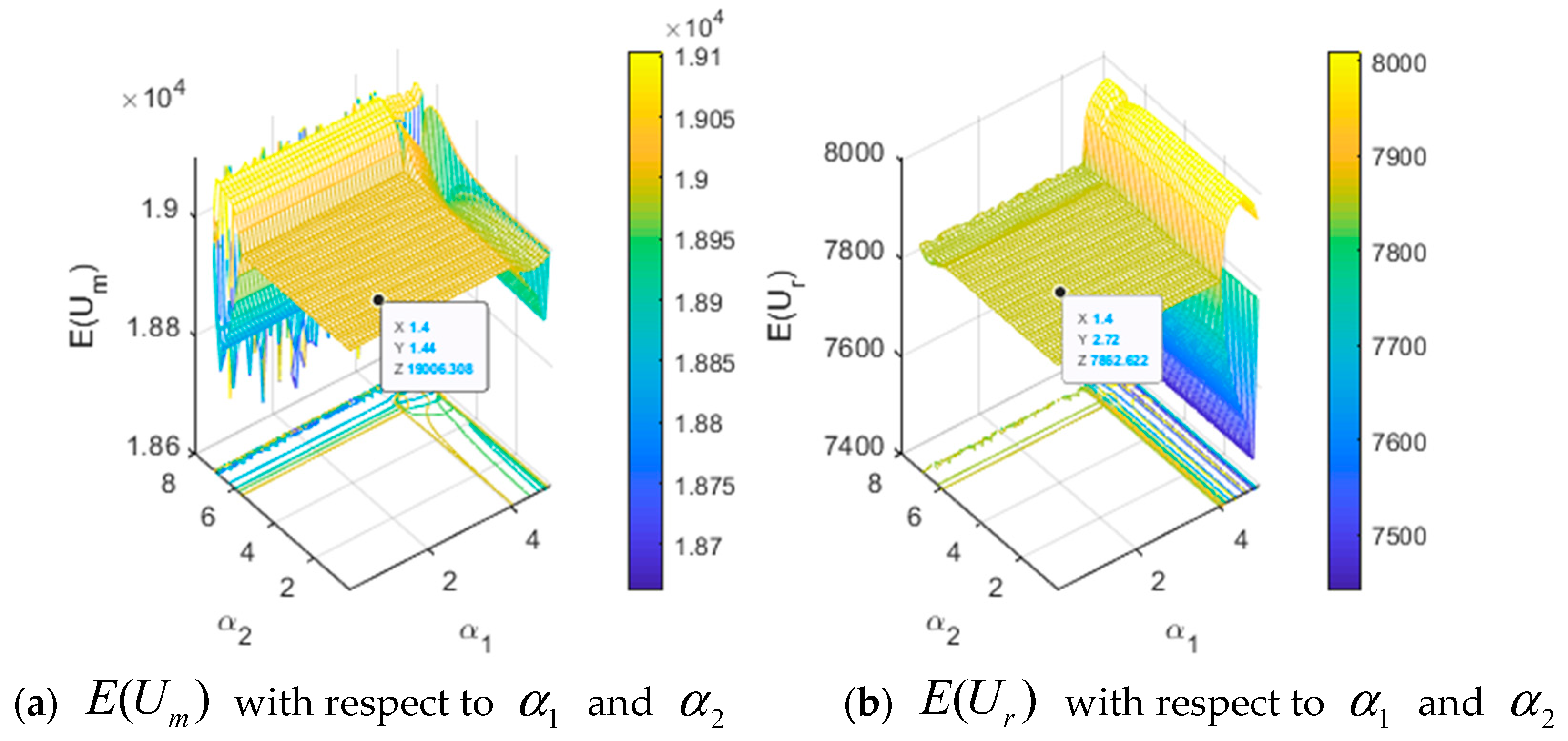
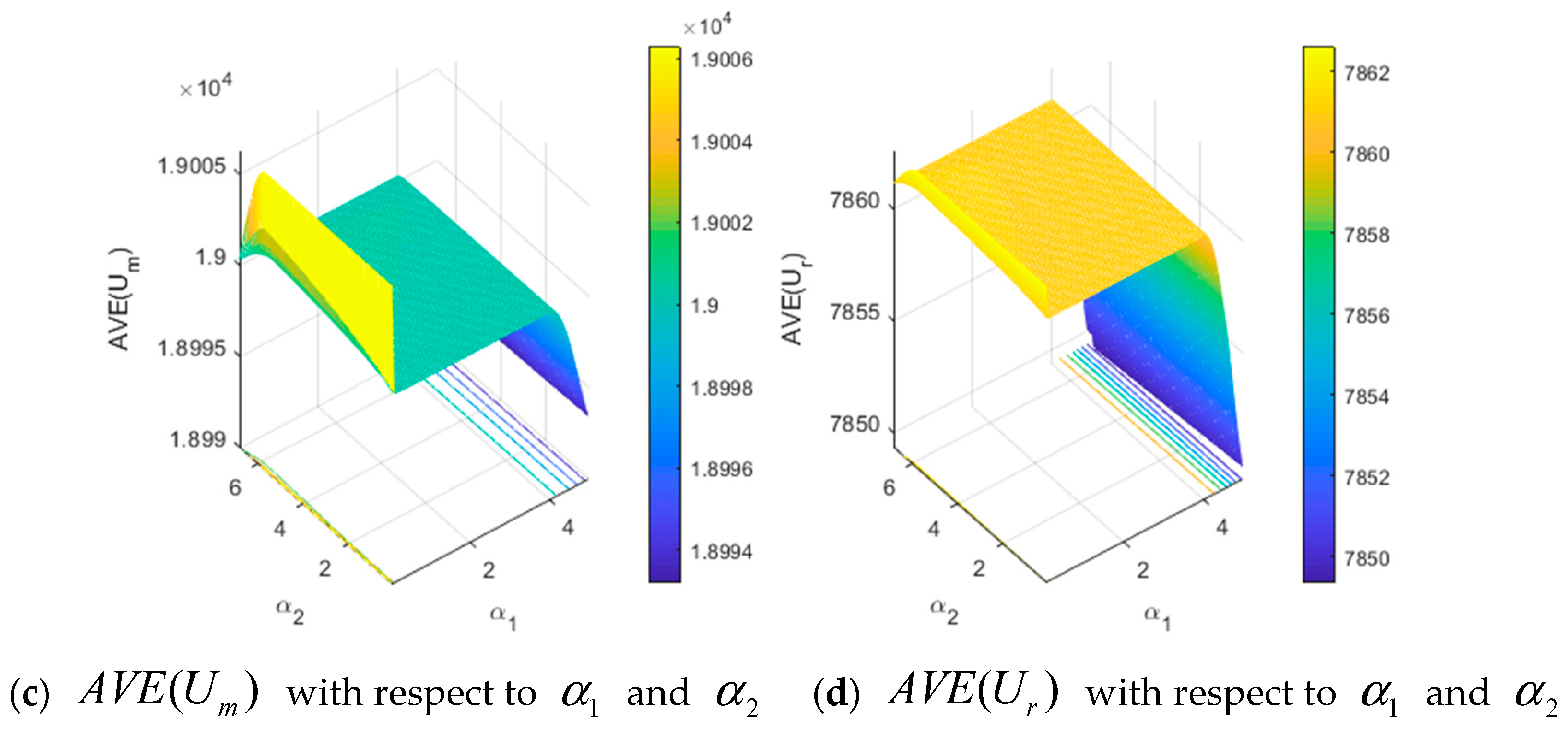
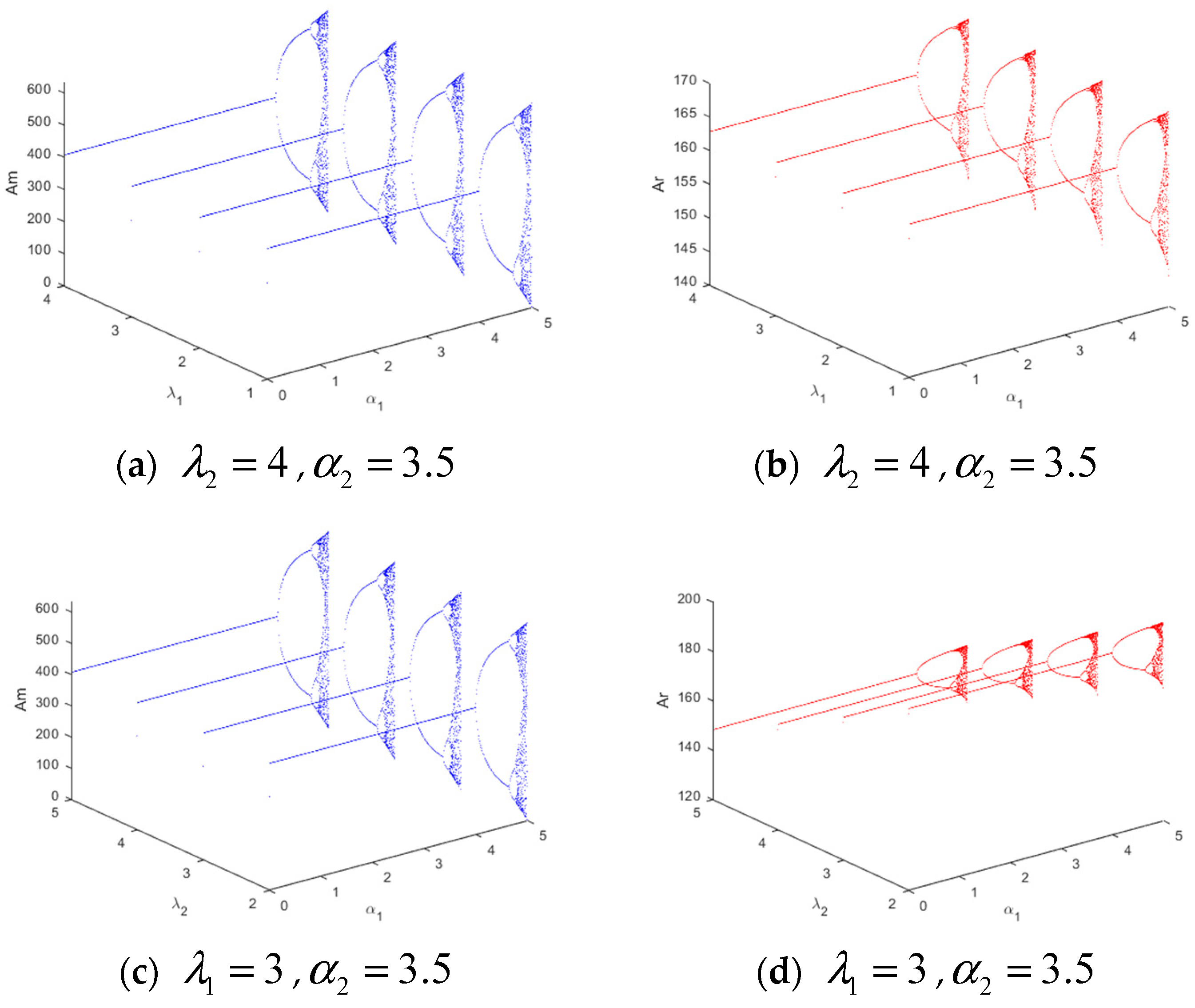
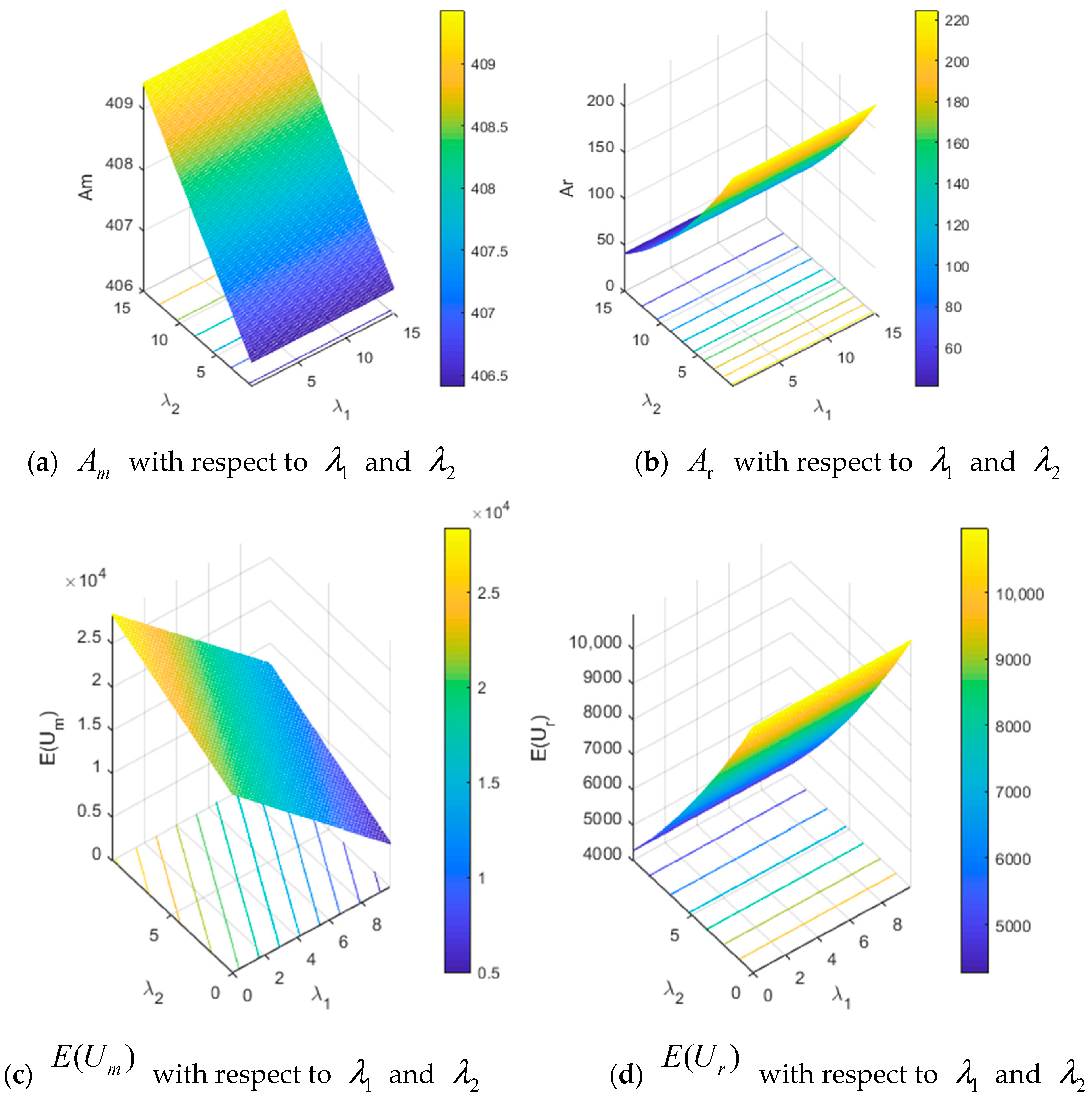
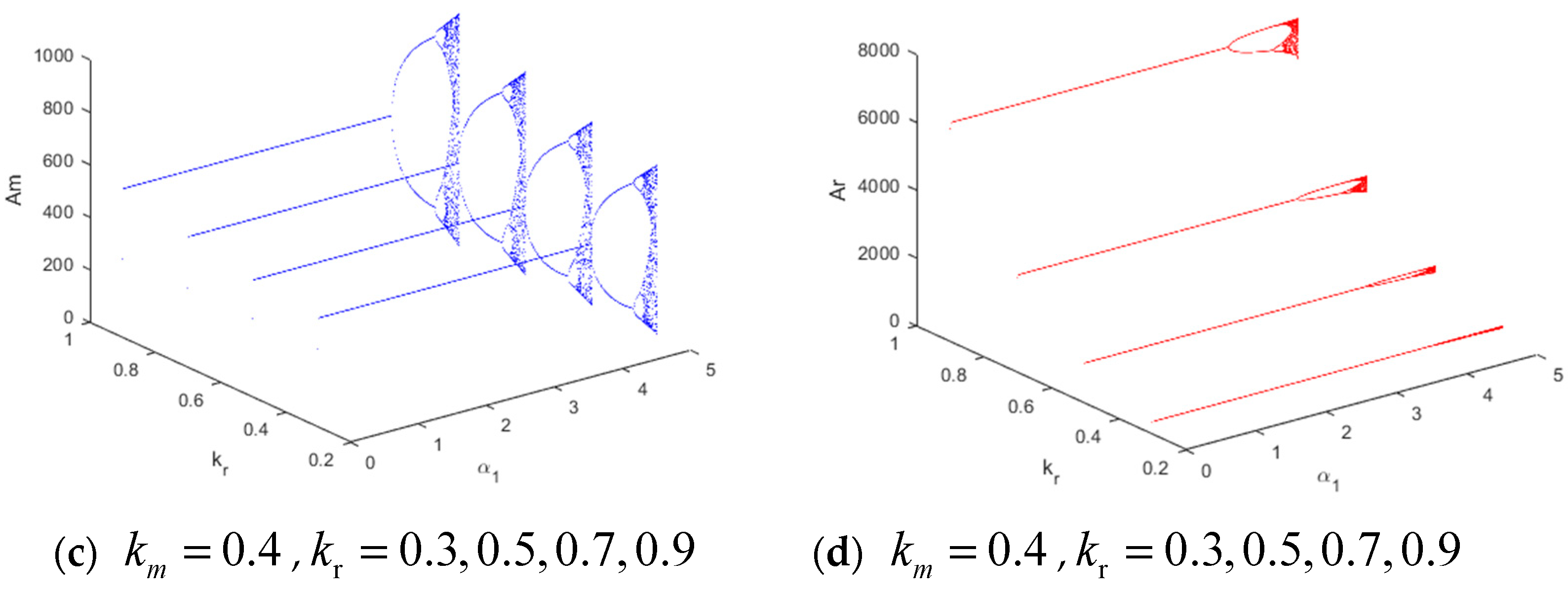
4.1. The Dynamics with Respect to Adjustment Speeds and
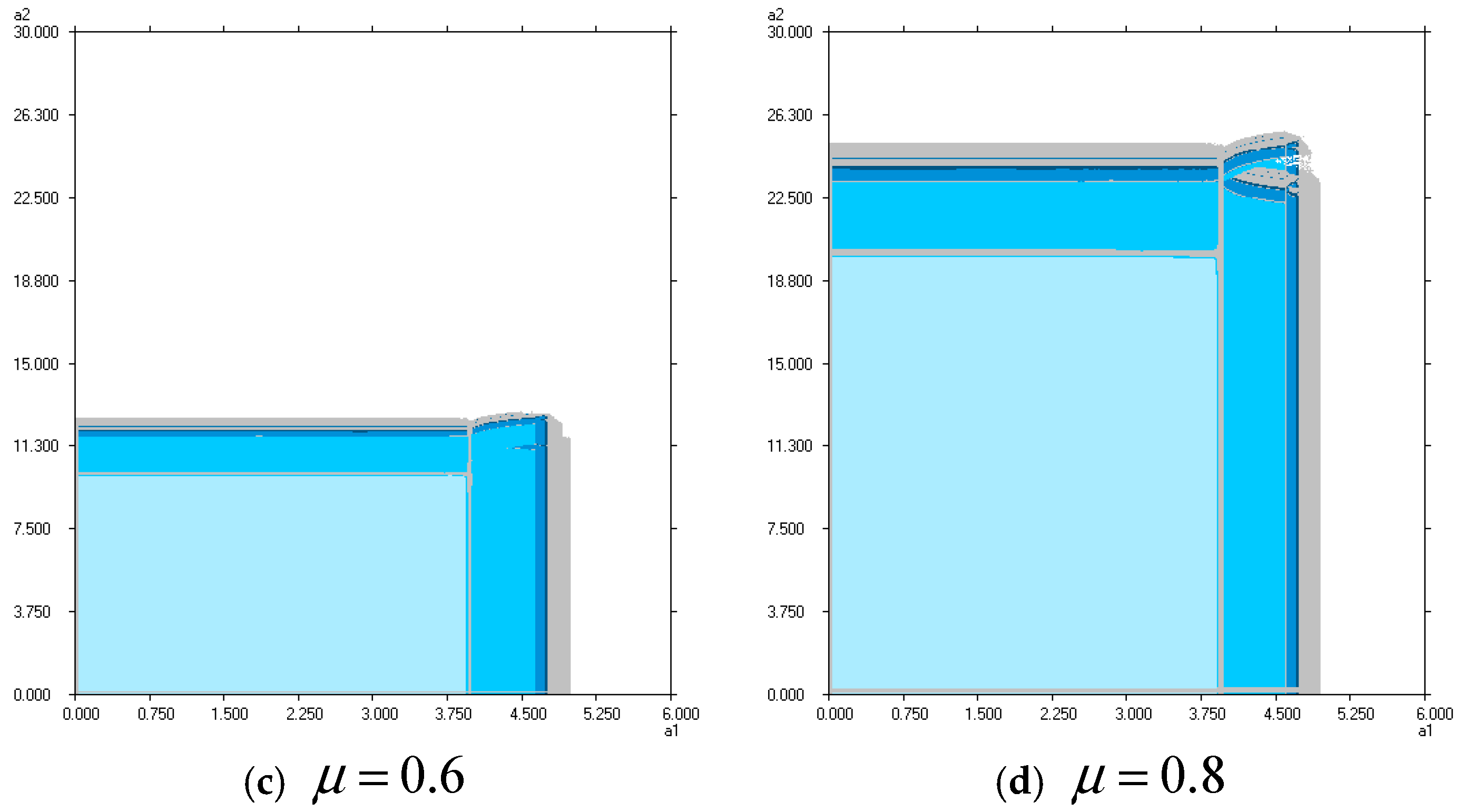
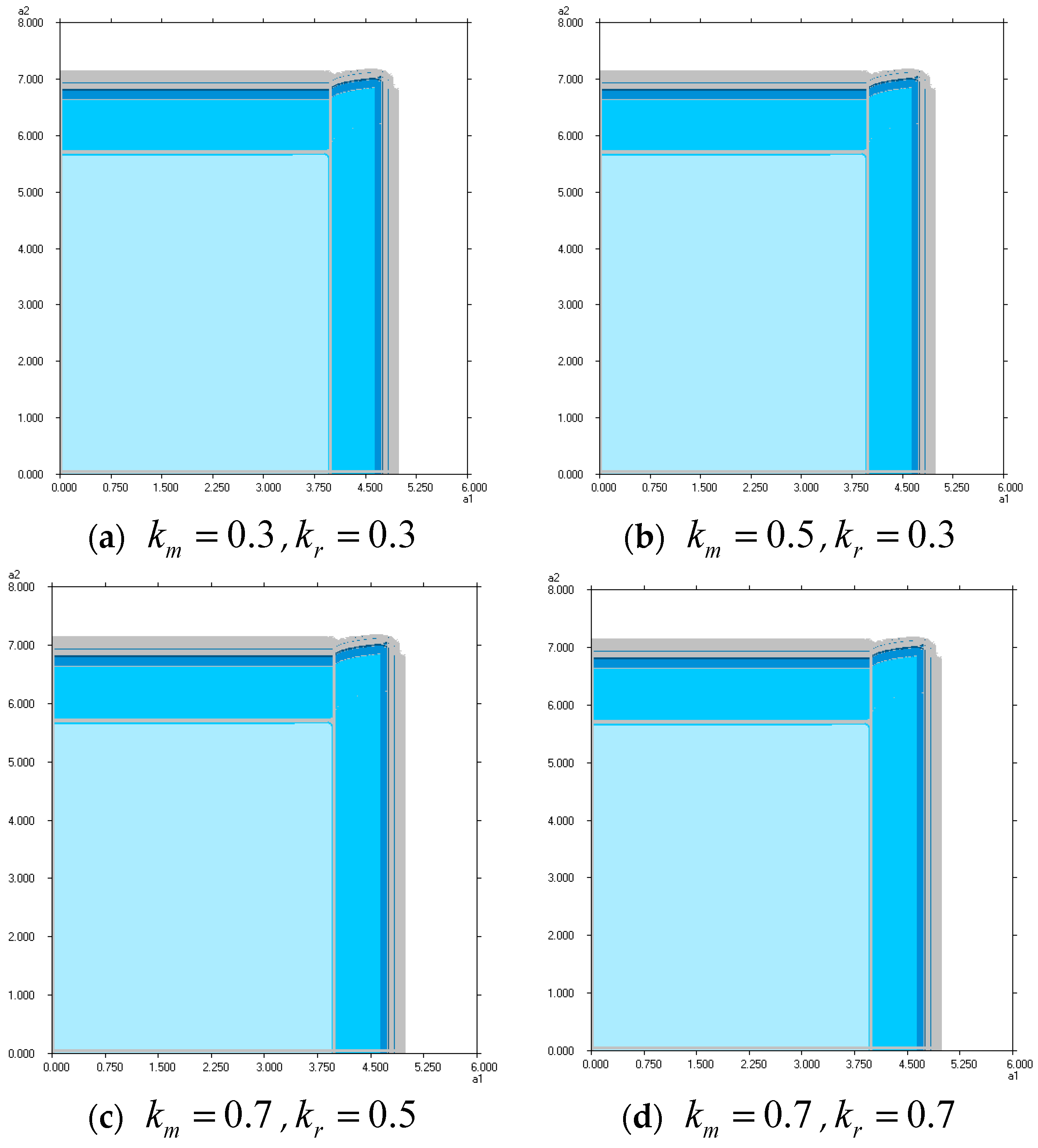
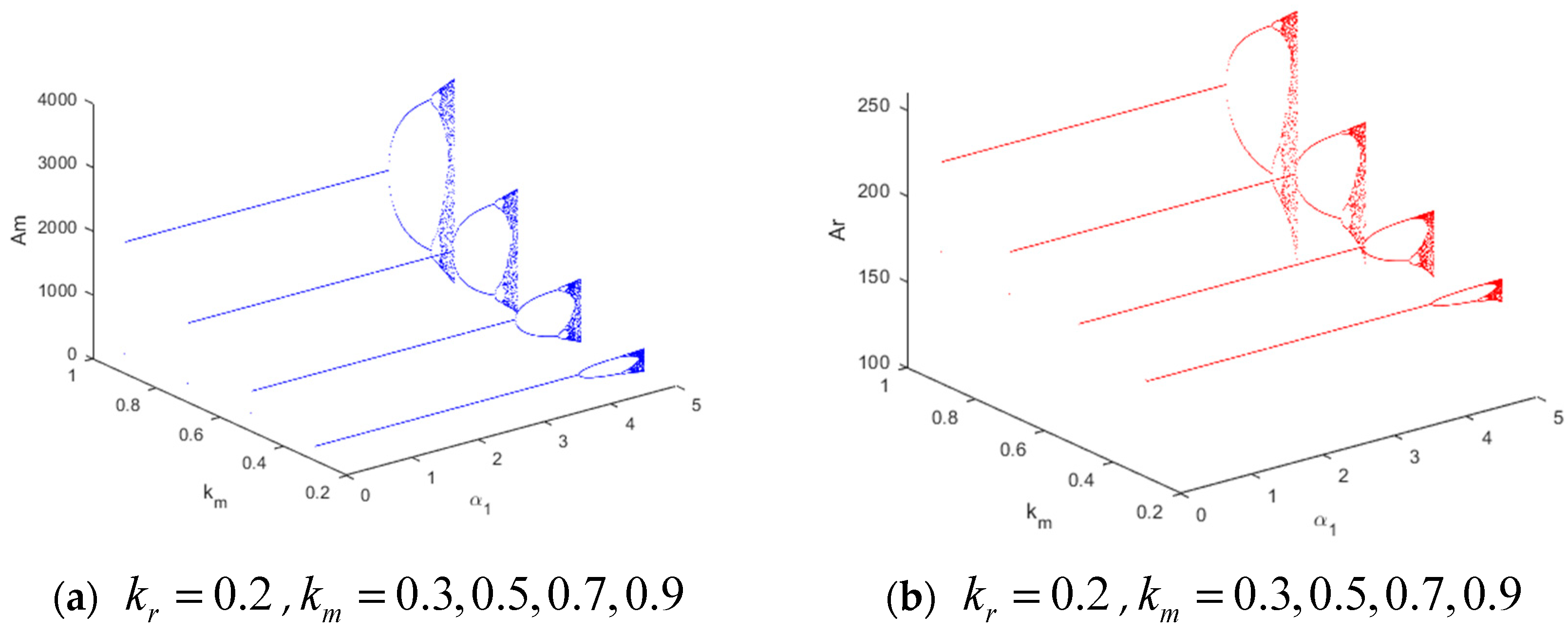
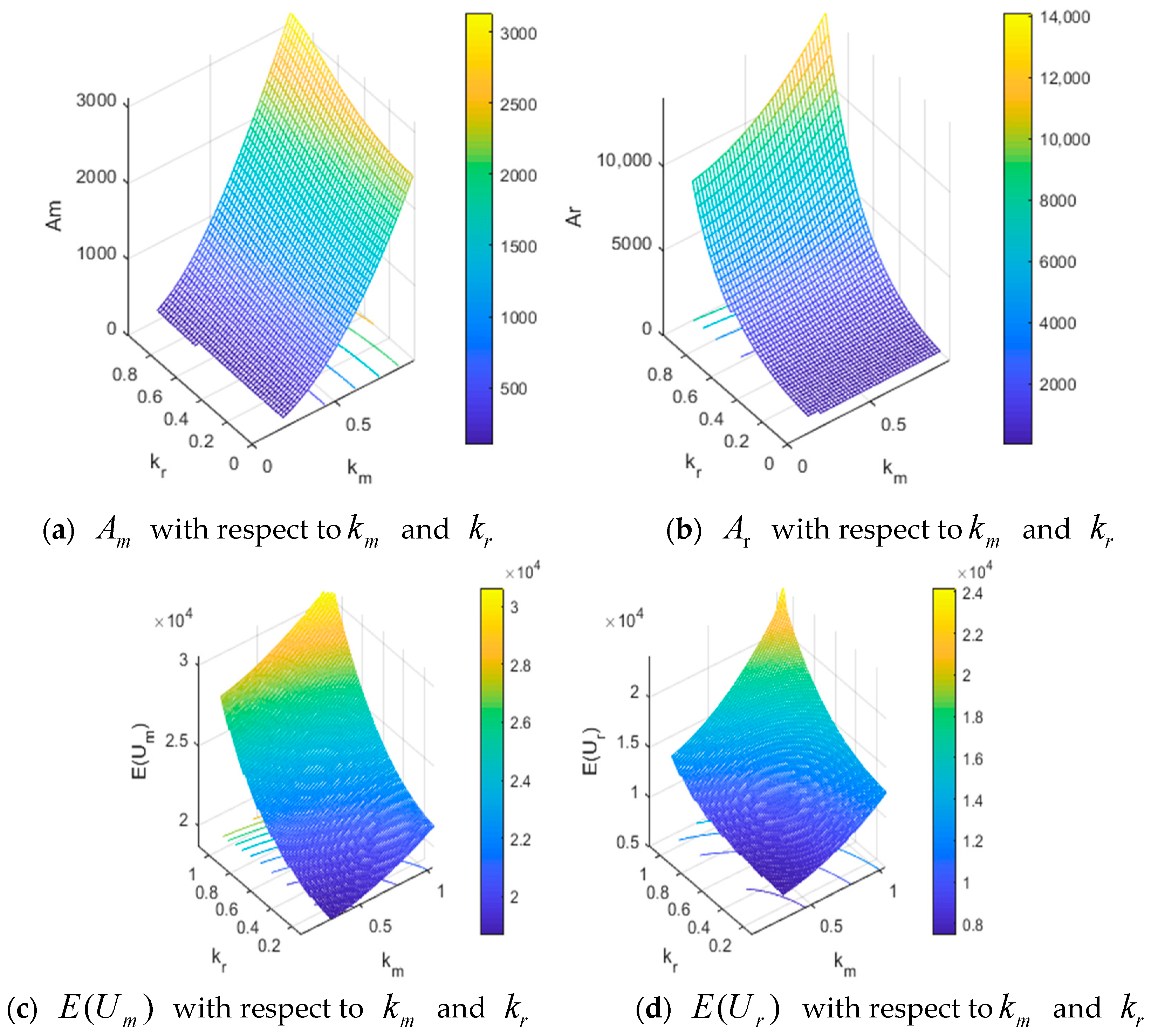
4.2. The Influence of the Manufacturer Participation Rate
4.3. The Influence of Risk Tolerance Levels and
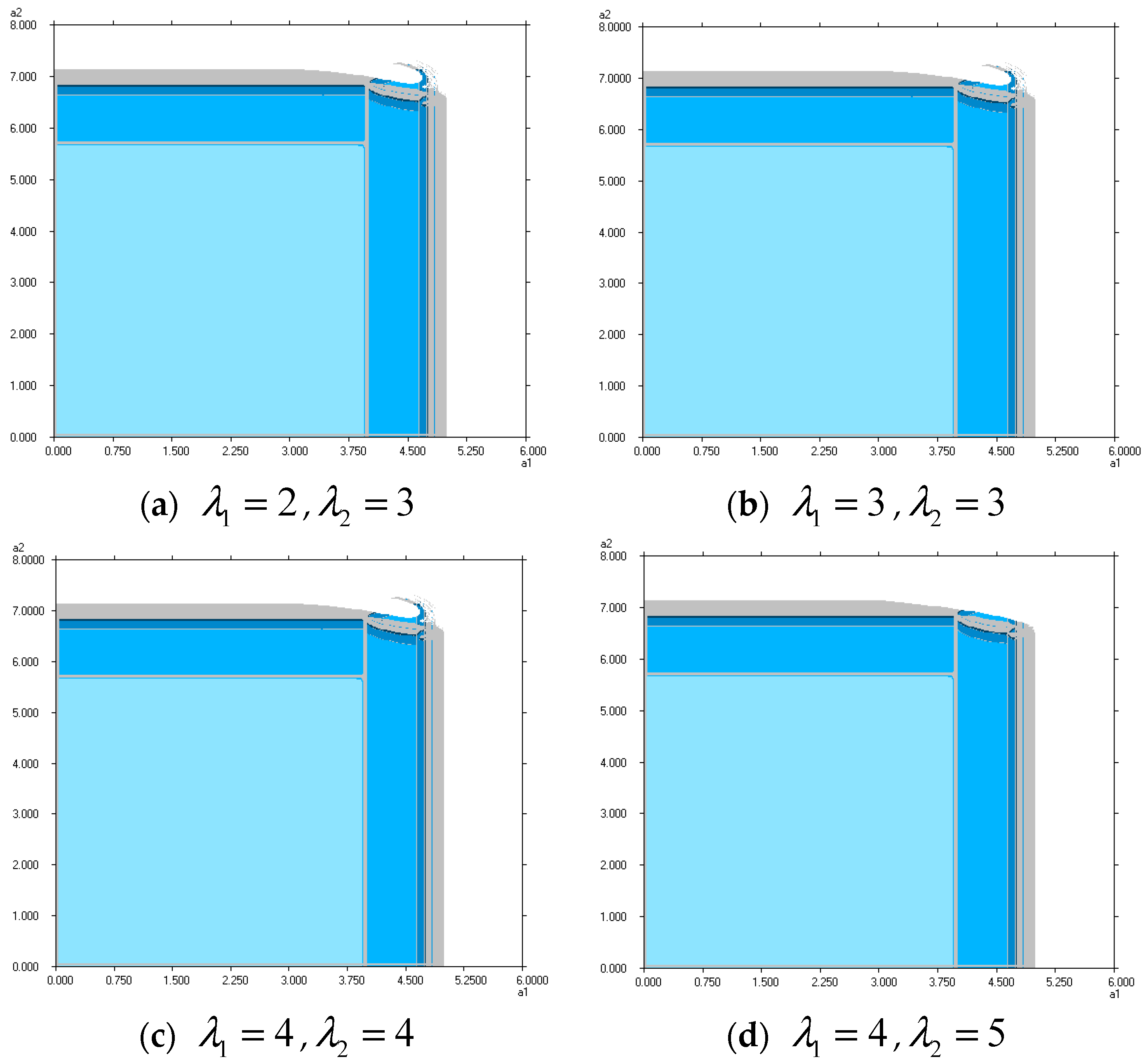
4.4. The Influence of Advertising Expenditure Effect Coefficients and
5. Chaos Control
6. Contribution and Implication
- (1)
- If the enterprises keep adjustment speeds within the stability region, no matter what initial advertising expenditures are chosen by the enterprises, the market will eventually reach the Nash equilibrium after a series of games. As a result, the enterprises can obtain optimal strategies. Otherwise, if the adjustment speeds of advertising expenditure are too fast, the system loses stability and enters chaotic states, which lead to a rapid decrease in expected utilities. The manufacturer and retailer will control their adjustment speeds to maintain the stability of the supply chain market for the maximum revenue.
- (2)
- The stability range of the system expands with an increase in the participation rate of local advertising expenditure by the manufacturer. As the manufacturer increases the participation rate of local advertising, the retailer spends more on local advertising expenditures. However, the national advertising expenditure of the manufacturer only has a slight downward adjustment with the increase in the participation rate. The expected utility of the manufacturer decreases, while the retailer increases slightly on the whole by an increase in the participation rate. For market stability and maximizing revenue, the manufacturer should adjust the participation rate appropriately, avoiding too high or too low values.
- (3)
- The stable region has no variation with risk tolerance levels of the manufacturer and retailer. The risk tolerance level of the manufacturer has no effect on the national advertising expenditure by the manufacturer and local advertising expenditure by the retailer. However, the manufacturer’s national advertising expenditure rises and the retailer’s local advertising expenditure reduces with an increase in the risk tolerance level of the retailer when the system is in a stable state. The expected utility of the manufacturer decreases and the expected utility of retailer remains unchanged with an increase in the risk tolerance level of the manufacturer. The expected utility of the manufacturer rises and the expected utility of the retailer decreases with an increase in the risk tolerance level of the retailer. Hence, the manufacturer will try to reduce their own risk tolerance level for economic revenue. In order to make neither too much advertising expenditure nor too little expected utility, the retailer will appropriately adjust the risk tolerance level to adapt to their own development according to their own enterprise strategy in the supply chain market competition.
- (4)
- With increasing effect coefficients of advertising expenditure, the stable region remains unchanged. The advertising expenditures and expected utilities rise with an increase in effect coefficients of advertising expenditure. The increase in its effect coefficient has a greater impact on its own advertising investment. In order to obtain more expected utilities and less advertising expenditures, both the manufacturer and retailer will reduce their own effect coefficients of advertising expenditure; meanwhile, they will attempt to increase their opponent’s effect coefficients to gain the most revenue.
- (5)
- It is profitable to keep the relevant factors in a certain range for manufacturer and retailer. Once the system falls into chaos, the chaos phenomenon can be delayed or eliminated effectively by the parameters control method.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berger, P.D. Vertical Cooperative Advertising Ventures. J. Mark. Res. 1972, 9, 309–312. [Google Scholar] [CrossRef]
- Fulop, C. The Role of Advertising in the Retail Marketing Mix. Int. J. Advert. 1988, 7, 99–117. [Google Scholar] [CrossRef]
- Bergen, M.; John, G. Understanding Cooperative Advertising Participation Rates in Conventional Channels. J. Mark. Res. 1997, 34, 357–369. [Google Scholar] [CrossRef]
- Zhang, J.; Gou, Q.; Liang, L.; Huang, Z. Supply chain coordination through cooperative advertising with reference price effect. Omega 2013, 41, 345–353. [Google Scholar] [CrossRef]
- Giri, B.C.; Sharma, S. Manufacturer’s pricing strategy in a two-level supply chain with competing retailers and advertising cost dependent demand. Econ. Model. 2014, 38, 102–111. [Google Scholar] [CrossRef]
- Stuart, A. Portfolio Selection: Efficient Diversification of Investment. OR 1959, 10, 253–254. [Google Scholar] [CrossRef]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investments; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Eeckhoudt, L.; Gollier, C.; Schlesinger, H. The Risk-Averse (and Prudent) Newsboy. Manag. Sci. 1995, 41, 786–794. [Google Scholar] [CrossRef]
- Martínez-de-Albéniz, V.; Simchi-Levi, D. Mean-variance trade-offs in supply contracts. Nav. Res. Logist. 2006, 53, 603–616. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, H.; Liu, W.; Song, S.; Liao, Y. Supply Chain Coordination with a Risk-Averse Retailer and the Call Option Contract in the Presence of a Service Requirement. Mathematics 2021, 9, 787. [Google Scholar] [CrossRef]
- Marshall Fisher, A.R. Reducing the Cost of Demand Uncertainty Through Accurate Response to Early Sales. Oper. Res. 1996, 44, 87–99. [Google Scholar] [CrossRef]
- Anupindi, R.; Bassok, Y. Centralization of stocks: Retailers vs. manufacturer. Manag. Sci. 1999, 45, 178–191. [Google Scholar] [CrossRef]
- Gan, X.; Sethi, S.P.; Yan, H. Channel Coordination with a Risk-Neutral Supplier and a Downside-Risk-Averse Retailer. Prod. Oper. Manag. 2005, 14, 80–89. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef]
- Gao, T.; Wang, K.; Mei, Y.; He, S.; Wang, Y. Supply Chain Pricing Models Considering Risk Attitudes under Free-Riding Behavior. Mathematics 2022, 10, 1723. [Google Scholar] [CrossRef]
- Choi, T.-M.; Ma, C.; Shen, B.; Sun, Q. Optimal pricing in mass customization supply chains with risk-averse agents and retail competition. Omega 2019, 88, 150–161. [Google Scholar] [CrossRef]
- Xiao, T.; Yang, D. Price and service competition of supply chains with risk-averse retailers under demand uncertainty. Int. J. Prod. Econ. 2008, 114, 187–200. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J. Coordination of the traditional and the online channels for a short-life-cycle product. Eur. J. Oper. Res. 2017, 258, 639–651. [Google Scholar] [CrossRef]
- Ma, J.; Wang, H. Complexity analysis of dynamic noncooperative game models for closed-loop supply chain with product recovery. Appl. Math. Model. 2014, 38, 5562–5572. [Google Scholar] [CrossRef]
- Liu, J.; Liu, G.; Li, N.; Xu, H. Dynamics Analysis of Game and Chaotic Control in the Chinese Fixed Broadband Telecom Market. Discret. Dyn. Nat. Soc. 2014, 2014, 275123. [Google Scholar] [CrossRef]
- Askar, S.S.; Al-Khedhairi, A. Local and Global Dynamics of a Constraint Profit Maximization for Bischi–Naimzada Competition Duopoly Game. Mathematics 2020, 8, 1458. [Google Scholar] [CrossRef]
- Askar, S.S. The Influences of Asymmetric Market Information on the Dynamics of Duopoly Game. Mathematics 2020, 8, 1132. [Google Scholar] [CrossRef]
- Sun, L.; Ma, J. Study and Simulation on Dynamics of a Risk-Averse Supply Chain Pricing Model with Dual-Channel and Incomplete Information. Int. J. Bifurc. Chaos 2016, 26, 1650146. [Google Scholar] [CrossRef]
- Berger, P.D.; Magliozzi, T. Optimal Co-Operative Advertising Decisions in Direct-Mail Operations. J. Oper. Res. Soc. 1992, 43, 1079–1086. [Google Scholar] [CrossRef]
- Dant, R.P.; Berger, P.D. Modelling Cooperative Advertising Decisions in Franchising. J. Oper. Res. Soc. 1996, 47, 1120–1136. [Google Scholar] [CrossRef]
- Karray, S.; Zaccour, G. Could co-op advertising be a manufacturer’s counterstrategy to store brands? J. Bus. Res. 2006, 59, 1008–1015. [Google Scholar] [CrossRef]
- Xie, J.; Wei, J.C. Coordinating advertising and pricing in a manufacturer–retailer channel. Eur. J. Oper. Res. 2009, 197, 785–791. [Google Scholar] [CrossRef]
- Sarkar, B.; Omair, M.; Kim, N. A cooperative advertising collaboration policy in supply chain management under uncertain conditions. Appl. Soft Comput. 2020, 88, 105948. [Google Scholar] [CrossRef]
- Xiao, D.; Zhou, Y.-W.; Zhong, Y.; Xie, W. Optimal cooperative advertising and ordering policies for a two-echelon supply chain. Comput. Ind. Eng. 2019, 127, 511–519. [Google Scholar] [CrossRef]
- Agrawal, V.; Seshadri, S. Impact of Uncertainty and Risk Aversion on Price and Order Quantity in the Newsvendor Problem. Manuf. Serv. Oper. Manag. 2000, 2, 410–423. [Google Scholar] [CrossRef]
- Xu, G.; Dan, B.; Zhang, X.; Liu, C. Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract. Int. J. Prod. Econ. 2014, 147, 171–179. [Google Scholar] [CrossRef]
- Yan, B.; Jin, Z.; Liu, Y.; Yang, J. Decision on risk-averse dual-channel supply chain under demand disruption. Commun. Nonlinear Sci. Numer. Simul. 2018, 55, 206–224. [Google Scholar] [CrossRef]
- Zhou, Y.-W.; Li, J.; Zhong, Y. Cooperative advertising and ordering policies in a two-echelon supply chain with risk-averse agents. Omega 2018, 75, 97–117. [Google Scholar] [CrossRef]
- Karray, S.; Amin, S.H. Cooperative advertising in a supply chain with retail competition. Int. J. Prod. Res. 2014, 53, 88–105. [Google Scholar] [CrossRef]
- Ma, J.; Ren, H.; Yu, M.; Zhu, M. Research on the Complexity and Chaos Control about a Closed-Loop Supply Chain with Dual-Channel Recycling and Uncertain Consumer Perception. Complexity 2018, 2018, 9853635. [Google Scholar] [CrossRef]
- Ma, J.; Hong, Y. Dynamic game analysis on pricing and service strategy in a retailer-led supply chain with risk attitudes and free-ride effect. Kybernetes 2021, 51, 1199–1230. [Google Scholar] [CrossRef]
- Khademi, M.; Ferrara, M.; Pansera, B.; Salimi, M. A dynamic game on Green Supply Chain Management. arXiv 2015, arXiv:1503.04772. [Google Scholar]
- Ma, J.; Tian, Y.; Xu, T.; Koivumäki, T.; Xu, Y. Dynamic game study of multi-channel supply chain under cap-and-trade regulation. Chaos Solitons Fractals 2022, 160, 112131. [Google Scholar] [CrossRef]
- Karray, S. Periodicity of pricing and marketing efforts in a distribution channel. Eur. J. Oper. Res. 2013, 228, 635–647. [Google Scholar] [CrossRef]
- Xie, G.; Yue, W.; Wang, S.; Lai, K.K. Quality investment and price decision in a risk-averse supply chain. Eur. J. Oper. Res. 2011, 214, 403–410. [Google Scholar] [CrossRef]
- Walls, M.R. Combining decision analysis and portfolio management to improve project selection in the exploration and production firm. J. Pet. Sci. Eng. 2004, 44, 55–65. [Google Scholar] [CrossRef]
- Avinadav, T.; Chernonog, T.; Perlman, Y. Mergers and acquisitions between risk-averse parties. Eur. J. Oper. Res. 2017, 259, 926–934. [Google Scholar] [CrossRef]
- Choi, T.-M.; Li, D.; Yan, H. Mean–variance analysis of a single supplier and retailer supply chain under a returns policy. Eur. J. Oper. Res. 2008, 184, 356–376. [Google Scholar] [CrossRef]
- Guo, Z.; Ma, J. Dynamics and implications on a cooperative advertising model in the supply chain. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 198–212. [Google Scholar] [CrossRef]
- Li, T.; Ma, J. Complexity analysis of dual-channel game model with different managers’ business objectives. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 199–208. [Google Scholar] [CrossRef]
- Ma, J.; Li, Q.; Bao, B. Study on Complex Advertising and Price Competition Dual-Channel Supply Chain Models Considering the Overconfidence Manufacturer. Math. Probl. Eng. 2016, 2016, 2027146. [Google Scholar] [CrossRef]
- Ma, J.; Guo, Z. The influence of information on the stability of a dynamic Bertrand game. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 32–44. [Google Scholar] [CrossRef]
- Xi, X.; Zhang, Y. Complexity analysis of production, fertilizer-saving level, and emission reduction efforts decisions in a two-parallel agricultural product supply chain. Chaos Solitons Fractals 2021, 152, 111358. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, J.; Xie, L.; Koivumäki, T.; Seppänen, V. Coordination and control of multi-channel supply chain driven by consumers’ channel preference and sales effort. Chaos Solitons Fractals 2020, 132, 109576. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, J. The complexity analysis and chaos control in omni-channel supply chain with consumer migration and advertising cost sharing. Chaos Solitons Fractals 2021, 146, 110884. [Google Scholar] [CrossRef]



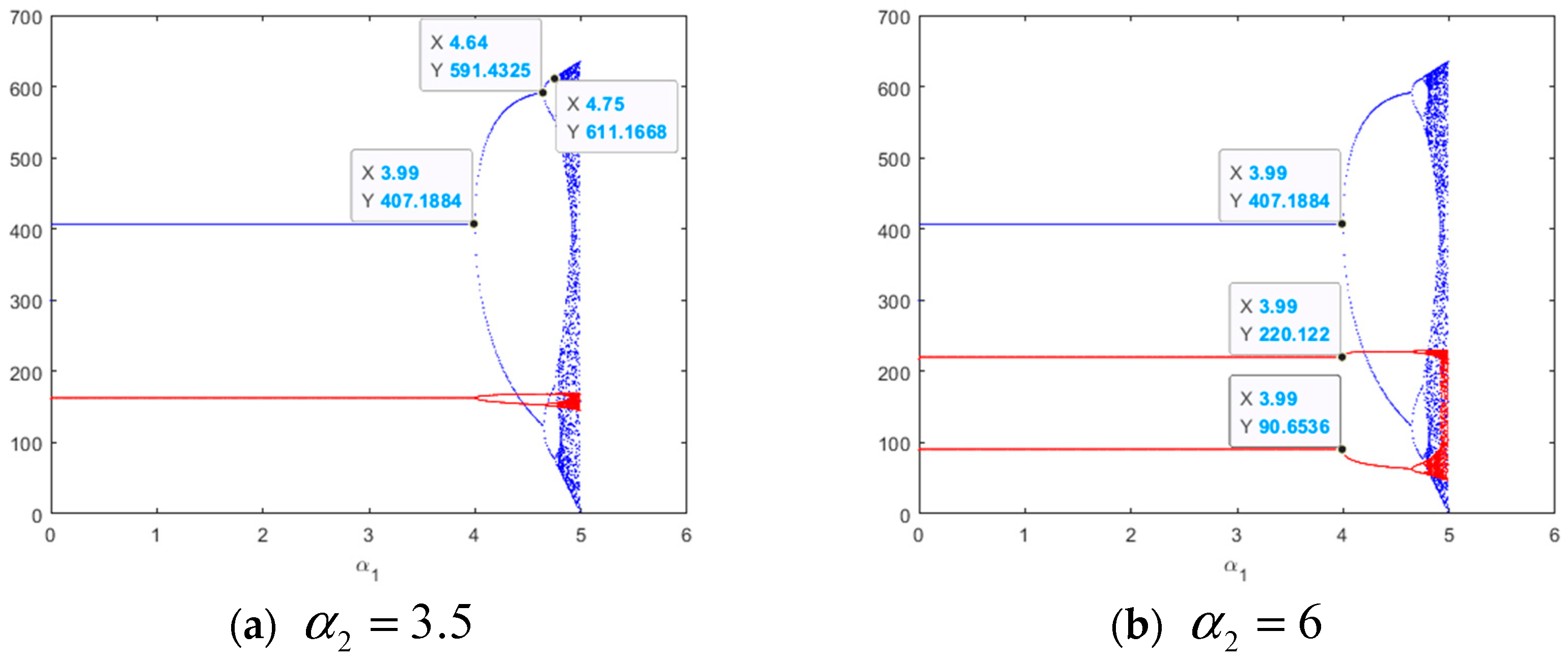
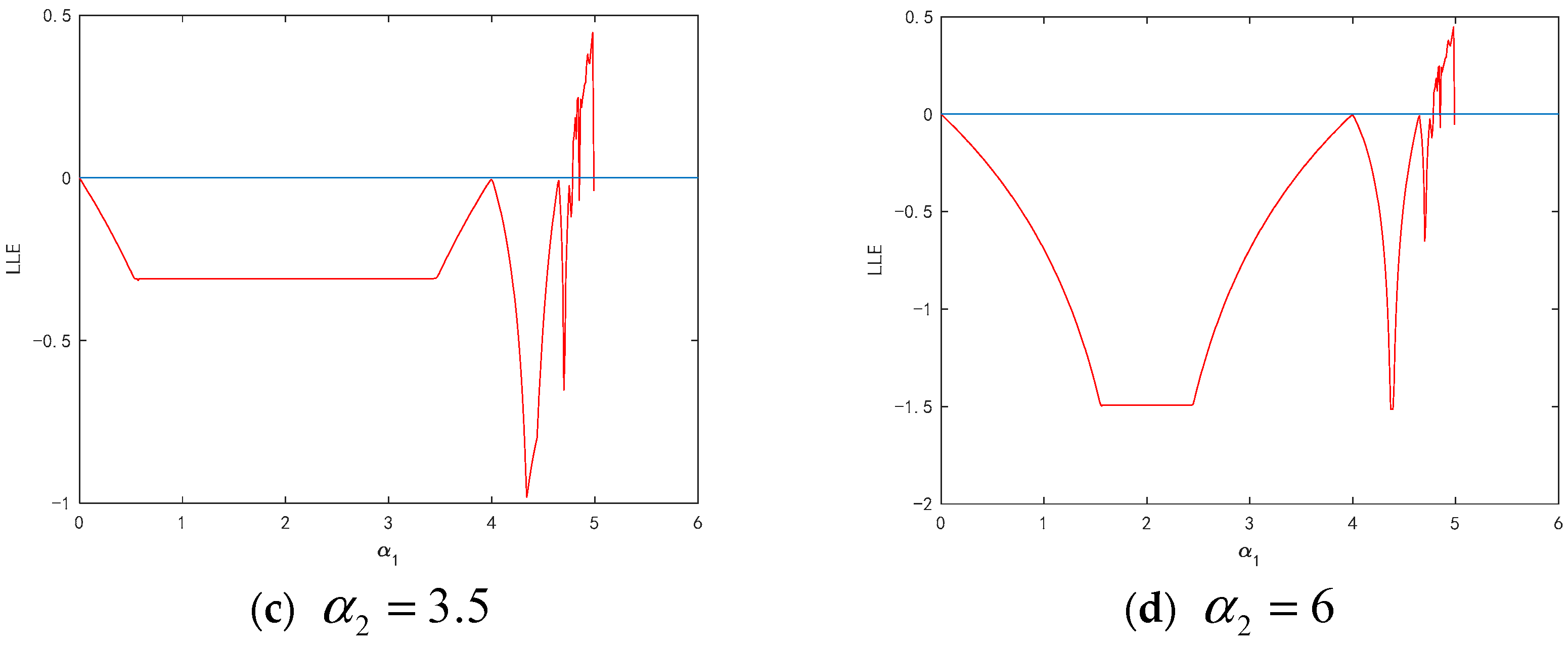
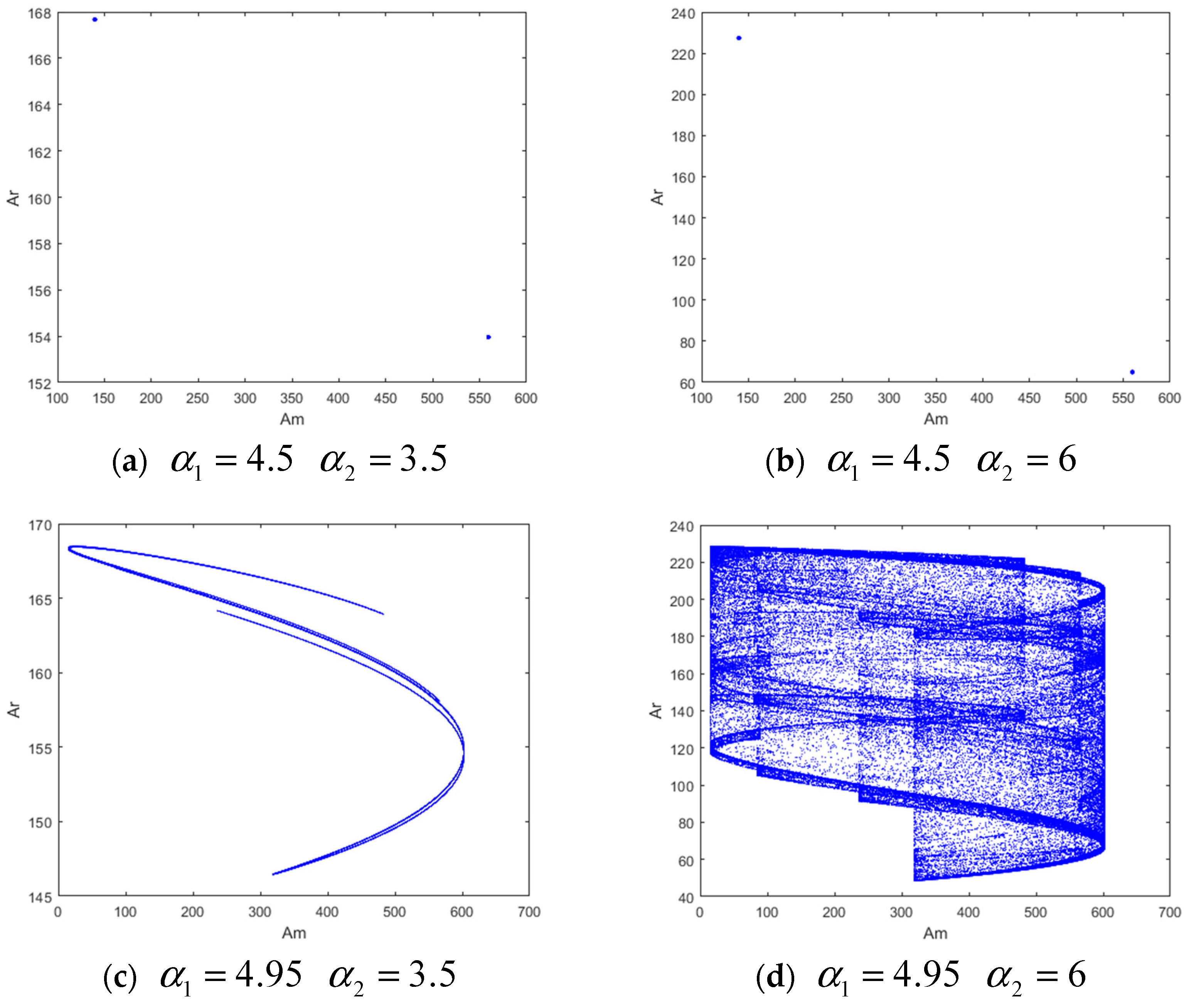
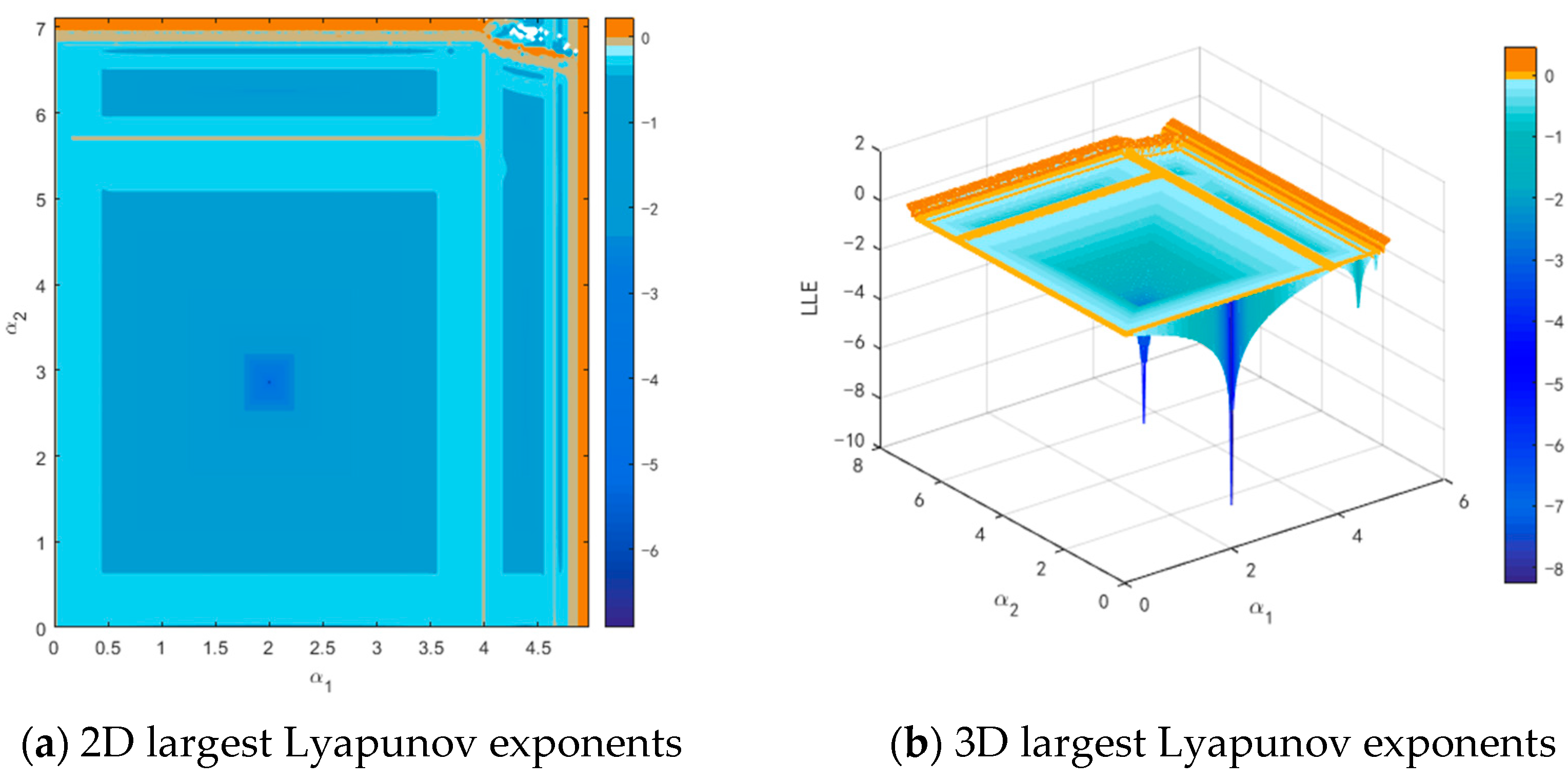






| Notation | Explanation |
|---|---|
| Price of retailer, | |
| Baseline demand, | |
| National advertising expenditure of manufacturer, | |
| Local advertising expenditure of retailer, | |
| Effect coefficient of national advertising expenditure, | |
| Effect coefficient of local advertising expenditure, | |
| Wholesale price (manufacturer’s price to the retailers) | |
| Manufacturer participation rate in percentage, | |
| Adjustment speed of manufacturer advertising expenditure, | |
| Adjustment speed of retailer advertising expenditure, | |
| Risk tolerance level of manufacturer, | |
| Risk tolerance level of retailer, |
| (406.8, 193.7) (19,020, 9356) | (406.8, 193.7) (17,420, 9356) | (406.8, 193.7) (15,820, 9356) | (406.8, 193.7) (14,220, 9356) | (406.8, 193.7) (12,620, 9356) | |
| (407, 177.9) (19,810, 8593) | (407, 177.9) (18,210, 8593) | (407, 177.9) (16,610, 8593) | (407, 177.9) (15,010, 8593) | (407, 177.9) (13,410, 8593) | |
| (407.2, 162.8) (20,610, 7863) | (407.2, 162.8) (19,010, 7863) | (407.2, 162.8) (17,401, 7863) | (407.2, 162.8) (15,810, 7863) | (407.2, 162.8) (14,210, 7863) | |
| (407.4, 148.3) (21,400, 7165) | (407.4, 148.3) (19,800, 7165) | (407.4, 148.3) (18,200, 7165) | (407.4, 148.3) (16,600, 7165) | (407.4, 148.3) (15,000, 7165) | |
| (407.6, 134.6) (22,190, 6499) | (407.6, 134.6) (20,590, 6499) | (407.6, 134.6) (18,990, 6499) | (407.6, 134.6) (17,390, 6499) | (407.6, 134.6) (15,790, 6499) |
| (234.3, 365) (19,090, 7694) | (650.1, 400.4) (19,500, 8439) | (1272, 456.3) (20,130, 9618) | (2098, 536.4) (20,960, 11,310) | |
| (251.9, 1148) (19,970, 8193) | (697.3, 1262) (20,420, 9013) | (1359, 1444) (21,090, 10,310) | (2230, 1704) (21,970, 12,160) | |
| (280.6, 2749) (21,470, 9072) | (772.7, 3038) (21,960, 10,030) | (1459, 3494) (22,700, 11,530) | (2429, 4141) (23,670, 13,660) | |
| (320.9, 6148) (23,830, 10,570) | (874.3, 6834) (24,390, 11,750) | (1665, 7903) (25,220, 13,590) | (2650, 9396) (26,290, 16,160) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, C. Dynamic Game Analysis on Cooperative Advertising Strategy in a Manufacturer-Led Supply Chain with Risk Aversion. Mathematics 2023, 11, 512. https://doi.org/10.3390/math11030512
Liu J, Li C. Dynamic Game Analysis on Cooperative Advertising Strategy in a Manufacturer-Led Supply Chain with Risk Aversion. Mathematics. 2023; 11(3):512. https://doi.org/10.3390/math11030512
Chicago/Turabian StyleLiu, Jia, and Cuixia Li. 2023. "Dynamic Game Analysis on Cooperative Advertising Strategy in a Manufacturer-Led Supply Chain with Risk Aversion" Mathematics 11, no. 3: 512. https://doi.org/10.3390/math11030512
APA StyleLiu, J., & Li, C. (2023). Dynamic Game Analysis on Cooperative Advertising Strategy in a Manufacturer-Led Supply Chain with Risk Aversion. Mathematics, 11(3), 512. https://doi.org/10.3390/math11030512





