Deep Learning Method Based on Physics-Informed Neural Network for 3D Anisotropic Steady-State Heat Conduction Problems
Abstract
:1. Introduction
2. Equations of 3D Anisotropic Steady-State Heat Conduction Problems
3. The PINN for 3D Anisotropic Steady-State Heat Conduction Problem
| Algorithm 1 Algorithmic Procedure | |
| Input: Internal training data, (xi); boundary training data, (xj); | |
| Output: Prediction of DNN, ; | |
| 1: | Initialize the parameters of DNN; |
| 2: | Define the loss function: loss = lossf + lossb; |
| 3: | for epoch = 1:numEpochs |
| 4: | U1 = ξ (xi; θ), ξ (xj; θ); |
| 5: | compute loss; |
| 6: | obtain gradients by automatic differential; |
| 7: | minimize the loss by Adam method; |
| 8: | end; |
| 9: | Obtain the prediction U = ξ (xk; θ); |
| 10: | return U. |
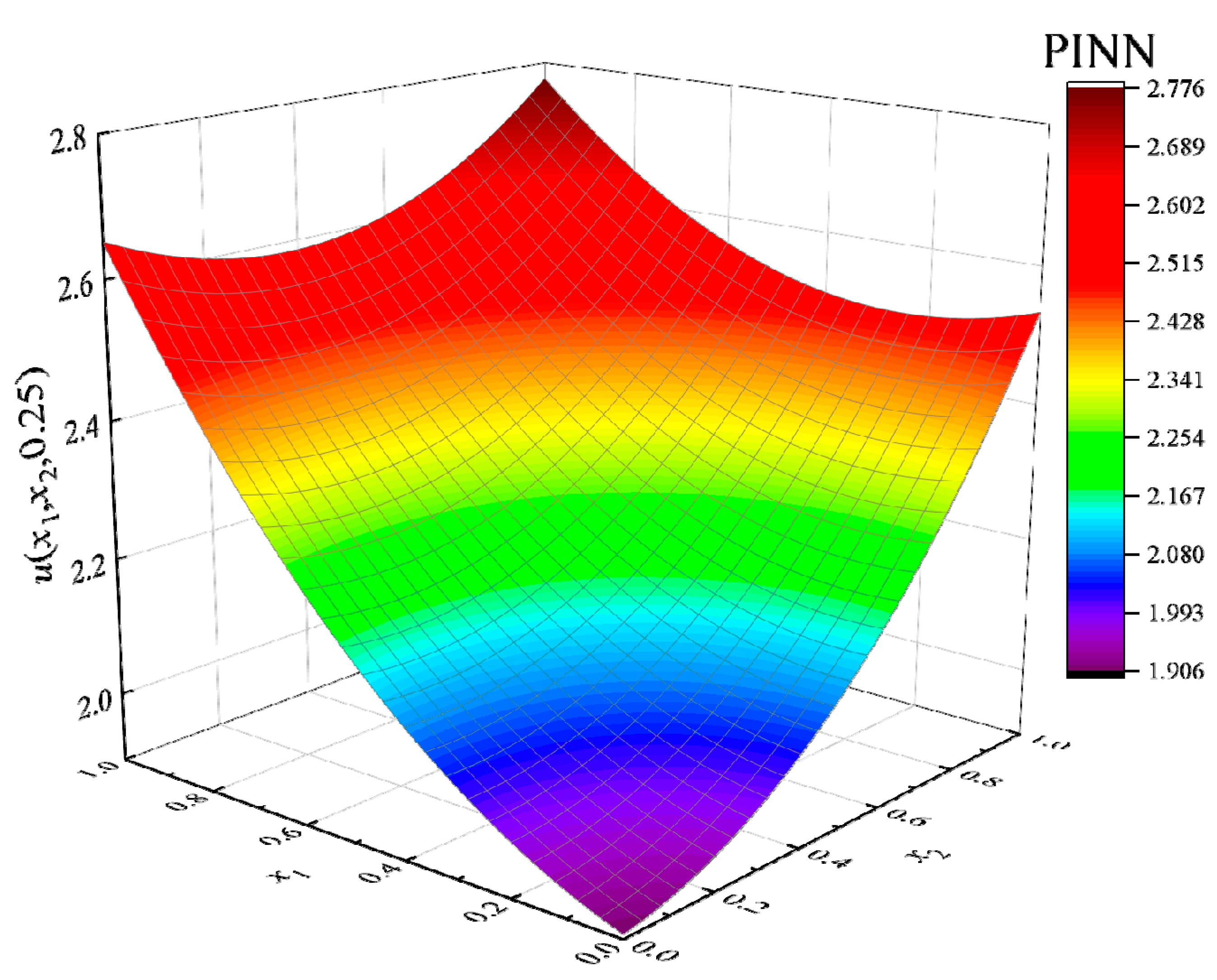
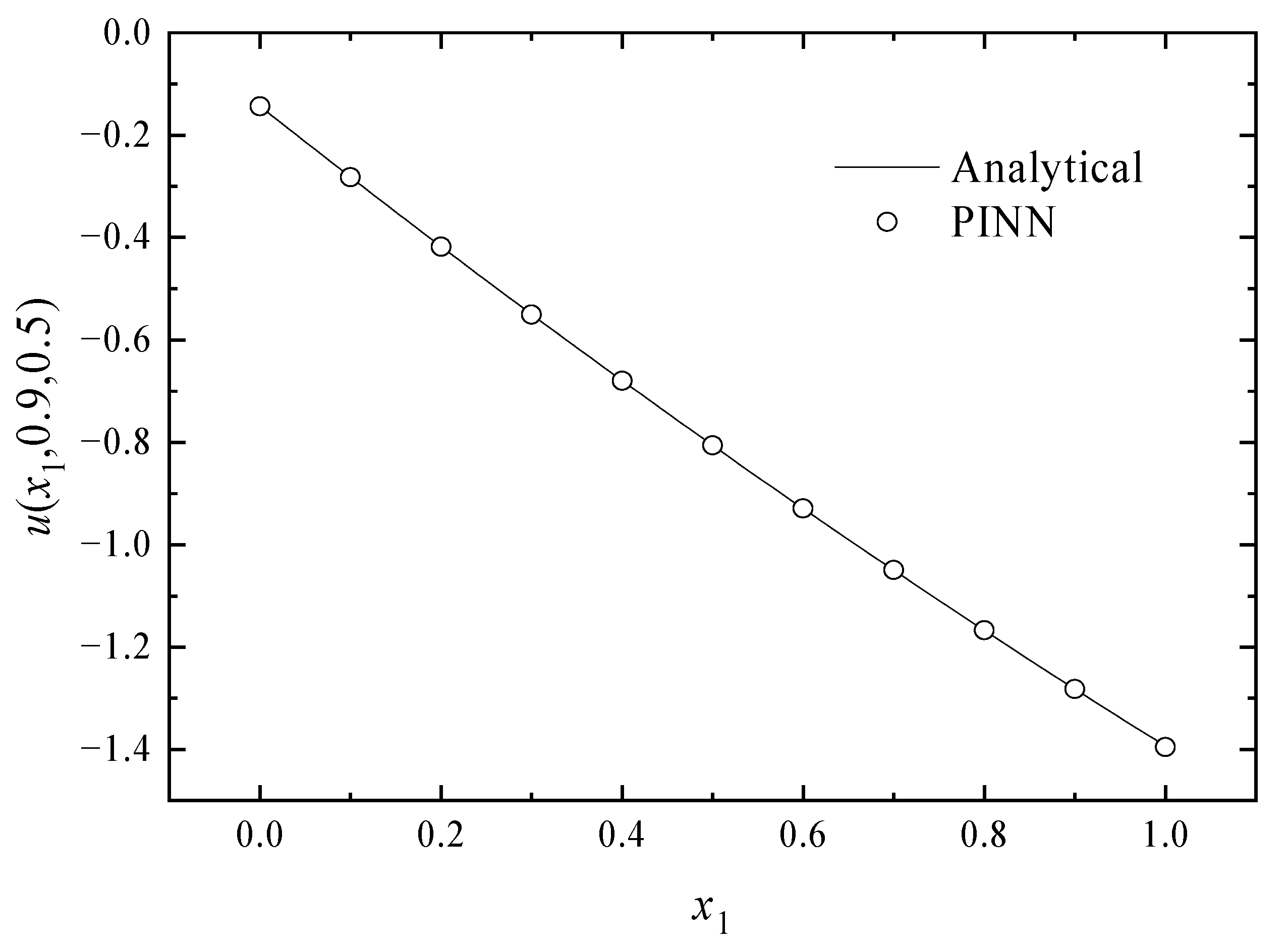
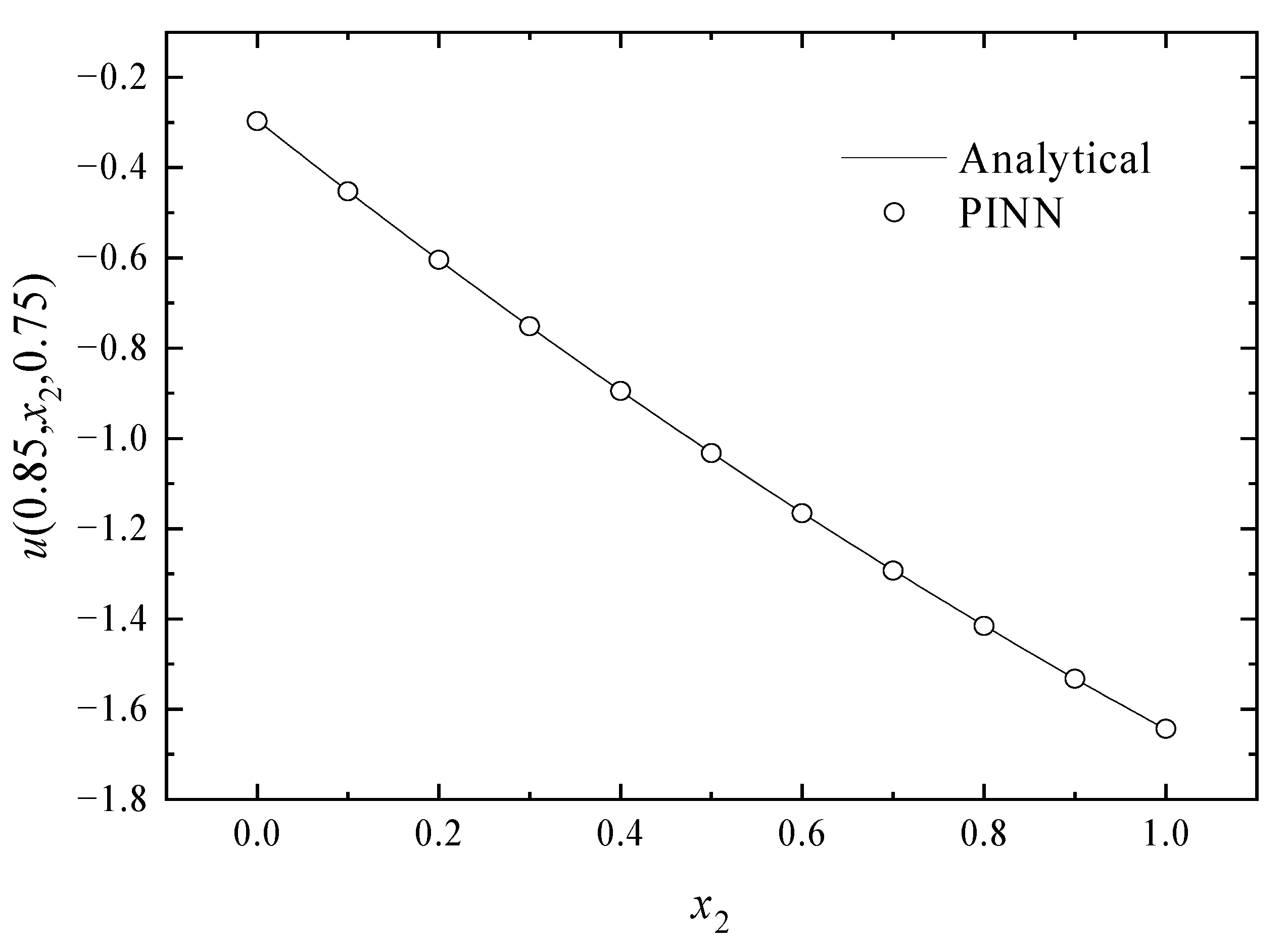
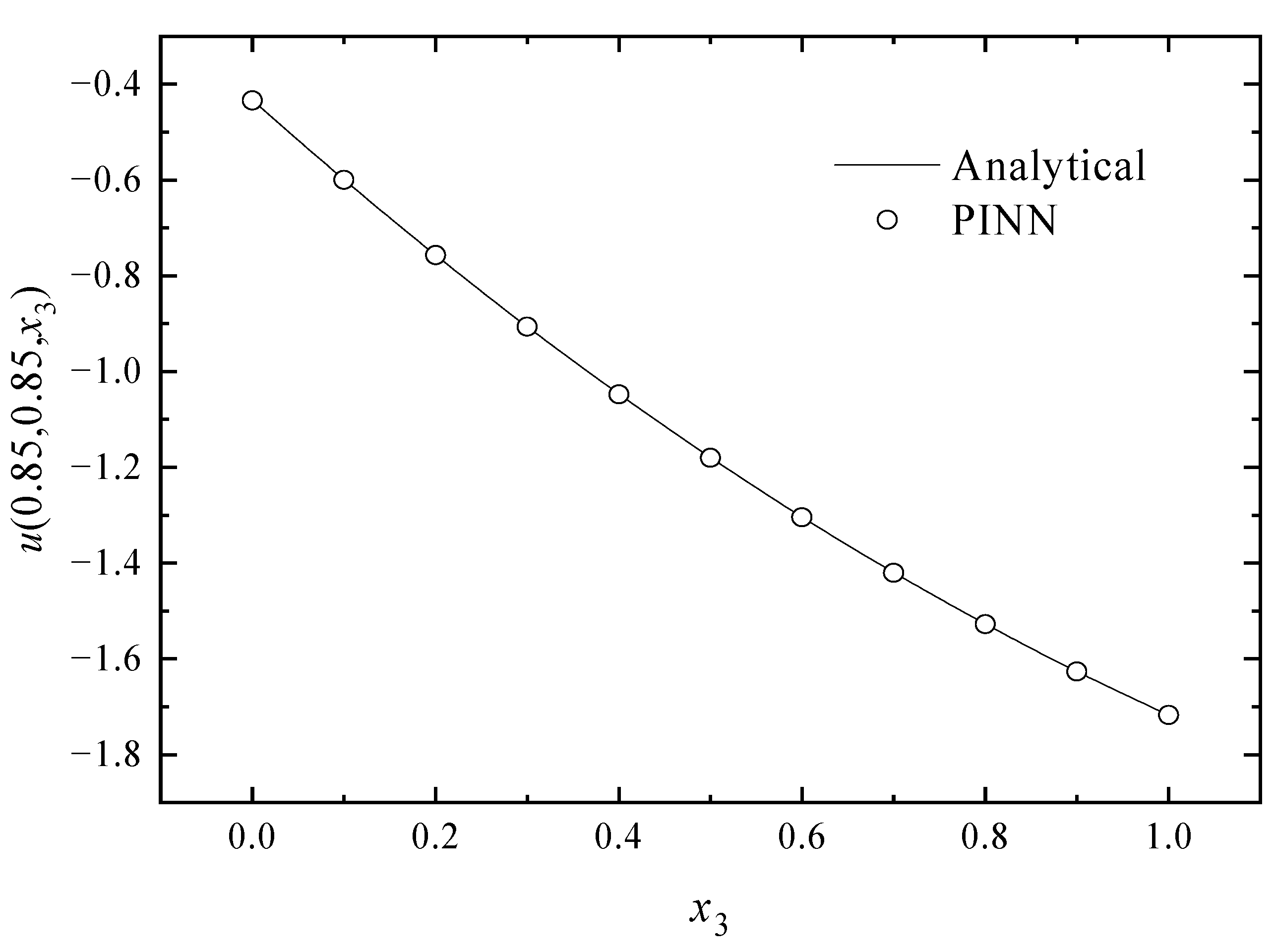
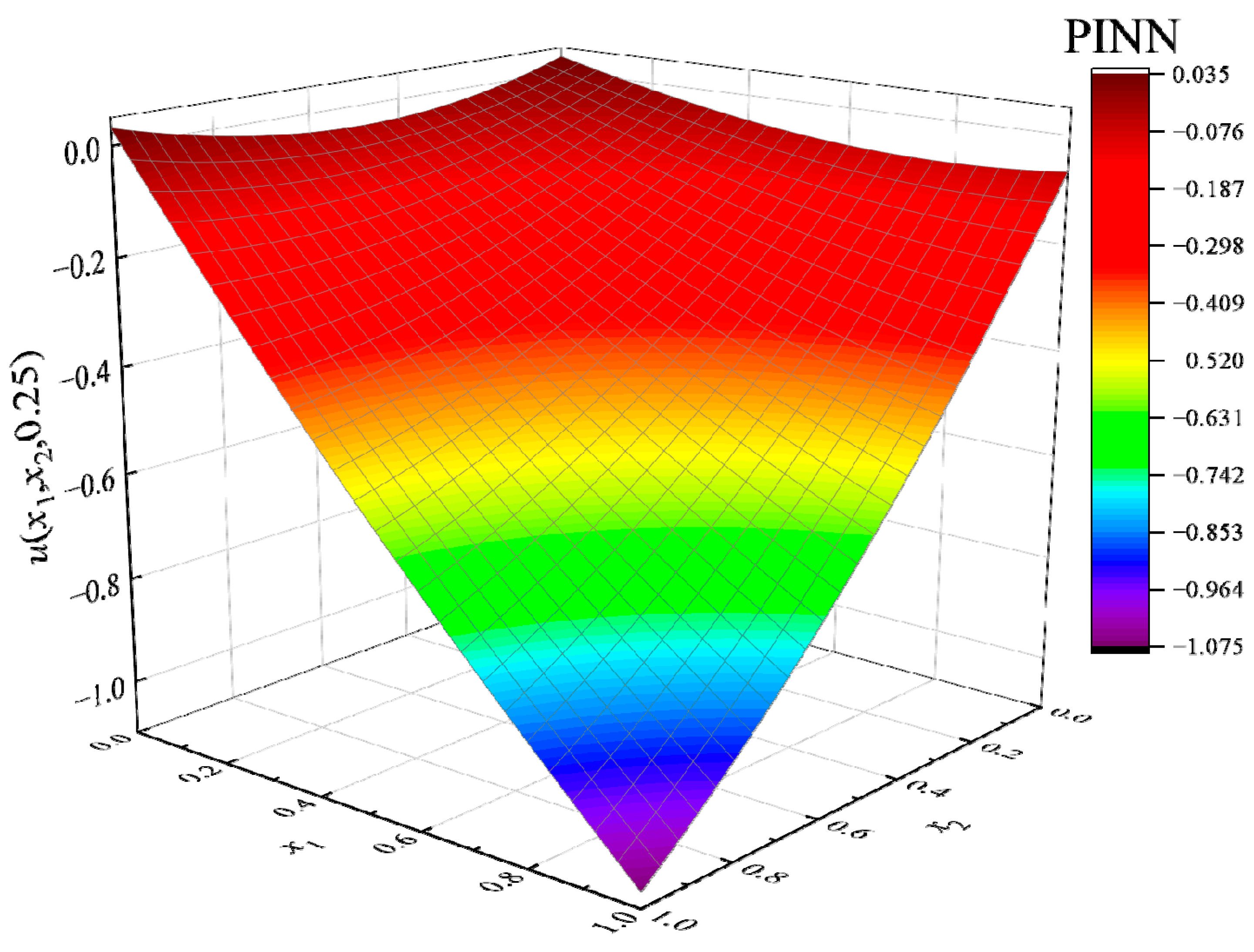
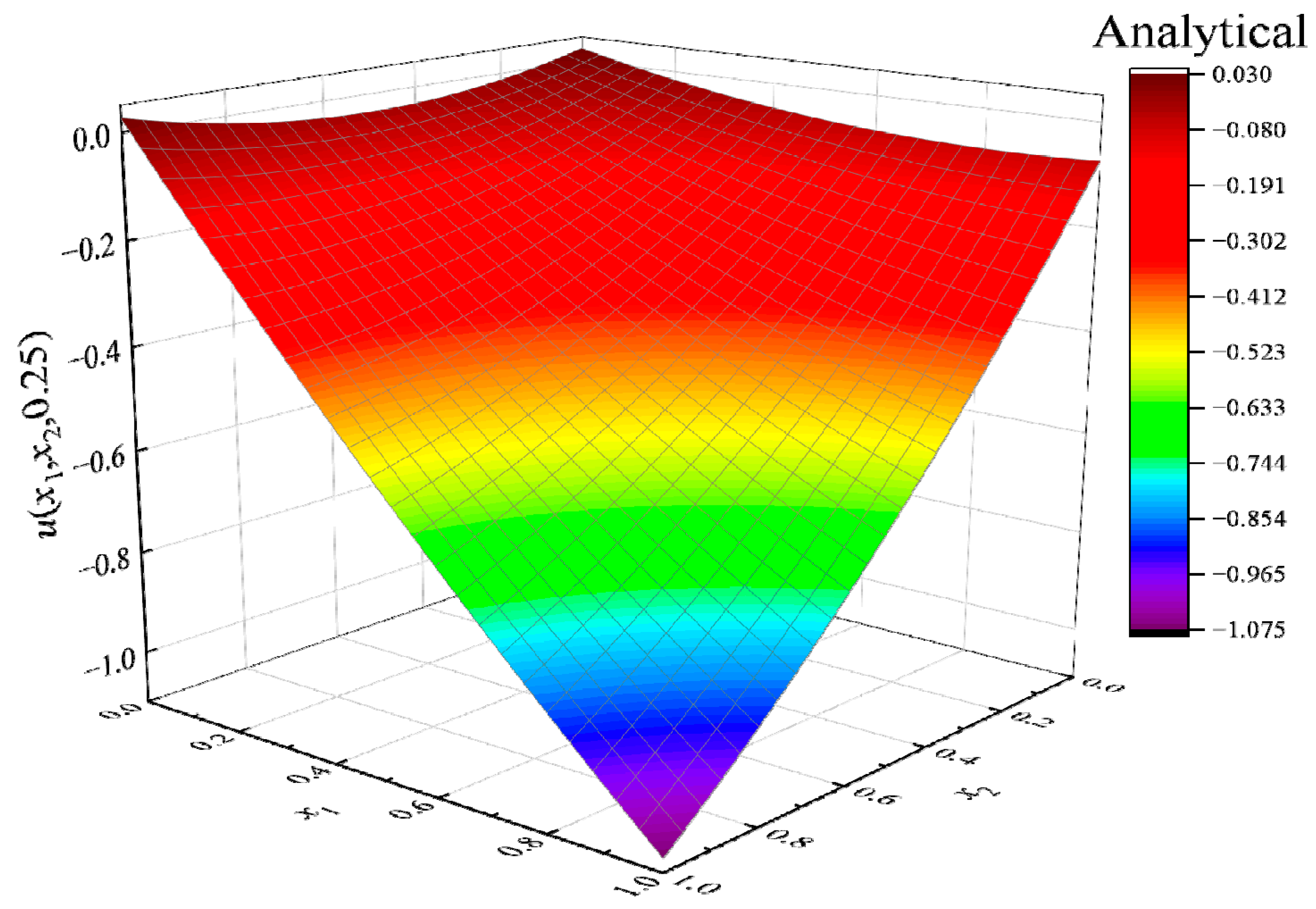
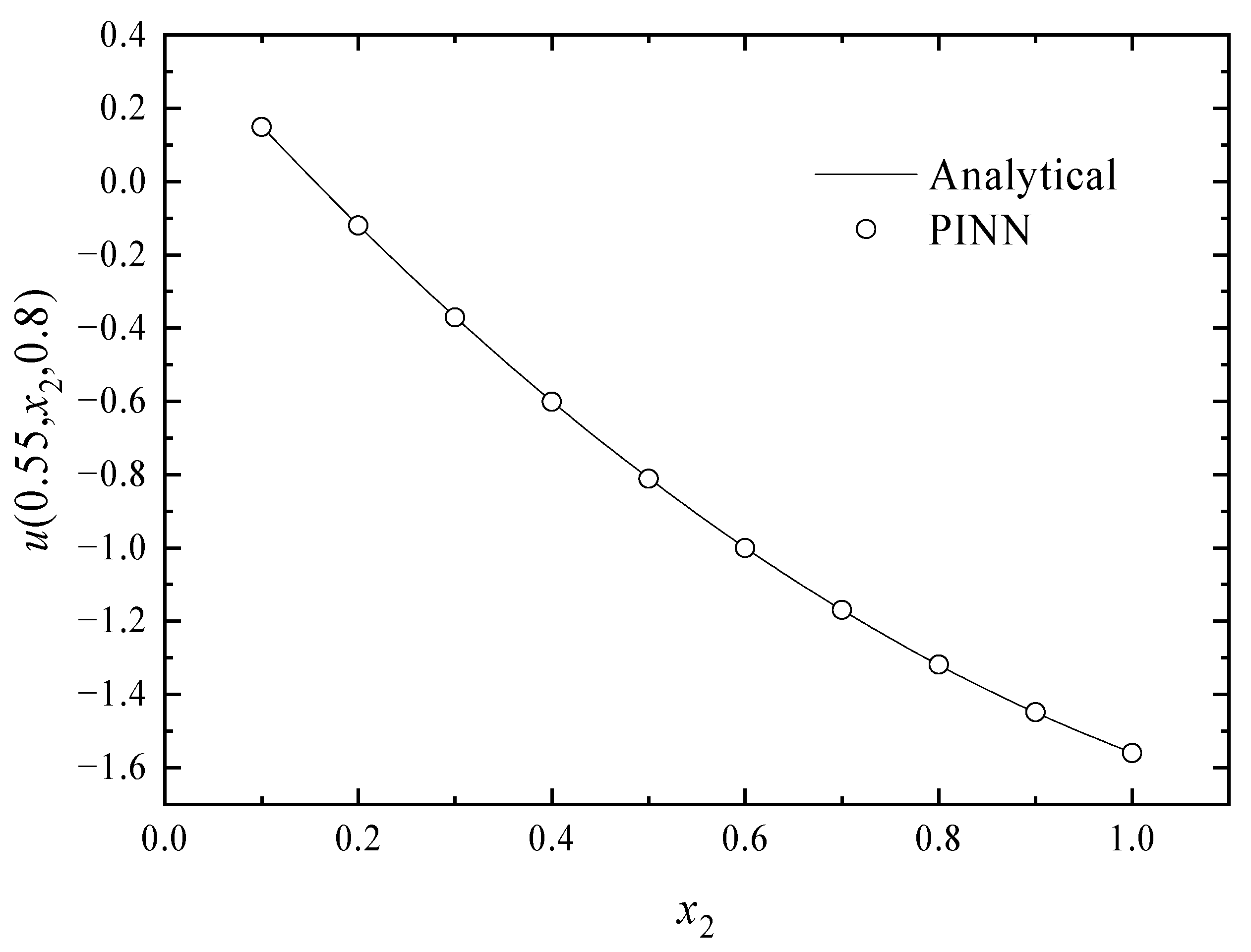
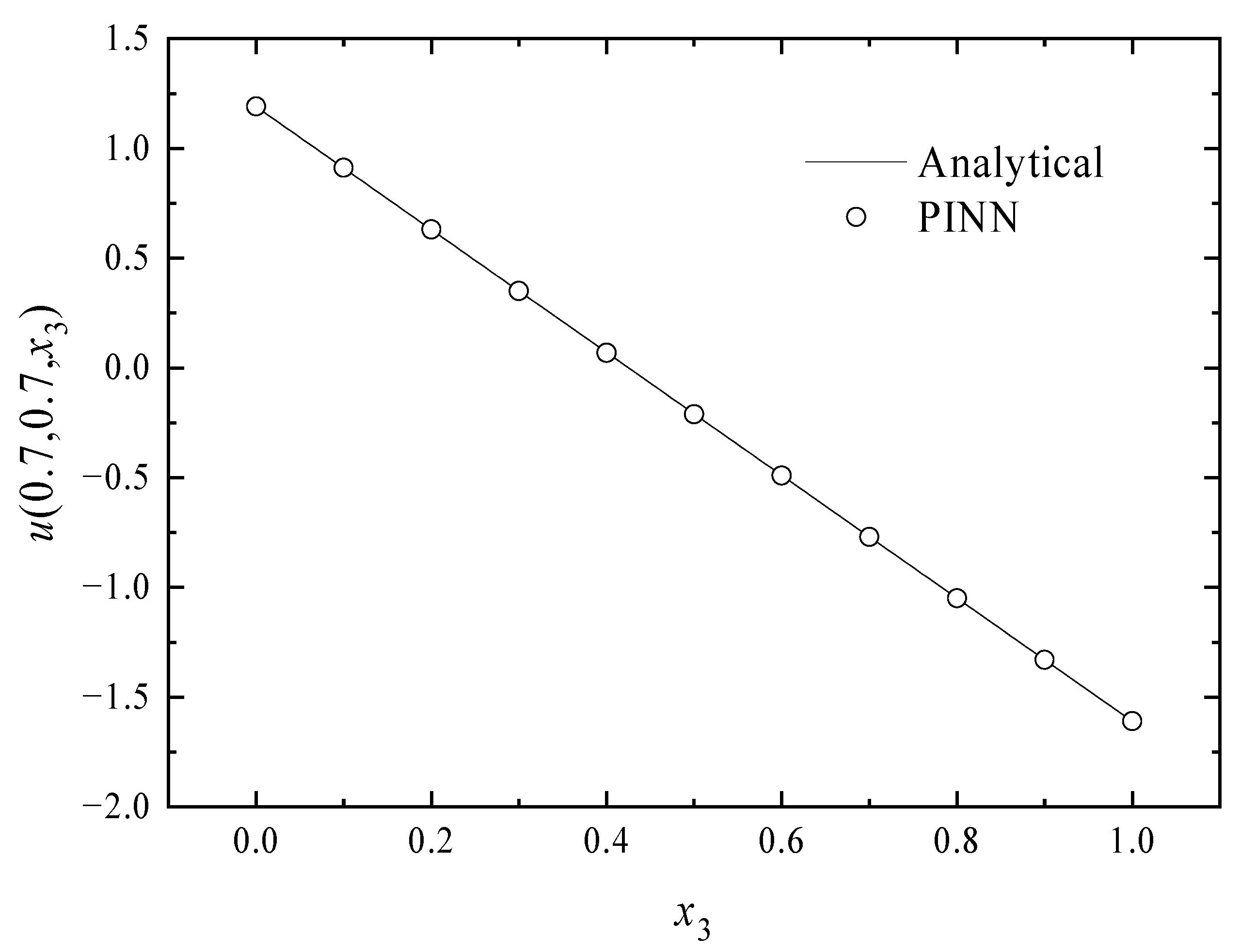
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arora, G.; Joshi, V. A computational approach for solution of one dimensional parabolic partial differential equation with application in biological processes. Ain Shams Eng. J. 2018, 9, 1141–1150. [Google Scholar] [CrossRef]
- Koroche, K.A. Numerical solution for one dimensional linear types of parabolic partial differential equation and application to heat equation. Math. Comput. Sci. 2020, 5, 76. [Google Scholar] [CrossRef]
- Voinea-Marinescu, A.P.; Marin, L. Fading regularization MFS algorithm for the Cauchy problem in anisotropic heat conduction. Comput. Mech. 2021, 68, 921–941. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Ying, S. DeLISA: Deep learning based iteration scheme approximation for solving PDEs. J. Comput. Phys. 2022, 451, 110884. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Ying, S. DWNN: Deep wavelet neural network for solving partial differential equations. Mathematics 2022, 10, 1976. [Google Scholar] [CrossRef]
- Zhu, J.-A.; Jia, Y.; Lei, J.; Liu, Z. Deep learning approach to mechanical property prediction of single-network hydrogel. Mathematics 2021, 9, 2804. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, Z. The machine learning embedded method of parameters determination in the constitutive models and potential applications for hydrogels. Int. J. Appl. Mech. 2021, 13, 2150001. [Google Scholar] [CrossRef]
- Huang, R.; Zheng, S.; Liu, Z.; Ng, T.Y. Recent advances of the constitutive models of smart materials—Hydrogels and shape memory polymers. Int. J. Appl. Mech. 2020, 12, 2050014. [Google Scholar] [CrossRef]
- Zheng, S.; Li, Z.; Liu, Z. The fast homogeneous diffusion of hydrogel under different stimuli. Int. J. Mech. Sci. 2018, 137, 263–270. [Google Scholar] [CrossRef]
- Dai, B.D.; Cheng, Y.M. Local boundary integral equation method based on radial basis functions for potential problems. Acta Phys. Sin. 2007, 56, 597–603. [Google Scholar]
- Peng, M.; Cheng, Y. A boundary element-free method (BEFM) for two-dimensional potential problems. Eng. Anal. Bound. Elem. 2009, 33, 77–82. [Google Scholar] [CrossRef]
- Lei, J.; Li, Z.; Xu, S.; Liu, Z. Recent advances of hydrogel network models for studies on mechanical behaviors. Acta Mech. Sin. 2021, 37, 367–386. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Ng, T.Y.; Sharma, P. The effect of water content on the elastic modulus and fracture energy of hydrogel. Extrem. Mech. Lett. 2020, 35, 100617. [Google Scholar] [CrossRef]
- Xu, S.; Liu, Z. A nonequilibrium thermodynamics approach to the transient properties of hydrogels. J. Mech. Phys. Solids 2019, 127, 94–110. [Google Scholar] [CrossRef]
- Jia, Y.T.; Zhou, Z.D.; Jiang, H.L.; Liu, Z.S. Characterization of fracture toughness and damage zone of double network hydrogels. J. Mech. Phys. Solids 2022, 169, 105090. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Li, J.H. A meshless method with complex variables for elasticity. Acta Phys. Sin. 2005, 54, 4463–4471. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, Y.M. Reproducing kernel particle method with complex variables for elasticity. Acta Phys. Sin. 2008, 57, 1–10. [Google Scholar] [CrossRef]
- Cheng, Y.-M.; Wang, J.-F.; Bai, F.-N. A new complex variable element-free Galerkin method for two-dimensional potential problems. Chin. Phys. B 2012, 21, 090203. [Google Scholar] [CrossRef]
- Sun, F.-X.; Wang, J.-F.; Cheng, Y.-M. An improved interpolating element-free Galerkin method for elasticity. Chin. Phys. B 2013, 22, 120203. [Google Scholar] [CrossRef]
- Peng, P.; Fu, Y.; Cheng, Y. A hybrid reproducing kernel particle method for three-dimensional advection-diffusion problems. Int. J. Appl. Mech. 2021, 13, 2150085. [Google Scholar] [CrossRef]
- Peng, P.; Cheng, Y. Analyzing three-dimensional wave propagation with the hybrid reproducing kernel particle method based on the dimension splitting method. Eng. Comput. 2022, 38, S1131–S1147. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, M.; Cheng, Y. The interpolating dimension splitting element-free Galerkin method for 3D potential problems. Eng. Comput. 2022, 38, S2703–S2717. [Google Scholar] [CrossRef]
- Cheng, R.-J.; Cheng, Y.-M. The meshless method for solving the inverse heat conduction problem with a source parameter. Acta Phys. Sin. 2007, 56, 5569–5574. [Google Scholar] [CrossRef]
- Cheng, R.-J.; Cheng, Y.-M. The meshless method for a two-dimensional inverse heat conduction problem with a source parameter. Acta Mech. Sin. 2007, 39, 843–847. [Google Scholar]
- Weng, Y.; Zhang, Z.; Cheng, Y. The complex variable reproducing kernel particle method for two-dimensional inverse heat conduction problems. Eng. Anal. Bound. Elem. 2014, 44, 36–44. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, Y.-M. Complex variable reproducing kernel particle method for transient heat conduction problems. Acta Phys. Sin. 2008, 57, 6047–6055. [Google Scholar] [CrossRef]
- Chen, L.; Ma, H.-P.; Cheng, Y.-M. Combining the complex variable reproducing kernel particle method and the finite element method for solving transient heat conduction problems. Chin. Phys. B 2013, 22, 050202. [Google Scholar] [CrossRef]
- Wang, J.-F.; Cheng, Y.-M. A new complex variable meshless method for transient heat conduction problems. Chin. Phys. B 2012, 21, 120206. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, W.; He, X.-Q. Singular boundary method for steady-state heat conduction in three dimensional general anisotropic media. Int. J. Heat Mass Transf. 2012, 55, 4837–4848. [Google Scholar] [CrossRef]
- Lu, S.; Liu, J.; Lin, G.; Zhang, P. Modified scaled boundary finite element analysis of 3D steady-state heat conduction in anisotropic layered media. Int. J. Heat Mass Transf. 2017, 108, 2462–2471. [Google Scholar] [CrossRef]
- Guan, Y.; Atluri, S.N. Meshless fragile points methods based on Petrov-Galerkin weak-forms for transient heat conduction problems in complex anisotropic nonhomogeneous media. Int. J. Numer. Methods Eng. 2021, 122, 4055–4092. [Google Scholar] [CrossRef]
- Shiah, Y.; Lee, R. Boundary element modeling of 3D anisotropic heat conduction involving arbitrary volume heat source. Math. Comput. Model. 2011, 54, 2392–2402. [Google Scholar] [CrossRef]
- Gu, Y.; Fan, C.-M.; Qu, W.; Wang, F. Localized method of fundamental solutions for large-scale modelling of three-dimensional anisotropic heat conduction problems—Theory and MATLAB code. Comput. Struct. 2019, 220, 144–155. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, G.; Gong, S.; Wang, S. Transient heat transfer analysis of anisotropic material by using element-free Galerkin method. Int. Commun. Heat Mass Transf. 2017, 84, 134–143. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Cheng, Y.; Liew, K.M. The improved element-free Galerkin method for three-dimensional transient heat conduction problems. Sci. China—Phys. Mech. Astron. 2013, 56, 1568–1580. [Google Scholar] [CrossRef]
- Cheng, H.; Xing, Z.; Peng, M. The improved element-free Galerkin method for anisotropic steady-state heat conduction problems. Comput. Model. Eng. Sci. 2022, 132, 945–964. [Google Scholar] [CrossRef]
- Cheng, J. Analyzing the factors influencing the choice of the government on leasing different types of land uses: Evidence from Shanghai of China. Land Use Policy 2019, 90, 104303. [Google Scholar] [CrossRef]
- Cheng, J. Residential land leasing and price under public land ownership. J. Urban Plan. Dev. 2021, 147, 05021009. [Google Scholar] [CrossRef]
- Cheng, J.; Luo, X. Analyzing the land leasing behavior of the government of Beijing, China, via the multinomial logit model. Land 2022, 11, 376. [Google Scholar] [CrossRef]
- Wu, S.-S.; Cheng, J.; Lo, S.-M.; Chen, C.C.; Bai, Y. Coordinating urban construction and district-level population density for balanced development: An explorative structural equation modeling analysis on Shanghai. J. Clean. Prod. 2021, 312, 127646. [Google Scholar] [CrossRef]
- Cheng, J.; Xie, Y.; Zhang, J. Industry structure optimization via the complex network of industry space: A case study of Jiangxi Province in China. J. Clean. Prod. 2022, 338, 130602. [Google Scholar] [CrossRef]
- Ren, H.; Wang, L.; Zhao, N. An interpolating element-free Galerkin method for steady-state heat conduction problems. Int. J. Appl. Mech. 2014, 6, 1450024. [Google Scholar] [CrossRef]
- Liu, D.; Cheng, Y. The interpolating element-free Galerkin method for three-dimensional transient heat conduction problems. Results Phys. 2020, 19, 103477. [Google Scholar] [CrossRef]
- Liu, F.; Cheng, Y. The improved element-free Galerkin method based on the nonsingular weight functions for inhomogeneous swelling of polymer gels. Int. J. Appl. Mech. 2018, 10, 1850047. [Google Scholar] [CrossRef]
- Cheng, H.; Peng, M.; Cheng, Y. The dimension splitting and improved complex variable element-free Galerkin method for 3-dimensional transient heat conduction problems. Int. J. Numer. Methods Eng. 2018, 114, 321–345. [Google Scholar] [CrossRef]
- Meng, Z.; Cheng, H.; Ma, L.; Cheng, Y. The dimension splitting element-free Galerkin method for 3D transient heat conduction problems. Sci. China Phys. Mech. Astron. 2018, 62, 040711. [Google Scholar] [CrossRef]
- Peng, P.P.; Cheng, Y.M. Analyzing three-dimensional transient heat conduction problems with the dimension splitting reproducing kernel particle method. Eng. Anal. Bound. Elem. 2020, 121, 180–191. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, M.; Fu, Y.; Cheng, Y. The dimension splitting interpolating element-free Galerkin method for solving three-dimensional transient heat conduction problems. Eng. Anal. Bound. Elem. 2021, 128, 326–341. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, G.; Gu, Y.; Wang, X.; Wang, F. Multi-domain physics-informed neural network for solving forward and inverse problems of steady-state heat conduction in multilayer media. Phys. Fluids 2022, 34, 116116. [Google Scholar] [CrossRef]
- Manavi, S.; Becker, T.; Fattahi, E. Enhanced surrogate modelling of heat conduction problems using physics-informed neural network framework. Int. Commun. Heat Mass Transf. 2023, 142, 106662. [Google Scholar] [CrossRef]
- Paulin, L.; Coeurjolly, D.; Iehl, J.-C.; Bonneel, N.; Keller, A.; Ostromoukhov, V. Cascaded sobol’ sampling. ACM Trans. Graph. 2021, 40, 275. [Google Scholar] [CrossRef]
- Yi, D.; Ahn, J.; Ji, S. An effective optimization method for machine learning based on ADAM. Appl. Sci. 2020, 10, 1073. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Cheng, H.; Cheng, J. Deep Learning Method Based on Physics-Informed Neural Network for 3D Anisotropic Steady-State Heat Conduction Problems. Mathematics 2023, 11, 4049. https://doi.org/10.3390/math11194049
Xing Z, Cheng H, Cheng J. Deep Learning Method Based on Physics-Informed Neural Network for 3D Anisotropic Steady-State Heat Conduction Problems. Mathematics. 2023; 11(19):4049. https://doi.org/10.3390/math11194049
Chicago/Turabian StyleXing, Zebin, Heng Cheng, and Jing Cheng. 2023. "Deep Learning Method Based on Physics-Informed Neural Network for 3D Anisotropic Steady-State Heat Conduction Problems" Mathematics 11, no. 19: 4049. https://doi.org/10.3390/math11194049
APA StyleXing, Z., Cheng, H., & Cheng, J. (2023). Deep Learning Method Based on Physics-Informed Neural Network for 3D Anisotropic Steady-State Heat Conduction Problems. Mathematics, 11(19), 4049. https://doi.org/10.3390/math11194049





