Mathematical Modeling of Toxoplasmosis in Cats with Two Time Delays under Environmental Effects
Abstract
1. Introduction
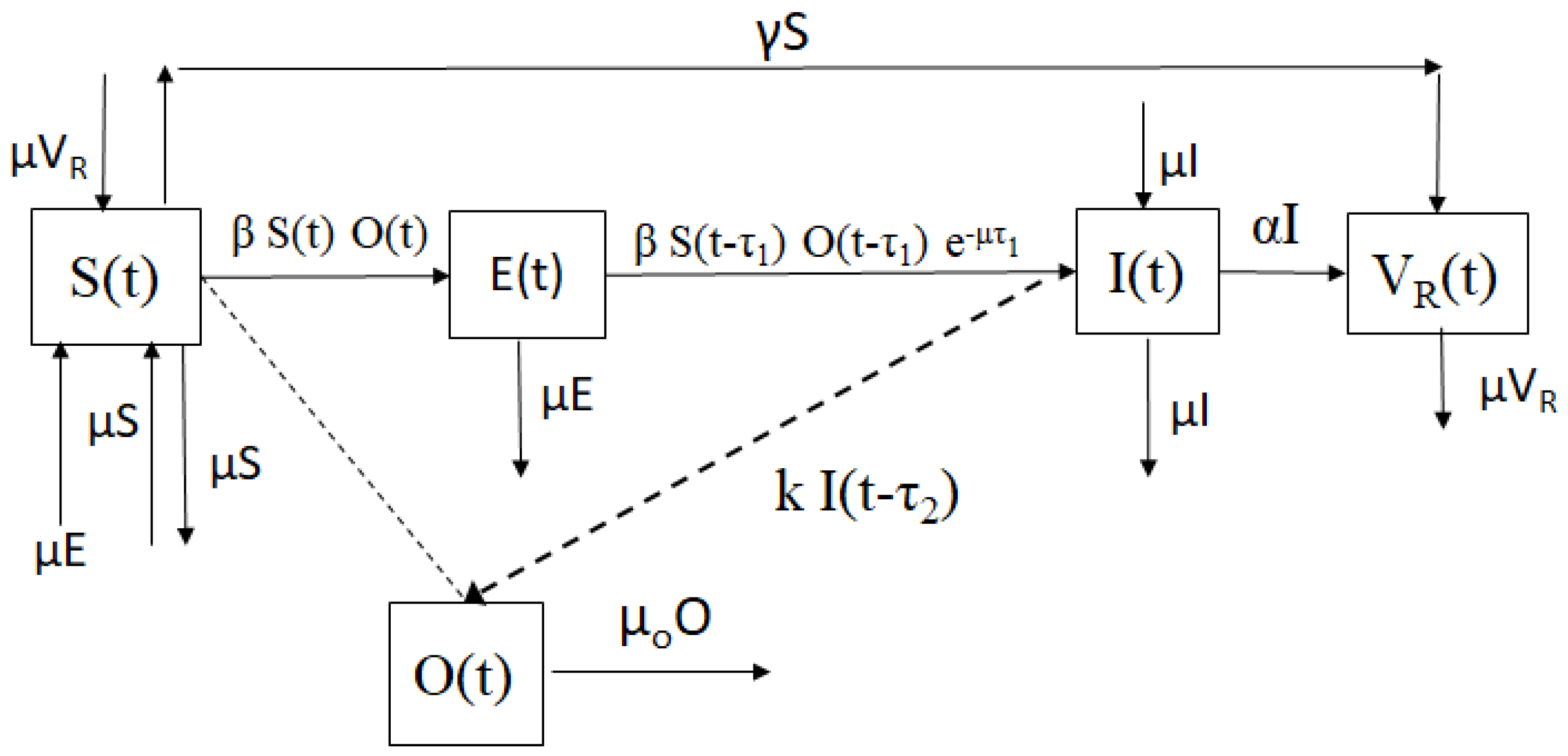
2. Mathematical Model
3. Stability Analysis of the Model
3.1. Disease-Free Steady State for the Model without Delay
3.2. Endemic Steady State
3.3. Toxoplasmosis-Free Steady State Analysis
3.4. Global Stability Analysis of the Toxoplasmosis-Free Equilibrium
3.5. Stability Analysis of the Toxoplasmosis-Endemic Steady State
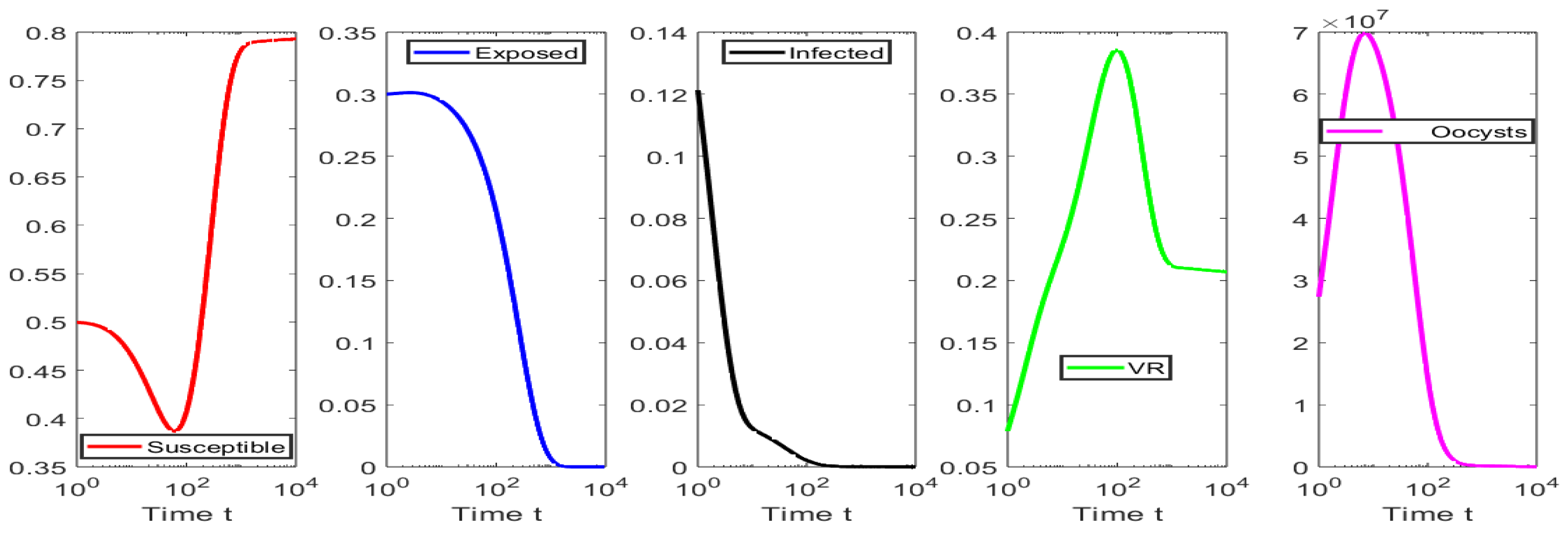
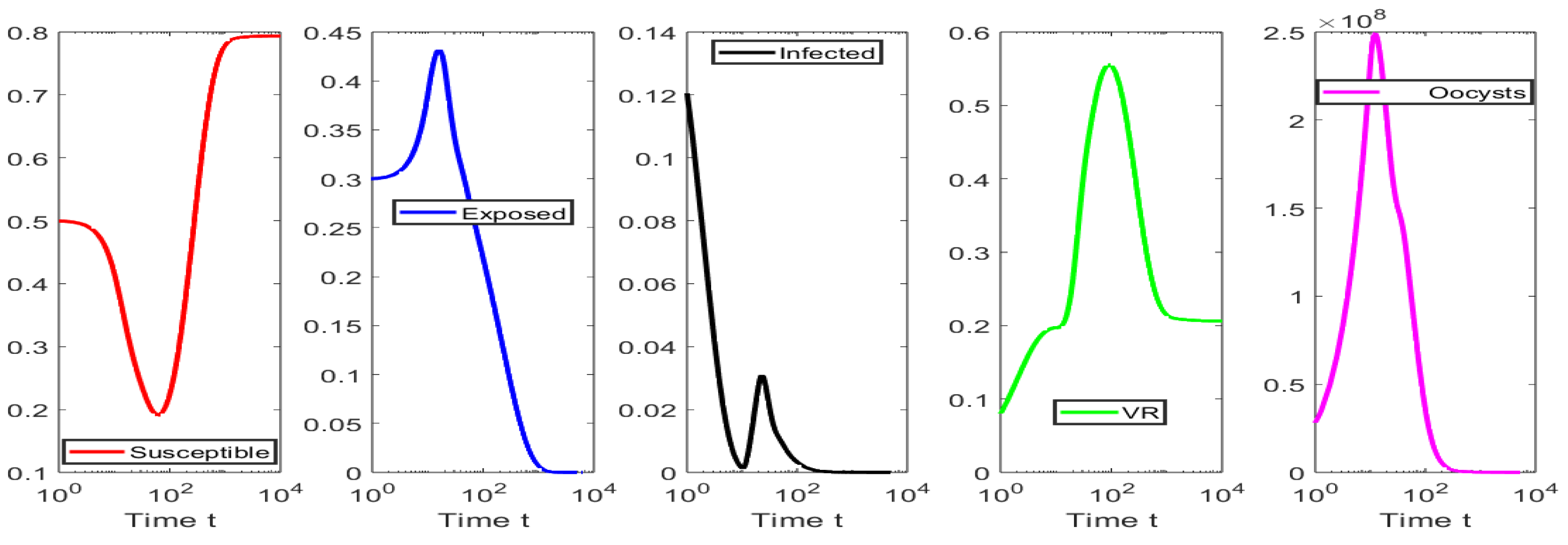
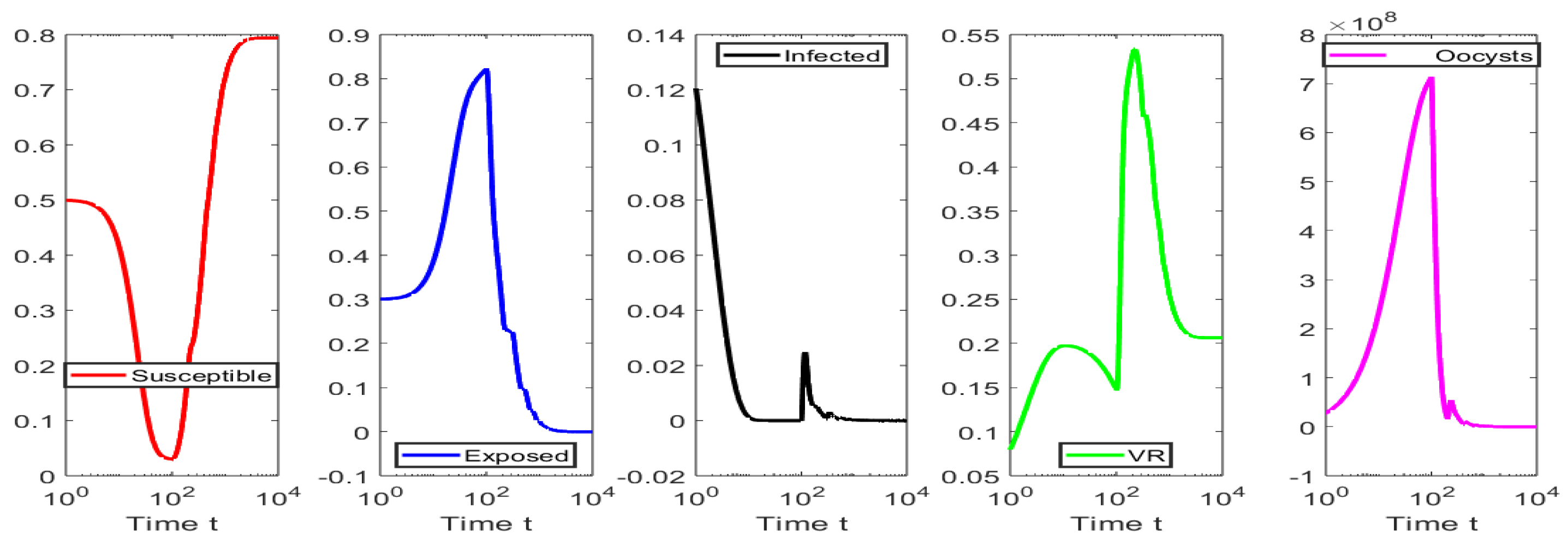
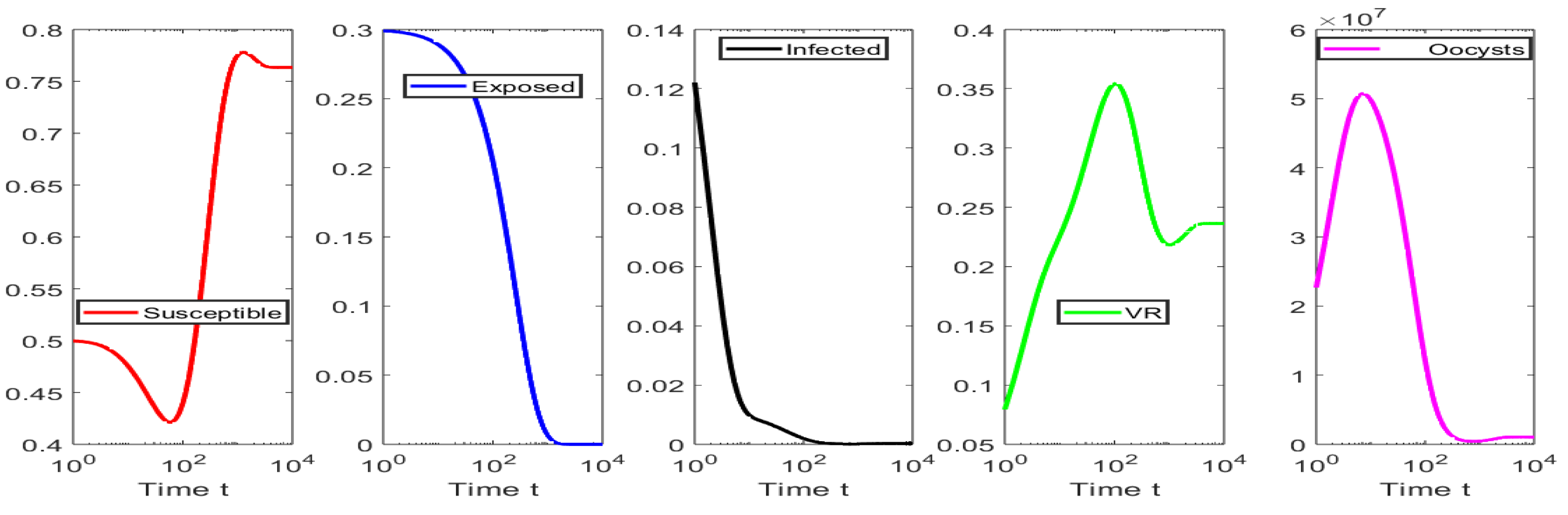
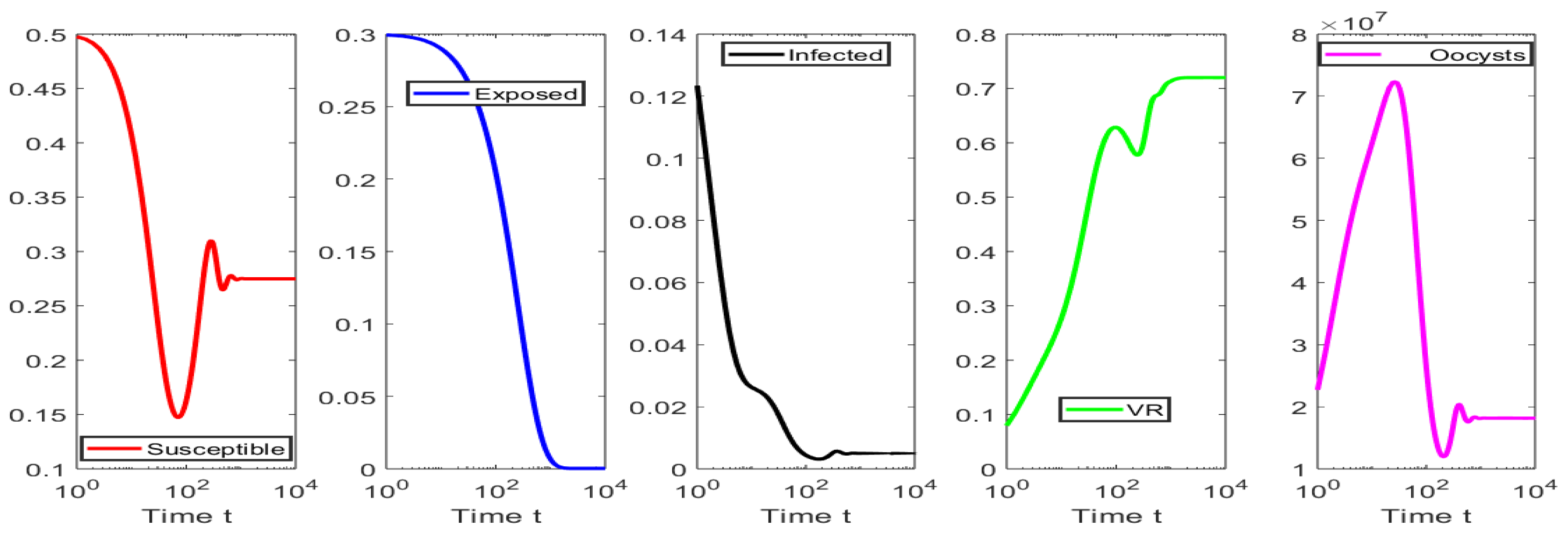
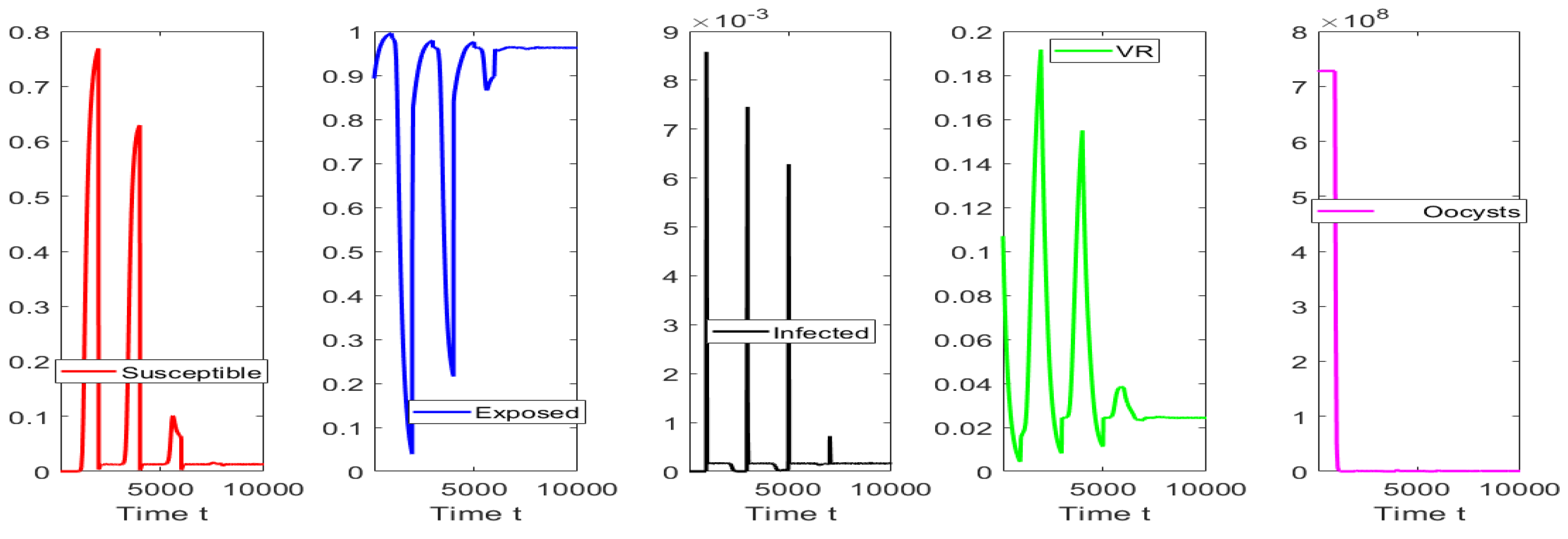
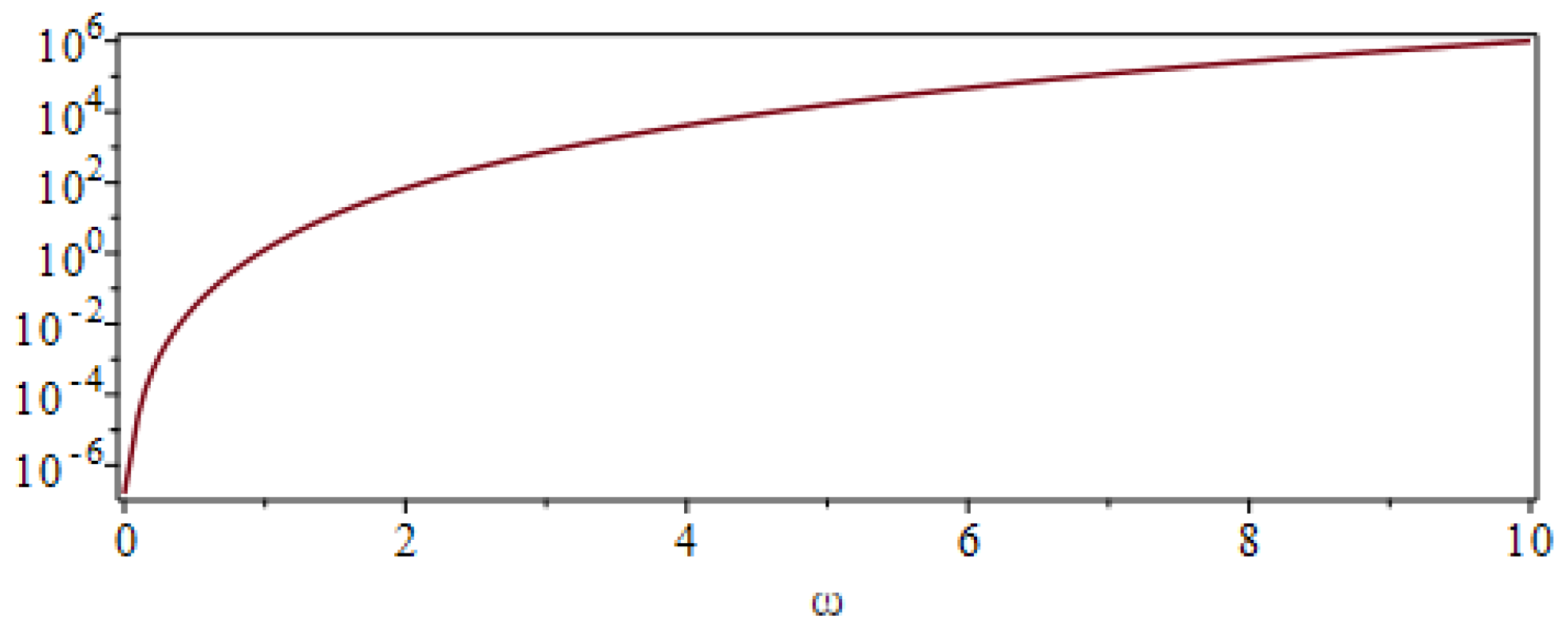
4. Numerical Simulations
4.1. Numerical Simulations for the Scenarios When
4.2. Numerical Simulations for the Scenarios When
4.3. Numerical Tests for Hopf Bifurcation When
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Attias, M.; Teixeira, D.E.; Benchimol, M.; Vommaro, R.C.; Crepaldi, P.H.; De Souza, W. The life-cycle of Toxoplasma gondii reviewed using animations. Parasites Vectors 2020, 13, 588. [Google Scholar] [CrossRef] [PubMed]
- Dubey, J. Advances in the life cycle of Toxoplasma gondii. Int. J. Parasitol. 1998, 28, 1019–1024. [Google Scholar] [CrossRef] [PubMed]
- Thomas, F.; Lafferty, K.D.; Brodeur, J.; Elguero, E.; Gauthier-Clerc, M.; Missé, D. Incidence of adult brain cancers is higher in countries where the protozoan parasite Toxoplasma gondii is common. Biol. Lett. 2012, 8, 101–103. [Google Scholar] [CrossRef] [PubMed]
- Dubey, J.P. Outbreaks of clinical toxoplasmosis in humans: Five decades of personal experience, perspectives and lessons learned. Parasites Vectors 2021, 14, 263. [Google Scholar] [CrossRef]
- McLeod, R.; Cohen, W.; Dovgin, S.; Finkelstein, L.; Boyer, K.M. Human toxoplasma infection. In Toxoplasma gondii; Elsevier: Amsterdam, The Netherlands, 2020; pp. 117–227. [Google Scholar]
- Dubey, J. History of the discovery of the life cycle of Toxoplasma gondii. Int. J. Parasitol. 2009, 39, 877–882. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, R.E.; Stanford, M.R. Is ocular toxoplasmosis caused by prenatal or postnatal infection? Br. J. Ophthalmol. 2000, 84, 224–226. [Google Scholar] [CrossRef]
- Gonzalez, A.J.C.; Matos, I.V.; Revoredo, V.M. Acute toxoplasmosis complicated with myopericarditis and possible encephalitis in an immunocompetent patient. IDCases 2020, 20, e00772. [Google Scholar] [CrossRef]
- Alvarado-Esquivel, C.; Estrada-Martínez, S.; Pérez-Álamos, A.R.; Ramos-Nevárez, A.; Botello-Calderón, K.; Alvarado-Félix, Á.O.; Vaquera-Enríquez, R.; Alvarado-Félix, G.A.; Sifuentes-Álvarez, A.; Guido-Arreola, C.A.; et al. Toxoplasma gondii infection and insomnia: A case control seroprevalence study. PLoS ONE 2022, 17, e0266214. [Google Scholar] [CrossRef]
- Alvarado-Esquivel, C.; Estrada-Martínez, S.; Ramos-Nevárez, A.; Pérez-Álamos, A.R.; Beristain-García, I.; Alvarado-Félix, Á.O.; Cerrillo-Soto, S.M.; Sifuentes-Álvarez, A.; Alvarado-Félix, G.A.; Guido-Arreola, C.A.; et al. Association between Toxoplasma gondii exposure and suicidal behavior in patients attending primary health care clinics. Pathogens 2021, 10, 677. [Google Scholar] [CrossRef]
- Hosseininejad, Z.; Sharif, M.; Sarvi, S.; Amouei, A.; Hosseini, S.A.; Nayeri Chegeni, T.; Anvari, D.; Saberi, R.; Gohardehi, S.; Mizani, A.; et al. Toxoplasmosis seroprevalence in rheumatoid arthritis patients: A systematic review and meta-analysis. PLoS Neglect. Trop. Dis. 2018, 12, e0006545. [Google Scholar] [CrossRef]
- Beshay, E.V.N.; El-Refai, S.A.; Helwa, M.A.; Atia, A.F.; Dawoud, M.M. Toxoplasma gondii as a possible causative pathogen of type-1 diabetes mellitus: Evidence from case-control and experimental studies. Exp. Parasitol. 2018, 188, 93–101. [Google Scholar] [CrossRef] [PubMed]
- De Haan, L.; Sutterland, A.L.; Schotborgh, J.V.; Schirmbeck, F.; de Haan, L. Association of Toxoplasma gondii seropositivity with cognitive function in healthy people: A systematic review and meta-analysis. JAMA Psychiatry 2021, 78, 1103–1112. [Google Scholar] [CrossRef]
- Caldrer, S.; Vola, A.; Ferrari, G.; Ursini, T.; Mazzi, C.; Meroni, V.; Beltrame, A. Toxoplasma gondii Serotypes in Italian and Foreign Populations: A Cross-Sectional Study Using a Homemade ELISA Test. Microorganisms 2022, 10, 1577. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Escobar, M.; Schares, G.; Maksimov, P.; Joeres, M.; Ortega-Mora, L.M.; Calero-Bernal, R. Toxoplasma gondii Genotyping: A Closer Look Into Europe. Front. Cell. Infect. Microbiol. 2022, 12, 842595. [Google Scholar] [CrossRef]
- Galal, L.; Hamidović, A.; Dardé, M.L.; Mercier, M. Diversity of Toxoplasma gondii strains at the global level and its determinants. Food Waterborne Parasitol. 2019, 15, e00052. [Google Scholar] [CrossRef] [PubMed]
- CDC. Center for Disease Control and Prevention, Toxoplasmosis. Available online: https://www.cdc.gov/parasites/toxoplasmosis/ (accessed on 1 May 2021).
- Morris, J.G., Jr.; Havelaar, A. Toxoplasma gondii. In Foodborne Infections and Intoxications; Elsevier: Amsterdam, The Netherlands, 2021; pp. 347–361. [Google Scholar]
- Zhu, S.; VanWormer, E.; Martínez-López, B.; Bahia-Oliveira, L.M.G.; DaMatta, R.A.; Rodrigues, P.S.; Shapiro, K. Quantitative Risk Assessment of Oocyst Versus Bradyzoite Foodborne Transmission of Toxoplasma gondii in Brazil. Pathogens 2023, 12, 870. [Google Scholar] [CrossRef] [PubMed]
- Dubey, J.P. The history of Toxoplasma gondii—The first 100 years. J. Eukaryot. Microbiol. 2008, 55, 467–475. [Google Scholar] [CrossRef]
- Havelaar, A.H.; Kirk, M.D.; Torgerson, P.R.; Gibb, H.J.; Hald, T.; Lake, R.J.; Praet, N.; Bellinger, D.C.; De Silva, N.R.; Gargouri, N.; et al. World Health Organization global estimates and regional comparisons of the burden of foodborne disease in 2010. PLoS Med. 2015, 12, e1001923. [Google Scholar] [CrossRef]
- Opsteegh, M.; Kortbeek, T.M.; Havelaar, A.H.; van der Giessen, J.W. Intervention strategies to reduce human Toxoplasma gondii disease burden. Clin. Infect. Dis. 2015, 60, 101–107. [Google Scholar] [CrossRef]
- Torgerson, P.R.; Mastroiacovo, P. The global burden of congenital toxoplasmosis: A systematic review. Bull. World Health Organ. 2013, 91, 501–508. [Google Scholar] [CrossRef]
- Scallan, E.; Hoekstra, R.M.; Angulo, F.J.; Tauxe, R.V.; Widdowson, M.A.; Roy, S.L.; Jones, J.L.; Griffin, P.M. Foodborne illness acquired in the United States—Major pathogens. Emerg. Infect. Dis. 2011, 17, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Batz, M.B.; Hoffmann, S.; Morris, J.G., Jr. Ranking the disease burden of 14 pathogens in food sources in the United States using attribution data from outbreak investigations and expert elicitation. J. Food Prot. 2012, 75, 1278–1291. [Google Scholar] [CrossRef]
- Deng, H.; Cummins, R.; Schares, G.; Trevisan, C.; Enemark, H.; Waap, H.; Srbljanovic, J.; Djurkovic-Djakovic, O.; Pires, S.M.; van der Giessen, J.W.; et al. Mathematical modelling of Toxoplasma gondii transmission: A systematic review. Food Waterborne Parasitol. 2021, 22, e00102. [Google Scholar] [CrossRef]
- Aramini, J.; Stephen, C.; Dubey, J.P.; Engelstoft, C.; Schwantje, H.; Ribble, C.S. Potential contamination of drinking water with Toxoplasma gondii oocysts. Epidemiol. Infect. Camb. Univ. Press 1999, 122, 305–315. [Google Scholar] [CrossRef] [PubMed]
- Hill, D.; Dubey, J. Toxoplasma gondii: Transmission, diagnosis and prevention. Clin. Microbiol. Infect. 2002, 8, 634–640. [Google Scholar] [CrossRef]
- Frenkel, J.; Ruiz, A.; Chinchilla, M. Soil survival of Toxoplasma oocysts in Kansas and Costa Rica. Am. J. Trop. Med. Hyg. 1975, 24, 439–443. [Google Scholar] [CrossRef]
- Kuruca, L.; Belluco, S.; Vieira-Pinto, M.; Antic, D.; Blagojevic, B. Current control options and a way towards risk-based control of Toxoplasma gondii in the meat chain. Food Control 2023, 146, 109556. [Google Scholar] [CrossRef]
- Fayer, R. Toxoplasmosis update and public health implications. Can. Vet. J. 1981, 22, 344–352. [Google Scholar]
- Innes, E.A.; Hamilton, C.; Garcia, J.L.; Chryssafidis, A.; Smith, D. A one health approach to vaccines against Toxoplasma gondii. Food Waterborne Parasitol. 2019, 15, e00053. [Google Scholar] [CrossRef] [PubMed]
- Marinović, A.A.B.; Opsteegh, M.; Deng, H.; Suijkerbuijk, A.W.; van Gils, P.F.; Van Der Giessen, J. Prospects of toxoplasmosis control by cat vaccination. Epidemics 2020, 30, 100380. [Google Scholar] [CrossRef]
- Smith, N.C.; Goulart, C.; Hayward, J.A.; Kupz, A.; Miller, C.M.; van Dooren, G.C. Control of human toxoplasmosis. Int. J. Parasitol. 2021, 51, 95–121. [Google Scholar] [CrossRef] [PubMed]
- Wolf, P.J.; Hamilton, F. Managing free-roaming cats in US cities: An object lesson in public policy and citizen action. J. Urban Aff. 2020, 44, 221–242. [Google Scholar] [CrossRef]
- Dubey, J. A review of Toxoplasmosis in cattle. Vet. Parasitol. 1986, 22, 177–202. [Google Scholar] [CrossRef]
- Dubey, J. A review of Toxoplasmosis in pigs. Vet. Parasitol. 1986, 19, 181–223. [Google Scholar] [CrossRef] [PubMed]
- Dubey, J.; Beattie, C. Toxoplasmosis of Animals and Man; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Dubey, J.P. Strategies to reduce transmission of Toxoplasma gondii to animals and humans. Vet. Parasitol. 1996, 64, 65–70. [Google Scholar] [CrossRef]
- Dubey, J.; Mattix, M.; Lipscomb, T. Lesions of neonatally induced toxoplasmosis in cats. Vet. Pathol. 1996, 33, 290–295. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.; Morley, E.; Hughes, J.; Duncanson, P.; Terry, R.; Smith, J.; Hide, G. High levels of congenital transmission of Toxoplasma gondii in longitudinal and cross-sectional studies on sheep farms provides evidence of vertical transmission in ovine hosts. Parasitology 2005, 130, 301–307. [Google Scholar] [CrossRef]
- Sacks, J.J.; Roberto, R.R.; Brooks, N.F. Toxoplasmosis infection associated with raw goat’s milk. JAMA 1982, 248, 1728–1732. [Google Scholar] [CrossRef]
- Simon, J.A.; Pradel, R.; Aubert, D.; Geers, R.; Villena, I.; Poulle, M.L. A multi-event capture-recapture analysis of Toxoplasma gondii seroconversion dynamics in farm cats. Parasites Vectors 2018, 11, 339. [Google Scholar] [CrossRef]
- Webster, J.P. The effect of Toxoplasma gondii on animal behavior: Playing cat and mouse. Schizophr. Bull. 2007, 33, 752–756. [Google Scholar] [CrossRef]
- Dabritz, H.; Conrad, P.A. Cats and Toxoplasma: Implications for public health. Zoonoses Public Health 2010, 57, 34–52. [Google Scholar] [CrossRef] [PubMed]
- Murphy, R.G.; Williams, R.H.; Hughes, J.M.; Hide, G.; Ford, N.J.; Oldbury, D.J. The urban house mouse (Mus domesticus) as a reservoir of infection for the human parasite Toxoplasma gondii: An unrecognised public health issue? Int. J. Environ. Health Res. 2008, 18, 177–185. [Google Scholar] [CrossRef]
- Arenas, A.J.; González-Parra, G.; Micó, R.J.V. Modeling toxoplasmosis spread in cat populations under vaccination. Theor. Popul. Biol. 2010, 77, 227–237. [Google Scholar] [CrossRef]
- Ferreira, J.D.; Echeverry, L.M.; Rincon, C.A.P. Stability and bifurcation in epidemic models describing the transmission of toxoplasmosis in human and cat populations. Math. Methods Appl. Sci. 2017, 40, 5575–5592. [Google Scholar] [CrossRef]
- González-Parra, G.C.; Arenas, A.J.; Aranda, D.F.; Villanueva, R.J.; Jódar, L. Dynamics of a model of Toxoplasmosis disease in human and cat populations. Comput. Math. Appl. 2009, 57, 1692–1700. [Google Scholar] [CrossRef]
- Turner, M.; Lenhart, S.; Rosenthal, B.; Zhao, X. Modeling effective transmission pathways and control of the world’s most successful parasite. Theor. Popul. Biol. 2013, 86, 50–61. [Google Scholar] [CrossRef]
- Lélu, M.; Langlais, M.; Poulle, M.L.; Gilot-Fromont, E. Transmission dynamics of Toxoplasma gondii along an urban–rural gradient. Theor. Popul. Biol. 2010, 78, 139–147. [Google Scholar] [CrossRef]
- González-Parra, G.; Arenas, A.J.; Chen-Charpentier, B.; Sultana, S. Mathematical modeling of toxoplasmosis with multiple hosts, vertical transmission and cat vaccination. Comput. Appl. Math. 2023, 42, 88. [Google Scholar] [CrossRef]
- Sultana, S.; González-Parra, G.; Arenas, A.J. A Generalized Mathematical Model of Toxoplasmosis with an Intermediate Host and the Definitive Cat Host. Mathematics 2023, 11, 1642. [Google Scholar] [CrossRef]
- Mateus-Pinilla, N.; Hannon, B.; Weigel, R. A computer simulation of the prevention of the transmission of Toxoplasma gondii on swine farms using a feline T. gondii vaccine. Prev. Vet. Med. 2002, 55, 17–36. [Google Scholar] [CrossRef]
- Sullivan, A.; Agusto, F.; Bewick, S.; Su, C.; Lenhart, S.; Zhao, X. A mathematical model for within-host Toxoplasma gondii invasion dynamics. Math. Biosci. Eng. 2012, 9, 647. [Google Scholar] [PubMed]
- Dubey, J. Duration of Immunity to Shedding of Toxoplasma gondii Oocysts by Cats. J. Parasitol. 1995, 81, 410–415. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, J.; Dubey, J.; Miller, N.L. Toxoplasma gondii in cats: Fecal stages identified as coccidian oocysts. Science 1970, 167, 893–896. [Google Scholar] [CrossRef]
- Dubey, J.; Lindsay, D.S.; Lappin, M.R. Toxoplasmosis and other intestinal coccidial infections in cats and dogs. Vet. Clin. Small Anim. Pract. 2009, 39, 1009–1034. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Sullivan, A.M.; Su, C.; Zhao, X. An agent-based model for the transmission dynamics of Toxoplasma gondii. J. Theor. Biol. 2012, 293, 15–26. [Google Scholar] [CrossRef]
- Lappin, M. Feline toxoplasmosis. InPractice 1999, 21, 578–589. [Google Scholar] [CrossRef]
- Burrells, A.; Bartley, P.; Zimmer, I.; Roy, S.; Kitchener, A.C.; Meredith, A.; Wright, S.; Innes, E.; Katzer, F. Evidence of the three main clonal Toxoplasma gondii lineages from wild mammalian carnivores in the UK. Parasitology 2013, 140, 1768–1776. [Google Scholar] [CrossRef]
- Dardé, M. Toxoplasma gondii “new” genotypes and virulence. Parasite 2008, 15, 366–371. [Google Scholar] [CrossRef]
- Lindsay, D.; Dubey, J. Toxoplasma gondii: The changing paradigm of congenital toxoplasmosis. Parasitology 2011, 138, 1829–1831. [Google Scholar] [CrossRef]
- Arenas, A.J.; González-Parra, G.; Naranjo, J.J.; Cogollo, M.; De La Espriella, N. Mathematical Analysis and Numerical Solution of a Model of HIV with a Discrete Time Delay. Mathematics 2021, 9, 257. [Google Scholar] [CrossRef]
- Chen-Charpentier, B.M.; Jackson, M. Direct and indirect optimal control applied to plant virus propagation with seasonality and delays. J. Comput. Appl. Math. 2020, 380, 112983. [Google Scholar] [CrossRef]
- Smith, H.L. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: Berlin/Heidelberg, Germany, 2011; Volume 57. [Google Scholar]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Hethcote, H. Mathematics of infectious diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef]
- Xu, R. Global dynamics of an {SEIS} epidemiological model with time delay describing a latent period. Math. Comput. Simul. 2012, 85, 90–102. [Google Scholar] [CrossRef]
- Yan, P.; Liu, S. SEIR epidemic model with delay. ANZIAM J. 2006, 48, 119–134. [Google Scholar] [CrossRef]
- Guo, B.Z.; Cai, L.M. A note for the global stability of a delay differential equation of hepatitis B virus infection. Math. Biosci. Eng. 2011, 8, 689–694. [Google Scholar]
- Samanta, G.P. Dynamic behaviour for a nonautonomous heroin epidemic model with time delay. J. Appl. Math. Comput. 2011, 35, 161–178. [Google Scholar] [CrossRef]
- Nelson, P.W.; Murray, J.D.; Perelson, A.S. A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 2000, 163, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Castro, M.Á.; García, M.A.; Martín, J.A.; Rodríguez, F. Exact and nonstandard finite difference schemes for coupled linear delay differential systems. Mathematics 2019, 7, 1038. [Google Scholar] [CrossRef]
- García, M.; Castro, M.; Martín, J.A.; Rodríguez, F. Exact and nonstandard numerical schemes for linear delay differential models. Appl. Math. Comput. 2018, 338, 337–345. [Google Scholar] [CrossRef]
- Kerr, G.; González-Parra, G.; Sherman, M. A new method based on the Laplace transform and Fourier series for solving linear neutral delay differential equations. Appl. Math. Comput. 2022, 420, 126914. [Google Scholar] [CrossRef]
- Shampine, L.F.; Thompson, S. Numerical solution of delay differential equations. In Delay Differential Equations; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–27. [Google Scholar]
- Bachar, M. On periodic solutions of delay differential equations with impulses. Symmetry 2019, 11, 523. [Google Scholar] [CrossRef]
- Bartłomiejczyk, A.; Bodnar, M. Hopf bifurcation in time-delayed gene expression model with dimers. Math. Methods Appl. Sci. 2023, 46, 12087–12111. [Google Scholar] [CrossRef]
- Gökçe, A. A dynamic interplay between Allee effect and time delay in a mathematical model with weakening memory. Appl. Math. Comput. 2022, 430, 127306. [Google Scholar] [CrossRef]
- Liu, Y.; Cai, J.; Xu, H.; Shan, M.; Gao, Q. Stability and Hopf bifurcation of a love model with two delays. Math. Comput. Simul. 2023, 205, 558–580. [Google Scholar] [CrossRef]
- Maji, C.; Al Basir, F.; Mukherjee, D.; Ravichandran, C.; Nisar, K. COVID-19 propagation and the usefulness of awareness-based control measures: A mathematical model with delay. AIMS Math 2022, 7, 12091–12105. [Google Scholar] [CrossRef]
- Najm, F.; Yafia, R.; Aziz-Alaoui, M. Hopf Bifurcation in Oncolytic Therapeutic Modeling: Viruses as Anti-Tumor Means with Viral Lytic Cycle. Int. J. Bifurc. Chaos 2022, 32, 2250171. [Google Scholar] [CrossRef]
- Ruschel, S.; Pereira, T.; Yanchuk, S.; Young, L.S. An SIQ delay differential equations model for disease control via isolation. J. Math. Biol. 2019, 79, 249–279. [Google Scholar] [CrossRef]
- Sepulveda, G.; Arenas, A.J.; González-Parra, G. Mathematical Modeling of COVID-19 Dynamics under Two Vaccination Doses and Delay Effects. Mathematics 2023, 11, 369. [Google Scholar] [CrossRef]
- Achouri, H.; Aouiti, C. Bogdanov–Takens and triple zero bifurcations for a neutral functional differential equations with multiple delays. J. Dyn. Differ. Equ. 2021, 35, 355–380. [Google Scholar] [CrossRef]
- Angelova, M.; Shelyag, S. Delay-differential equations for glucose-insulin regulation. In 2019–20 MATRIX Annals; Springer: Berlin/Heidelberg, Germany, 2021; pp. 299–306. [Google Scholar]
- Diekmann, O.; Van Gils, S.A.; Lunel, S.M.; Walther, H.O. Delay Equations: Functional-, Complex-, and Nonlinear Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 110. [Google Scholar]
- Masood, F.; Moaaz, O.; Askar, S.S.; Alshamrani, A. New Conditions for Testing the Asymptotic Behavior of Solutions of Odd-Order Neutral Differential Equations with Multiple Delays. Axioms 2023, 12, 658. [Google Scholar] [CrossRef]
- Pospíšil, M. Representation of solutions of systems of linear differential equations with multiple delays and nonpermutable variable coefficients. Math. Model. Anal. 2020, 25, 303–322. [Google Scholar] [CrossRef]
- Santra, S.S.; Bazighifan, O.; Ahmad, H.; Yao, S.W. Second-order differential equation with multiple delays: Oscillation theorems and applications. Complexity 2020, 2020, 8853745. [Google Scholar] [CrossRef]
- Ge, J.; Xu, J. An analytical method for studying double Hopf bifurcations induced by two delays in nonlinear differential systems. Sci. China Technol. Sci. 2020, 63, 597–602. [Google Scholar] [CrossRef]
- Lin, X.; Wang, H. Stability analysis of delay differential equations with two discrete delays. Can. Appl. Math. Q. 2012, 20, 519–533. [Google Scholar]
- Pal, S.; Gupta, A.; Misra, A.K.; Dubey, B. Chaotic dynamics of a stage-structured prey-predator system with hunting cooperation and fear in presence of two discrete time delays. J. Biol. Syst. 2023, 31, 611–642. [Google Scholar] [CrossRef]
- Cheng, Z.; Song, Q.; Xiao, M. Bifurcation and control of disease spreading networks model with two delays. Asian J. Control 2023, 25, 1323–1335. [Google Scholar] [CrossRef]
- Gu, K.; Niculescu, S.I.; Chen, J. On stability crossing curves for general systems with two delays. J. Math. Anal. Appl. 2005, 311, 231–253. [Google Scholar] [CrossRef]
- Gao, S.; Chen, L.; Teng, Z. Pulse vaccination of an SEIR epidemic model with time delay. Nonlinear Anal. Real World Appl. 2008, 9, 599–607. [Google Scholar] [CrossRef]
- Sykes, D.; Rychtář, J. A game-theoretic approach to valuating toxoplasmosis vaccination strategies. Theor. Popul. Biol. 2015, 105, 33–38. [Google Scholar] [CrossRef]
- Freyre, A.; Choromanski, L.; Fishback, J.; Popiel, I. Immunization of cats with tissue cysts, bradyzoites, and tachyzoites of the T-263 strain of Toxoplasma gondii. J. Parasitol. 1993, 79, 716–719. [Google Scholar] [CrossRef]
- Frenkel, J. Transmission of toxoplasmosis and the role of immunity in limiting transmission and illness. J. Am. Vet. Med. Assoc. 1990, 196, 233–240. [Google Scholar] [PubMed]
- Powell, C.C.; Lappin, M.R. Clinical ocular toxoplasmosis in neonatal kittens. Vet. Ophthalmol. 2001, 4, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Iwamoto, I.; Yoshiki, K. Experimental toxoplasmosis in pregnant cats. Vet. Ophthalmol. 1993, 55, 1005–1009. [Google Scholar] [CrossRef][Green Version]
- Dubey, J.; Lappin, M.; Thulliez, P. Diagnosis of induced toxoplasmosis in neonatal cats. J. Am. Vet. Med. Assoc. 1995, 207, 179–185. [Google Scholar] [PubMed]
- Powell, C.C.; Brewer, M.; Lappin, M.R. Detection of Toxoplasma gondii in the milk of experimentally infected lactating cats. Vet. Parasitol. 2001, 102, 29–33. [Google Scholar] [CrossRef] [PubMed]
- Kuang, Y. Delay Differential Equations: With Applications in Population Dynamics; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Gourley, S.A.; Kuang, Y.; Nagy, J.D. Dynamics of a delay differential equation model of hepatitis B virus infection. J. Biol. Dyn. 2008, 2, 140–153. [Google Scholar] [CrossRef]
- Jack, K.; Hale, S.M.V.L. Introduction to Functional Differential Equations, 1st ed.; Applied Mathematical Sciences 99; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Hale, J. Ordinary Differential Equations; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Hirsh, M.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems and an Introduction to Chaos; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Murray, J.D. Mathematical Biology I. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- González-Parra, G.; Sultana, S.; Arenas, A.J. Mathematical modeling of toxoplasmosis considering a time delay in the infectivity of oocysts. Mathematics 2022, 10, 354. [Google Scholar] [CrossRef]
- Sultana, S.; González-Parra, G.; Arenas, A.J. Dynamics of toxoplasmosis in the cat’s population with an exposed stage and a time delay. Math. Biosci. Eng. 2022, 19, 12655–12676. [Google Scholar] [CrossRef]
- La Salle, J.P. The Stability of Dynamical Systems; SIAM: Philadelphia, PA, USA, 1976. [Google Scholar]
- Shampine, L.F.; Thompson, S. Solving ddes in matlab. Appl. Numer. Math. 2001, 37, 441–458. [Google Scholar] [CrossRef]
- Berthier, K.; Langlais, M.; Auger, P.; Pontier, D. Dynamics of a feline virus with two transmission modes within exponentially growing host populations. Proc. R. Soc. B Biol. Sci. 2000, 267, 2049–2056. [Google Scholar] [CrossRef]
- Fayer, R. Toxoplasma gondii: Transmission, diagnosis and prevention. Can. Vet. 1981, 22, 344–352. [Google Scholar]
- Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. [Google Scholar] [CrossRef] [PubMed]
- González-Parra, G.; Díaz-Rodríguez, M.; Arenas, A.J. Mathematical modeling to study the impact of immigration on the dynamics of the COVID-19 pandemic: A case study for Venezuela. Spat. Spatio-Temp. Epidemiol. 2022, 43, 100532. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultana, S.; González-Parra, G.; Arenas, A.J. Mathematical Modeling of Toxoplasmosis in Cats with Two Time Delays under Environmental Effects. Mathematics 2023, 11, 3463. https://doi.org/10.3390/math11163463
Sultana S, González-Parra G, Arenas AJ. Mathematical Modeling of Toxoplasmosis in Cats with Two Time Delays under Environmental Effects. Mathematics. 2023; 11(16):3463. https://doi.org/10.3390/math11163463
Chicago/Turabian StyleSultana, Sharmin, Gilberto González-Parra, and Abraham J. Arenas. 2023. "Mathematical Modeling of Toxoplasmosis in Cats with Two Time Delays under Environmental Effects" Mathematics 11, no. 16: 3463. https://doi.org/10.3390/math11163463
APA StyleSultana, S., González-Parra, G., & Arenas, A. J. (2023). Mathematical Modeling of Toxoplasmosis in Cats with Two Time Delays under Environmental Effects. Mathematics, 11(16), 3463. https://doi.org/10.3390/math11163463










