Cutting-Edge Analytical and Numerical Approaches to the Gilson–Pickering Equation with Plenty of Soliton Solutions
Abstract
1. Introduction
2. Transforming PDE to ODE
3. Brief Description of Paul–Painlevé Approach
- Step 1: Consider a nonlinear partial differential equation in as a function of space variable x and time variable t aswhere is contained the nonlinear terms as well.
- Step 4: Solution of the Riccati-equation is obtained aswhere and K are the constants.
Application of the PPA on GPE
4. Standard -Expansion Technique
- Step 1.where is a polynomial of and its partial derivatives.
- Step 2. Employing the traveling wave transformationwhere and are the non-zero values, allows us to diminish Equation (22) to an ODE of in the below form:
4.1. The Soliton Solutions
4.1.1. Set I
4.1.2. Set II
4.1.3. Set III
4.1.4. Set IV
4.1.5. Set V
4.1.6. Set VI
4.1.7. Set VII
4.1.8. Set VIII
4.1.9. Set IX
4.1.10. Set X
4.1.11. Set XI
4.1.12. Set XII
4.1.13. Set XIII
4.1.14. Set XIV
4.1.15. Set XV
4.1.16. Set XVI
4.1.17. Set XVII
4.1.18. Set XVIII
4.1.19. Set XIX
4.1.20. Set XX
4.1.21. Set XXI
4.1.22. Set XXII
4.1.23. Set XXIII
4.1.24. Set XXIV
4.1.25. Set XXV
4.1.26. Set XXVI
4.1.27. Set XXVII
4.1.28. Set XXVIII
4.1.29. Set XXIX
4.1.30. Set XXX
4.1.31. Set XXXI
4.1.32. Set XXXII
4.1.33. Set XXXIII
5. He’s Variational Direct Technique
- Step 1. Let a nonlinear PDE be stated in the general formWe commence the below transformations:where a and b are values that will be determined.
- Step 2. Engaging the reduction (141), one becomeswhere and so on.
- Step 3. By utilizing the variational technique to Equation (142), the following functional can be presented as
- Step 5. Employing the Ritz-like technique with the stationary requirement, we reach:
5.1. Performance of He’s VDT for a GP Equation
5.1.1. Periodic Wave Solution
5.1.2. Soliton Solution
5.1.3. Bright Soliton Solution
5.1.4. Periodic Wave form Solution
5.1.5. Another form of Periodic Wave Solution
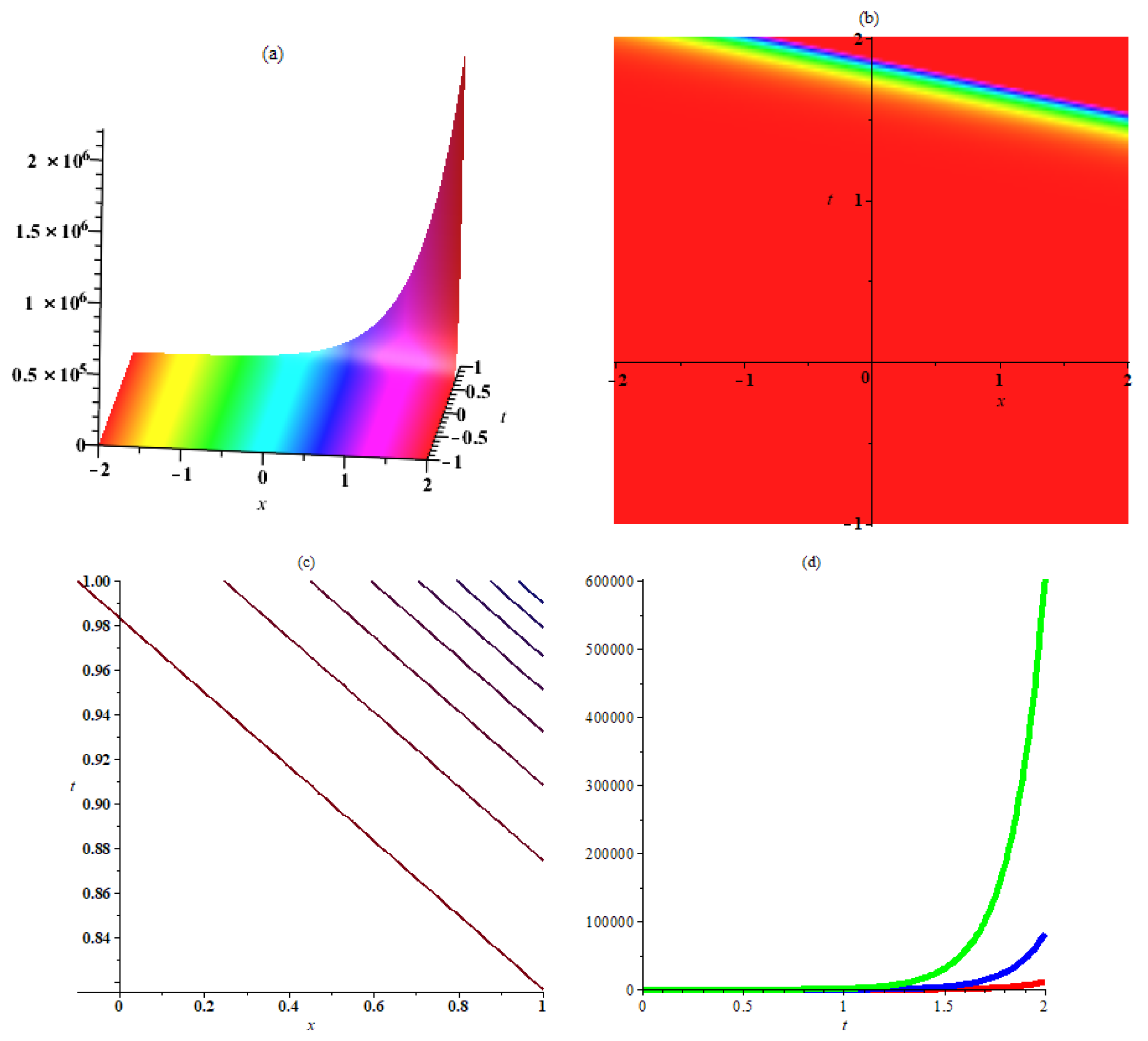
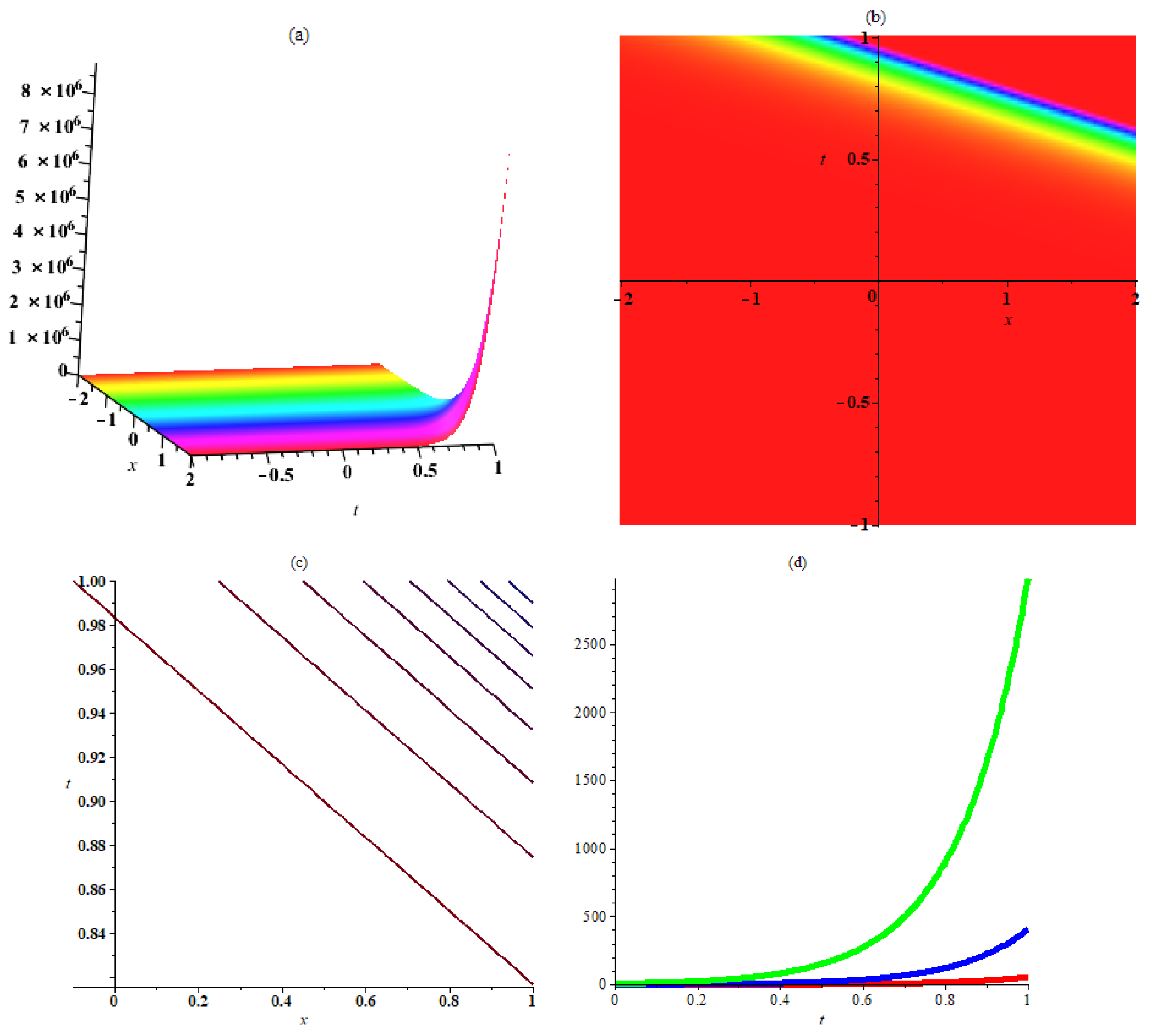
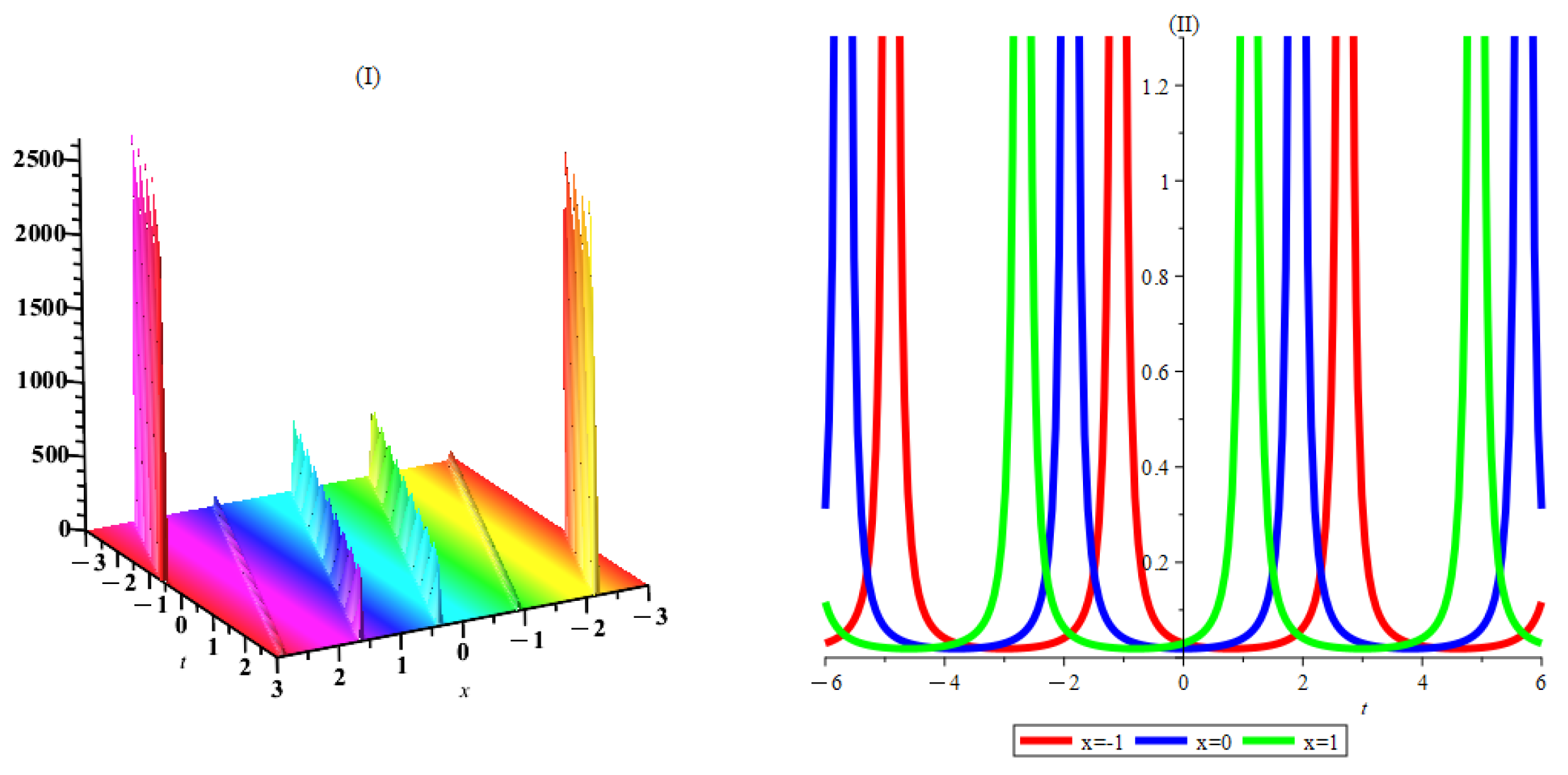
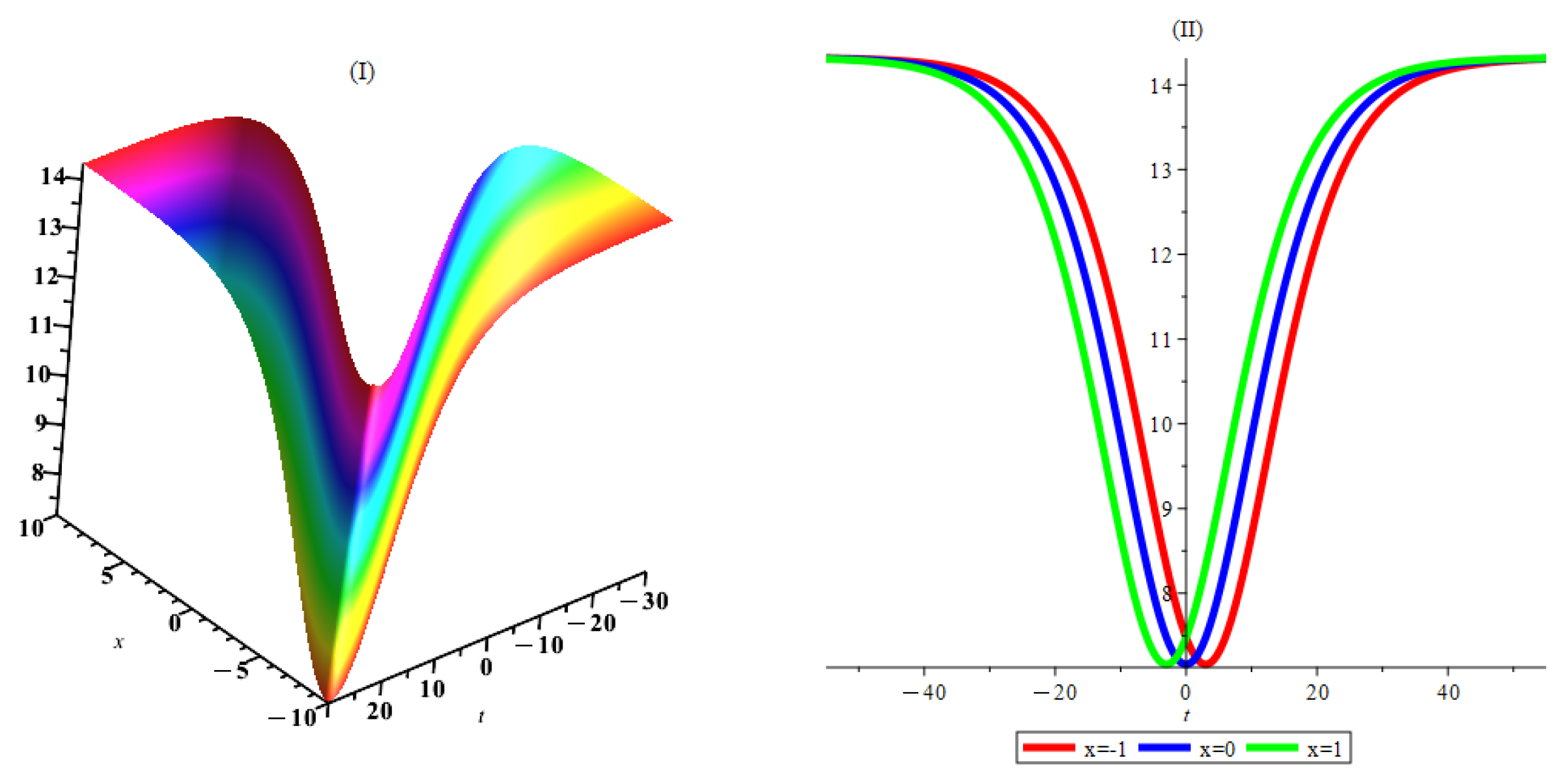
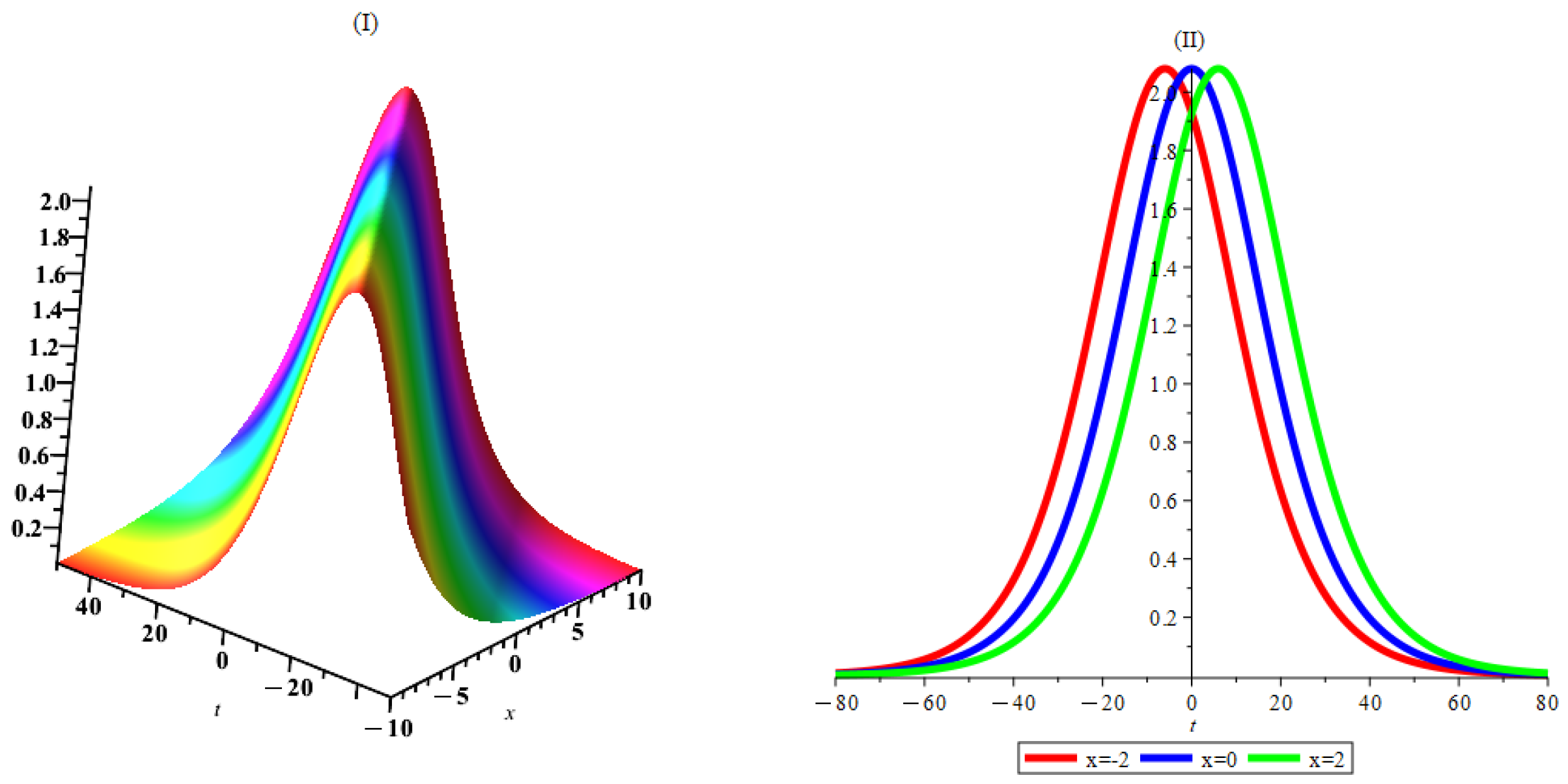
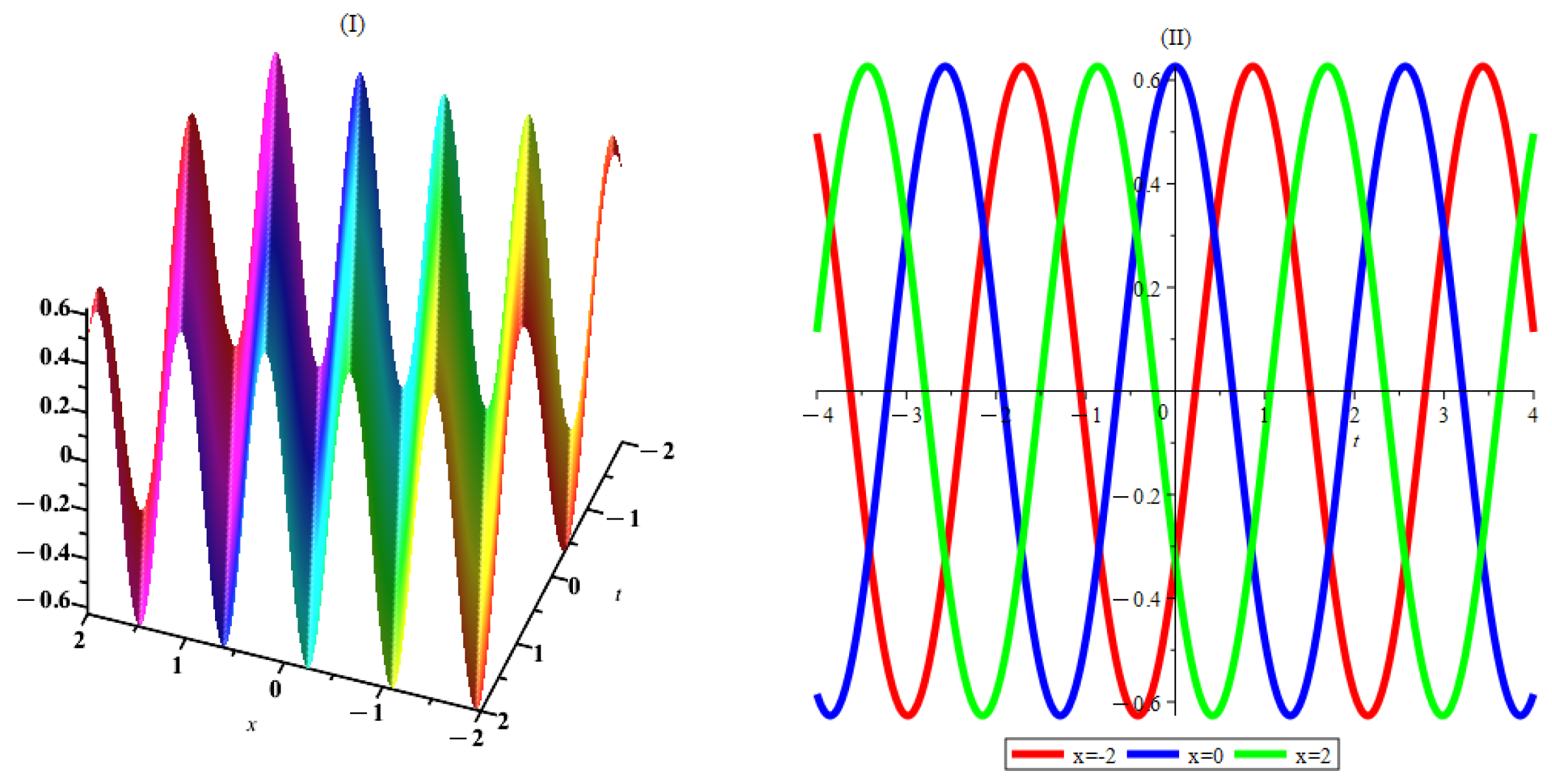
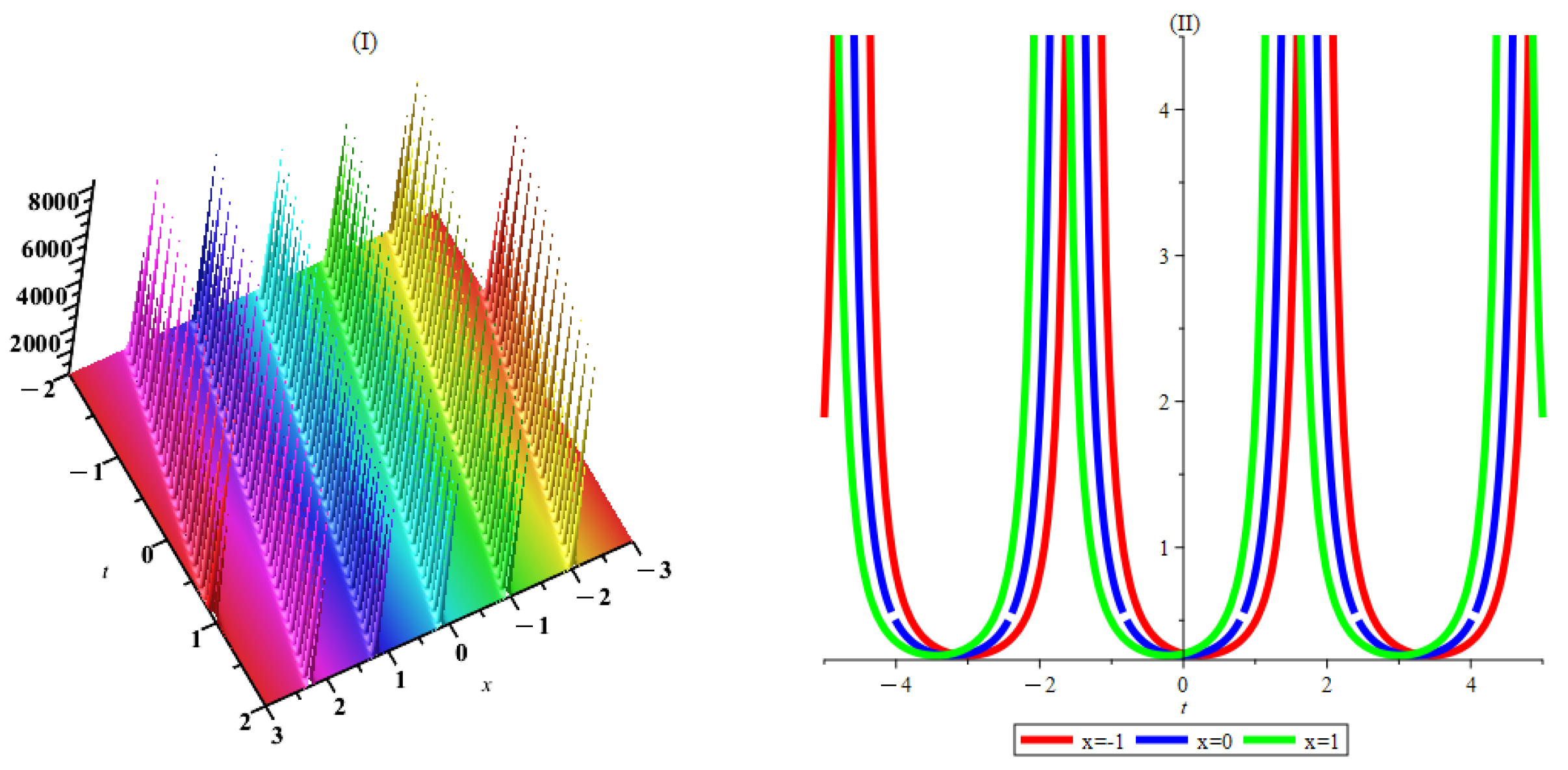
6. Interpretation and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Samir, I.; Badra, N.; Ahmed, H.M.; Arnous, A.H.; Ghanem, A.S. Solitary wave solutions and other solutions for Gilson-Pickering equation by using the modified extended mapping method. Results Phys. 2022, 36, 105427. [Google Scholar] [CrossRef]
- Rani, A.; Zulfiqar, A.; Ahmad, J.; Hassan, Q.M.U. New soliton wave structures of fractional Gilson-Pickering equation using tanh-coth method and their applications. Results Phys. 2021, 29, 104724. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Jhangeer, A.; Tala-Tebue, E.; Hashemi, M.S.; Sharif, S.; Ahmad, H.; Yao, S.W. New wave surfaces and bifurcation of nonlinear periodic waves for Gilson-Pickering equation. Results Phys. 2021, 24, 104192. [Google Scholar] [CrossRef]
- Kai, Y.; Li, Y.; Huang, L. Topological properties and wave structures of Gilson-Pickering equation, Chaos. Solitons Fractals 2022, 157, 111899. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Nikan, O.; Avazzadeh, Z. Traveling wave solutions of the nonlinear Gilson-Pickering equation in crystal lattice theory. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar]
- Ali, K.K.; Mehanna, M.S. Traveling wave solutions and numerical solutions of Gilson-Pickering equation. Results Phys. 2021, 28, 104596. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, M. Homotopy perturbation method for fractional Fornberg-Whitham equation. Comput. Math. Appl. 2011, 61, 250–254. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Bayram, M. An application of genocchi wavelets for solving the fractional Rosenau-Hyman equation. Alex. Eng. J. 2021, 60, 5331–5340. [Google Scholar] [CrossRef]
- Sun, Y.L.; Ma, W.X.; Yu, J.-P.; Khalique, C.M. Exact solutions of the Rosenau-Hyman equation, coupled KdV system and Burgers-Huxley equation using modified transformed rational function method. Mod. Phys. Lett. B 2018, 32, 1850282. [Google Scholar] [CrossRef]
- Du, L.; Wu, X. Singularities in finite time of a 3-component Camassa-Holm equations. Appl. Math. Lett. 2022, 134, 10831. [Google Scholar] [CrossRef]
- Saha, A.; Banerjee, S. Dynamical Systems and Nonlinear Waves in Plasmas; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Khater, M.M. Two–component plasma and electron trapping’s influence on the potential of a solitary electrostatic wave with the dust-ion-acoustic speed. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Mahmoud, E.E.; Abdel-Aty, A.H.; Abualnaja, K.; Mohamed, A.-B.; Eleuch, H. On the interaction between (low & high) frequency of (ion-acoustic & langmuir) waves in plasma via some recent computational schemes. Results Phys. 2020, 19, 103684. [Google Scholar]
- Khater, M.M. Abundant stable and accurate solutions of the three-dimensional magnetized electron-positron plasma equations. J. Ocean. Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Zhao, D.; Lu, D.; Salama, S.A.; Yongphet, P.; Khater, M.M. Soliton wave solutions of ion-acoustic waves a cold plasma with negative ions. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 852–895. [Google Scholar] [CrossRef]
- Khater, M.M.; Seadawy, A.R.; Lu, D. Bifurcations of solitary wave solutions for (two and three)-dimensional nonlinear partial differential equation in quantum and magnetized plasma by using two different methods. Results Phys. 2018, 9, 142–150. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Iqbal, J.; Arif, M.; Khan, A.; Gasimov, Y.S.; Chinram, R. A new application of Gauss quadrature method for solving systems of nonlinear equations. Symmetry 2021, 13, 432. [Google Scholar] [CrossRef]
- Gasimov, Y.S. On a shape design problem for one spectral functional. J. Inverse Ill-Posed Probl. 2013, 21, 629–637. [Google Scholar] [CrossRef]
- Aslanova, F. A comparative study of the hardness and force analysis methods used in truss optimization with metaheuristic algorithms and under dynamic loading. Journal of Research in Science. Eng. Technol. 2020, 8, 25–33. [Google Scholar] [CrossRef]
- Madina, B.; Gumilyov, L.N. Determination of the Most Effective Location of Environmental Hardenings in Concrete Cooling Tower Under Far-Source Seismic Using Linear Spectral Dynamic Analysis Results. J. Res. Sci. Eng. Technol. 2020, 8, 22–24. [Google Scholar] [CrossRef]
- Bouchaala, F.; Ali, M.Y.; Matsushima, J.; Bouzidi, Y.; Takougang, E.M.T.; Mohamed, A.A.; Sultan, A. Azimuthal investigation of compressional seismic-wave attenuation in a fractured reservoirSeismic wave attenuation anisotropy. Geophysics 2019, 84, B437–B446. [Google Scholar] [CrossRef]
- Diaz-Acosta, A.; Bouchaala, F.; Kishida, T.; Jouini, M.S.; Ali, M.Y. Investigation of fractured carbonate reservoirs by applying shear-wave splitting concept. Adv. Geo-Energy Res. 2023, 7, 99–110. [Google Scholar] [CrossRef]
- Velidi, G. Pressure and velocity variation in remote-controlled plane using cfd analysis. J. Airl. Oper. Aviat. Manag. 2022, 1, 9–18. [Google Scholar] [CrossRef]
- Rajan, R.A.; Bharathi, A.P.; Sarika, A.S. Multimodal Biometric Template Transformation Approach using a List Ranking Algorithm. Rev. Comput. Eng. Res. 2022, 9, 239–249. [Google Scholar]
- Cai, W.; Mohammaditab, R.; Fathi, G.; Wakil, K.; Ebadi, A.G.; Ghadimi, N. Optimal bidding and offering strategies of compressed air energy storage: A hybrid robust-stochastic approach. Renew Energy 2019, 143, 1–8. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, T.; He, G.; Nojavan, S.; Jermsittiparsert, K.; Ghadimi, N. Energy management of wind-PV-storage-grid based large electricity consumer using robust optimization technique. J. Energy Storage 2020, 27, 101054. [Google Scholar] [CrossRef]
- Mehrpooya, M.; Ghadimi, N.; Marefati, M.; Ghorbanian, S.A. Numerical investigation of a new combined energy system includes parabolic dish solar collector, stirling engine and thermoelectric device. Int. J. Energy Res. 2021, 45, 16436–16455. [Google Scholar] [CrossRef]
- Gu, Y.; Malmir, S.; Manafian, J.; Ilhan, O.A.; Alizadeh, A.; Othman, A.J. Variety interaction between k-lump and k-kink solutions for the (3+1)-D Burger system by bilinear analysis. Results Phys. 2022, 43, 106032. [Google Scholar] [CrossRef]
- Guo, B.; Dong, H.; Fang, Y. Lump Solutions and Interaction Solutions for the Dimensionally Reduced Nonlinear Evolution Equation. Complexity 2019, 2019, 5765061. [Google Scholar] [CrossRef]
- Manafian, J.; Lakestani, M. N–lump and interaction solutions of localized waves to the (2+1)-dimensional variable-coefficient Caudrey–Dodd-Gibbon-Kotera-Sawada equation. J. Geom. Phys. 2020, 150, 103598. [Google Scholar] [CrossRef]
- Li, R.; Bu Sinnah, Z.A.; Shatouri, Z.M.; Manafian, J.; Aghdaei, M.F.; Kadi, A. Different forms of optical soliton solutions to the Kudryashov’s quintuple self-phase modulation with dual-form of generalized nonlocal nonlinearity. Results Phys. 2023, 46, 106293. [Google Scholar] [CrossRef]
- Riahi, R.; Ghasemi, M.; Shatouri, Z.M.; Gharipour, M.; Maghami, M.; Melali, H.; Sami, R.; Tabatabaei, A.; Hosseini, S.M. Risk Factors for In-Hospital Mortality among Patients with Coronavirus-19 in Isfahan City, Iran. Adv. Biomed. Res. 2022, 11, 121. [Google Scholar]
- Zhao, C.; Cheung, C.F.; Xu, P. High-efficiency sub-microscale uncertainty measurement method using pattern recognition. ISA Trans. 2020, 101, 503–514. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xie, J.; Shi, W.; Huo, Y.; Ren, Z.; He, D. Resonance and bifurcation of fractional quintic Mathieu–Duffing system. Chaos: Int. J. Nonlinear Sci. 2023, 33, 23131. [Google Scholar] [CrossRef]
- Xie, X.; Huang, L.; Marson, S.M.; Wei, G. Emergency response process for sudden rainstorm and flooding: Scenario deduction and Bayesian network analysis using evidence theory and knowledge meta-theory. Nat. Hazards 2023, 117, 3307–3329. [Google Scholar] [CrossRef]
- Guo, C.; Hu, J. Fixed-Time Stabilization of High-Order Uncertain Nonlinear Systems: Output Feedback Control Design and Settling Time Analysis. J. Syst. Sci. Complex. 2023. [Google Scholar] [CrossRef]
- Luo, R.; Peng, Z.; Hu, J. On Model Identification Based Optimal Control and It’s Applications to Multi-Agent Learning and Control. Mathematics 2023, 11, 906. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time observer based tracking control of uncertain heterogeneous underwater vehicles using adaptive sliding mode approach. Neurocomput. 2022, 481, 322–332. [Google Scholar] [CrossRef]
- Manafian, J.; Mohammed, S.A.; Alizadeh, A.; Baskonus, H.M.; Gao, W. Investigating lump and its interaction for the third–order evolution equation arising propagation of long waves over shallow water. Eur. J. Mech.-B/Fluids 2020, 84, 289–301. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, X.; Huang, H.; Zhang, D.; Ghadimi, N. Optimal economic scheduling of microgrids considering renewable energy sources based on energy hub model using demand response and improved water wave optimization algorithm. J. Energy Storage 2022, 55, 105311. [Google Scholar] [CrossRef]
- Erfeng, H.; Ghadimi, N. Model identification of proton-exchange membrane fuel cells based on a hybrid convolutional neural network and extreme learning machine optimized by improved honey badger algorithm. Sustain. Energy Technol. Assessments 2022, 52, 102005. [Google Scholar]
- Saeedi, M.; Moradi, M.; Hosseini, M.; Emamifar, A.; Ghadimi, N. Robust optimization based optimal chiller loading under cooling demand uncertainty. Appl. Therm. Eng 2019, 148, 1081–1091. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Ghadimi, N. Probabilistic decomposition-based security constrained transmission expansion planning incorporating distributed series reactor. IET Gener. Trans. Distrib. 2020, 14, 3478–3487. [Google Scholar] [CrossRef]
- Mir, M.; Shafieezadeh, M.; Heidari, M.A.; Ghadimi, N. Application of hybrid forecast engine based intelligent algorithm and feature selection for wind signal prediction. Evolv. Syst. 2020, 11, 559–573. [Google Scholar] [CrossRef]
- Rao, X.; Manafian, J.; Mahmoud, K.H.; Hajar, A.; Mahdi, A.B.; Zaidi, M. The nonlinear vibration and dispersive wave systems with extended homoclinic breather wave solutions. Open Phys. 2022, 20, 795–821. [Google Scholar] [CrossRef]
- Zhong, Q.; Han, S.; Shi, K.; Zhong, S.; Kwon, O. Co-Design of Adaptive Memory Event-Triggered Mechanism and Aperiodic Intermittent Controller for Nonlinear Networked Control Systems. IEEE Trans. Circuits Sys. II Express Briefs 2022, 69, 4979–4983. [Google Scholar] [CrossRef]
- Ma, Q.; Meng, Q.; Xu, S. Distributed Optimization for Uncertain High-Order Nonlinear Multiagent Systems via Dynamic Gain Approach. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4351–4357. [Google Scholar] [CrossRef]
- Chen, D.; Wang, Q.; Li, Y.; Li, Y.; Zhou, H.; Fan, Y. A general linear free energy relationship for predicting partition coefficients of neutral organic compounds. Chemosphere 2020, 247, 125869. [Google Scholar] [CrossRef]
- Alimirzaluo, E.; Nadjafikhah, M.; Manafian, J. Some new exact solutions of (3+1)-dimensional Burgers system via Lie symmetry analysis. Adv. Diff. Equ. 2021, 2021, 60. [Google Scholar] [CrossRef]
- Wu, W.; Manafian, J.; Ali, K.K.; Karakoc, S.B.; Taqik, A.H.; Mahmoud, M.A. Numerical and analytical results of the 1D BBM equation and 2D coupled BBM-system by finite element method. Int. J. Mod. Phys. B 2022, 36, 2250201. [Google Scholar] [CrossRef]
- Pan, Y.; Manafian, J.; Zeynalli, S.M.; Al-Obaidi, R.; Sivaraman, R.; Kadi, A. N-Lump Solutions to a (3+1)-Dimensional Variable-Coefficient Generalized Nonlinear Wave Equation in a Liquid with Gas Bubbles. Qual. Theory Dynamical. Syst. 2022, 21, 127. [Google Scholar] [CrossRef]
- Shen, X.; Manafian, J.; Jiang, M.; Ilhan, O.A.; Shafikk, S.S.; Zaidi, M. Abundant wave solutions for generalized Hietarinta equation with Hirota’s bilinear operator. Mod. Phys. Lett. B 2022, 36, 2250032. [Google Scholar] [CrossRef]
- Yang, Z.; Ghadamyari, M.; Khorramdel, H.; Alizadeh, S.M.S.; Pirouzi, S.; Milani, M.; Banihashemi, F.; Ghadimi, N. Robust multi-objective optimal design of islanded hybrid system with renewable and diesel sources/stationary and mobile energy storage systems. Renew. Sustain. Energy Rev. 2021, 148, 111295. [Google Scholar] [CrossRef]
- Yu, D.; Noradin, G. Reliability constraint stochastic UC by considering the correlation of random variables with Copula theory. IET Renew. Power Gener. 2019, 13, 2587–2593. [Google Scholar] [CrossRef]
- Li, R.; Ilhan, O.A.; Manafian, J.; Mahmoud, K.H.; Abotaleb, M.; Kadi, A. A Mathematical Study of the (3+1)-D Variable Coefficients Generalized Shallow Water Wave Equation with Its Application in the Interaction between the Lump and Soliton Solutions. Mathematics 2022, 10, 3074. [Google Scholar] [CrossRef]
- Ak, T.; Saha, A.; Dhawan, S. Performance of a hybrid computational scheme on traveling waves and its dynamic transition for Gilson-Pickering equation. Int. J. Mod. Phys. C 2019, 30, 1950028. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Khodadadian, A.; Parvizi, M.; Dehghan, M.; Heitzinger, C. A direct meshless local collocation method for solving stochastic Cahn-Hilliard-Cook and stochastic Swift-Hohenberg equations. Eng. Anal. Bound. Elem. 2019, 98, 253–264. [Google Scholar] [CrossRef]
- Ak, T.; Abbaszadeh, M.; Dehghan, M.; Khodadadian, A.; Noii, N.; Heitzinger, C.; Wick, T. A reduced-order variational multiscale interpolating element free Galerkin technique based on proper orthogonal decomposition for solving Navier-Stokes equations coupled with a heat transfer equation: Nonstationary incompressible Boussinesq equations. J. Comput. Phys. 2021, 426, 109875. [Google Scholar]
- Kudryashov, N.A. The Painlevé approach for finding solitary wave solutions of nonlinear nonintegrable differential equations. Optik 2019, 183, 642–649. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Manafian, J.; Mahmoud, K.H.; Alsubaie, A.S.; Aldurayhim, A.; Alkader, A. Cutting-Edge Analytical and Numerical Approaches to the Gilson–Pickering Equation with Plenty of Soliton Solutions. Mathematics 2023, 11, 3454. https://doi.org/10.3390/math11163454
Chen W, Manafian J, Mahmoud KH, Alsubaie AS, Aldurayhim A, Alkader A. Cutting-Edge Analytical and Numerical Approaches to the Gilson–Pickering Equation with Plenty of Soliton Solutions. Mathematics. 2023; 11(16):3454. https://doi.org/10.3390/math11163454
Chicago/Turabian StyleChen, Wensheng, Jalil Manafian, Khaled Hussein Mahmoud, Abdullah Saad Alsubaie, Abdullah Aldurayhim, and Alabed Alkader. 2023. "Cutting-Edge Analytical and Numerical Approaches to the Gilson–Pickering Equation with Plenty of Soliton Solutions" Mathematics 11, no. 16: 3454. https://doi.org/10.3390/math11163454
APA StyleChen, W., Manafian, J., Mahmoud, K. H., Alsubaie, A. S., Aldurayhim, A., & Alkader, A. (2023). Cutting-Edge Analytical and Numerical Approaches to the Gilson–Pickering Equation with Plenty of Soliton Solutions. Mathematics, 11(16), 3454. https://doi.org/10.3390/math11163454





