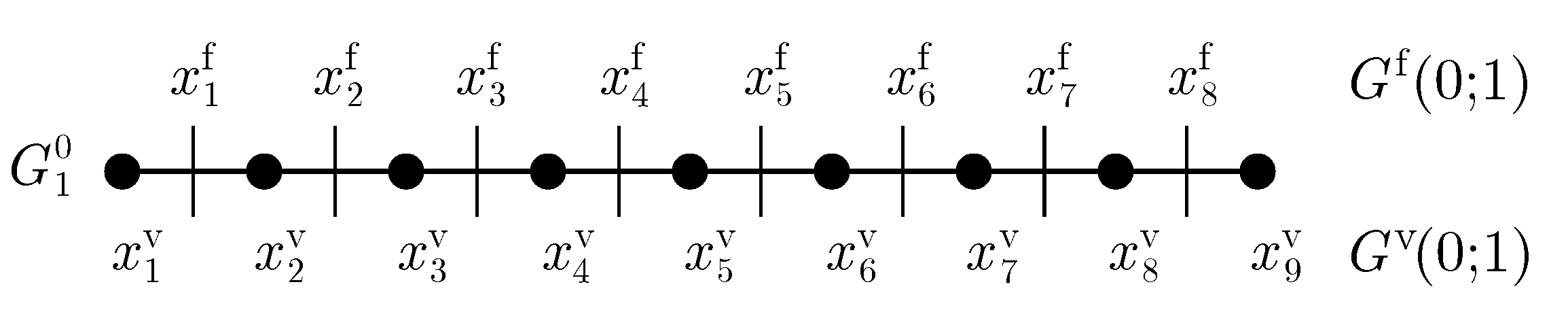Black-Box Solver for Numerical Simulations and Mathematical Modelling in Engineering Physics

Abstract

This article presents a two-grid approach for developing a black-box iterative solver for a large class of real-life problems in continuum mechanics (heat and mass transfer, fluid dynamics, elasticity, electromagnetism, and others). The main requirements on this (non-)linear black-box solver are: (1) robustness (the lowest number of problem-dependent components), (2) efficiency (close-to-optimal algorithmic complexity), and (3) parallelism (a parallel robust algorithm should be faster than the fastest sequential one). The basic idea is to use the auxiliary structured grid for more computational work, where (non-)linear problems are simpler to solve and to parallelize, i.e., to combine the advantages of unstructured and structured grids: simplicity of generation in complex domain geometry and opportunity to solve (non-)linear (initial-)boundary value problems by using the Robust Multigrid Technique. Topics covered include the description of the two-grid algorithm and estimation of their robustness, convergence, algorithmic complexity, and parallelism. Further development of modern software for solving real-life problems justifies relevance of the research. The proposed two-grid algorithm can be used in black-box parallel software for the reduction in the execution time in solving (initial-)boundary value problems.

1. Introduction

Mathematical modelling of physical and chemical processes has always been an important activity in science and engineering [1]. Scientists and engineers, however, cannot understand all the details of the mathematical models, numerical algorithms, parallel computing technologies, and parallel supercomputer architectures. This fact motivates the development of black-box software.

Several industries, as well as engineering and consulting companies worldwide, use commercially available general-purpose CFD codes for the simulation of fluid flow, heat and mass transfer, and combustion in aerospace applications (Fluent, Star-CCM+, COMSOL’s CFD Module, Altair’s AcuSolve, and others). Also, many universities and research institutes worldwide apply commercial codes, in addition to using those developed in house. Today, open-source codes such as OpenFOAM are also freely available. Other important issues are the description of complex domain geometries and the generation of suitable grids. However, to successfully apply such codes and to interpret the computed results, it is necessary to understand the fundamental concepts of computational methods. A promising and challenging trend in numerical simulation and scientific computing is to devise a single code to handle all problems which already be solved.

As a rule, mathematical modelling consists of the following stages:

(1)

The formulation of the mathematical model for the studied physical and chemical processes in form

$$\mathcal{N}\left(u\right)=f;$$

(1)

(2)

The approximation of the space-time continuum (generation of computational grid G);

(3)

The approximation of the differential problems (1) on grid G to obtain a discrete analogue of the mathematical model

$${\mathcal{N}}_h^{}\left(u_h^{}\right)=f_h^{};$$

(2)

(4)

A numerical solution for the (non-)linear discrete equations

$$u_h^{}={\mathcal{N}}_h^{-1}{f}_h^{}$$

(3)

on a sequential or parallel computer;

(5)

The visualisation and analysis of computational results.

Here, $\mathcal{N}\left(u\right)=f$ denotes a system of (non-)linear PDEs and (initial-)boundary conditions (mathematical model), ${\mathcal{N}}_h^{}\left(u_h^{}\right)=f_h^{}$ denotes the resulting system of (non-)linear algebraic Equations (the discrete analogue of the mathematical model), and $u_h^{}={\mathcal{N}}_h^{-1}{f}_h^{}$ is the numerical solution.

Unfortunately, each stage of the mathematical modelling is a very complex problem which has not yet been solved robustly. The most time consuming step in execution is the numerical solution of (non-)linear discrete Equation (3).

Some remarks need to be added to the concept of black-box solver. Previously, an algorithm for solving a system of linear algebraic equations was called black-box solver if it required only the matrix formulation of problem $A\mathbf{x}=\mathbf{b}$, i.e., the coefficient matrix A, the right-hand side vector $\mathbf{b}$, and a starting guess ${\mathbf{x}}_{}^{\left(0\right)}$ to the solution $A_{}^{-1}\mathbf{b}$ [2]. A similar approach is applicable to solving the linear problems or to solving globally linearized nonlinear problems without any geometric input [3].

Monolithic methods applied to the entire system in a coupled manner demonstrate robust convergence for the saddle point problems and multiphysics simulation [4,5]. The most elegant conservative approach to construct the monolithic algorithm is finite volume-coupled ordering of unknowns, i.e., with usage of geometric data on computational grid. It is clear that efficient monolithic method is too difficult to construct for solving systems of strongly coupled nonlinear PDEs using only local linearization.

We define software as black-box if it does not require any additional input from the user apart from a specification of the physical problem consisting of the domain geometry, boundary and initial conditions, source terms, the enumeration of the equations to be solved (heat conductivity equation, Navier–Stokes equations, Maxwell equations, etc.), and mediums. The user does not need to know anything about numerical methods or high-performance and parallel computing [6]. The idea behind robust algorithms is to choose the components independently of a given problem to match large a class of problems as possible [7]. The robust approach is often used in software packages where attaining the highest efficiency for a single problem is not so important [3,8].

In fact, we have the numerous mathematical models of various physical and chemical processes for multiphysics simulation in real-life problems, the numerous methods for generating adaptive unstructured or (block-)structured grids [9], numerous methods for approximating the nonlinear (initial-)boundary value problems on these grids, the orderings of unknowns and the numerous iterative methods for parallel segregated/coupled solution of globally/locally linearized discrete analogues of these nonlinear (initial-)boundary value problems. If it possible to develop «one parallel solver for all problems», then this solver can be putted into black-box software for parallel handling a wide class of real-life problems. It should be emphasized that the execution time critically depends on the computational algorithm used to solve the real-life problems in parallel.

The development of classical solvers can be regarded as the attempts to improve either robustness or convergence rate, or efficiency of parallel algorithm [3]. In our view, the development of black-box solver can be regarded as the attempt to simultaneously improve robustness, convergence rate, and efficiency of parallel algorithm, despite mutual exclusive nature of these requirements.

This paper will focus on mathematical background of the black-box solver development. First, it is necessary to formulate the problem of constructing black-box solver. Next, a two-grid algorithm consisting of the original and auxiliary grids for solving nonlinear (initial-) boundary value problems will be presented. Then Robust Multigrid Technique (RMT) for solving the nonlinear (initial-) boundary value problems on the auxiliary grid will be presented. The goal of the paper is to develop a black-box computational approach for parallel solution of a wide class of applied problems starting with the Poisson equation up to systems of nonlinear strongly coupled partial differential equations (multiphysics simulation) in domains with complex geometry, which we already know how to solve. The main difficulty is that this algorithm must satisfy three mutually exclusive requirements (robustness, efficiency, and parallelism).

Modern software (Fluent, Star-CCM+, COMSOL’s CFD Module, Altair’s AcuSolve, and others) use general building blocks, which helps users to develop their own software for particular applications without having to start from scratch. The efficiency of users algorithm assembled from these building blocks is difficult to estimate, finding their optimal forms can impose challenges for many applications. The attempts are made to optimize the iterative algorithms using neural networks [10,11]. For example, the transfer operators are crucial for fast convergence of multigrid methods, but they are unknown in advance. To find them original approach based on a reformulation of the two-grid method in terms of a deep neural network with a specific architecture has been proposed and developed [12]. A more attractive approach is to minimize the number of problem-dependent components, i.e., to develop Robust Multigrid Technique with the problem-independent transfer operators (Section 4). This one of reasons for indicating the practical significance of the work.

The article is structured as follows: In Section 1, we briefly introduce main problems caused by further development of black-box software for scientific and technical computations. Section 2 describes general requirements on black-box solver such as robustness, complexity, and parallelism. Section 3 introduces two-grid algorithm with auxiliary structured grid for simplifying coupled solution of nonlinear (initial-)boundary value problems. Section 4 represents Robust Multigrid Technique used on the auxiliary grid. Discussion on the multigrid methods is given in Section 5. Section 6 summarizes advantages of the two-grid algorithm.

2. General Requirements on Black-Box Solver

In order to clarify our understanding of black-box solver, we want to briefly discuss different computational aspects of real-life problems and to point out those problem features which we regard as the most significant ones:

(1)

Generation and adaptive refinement of the computational grids in complex domains. Unstructured automatic mesh generation is much easier than the generation of (block-)structured grids for very complicated domains, but the construction of efficient solver is much easier for structured grids [13,14]. Adaptivity and parallelism are numerically important principles, which, however, partly conflict with each other [3].

(2)

Multiphysics simulation. Multiphysics simulation involves the numerical analysis of multiple, simultaneous physical and chemical phenomena (such as heat transfer, fluid flow, deformation, electromagnetics, acoustics, mass transport, and others). The systems of nonlinear partial differential equations describing the phenomena can be solved in (de-)coupled manner. The coupled and decoupled iterations show a certain difference in the computational work, which is not known in advance but detected during the iterative solution process.

(3)

Stationary or non-stationary solution. The initial-boundary value problems for the time-dependent PDEs of engineering physics and the efficient algorithms for their numerical solution are of considerable scientific and practical interest [15]. The following are reasons for this:

(a)

Some physical processes (for example, turbulence) are purely non-stationary 3D phenomena;

(b)

The initial-boundary value problems are particularly useful if the solution shows an unsteady behaviour which is not known in advance. A steady-state solution can be obtained through pseudo-time marching. Using semi-implicit or fully implicit discretizations, large and adaptable time steps can be used, and parallel processing across space and/or time is feasible;

(c)

The systems of strongly coupled nonlinear PDEs are used for multiphysics simulation in real-life problems. In this case, the time step can be used as an under-relaxation factor for convergence control of the nonlinear iterations.

Therefore, a time-dependent formulation of PDEs is more preferable for black-box implementation. The computational algorithm must be efficient for different grid aspect ratio in time and in space.

What properties should the true black-box algorithm have? From our point of view, the most significant properties are: robustness, optimal computational work. Remember that here the number of problem-dependent component defines the robustness of algorithms: an algorithm is called robust if it has the least number of problem-dependent components among algorithms of the same class and optimal computational work is the opportunity to solve many problems to within truncation error at a cost of $CN$ arithmetic operations, where N is the number of unknowns. The development of black-box solvers for multidisciplinary applications based on the solution of the “robustness–efficiency–parallelism” problem is a new challenge for scientific computing. Unfortunately, the true black-box solver cannot be constructed because the above requirements are mutually exclusive. Therefore, it is necessary to soften the “robustness–efficiency–parallelism” requirements in order to construct a close-to-black-box solver.

Algorithmic complexity $\left(\mathcal{W}\right)$ is a way of comparing the efficiency of computational algorithms. Complexity can be measured in terms of the number of arithmetic operations that it takes for the algorithm to solve the given problem.

We start our discussion with linear PDEs since the analysis is particularly easy and illustrative: let $\mathcal{N}$ be a linear elliptic operator in (1) (for example, $\mathcal{N}$ is a Laplace operator) and the domain $\Omega$ be d-dimensional unit cube ($d=2,3$). A uniform computational grid G is generated by dividing each edge of the cube $\Omega$ into n subintervals. In the following, n and $h=1/n$ denote the discretization parameter and mesh size, respectively. Some approximation of the problem (1) on the grid G results in the discrete analogue (2).

Using some ordering of unknowns, the linear discrete problem (2) can be rewritten in the matrix form

$$A\mathbf{u}=\mathbf{b},$$

(4)

where A is a coefficient matrix, $\mathbf{u}$ is a vector of unknowns, and $\mathbf{b}$ is a right-hand side vector. General linear iterations for solving the system (4) can be represented in the form

$$W\left({\mathbf{u}}_{}^{(s+1)}-{\mathbf{u}}_{}^{\left(s\right)}\right)=\mathbf{b}-A{\mathbf{u}}_{}^{\left(s\right)},s=0,1,2,\dots ,$$

(5)

where the splitting matrix W defines a basic linear iterative algorithm

$${\mathbf{u}}_{}^{(s+1)}=\left(I-W_{}^{-1}A\right){\mathbf{u}}_{}^{\left(s\right)}+W_{}^{-1}\mathbf{b},$$

where I is the unity matrix, and s is the iteration counter. In the following, we will assume that the system (4) has an unique solution $\mathbf{u}=A_{}^{-1}\mathbf{b}$ and iterations (5) converge to this solution: ${\mathbf{u}}_{}^{\left(s\right)}\to \mathbf{u}=A_{}^{-1}\mathbf{b}$ for $s\to +\infty$. The basic linear algorithm (5) for iterative solving (4) has three problem-dependent components: the ordering of unknowns, the splitting matrix W and a stopping criterion for these iterations.

For estimating the algorithmic complexity, we assume that a block ordering of the unknowns is used, i.e., the number of unknowns becomes

$$N=n_{}^d=n_b^{}{N}_b^{},$$

where $n_b^{}$ is the number of blocks, $N_b^{}$ is the number of unknowns forming each block, $N=n_{}^d,d=2,3$ is the number of unknowns, and n is the discretization parameter ($h=1/n$). The computational cost of each Vanka-type iteration (block Gauss–Seidel method used for the coupled numerical solution of systems of PDEs including the saddle-point problems [16,17]) is

$${\mathcal{W}}_1^{}=C{n}_b^{}{N}_b^3=C{n}_b^{-2}{N}_{}^3$$

arithmetic operations (ao), where C is some constant. The number of iterations (5) can be estimated as

$$\Theta =n_{}^{\varkappa }=N_{}^{\varkappa /d},$$

where the parameter $\varkappa$ depends on the condition number of the coefficient matrix A and the block size $N_b^{}$, $d=2,3$. Then the algorithmic complexity of the block iterative method becomes

$$\mathcal{W}=\Theta {\mathcal{W}}_1^{}=C{n}_b^{-2}{N}_{}^{3+\varkappa /d}\mathtt{ao}.$$

(6)

Use of the uniform grid in the above-mentioned linear analysis makes it possible to obtain the expression (6) for estimating the computational work. If $n_b^{}=1$, then the block iteration coincides with the Gaussian elimination

$$\varkappa =0\Rightarrow \mathcal{W}=C{N}_{}^3\mathtt{ao},$$

i.e., the complexity $\mathcal{W}$ is $\varkappa$-independent and

$$n_b^{}\to 1\Rightarrow \varkappa \to 0.$$

The Gaussian elimination with partial/complete pivoting is implemented without the problem-dependent components, but large complexity ($\mathcal{W}=O\left(N_{}^3\right)\mathtt{ao}$) allows this direct method to be used for solving small systems of linear algebraic Equations (SLAEs).

The point ordering of an unknown corresponds to $n_b^{}=N$. In this case, the algorithmic complexity becomes

$$\mathcal{W}=C{N}_{}^{1+\varkappa /d}\mathtt{ao}.$$

It is expected that the point iterative method (5) will be faster than the Gaussian elimination for sufficiently large N, i.e., $0\le \varkappa <2d$.

The parameter $\varkappa$ depends on the coefficient matrix A: $\varkappa \to 0$ for well-conditioned problems and the point iterative method has almost optimal algorithmic complexity

$$\mathcal{W}\to CN\mathtt{ao}\mathrm{for}\varkappa \to 0.$$

As a rule, it is not useful to accelerate a highly efficient solver. The extra effort does not pay off.

Thus, the simplest problem of constructing a robust iterative algorithm for numerical solving linear (initial-)boundary value problems on a uniform grid can be formulated as follows:

(1)

If A in (4) is a well-conditioned coefficient matrix ($\varkappa \to 0$), then the robust iterative algorithm must coincide with the basic linear algorithm (5);

(2)

If A in (4) is an ill-conditioned coefficient matrix ($0<\varkappa <2d$), then it is necessary to add the lowest number of problem-dependent components to the basic linear algorithm (5) to:

(a)

Reduce the algorithmic complexity (6) down to a close-to-optimal value

$$\mathcal{W}=C{n}_b^{-2}{N}_{}^{3}logN\mathtt{ao},1\ll n_b^{}\le N$$

(7)

in sequential implementation;

(b)

Ensure that a parallel algorithm should be faster than the fastest sequential solver.

The above considerations imply that it is necessary to coupled consider the two requirements of close-to-optimal complexity (7) and parallelism. For the given purpose, the execution time of a parallel close-to-black-box algorithm should be compared with the execution time of the fastest (optimal) sequential algorithm. Let

$${\mathcal{W}}_o^{}=C_o^{}{n}_b^{-2}{N}_{}^3\mathtt{ao}$$

(8)

be the algorithmic complexity of optimal solver and

$${\mathcal{W}}_p^{}=C_p^{}{\displaystyle \frac{1}{p}}{n}_b^{-2}{N}_{}^{3}logN\mathtt{ao}$$

be the algorithmic complexity of fully parallel close-to-black-box solver (7). Here, p is the number of independent computing units in parallel implementation and $C_o^{}$ and $C_p^{}$ are some constant. Assuming that the execution time is proportional to the complexity in the algorithm considered ($T\sim \mathcal{W}$), we have

$$S={\displaystyle \frac{T_o^{}}{T_p^{}}}\approx {\displaystyle \frac{C_o^{}}{C_p^{}}}{\displaystyle \frac{p}{logN}},$$

where S is the speed-up of the parallel solver over the optimal one, $T_o^{}$ is the execution time of the sequential optimal algorithm, and $T_p^{}$ is the execution time of the parallel close-to-black-box algorithm, N and p are the number of unknowns and independent computing units, respectively. If $C_o^{}\approx C_p^{}$ then

$$S>1\Rightarrow p>logN.$$

From the above results and considerations, one can conclude that parallel implementation of the close-to-black-box algorithm (7) will not lead to impressive reduction in the execution time as compared with the optimal sequential one (8) with N large.

Constructing the iterative algorithm for numerically solving nonlinear (initial-)boundary value problems remains the same:

(1)

If the sequential Newton-type iterations converge slowly, then convergence should be accelerated up to close-to-optimal value (7) using the least number of extra problem-dependent components;

(2)

The parallel nonlinear algorithm should be faster than the fastest sequential one.

In general, development of the robust algorithm is more difficult than that of solving linear problems on a uniform grid. We summarize these considerations as follows:

(1)

As a rule, systems of nonlinear strongly coupled PDEs in complex domains (multiphysics simulation) are needed to solve in a (de)coupled manner for industrial applications, so theoretical analysis of algorithmic complexity such as (6) becomes more difficult;

(2)

Simplicity of Gauss–Seidel iterations makes this algorithm attractive for smoothing in low-memory sequential or parallel multigrid. For real-life applications, it is far from trivial to choose optimal robust algorithm components uniformly for a large class of problems. In many cases, the Krylov subspace methods may have advantages. Therefore, each iterative algorithm for the numerical solution of nonlinear (initial-)boundary value problems has at least three problem-dependent components: the ordering of unknowns, (de)coupled iterations for a locally/globally linearised discrete problems and a stopping criterion for this iterative process. As a result, a black-box solver requires black-box optimization (i.e., the optimal choice of the problem-dependent components of the robust algorithm for the given problem without user control).

The question remains: Is it possible to construct a close-to-optimal black-box solver (the least number of problem-dependent components, close-to-optimal complexity (7), the parallel algorithm should be faster than the fastest sequential one) instead of the true black-box one (absence of the problem-dependent components, optimal complexity (8), and full parallelism)? Yes! First, a general computational approach for combining the advantages of unstructured and structured grids (two-grid algorithm) will be presented. Second, a robust method for solving the discrete initial-boundary value problems on the auxiliary structured grid will be analysed.

3. Two-Grid Algorithm

Close-to-black-box solver can be constructed by combining the advantages of unstructured and structured grids: simplicity of automatic generation in complex domain geometry and opportunity to solve nonlinear (initial-)boundary value problems by very efficient geometric multigrid methods in parallel (de-)coupled manner. The Auxiliary Space Method is a (non-)nested two-level preconditioning technique based on a simple relaxation scheme (smoother) and an auxiliary space (here a structured grid is the auxiliary space). The basic idea of the Auxiliary Space Method is to use an auxiliary (non-)linear problem in the auxiliary space, where it is simpler to solve [18,19]. The solution of auxiliary problem (auxiliary grid correction) is then transferred back to the original space. The mismatch between auxiliary space and the original space is corrected by a few smoothing iterations.

For reason of simplicity, we consider a linear boundary value problem

$$\begin{array}{cc}\hfill \mathcal{L}\left(u\right)& =f\hfill \end{array}$$

(9a)

on domain $\Omega \in {\mathbb{R}}_{}^d$, together with a set of appropriate boundary conditions

$$\begin{array}{cc}\hfill 1-1{\mathcal{L}}_{\partial \Omega }^{}\left(u\right)& =g\hfill \end{array}$$

(9b)

at the domain boundary $\partial \Omega$. Here, $\mathcal{L}$ is a linear elliptic operators, f is a known functions and u is the desired solution.

Let $\widehat{u}$ be an approximation to the solution u and $c=u-\widehat{u}$ is a correction, i.e., difference between the solution and the approximation to it. The representation of the solution

$$u=\widehat{u}+c,$$

(10)

is called $\Sigma$-modification of the solution [15,20]. Substitution of (10) into (9) leads to $\Sigma$-modified form of this problem

$$\begin{array}{cc}\hfill \mathcal{L}\left(c\right)& =f-\mathcal{L}\left(\widehat{u}\right),\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\partial \Omega }^{}\left(c\right)& =g-{\mathcal{L}}_{\partial \Omega }^{}\left(\widehat{u}\right).\hfill \end{array}$$

(11b)

$\Sigma$-modification can be used for solving some nonlinear problems (for example, the Navier–Stokes equations), but $\Pi$-modification $u=\widehat{u}·c$ can be preferable for another nonlinear problems. The general approach for solving the nonlinear problems solution is Full Approximation Storage scheme [3].

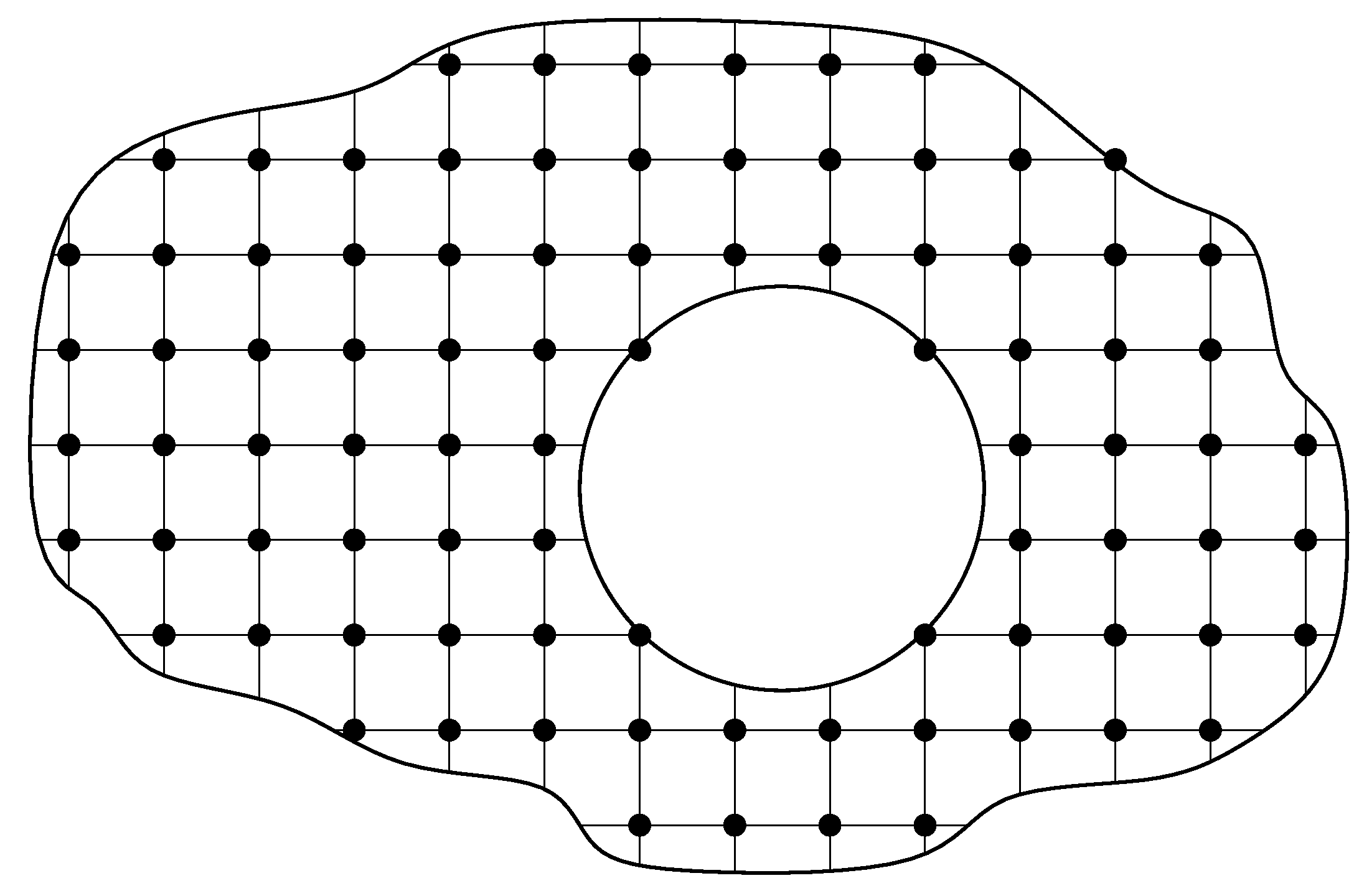
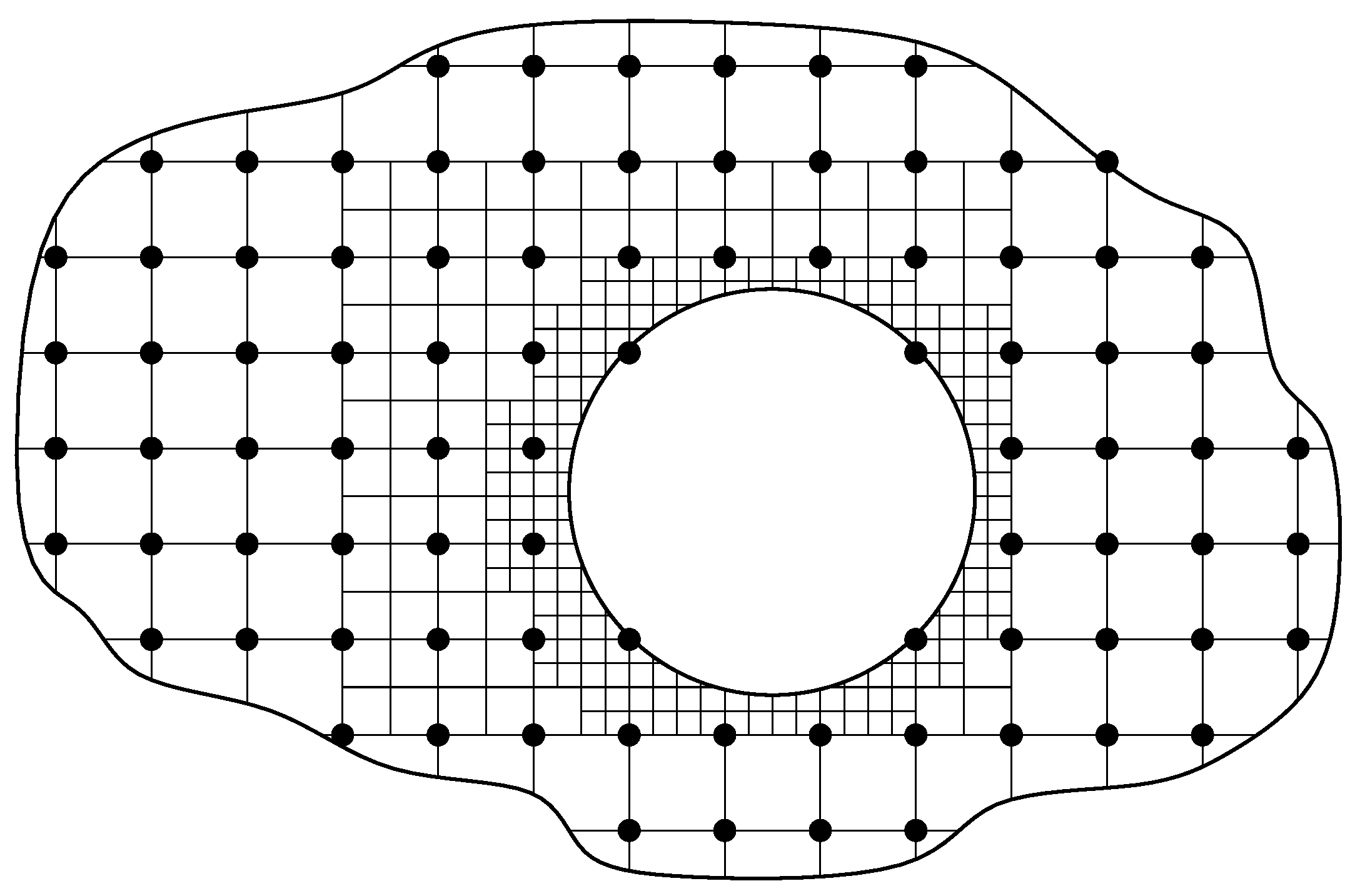
Let an original (un-)structured grid $G_o^{}$ and an auxiliary structured grids $G_a^{}$ be generated in the domain $\Omega$. Figure 1 and Figure 2 represents example of such computational grids. Approximation of (11) on these grids $G_o^{}$ and $G_a^{}$ leads to the discrete problems written in the matrix form (with the eliminated boundary conditions):

(a)

the original grid $G_o^{}$

$$A_o^{}{\mathbf{c}}_o^h={\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^h,$$

(12)

(b)

the auxiliary grids $G_a^{}$

$$A_a^{}{\mathbf{c}}_a^h={\mathbf{f}}_a^h-A_a^{}{\widehat{\mathbf{u}}}_a^h.$$

(13)

It should be emphasized that the problem (11) is discretized on these grids $G_o^{}$ and $G_a^{}$ independently. So, the systems (12) and (13) are independent from each other. It simplifies the coupled iterative solution of systems of PDEs. For interface between (12) and (13), a restriction operator ${\mathcal{R}}_{o\to a}^{}$ transferring the residual ${\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^h$ from the grid $G_o^{}$ onto the grid $G_a^{}$

$${\mathbf{f}}_a^h-A_a^{}{\widehat{\mathbf{u}}}_a^h={\mathcal{R}}_{o\to a}^{}({\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^h),$$

(14)

and a prolongation operator ${\mathcal{P}}_{a\to o}^{}$ transferring the correction ${\mathbf{c}}_a^h$ from the grid $G_a^{}$ onto the grid $G_o^{}$

$${\mathbf{c}}_o^h={\mathcal{P}}_{a\to o}^{}{\mathbf{c}}_a^h$$

(15)

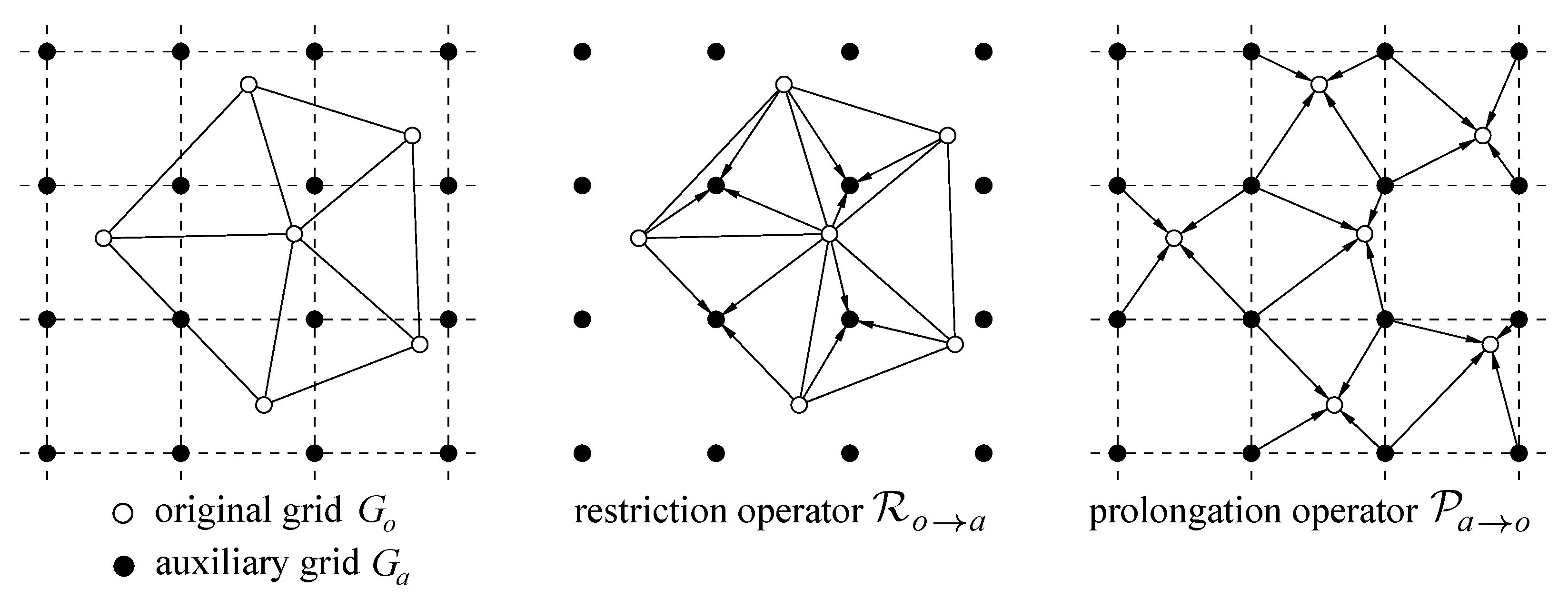
should be defined. Figure 3 demonstrates an example of the transfer operators ${\mathcal{R}}_{o\to a}^{}$ and ${\mathcal{P}}_{a\to o}^{}$. Using (14) and (15), the correction ${\mathbf{c}}_o^h$ can be computed as

$${\mathbf{c}}_o^h={\mathcal{P}}_{a\to o}^{}{A}_a^{-1}{\mathcal{R}}_{o\to a}^{}({\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^h).$$

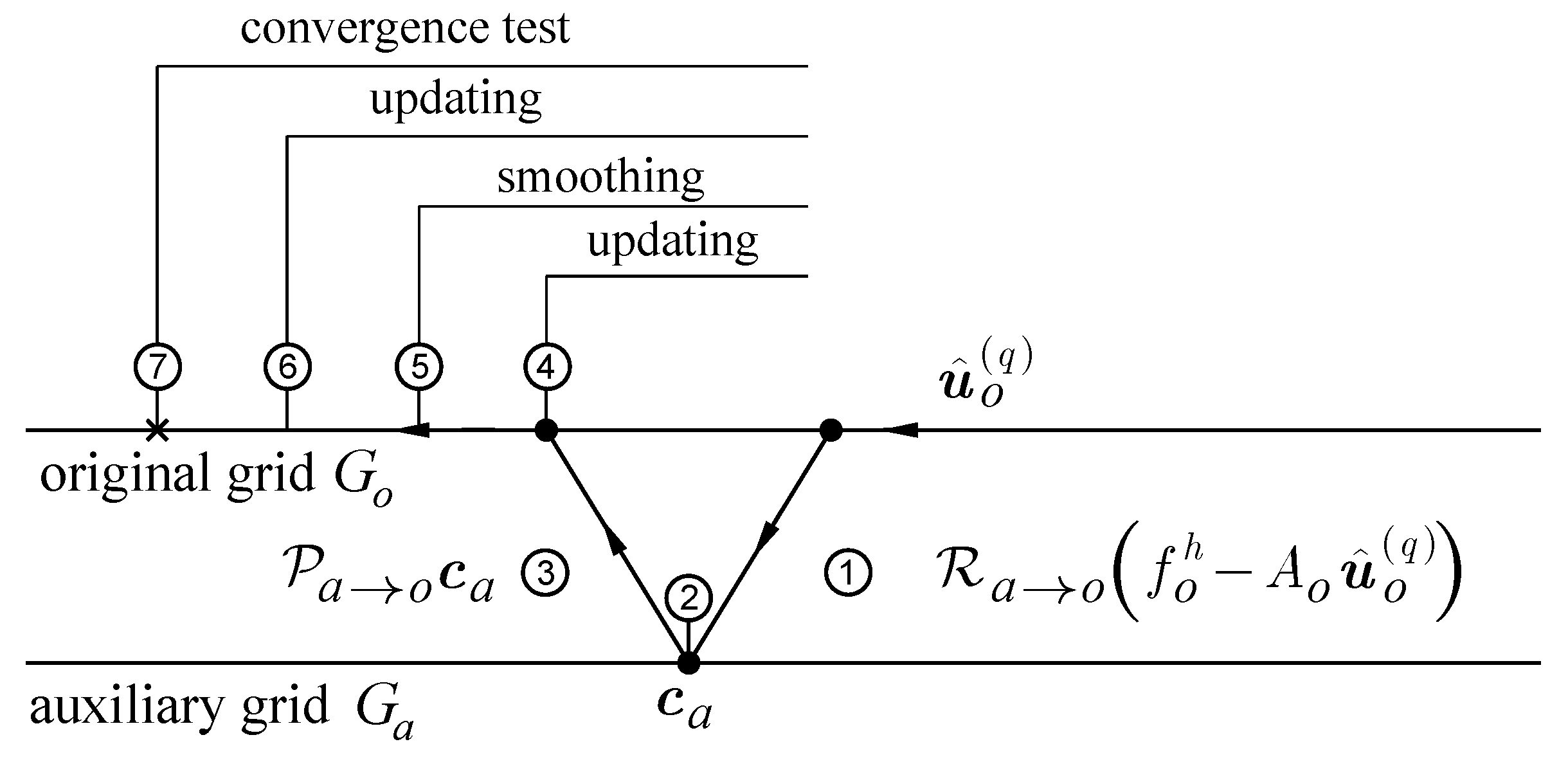
Figure 4 represent the linear two-grid algorithm:

• Transfer of the residual ${\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(q\right)}$ to the auxiliary grid $G_a^{}$, where q is a counter of the intergrid iterations;
• Solution of the auxiliary system by some numerical method

  $$A_a^{}{\mathbf{c}}_a^{}={\mathcal{R}}_{o\to a}^{}\left({\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(q\right)}\right)\Rightarrow c_a^{};$$
• Prolongation of the correction ${\mathbf{c}}_a^{}$ to the original grid $G_o^{}$

  $${\mathbf{c}}_o^{}={\mathcal{P}}_{a\to o}^{}{\mathbf{c}}_a^{},$$

  where ${\mathcal{P}}_{a\to o}^{}$ is a prolongation operator transferring the correction to $G_o^{}$;
• Computation of the starting guess for the smoothing iterations on $G_o^{}$

  $${\widehat{\mathbf{u}}}_o^{\left(0\right)}={\mathbf{c}}_o^{}+{\widehat{\mathbf{u}}}_o^{\left(q\right)};$$
• Smoothing iterations on the original grid $G_o^{}$

  $$W_o^{}\left({\widehat{\mathbf{u}}}_o^{(s+1)}-{\widehat{\mathbf{u}}}_o^{\left(s\right)}\right)={\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(s\right)},s=0,1,2,\dots ,$$

  where s is the smoothing iteration counter;
• Updating the approximation to the solution

  $${\widehat{\mathbf{u}}}_o^{(q+1)}={\widehat{\mathbf{u}}}_o^{(s+1)},$$

  where q is the intergrid iteration counter;
• check convergence, repeat if necessary.

The linear two-grid algorithm can be rewritten in the matrix form

$${\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{(q+1)}=M\left({\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(q\right)}\right),$$

(16)

where the iteration matrix of the linear two-grid algorithm is

$$M=A_o^{}{S}_o^{\nu }\left(A_o^{-1}-{\mathcal{P}}_{a\to o}^{}{A}_a^{-1}{\mathcal{R}}_{o\to a}^{}\right),$$

(17)

and $S_o^{}=I-W_o^{-1}{A}_o^{}$ is a smoothing iteration matrix and $\nu$ is the smoothing iterations counter ($\parallel S_o^{}\parallel <1$).

The convergence properties of the linear two-grid algorithm can be easily analysed by considering factor ${\rho }_q^{}$ of the averaged reduction in the residual ${\mathbf{r}}_o^{\left(q\right)}={\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(q\right)}$

$${\rho }_q^{}={\left({\displaystyle \frac{\parallel {\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(q\right)}\parallel }{\parallel {\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(0\right)}\parallel }}\right)}^{1/q},$$

(18)

which shows the averaged reduction in the residual over q integrid iterations [21].

The classical multigrid theory is based on the approximation and smoothing property as introduced by W. Hackbusch [22]:

• Smoothing property: a monotonically decreasing function $\eta \left(\nu \right):{\mathbb{R}}_{+}^{}\to {\mathbb{R}}_{+}^{}$ exist such that $\eta \left(\nu \right)\to 0$ for $\nu \to \infty$ and

  $$\parallel A_o^{}{S}_o^{\nu }\parallel ⩽\eta \left(\nu \right)\parallel A_o^{}\parallel ,$$

  (19)

  $$\eta \left(\nu \right)\sim \left\{\begin{array}{cc}\hfill 1/\nu ,& \mathrm{for}\mathrm{symmetric}\mathrm{problems}\hfill \\ \hfill 1/\sqrt{\nu },& \mathrm{for}\text{non-symmetric}\mathrm{problems}\hfill \end{array}\right..$$
• Approximation property: there exists a constant $C_A^{}>0$ such that

  $$\parallel A_o^{-1}-{\mathcal{P}}_{a\to o}^{}{A}_a^{-1}{\mathcal{R}}_{o\to a}^{}\parallel ⩽C_A^{}{\parallel A_o^{}\parallel }_{}^{-1}.$$

  (20)

The smoothing property states, in principle, that the smoother reduces the high-frequency components of the error (without amplifying the low-frequency components). The approximation property requires the coarse grid correction to be reasonable [22]. The basis of this theory is a splitting (factorization) of the two-grid iteration matrix M (17).

Theorem 1.

Assuming that the smoothing property (19) and approximation property (20) hold, then the N-independent convergence of the intergrid iterations (16) follows immediately for ν that is large enough.

Proof of Theorem 1.

The intergrid iterations (16) can be rewritten as

$${\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(q\right)}=M_{}^q\left({\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(0\right)}\right).$$

This leads to the following estimation

$$\parallel {\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(q\right)}{\parallel \le \parallel M\parallel }_{}^q\parallel {\mathbf{f}}_o^h-A_o^{}{\widehat{\mathbf{u}}}_o^{\left(0\right)}\parallel \Rightarrow {\rho }_q^{}\le \parallel M\parallel .$$

The splitting of the two-grid iteration matrix M (17), the smoothing property (19), and approximation property (20) lead to the estimation

$${\rho }_q^{}\le \parallel M\parallel \le \parallel A_o^{}{S}_o^{\nu }\parallel ·\parallel A_o^{-1}-{\mathcal{P}}_{a\to o}^{}{A}_a^{-1}{\mathcal{R}}_{o\to a}^{}\parallel \le \eta \left(\nu \right)\parallel A_o^{}\parallel C_A^{}{\parallel A_o^{}\parallel }_{}^{-1}=C_A^{}\eta \left(\nu \right).$$

Since $\eta \left(\nu \right)$ is the monotonically decreasing function, it should be noted that

$${\rho }_q^{}\le C_A^{}\eta \left(\nu \right)<1$$

for a sufficiently large $\nu$. □

This theorem predicts that the number of intergrid iterations of the two-grid algorithm does not depend on the number of unknowns N, i.e., ${\rho }_q^{}\ne {\rho }_q^{}\left(N\right)$ (18).

The main features of the two-grid algorithm can be summarized as follows:

(1)

The number of extra problem-dependent components as compared with the basic algorithm (5) are:

(a)

A non-nested case: let $G_o^{}$ and $G_a^{}$ be the unstructured and structured grid, respectively. The two-grid algorithm has two extra problem-dependent components: transfer operators ${\mathcal{R}}_{o\to a}^{}$ and ${\mathcal{P}}_{a\to o}^{}$ (Figure 3);

(b)

A nested case: let $G_o^{}$ and $G_a^{}$ be the block-structured grids [9]. In this case, we suppose $G_a^{}=G_o^{}\Rightarrow {\mathcal{R}}_{o\to a}^{}={\mathcal{P}}_{a\to o}^{}=I$ in absence of smoothing on the original grid ($S_o^{}=I$) and the two-grid algorithm has extra problem-dependent components (interblock interpolation);

(c)

A nested case: let $G_o^{}$ and $G_a^{}$ be the structured grids. In this case, we suppose $G_a^{}=G_o^{}\Rightarrow {\mathcal{R}}_{o\to a}^{}={\mathcal{P}}_{a\to o}^{}=I$ in absence of smoothing on the original grid ($S_o^{}=I$) and the two-grid algorithm has no extra problem-dependent components.

(2)

The nonlinear two-grid algorithm based on Full Approximation Scheme approach is given in [15].

(3)

The nonlinear two-grid algorithm offers a general possibility to employ low order schemes and obtain high order accuracy (the high order defect correction iteration [3]). Remember that mathematical modelling in continuum mechanics is a chain of approximations:

(a)

The difference schemes approximate the governing differential Equation (1). (A difference scheme is a finite system of algebraic equations replacing some differential problem);

(b)

The differential Equation (1) approximate the fundamental conservation laws of continuum mechanics. (In fact, the hypothesis of continuity prohibits the limit leading to the differential equations);

(c)

A continuous medium approximates a real one. Since any chemical reaction is the result of intermolecular interactions, modelling chemical processes in continuum mechanics is only possible by using empirical hypotheses and experimental data to approximate the quantum nature of these intermolecular interactions.

As a rule, the mathematical description errors of physical and chemical processes in real-life problems has a physical nature (inaccurate the initial and∖or the boundary conditions, equation state errors, approximate description of the turbulent transport and the chemical reactions, etc.) and they exceed the discretization errors of the governing (integro-)differential Equations [23]. In many cases, the second-order accurate finite volume discretization does not damage the discrete solution accuracy of the mathematical model equations required for practical applications. However, advanced software can use the high-order discretization without significant changes in the computational algorithm. For reasons of robustness, the finite volume method of the second order discretization will be used on the auxiliary grid $G_a^{}$, but high order discretization approaches can be used on the original grid $G_o^{}$.

(4)

The basic ingredients of the two-grid algorithm are computation of correction ${\mathbf{c}}_a^{}$ on the auxiliary grid $G_a^{}$ and smoothing iterations on the original grid $G_a^{}$. The most time-consuming component of the solver is numerical inversion of the coefficient matrix $A_a^{}$, i.e., the matrix $A_a^{-1}$ in (17).

(5)

The differential problem is approximated on the grids $G_o^{}$ and $G_a^{}$ separately in order to simplify coupled iterative solution of systems of PDEs on the auxiliary structured grid $G_a^{}$ (for example, the Vanka-type iterations or the volume-coupled approach used in monolithic algebraic multigrid methods [5]).

The two-grid algorithm puts more computational work on the auxiliary (structured) grid $G_a^{}$, where the (non-)linear problems are simpler to solve and parallelize. The final effort is the construction of an efficient iterative algorithm for solving the (non-)linear (initial-)boundary value problems on the auxiliary grid $G_a^{}$.

4. Robust Multigrid Technique

An epochal event in world computational mathematics was publication of R.P. Fedorenko’s paper (Keldysh Institute of Applied Mathematics of Russian Academy of Sciences, Moscow, USSR/Russia) in 1961 [24], where the author formulated a new iterative method for solving discrete boundary value problems (BVPs) on structured grids (https://team.kiam.ru/botchev/fedorenko/, accessed on 1 August 2023). Thoughtful conclusions on the basis of elementary analysis were far ahead of their time, and after many years this paper was called the “first true multigrid publication” in the scientific literature. The first theoretical results were reported in the pioneering papers of N.S. Bakhvalov and G.P. Astrakhantsev.

At the end of the 1970s and at the beginning of the 1980s research on the multigrid methods increased. Very interesting multigrid approaches were proposed and developed in the Theoretical Division of the Los Alamos National Laboratory, USA. In papers [25,26], P.O. Frederickson and O.A. McBryan studied the efficiency of the Parallel Superconvergent Multigrid Method (PSMG). The basic idea behind the PSMG is the observation that for each fine grid there are two natural coarse grids—the even and odd points of the fine grid (Figure 5). The authors tried to develop a optimized multigrid algorithm by combining these coarse grid solutions for more accurate correction.

Although P.O. Frederickson and O.A. McBryan restrict themselves to a theoretical analysis of the PSMG, they demonstrate that besides numerical efficiency, the algorithm is also highly parallel. The PSMG and related ideas essentially refer to massively parallel computing. However, combinations or the extrapolation of the coarse grid corrections is a very efficient approach only for the simplest BVPs.

Also in 1990, a similar multiple coarse grid correction strategy had been proposed for the development of a robust multigrid method for black-box software in Baranov Central Institute of Aviation Motors, Moscow, USSR/Russia. A developed solver is called Robust Multigrid Technique (RMT). The RMT uses a multiple coarsening strategy coupled with the finite volume discretization in order to obtain the problem-independent transfer operators and coarse grid operator (i.e., the matrix $A_a^{}$ in (13)), high parallel efficiency, and to make the smoother’s task the least demanding. The history of RMT is given in [20], and for the theoretical description of RMT and corresponding parallel analysis, we refer interested readers to [6,15,20,27].

The uniform finest grid $G_1^0$ consists of two sets of points $G^{\mathrm{v}}(0;1)$ and $G^{\mathrm{f}}(0;1)$:

$$\begin{array}{cc}\hfill G^{\mathrm{v}}(0;1)& =\left\{x_i^{\mathrm{v}}\right|x_i^{\mathrm{v}}=h(i-1),i=1,2,\dots ,n_{}^0+1,h=1/n_1^0\},\hfill \\ \hfill G^{\mathrm{f}}(0;1)& =\left\{x_i^{\mathrm{f}}\right|x_i^{\mathrm{f}}=(x_i^{\mathrm{v}}+x_{i+1}^{\mathrm{v}})/2,i=1,2,\dots ,n_1^0\},\hfill \end{array}$$

where the discretization parameter $n_1^0$ defines the finest grid $G_1^0$. Figure 6 represents the finest uniform grid $G_1^0=G^{\mathrm{v}}(0;1)\cup G^{\mathrm{f}}(0;1)$ generated with $n_1^0=8$ or mesh size $h=1/8$ in the unit segment: $x_1^{\mathrm{v}}=0$, $x_9^{\mathrm{v}}=1$.

Each d-dimensional computational grid used in RMT can be represented as product of d one-dimensional grids, so the one-dimensional grid $G_1^0=G^{\mathrm{v}}(0;1)\cup G^{\mathrm{f}}(0;1)$ will be considered in detail. Figure 7 represents triple coarsening of RMT. This triple coarsening is independent of the assignment of grid functions to points $x_i^{\mathrm{v}}$ ($x_i^{\mathrm{v}}$ are the vertices, $x_i^{\mathrm{f}}$ are the finite volume faces) or to points $x_i^{\mathrm{f}}$ ($x_i^{\mathrm{f}}$ are the vertices, $x_i^{\mathrm{v}}$ are the finite volume faces). This triple coarsening, which does not depend on the configuration of finite volumes, gives a straightforward generalization to multidimensional (un-)staggered discretization of the (initial-)boundary value problems. Later, the triple coarsening was proposed in the Theoretical Division of the Los Alamos National Laboratory [28].

PSMG and RMT are the single-grid algorithms based on the essential multigrid principle of iterations with a basic iterative method on the fine grid [21], but representation of these single-grid algorithms as the multigrid solvers allows analyse their convergence and complexity by elementary methods. The essential multigrid principle is to approximate the smooth (long wavelength) part of the error on coarser grids. The non-smooth or rough part is reduced with a small number (independent of mesh size) h.

Figure 7 illustrates the main properties of the coarse grids of RMT:

Property 1: 

all coarse grids $G_1^1$, $G_2^1$ and $G_3^1$ have no common grid points:

$$G_n^1\cap G_m^1=⌀,n\ne m.$$

It result in the massive parallelization of computations.

Property 2: 

the fine grid $G_1^0$ is represented as a union of the coarse grids $G_1^1$, $G_2^1$ and $G_3^1$:

$$G_1^0=\bigcup _{k=1}^3{G}_k^1.$$

It result in the problem-independent prolongation operator $\mathcal{P}$.

Property 3: 

all grids are geometrically similar, but the mesh size of the coarse grids $G_1^1$, $G_2^1$ and $G_3^1$ is three times larger than the mesh size of the finest grid $G_1^0$. It result in the unified finite volume discretization of the modified (initial-)boundary value problems on the multigrid structures, i.e., to the problem-independent construction of the coarse grid operator $A_a^{}$ in (17).

Property 4: 

independent of the grid functions assignment, each finite volume on the coarse grids $G_1^1$, $G_2^1$ and $G_3^1$ is a union of three finite volumes on the fine grid $G_1^0$. It result in the problem-independent restriction operator $\mathcal{R}$ based on the additive interval property to evaluate integrals in the finite volume discretization.

The finest grid $G_1^0$ forms zero grid level, but the coarse grids $G_1^1$, $G_2^1$ and $G_3^1$ form the first grid level. The following coarsening is carried out recursively: each computational grid $G_i^l,i=1,\dots ,3^l$ of level l is considered to be the finest grid for three coarse grids of level $l+1$. Nine coarser grids obtained from three coarse grids of the first level form a second level as shown in Figure 8. The coarsening stops when the coarse grids will have a few points $x_{}^{\mathrm{v}}$ and $x_{}^{\mathrm{f}}$, and further coarsening cannot be performed. The coarsest level will be denoted by $L_3^{+}$. The total number of levels (coarse levels $L_3^{+}$ and the finest grid (zero level)) is $L_3^{+}+1$. The grid hierarchy $G_m^l,m=1,\dots ,3_{}^l,l=0,\dots ,L_3^{+}$ will be called a multigrid structure ($\mathcal{MS}$) generated by the grid $G_1^0$:

$$\mathcal{MS}\left(G_1^0\right)=\left\{G_m^l|m=1,2,\dots ,3_{}^l,l=0,1,\dots ,L_3^{+}\right\}.$$

Here the coarse grids are used the only for obviousness of the technique description, since RMT is a single-grid algorithm, the index mapping gives the multigrid illusion [6,15,20,27].

Figure 9 represents the finest grid $G_1^0$ ($n_1^0=30,h=1/n_1^0=1/30$) and the coarse grids of the first and second levels. The number of coarse levels $L_3^{+}+1$ can be computed before the generation of a multigrid structure. Assume that many of the coarsest grids of level $L_3^{+}$ have three points $x_{}^{\mathrm{v}}$ or $x_{}^{\mathrm{f}}$. Then the number of points on the finest grid $G_1^0$ is $n_1^0+1\approx 3^{L_3^{+}+1}$ or

$$n_1^0+1\approx 3^{L_3^{+}+1}\Rightarrow L_3^{+}\approx [{\log }_3(n_1^0+1)-1]\approx \left[{\log }_3{\displaystyle \frac{n_1^0}{3}}\right],$$

(21)

where the square brackets indicate an integer part. The procedure of the fast approximation of integrals on the multigrid structures uses the ghost points of each grid [20,27].

The multigrid schedule of RMT is the V-cycle with no pre-smoothing (the so-called sawtooth cycle [21]). The sawtooth cycle is a special case of the V-cycle, in which smoothing before the coarse grid correction (pre-smoothing) is deleted. The computational cost of each multigrid iteration of RMT can be estimated as

$${\mathcal{W}}_q^{}={\mathcal{W}}_0^{}(L_3^{+}+1)\mathtt{ao},$$

where ${\mathcal{W}}_0^{}=CN$ ao is cost of the finest grid smoothing, N is the number of unknowns, C is some constant, and $L_3^{+}+1$ is the number of levels. Since

$$L_3^{+}+1\approx \left[{log}_3(n_1^0+1)\right]\approx {\displaystyle \frac{1}{d}}\left[{log}_{3}N\right]$$

(21) and all grids of the some level have the same number of points, the algorithmic complexity of RMT can be estimated as

$${\mathcal{W}}_{\mathrm{RMT}}^{}=q{\mathcal{W}}_q^{}=q{\mathcal{W}}_0^{}(L_3^{+}+1)=C{\displaystyle \frac{q}{d}}N\left[{log}_{3}N\right]\le C{\displaystyle \frac{q}{d}}N{log}_{3}N=O(NlogN)\mathtt{ao},$$

i.e., RMT has the required close-to-optimal algorithmic complexity (7). Theoretical analysis predicts that the single-grid RMT has the most attractive property of classic multigrid methods, namely h-independent convergence in general situations [6,15,20,27].

We summarize some well-known facts about sequential RMT here:

(1)

RMT is a single-grid algorithm having close-to-optimal algorithmic complexity and h-independent convergence;

(2)

RMT uses a multiple coarsening strategy coupled with the finite volume discretization in order to obtain the problem-independent transfer operators and coarse grid operator, high parallel efficiency, and to make the smoother’s task the least demanding. The history of RMT is given in [6], for the theoretical description of RMT and corresponding examples and parallel analysis, we refer to [6,15,20,27];

(3)

RMT has extra problem-dependent component (the number of smoothing iterations on the coarse levels);

(4)

All problem-dependent components of RMT can be optimized on the multigrid structure in the black-box manner. The basic idea of black-box optimization is the experimental study of the iteration convergence rate on a multigrid structure starting from the same initial guess. For example, a discrete problem can be solved using different problem-dependent components on several grids of the same level starting from the same initial guess. Analysis of reduction in the residual norm during the smoothing iterations makes it possible to choose close-to-optimal problem-dependent components of the algorithm. Figure 9 illustrates that the similarity of all grids of the same level leads to almost the same problem-dependent components of the algorithm at this level. It should be emphasized that this black-box optimization does not require any theoretical input or a priori information on problem to be solved. The extra effort for this black-box optimization is negligible compared to the effort for smoothing.

Finally, analysis of the parallel RMT completes analysis of the two-grid algorithm. Assuming that the finest grid is deleted, we can solve the discrete problems on $3_{}^d,d=2,3$ independent coarse grids of the first level. This geometric parallelism of RMT is based on non-overlapping the finest grid partition for distribution of $3_{}^d,d=2,3$ independent tasks over $p=3_{}^{\kappa },\kappa =1,2,\dots ,d$ computing units. In the following, the coarse grids, which are considered the finest grids in the solution process, will be called dynamic finest grids. The difference between this starting guess and the finest grid numerical solution does not exceed ℓ significant digits for the second order finite volume discretization, where ℓ is the serial number of the dynamic level.

To illustrate the parallel RMT, we consider the following example:

$${\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial z^2}}=-f(x,y,z)$$

(22)

in the unit cube $\Omega ={(0,1)}^3$. If the exact solution is given by

$$u_a^{}(x,y,z)=exp(x+y+z),$$

(23)

then substitution of (23) into (22) gives the right-hand side function

$$f(x,y,z)=-3exp(x+y+z)$$

and the Dirichlet boundary conditions.

Standard seven-point finite volume discretization of (22) on the uniform grid $G_1^0$ is abbreviated as

$${\Delta }_{}^h{u}_{}^h=-f_{}^h,$$

where ${\Delta }_{}^h$, $u_{}^h$, and $f_{}^h$ are the discrete analogues of the Laplace operator, the solution u, and the right-hand side function f, respectively.

This boundary value problem is solved by RMT with ($h_x^{}=h_y^{}=h_z^{}=1/100$) using the stopping criterion

$$\underset{ijk}{max}\left|{\Delta }_{}^h{u}_{}^h+f_{}^h\right|<{10}_{}^{-6}.$$

The error of the numerical solution is defined by comparison of the exact and approximated solutions

$${\parallel \mathbf{e}\parallel }_{\infty }^{}=\underset{ijk}{max}\left|u_a^{}(x_i^{\mathrm{v}},y_j^{\mathrm{v}},z_k^{\mathrm{v}})-u_{ijk}^h\right|,$$

where $u_a^{}$ and $u_{}^h$ are the exact (23) and the numerical solutions, respectively.

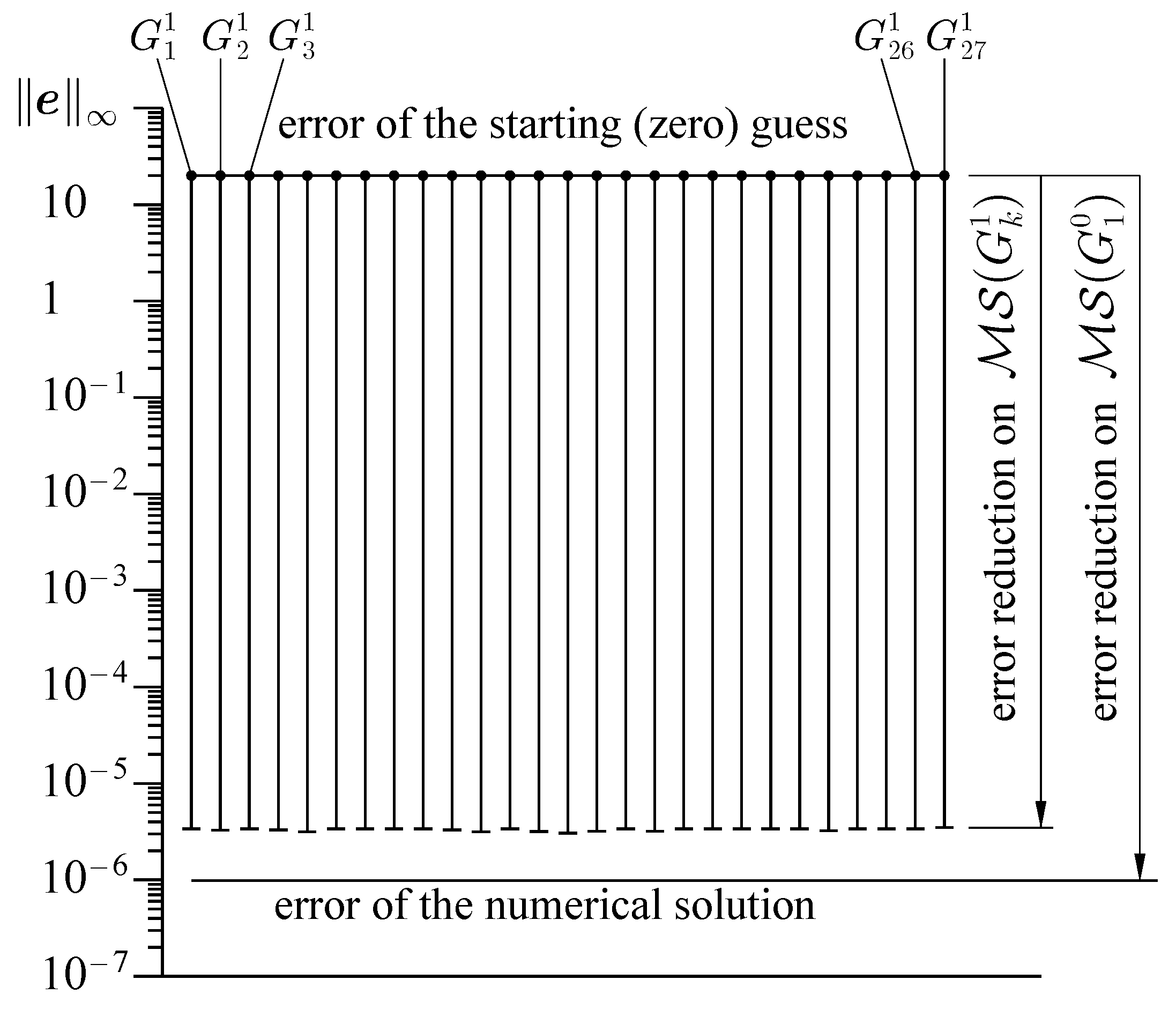
Figure 10 represents the error of the numerical solutions ${\parallel \mathbf{e}\parallel }_{\infty }^{}$ obtained on the multigrid structures $\mathcal{MS}\left(G_1^0\right)$ and $\mathcal{MS}\left(G_k^1\right),k=1,\dots ,3_{}^d$ starting with the iterant zero on $101\times 101\times 101$ uniform finest grid $G_1^0$ ($n_1^0=100,h=1/100$). Taking into account the stopping criterion, the iterative solution of the model BVP on the finest grid $G_1^0$ is a reduction in the error of the zero starting guess ($\parallel {\mathbf{e}}_{}^{\left(0\right)}{\parallel }_{\infty }^{}\approx e^3\approx 20$) down to ${\parallel \mathbf{e}\parallel }_{\infty }^{}\approx {10}_{}^{-6}$. Figure 10 illustrates the accuracy of the starting guess to the finest grid solution assembled from the solutions obtained in parallel on the coarse grids of the first level (dynamic finest grids). This geometric parallelism does not require parallelization of the iterative/direct solvers.

The algebraic parallelism of RMT is based on the multicolour orderings of unknowns (or block of unknowns) to parallelize the smoothing iterations on the finer levels where the number of grids is less than the number of computing units. The small-scale granular algebraic parallelism is grid-independent.

The solution of the modified boundary value problem starts on the auxiliary grid. $3_{}^d$ multigrid structures generated by the dynamic grids of the first level makes it possible to obtain accurate approximation to the solution in parallel by handling $3_{}^d$ independent discrete problems. In addition to black-box optimization of the problem-dependent components, the dynamic grid refinements are carried out during the solution process on the multigrid structures generated by the dynamic grids, controlled by some appropriate adaptation criteria. Figure 11 demonstrates an example of the adaptive grid refinement. Stopping of iterative computation of the auxiliary grid correction on the finest grid means that the sufficiently accurate approximation to the solution on the original grid obtained and subdomains for the grid refinement are determined. The next step is generation of an original (un)structured grid taking into account the subdomains for the auxiliary grid refinement. The auxiliary grid correction is prolonged to the original grid and it is corrected by a few smoothing iterations. The iterative process is continued with restriction of residual to the auxiliary grid if the required accuracy is not yet achieved. Otherwise, the two-grid algorithm stops. Subsequent intergrid iterations are performed without dynamic grids, the black-box optimization and the auxiliary grid refinement.

The initial-boundary value problems are solved in the same parallel manner: parallel in space as that for the boundary value problems and parallel in time (waveform relaxation) [15,29,30].

Theoretically, the execution time of the parallel RMT implemented over nine computing units is approximately equal to the execution time of the sequential V-cycle [15].

5. Discussion

In our opinion, black-box algorithm for solving the real-life problems should be based on the following principles:

(1)

Dominance of physical errors. In many cases, the second-order accurate finite volume discretization does not damage the discrete solution accuracy of the real-life problems, but advanced software can use the high-order discretization without significant changes in the algorithm [31].

(2)

Formalization of computations. The black-box algorithm is intended to solve the nonlinear initial-boundary value problems in unified manner, which we already know how to solve. In other words, the black-box algorithm is development of well-known methods for solving well-known problems, but not a new method for solving new problems.

(3)

Requirements on robustness, efficiency and parallelism. The triad of requirements on robustness, efficiency, and parallelism defines black-box algorithm. Attempts to satisfy one requirement without considering the others is a waste of time.

(4)

(De)coupled solution of the most difficult problem. The strongly coupled systems of nonlinear partial (integro-)differential equations (for example, steady Navier–Stokes equations) are the most difficult problem for black-box algorithm. This solver must solve such systems not only in segregated manner, but also in coupled one on (un)structured grids.

Modern general-purpose codes (Fluent, Star-CCM+, COMSOL’s CFD Module, Altair’s AcuSolve, and others) use multigrid methods for solving the real-life problems. The geometric multigrid (GMG) solver accelerates the convergence of the iterative methods (smoothers) by solving the discrete (non)linear problem on a grid hierarchy [32]. The GMG cannot be represented as a fixed algorithm: a priori information about the problem being solved is used to optimize the problem-dependent components [33,34]. For complicated applications, it is far from trivial to choose optimal multigrid components uniformly for a large class of problems. Another difficulty is application of GMG in the complex domain geometries.

From the multigrid point of view, the unstructured grids are a complication. In contrast to GMG, algebraic multigrid (AMG) does not require a given problem to be defined on a grid but rather operates directly on algebraic Equation (4). In fact, the real-life problems lead to a system of nonlinear algebraic Equation (2) which often have to be solved without global linearization. In addition, a coupled solver for systems of PDEs is difficult to construct without geometric input.

It should be emphasized that standard multigrid methods is intrinsically not fully parallel due to the grid levels are run through sequentially and problem of communication (large communication overhead on very coarse grids) [35].

From the considerations, one can conclude that the standard multigrid methods (GMG and AMG) have optimal convergence rate and unsatisfactory robustness and parallelism.

It is clear that true black-box solver (all problem-independent components, optimal convergence rate, full parallelism) cannot be constructed, but the above mentioned two-grid algorithm (the least number of problem-dependent components, close-to-optimal convergence rate, high unified parallelism in RMT-based two-grid approach for (initial-)boundary value problems) is good approximation to desired solver for black-box software. From a scientific point of view, it is interesting to construct other computational techniques for solving a large class of nonlinear (initial-)boundary value problems in (de)coupled manner comparable in robustness, efficiency and parallelism with the two-grid algorithm.

6. Conclusions

We summarize advantages of the two-grid algorithm:

The two-grid algorithm satisfies to above mentioned conditions for black-box solvers:

(a)

Robustness (the lowest number of problem-dependent components);

(b)

Efficiency (close-to-optimal algorithmic complexity);

(c)

Parallelism (a parallel robust algorithm should be faster than the fastest sequential one).

The number of extra problem-dependent components as compared with the basic algorithm (5) are:

(a)

A non-nested case: let $G_o^{}$ and $G_a^{}$ be the unstructured and structured grid, respectively. The two-grid algorithm has three extra problem-dependent components: transfer operators (${\mathcal{R}}_{o\to a}^{}$ and ${\mathcal{P}}_{a\to o}^{}$) and the number of smoothing iterations on the auxiliary grid;

(b)

A nested case: let $G_o^{}$ and $G_a^{}$ be the block-structured grids. In this case, we suppose $G_a^{}=G_o^{}\Rightarrow {\mathcal{R}}_{o\to a}^{}={\mathcal{P}}_{a\to o}^{}=I$ in absence of smoothing on the original grid ($S_o^{}=I$) and the two-grid algorithm has two extra problem-dependent components (interblock interpolation) and the number of smoothing iterations on the auxiliary grid;

(c)

A nested case: let $G_o^{}$ and $G_a^{}$ be the structured grids. In this case, we suppose $G_a^{}=G_o^{}\Rightarrow {\mathcal{R}}_{o\to a}^{}={\mathcal{P}}_{a\to o}^{}=I$ in absence of smoothing on the original grid ($S_o^{}=I$) and the two-grid algorithm has extra problem-dependent components (the number of smoothing iterations on the auxiliary grid).

The general nonlinear two-grid algorithm is based on Full Approximation Scheme approach. The nonlinear two-grid algorithm offers a general possibility to employ low order schemes and obtain high order accuracy (the high order defect correction iteration). In general, different approaches are used to discretize the same differential problem on different grids (for example, the finite element method on the original grid and the finite volume method on the auxiliary grid). The increased discretization complexity is disadvantage of the two-grid algorithm. The problem-dependent components of the two-grid algorithm (the original grid, the smoothing procedure, segregated/coupled type of the smoothing iterations, and others) can be optimized using black-box optimization of the multigrid structures without any theoretical input or a priori information on problem to be solved.

The most elegant large-scale granular geometric parallelization of RMT can be achieved by distributing the $3_{}^d$ independent discrete tasks over $3_{}^d$ computing units. This parallelization is smoother-independent. The small-scale granular algebraic parallelism is used on the finer levels. This parallelization is grid-independent. Theoretical analysis predicts that the parallel RMT implemented over nine computing units is approximately equal to the sequential V-cycle in execution time. The initial-boundary value problems are solved in the same parallel manner as the boundary value problems, but including parallelism in time.

The results of numerical experiments for the illustration of the robustness and the efficiency of RMT are given in [6,15]. The sequential and parallel software are presented in [20,27].