Abstract
With the dramatic increase in the number of mobile users and wireless devices accessing the network, the performance of fifth generation (5G) wireless communication systems has been severely challenged. Reconfigurable intelligent surface (RIS) has received much attention as one of the promising technologies for the sixth generation (6G) due to its ease of deployment, low power consumption, and low price. RIS is an electromagnetic metamaterial that serves to reconfigure the wireless environment by adjusting the phase, amplitude, and frequency of the wireless signal. To maximize channel transmission efficiency and improve the reliability of communication systems, the acquisition of channel state information (CSI) is essential. Therefore, an effective channel estimation method guarantees the achievement of excellent RIS performance. This survey presents a comprehensive study of existing channel estimation methods for RIS. Firstly, channel estimation methods in high and low frequency bands are overviewed and compared. We focus on channel estimation in the high frequency band and analyze the system model. Then, the comprehensive description of the different channel estimation methods is given, with a focus on the application of deep learning. Finally, we conclude the paper and provide an outlook on the future development of RIS channel estimation.
Keywords:
wireless communication system; sixth generation (6G); reconfigurable intelligent surface (RIS); channel estimation MSC:
94A40
1. Introduction
With the explosion of mobile data and the demand for better quality of service (QoS), effective, and reliable communications are becoming increasingly important. The advent of the internet of things (IoT) marks the interconnection of everything, while providing great convenience. This is a great challenge for information transmission. In the past few decades, researchers have worked to improve the QoS of wireless channels. Now, it is important to find a technology with low energy consumption while ensuring the QoS. The fifth generation (5G) may face problems such as inability to meet larger connection capacity and more energy loss. To solve these problems, the development of the sixth generation (6G) has become a hot topic of increasing interest [1].
The development of 5G has become increasingly saturated, and in the upcoming era of IoT, communication systems need greater spectral efficiency and higher effectiveness. Massive multiple input multiple output (MIMO) technology has become the core technology of 5G, in which a large number of radio frequency (RF) antennas lead to high hardware costs and maintenance costs. The short propagation distance of electromagnetic waves in the high frequency bands and the limited coverage of electromagnetic waves require an increase in the number of base stations (BS), which will further increase the hardware and maintenance costs of 5G. At the same time, the dense distribution of BS and antennas reinforces the signal interference of 5G, deteriorates the performance of the network, increases the computational complexity of network coordination, and creates a serious dilemma in the development of 5G. We need an effective solution to realize the future of 6G [2,3].
To meet the requirements of superior performance and sustainability 6G, many options have been proposed. Reconfigurable intelligent surface (RIS) has received much attention from academia and industry as a potential technology for 6G. RIS, which is also called intelligent reflecting surface (IRS), is a new paradigm of electromagnetic metamaterials, which is composed of many passive reflective elements. It can reconfigure the wireless communication environment by intelligently modulating electromagnetic waves through digital coding to modulate the amplitude, phase, and frequency of the signal, which can improve the performance of wireless communication systems [4,5]. In 5G, millimeter wave (mmWave) as one of the main methods can increase the communication capacity to help solve the spectrum shortage problem. However, its small wavelength drawback can lead to transmission difficulties [6].
The coverage capacity of the signal can be increased by arranging RIS. Prior to the proposal of RIS, techniques such as active frequency selective surfaces were proposed [7], followed by theories such as space-time modulated digital coding metasurfaces, which laid the foundation for the emergence of RIS [8]. RIS can increase the network capacity by changing the phase shift to complete passive beam assignment [9]. RIS has been developed continuously and currently there is not only reflective RIS but also transmissive RIS with the advantages of higher aperture efficiency and operating bandwidth [10]. Furthermore, RIS has the advantages of low power consumption and low cost compared with amplify and forward relay system due to its passive characteristics [11]. The above advantages of RIS make it useful in high frequency bands, orthogonal frequency division multiplexing (OFDM) [12], non-orthogonal multiple access (NOMA) [13], and multi-antenna systems. However, to perform the role of RIS and accomplish effective and reliable wireless communication, it is required to obtain accurate channel state information (CSI) using channel estimation techniques, which is a great challenge. There have been many studies in channel estimation, and this paper provides a basic overview of RIS channel estimation.
We first analyze the full range of transmitted frequency wireless signals briefly and then focus on the 6G band. Channel estimation plays a critical role in the performance of wireless communication systems; this paper overviews RIS channel estimation schemes in various scenarios. In Section 2, we organised reviews about RIS channel estimation, which are based on the main directions and main contributions. In Section 3, channel estimation schemes in different frequency bands are introduced. In Section 4, different channel estimation signal processing algorithms are introduced, and this paper is concluded in Section 5. The notations used in the paper and their meanings are summarized in Table 1.

Table 1.
Notation description.
2. Objectives and Contributions
With RIS gradually gaining attention, a number of reviews on RIS channel estimation have appeared in recent years. Wu et al. [4] provided an overview of RIS-assisted wireless communication systems, describing the principles, hardware architecture, and applications relating to RIS. Zheng et al. [14] focused on promising research directions and emerging RIS architectures. Pan et al. [15] and Jian et al. [16] outlined channel estimation schemes for RIS-assisted communication systems and channel modeling. Liang et al. [17] presented RIS-aided wireless communications and RIS-based information transmission when the RIS acts as transmitter and reflector, respectively. Noh et al. [6] and Chen et al. [18] reviewed the relevant knowledge about RIS in the high frequency band. Swindlehurst et al. [19] mainly summarized the structured and unstructured system models of RIS. The authors analyze and balance the two systems through several metrics. Finally, the authors briefly add the study of algorithms such as deep learning.
Table 2 describes the ten public overviews for RIS-assisted wireless communication systems, presenting the main direction and major contribution for each overview.

Table 2.
Representative overview/survey papers on RIS.
In this paper, we provide an overview of channel estimation methods for RIS-assisted communication systems in terms of both different frequency bands and different algorithms. Specifically, we focus on the RIS-assisted channel estimation models in different frequency bands. We have focused on comparing the differences in channel estimation methods in different frequency bands. We found representative works and performed a quantitative analysis. In the following classification of the different algorithms, we focus on techniques related to deep learning RIS channel estimation algorithms, such as building end-to-end networks, introducing image processing algorithms and fusing conventional schemes with deep learning. This paper focuses on summarizing the different RIS channel estimation schemes and signal processing algorithms in different frequency bands, considering a comprehensive overview of the existing literature on channel estimation schemes.
3. Channel Estimation in Different Frequency Bands
In the 5G wireless communications, as the low frequency band is utilized fully, the target is shifted to the higher frequency bands with higher bandwidth. MmWave technology is considered to be an effective solution to the problem of spectrum resource shortage, and THz with higher spectrum will also become an important direction for the future beyond 5G (B5G) and 6G wireless communication systems. Although the communication in high frequency bands can solve the problem of spectrum resource shortage, due to its small wavelength characteristics, it will produce serious path loss, resulting in small coverage of mmWave. RIS can improve the coverage of its communication at a lower cost. As shown in Figure 1, the mmWave frequency bands is 30–300 GHz, and its wavelength is only 1–10 mm. The THz has the frequency of 300 GHz–10 THz and it has a much shorter wavelength. The higher frequency band reaches the visible light band, which is 395–750 THz. RIS not only extends wireless coverage, but also plays a role in improving communication quality and expanding communication capacity. However, the optimization of both beamforming and reflection coefficient matrix of RIS transceivers cannot be achieved without accurate CSI; it is crucial to use efficient, low-overhead, and low-complexity channel estimation methods. Due to the difference in frequency bands and hardware architecture, the chosen estimation method will be different. The method chosen will also vary in different system settings such as single input single output (SISO), multiple input single output (MISO), single input multiple output (SIMO), and MIMO. In the following, we outline the advantages and disadvantages of different channel estimation methods in the high and low frequency bands, discuss representative work and present the basic principles.

Figure 1.
Frequency bandwidth and wavelength of wireless radio waves.
In this discussion, since the channel estimation for BS-user equipment (UE) can often be obtained using common channel estimation methods to obtain CSI or directly propagate blocked, only the channel reflected through the RIS is discussed. As shown in Figure 2, we considered an uplink MIMO system model. Assume that the BS is equipped with M = × antennas uniform planar array (UPA), where is the number of antennas in the horizontal direction and is the number of antennas in the vertical direction. The RIS is equipped with N = × reflecting elements UPA, where and are the number of reflecting elements in the horizontal and vertical directions, respectively. In this communication system, there are K single antenna users. The channel from the RIS to the BS can be denoted by , and the channel from the kth () user to the RIS can be denoted by . The reflection matrix of the RIS element can be denoted by , where and denote the reflection amplitude and phase of the nth RIS reflector, respectively [22,23,24].
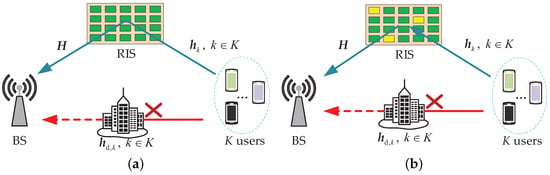
Figure 2.
A RIS-aided multi-user MIMO system consisting of a BS with M antennas, a RIS with N reflective elements, and K single-antenna users, green elements in RIS are passive, yellow elements in RIS are active: (a) Cascade channel estimation and (b) separate channel estimation.
As shown in Figure 2, assuming that user k sends the pilot symbol at time slot , the received signal at BS can be expressed as:
where represents additive white Gaussian noise (AWGN), assuming , and is the noise power. is the direct channel between the BS and user k. This paper assumes that the direct channel is blocked; therefore, . The cascade channel can be expressed as:
Stacking T time slots of Equation (1) and combining Equation (2), by assuming the received signal can be expressed as:
where and . With the finite scattering properties of mmWave, it can be represented using the Saleh-Valenzuela (SV) model [22,23,24,25]. There is a one-to-one relationship between spatial frequency and physical angle on the UPA side. Therefore, for simplicity of illustration, we will refer to the independent variable of the array steering vector as the angle or spatial frequency. The channel matrix between the RIS and the BS can be written as:
where L represents the propagation scattering path between the BS and the RIS; , , and are the complex gain, angle of arrival (AoA), and angle of departure (AoD) of the lth path, respectively. The channel matrix between user k and the RIS can be written as:
where represents the propagation scattering path between the k users and the RIS; and are the complex gain and AoD of the jth path to the kth user, respectively. A steering vector of the UPA is , which can be expressed as [22,23,24]:
where and can be expressed as Equations (7) and (8), respectively:
where the variables z and x can be considered as the corresponding equivalent spatial frequencies with respect to the z axis and x axis of the UPA, respectively. The and are the two uniform linear arrays (ULAs) on the vertical (z-axis) and horizontal (x-axis) directions, respectively. The UPA is obtained by performing a Kronecker product calculation from two ULAs. The and are expressed as the signal elevation and azimuth angles of the UPA, respectively. The relationship between the spatial frequency pair and the physical angle pair can be expressed as [23]:
where is the carrier wavelength, and d is the component spacing. We assume a one-to-one correspondence between physical angle and spatial frequency on the UPA side; then, it is necessary to satisfy .
The following evaluation metrics are commonly used in RIS channel estimation. Mean squared error (MSE) and normalised MSE (NMSE) are commonly used to express the accuracy of channel estimation. The MSE and NMSE can be expressed as Equations (10) and (11), respectively:
where is the estimated value. The signal-to-noise ratio (SNR) represents the ratio of signal power to noise power. It can be expressed as:
where is the signal power and is the power of the noise. The pilot overhead is also one of the important metrics for evaluating channel estimation methods. The bit error rate (BER) and achievable rate can indicate the efficiency of the message delivery after channel estimation and beamforming.
3.1. Channel Estimation for RIS Systems in High Frequency Bands
In this section, we focus on the channel estimation for RIS systems in high frequency bands. As one of the key technologies of 5G, the larger bandwidth of mmWave brings greater channel capacity and higher communication rates. Higher band THz communication is also considered one of the key technologies for future 6G development. However, the path propagation process generates severe path loss and the path is easily blocked by obstacles; the hardware complexity and huge power consumption associated with the high frequency bands are the main problems it currently faces. The RIS, with its low cost, low power consumption, and the advantage of reducing the path loss by reflecting the signal, can make up for the shortage in the high frequency bands. Accurate CSI can design the optimal phase dependence of RIS and thus improve the performance, while the accuracy of channel estimation determines the acquisition of CSI. A suitable method with high accuracy, low training overhead, and complexity is difficult to achieve at the same time slot when selecting a method for channel estimation.
In the high frequency bands, multipath scattering is sparse and can be modeled by the angular domain. This modeling approach uses only a small number of parameters, which reduces the pilot overhead. RIS cannot transmit or receive signals due to its passive characteristic; therefore, the channel estimation is accomplished by designing from the hardware and transmission protocol aspects. In terms of hardware design, there are fully-passive RIS and semi-passive RIS. The difference is that fully-passive RIS is a passive reflective element that can only reflect signals, while semi-passive RIS can receive signals by installing a small number of active elements. Due to the difference in hardware, the existing channel estimation methods can be divided into cascaded channel estimation and separate channel estimation.
In the mmWave band, due to its channel sparsity, only the angle, gain, and time delay need to be estimated for channel estimation, and the required pilot overhead is reduced greatly. In the RIS-assisted wireless communication system, cascaded channel estimation methods and separated channel estimation methods have their own advantages and disadvantages. The channel estimation methods in high frequency bands are described in Figure 3. Methods are based on fully passive RIS and semi-passive RIS in different scenarios, which are divided into five main aspects: single-user, multi-user, practical application, assistance, and wideband systems.
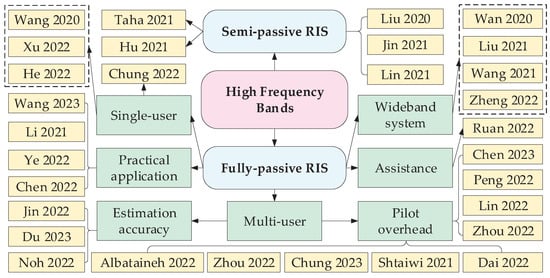
Figure 3.
Channel estimation for RIS systems in high frequency bands.
3.1.1. Channel Estimation for Fully-Passive RIS
Single-user: With passive characteristics of fully-passive RIS, it cannot complete the reception and transmission of the signal. Therefore, the existing channel estimation method is to complete the estimation of the cascaded channel, as shown in Figure 2a. To achieve good reflection characteristics, the channels of BS-RIS and RIS-UE are considered as the overall channel, and the CSI obtained through the cascaded channel is sufficient to complete the phase shift setting of the RIS. The sparsity of mmWave can be exploited to convert the channel estimation problem into a sparse channel recovery problem, which can be solved using a compressive sensing (CS) algorithm.
Wang et al. [26] converted the channel estimation problem into a sparse recovery representation of the cascaded channel using the property of Khatri-Rao and Kronecker products. The problem was solved using the orthogonal matching pursuit (OMP) and generalized approximate message passing (GAMP) algorithms. Compared with the least square (LS) method, which requires at least 1024 overheads, the GAMP algorithm in this paper requires only 100 overheads and has an NMSE of 0.04. In channel estimation, excessive training overhead can lead to a reduction in signal efficiency. Therefore, different approaches are proposed in the following literatures.
Chung et al. [27] proposed a two-stage beam training and channel estimation method based on fast alternating LS (FALS), which can reduce the complexity. The training overhead can be reduced by recovering the complete channel matrix using the observed partial channel matrix. Compared with the OMP and atomic norm minimization (ANM) algorithms, the method used in this paper can reduce the number of training symbols by about 45% and is second only to the OMP algorithm in terms of complexity.
Deep learning methods have attracted much attention in recent years and can be effectively applied to channel estimation. Xu et al. [28] proposed a channel subsampling and a two-part deep neural network (DNN) approach to reduce the training overhead in dynamic time-varying channels. The first part describes the RIS dynamic channel using the neural ordinary differential equation (ODE), and the latter part uses the ODE to modify the structure of the neural network to complete the channel extrapolation. He et al. [29] simulated a conventional gradient descent algorithm using a model-driven depth unfolding approach. A computationally intensive training process was performed in the offline phase, and only low-complexity computations are required in the projection phase. The deep learning approach used in this paper reduces the overhead by 25% compared with the LS algorithm.
Multi-user: More pilot overhead and interference among UEs need to be considered in multi-user scenarios; therefore, a more suitable method for channel estimation needs to be found. Since the number of paths in the BS-RIS-UE will be few unlike conventional MIMO mmWave channels where only row sparsity is available, in RIS-assisted mmWave communication systems with row block sparsity, this feature can be exploited to further reduce the training overhead [25].
To reduce training overhead and pilot overhead, Chen et al. [22] used row-column block sparsity on the foundation of [25]. Using this property, a method was proposed to exploit inter-user correlation to achieve joint channel recovery for multiple users. The proposed method reduces the pilot overhead compared with LS, multiple measurement vector (MMV), etc. By projecting and exploiting the scaling relationships among different users, the approach in this paper reduces the overhead by 80% and 60%, respectively, compared with the LS algorithm and MMV.
Channel estimation efficiency can be improved by setting up a reasonable transmission protocol. To reduce the pilot overhead, the sparsity, and correlation of mmWave multi-user were exploited in [23,30]. Partial information of a single user can be estimated in the first. Further, the channel between BS and RIS is estimated in a large time scale using the quasi-static property between BS-RIS, and the channel estimation for multi-user is completed using channel recovery. Additionally, using the case that the physical locations of BS, RIS and UEs do not vary significantly over multiple consecutive channel coherence blocks, the remaining channel coherence blocks only need to estimate the rapidly varying channel gain. Compared with the baseline solution, only 50% of the pilot overhead is used to achieve better results.
Moreover, a RIS-assisted mmWave channel estimation method based on the Re’nyi entropy function was proposed in [31]. The Re’nyi entropy function is utilized as a sparse promoting regularizer for the purpose of reducing the pilot overhead. When utilizing CS algorithms, the complexity is cube proportional to the number of RIS components. Lin et al. [24] transform the channel estimation problem into a fixed constraint rank one parametric regularization optimization problem. The manifold optimisation (MO) and alternating minimisation (AM) methods are used to find the local optimal solution. To further reduce the complexity, a three-part CS-based channel estimation method was proposed [24]. Optimisation-based algorithms can improve accuracy, but they also introduce a greater degree of complexity. On the other hand, greedy algorithms can reduce the complexity relatively well, but also the accuracy.
To improve the estimation performance and robustness, in sparse channel recovery, a predefined dictionary is used which leads to grid mismatch and performance degradation. Zhou et al. [32] proposed to optimize the dictionary to adapt to the channel characteristics. BS and RIS keep the position constant in most cases. Chung et al. [33] estimated the angular information by using the position information to achieve the purpose of reducing the pilot overhead. The one-dimensional (1D) and two-dimensional (2D) ANM-based channel estimation method is further proposed to achieve excellent estimation accuracy.
To improve the ability to apply different scenarios and reduce the pilot overhead, Shtaiwi et al. [34] first estimated some of the active users and in the second stage estimated inactive users based on the spatial-temporal-spectral (STS) framework of deep convolutional neural networks (CNN). Deep learning networks can sometimes have a low generalisation ability and cannot be applied to changing scenarios. Taking it a step further, Dai et al. [35] proposed a distributed machine learning (DML) technique to achieve reliable downlink cascaded channel estimation and neural network architectures.
Deep learning is an effective way to improve the estimation performance. Three practical residual neural networks, namely, generative adversarial networks based convolutional blind denoising (GAN-CBD) network, convolutional blind denoising network (CBDNet), and multiple residual dense network (MRDNet), were proposed in [36] using the low-rank structure of the channel. Specifically, the GAN-CBD and CBDNet based on the generative adversarial network were used in the offline phase to obtain accurate CSI, and then the MRDNet was used to adapt the online cascaded channel estimation with improved generalization and fitting capabilities flexibly. A semi-blind joint channel estimation and symbol detection scheme was proposed in [37]. The method proves that the BS received signal follows the PARATUCK2 tensor model and there is no training phase, symbol detection, and channel estimation are done simultaneously. It is difficult to meet the demand for a large number of training symbols in practice, and two Cramér-Rao lower bound (CRB)-based training signal design methods for enhanced sparse channel estimation were proposed in [38]. The CRB for the channel parameters consisting of path gain and path angle is derived under the assumption of Bayesian mixture parameters.
Practical application: The impact of its hardware cost and accidents on RIS need to be considered. The increase in the number of antennas in large-scale MIMO systems leads to high power consumption and high cost. Wang et al. [39] proposed to equip the BS with a small number of analog-to-digital converters (ADCs). The channel estimation was then completed using the bilinear generalized approximate message passing (BiG AMP) algorithm. The method in this paper requires only 8 bit quantization to achieve the same results as infinite bit.
To address the information loss due to quantization, a Bayesian optimal estimation framework was introduced to reduce the cost and power consumption. RIS was proposed in [40] to apply low-precision ADC quantization in large-scale MIMO communication systems. Further, a channel estimation algorithm based on GAMP algorithm and combined with expectation maximization (EM) and nearest neighbor learning (NNL) algorithms was proposed. It compensated for the loss caused by low precision ADC quantization, which can guarantee the estimation performance while reducing power consumption.
To solve array blocking problems caused by sand, dust, rain, and snow cover in practical applications, the joint array diagnosis and channel estimation methods applied to single-user and multi-users were proposed in [40], respectively. It reduced the influence caused by the outside world to improve channel estimation accuracy and usage efficiency.
To eliminate inter-cell and intra-cell interference, Ye et al. [41] achieved a proper phase shift for each element design by designing different reflection coefficients. It ensured that the performance of the desired user was maximised and that interference to the undesired user was minimised. An efficient 2D line spectrum optimization based on ANM was also proposed for channel estimation, and the design of reflection beamforming was accomplished using this method, but the performance was limited when the number of users increased.
Integrating RIS into vehicles can achieve good applications in the future. The mobility of vehicles makes the CSI change contiguously, which makes it difficult to obtain accurate instantaneous CSI. Therefore, a transmission protocol with a reasonable configuration of CSI acquisition time scale was proposed in [42], which can reduce the channel information update frequency, the proposed method can reduce the complexity and training overhead effectively.
Wideband systems: The proposed method for narrowband systems is not generally applicable in wideband systems. Wan et al. [43] proposed to use OFDM to overcome frequency selective fading in wideband, and then used BS-RIS as prior knowledge to design the pilot to estimate BS-UE and RIS-UE by the distributed OMP (DOMP) method jointly. Liu et al. [44] transformed the wideband channel estimation into a parameter recovery problem. Several pilot symbols were used to detect the channel parameters by a newtonian OMP (NOMP) algorithm. This method considered the phase and delay differences between the received signals at different BS antennas and RIS elements.
Wang et al. [45] applied the super-resolution (SR) method in images to channel estimation. Then, they proposed a switch-based method for LS estimation and super-resolution, which can reduce the training overhead while ensuring the channel estimation accuracy.
Zheng et al. [46] proposed a channel estimation method based on canonical polyadic decomposition (CPD) by representing the received signal as a third-order tensor using the inherent sparsity of mmWave. Then, the channel parameters were estimated based on the structured CPD method.
The problem of high pilot overhead due to a fully passive RIS can often also be solved by assisted methods. Ruan et al. [47] proposed an approach of using reference points for separate channel estimation to overcome the problem of large training overhead for cascaded channels. The proposed method achieves a 2 dB reduction in NMSE compared with the best benchmark solution.
Due to the passive characteristic of the RIS, setting up active elements in the passive RIS is necessary to estimate the channels of the BS-RIS and RIS-UE separately. In the next part of this section, the fully passive hardware architecture of the RIS changes to a semi-passive structure, and the corresponding channel estimation methods change.
3.1.2. Channel Estimation for Semi-Passive RIS
The fully passive RIS can perform cascaded channel estimation due to the inability to transmit and receive signals. Due to the inability to decouple well in high-dimensional channels and the scaling ambiguity, it is difficult to obtain CSI for BS-RIS and RIS-UE. Therefore, several active RIS elements are proposed to be placed in the RIS, as shown in Figure 2b, which can both exploit the advantages of RIS in saving power to a certain extent and accomplish signal processing more efficiently.
An architecture with only a few active elements was proposed in [48]. A CS method was proposed to perform channel reconstruction for sampled channels sensed by a few elements. Another method was to use deep learning to learn the best mapping from the best reflection matrix.
Hu et al. [49] proposed a receiver element RIS structure equipped with only a portion of 1-bit quantization. The training signal at the passive RIS element was first recovered using the alternating direction method of multipliers (ADMM), and then the full channel information was obtained using channel sparsity and the GAMP algorithm.
A deep denoising neural network-assisted compressed channel estimation method was proposed in [50]. The complete channel matrix was obtained from partial cells using the channel reconstruction method. The use of denoising networks can achieve performance gains of up to 4 dB above the initial estimation.
Jin et al. [51] proposed an approach to reshape the channel matrix into a two-dimensional image, using single-scale enhanced deep super-resolution (EDSR) neural network and multi-scale deep super-resolution (MDSR) neural network to recover the channel using low sparse channel properties. This approach can increase the generalization capability and reduce the hardware complexity.
Lin et al. [52] considered time-varying channels and proposed a hybrid RIS structure composed of active and passive elements. The narrowband was modeled as a third-order CPD problem and the wideband problem as a fourth-order CPD problem. Then, the tensor problem was solved by an algebraic method to recover the channel parameters and complete the channel estimation. This can help to improve the accuracy of estimating and reduce the complexity of estimating.
In the high frequency band, the channel estimation problem is mostly converted to a compressed sensing problem because of its channel sparsity characteristics. It can be solved using greedy algorithms, message passing algorithms, and optimisation algorithms. Using this feature and the channel estimation protocol, up to 80% reduction in pilot overhead can be achieved in the method proposed in this paper. In practical situations, the hardware losses and costs associated with high frequency bands need to be considered. It is also necessary to consider the Doppler shift caused by the actual movement of cars, high-speed trains, etc. Therefore, a suitable channel estimation method needs to be selected. The complexity can be reduced by using deep learning methods instead of algorithms, and of course also for denoising purposes. The channel estimation algorithms, and performance comparison in high frequency bands are described in Table 3. Table 3 describes the methods from four aspects: system setup, problem, method, and results analysis.

Table 3.
Channel estimation in high frequency bands sorted by publication years.
3.2. Channel Estimation for RIS Systems in Low Frequency Bands
In this section, the focus is on the channel estimation method for RIS systems in low frequency bands. At low frequency bands, due to its rich multipath scattering, an unstructured channel model is used, but it is difficult to describe the overall characteristics of the propagation environment with the method. Unstructured CSI requires a large training overhead; therefore, many channel estimation methods have been proposed to reduce the training overhead.
The channel estimation methods in low frequency bands are described in Figure 4. Methods are based on fully-passive RIS and semi-passive RIS in different scenarios, which are divided into four main aspects: MISO, MIMO, massive MIMO, and wideband system.
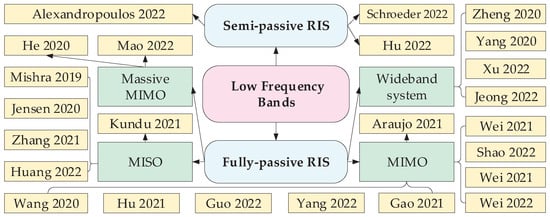
Figure 4.
Channel estimation for RIS systems in low frequency bands.
The channel estimation methods of different RIS systems are presented by different RIS architectures. Similar to the high band, the fully-passive RIS mostly uses the estimation method of cascaded channels, while the semi-passive can use the method of separate channel estimation.
3.2.1. Channel Estimation for Fully-Passive RIS
In a fully passive RIS-assisted low frequency system, channel estimation can be accomplished for the cascaded channel. In addition, the obtained CSI is sufficient to accomplish setting the optimal phase to achieve maximum transmission efficiency. The methods applied will be varied for different system settings, we will present the channel estimation methods for different system settings in the following.
MISO systems: Mishra et al. [53] first proposed the ON/OFF channel estimation method. This method accomplishes channel estimation by sequentially turning on the RIS element. Since the cascaded channels are only estimated one by one, the estimated variance of each element is equal to 2. To reduce the variance, a minimum variance unbiased (MVU) estimator was proposed in [54]. This method can be T (training periods) times more accurate than the ON/OFF method of estimation. However, it required large pilot overhead.
To further reduce the pilot overhead, different approaches were proposed in [55,56]. Zhang et al. [55] proposed a rank-one matrix factorization (MF) approach. AM and gradient descent methods were then used to find the approximate optimal solution. An iterative expectation maximization (EM) algorithm for semi-blind channel estimation was proposed in [56]. The method first transforms the channel estimation problem into a maximum likelihood estimation problem by initializing the semi-blind channel estimation with pilots and solving it using EM. This method can reduce the pilot overhead by 85% compared with the benchmark solution.
Kundu et al. [57] proposed an linear minimum mean square error (LMMSE) based channel estimation method that further utilized CNN to approximate the optimal solution. Both denoising CNN (DnCNN) and fast and flexible denoising network (FFDNet) were considered in this paper. Improved MSE performance of DnCNN and FFDNet-based channel estimators as channels become more highly correlated. This method offered high performance and relatively low implementation complexity.
MIMO systems: The increased number of users and antennas can make channel estimation more challenging. In [58], a three-stage channel estimation method was proposed considering the redundancy among channels without any assumption of sparsity and low rank. The channel matrix of a typical user directly to the BS and the channel matrix reflected by the RIS were estimated in the first two stages, respectively. Finally, the channel estimation for other users was completed using the strong correlation between other users and that user. This can reduce the pilot overhead and save estimation time in MIMO systems.
Hu et al. [59] used the quasi static property of BS-RIS to perform channel estimation at the time scale. Small-scale channel estimation was performed between UE and RIS, which can reduce the pilot overhead significantly. Although this method reduces pilot overhead, performance is worse than MVU. This property is used in later channel estimation methods frequently.
A normally open training protocol was proposed in [60] and utilized a common link structure to reduce the pilot overhead. This method offers a performance gain of approximately 15 dB compared with the ON/OFF method.
To reduce the training overhead, Yang et al. [61] proposed the anchor-assisted approach, which assisted RIS in channel estimation by setting anchor points. While achieving the same performance as the baseline solution, this method reduces the number of training symbols by approximately 50.
The tensor modeling approach is also applicable to channel estimation. Dearaujo et al. [62] proposed channel estimation method relying on parallel factor (PARAFAC) of received signal tensor modeling. This method dealt with the non-ideal case, when there is phase perturbation and when the receiver does not know the RIS phase shift.
Deep learning methods have received much attention in recent years and can be applied to channel estimation to achieve better performance. Gao et al. [63] proposed a three-stage DNN framework, which can achieve better performance without relying on high pilot overhead and accurate channel statistics. Compared with the OMP method, this method can reduce the pilot overhead by approximately 50%.
A cascaded channel estimation scheme based on dual-structured OMP (DS-OMP) was proposed in [64] by exploiting dual structural sparsity of inter-user angular cascade channels.
In RIS-assisted wireless communication systems, not all devices are active at the same time, and assigning potential devices to pilot sequences as well would lead to excessive overhead. Shao et al. [65] proposed an unsourced random access (URA) scheme and proposed a rank one decomposition-based message recovery and channel estimation method for RIS-assisted URAs. Both channel estimation and signal recovery alone require a lot of training and computation; therefore, Refs. [66,67] proposed joint channel estimation and signal recovery methods that were able to cost lower complexity.
Massive MIMO systems: The larger number of antennas can make channel estimation more difficult to achieve. To complete the channel estimation, He et al. [68] proposed a two-stage cascaded channel estimation method. In the first stage, a BiG AMP algorithm with sparse matrix decomposition was used. In the second stage, a matrix-completed Riemannian streamlined gradient algorithm was used to accomplish accurate channel estimation. The size of sparsity affects matrix decomposition and completion.
The deep learning approach is further utilized. Mao et al. [69] brought the results of channel recovery into the residual network to reduce the errors caused by grid mismatch. In order to improve the accuracy of the OMP algorithm, a residual structure-based OMP (RS-OMP) network was proposed. Then, a straightforward network (SN) structure was proposed instead of the OMP algorithm.
Wideband systems: Zheng et al. [70] designed a novel phase-shifted channel estimation model for RIS-OFDM systems that satisfies the unit-mode constraint. With the same pilot overhead, this method improves gain by 14 dB over the ON/OFF method. Yang et al. [71] proposed a method using RIS grouping in SISO systems. Both methods provide accurate channel estimation results and a reduction in training overhead.
Xu et al. [72] extrapolated the partial RIS elements to the complete channel by closing them and obtaining partial channel information. Using the compression idea, the extrapolation problem was transformed into a problem of recovering the channel parameters. The complete channel was reconstructed using the sparse Bayesian learning (SBL) framework finally. This method can reduce the pilot overhead while ensuring the accuracy. SNR is improved by 12 dB gain compared with the LS method.
In OFDM systems, the carrier frequency offset problem is encountered. Jeong et al. [73] proposed a joint carrier frequency offset (CFO) and channel impulse response (CIR) estimation method to solve this problem. The method improved the channel estimation accuracy under OFDM systems. This method can improve performance gains up to 30 times compared with the benchmark scheme.
3.2.2. Channel Estimation for Semi-Passive RIS
The estimation of separate channels can be easily accomplished by setting active elements with transceiver signal capability installed on the RIS. However, in semi-passive RIS, it is necessary to consider not only the method of channel estimation, but also to set the number and location of active RIS elements in a reasonable way. The goal is to be able to improve the accuracy or reduce the complexity of channel estimation while ensuring that the hardware complexity and power consumption are acceptable.
An architecture consisting of a passive RIS and an active RF chain for baseband reception was proposed in [74]. Using this architecture and assuming sparse wireless channels in the beamspace domain, an alternating optimization method was proposed to achieve explicit channel estimation on the RIS side. This method saves pilot overhead and training time.
Schroeder et al. [75] proposed a two-stage channel estimation scheme based on ANM. A new two-stage channel estimation approach was developed in a hybrid RIS architecture. The proposed channel estimation required fewer active RIS elements and only one-way training, which has better estimation performance.
Hu et al. [76] proposed a semi-passive RIS using a grouping structure. Based on this structure, a two-stage channel estimation method was proposed. The first stage estimated the BS-RIS channel signal parameters by the estimation of signal parameters via rotational invariance technique (ESPRIT). The second stage estimated the channel using the total LS (TLS) ESPRIT and multi-signal classification (MUSIC) methods. This method has better performance and lower training overhead, and the performance can be further improved by flexibly allocating the training time between the two phases. The best performance is achieved when the ratio of first stage to total time is 0.1. However, the grouping structure made the beamforming performance degraded.
Compared with the high frequency bands, the low frequency bands lack channel sparsity characteristics. Sparse matrices can be created by assuming a partial opening of the RIS or other assumptions. High-dimensional matrices can be reduced in complexity by matrix decomposition or by using tensor methods. Further, deep learning methods can be used to improve the estimation performance and reduce the pilot overhead. The channel estimation algorithms and performance comparison in low frequency bands are described in Table 4. Table 4 describes the methods from four aspects: system setup, problem, method, and results analysis.

Table 4.
Channel estimation in low frequency bands sorted by publication years.
4. Signal Processing Algorithms for RIS Channel Estimation
Based on different parameter acquisition schemes and mathematical modeling, we divide channel estimation algorithms into five aspects: conventional-based, optimization-based, CS-based, deep-learning-based, and composition-based algorithms.
4.1. The Conventional Algorithms for RIS Channel Estimation
In the generic channel estimation method, the transmitter transmits the pilot sequence and the receiver receives the signal sequence to recover the channel matrix in the constructed channel model.
LS/LMMSE: LS estimation [77] and LMMSE are classical channel estimation methods for finding model solutions for channel estimation, which was widely used in RIS-aided systems for pilot-based channel estimation. The RIS channel estimation of conventional LS/LMMSE has a large channel estimation pilot overhead; to minimize the LS/LMMSE channel estimation error, the training reflection pattern and the transmit pilot sequence can be designed jointly [78,79].
The conventional LS estimation scheme had a high pilot overhead, which was reduced in [80]. Using a low-rank subspace, a reduced subspace LS estimation scheme and the RIS phase shift pattern was optimized to minimize the MSE of the channel estimation. Xu et al. [81] applied minimum MSE (MMSE) channel estimation to unmanned aerial vehicle (UAV) scenarios with low-complexity optimization of the RIS phase shift matrix.
At high Doppler frequencies, the existing RIS channel estimation techniques assuming block fading model pairs cause large errors. In [82], the characteristic of Doppler frequency shift of the time-varying channel leads to a large estimation overhead. To reduce the computational complexity, a correlation coefficient between direct line-of-sight and non-line-of-sight was established. The function of the channel was modeled and the MMSE estimation process was refined to improve the accuracy.
Grouping RIS: To reduce the training overhead and make full use of the spatial correlation of the channel, a scheme of grouping RIS elements was proposed in [71]. The large RIS was divided into several small RIS groups and each group shared the same common reflection coefficients, which was widely used in the subsequent RIS channel estimation process.
For the channel estimation problem of the uplink channel of a RIS-assisted multi-user MIMO (MU-MIMO) system, the entire RIS surface was divided into sub-RISs and an algorithm for estimating the channel using the symmetric positive definite (SPD) matrix [83] was proposed.
Kalman filtering (KF): The channel coefficient matrix was kept constant during the coherent time and the channel was estimated for the elements of the multiple time blocks [84]. Mao et al. [85] used KF for mobile scenes and derived the best reflection coefficients for RIS elements according to the MMSE.
For downlink communication system in a frequency division duplex MIMO system, Cai et al. [86] proposed that the direct channel and the cascaded channel were estimated by two KF tracking. The reflection coefficients at the pilot and RIS were designed jointly and the optimal coefficient matrix was approximated by the columns of the discrete Fourier transform (DFT) matrix.
Multi-stages: To further improve the estimation accuracy, the distributed multi-stage algorithm was used for RIS channel estimation widely. To obtain higher accuracy channel estimation with lower pilot overhead, in [87], an anchor-assisted multi-stage multiuser wideband cascaded channel estimation scheme was proposed to estimate the cascaded channels. In the first stage, Qian et al. [87] obtained BS-RIS CSI based on cyclic prefix single carrier transmission and phase configuration at RIS. In the second stage, the cascade channel information was estimated in the frequency domain using partial BS-RIS channel states.
The conventional-based channel estimation algorithms and performance comparison are described in Table 5. Table 5 describes the methods from four aspects: antenna/RIS architecture, channel model, major algorithm, and performance analysis.

Table 5.
Comparison of conventional algorithms for RIS channel estimation.
4.2. Optimization-Based Algorithms for RIS Channel Estimation
Optimization algorithms are also used in the RIS channel estimation process commonly. The generalized EM (GEM) algorithm is used to estimate the parameters in the absence of variables, the model and parameters are adjusted to obtain the optimal solution continuously. A spatially alternating GEM-based scheme for RIS-assisted channel measurements was presented in [88]. The scheme was estimated by multipath component tracking and maximum likelihood (ML) calculations.
In [89], a new over-the-air (OTA) method to estimate the true phase shift of the RIS elements was modeled as a high-dimensional non-convex optimization problem. The ML estimates were obtained by iterative algorithm. The root MSE (RMSE) of the phase estimation was closed to the CRB, thus verifying the effectiveness of the proposed algorithm.
To reduce the pilot overhead by exploiting the common-link variables and the user-specific variables, Guo et al. [60] used an alternating optimization algorithm to achieve a locally optimal solution for a non-convex optimization problem, with a low computational complexity.
Modelling the millimetre wave channel estimation problem as a non-convex optimisation problem, Lin et al. [24] used alternating minimisation and manifold optimization algorithms to generate locally optimal solutions. To reduce the computational complexity, a multi-stage computer-based algorithm is further designed.
The optimization-based channel estimation algorithms and performance comparison are described in Table 6. Table 6 describes the methods from four aspects: antenna/RIS architecture, channel model, major algorithm, and performance analysis.

Table 6.
Comparison of optimization-based algorithms for RIS channel estimation.
4.3. Compressed Sensing-Based Algorithms for RIS Channel Estimation
The problem is formulated as an optimization algorithm to recover the original signal as accurately as possible from the sparse projection matrix, which is often used to deal with the channel estimation problem of RIS [90].
The greedy algorithm, a common algorithm for CS, has low computational complexity and is often used in the signal recovery process [91,92]. Common CS techniques such as ANM [75], OMP algorithm [64], approximation messaging passing (AMP) [93], and tensor decomposition technique [37] were widely used for the channel estimation process. The CS algorithm constantly searches for the most suitable transform base to represent the channel matrix as sparse, which is an optimization problem. The channel matrix is computed accurately using a small amount of information, which reduces the pilot overhead during channel estimation significantly.
OMP algorithm: The conventional OMP algorithm directly used for RIS channel estimation leads to large complexity, and how to reduce the training overhead becomes a topic worth discussing. The number of RIS components is large and the calculated pressure of the composite channel is high. For the composite channel models, the channel estimation problem was formulated as a sparse recovery problem for a set of independent dictionaries in the angular and temporal domains.
The computational complexity of the multidimensional OMP strategy [94] was based on compressed channel estimation, which was greatly reduced by not computing on the large dictionary directly. The OMP algorithm was modified to exploit the joint corner-domain sparse structure of the cascaded channels associated with different users. The matrices of the corner domain channels for different users had common non-zero rows. The joint estimation of a large number of common corner domain cascaded channels increased the number of training samples and reduced the effect of noise.
AMP algorithm: The sparsity of the OMP algorithm is a fixed value, which is not compatible with the actual situation. The further proposed AMP algorithm has adaptive sparsity. A two-stage algorithm including matrix decomposition stage and matrix completion stage was proposed in [68].
In [93], in the first stage, conventional channel training methods were used to estimate the direct MIMO channel among UE terminals. In the second stage, the bilinear adaptive vector approximation messaging algorithm was used for dictionary matrix learning. The sparsity of the phase-shifted coefficient matrix was used to remove the permutation ambiguity from the channel during the training process. By using the statistical properties of the user-to-RIS and RIS-to-BS channels and the central limit theorem (CLT), it can verify the approximate Gaussian distribution when the channel propagates in the sub-6 GHz band.
By using Gaussian approximation, the joint channel estimation and data detection technique of the BiG AMP algorithm [95] was proposed. In the improved BiG AMP algorithm, a pilot was used to eliminate the effect of quantization and the paper used a quantization-aware approach to estimate the CSI. The performance was further improved relative to Ref. [93].
During numerical processing, the row sparse matrix elements were coupled to each other causing a certain degree of error in the conventional estimation scheme. A hybrid approximate message passing framework was proposed in [96] to decompose the derivative frequency matrix, and recover the row sparse representation in the model. The hybrid architecture compensates for the problem that GAMP cannot operate in the non-Gaussian distribution dictionary.
In this section, we give an overview of the idea and use of CS algorithms in the RIS channel estimation process, mainly describing the shortcomings of the classical OMP algorithm, such as high computational complexity and fixed sparsity leading to large application limitations. The extension literature improves on the shortcomings, how to reduce the computational complexity, and the joint adaptive sparsity AMP algorithm.
The compressed sensing-based channel estimation algorithms and performance comparison are described in Table 7. Table 7 describes the methods from four aspects: antenna/RIS architecture, channel model, major algorithm, and performance analysis.

Table 7.
Comparison of compressed sensing-based algorithms for RIS channel estimation.
4.4. Deep Learning-Based Algorithms for RIS Channel Estimation
Deep learning has been widely used for RIS channel estimation [98,99]. The learning ability of neural networks can be used to estimate the full channel from the partial pilot channel information [100,101]; it can also be combined with image processing techniques to imagine the RIS channel information as two images: one corresponding to the real part channel information and one corresponding to the imaginary part channel information. Image processing techniques are more mature, and common interpolation and denoising methods for images are further applied in RIS. The coarse channel information is extracted, preprocessed, and then trained in the network to get the accurate CSI image. The introduction of image processing techniques has opened up a new area worth exploring for CSI [102,103].
Most of the data processed by the channel estimation are complex numbers, but the existing deep learning library functions do not support the operation of the complex number domain. The general practice is that the data need to be preprocessed before input to the network, and the real and imaginary parts of the complex numbers are extracted and then input to the neural network. Due to there being two kinds of real numbers without mining the phase information of the complex numbers, this preprocessing scheme brings much information loss.
The deep learning-based algorithms for RIS channel estimation are presented by different network architectures, which are divided into six main aspects: end to end, CNN, graph attention network (GANet), DNN, recurrent neural network (RNN), and long short-term memory (LSTM).
End to end network: Existing RIS systems have separate functions for coding and modulation, channel estimation, channel equalisation, decoding and demodulation. Actually, these modules can be also considered as a whole and modelled as an end to end network. The end to end network can further optimise the performance of the system by avoiding the system falling into local optima. Simultaneously, it optimizes the connection weight coefficients of the sender, RIS and receiver to minimize the cross-entropy loss function of the system [100].
CNN: Ahmet et al. [104] designed CNN networks for direct channel and cascade channel estimation, where the users accessed the network directly to estimate their own channels. A large amount of reflective surface channel information was coupled with each other, which were computationally difficult. Compensated learning-based neural network was proposed in [105] to dynamically track the CSI. Due to the powerful adaptive capability of deep learning networks, the estimation process learned the fading channel knowledge directly without the priori knowledge. Chen et al. [105] reduced the number of hidden nodes and introduced an offset learning module to improve the performance in the network. Kundu et al. [57] modelled the channel estimation as an image problem, using CNN networks to denoise and approximate the optimal MMSE channel results.
Liu et al. [106] developed a deep residual learning (DReL) framework applied to multi-user cascaded RIS channel estimation. The correctness of DReL is verified by applying it to CNN networks using Bayesian estimation theory derivation, avoiding the multi-dimensional integral calculation of MMSE estimation. The accuracy of channel estimation is further improved by exploiting the advantages of CNN and DReL in feature extraction and denoising.
GANet: Tekbiyik et al. [107] used GANet for full duplex wireless communication link channel estimation. The training results are robust under different propagation channels with better performance compared with conventional LS estimation.
DNN: During the estimation of partially activated RIS element channel coefficients, a three-stage estimation scheme was proposed in [63] for direct channel. Active RIS element cascade channel and inactive RIS element cascade channel was continuously trained to achieve good accuracy. Jin et al. [36] used residual neural networks for cascaded channel estimation. The online cascade channel estimation was proposed to use the network as a multi-residual dense network.
As shown in Figure 5, Zhang et al. [108] proposed a deep learning network architecture for RIS channel estimation.
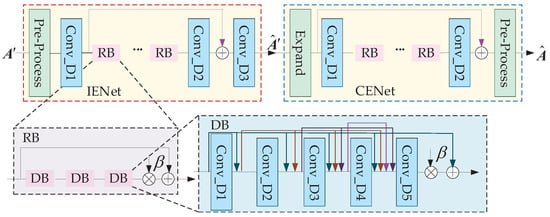
Figure 5.
A deep learning network architecture for RIS channel estimation.
To reduce the pilot overhead, a strategy of RIS grouping was used. The grouping assumes that each group of RIS shares the same reflection coefficient, which is not consistent with reality and causes channel interference under a certain degree. Zhang et al. [108] designed two deep learning networks. The first network eliminates channel interference when RIS grouping was used, and the second network extrapolated the full channel from a partial channel. To separate the real part from the imaginary part, the network consists of three convolutional layers and multiple residual blocks (RBs) of the same structure. Each RB contains three identical dense blocks (DBs); each DB consists of five convolutional layers. A leaky rectified linear unit (LReLU) was used as the activation function for the first four layers in a DB. The output feature information from the previous layers was used as input to each subsequent convolutional layer, and was the output of IENet to improved estimation accuracy for the partial channels. the result learned by the nonlinear transformations, was multiplied by a constant and then added to the result. CENet was constructed from two convolutional layers and the same RBs. was the output of CENet. In turn, all channel information was obtained.
RNN: Considering the large number of RIS components and the relatively short coherence time, Xu et al. [28] considered a deep learning scheme to infer the full channel from partial channels in the antenna domain. Xu et al. used a RNN network in the time domain to explore the connection among different time blocks.
In [109], the deep deterministic policy gradient-based scheme was developed to adapt to the dynamic channel variations to suppress the interference of time-varying channels. Machine learning for channel estimation using reinforcement learning correlation algorithms was not applicable in RIS systems. For the RIS phase shift problem, the data samples associated with the transition from one state to another, and it was difficult to define. In [110], a deep neural network model consisting of two DNNs was proposed which was more effective for a large number of RIS elements.
LSTM: The work in [111] exploited the dual time-scale channel property, where the BS and RIS channels were static and the channel between the RIS and the user was dynamic. In the subsequent channel estimation process, Xu et al. designed a LSTM based neural network framework for the channel decomposition process and the channel prediction process. Xu et al. changed the connection layer according to the nonlinear mapping relationship between the input and the output, thus reducing the complexity.
The specific application scenarios of various network architectures in the process of RIS channel estimation were described above. Suitable networks improve channel estimation performances in unfavorable scenarios such as high-speed time-varying, noisy, etc.
The deep learning-based channel estimation algorithms and performance comparison are described in Table 8. Table 8 describes the methods from three aspects: antenna/RIS architecture, channel model, and performance analysis of deep learning model.

Table 8.
Deep learning-based algorithms comparison for RIS channel estimation.
4.5. Composition-Based Algorithms for RIS Channel Estimation
The direction of algorithm evolution has been described, it is found that deep learning algorithms are being integrated with conventional algorithms and used in the channel estimation process widely. Deep learning can make up for the shortcomings of conventional algorithms, such as improving the channel estimation accuracy and joint optimization of multiple modules. The deficiencies of conventional algorithms with insufficient accuracy can be further improved by using the good denoising function of neural networks to improve the channel estimation accuracy.
SemiDefinite relaxation (SDR)-deep learning: Elements on the RIS were usually arranged in two dimensions, treating the channel information as a single image. Yin et al. [112] first used a SDR scheme and then built an end to end deep learning channel prediction model that predicted the entire CSI based on the pilot information. It outperforms existing approaches based on grouping of RIS elements in terms of achievable rate.
LS-deep learning: Wang et al. [45] modelled the channel information estimated by LS as a low-resolution image and then interpolate it into a high-resolution image linearly.
OMP-deep learning: Using the conventional CS OMP algorithm, it is assumed that the arrival and departure angle bases fall on the discrete grid during the computation exactly, which does not match the reality causing errors. Mao et al. [69] fused deep learning in the OMP algorithm to get results after the residual network to improve the performance.
AMP-deep learning: Conventional CS algorithms AMP algorithm can reduce the pilot overhead substantially, but the estimation accuracy is insufficient. Tsai et al. [113] proposed a hypernetwork-assisted based learned AMP network with dynamic shrinkage parameters, where the adaptive shrinkage parameters of the network output are used among layers instead of a fixed value, thus improving the estimation accuracy.
The core of the conventional approach is in the human perception and modeling of the target problem, as well as proposing a solver to solve the model. Deep learning methods that use parameters to fit the problem can outperform conventional methods in case of good convergence. In most cases, the ability to fit a large number of network parameters is stronger than that of the models constructed using some prior knowledge in conventional methods. As the complexity of the problem increases, the advantage of deep learning becomes more obvious; the conventional solution incorporating deep learning solution has a broad development prospect.
The composition-based channel estimation algorithms and performance comparison are described in Table 9. Table 9 describes the methods from three aspects: antenna/RIS architecture, major problem, and performance analysis of deep learning model.

Table 9.
Composition-based algorithms comparison for RIS channel estimation.
5. Conclusions
5.1. Overall Discussion
RIS, as a fundamental and innovative technology, has great potential and development prospects in future 6G. In this paper, we investigate the key technology of channel estimation for the emerging of RIS. The focus is on investigating the channel estimation methods for RIS-assisted wireless communication systems in high and low frequency bands applications and the comparison under different channel estimation algorithms. Specifically, we first compare the RIS channel estimation methods in different frequency bands, and analyze the differences and development directions of channel estimation methods in fully-passive RIS and semi-passive RIS. We introduce a system model using angular domain modeling to accomplish channel estimation, in which fewer parameters can save training overhead.
We analyze the channel estimation methods in real situations, wideband, and different system settings. Completing channel estimation in the real case requires consideration of cost, fault detection, and mobility issues. Issues such as frequency selective fading need to be considered in wideband, and issues such as mutual interference and pilot pollution need to be considered in different system settings. Therefore, different channel estimation methods need to be used in different scenarios.
We classify the channel estimation methods of RIS into conventional-based algorithms, optimization-based algorithms, CS-based algorithms, deep learning-based algorithms, and composition-based algorithms, and investigate the application of channel estimation in RIS with different algorithms. We analyze the advantages and disadvantages of different methods, use the advantages and improve the disadvantages of different channel methods, and continuously search for more efficient channel estimation methods. We focus on emerging applications of deep learning in the field of RIS channel estimation, such as fusing deep learning with conventional solutions, combining the field of deep learning image processing with channel estimation and building end to end networks.
5.2. Future Work
Finally, RIS has great potential for development in the future, and it is crucial to obtain accurate CSI to guarantee the efficient functioning of RIS. With the increase in cascaded links in multi-RIS systems, the channel estimation complexity increases further and the channel estimation method of single RIS may no longer be applicable. How to integrate more efficiently with RIS in higher frequency bands, such as the THz band, is also an issue of concern. Deploying RIS in complex and changing environments, such as cities with tall buildings, moving vehicles or satellites, requires more appropriate channel estimation methods to guarantee effective communication. The idea of fusing deep learning algorithms with conventional schemes and using the powerful data fitting capability of deep learning to improve the performance of conventional algorithms has a broad development prospect. In summary, RIS has great potential and deserves further exploration and research. We hope that this review can provide sufficient information and promote the development of RIS, regarding which the method of RIS channel estimation is still an evolving process. It is hoped that this research and analysis of RIS for wireless communication channel estimation will stimulate further research into the next-generation wireless communication technologies and their practical application in future wireless communication.
Author Contributions
Y.Y., J.W. and X.Z. chose the topic and designed the structure of the paper. J.W. and X.Z. sorted out and analyzed RIS channel estimation in different frequency bands. Y.Y. and X.Z. reviewed the signal processing algorithms. C.W., Z.B. and Z.Y. classified the involved algorithms and analyzed the data. Y.Y., J.W., X.Z., C.W., Z.B. and Z.Y. performed investigation and revised the manuscript. X.Z., C.W., Z.B. and Z.Y. performed funding acquisition. X.Z. performed supervision and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Shandong Provincial Natural Science Foundation (Nos. ZR2022MF256, ZR2020MF008), in part by the Joint Fund of Shandong Provincial Natural Science Foundation (No. ZR2021LZH003), in part by the Shandong Province Science and Technology Small and Medium-Sized Enterprises Innovation Ability Enhancement Project (No. 2023TSGC0702), in part by the Scientific Research Project of Shandong University–Weihai Research Institute of Industrial Technology (No. 0006202210020011), in part by the Science and Technology Development Plan Project of Weihai Municipality (No. 2022DXGJ13), in part by the Shandong University Graduate Education Quality Curriculum Construction Project (No. 2022038), in part by the Education and Teaching Reform Research Project of Shandong University, Weihai (No. Y2023024), in part by the 17th Student Research Training Program (SRTP) at Shandong University, Weihai (Nos. A22298, A22085), and in part by the 18th Student Research Training Program (SRTP) at Shandong University, Weihai (Nos. A23247, A23249).
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declare no conflict of interest.
References
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Di Renzo, M.; Al-Dhahir, N. Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Commun. Surv. Tutor. 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- Dajer, M.; Ma, Z.; Piazzi, L.; Prasad, N.; Qi, X.F.; Sheen, B.; Yang, J.; Yue, G. Reconfigurable intelligent surface: Design the channel—A new opportunity for future wireless networks. Digit. Commun. Netw. 2022, 8, 87–104. [Google Scholar] [CrossRef]
- Zhao, Y.; Lv, X. Network coexistence analysis of RIS-assisted wireless communications. IEEE Access 2022, 10, 63442–63454. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, S.; Zheng, B.; You, C.; Zhang, R. Intelligent reflecting surface-aided wireless communications: A tutorial. IEEE Trans. Commun. 2021, 69, 3313–3351. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.; Abdullah, Z.; Kourtessis, P.; Kisseleff, S.; Krikidis, I. Coverage probability of STAR-RIS-assisted massive MIMO systems with correlation and phase errors. IEEE Wirel. Commun. Lett. 2022, 11, 1738–1742. [Google Scholar] [CrossRef]
- Noh, S.; Lee, J.; Lee, G.; Seo, K.; Sung, Y.; Yu, H. Channel estimation techniques for RIS-assisted communication: Millimeter-wave and sub-THz systems. IEEE Veh. Technol. Mag. 2022, 17, 64–73. [Google Scholar] [CrossRef]
- Elzwawi, G.H.; Elzuwawi, H.H.; Tahseen, M.M.; Denidni, T.A. Frequency selective surface-based switched-beamforming antenna. IEEE Access 2018, 6, 48042–48050. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.Q.; Liu, S.; Zhang, Q.; Zhao, J.; Dai, J.Y.; Bai, G.D.; Wan, X.; Cheng, Q.; Castaldi, G.; et al. Space-time-coding digital metasurfaces. Nat. Commun. 2018, 9, 4334. [Google Scholar] [CrossRef]
- Tan, X.; Sun, Z.; Jornet, J.M.; Pados, D. Increasing indoor spectrum sharing capacity using smart reflect-array. In Proceedings of the IEEE International Conference on Communications, Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Cao, H. Beamforming design and power allocation for transmissive RMS-Based transmitter architectures. IEEE Wirel. Commun. Lett. 2022, 11, 53–57. [Google Scholar] [CrossRef]
- Di Renzo, M.; Ntontin, K.; Song, J.; Danufane, F.H.; Qian, X.; Lazarakis, F.; de Rosny, J.; Phan-Huy, D.T.; Simeone, O.; Zhang, R.; et al. Reconfigurable intelligent surfaces vs. relaying: Differences, similarities, and performance comparison. IEEE Open J. Commun. Soc. 2020, 1, 798–807. [Google Scholar] [CrossRef]
- Pradhan, C.; Li, A.; Song, L.; Li, J.; Vucetic, B.; Li, Y. Reconfigurable intelligent surface (RIS)-enhanced two-way OFDM communications. IEEE Trans. Veh. Technol. 2020, 69, 16270–16275. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Y.; Chen, Y.; Al-Dhahir, N. Machine learning for user partitioning and phase shifters design in RIS-aided NOMA networks. IEEE Trans. Commun. 2021, 69, 7414–7428. [Google Scholar] [CrossRef]
- Zheng, B.; You, C.; Mei, W.; Zhang, R. A survey on channel estimation and practical passive beamforming design for intelligent reflecting surface aided wireless communications. IEEE Commun. Surv. Tutor. 2022, 24, 1035–1071. [Google Scholar] [CrossRef]
- Pan, C.; Zhou, G.; Zhi, K.; Hong, S.; Wu, T.; Pan, Y.; Ren, H.; Renzo, M.D.; Swindlehurst, A.L.; Zhang, R.; et al. An overview of signal processing techniques for RIS/IRS-aided wireless systems. IEEE J. Sel. Top. Signal Process. 2022, 1–35. [Google Scholar] [CrossRef]
- Jian, M.; Alexandropoulos, G.C.; Basar, E.; Huang, C.; Liu, R.; Liu, Y.; Yuen, C. Reconfigurable intelligent surfaces for wireless communications: Overview of hardware designs, channel models, and estimation techniques. Intell. Converg. Netw. 2022, 3, 1–32. [Google Scholar] [CrossRef]
- Liang, Y.C.; Chen, J.; Long, R.; He, Z.Q.; Lin, X.; Huang, C.; Liu, S.; Shen, X.S.; Di Renzo, M. Reconfigurable intelligent surfaces for smart wireless environments: Channel estimation, system design and applications in 6G networks. Sci. China-Inf. Sci. 2021, 64, 200301. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, X.; Han, C.; Wen, Q. Towards intelligent reflecting surface empowered 6G terahertz communications: A survey. China Commun. 2021, 18, 93–119. [Google Scholar] [CrossRef]
- Swindlehurst, A.L.; Zhou, G.; Liu, R.; Pan, C.; Li, M. Channel estimation with reconfigurable intelligent surfaces—A general framework. Proc. IEEE 2022, 110, 1312–1338. [Google Scholar] [CrossRef]
- Basharat, S.; Khan, M.; Iqbal, M.; Hashmi, U.S.; Zaidi, S.A.R.; Robertson, I. Exploring reconfigurable intelligent surfaces for 6G: State-of-the-art and the road ahead. IET Commun. 2022, 16, 1458–1474. [Google Scholar] [CrossRef]
- Babiker, J.M.S.D.; Huang, X. A survey channel estimation for intelligent reflecting surface (IRS). In Cognitive Radio Oriented Wireless Networks and Wireless Internet; Springer: Berlin/Heidelberg, Germany, 2022; Volume 427, pp. 169–180. [Google Scholar] [CrossRef]
- Chen, J.; Liang, Y.C.; Cheng, H.V.; Yu, W. Channel estimation for reconfigurable intelligent surface aided multi-user mmWave MIMO systems. IEEE Trans. Wirel. Commun. 2023, 1–17. [Google Scholar] [CrossRef]
- Peng, Z.; Zhou, G.; Pan, C.; Ren, H.; Swindlehurst, A.L.; Popovski, P.; Wu, G. Channel estimation for RIS-aided multi-user mmWave systems with uniform planar arrays. IEEE Trans. Commun. 2022, 70, 8105–8122. [Google Scholar] [CrossRef]
- Lin, T.; Yu, X.; Zhu, Y.; Schober, R. Channel estimation for IRS-assisted millimeter-wave MIMO systems: Sparsity-inspired approaches. IEEE Trans. Commun. 2022, 70, 4078–4092. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, X.; Zhang, Y.J.A. Matrix-calibration-based cascaded channel estimation for reconfigurable intelligent surface assisted multiuser MIMO. IEEE J. Sel. Areas Commun. 2020, 38, 2621–2636. [Google Scholar] [CrossRef]
- Wang, P.; Fang, J.; Duan, H.; Li, H. Compressed channel estimation for intelligent reflecting surface-assisted millimeter wave systems. IEEE Signal Process. Lett. 2020, 27, 905–909. [Google Scholar] [CrossRef]
- Chung, H.; Kim, S. Efficient two-stage beam training and channel estimation for RIS-aided mwave systems via fast alternating least squares. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 23–27 May2022; pp. 5188–5192. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, S.; Ma, J.; Dobre, O.A. Deep learning-based time-varying channel estimation for RIS assisted communication. IEEE Commun. Lett. 2022, 26, 94–98. [Google Scholar] [CrossRef]
- He, J.; Wymeersch, H.; Di Renzo, M.; Juntti, M. Learning to estimate RIS-aided mmWave channels. IEEE Wirel. Commun. Lett. 2022, 11, 841–845. [Google Scholar] [CrossRef]
- Zhou, G.; Pan, C.; Ren, H.; Popovski, P.; Swindlehurst, A.L. Channel estimation for RIS-aided multiuser millimeter-wave systems. IEEE Trans. Signal Process. 2022, 70, 1478–1492. [Google Scholar] [CrossRef]
- Albataineh, Z.; Hayajneh, K.F.; Shakhatreh, H.; Athamneh, R.A.; Anan, M. Channel estimation for reconfigurable intelligent surface-assisted mmWave based on Re`nyi entropy function. Sci. Rep. 2022, 12, 22301. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, B.; Chen, J.; Liang, Y.C. Dictionary learning-based channel estimation for RIS-aided MISO communications. IEEE Wirel. Commun. Lett. 2022, 11, 2125–2129. [Google Scholar] [CrossRef]
- Chung, H.; Kim, S. Location-aware beam training and multi-dimensional ANM-based channel estimation for RIS-aided mmWave systems. IEEE Trans. Wirel. Commun. 2023, 1–15. [Google Scholar] [CrossRef]
- Shtaiwi, E.; Zhang, H.; Abdelhadi, A.; Han, Z. RIS-assisted mmWave channel estimation using convolutional neural networks. In Proceedings of the IEEE Wireless Communications and Networking Conference Workshops, Nanjing, China, 29 March 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Dai, L.; Wei, X. Distributed machine learning based downlink channel estimation for RIS assisted wireless communications. IEEE Trans. Commun. 2022, 70, 4900–4909. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, J.; Huang, C.; Yang, L.; Xiao, H.; Ai, B.; Wang, Z. Multiple residual dense networks for reconfigurable intelligent surfaces cascaded channel estimation. IEEE Trans. Veh. Technol. 2022, 71, 2134–2139. [Google Scholar] [CrossRef]
- Du, J.; Luo, X.; Li, X.; Zhu, M.; Rabie, K.M.; Kara, F. Semi-blind joint channel estimation and symbol detection for RIS-empowered multiuser mmWave systems. IEEE Commun. Lett. 2023, 27, 362–366. [Google Scholar] [CrossRef]
- Noh, S.; Yu, H.; Sung, Y. Training signal design for sparse channel estimation in intelligent reflecting surface-assisted millimeter-wave communication. IEEE Trans. Wirel. Commun. 2022, 21, 2399–2413. [Google Scholar] [CrossRef]
- Wang, R.; Ren, H.; Pan, C.; Fang, J.; Dong, M.; Dobre, O.A. Channel estimation for RIS-aided mmWave massive MIMO system using few-bit ADCs. IEEE Commun. Lett. 2023, 27, 961–965. [Google Scholar] [CrossRef]
- Li, B. Sparse Channel Estimation for Reconfigurable Intelligent Surface Assisted Millimeter Wave Massive MIMO System. Ph.D. Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2021. [Google Scholar] [CrossRef]
- Ye, J.; Kammoun, A.; Alouini, M.S. Reconfigurable intelligent surface enabled interference nulling and signal power maximization in mmWave bands. IEEE Trans. Wirel. Commun. 2022, 21, 9096–9113. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Jiao, L. Robust transmission for reconfigurable intelligent surface aided millimeter wave vehicular communications with statistical CSI. IEEE Trans. Wirel. Commun. 2022, 21, 928–944. [Google Scholar] [CrossRef]
- Wan, Z.; Gao, Z.; Alouini, M.S. Broadband channel estimation for intelligent reflecting surface aided mmWave massive MIMO systems. In Proceedings of the IEEE International Conference on Communications; IEEE: Dublin, Ireland, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Gao, F.; Tang, J.; Dobre, O.A. Cascaded channel estimation for RIS assisted mmWave MIMO transmissions. IEEE Wirel. Commun. Lett. 2021, 10, 2065–2069. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, H.; Sun, H. Channel estimation in IRS-enhanced mmWave system with super-resolution network. IEEE Commun. Lett. 2021, 25, 2599–2603. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, P.; Fang, J.; Li, H. Compressed channel estimation for IRS-assisted millimeter wave OFDM systems: A low-rank tensor decomposition-based approach. IEEE Wirel. Commun. Lett. 2022, 11, 1258–1262. [Google Scholar] [CrossRef]
- Ruan, C.; Zhang, Z.; Jiang, H.; Dang, J.; Wu, L.; Zhang, H. Approximate message passing for channel estimation in reconfigurable intelligent surface aided MIMO multiuser systems. IEEE Trans. Commun. 2022, 70, 5469–5481. [Google Scholar] [CrossRef]
- Taha, A.; Alrabeiah, M.; Alkhateeb, A. Enabling large intelligent surfaces with compressive sensing and deep learning. IEEE Access 2021, 9, 44304–44321. [Google Scholar] [CrossRef]
- Hu, J.; Yin, H.; Bjornson, E. MmWave MIMO communication with semi-passive RIS: A low-complexity channel estimation scheme. In Proceedings of the IEEE Global Communications Conference, Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, S.; Gao, Z.; Zhang, J.; Renzo, M.D.; Alouini, M.S. Deep denoising neural network assisted compressive channel estimation for mmWave intelligent reflecting surfaces. IEEE Trans. Veh. Technol. 2020, 69, 9223–9228. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, J.; Zhang, X.; Xiao, H.; Ai, B.; Ng, D.W.K. Channel estimation for semi-passive reconfigurable intelligent surfaces with enhanced deep residual networks. IEEE Trans. Veh. Technol. 2021, 70, 11083–11088. [Google Scholar] [CrossRef]
- Lin, Y.; Jin, S.; Matthaiou, M.; You, X. Tensor-based algebraic channel estimation for hybrid IRS-assisted MIMO-OFDM. IEEE Trans. Wirel. Commun. 2021, 20, 3770–3784. [Google Scholar] [CrossRef]
- Mishra, D.; Johansson, H. Channel estimation and low-complexity beamforming design for passive intelligent surface assisted MISO wireless energy transfer. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019; pp. 4659–4663. [Google Scholar] [CrossRef]
- Jensen, T.L.; De Carvalho, E. An optimal channel estimation scheme for intelligent reflecting surfaces based on a minimum variance unbiased estimator. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020; pp. 5000–5004. [Google Scholar] [CrossRef]
- Zhang, W.; Tay, W.P. Cost-efficient RIS-aided channel estimation via rank-one matrix factorization. IEEE Wirel. Commun. Lett. 2021, 10, 2562–2566. [Google Scholar] [CrossRef]
- Huang, C.; Xu, J.; Zhang, W.; Xu, W.; Ng, D.W.K. Semi-blind channel estimation for RIS-assisted MISO systems using expectation maximization. IEEE Trans. Veh. Technol. 2022, 71, 10173–10178. [Google Scholar] [CrossRef]
- Kundu, N.K.; McKay, M.R. Channel estimation for reconfigurable intelligent surface aided MISO communications: From LMMSE to deep learning solutions. IEEE Open J. Commun. Soc. 2021, 2, 471–487. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Cui, S. Channel estimation for intelligent reflecting surface assisted multiuser communications: Framework, algorithms, and analysis. IEEE Trans. Wirel. Commun. 2020, 19, 6607–6620. [Google Scholar] [CrossRef]
- Hu, C.; Dai, L.; Han, S.; Wang, X. Two-timescale channel estimation for reconfigurable intelligent surface aided wireless communications. IEEE Trans. Commun. 2021, 69, 7736–7747. [Google Scholar] [CrossRef]
- Guo, H.; Lau, V.K.N. Uplink cascaded channel estimation for intelligent reflecting surface assisted multiuser MISO systems. IEEE Trans. Signal Process. 2022, 70, 3964–3977. [Google Scholar] [CrossRef]
- Yang, W.; Li, M.; Liu, Q. A novel anchor-assisted channel estimation for RIS-aided multiuser communication systems. IEEE Commun. Lett. 2022, 26, 2740–2744. [Google Scholar] [CrossRef]
- De Araujo, G.T.; De Almeida, A.L.F.; Boyer, R. Channel estimation for intelligent reflecting surface assisted MIMO systems: A tensor modeling approach. IEEE J. Sel. Top. Signal Process. 2021, 15, 789–802. [Google Scholar] [CrossRef]
- Gao, S.; Dong, P.; Pan, Z.; Li, G.Y. Deep multi-stage CSI acquisition for reconfigurable intelligent surface aided MIMO systems. IEEE Commun. Lett. 2021, 25, 2024–2028. [Google Scholar] [CrossRef]
- Wei, X.; Shen, D.; Dai, L. Channel estimation for RIS assisted wireless communications—Part II: An improved solution based on double-structured sparsity. IEEE Commun. Lett. 2021, 25, 1403–1407. [Google Scholar] [CrossRef]
- Shao, X.; Cheng, L.; Chen, X.; Huang, C.; Ng, D.W.K. Reconfigurable intelligent surface-aided 6G massive access: Coupled tensor modeling and sparse Bayesian learning. IEEE Trans. Wirel. Commun. 2022, 21, 10145–10161. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Alexandropoulos, G.C.; Yang, Z.; Yuen, C.; Zhang, Z. Joint channel estimation and signal recovery in RIS-assisted multi-user MISO communications. In Proceedings of the IEEE Wireless Communications and Networking Conference, Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Guo, Q.; Yang, Z.; Zhang, Z.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Joint channel estimation and signal recovery for RIS-empowered multiuser communications. IEEE Trans. Commun. 2022, 70, 4640–4655. [Google Scholar] [CrossRef]
- He, Z.Q.; Yuan, X. Cascaded channel estimation for large intelligent metasurface assisted massive MIMO. IEEE Wirel. Commun. Lett. 2020, 9, 210–214. [Google Scholar] [CrossRef]
- Mao, Z.; Liu, X.; Peng, M. Channel estimation for intelligent reflecting surface assisted massive MIMO systems—A deep learning approach. IEEE Commun. Lett. 2022, 26, 798–802. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, R. Intelligent reflecting surface-enhanced OFDM: Channel estimation and reflection optimization. IEEE Wirel. Commun. Lett. 2020, 9, 518–522. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, B.; Zhang, S.; Zhang, R. Intelligent reflecting surface meets OFDM: Protocol design and rate maximization. IEEE Trans. Commun. 2020, 68, 4522–4535. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, S.; Gao, F.; Wang, J. Sparse Bayesian learning based channel extrapolation for RIS assisted MIMO-OFDM. IEEE Trans. Commun. 2022, 70, 5498–5513. [Google Scholar] [CrossRef]
- Jeong, S.; Farhang, A.; Perovic, N.S.; Flanagan, M.F. Low-complexity joint CFO and channel estimation for RIS-aided OFDM systems. IEEE Wirel. Commun. Lett. 2022, 11, 203–207. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C.; Vlachos, E. A hardware architecture for reconfigurable intelligent surfaces with minimal active elements for explicit channel estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020; pp. 9175–9179. [Google Scholar] [CrossRef]
- Schroeder, R.; He, J.; Juntti, M. Channel estimation for hybrid RIS aided MIMO communications via atomic norm minimization. In Proceedings of the IEEE International Conference on Communications Workshops, Seoul, Republic of Korea, 16–20 May 2022; pp. 1219–1224. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, R.; Zhong, C. Semi-passive elements assisted channel estimation for intelligent reflecting surface-aided communications. IEEE Trans. Wirel. Commun. 2022, 21, 1132–1142. [Google Scholar] [CrossRef]
- Zhou, G.; Pan, C.; Ren, H.; Wang, K. Channel estimation for RIS-aided millimeter-wave massive MIMO systems. In Proceedings of the 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October 2021–3 November 2021; pp. 698–703. [Google Scholar] [CrossRef]
- Zheng, B.; You, C.; Zhang, R. Intelligent reflecting surface assisted multi-user OFDMA: Channel estimation and training design. IEEE Trans. Wirel. Commun. 2020, 19, 8315–8329. [Google Scholar] [CrossRef]
- Abeywickrama, S.; You, C.; Zhang, R.; Yuen, C. Channel estimation for intelligent reflecting surface assisted backscatter communication. IEEE Wirel. Commun. Lett. 2021, 10, 2519–2523. [Google Scholar] [CrossRef]
- Demir, O.T.; Bjornson, E.; Sanguinetti, L. Exploiting array geometry for reduced-subspace channel estimation in RIS-aided communications. In Proceedings of the IEEE 12th Sensor Array and Multichannel Signal Processing Workshop, Trondheim, Norway, 20–23 June 2022; pp. 455–459. [Google Scholar] [CrossRef]
- Xu, C.; An, J.; Bai, T.; Xiang, L.; Sugiura, S.; Maunder, R.G.; Yang, L.L.; Hanzo, L. Reconfigurable intelligent surface assisted multi-carrier wireless systems for doubly selective high-mobility Ricean channels. IEEE Trans. Veh. Technol. 2022, 71, 4023–4041. [Google Scholar] [CrossRef]
- Xu, C.; An, J.; Bai, T.; Sugiura, S.; Maunder, R.G.; Wang, Z.; Yang, L.L.; Hanzo, L. Channel estimation for reconfigurable intelligent surface assisted high-mobility wireless systems. IEEE Trans. Veh. Technol. 2023, 72, 718–734. [Google Scholar] [CrossRef]
- Shtaiwi, E.; Zhang, H.; Vishwanath, S.; Youssef, M.; Abdelhadi, A.; Han, Z. Channel estimation approach for RIS assisted MIMO systems. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 452–465. [Google Scholar] [CrossRef]
- You, C.; Zheng, B.; Zhang, R. Channel estimation and passive beamforming for intelligent reflecting surface: Discrete phase shift and progressive refinement. IEEE J. Sel. Areas Commun. 2020, 38, 2604–2620. [Google Scholar] [CrossRef]
- Mao, Z.; Peng, M.; Liu, X. Channel estimation for reconfigurable intelligent surface assisted wireless communication systems in mobility scenarios. China Commun. 2021, 18, 29–38. [Google Scholar] [CrossRef]
- Cai, P.; Zong, J.; Luo, X.; Zhou, Y.; Chen, S.; Qian, H. Downlink channel tracking for intelligent reflecting surface-aided FDD MIMO systems. IEEE Trans. Veh. Technol. 2021, 70, 3341–3353. [Google Scholar] [CrossRef]
- Qian, S.; Chen, Y.; Li, Q.; Li, P.; Xia, X.; Wen, M. Anchor-aided channel estimation for RIS-assisted multiuser broadband communications. IEEE Wirel. Commun. Lett. 2023, 12, 89–93. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, C.X.; Zhou, Z.; Feng, R.; Xin, L.; Huang, J. A novel SAGE-based channel parameter estimation scheme for 6G RIS-assisted wireless channel measurements. In Proceedings of the IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 3305–3310. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, Y. Over-the-air phase calibration of reconfigurable intelligent surfaces. IEEE Wirel. Commun. Lett. 2023, 12, 664–668. [Google Scholar] [CrossRef]
- Ardah, K.; Gherekhloo, S.; de Almeida, A.L.F.; Haardt, M. TRICE: A channel estimation framework for RIS-aided millimeter-wave MIMO systems. IEEE Signal Process. Lett. 2021, 28, 513–517. [Google Scholar] [CrossRef]
- Jia, C.; Cheng, J.; Gao, H.; Xu, W. High-resolution channel estimation for intelligent reflecting surface-assisted mmWave communications. In Proceedings of the IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, X.; Chen, Z.; Chen, W.; Li, Z.; Chi, Y.; Han, C.; Li, S. Joint channel estimation and data rate maximization for intelligent reflecting surface assisted terahertz MIMO communication systems. IEEE Access 2020, 8, 99565–99581. [Google Scholar] [CrossRef]
- Mirza, J.; Ali, B. Channel estimation method and phase shift design for reconfigurable intelligent surface assisted MIMO networks. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 441–451. [Google Scholar] [CrossRef]
- Bayraktar, M.; Palacios, J.; Gonzalez-Prelcic, N.; Zhang, C.J. Multidimensional orthogonal matching pursuit-based RIS-aided joint localization and channel estimation at mmWave. In Proceedings of the IEEE 23rd International Workshop on Signal Processing Advances in Wireless Communication, Oulu, Finland, 4–6 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Xiong, Y.; Qin, L.; Sun, S.; Liu, L.; Mao, S.; Zhang, Z.; Wei, N. Joint effective channel estimation and data detection for RIS-aided massive MIMO systems with low-resolution ADCs. IEEE Commun. Lett. 2023, 27, 721–725. [Google Scholar] [CrossRef]
- Zhou, L.; Dai, J.; Xu, W.; Chang, C. Sparse channel estimation for intelligent reflecting surface assisted massive MIMO systems. IEEE Trans. Green Commun. Netw. 2022, 6, 208–220. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Xin, L. Joint channel estimation for RIS-assisted wireless communication system. In Proceedings of the IEEE Wireless Communications and Networking Conference, Austin, TX, USA, 10–13 April 2022; pp. 1087–1092. [Google Scholar] [CrossRef]
- Huang, C.; Mo, R.; Yuen, C. Reconfigurable intelligent surface assisted multiuser MISO systems exploiting deep reinforcement learning. IEEE J. Sel. Areas Commun. 2020, 38, 1839–1850. [Google Scholar] [CrossRef]
- Yerzhanova, M.; Kim, Y.H. Channel estimation via model and learning for monostatic multiantenna backscatter communication. IEEE Access 2021, 9, 165341–165350. [Google Scholar] [CrossRef]
- Jiang, H.; Dai, L.; Hao, M.; MacKenzie, R. End-to-end learning for RIS-aided communication systems. IEEE Trans. Veh. Technol. 2022, 71, 6778–6783. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, T.; Yu, W. Learning based user scheduling in reconfigurable intelligent surface assisted multiuser downlink. IEEE J. Sel. Top. Signal Process. 2022, 16, 1026–1039. [Google Scholar] [CrossRef]
- Xu, J.; Ai, B. When mmWave high-speed railway networks meet reconfigurable intelligent surface: A deep reinforcement learning method. IEEE Wirel. Commun. Lett. 2022, 11, 533–537. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, S.; Zhong, C.; Ma, J.; Dobre, O.A. Ordinary differential equation-based CNN for channel extrapolation over RIS-assisted communication. IEEE Commun. Lett. 2021, 25, 1921–1925. [Google Scholar] [CrossRef]
- Ahmet M., E.; Papazafeiropoulos, A.; Kourtessis, P.; Chatzinotas, S. Deep channel learning for large intelligent surfaces aided mm-wave massive MIMO systems. IEEE Wirel. Commun. Lett. 2020, 9, 1447–1451. [Google Scholar] [CrossRef]
- Chen, Z.; Tang, J.; Zhang, X.Y.; Wu, Q.; Wang, Y.; So, D.K.C.; Jin, S.; Wong, K.K. Offset learning based channel estimation for intelligent reflecting surface-assisted indoor communication. IEEE J. Sel. Top. Signal Process. 2022, 16, 41–55. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X.; Ng, D.W.K.; Yuan, J. Deep residual learning for channel estimation in intelligent reflecting surface-assisted multi-user communications. IEEE Trans. Wirel. Commun. 2022, 21, 898–912. [Google Scholar] [CrossRef]
- Tekbiyik, K.; Kurt, G.K.; Huang, C.; Ekti, A.R.; Yanikomeroglu, H. Channel estimation for full-duplex RIS-assisted HAPS backhauling with graph attention networks. In Proceedings of the IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Gao, F.; Ma, J.; Dobre, O.A. Deep learning-based RIS channel extrapolation with element-grouping. IEEE Wirel. Commun. Lett. 2021, 10, 2644–2648. [Google Scholar] [CrossRef]
- Xu, J.; Ai, B.; Quek, T.Q.S.; Liuc, Y. Deep reinforcement learning for interference suppression in RIS-aided high-speed railway networks. In Proceedings of the IEEE International Conference on Communications Workshops, Seoul, Republic of Korea, 16–20 May 2022; pp. 337–342. [Google Scholar] [CrossRef]
- Li, K.; Huang, C.; Gong, Y.; Chen, G. Double deep learning for joint phase-shift and beamforming based on cascaded channels in RIS-assisted MIMO networks. IEEE Wirel. Commun. Lett. 2023, 12, 659–663. [Google Scholar] [CrossRef]
- Xu, W.; An, J.; Xu, Y.; Huang, C.; Gan, L.; Yuen, C. Time-varying channel prediction for RIS-assisted MU-MISO networks via deep learning. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1802–1815. [Google Scholar] [CrossRef]
- Yin, S.; Li, Y.; Tian, Y.; Yu, F.R. Intelligent reflecting surface enhanced wireless communications with deep-learning-based channel prediction. IEEE Trans. Veh. Technol. 2022, 71, 1049–1053. [Google Scholar] [CrossRef]
- Tsai, W.C.; Chen, C.W.; Teng, C.F.; Wu, A.Y. Low-complexity compressive channel estimation for IRS-aided mmWave systems with hypernetwork-assisted LAMP network. IEEE Commun. Lett. 2022, 26, 1883–1887. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).