Representing Blurred Image without Deblurring

Abstract

The effective recognition of patterns from blurred images presents a fundamental difficulty for many practical vision tasks. In the era of deep learning, the main ideas to cope with this difficulty are data augmentation and deblurring. However, both facing issues such as inefficiency, instability, and lack of explainability. In this paper, we explore a simple but effective way to define invariants from blurred images, without data augmentation and deblurring. Here, the invariants are designed from Fractional Moments under Projection operators (FMP), where the blur invariance and rotation invariance are guaranteed by the general theorem of blur invariants and the Fourier-domain rotation equivariance, respectively. In general, the proposed FMP not only bears a simpler explicit definition, but also has useful representation properties including orthogonality, statistical flexibility, as well as the combined invariance of blurring and rotation. Simulation experiments are provided to demonstrate such properties of our FMP, revealing the potential for small-scale robust vision problems.

1. Introduction

In many real-world vision tasks, it is an inevitablity that researchers conduct analyses on degraded versions of the original scene. Blurring is a common type of image degradation that usually occurs in imperfect imaging, e.g., out of focus, camera or object motion. In this paper, the blur is formalized as the following simple but reasonably accurate model [1]. The blurred image $f_h$ is the result of ideal scene f convolved by a Point-Spread Function (PSF) h, i.e., $f_h(x,y)=(f\ast h)(x,y)$. Moreover, the modern image processing software, e.g., Photoshop, can simulate blurring effects based on the above formalization, with potential use in general image retouching and even malicious adversary attacks against automatic systems. Therefore, an efficient and secure vision algorithm naturally requires the robustness to blur.

1.1. Current Solutions

Robust visual algorithms heavily rely on robust data representations [2]. In this regard, current typical deep-learning representations [3], mainly Convolutional Neural Networks (CNN), are not designed to be robust to blurring at the architectural level. As a remedy, there are two popular data-level ideas to improve the robustness of learning representations:

• Data augmentation which includes blurred image samples in the training phase for boosting the CNN to adapt to blurred patterns;
• Deblurring as data pre-processing, which attempts to restore an ideal scene from blurred images for the regular (without blur augmentation) CNN inference.

However, the above two ideas face issues such as inefficiency, instability, and lack of explainability:

• Regarding the efficiency, data augmentation and pre-processing clearly increase the computational cost of the training and inference phases, respectively;
• Regarding the stability, blind deblurring is an ill-posed inverse problem, and the introduced recovery artifacts also strongly disturb the CNN representations [4];
• Regarding the explainability, neither of these ideas can achieve a guaranteed robustness with respect to a given class of blurs—their effectiveness is somewhat empirical.

On the non-learning path, moments and moment invariants have been well established, towards the in-form robustness with respect to various forms of image distortion [5].

In particular, orthogonal moments and moment invariants may be the most popular class for real-world tasks. They provide geometric invariance while providing a certain robustness to signal loss (including blurring) due to the orthogonality. However, such robustness is restricted from a Fourier perspective: only a few low-order moments capturing low-frequency information are stable while the rest remain sensitive to signal loss. One will have to face a tricky contradiction between discriminability and robustness in the design of the algorithm.

Recently, such moments and invariants have been extended to a fractional domain of orders, yielding new time-frequency discriminability and hence somewhat alleviating the above contradiction. However, both integer and fractional moment invariants still lack the guaranteed robustness to blurring.

To address above issue, the researchers have specifically designed blur invariants, formed in Fourier domain by special projection operator [6]. As a key theoretical contribution, such projection-based methods are recently integrated and generalized into a unified theorem, General Theorem of Blur Invariants (GTBI) [7], which does not require any prior knowledge of the blur type.

1.2. Motivations

On the other hand, such Fourier-domain blur invariants are not robust to geometric transformations. With this lack, the existing ideas expand above blur invariants via integer geometric/complex moments, and then introducing combined invariance by Substitution Theorem (ST) based on corresponding geometric invariants. However, this expanded version has a quite complicated explicit form, and it is even more complicated after introducing the combined invariance.

1.3. Contributions

In this paper, we explore a simple but effective way to define combined invariants, which are designed from Fractional Moments under Projection operators (FMP).

Theoretically, the blur invariance and rotation invariance of FMP are guaranteed by the GTBI and the Fourier-domain rotation equivariance, respectively. From a statistical perspective, the proposed FMP representations can be considered as flexible and orthogonal statistics in frequency domain, where both properties are beneficial for the discriminability.

In summary, the proposed FMP not only has a simpler explicit definition, but also has useful representation properties including orthogonality, statistical flexibility, as well as the combined invariance of blurring and rotation.

1.4. Organizations

The rest of this paper is organized as follows. We first briefly review the studies of blur invariants and fractional moments in the following Section 2. As the core of this paper, we formulate the basic definitions of FMP and the derived important properties in Section 3 and Section 4, respectively. Furthermore, Section 5 reports the comparative results of our FMP with state-of-the-art orthogonal moments and deep learning representations with data augmentation or deblurring. In Section 6, we give the conclusion of this paper and point out future work on stability.

2. Related Works

In this section, we briefly review the relevant studies on blur invariants and fractional moments, which are linked to the proposed methodology.

2.1. Blur Invariants

In the community of moment and moment invariants, the blur invariants are a recent idea compared to the geometric invariants, where geometric ones can even be traced back to David Hilbert (1890s) [8].

In pioneer papers (1990s) [9], Flusser et al. achieved heuristic blur invariance by restricting the definition of PSF. Such problem modeling and solving ideas have been adopted by many later researchers. Therefore, a series of blur invariants are derived with respect to centrosymmetric blur [10], axially symmetric blur [11], motion blur [12], circularly symmetric blur [13], arbitrary N-fold symmetric blur [6], and arbitrary (anisotropic) Gaussian blur [14]. In the last two works, the authors developed projection-based invariants in the Fourier domain, and the restrictions on the PSF were greatly relaxed.

Recently, the above projection-based approach was extended to a very strong theorem, i.e., General Theorem of Blur Invariants (GTBI) [7], where the construction of invariants occurs regardless of the specific form of the PSF and the dimensionality of the image. This remarkable work moves blur invariants from being constructed heuristically to being constructed by a unified theory.

Turning to the topic of combined invariants for image representation, i.e., geometric invariance is further introduced into the above blur invariants. A typical solution in this regard is to expand the Fourier-domain blur invariants by means of classical moments, e.g., geometric moments and complex moments. Then, the combined invariance is introduced in the expanded version by Substitution Theorem (ST) [7] with geometric/complex moment invariants.

Note that such expanded blur invariants as well as the corresponding combined invariants exhibit quite complicated explicit forms. Therefore, this paper attempts to give an alternative path for the construction of combined invariance with respect to blurring and rotation, without going through the tricky moment expansion.

2.2. Fractional Moments

We start the topic of fractional moments with the information suppression problem [15]. Indeed, the regional information of the image represented by the moments is closely related to the distribution of zeros of basis functions [15]. The suppression is a unnecessary bias of zeros toward certain non-discriminative regions, causing the information in other more discriminative regions to be ignored.

This information suppression problem was first analyzed in Zernike Moments (ZM), both theoretically and empirically [16]. Here, the solution suggested by the authors is to use the moments with uniformly distributed zeros, e.g., Orthogonal Fourier–Mellin Moments (OFMM).

As a more systematic idea, Hoang et al. [17] proposed a class of fractional moments with adjustable zeros, i.e., Generic Polar Harmonic Transforms (GPHT). From a classical signal processing perspective, such fractional moments are time-frequency analysis methods. Its apparent ability to resolve the phenomenon of information suppression and, more generally, to alleviate the inherent contradiction between robustness and discriminability of classical moments. In this path, many classical moments are extended to the fractional domain of orders, e.g., fractional Legendre moments [18], fractional OFMM [19], fractional ZM [20], fractional Chebyshev moments [21], and Fractional Jacobi–Fourier Moments (FJFM) [22]. As unified mathematical tools, GPHT and FJFM are more general definitions covering other fractional moments.

Note that the above fractional moments are all designed in the original image domain and robustness/invariance to blurring is not discussed. Therefore, this paper focus on fractional moments in transformation domains, for satisfying both blurring invariance and rotation invariance.

3. Fractional Moments under Projection: Definition

In this section, we formulate the most basic components in this paper, covering the general definition of FMP and two kinds of radial basis functions.

Definition 1.

(Fractional moments under projection). For an image function f, the fractional moments under projection are defined as the following inner product:

$$〈{\mathcal{I}}_f,V_{nm}^{\alpha }〉={\int \int }_D{\left[V_{nm}^{\alpha }({\xi }_x,{\xi }_y)\right]}^{\ast }{\mathcal{I}}_f({\xi }_x,{\xi }_y)d{\xi }_{x}d{\xi }_y,$$

(1)

where ${\mathcal{I}}_f$ is of blur invariance and is defined in the Fourier domain by GTBI [7]:

$${\mathcal{I}}_f({\xi }_x,{\xi }_y)=\frac{\mathcal{F}\left(f\right)({\xi }_x,{\xi }_y)}{\mathcal{F}\left(Pf\right)({\xi }_x,{\xi }_y)},$$

(2)

with orthogonal projector $P:\mathcal{L}\to \mathcal{S}$, mapping the image space $\mathcal{L}$ into a given class (which we want to design the invariants) of PSFs $\mathcal{S}\subset \mathcal{L}$, where $P^2=P$ and the P is called orthogonal when $\mathcal{S}\perp (\mathcal{L}\ominus \mathcal{S})$.

The $V_{nm}^{\alpha }$ is the basis function of order parameter $(n,m)\in {\mathbb{Z}}^2$ and fractional parameter $\alpha \in {\mathbb{R}}^{+}$ over the domain $D\in {\mathbb{R}}^2$, where * is the complex conjugate. Here, orthogonality and rotation invariance structures are imposed on the definition of basis functions [5]:

$$V_{nm}^{\alpha }(rcos\theta ,rsin\theta )\equiv V_{nm}^{\alpha }(r,\theta )\stackrel{\Delta }{=}{R}_n^{\alpha }\left(r\right)A_m\left(\theta \right),$$

(3)

with angular basis function $A_m\left(\theta \right)=exp\left(\mathit{j}m\theta \right)$ ($\mathit{j}=\sqrt{-1}$) and radial basis function $R_n^{\alpha }\left(r\right)$ satisfying the weighted orthogonality condition: $\underset{0}{\overset{1}{\int }}{R}_n^{\alpha }\left(r\right){\left[R_{n^{\prime }}^{\alpha }\left(r\right)\right]}^{\ast }rdr=\frac{1}{2\pi }{\delta }_{n{n}^{\prime }}$ over a unit-disk domain $D=\left\{\right(r,\theta ):r\in [0,1],\theta \in [0,2\pi \left)\right\}$.

In the Definition 1, ${\mathcal{I}}_f$ can be considered as the blur-invariant part of f in the Fourier domain. Here, its invariance derives from the equivariance of projector P with respect to blurring, i.e., $P(f\ast h)=Pf\ast h$ for any $h\in \mathcal{S}$. Furthermore, this equivariance is in fact ensured by the orthogonality of projector P. For more details on the proof, we refer the reader to the GTBI by Flusser et al. [7].

Note that the explicit definition of $R_n^{\alpha }$ is not yet given and bears numerous potential forms (see [5] for a survey). Considering the representation capability and discussion generality, we introduce two classes of radial basis functions based on harmonic and polynomial functions, respectively.

Definition 2.

(Harmonic radial basis function). The complex exponential functions  [23] in Fourier analysis can satisfy the weighted orthogonality condition in Definition 1, leading to an explicit form:

$$R_n^{\alpha }\left(r\right)=\sqrt{\frac{\alpha r^{\alpha -2}}{2\pi }}exp\left(\mathit{j}2n\pi r^{\alpha }\right),$$

(4)

where the orthogonality holds for all possible α.

Definition 3.

(Polynomial radial basis function). A class of classical orthogonal polynomials, Jacobi polynomials [22], can satisfy the weighted orthogonality condition in Definition 1, leading to an explicit form:

$$\begin{array}{c}\hfill R_n^{\alpha }(r;p,q)=\sqrt{\frac{\alpha r^{\alpha q-2}{(1-r^{\alpha })}^{p-q}(p+2n)\mathsf{\Gamma }(q+n)n!}{2\pi \mathsf{\Gamma }(p+n)\mathsf{\Gamma }(p-q+n+1)}}\\ \hfill \times \sum _{k=0}^n\frac{{(-1)}^k\mathsf{\Gamma }(p+n+k)r^{\alpha k}}{k!(n-k)!\mathsf{\Gamma }(q+k)},\end{array}$$

(5)

where $n\in \mathbb{N}$ and the polynomial parameters $p,q\in \mathbb{R}$ must fulfill: $p-q>-1$, $q>0$; similarly, the orthogonality holds for all possible α, p, and q.

Here, we have specified the FMP of Definition 1 into harmonic and polynomial versions, corresponding Definitions 2 and 3, respectively. As to be discussed later, the proposed harmonic/polynomial FMP is a generic and flexible representation in Fourier domain, with in-form blurring and rotation invariance.

4. Fractional Moments under Projection: Property

In this section, we give some important properties derived from above definitions, covering the generic/flexible nature, rotation invariance, and blurring robustness.

Property 3.

(Generic and flexible nature). By changing the parameter value of α, a specific class of FMP representations can be obtained from the generic Definitions 1∼3. Note that members of this class share beneficial Properties 2 and 3, while also being complementary in discriminative information since the distribution of zeros of $R_n^{\alpha }\left(r\right)$ is flexible depending on α.

Remark 1.

As can be seen from the above property, the fractional parameter α in Definitions 2 and 3 allows a generic and flexible representation, meaning potential discriminability for various vision tasks. Mathematically, the number and location of zeros of the basis functions determine the frequency and spatial properties of the represented information, respectively, [15]. In our FMP, $(n,m)$ and α explicitly encode the number and location of zeros of the basis functions:

• The number of zeros in the radial and angular directions is proportional to n and m, respectively.
• The location of zeros in the radial direction is biased towards 0 or 1 corresponding to $\alpha <1$ or $\alpha >1$, where $\alpha =1$ means a uniformly distributed zeros.

Property 3.

(Rotation invariance). Suppose $f_R$ is a rotated version of image f by an angle φ about the center, when projector P is rotation equivariance, there must be a function $\mathcal{J}$ other than constant functions such that:

$$\mathcal{J}\left(\left\{〈{\mathcal{I}}_{f_R},V_{nm}^{\alpha }〉\right\}\right)\equiv \mathcal{J}\left(\left\{〈{\mathcal{I}}_f,V_{nm}^{\alpha }〉\right\}\right),$$

(6)

i.e., satisfying the rotation invariance, for all possible input images and FMP parameters.

Proof. 

The proof of (6) is based on the 2D-Fourier rotation equivariance for ${\mathcal{I}}_f({\xi }_x,{\xi }_y)$ and the 1D-Fourier translation theorem for $A_m\left(\theta \right)$.

For convenience, we denote the rotation operator about the center as $\mathsf{\Theta }$, i.e., $f_R=\mathsf{\Theta }f$. Firstly, the Fourier transform $\mathcal{F}$ is widely known to have equivariance to rotations in the classical literature as $\mathcal{F}\left(\mathsf{\Theta }f\right)=\mathsf{\Theta }\mathcal{F}\left(f\right)$. Secondly, we have assumed the equivariance of projector P to rotation, i.e., $P\mathsf{\Theta }f=\mathsf{\Theta }Pf$. With the above properties, it is easy to derive:

$${\mathcal{I}}_{\mathsf{\Theta }f}=\frac{\mathcal{F}\left(\mathsf{\Theta }f\right)}{\mathcal{F}\left(P\mathsf{\Theta }f\right)}=\frac{\mathsf{\Theta }\mathcal{F}\left(f\right)}{\mathcal{F}\left(\mathsf{\Theta }Pf\right)}=\frac{\mathsf{\Theta }\mathcal{F}\left(f\right)}{\mathsf{\Theta }\mathcal{F}\left(Pf\right)}=\mathsf{\Theta }\left(\frac{\mathcal{F}\left(f\right)}{\mathcal{F}\left(Pf\right)}\right)=\mathsf{\Theta }{\mathcal{I}}_f.$$

(7)

We introduce a polar form of the frequency domain: $\mathcal{I}({\xi }_x,{\xi }_y)=\mathcal{I}(rcos\theta ,rsin\theta )=\mathcal{I}(r,\theta )$. Then (7) can be rewritten as ${\mathcal{I}}_{f_R}(r,\theta )={\mathcal{I}}_f(r,\theta +\phi )$.

With the above rotation equivariance of $\mathcal{I}$, it can be derived that the FMP representations before and after image rotation will differ by only a phase term (with respect to the rotation angle):

$$\begin{array}{cc}\hfill & 〈{\mathcal{I}}_{f_R}(r,\theta ),V_{nm}^{\alpha }(r,\theta )〉\hfill \\ \hfill & =〈{\mathcal{I}}_f(r,\theta +\phi ),V_{nm}^{\alpha }(r,\theta )〉\hfill \\ \hfill & =〈{\mathcal{I}}_f(r,{\theta }^{\prime }),V_{nm}^{\alpha }(r,{\theta }^{\prime }-\phi )〉\hfill \\ \hfill & =〈{\mathcal{I}}_f(r,{\theta }^{\prime }),V_{nm}^{\alpha }(r,{\theta }^{\prime })〉{\left[A_m(-\phi )\right]}^{\ast }\hfill \\ \hfill & =〈{\mathcal{I}}_f,V_{nm}^{\alpha }〉A_m\left(\phi \right),\hfill \end{array}$$

(8)

with ${\theta }^{\prime }=\theta +\phi$, where the second pass holds due to Fourier translation theorem of $A_m\left(\theta \right)$.

Here, a naive definition of $\mathcal{J}$ is the magnitude operator:

$$\mathcal{J}\left(\left\{〈{\mathcal{I}}_{•},V_{nm}^{\alpha }〉\right\}\right)\stackrel{\Delta }{=}\left|〈{\mathcal{I}}_{•},V_{nm}^{\alpha }〉\right|,$$

(9)

hence $|〈{\mathcal{I}}_{f_R},V_{nm}^{\alpha }〉|=|〈{\mathcal{I}}_f,V_{nm}^{\alpha }〉A_m\left(\phi \right)|=|〈{\mathcal{I}}_f,V_{nm}^{\alpha }〉|$. For the more generalized definition of $\mathcal{J}$, interested readers are referred to [24].    □

Property 3.

(Blurring robustness). Suppose $f_h$ is a blurred version of image f convolved by a function h: $f_h=f\ast h$, the FMP is more robust than the counterpart in the original image domain [22,23] under the sense of l-norm distance of representation variations:

$$\begin{array}{c}\hfill \left|\right|\left\{〈{\mathcal{I}}_{f_h},V_{nm}^{\alpha }〉\right\}-\left\{〈{\mathcal{I}}_f,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l\le \left|\right|\left\{〈f_h,V_{nm}^{\alpha }〉\right\}-\left\{〈f,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l,\end{array}$$

(10)

and the equality holds if and only if $h=\mathrm{id}$.

Proof. 

The proof of (10) is based on the blur invariance of $\mathcal{I}$, the linearity of inner product, the positive definiteness of norm, as well as the completeness and orthogonality of the basis functions V.

For the left side of (10), i.e., the variation of FMP representation, we can rewrite it as:

$$\begin{array}{cc}\hfill & \left|\right|\left\{〈{\mathcal{I}}_{f_h},V_{nm}^{\alpha }〉\right\}-\left\{〈{\mathcal{I}}_f,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l\hfill \\ \hfill & =\left|\right|\left\{〈{\mathcal{I}}_{f_h}-{\mathcal{I}}_f,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l\hfill \\ \hfill & =\left|\right|\left\{〈0,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l=0,\hfill \end{array}$$

(11)

where the first pass holds due to the linearity of inner product and the second pass holds as the blur invariance of (2) is guaranteed by GTBI.

For the right side of (10), i.e., the variation of the image-domain counterpart representation, we can rewrite it as:

$$\begin{array}{cc}\hfill & \left|\right|\left\{〈f_{\eta },V_{nm}^{\alpha }〉\right\}-\left\{〈f,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l\hfill \\ \hfill & =\left|\right|\left\{〈f_h-f,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l\hfill \\ \hfill & =\left|\right|\left\{〈d,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l\ge 0,\hfill \end{array}$$

(12)

where $d=f\ast h-f=f\ast (h-\mathrm{id})$ can be considered as image residual. Here, we assert that $\left|\right|\left\{〈d,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l\ge 0$ and the equality holds if and only if $d=0$, i.e., $h=\mathrm{id}$.

Without loss of generality, we assume that there exists $d\ne 0$, such that $\left|\right|\left\{〈d,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l=0$. Based on this assumption, it is known that $d\notin \left\{V_{nm}^{\alpha }\right\}$, due to $\left|\right|\left\{〈d,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l={\left|\right|\delta \left|\right|}_l\ne 0$ if $d\in \left\{V_{nm}^{\alpha }\right\}$. Taken together, the above assumption means that d is a nonzero element that does not belong to the set of basis functions, while being orthogonal to any element in this set for guaranteeing $\left|\right|\left\{〈d,V_{nm}^{\alpha }〉\right\}{\left|\right|}_l=0$. This obviously conflicts with the completeness and orthogonality of the basis functions in a Hilbert space. Therefore, this assumption does not hold.

It can be noted that the correctness of (11) and (12) implies in fact the correctness of the original property (10).    □

Note that the ideal identities in Properties 2 and 3 may no longer hold for the discrete domain, which involve resampling and requantization errors. Interested readers can access our symmetrical work on noise-invariant representation in [25].

5. Experiments

In this section, we will evaluate the robustness and discriminability of the proposed FMP, by intuitive feature histogram and quantitative pattern recognition on challenging blurred images.

5.1. Implementation Details

Before giving the results, we first specify the implementation details of our FMP. In fact, the Definition 1 of FMP is a very broad formulation that does not rely on the specific type of image blurring.

Throughout the experimental section, we take the centrosymmetric blurring as an example and form a specific practice of FMP accordingly. Hence, the set of centrosymmetric PSFs is $\mathcal{S}=\{h:h(x,y)=h(-x,-y\left)\right\}$. With the relevant papers on GTBI [7], we define the orthogonal projector as $Pf(x,y)=\left(f\right(x,y)+f(-x,-y\left)\right)/2$, yielding a special form of (2) as ${\mathcal{I}}_f=tan(\angle \mathcal{F}\left(f\right))$.

Note that the ${\mathcal{I}}_f({\xi }_x,{\xi }_y)$ is of a fractional form (2), with certain numerical instability when the denominator is small. In our implementation, we evade this issue by restricting the frequency range with the natural image prior: $\{({\xi }_x,{\xi }_y):|\left|({\xi }_x,{\xi }_y)\right|{|}_{\infty }\le 10\}$.

5.2. Feature Histogram

For this part, we evaluate the robustness by visualizing the FMP representation with different blurring conditions, which will also demonstrate the non-trivial nature of the representation.

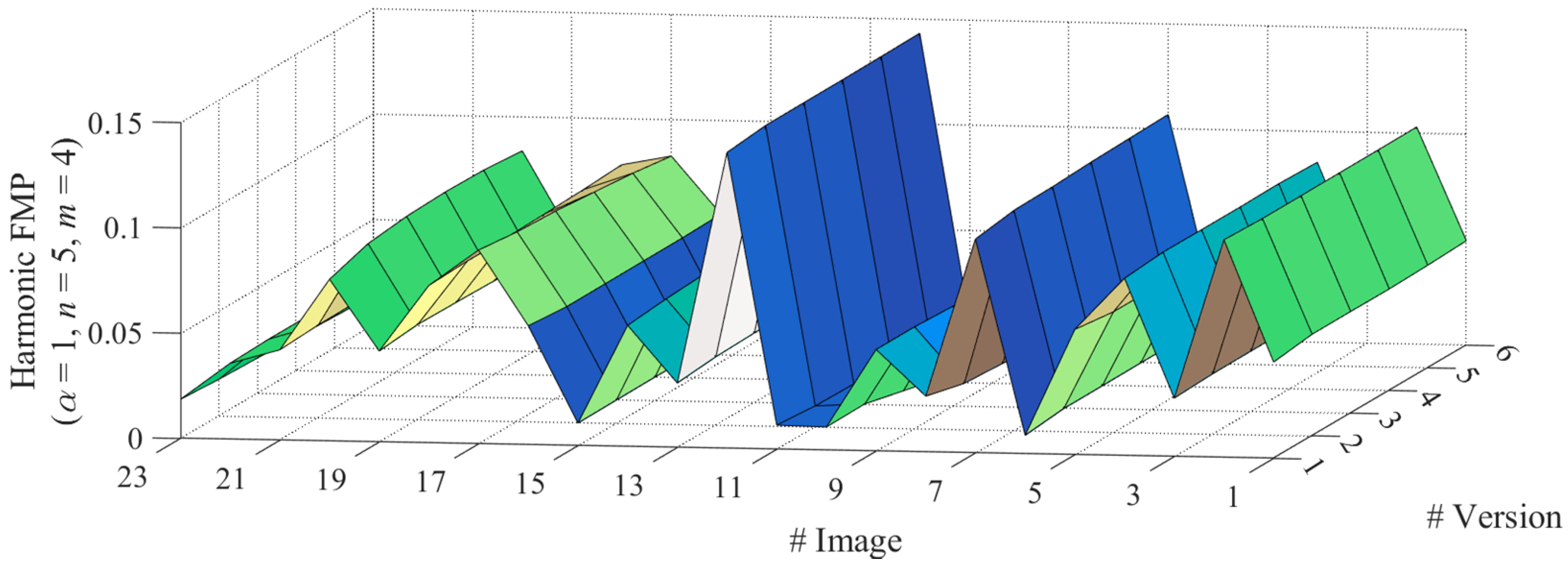
As shown in Figure 1, the experiment is executed on the well-known degraded image dataset CIDIQ [26] involving centrosymmetric Gaussian blurring. Here, the CIDIQ includes 23 clean images, each one corresponds to 5 blurred versions at different levels, for a total of 115 images.

As shown in Figure 2 and Figure 3, we present the magnitude of harmonic/polynomial FMP over clean and blurred images, where the harmonic FMP is of $\alpha =1$, $n=5$, and $m=4$, and the polynomial FMR is of $\alpha =1$, $p=1$, $q=1$, $n=5$, and $m=4$. Note that the value is always almost constant within each individual blurring series (regardless of blurring level) while significantly different for distinct images. This phenomenon means that our FMP has ideal blurring robustness as well as sufficient discriminability for distinct images (i.e., non-trivial nature of such invariants).

5.3. Pattern Recognition

For this part, we directly verify the robustness to rotation and blurring as well as the discriminability to distinct images, by employing pattern recognition with different blurring and orientation conditions.

The testing images are derived from the COREL dataset [27], with four orientations and also with blurring of:

• Gaussian: G1 (${\sigma }_x=5$, ${\sigma }_y=10$, $\theta =0$, and $L=10\times 10$), G2 (same as G1 except $\theta ={45}^{\circ }$), and G3 (same as G1 except ${\sigma }_x=10$ and $L=20\times 20$);
• Disc: D1 ($L=7\times 7$) and D2 ($L=9\times 9$);
• Motion: M1 ($L=10$ and $\theta ={20}^{\circ }$) and M2 ($L=20$ and $\theta ={45}^{\circ }$).

The comparison methods involved in this experiment include:

• Classical moment representations: ART [28], GFD [29], and ZM [30];
• Fractional moments (FM) representations, as the image-domain counterpart of FMP, i.e., FJFM (p, q, $\alpha$) [22] and GPCET ($\alpha$) [23], with their popular special cases OFMM [31], JFM [32], EFM [33], and PCET [34];
• FMP representations, i.e., all FMP counterparts for the above FM;
• Deep learning representations: GoogLeNet [35] and ResNet-50 [36] with rotation/blur data augmentation and deblurring [37] as data preprocessing.

In

Table 1. Correct Classification Percentages (%) for Classical Moment Representations, FM Representations, and FMP Representations.

Method	Blurring Type
	G1	G2	G3	D1	D2	M1	M2
ART	83	83	47	99	93	100	99
GFD	76	75	43	99	88	100	98
ZM	99	99	81	100	100	100	100
OFMM/FJFM(2,2,1)	73	70	33	99	88	100	98
JFM(3,3)/FJFM(3,3,1)	76	76	45	99	86	100	98
FJFM(3,3,2)	78	78	42	99	92	100	99
EFM/GPCET(1)	66	66	38	93	78	100	90
PCET/GPCET(2)	62	62	31	95	70	99	93
GPCET(1.5)	65	62	33	91	75	99	91
OFMMP/FJFMP(2,2,1)	100	100	100	100	100	100	100
JFMP(3,3)/FJFMP(3,3,1)	100	100	100	100	100	100	100
FJFMP(3,3,2)	100	100	100	100	100	100	100
EFMP/GPCETP(1)	100	100	100	100	100	100	100
PCETP/GPCETP(2)	100	100	100	100	100	100	100
GPCETP(1.5)	100	100	100	100	100	100	100

, we list the correct classification percentages for non-learning representations, i.e., classical moment representations, FM representations, and FMP representations.

• Classical moment representations and FM representations do not have guaranteed blur invariance. Their scores are unstable under various blurring types or intensities. Here, the worst case occurs for high-intensity Gaussian blurring G3.
• Our FMP achieves robustness gains with respect to its FM counterpart, while being sufficient in discriminability. All the FMP representations achieve ∼100% correct classification on rotated and centrosymmetric blurred images just as expected in Section 4.

In

Table 2. Correct Classification Percentages (%) for Learning Methods (With Augmentation and Deblurring) Compared to the Average Results of FM and FMP Representations.

Method	Training Size	Blurring Type
		G1	G2	G3	D1	D2	M1	M2
GoogLeNet (rotation data augmentation)	×8	26	22	5	43	27	74	28
GoogLeNet (rotation and blur data augmentation)	×16	72	69	60	81	76	85	60
GoogLeNet (rotation data augmentation and deblurring)	×8	23	21	5	34	26	45	17
ResNet-50 (rotation data augmentation)	×8	20	20	6	44	23	77	46
ResNet-50 (rotation and blur data augmentation)	×16	78	75	68	88	81	87	67
ResNet-50 (rotation data augmentation and deblurring)	×8	12	11	4	25	18	31	24
FM (average results)	×1	70	69	37	96	82	100	95
FMP (average results)	×1	100	100	100	100	100	100	100

, we list the correct classification percentages for learning representations with rotation and blur data augmentation or deblurring as data preprocessing.

• With only rotation data augmentation, learning representations cannot yet achieve satisfactory classification accuracy, where the additional cost is an 8-fold increase in training size.
• Concerning both rotation and blur data augmentation, learning representations perform significantly better but still do not achieve >90% accuracy for any blurring types, where the additional cost is a 16-fold increase in training size.
• With rotation data augmentation and deblurring, learning representations perform even worse than without the blur data augmentation, potentially due to the recovery error introduced by the deblurring algorithm [37], where the additional cost is the preprocessing for each testing image. Note that such a performance gap was also observed in [4].
• Further, our FMP achieves significantly better scores with respect to the state-of-the-art learning representations, meaning FMP is competitive for small-scale robust vision problems even in the deep-learning era.

6. Conclusions

In this paper, we have provided a simple but effective way to define robust image representation for blur and orientation variants. We refer to this approach as “Fractional Moments under Projection operators (FMP)”, which is characterized by orthogonality, generality, flexibility, as well as the combined invariance of blurring and rotation.

The definitions and properties of FMP have been well formalized through the general theorem of blur invariants and the general theorem of in-/equi-/co-variance. Moreover, simulation experiments validate the beneficial properties of FMP, revealing the potential for small-scale robust vision problems.

Since the GTBI definition involves a fractional form, the direct discrete implementation exhibits a certain numerical instability when the denominator is small. Therefore, our future work will address numerical issues related to the discrete implementation of FMP.