Enhanced Automated Deep Learning Application for Short-Term Load Forecasting
Abstract
1. Introduction
- Proposal of a hybrid model called Convolutional LSTM Encoder–Decoder for power production time series.
- Presentation of an automated STLF algorithm which incorporates data pre-processing techniques, training, optimization of several AI models, testing and prediction of results.
2. Materials and Methods
2.1. Forecasting Approaches
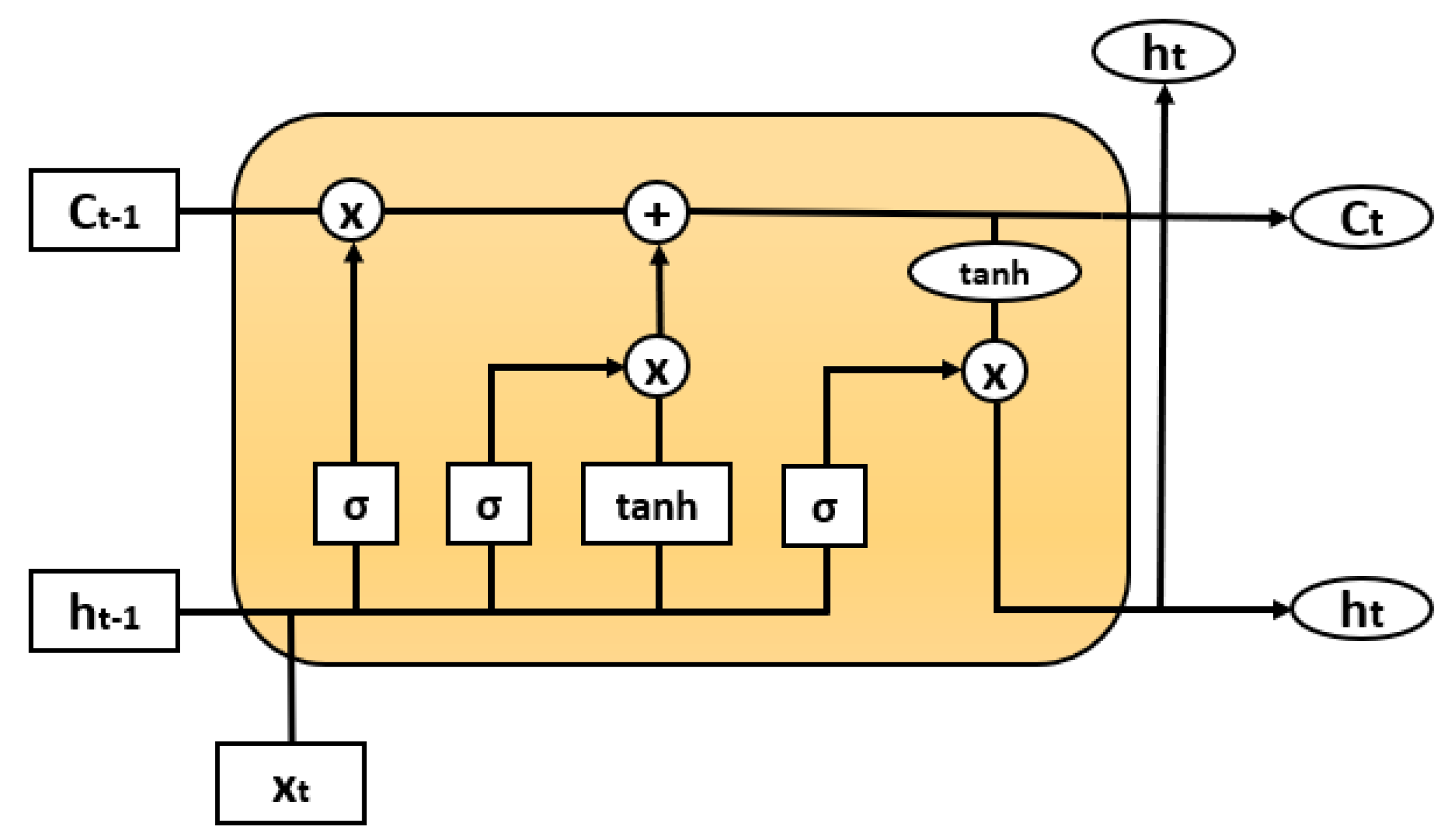
2.1.1. Long Short-Term Memory Networks
- Forget Gate (): the useful bits of the cell state (long-term memory of the network) are decided on given both the previous hidden state and new input data . At the bottom, the forget gate controls which part of the long-term memory must be forgotten.
- Input Gate (): The main operation of the input gate is to update the cell state of the LSTM unit. Firstly, a sigmoid layer decides which values it is going to update. Next, a layer creates a vector () of all possible values that can be added to the cell state and, finally, these two are combined to update the cell state.
- Cell State (): The Cell State multiplies the old state by and then adds .
- Output Gate (): The output gate decides what information is going to be output. Using a sigmoid and a tanh function to multiply the two outputs they create, what information the hidden state must carry is decided on.
2.1.2. MultiLayer Perceptron
- Firstly, MLP algorithms use a Forward Propagation Process to calculate their parameters at the training period, as they propagate data from the input to the output layer.
- Secondly, the network calculates the value of the loss function, which contains the difference between the actual and forecasting data and tries to find the optimal solution, minimizing any error [27].
- Then, using back-propagation algorithms, the gradient of loss function is calculated and the values of the synaptic weights between neurons updated [28].
2.1.3. Convolutional Neural Networks
- Convolutional Layer: The Convolutional layer is the core building block of a Convolutional Network that does most of the computational heavy lifting.
- Pooling Layer: The objective of the Pooling Layer is the progressive reduction of the spatial size of the representation in order to reduce computational volume of the system and, as a result, to reduce overfitting in the training process.
- Fully-Connected Layer: Neurons in a fully-connected layer have full connections to all activations in the previous layer, as seen in regular Neural Networks. Their activations can, hence, be computed with a matrix multiplication followed by a bias offset.
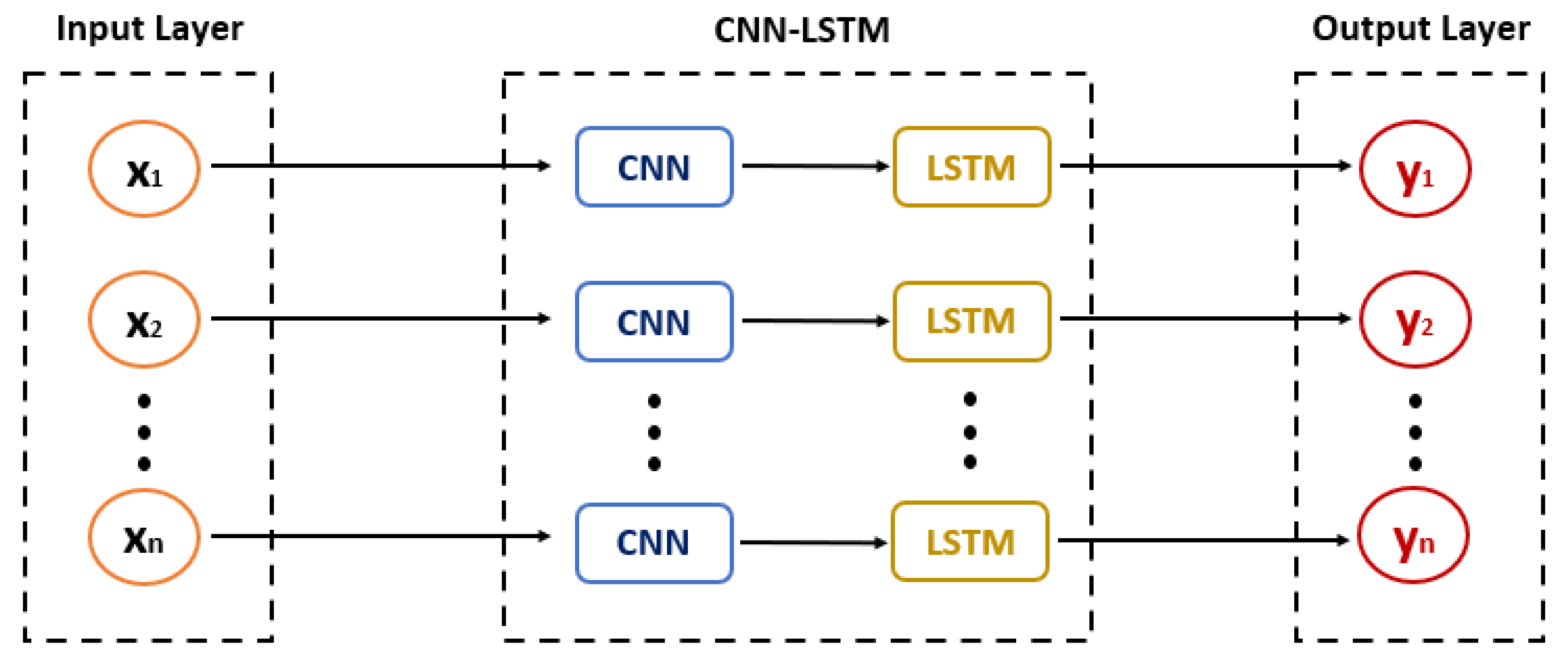
2.1.4. Hybrid CNN–LSTM Model
2.1.5. Temporal Convolutional Networks
- First, the model computes the low-level features using the CNN-1D modules encoding the spatial–temporal information,
- Second, the model feeds this information and classifies it using Recurrent Neural Networks.
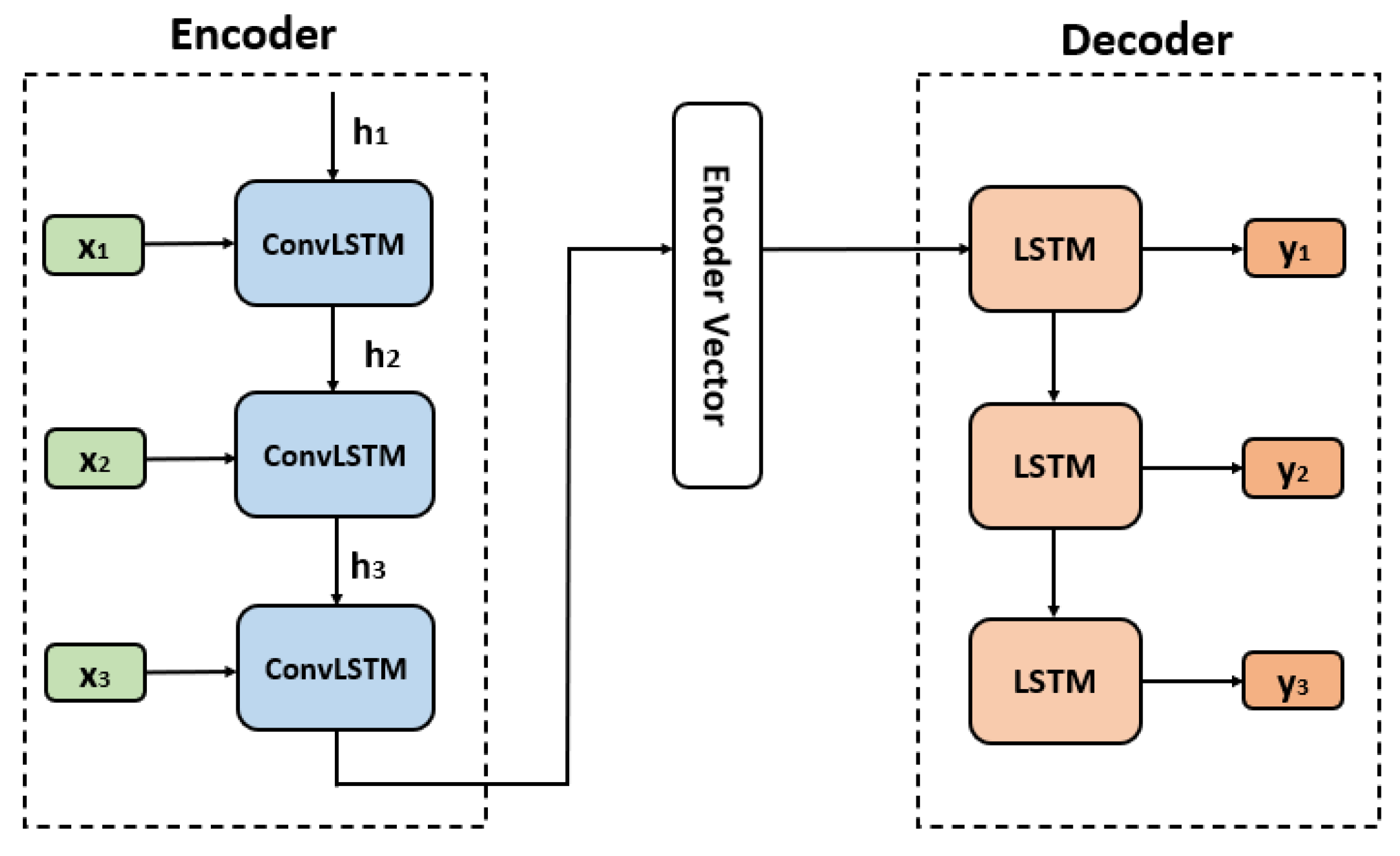
2.2. Proposed Approach: Convolutional LSTM Encoder–Decoder Model
- The Encoder Component: This is the first component of the Network and its main function is feature extraction of the input dataset, which is why it is called an ‘encoder’. It receives a sequence as input and passes the information values into the internal state vectors or Encoder Vectors, creating, in this way, a hidden state.
- The Encoder Vector: The encoder vector is the last hidden state of the Network which converts the 2D output of the RNN (ConvLSTM in our case) model to a high length 3D vector in order to help the Decoder Component make better predictions.
- The Decoder Component: The Decoder Component consists of one recurrent unit, or a stack of several recurrent units, each one of which predicts an output y at a time step t.

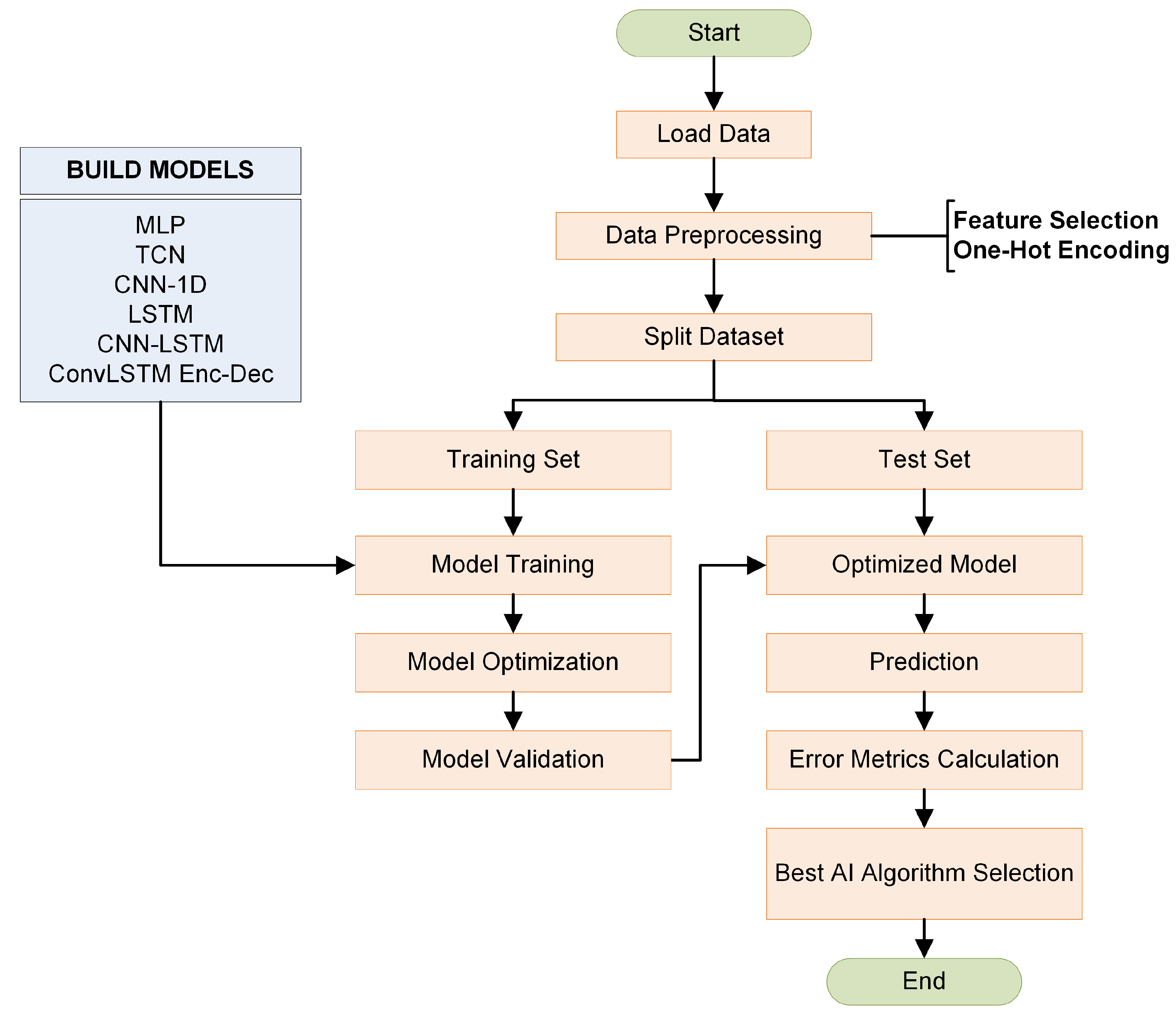
2.3. Automated STLF Algorithm
- The algorithm loads the dataset.
- The algorithm proceeds to the Pre-processing Step, in which the dataset is normalized using the Min–Max Scaling algorithm, and the Cyclical Time Features are created using One-Hot Encoding.
- The dataset is split into Training, Validation and Test sets.
- Every Deep Learning Model is trained and evaluated using the Bayesian Optimization Algorithm.
- The best model from the algorithm, in terms of higher prediction accuracy, is selected to be used for future predictions.
3. Case Study
3.1. Climate Dataset
3.2. Electrical Power Dataset and Exploratory Analysis
Correlation Heatmap
3.3. Feature Selection
3.4. Data Pre-Possessing
3.4.1. Min–Max Scaling
3.4.2. One-Hot Encoding
3.5. Data Partitioning
3.6. Model Architecture
3.6.1. LSTM Model
- Units of lstm network = 256
- Batch size = 128
- ReLU activation function for the LSTM Module, as well as the output Dense Layer
- Optimizer = Adam
- Learning rate = 0.0010
- Epochs = 100
3.6.2. CNN–LSTM Model
- filters = 64
- kernel size = 2
- ReLU activation function for the both the CNN and LSTM Module
- 48 units for the LSTM Module
- MaxPooling1D with pool size = 2
- Batch size = 128
- Optimizer = Adam
- Learning rate = 0.0010
- Epochs = 100
3.6.3. Multilayer Perceptron Model
- 480 Neurons for the Input Layer
- Batch size = 128
- ReLU activation function for the Input Layer, as well as the output Dense Layer
- Optimizer = Adam
- Learning rate = 0.0011
- Epochs = 100
3.6.4. Temporal Convolution Network
- Filters = 256
- Dilations = [1, 2, 4, 8, 16, 32]
- Batch size = 128
- Optimizer = Adam
- Learning rate = 0.0010
- Epochs = 100
3.6.5. CNN-1D Model
- Filters = 64
- Kernel size = 3
- MaxPooling1D (pool size = 2)
- Neurons of Dense Layer = 16
- ReLU activation function for the CNN Module, as well as the output Dense Layer
- Optimizer = Adam
- Learning rate = 0.0010
- Epochs = 100
3.6.6. ConvLSTM Encoder–Decoder Model
- Filters = 64
- Kernel size = (1,4)
- ReLU activation function for the ConvLSTM2D Module, for the LSTM Layer, as well as the output Dense Layer
- Encoder Vector with size = 1
- 64 Units for the LSTM module
- Optimizer = Adam
- Learning rate = 0.0068
- Epochs = 100
3.7. Software Environment
3.8. Performance Metrics (Evaluation Metrics)
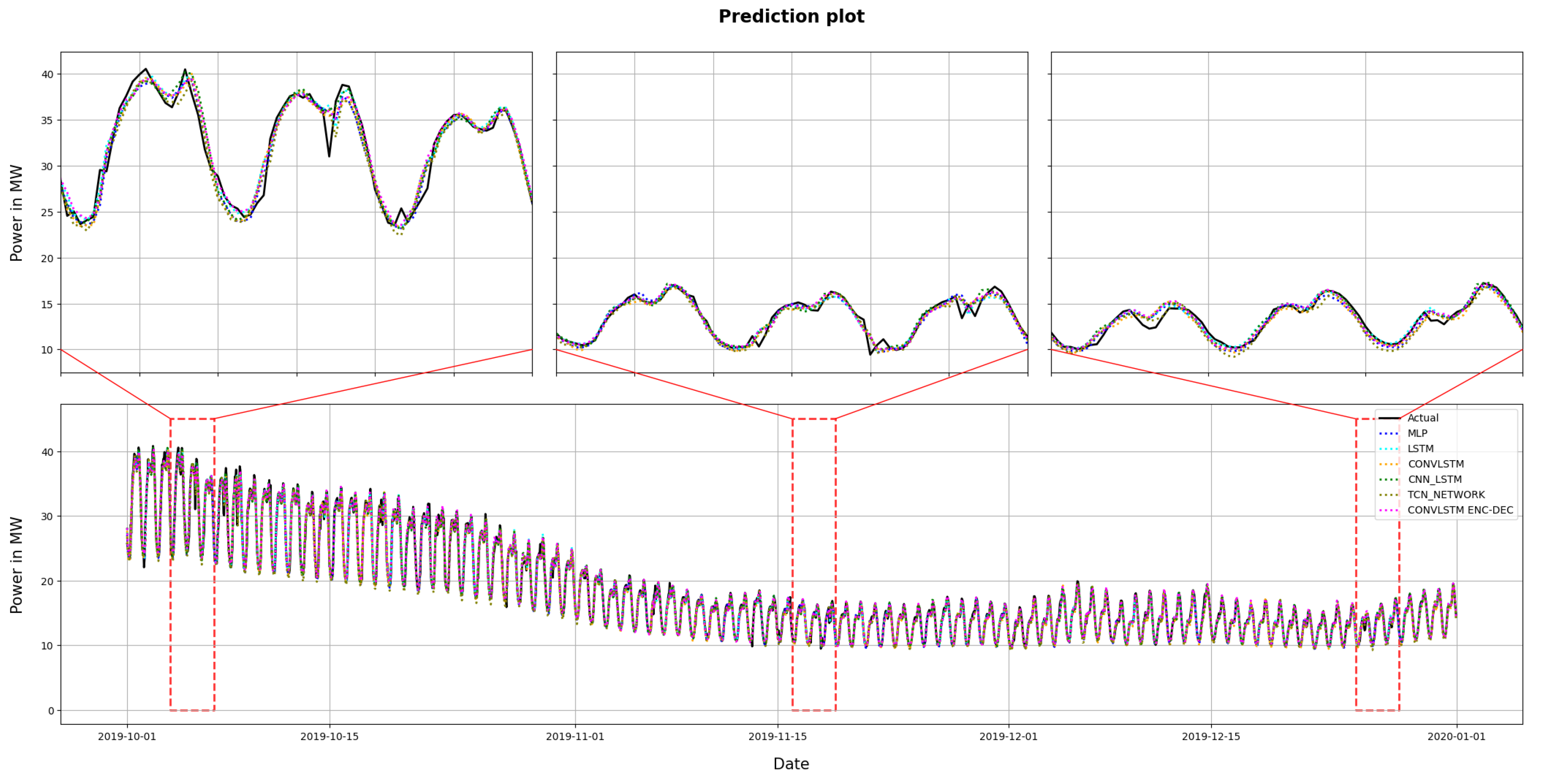
4. Results Analysis and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Attention Mechanism |
| BO | Bayesian Optimization |
| BEGA | Binary Encoding Genetic Algorithm |
| BPNN | Backpropagation Neural Network |
| CNN-1d | Convolutional Neural Network One Dimensional |
| CNN-LSTM | Convolutional Neural Network—Long Short-Term Memory |
| ConvLSTM | Convolutional Long Short-Term Memory |
| DTM | Dynamic Time Wrapping |
| FC | Fully-Connected |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MLP | Multilayer Perceptron |
| NLP | Natural language processing |
| R2 | R-Squared |
| RFR | Random Forests Regression |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| STLF | Short-Term Load Forecasting |
| SVR | Support Vector Regression |
| TCN | Temporal Convolutional Network |
References
- Karthik, N.; Parvathy, A.K.; Arul, R.; Padmanathan, K. Multi-objective optimal power flow using a new heuristic optimization algorithm with the incorporation of renewable energy sources. Int. J. Energy Environ. Eng. 2021, 12, 641–678. [Google Scholar] [CrossRef]
- Laitsos, V.M.; Bargiotas, D.; Daskalopulu, A.; Arvanitidis, A.I.; Tsoukalas, L.H. An incentive-based implementation of demand side management in power systems. Energies 2021, 14, 7994. [Google Scholar] [CrossRef]
- Poongavanam, E.; Kasinathan, P.; Kanagasabai, K. Optimal Energy Forecasting Using Hybrid Recurrent Neural Networks. Intell. Autom. Soft Comput. 2023, 36, 249–265. [Google Scholar] [CrossRef]
- Arvanitidis, A.I.; Kontogiannis, D.; Vontzos, G.; Laitsos, V.; Bargiotas, D. Stochastic Heuristic Optimization of Machine Learning Estimators for Short-Term Wind Power Forecasting. In Proceedings of the IEEE 2022 57th International Universities Power Engineering Conference (UPEC), Istanbul, Turkey, 30 August–2 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Vontzos, G.; Bargiotas, D. A Regional Civilian Airport Model at Remote Island for Smart Grid Simulation. In Proceedings of the Smart Energy for Smart Transport: Proceedings of the 6th Conference on Sustainable Urban Mobility, CSUM2022, Skiathos Island, Greece, 31 August–2 September 2022; Springer: Berlin/Heidelberg, Germany, 2023; pp. 183–192. [Google Scholar] [CrossRef]
- Mamun, A.A.; Sohel, M.; Mohammad, N.; Haque Sunny, M.S.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Hammad, M.A.; Jereb, B.; Rosi, B.; Dragan, D. Methods and models for electric load forecasting: A comprehensive review. Logist. Supply Chain. Sustain. Glob. Chall. 2020, 11, 51–76. [Google Scholar] [CrossRef]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Deep Learning Tutorial for Beginners: Neural Network Basics. Available online: https://www.guru99.com/deep-learning-tutorial.html{#}5 (accessed on 18 November 2022).
- Kontogiannis, D.; Bargiotas, D.; Daskalopulu, A. Minutely active power forecasting models using Neural Networks. Sustainability 2020, 12, 3177. [Google Scholar] [CrossRef]
- Arvanitidis, A.I.; Bargiotas, D.; Daskalopulu, A.; Laitsos, V.M.; Tsoukalas, L.H. Enhanced Short-Term Load Forecasting Using Artificial Neural Networks. Energies 2021, 14, 7788. [Google Scholar] [CrossRef]
- Arvanitidis, A.I.; Bargiotas, D.; Daskalopulu, A.; Kontogiannis, D.; Panapakidis, I.P.; Tsoukalas, L.H. Clustering Informed MLP Models for Fast and Accurate Short-Term Load Forecasting. Energies 2022, 15, 1295. [Google Scholar] [CrossRef]
- Kontogiannis, D.; Bargiotas, D.; Daskalopulu, A.; Arvanitidis, A.I.; Tsoukalas, L.H. Error compensation enhanced day-ahead electricity price forecasting. Energies 2022, 15, 1466. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Kwon, B.S.; Park, R.J.; Song, K.B. Short-term load forecasting based on deep neural networks using LSTM layer. J. Electr. Eng. Technol. 2020, 15, 1501–1509. [Google Scholar] [CrossRef]
- Jin, Y.; Guo, H.; Wang, J.; Song, A. A hybrid system based on LSTM for short-term power load forecasting. Energies 2020, 13, 6241. [Google Scholar] [CrossRef]
- Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A deep neural network model for short-term load forecast based on long short-term memory network and convolutional neural network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef]
- Rafi, S.H.; Nahid-Al-Masood; Deeba, S.R.; Hossain, E. A Short-Term Load Forecasting Method Using Integrated CNN and LSTM Network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Wu, K.; Wu, J.; Feng, L.; Yang, B.; Liang, R.; Yang, S.; Zhao, R. An attention-based CNN-LSTM-BiLSTM model for short-term electric load forecasting in integrated energy system. Int. Trans. Electr. Energy Syst. 2021, 31, e12637. [Google Scholar] [CrossRef]
- Farsi, B.; Amayri, M.; Bouguila, N.; Eicker, U. On Short-Term Load Forecasting Using Machine Learning Techniques and a Novel Parallel Deep LSTM-CNN Approach. IEEE Access 2021, 9, 31191–31212. [Google Scholar] [CrossRef]
- Peng, Q.; Liu, Z.W. Short-Term Residential Load Forecasting Based on Smart Meter Data Using Temporal Convolutional Networks. In Proceedings of the IEEE 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5423–5428. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-Term Load Forecasting for Industrial Customers Based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar] [CrossRef]
- Tang, X.; Chen, H.; Xiang, W.; Yang, J.; Zou, M. Short-term load forecasting using channel and temporal attention based temporal convolutional network. Electr. Power Syst. Res. 2022, 205, 107761. [Google Scholar] [CrossRef]
- Xia, G.; Zhang, F.; Wang, C.; Zhou, C. ED-ConvLSTM: A Novel Global Ionospheric Total Electron Content Medium-Term Forecast Model. Space Weather 2022, 20, e2021SW002959. [Google Scholar] [CrossRef]
- Wang, S.; Mu, L.; Liu, D. A hybrid approach for El Niño prediction based on Empirical Mode Decomposition and convolutional LSTM Encoder-Decoder. Comput. Geosci. 2021, 149, 104695. [Google Scholar] [CrossRef]
- Olah, C. Understanding LSTM Networks. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 12 January 2023).
- Banoula, M. An Overview on Multilayer Perceptron (MLP). Available online: https://www.simplilearn.com/tutorials/deep-learning-tutorial/multilayer-perceptron#forward_propagation (accessed on 7 January 2023).
- Andrew Zola, J.V. What Is a Backpropagation Algorithm? Available online: https://www.techtarget.com/searchenterpriseai/definition/backpropagation-algorithm (accessed on 7 January 2023).
- CS231n Convolutional Neural Networks for Visual Recognition. Available online: https://cs231n.github.io/convolutional-networks/#fc (accessed on 7 January 2023).
- Lara-Benítez, P.; Carranza-García, M.; Luna-Romera, J.M.; Riquelme, J.C. Temporal convolutional networks applied to energy-related time series forecasting. Appl. Sci. 2020, 10, 2322. [Google Scholar] [CrossRef]
- Tian, H.; Chen, J. Deep Learning with Spatial Attention-Based CONV-LSTM for SOC Estimation of Lithium-Ion Batteries. Processes 2022, 10, 2185. [Google Scholar] [CrossRef]
- Brownlee, J. How Does Attention Work in Encoder-Decoder Recurrent Neural Networks. Available online: https://machinelearningmastery.com/how-does-attention-work-in-encoder-decoder-recurrent-neural-networks/ (accessed on 12 January 2023).
- Kim, K.S.; Lee, J.B.; Roh, M.I.; Han, K.M.; Lee, G.H. Prediction of ocean weather based on denoising autoencoder and convolutional LSTM. J. Mar. Sci. Eng. 2020, 8, 805. [Google Scholar] [CrossRef]
- METAR-Wikipedia. Available online: https://en.wikipedia.org/wiki/METAR (accessed on 12 January 2023).
- Ogimet. Available online: https://www.ogimet.com/home.phtml.en (accessed on 12 January 2023).
- Thira ES-HEDNO. Available online: https://deddie.gr/en/themata-tou-diaxeiristi-mi-diasundedemenwn-nisiwn/leitourgia-mdn/dimosieusi-imerisiou-energeiakou-programmatismou/thira-es/ (accessed on 10 January 2022).
- Sammut, C.; Webb, G.I. (Eds.) Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2010; pp. 652–653. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]







| Power Consumption Descriptive Analysis | |
|---|---|
| Number of samples | 25,944 |
| Mean value | 23.31 MW |
| Standard deviation | 9.95 MW |
| Minimum value | 8.50 MW |
| Percentile 25% | 14.70 MW |
| Percentile 50% | 21.15 MW |
| Percentile 75% | 31.00 MW |
| Maximum value | 51.52 MW |
| Input Variable | Description |
|---|---|
| Power | The sequence of 24 h of load values for 1 day. |
| Temperature | The sequence of 24 h of temperature values for 1 day. |
| Dew Point | The sequence of 24 h of dew point values for 1 day. |
| Cosine of Day of Week/Sine of Day of Week | The Day of the Week converted by One-Hot Encoding to sine and cosine type. |
| Cosine of Hour of Day/Sine of Hour of Day | The Hour of Day 1–24, converted by One-Hot Encoding to sine and cosine type. |
| Cosine of Month of Year/Sine of Month of Year | The Month of the Year converted by One-Hot Encoding to sine and cosine type. |
| Is Weekend | A dummy variable, “Is Weekend”, takes 0 for working days and 1 for weekends. |
| Model Type | Input Length | Loss Function | Bayesian Optimization | Model Hyperparameters |
|---|---|---|---|---|
| LSTM | 24 | MSE | Objective: validation loss |
|
| MLP | 24 | MSE | Objective: validation loss |
|
| CNN-1D | 24 | MSE | Objective: validation loss |
|
| CNN-LSTM | 24 | MSE | Objective: validation loss |
|
| TCN | 24 | MSE | Objective: validation loss |
|
| Conv LSTM Encoder–Decoder | 24 | MSE | Objective: validation loss |
|
| Method | R2 (MW) | MAE (MW) | MSE (MW) | RMSE (MW) | MAPE (%) |
|---|---|---|---|---|---|
| CNN-1D | 0.9906 | 0.4936 | 0.5302 | 0.7282 | 2.66 |
| TCN | 0.9910 | 0.4576 | 0.5036 | 0.7096 | 2.40 |
| MLP | 0.9919 | 0.4477 | 0.4602 | 0.6784 | 2.38 |
| CNN-LSTM | 0.9917 | 0.4412 | 0.4714 | 0.6866 | 2.31 |
| LSTM | 0.9920 | 0.4275 | 0.4552 | 0.6747 | 2.25 |
| ConvLSTM Encoder-Decoder | 0.9921 | 0.4142 | 0.4454 | 0.6674 | 2.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laitsos, V.; Vontzos, G.; Bargiotas, D.; Daskalopulu, A.; Tsoukalas, L.H. Enhanced Automated Deep Learning Application for Short-Term Load Forecasting. Mathematics 2023, 11, 2912. https://doi.org/10.3390/math11132912
Laitsos V, Vontzos G, Bargiotas D, Daskalopulu A, Tsoukalas LH. Enhanced Automated Deep Learning Application for Short-Term Load Forecasting. Mathematics. 2023; 11(13):2912. https://doi.org/10.3390/math11132912
Chicago/Turabian StyleLaitsos, Vasileios, Georgios Vontzos, Dimitrios Bargiotas, Aspassia Daskalopulu, and Lefteri H. Tsoukalas. 2023. "Enhanced Automated Deep Learning Application for Short-Term Load Forecasting" Mathematics 11, no. 13: 2912. https://doi.org/10.3390/math11132912
APA StyleLaitsos, V., Vontzos, G., Bargiotas, D., Daskalopulu, A., & Tsoukalas, L. H. (2023). Enhanced Automated Deep Learning Application for Short-Term Load Forecasting. Mathematics, 11(13), 2912. https://doi.org/10.3390/math11132912









