Abstract
This article discusses the event-triggered consensus problem for a switched multi-agent system (MASs) with switching topologies. An observer-based dynamic event-triggered (DET) controller with a discontinuous nonlinear term is designed to reduce arduous communication. With the designed approach, the error system can reach a tracking consensus. Then, a continuous observer-based DET protocol is created using the boundary layer method to prevent chattering effects. Moreover, by employing the Riccati equation and the switched Lyapunov function method, some sufficient criteria are put forward to guarantee the tracking consensus of the systems. The suggested observer-based DET protocol can also exclude the Zeno behavior. Finally, two examples verify the validity of the analysis.
MSC:
93D23
1. Introduction
In recent decades, MASs have been widely studied in the engineering field such as spacecraft formation, sensor networks, mobile robots, and so on [1,2,3]. Particularly, the extensive application of the consensus control problems for MASs has attracted great interest among scholars [4]. To achieve system consensus, it is necessary to design effective control protocols or algorithms, so that each agent in MASs can continuously adjust its behavior based on the information sent by its neighbors.
Event-triggered control, as an effective control method, has attracted increasing attention in the past decade (see [5,6,7,8] and references therein). Unlike time-triggered control, which operates based on a fixed time schedule, event-triggered control adjusts system actions based on specific events or changes in the system’s state. It aims to activate control actions only when necessary, minimizing the utilization of system resources and improving efficiency. In the early work [9], the researchers introduced static event-triggered control into the study of MASs, which proved to be successful in extending the sampling period. After that, the static event-triggered control was combined with the observer. To name a few, a static event-triggered adaptive distributed observer was designed for studying the cooperative issue for heterogeneous linear MASs [10], and it was found that the rate of executing the operation in the processor can be enormously decreased. Recently, a data reduction and transmission method based on awareness is proposed to design asynchronous communication and event-triggered control scheme, which can avoid continuous communication between agents of both communication and control parties [11]. Different from the classical periodic sampling control [12], the above static event-triggered strategy can significantly prevent needless sampling and improve the utilization of restricted bandwidth resources. Nevertheless, when the threshold value in the triggering condition remains constant, some unnecessary communication is still going on. This results in a waste of sampling resources and computing resources. Thus, it is necessary to adjust the triggering threshold in the existing event-triggered strategy to further reduce the communication cost.
Considering the shortage of static event-triggered control, many scholars have studied the DET control method and reported corresponding results [13,14,15,16,17,18]. The core of this method is to introduce an auxiliary dynamic threshold in the triggering condition, so compared to the static threshold, the average time between events in the DET mechanism is longer. Therefore, it has the advantage of greatly reducing communication frequency in the implementation of the control process. For example, Ref. [13] provided a DET scheme to decrease the communication frequency. In detail, the total number of triggers determined by the DET strategy is less than the static one. Two independent DET strategies are designed to deal with the leader-following bounded consensus in MASs [14], which can avert frequent updates of the sensors and controllers simultaneously. Later, under the adaptive DET strategy, Ref. [15] extended the undirected graph to the directed graph and discussed the bounded consensus of MASs. In the present works on the DET method, most of them assume that the communication topology is fixed [14,15,17]. However, for most realistic circumstances, the fixed communication topologies are not adequate to characterize the interaction between agents. That is to say, the topologies may change in different time periods. In view of this, analysis of consensus for MASs with switching topologies is crucial, and substantial relevant systems (such as smart grid systems [19], general linear systems [20], and Euler–Lagrange systems [21]) have been reported.
It should be also pointed out that in some practical situations, many complex processes encompass switched modes, for example, traffic lights switch among different colors. Therefore, modeling each agent as a switched system is more general [22,23,24]. By introducing the idea of the switching method, a switching complex dynamic network describing a physical system more accurately is established. Recently, switched MASs with event-triggered control have drawn a large amount of attention [25,26,27,28,29,30,31,32]. For example, in [25], the event-triggered strategy is first used to investigate the tracking consensus of nonlinear switched MASs with unknown parameters, and an adaptive law is devised by utilizing the backstepping technique to analyze the unknown parameters. Ref. [27] discusses the security consensus problems for time-varying multi-agent systems with denial-of-service attacks and parameter uncertainty, updating the control input signal by adopting a new event-driven mechanism with a state-dependent threshold within a given limited range. A bumpless transfer control and event-triggered communication were discussed in [31] to handle the output consensus issue of a class of switched multi-agent systems. The cooperative output regulation for switched heterogeneous MASs under a switching strategy was proposed in [32]. The above references have proved that the consensus of switched MASs is affected by the subsystems and the switching rule. Moreover, in practical engineering applications, due to economic and technical limitations of measurement methods, it is difficult to obtain all state information, which makes implementing state feedback control challenging. The introduction of observers solves the contradiction between the performance superiority of state feedback and the physical difficulty of its realization. Thus, it is essential to consider observer-based control strategies for available measurement outputs. Unfortunately, the above literature [25,26,27,28,29,30,31,32] assumed that full state information can be obtained directly, and the control mechanisms only considered the static event-triggered mechanism. At present, there is little research on observer-based DET tracking consensus issues for switched MASs with a leader of nonzero control inputs, which inspired this research.
The above work inspired us to investigate tracking consensus for switched MASs where the leader system involves nonzero control inputs. In other words, we propose an observer-based DET protocol that includes a discontinuous nonlinear term and a continuous nonlinear term to ensure the stability of the switched MASs. The contributions are concluded below.
- Different from the existing results in [33,34,35] which focus on fixed network topology, this paper investigates the consensus for switched MASs with arbitrarily switching communication topologies.
- A more general observer-based DET consensus protocol with a variable threshold is provided, where the controller includes discontinuous function and continuous function. Compared with most relative works that handle the consensus of switched MASs adopting static event-triggered strategies [25,26,28,29], this paper can further reduce the expenses associated with system resource usage.
- Compared to the minimum switching law proposed in [30], this paper allows multiple modes of switching within an event interval, and the minimum dwell time of each subsystem is unlimited. The result obtained in this way is more general than the result in [30].
The rest of this paper is organized as follows. In Section 2, the preliminaries are described. Section 3 gives the tracking consensus criteria for switched MASs. In Section 4, some examples are shown to explain the validity of the provided approach. Section 5 concludes this paper.
Notations: represents the set of natural numbers. and are the n-dimensional Euclidean space and real matrices, respectively. and are the maximal and minimal eigenvalues of a real matrix, respectively. represents the Euclidean norm for vertices or matrices. The n-dimensional identity matrix is denoted as . ⊗ stands for the Kronecker product.
2. Preliminaries
2.1. Graph Theory
Denote , where is the switching signal. The switching instant sequence , satisfies . The interconnection topology among agents is described by an undigraph , where represents the set of all agents. stands for the induced subgraph of , where , . denotes the adjacency matrix of graph , where is the weight of the edge , and means agent v cannot receive any information from agent j, otherwise, . , otherwise, . The Laplacian matrix of a graph is defined as and with . Define the matrix as the connection relationship between the followers and the leader. If the v-th follower can receive information from the leader, , otherwise, . Let .
2.2. Problem Statement
Consider switched MASs containing N followers and one leader. The dynamics of the vth follower is expressed as
where () represents the system state, denotes the control input, and is the sensor output of v-th agent. , , and are constant system matrices.
The leader’s dynamics is expressed as
where and are the state and nonzero input, respectively. Suppose that , where .
To facilitate our major works, the following assumptions are presented.
Assumption 1.
The pairs are stabilizable. That is, for given , , the Riccati equation
has a solution . .
Assumption 2.
The pairs are observable.
Assumption 3.
is connected, and at least one follower can obtain information from the leader.
To facilitate the discussion in next section, we introduce the following definition.
Definition 1
([36]). For all , denotes number of switches of within the interval . If
holds for positive numbers and , then is called the chatter bound and is the average dwell time (ADT).
The following lemma is also useful for the analysis.
Lemma 1
([37]). If the ADT and satisfies
then is bounded and converges into the residual set:
where , , , , .
In engineering applications, the state information of the system (1) may not be fully achievable due to implementation costs. Therefore, utilizing an observer-based approach, the following state observer is designed:
where denotes the observer state vector, denotes the observer gain to be determined later.
In the following, the DET control schemes are proposed to reduce communication costs. Define as the measurement error. The trigger sequence is generated by
where , , is a variable, which satisfies
where , .
Next, we will give an important lemma to ensure that it remains Zeno-free.
Lemma 2
([16]). For prescribed scalars , , and , meets
Let . For each follower, the following event-based tracking control protocol is designed:
where represents the feedback gain matrix, . and nonlinear function will be designed later.
Remark 1.
Unlike the classical time-triggered control mechanism that periodically samples system states, our study introduces a DET control scheme. This scheme determines the interval based on specific triggering conditions proposed in our research.
Remark 2.
It is important to remember that some crucial results for event-triggered control have already been published [8,9,10]. These results are different from our DET control scheme in two ways. First, the insertion of the dynamic threshold makes DET conditions (4) dynamic for the measurement error. Second, this research takes switched systems into account as opposed to the current DET control approaches for deterministic systems.
Let as the tracking error and as the observation error. Based on the above discussion, it is easy to get
Incorporating the Kronecker product, the above error systems are further characterized as compact representation
where
3. Main Results
The major works that appeared are twofold. In Section 3.1, the DET protocol with a discontinuous term is considered. Under the proposed DET protocol, the Zeno behavior will be eliminated. On the other hand, a continuous observer-based DET protocol is designed by using the boundary layer method in Section 3.2.
3.1. DET Protocol with Discontinuous Term
Define the nonlinear function as
In what follows, we put forward an algorithm (Algorithm 1) to design the nonsmooth DET protocol.
| Algorithm 1 An algorithm to design the nonsmooth DET protocol |
If Assumptions 1–3 hold, the DET protocol can be taken into consideration in the following steps.
|
Theorem 1.
Proof.
We introduce the following Lyapunov function:
and
where will be given later.
Assume for . According to the above discussion, the stability will be analyzed from the following two cases.
Case 1. If there is no trigger moment in the interval , i.e., , The DET condition is not satisfied, and the last sampling system state is maintained. Define as
By virtue of the Cauchy inequality, we can obtain
using the Young’s inequality gives
According to the fact , it is easy to obtain
Then, from (8), one has
Since is Hurwitz, it is well known that there exists a such that , where . Then we can obtain
From the DET condition (4), for all
then, by using and Assumption 1, one has
where , , and . Then one obtains
Case 2. If there are trigger moments in the interval , i.e., , then one can have
Similarly, Equation (10) is also true on subintervals , , ⋯,, which renders (17) holding on these subintervals. Thus we can obtain that
It should be pointed out that since the Lyapunov function is continuous, then (18) can be derived from (19) on the interval .
Executing the similar steps in Case 1 and utilizing condition (3) in Algorithm 1, we have
Then, from that . Since , is bounded and , which denotes that and can asymptotically approach zero, and , thus , where . The proof is completed. □
Remark 3.
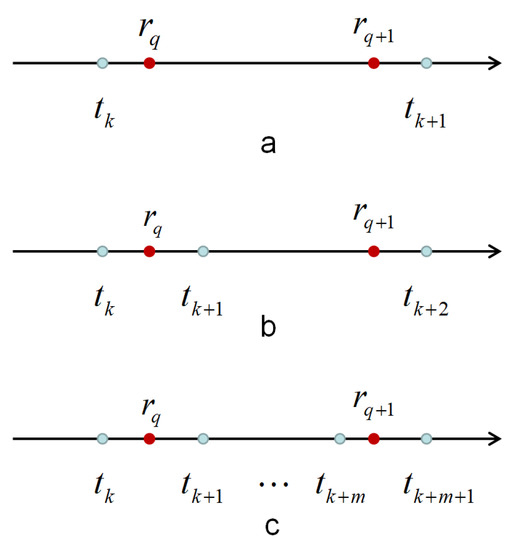
According to Theorem 1, multiple switching instances or no switching instance can occur within event intervals . The relationship between triggering instant and switching instant is given in Figure 1. This study introduces a more general scenario compared to the assumption of at most one switch each event interval [30] and synchronized switching and sampling within a fixed period [38]. It is important to note that is piecewise continuous and bounded, ensuring the continuity of [39], thus validating the conclusion (18).

Figure 1.
Relationship between trigger moments and switch moments.
Next, Theorem 2 is developed to prove Zeno-free. The so-called Zeno behavior refers to the event-triggered scheme we designed being excited infinitely within a limited time in the event-triggered control. Our purpose is to prove that any two adjacent triggering intervals are greater than zero.
Theorem 2.
Under consensus conditions in Algorithm 1, there is Zeno-free in the proposed DET protocol.
Proof.
The systems contain switching signals and event-triggered signals, respectively. Therefore, it is indispensable to clarify their relationship. Suppose that in the interval , . After that, the following two cases will be taken into account. □
Case 1. There is no switch on the interval . Then
From Theorem 1, we can know that the and are bounded for any finite time. Thus, let be the upper bound of , we obtain
where , . Then we have
thus
where .
According to the DET condition (4), the next triggering moment satisfies
from (22), we can obtain
Through calculation, we can further obtain
Case 2. There exist some switches on the triggering interval , i.e., , where . If system (1) has infinite triggering within a limited time interval, it is said that system (1) has Zeno behavior. Assume that M stands for the Zeno time, and , , thus . Nevertheless, , there are some , , such that , , ⋯, . Then , in other words, , which is contrary to converges to 0. Thus, it is Zeno free.
Remark 4.
The proof of Theorem 2 is inspired by [40] but different from [40]. In this paper, it is formidable to prohibit Zeno behavior since Theorem 2 needs to take into account how the triggering instants and switching instants are related.
One disadvantage of the DET protocol with the discontinuous term is that it produces the undesirable chattering effect in real implementation. To avoid the chattering effect, the next section will adopt the boundary layer technique to design a DET protocol with a continuous term .
3.2. DET Protocol with Continuous Term
Define the nonlinear function as
where represents the widths of the boundary layers.
Theorem 3 will clarify that the bounded consensus of switched MASs can be obtained under Algorithm 1, DET condition (4) and event-based tracking control protocols (5).
Theorem 3.
Proof.
Suppose is the Lyapunov function provided by (9). Combination Theorem 1, we obtain
Next, we consider the following three cases.
(1) , . Using the analysis method in Section 3.1, by introducing the auxiliary Lyapunov function , one obtains that
(3) for , and for , where . Then
Since , one has
According to Lemma 1, we obtain
Remark 5.
Although complete consensus can not be ensured by applying the continuous protocol (23), the chattering effect can be prevented. Keep in mind that the intrinsic shortcoming of the discontinuous controller is the unfavorable chattering effect in real-world application (8) [41]. From (27), we know that the bound of is decided by the nonzero control inputs and the maximum width , the number of followers, and the ADT. It can be noted that the smaller the , the smaller the bound of .
4. Numerical Simulation
Two numerical simulations verify the validity of the above results and the effectiveness of the proposed DET mechanism for switched MASs.
Assume that the topology switches between the graphs and are depicted by Figure 2a,b, where the switching signals are 1 and 2, respectively. The leader is
and the v-th followers are described by
with , and
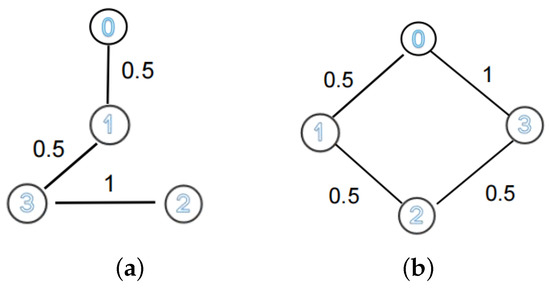
Figure 2.
Communication graphs. (a) ; (b) .
Then, , . Let .
Example 1.
Choose , , , solving conditions (1) and (2) in Algorithm 1, we have
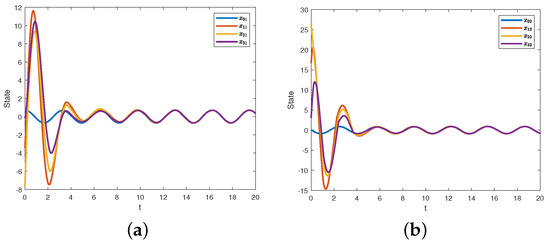
Through calculation, , we select , , and . Next, set and s. Then the trajectories of and are shown in Figure 2a,b, respectively. Then the trajectories of and are shown in Figure 3a,b, respectively. Figure 4a illustrates the consensus of the switched MASs. Meanwhile, Figure 4b is the sampling moments. The above simulation results verify the effectiveness of the proposed DET control strategy.

Figure 3.
In Example 1: (a) States trajectories of ; (b) States trajectories of .

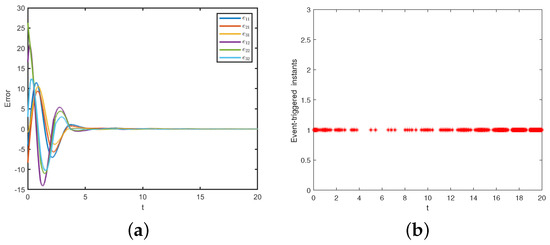
Figure 4.
In Example 1: (a) Time evolutions of ; (b) Triggering time sequences.
Example 2.
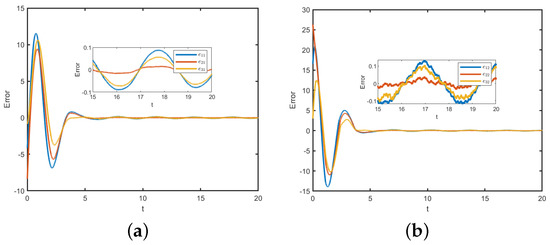
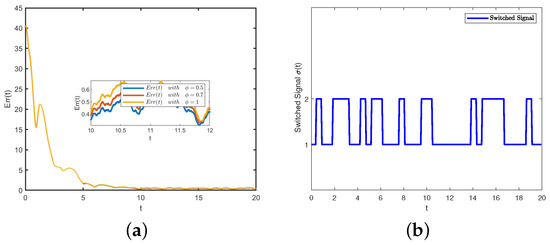
Consider the same parameters as those in Example 1. According to Theorem 3, switched MASs (1) and (2) will realize bounded consensus. The consensus error signal is displayed in Figure 5a,b. Assuming that Err(t). is determined by Theorem 3. Additionally, under any , Err (t) can achieve bounded consensus. Without losing generality, we select , the trajectories of Err(t) are illustrated in Figure 6a. In addition, the switching signal with two modes is given in Figure 6b.

Figure 5.
In Example 2: (a) Time evolutions of ; (b) Time evolutions of .

Figure 6.
In Example 2: (a) Time evolutions of Err(t); (b) Switching signal.
5. Conclusions
The tracking consensus control of switched MASs was discussed in this paper, where the system and communication topology were switched simultaneously and the leader system had nonzero control inputs. The proposed observer-based DET protocols include two nonlinear terms to handle the effect of nonzero control inputs. Moreover, the Zeno behavior for MASs under the observer-based DET protocols can be excluded. In addition, by employing the switched Lyapunov function method and Riccati equation, some sufficient criteria are put forward to ensure that all followers can track the leader. Compared with the existing works in the literature, the designed observer-based DET protocols can successfully limit the frequency of data transfer across agents while maintaining MASs consensus. Finally, two numerical examples show that the designed control protocol can reduce controller updates. In the future, the method suggested in this paper will be used to discuss the consensus problem of switched stochastic MASs with delay impulsive effects.
Author Contributions
X.R. performed the data analyses and wrote the manuscript; J.C. contributed to the conception of the study; Z.W. and C.W. helped perform the analysis with constructive discussions; H.Y. performed the experiment. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Science Foundation of China (62203337).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Jie, L.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Tang, Y.; Xing, X.; Karimi, H.R.; Kocarev, L.; Kurths, J. Tracking control of networked multi-agent systems under new characterizations of impulses and its applications in robotic systems. IEEE Trans. Ind. Electron. 2016, 63, 1299–1307. [Google Scholar] [CrossRef]
- Chen, S.; Ho, D.W.; Li, L.; Liu, M. Fault-tolerant consensus of multi-agent system with distributed adaptive protocol. IEEE Trans. Cybern. 2017, 45, 2142–2155. [Google Scholar] [CrossRef]
- Deng, C.; Wen, C.; Wang, W.; Li, X.; Yue, D. Distributed adaptive tracking control for high-order nonlinear multi-agent systems over event-triggered communication. IEEE Trans. Autom. Control 2022, 68, 1176–1183. [Google Scholar] [CrossRef]
- Guo, R.; Feng, J.; Wang, J.; Zhao, Y. Leader-following successive lag consensus of nonlinear multi-agent systems via observer-based event-triggered control. J. Frankl. Inst. 2022, in press. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, C.; Zhao, D.; Sun, B.; Li, Y. Event-triggered consensus control of continuous-time stochastic multi-agent systems. Automatica 2022, 137, 110022. [Google Scholar] [CrossRef]
- Luand, A.; Yang, G. Observer-based control for cyber-physical systems under denial-of-service with a decentralized event-triggered scheme. IEEE Trans. Cybern. 2020, 50, 4886–4895. [Google Scholar]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed event-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2012, 57, 1291–1297. [Google Scholar] [CrossRef]
- Qian, Y.; Liu, L.; Feng, G. Cooperative output regulation of linear multiagent systems: An event-triggered adaptive distributed observer approach. IEEE Trans. Autom. Control 2021, 66, 833–840. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z. Observer-based asynchronous communication and adaptive control protocols with intermittent updating and interaction. IEEE Trans. Netw. Sci. Eng. 2023, 10, 452–462. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, L. Sampled-data based consensus of continuous-time multi-agent systems with time-varying topology. IEEE Trans. Autom. Control 2011, 56, 1226–1231. [Google Scholar] [CrossRef]
- Girard, A. Dynamic triggering mechanisms for event-triggered control. IEEE Trans. Autom. Control 2015, 60, 1992–1997. [Google Scholar] [CrossRef]
- Ruan, X.; Feng, J.; Xu, C.; Wang, J. Observer-based dynamic event-triggered strategies for leader-following consensus of multi-agent systems with disturbances. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3148–3158. [Google Scholar] [CrossRef]
- Ruan, X.; Xu, C.; Feng, J.; Wang, J.; Zhao, Y. Adaptive dynamic event-triggered control for multi-agent systems with matched uncertainties under directed topologies. Phys. A Stat. Mech. Appl. 2022, 586, 126450. [Google Scholar] [CrossRef]
- Hu, S.; Qiu, J.; Chen, X.; Zhao, F.; Jiang, X. Dynamic event-triggered control for leader-following consensus of multiagent systems with the estimator. IET Control Theory Appl. 2022, 16, 1475–1484. [Google Scholar] [CrossRef]
- Du, S.L.; Liu, T.; Ho, D.W. Dynamic event-triggered control for leader-following consensus of multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3243–3251. [Google Scholar] [CrossRef]
- Yang, Y.; Yue, D.; Xu, C. Dynamic event-triggered leader-following consensus control of a class of linear multi-agent systems. J. Frankl. Inst. 2018, 355, 7706–7734. [Google Scholar] [CrossRef]
- Loia, V.; Terzija, V.; Vaccaro, A.; Wall, P. An affine-arithmetic-based consensus protocol for smart-grid computing in the presence of data uncertainties. IEEE Trans. Ind. Electron. 2015, 62, 2973–2982. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, L.; Wang, L. Observability of multi-agent systems with switching topology. IEEE Trans. Circuits Syst. II Exp. Briefs 2017, 64, 1317–1321. [Google Scholar] [CrossRef]
- Liu, Y.; Min, H.; Wang, S.; Ma, L.; Liu, Z. Consensus for multiple heterogeneous Euler–Lagrange systems with time-delay and jointly connected topologies. J. Frankl. Inst. 2014, 351, 3351–3363. [Google Scholar] [CrossRef]
- Lee, T.; Sreenath, K.; Kumar, V. Geometric control of cooperating multiple quadrotor UAVs with a suspended payload. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 5510–5515. [Google Scholar]
- Ye, J.; Roy, S.; Godjevac, M.; Baldi, S. A switching control perspective on the offshore construction scenario of heavy-lift vessels. IEEE Trans. Control Syst. Technol. 2021, 29, 70–477. [Google Scholar] [CrossRef]
- Yuan, S.; Schutter, B.; Baldi, S. Robust adaptive tracking control of uncertain slowly switched linear systems. Nonlinear Anal. Hybrid Syst. 2018, 27, 1–12. [Google Scholar] [CrossRef]
- Yao, D.; Dou, C.; Yue, D.; Zhao, N.; Zhang, T. Event-triggered adaptive consensus tracking control for nonlinear switching multi-agent systems. Neurocomputing 2020, 38, 157–164. [Google Scholar] [CrossRef]
- Zou, W.; Xiang, Z. Event-triggered leader-following consensus of non-linear multi-agent systems with switched dynamics. IET Control Theory Appl. 2019, 13, 1222–1228. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, C.; Zhang, B.; Jiang, Y. Event-triggered based security consensus control for multi-agent systems with DoS attacks. Neurocomputing 2022, 505, 214–224. [Google Scholar] [CrossRef]
- Li, S.; Liang, K.; He, W. Fully distributed event-triggered secure consensus of general linear multi-agent systems under sequential scaling attacks. ISA Trans. 2022, 127, 146–155. [Google Scholar] [CrossRef]
- Zou, W.; Shi, P.; Xiang, Z.; Shi, Y. Consensus tracking control of switched stochastic nonlinear multiagent systems via event-triggered strategy. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1036–1045. [Google Scholar] [CrossRef]
- Xiao, X.; Zhou, L.; Ho, D.W.C.; Lu, G. Event-triggered control of continuous-time switched linear systems. IEEE Trans. Autom. Control 2019, 64, 1710–1717. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Z.; Zhao, L. Output consensus for switched multi-agent systems with bumpless transfer control and event-triggered communication. Inf. Sci. 2021, 544, 585–598. [Google Scholar] [CrossRef]
- He, G.; Zhao, J. Fully distributed event-triggered cooperative output regulation for switched multi-agent systems with combined switching mechanism. Inf. Sci. 2023, 638, 118970. [Google Scholar] [CrossRef]
- Demirel, B.; Ghadimi, E.; Quevedo, D.E.; Johansson, M. Optimal control of linear systems with limited control actions: Threshold-based event-triggered control. IEEE Trans. Control Netw. Syst. 2018, 5, 1275–1286. [Google Scholar] [CrossRef]
- Liu, W.; Yang, C.; Sun, Y.; Qin, J. Observer-based event-triggered tracking control of leader-follower systems with time delay. J. Syst. Sci. Complex. 2016, 29, 865–880. [Google Scholar] [CrossRef]
- Lv, Y.; Li, Z.; Duan, Z.; Chen, J. Distributed adaptive output feedback consensus protocols for linear systems on directed graphs with a leader of bounded input. Automatica 2016, 74, 308–314. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, H.; Wu, Z.; Chen, G. Stability analysis for input saturated discrete-time switched systems with average dwell-time. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 412–419. [Google Scholar] [CrossRef]
- Wen, G.; Wang, P.; Yu, X.; Yu, W.; Cao, J. Pinning synchronization of complex switching networks with a leader of nonzero control inputs. IEEE Trans. Circuits Syst. I Reg. Papers 2019, 66, 3100–3112. [Google Scholar] [CrossRef]
- Ma, D.; Zhao, J. Stabilization of networked switched linear systems: An asynchronous switching delay system approach. Syst. Control Lett. 2015, 77, 46–54. [Google Scholar] [CrossRef]
- Adkins, W.A.; Davidson, M.G. Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- He, W.; Xu, B.; Han, Q.L.; Qian, F. Adaptive consensus control of linear multiagent systems with dynamic event-triggered strategies. IEEE Trans. Cybern. 2020, 50, 2996–3008. [Google Scholar] [CrossRef]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).