An Archive-Guided Equilibrium Optimizer Based on Epsilon Dominance for Multi-Objective Optimization Problems
Abstract
1. Introduction
- We propose a GMOEO method to solve multi-objective optimization problems;
- We incorporated an external archive to store the non-dominated solutions and to guide the particles toward the optimal Pareto set.
- -dominance was employed to update the archive solutions and to ensure improved diversity, exploitation, and exploration. In addition, cone--dominance was employed to update the archive solutions, and was compared with the -dominance relation;
- A fast non-dominating sort and crowding distances were introduced to preserve the diversity and to ensure the convergence of the particles, as well as to ensure an efficient solution distribution;
- The effectiveness of the proposed algorithm was validated through comprehensive experiments conducted on different benchmarks, including ZDT and DTLZ test functions. The performance was then compared with the known multi-objective optimization algorithms.
2. Background Information
2.1. Multi-Objective Optimization Problems
2.2. Pareto Dominance and Optimality
 s ∈ x|z ≺ s
s ∈ x|z ≺ s
2.3. Equilibrium Optimizer (EO)
| Algorithm 1 Equilibrium optimizer (EO) [45] |
| Initialize the particles |
| Assign equilibrium candidates’ fitness a large number |
| Assign the parameters , , |
| while Iteration < Maxiteration do |
 |
| end |
3. The Guided Multi-Objective Equilibrium Optimization
- An external archive that could store the best non-dominated solutions in order to guide the particles toward the optimal set;
- The use of an efficient -dominance/cone--dominance relation for updating the archive solutions;
- The integration of a candidate population that enhanced the diversity;
- The use of the fast non-dominated sort (FNS) and the crowding distance to ensure an efficient and diverse set of solutions with an efficient convergence toward the Pareto optimal.
3.1. Updating the Candidate Population
3.1.1. Double Population
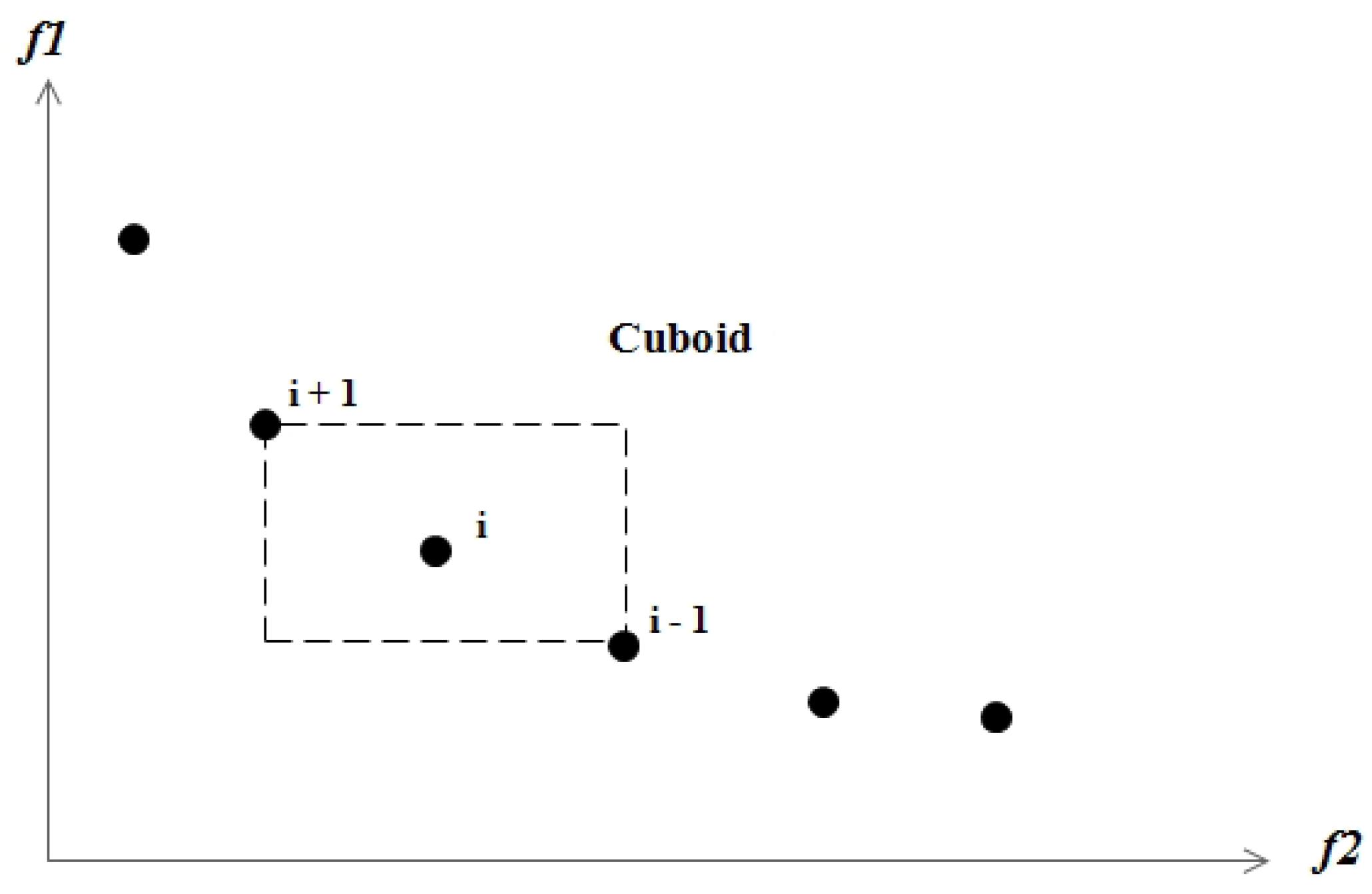
3.1.2. Sorting
| Algorithm 2 Steps of the fast non-dominated sort algorithm. |
| Input: Double population |
| foreachx ∈ Double population do |
 |
| end |
| Algorithm 3 Steps to compute crowding distance for each solution. |
| Input: F population based Front; |
| N solutions number in the front F |
| foreach k initialize the distance by Zero do |
 |
| end |
3.2. Updating the Archive Population
3.2.1. ϵ-Dominance
| Algorithm 4 Archive updating using ϵ-dominance. |
| Input: Archive population , iteration number t, candidate population c solution. |
| Calculate vector and for all archive population solutions , |
| if then |
 |
| end |
3.2.2. Cone-ϵ-Dominance
3.2.3. Evaluating the Archive Population Size
| Algorithm 5 Archive updating using the cone ϵ-dominance. |
| Input: Archive population A, candidate population solution |
| Calculate vector and b for all archive population solutions A |
| if c is cone-ϵ-dominated by any then |
 |
| end |
3.3. Updating the Particle Position
| Algorithm 6 Updating particles position. |
| Input: Particles population P, |
| Archive population , |
| =(+++)/4, |
| Equilibrium pool construction: |
| =,,,, |
| for i = 1: number of particles (n) do |
 |
| end |
| Algorithm 7 The guided multi-objective equilibrium optimizer (GMOEO). |
| Initialize the particles , |
| Assign equilibrium candidates’ fitness a large number, |
| Assign the parameters , , |
| while Iteration < Maxiterstion do |
 |
| end |
| Return: Archive population A |
4. Experimental Results
- SP was used to evaluate the uniformity of the distribution of non-dominated solutions and the diversity of the solutions. The spacing assisted in estimating the distribution of the obtained solution along the Pareto front. SP was defined as follows:wherewhere , with n as the number of solutions obtained in the front, while is the average of all with m as the number of objective functions f;
- MS was used to measure the diagonal length of the hyper-box generated by the extreme values of the objective functions in the non-dominated solution set. MS was defined as follows:where d represents the Euclidean distance between and the maximum value of the ith objective function, and is the minimum value of the ith objective function with M as the number of the objective functions;
- IGD was an inversion of the generational distance metric, which could be computed as the distance between the reference Pareto front and each of the closest non-dominated solutions. Generally, IGD is used as a measure of an algorithm’s convergence. It was formulated as follows:where n represents the number of the true Pareto solution set, while represents the Euclidean distance between the nearest Pareto solution obtained by the algorithm and the true Pareto front: the smaller the IGD and SP, the better the performance. Therefore, these were used to perform the comparison accordingly.
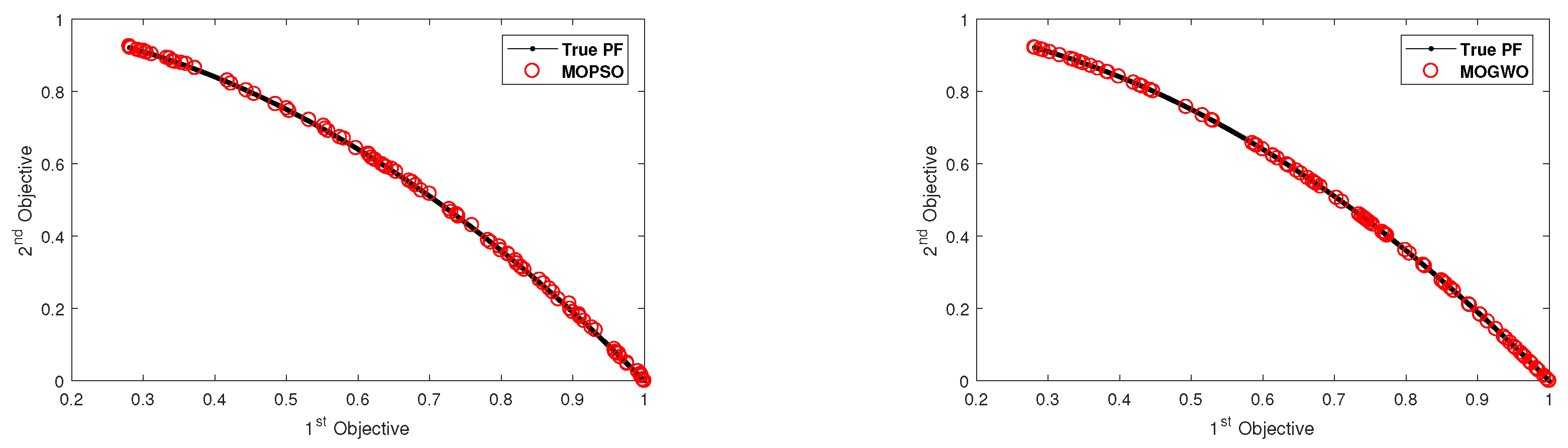
4.1. Results of the ZDT Test Functions
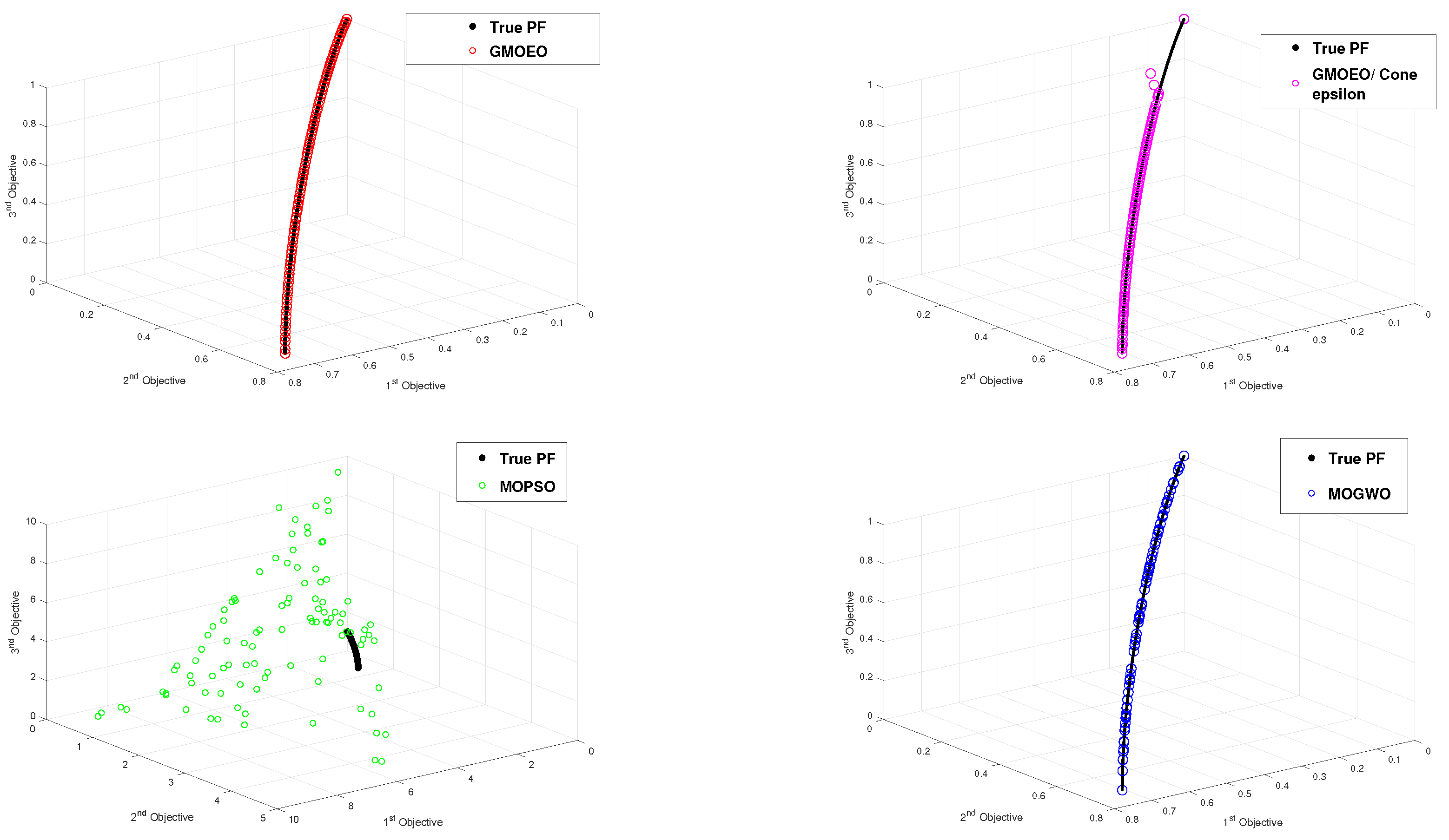
4.2. Results of the DTLZ Test Functions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dahou, A.; Chelloug, S.A.; Alduailij, M.; Elaziz, M.A. Improved Feature Selection Based on Chaos Game Optimization for Social Internet of Things with a Novel Deep Learning Model. Mathematics 2023, 11, 1032. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Abdellatif, A.D.; Alburaikan, A.; Khalifa, H.A.E.W.; Elaziz, M.A.; Abualigah, L.; AbdelMouty, A.M. A novel hybrid arithmetic optimization algorithm and salp swarm algorithm for data placement in cloud computing. Soft Comput. 2023, 27, 5769–5780. [Google Scholar] [CrossRef]
- Vijaya Bhaskar, K.; Ramesh, S.; Karunanithi, K.; Raja, S. Multi Objective Optimal Power Flow Solutions using Improved Multi Objective Mayfly Algorithm (IMOMA). J. Circuits Syst. Comput. 2023. [Google Scholar] [CrossRef]
- Perera, J.; Liu, S.H.; Mernik, M.; Črepinšek, M.; Ravber, M. A Graph Pointer Network-Based Multi-Objective Deep Reinforcement Learning Algorithm for Solving the Traveling Salesman Problem. Mathematics 2023, 11, 437. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, S.; Lei, Z.; Xiong, R.; Cheng, J. Pareto Dominance Archive and Coordinated Selection Strategy-Based Many-Objective Optimizer for Protein Structure Prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 2328–2340. [Google Scholar] [CrossRef]
- De, S.; Dey, S.; Bhattacharyya, S. Recent Advances in Hybrid Metaheuristics for Data Clustering; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Bhattacharyya, S. Hybrid Computational Intelligent Systems: Modeling, Simulation and Optimization; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Bhattacharyya, S.; Banerjee, J.S.; De, D. Confluence of Artificial Intelligence and Robotic Process Automation; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Mahmoodabadi, M. An optimal robust fuzzy adaptive integral sliding mode controller based upon a multi-objective grey wolf optimization algorithm for a nonlinear uncertain chaotic system. Chaos Solitons Fractals 2023, 167, 113092. [Google Scholar] [CrossRef]
- Chalabi, N.E.; Attia, A.; Bouziane, A.; Hassaballah, M. An improved marine predator algorithm based on Epsilon dominance and Pareto archive for multi-objective optimization. Eng. Appl. Artif. Intell. 2023, 119, 105718. [Google Scholar] [CrossRef]
- Feng, X.; Pan, A.; Ren, Z.; Fan, Z. Hybrid driven strategy for constrained evolutionary multi-objective optimization. Inf. Sci. 2022, 585, 344–365. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Hashim, F.A.; Shaban, H.; Hassaballah, M. Lévy flight distribution: A new metaheuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 94, 103731. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. M-PAES: A memetic algorithm for multiobjective optimization. In Proceedings of the Congress on Evolutionary Computation CEC00 (Cat. No. 00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 1, pp. 325–332. [Google Scholar]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK-Report 2001, 103. [Google Scholar] [CrossRef]
- Daliri, A.; Asghari, A.; Azgomi, H.; Alimoradi, M. The water optimization algorithm: A novel metaheuristic for solving optimization problems. Appl. Intell. 2022, 52, 17990–18029. [Google Scholar] [CrossRef]
- Qin, S.; Pi, D.; Shao, Z.; Xu, Y.; Chen, Y. Reliability-Aware Multi-Objective Memetic Algorithm for Workflow Scheduling Problem in Multi-Cloud System. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 1343–1361. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Abualigah, L.; Issa, M.; Abd El-Latif, A.A. Optimal parameters extracting of fuel cell based on Gorilla Troops Optimizer. Fuel 2023, 332, 126162. [Google Scholar] [CrossRef]
- Dutta, T.; Bhattacharyya, S.; Panigrahi, B.K. Multilevel Quantum Evolutionary Butterfly Optimization Algorithm for Automatic Clustering of Hyperspectral Images. In Proceedings of the 3rd International Conference on Artificial Intelligence and Computer Vision, Taiyuan, China, 26–28 May 2023; pp. 524–534. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Mohan, M.; Mishra, S. Evaluating the ε-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions. Evol. Comput. 2005, 13, 501–525. [Google Scholar] [CrossRef]
- Ma, X.; Qi, Y.; Li, L.; Liu, F.; Jiao, L.; Wu, J. MOEA/D with uniform decomposition measurement for many-objective problems. Soft Comput. 2014, 18, 2541–2564. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Jiao, Y.C.; Li, H.; Wang, X.K. MOEA/D-SQA: A multi-objective memetic algorithm based on decomposition. Eng. Optim. 2012, 44, 1095–1115. [Google Scholar] [CrossRef]
- Qiao, K.; Liang, J.; Yu, K.; Wang, M.; Qu, B.; Yue, C.; Guo, Y. A Self-Adaptive Evolutionary Multi-Task Based Constrained Multi-Objective Evolutionary Algorithm. IEEE Trans. Emerg. Top. Comput. Intell. 2023. [Google Scholar] [CrossRef]
- Wang, Q.; Gu, Q.; Chen, L.; Guo, Y.; Xiong, N. A MOEA/D with global and local cooperative optimization for complicated bi-objective optimization problems. Appl. Comput. 2023, 137, 110162. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Rabbani, M.; Oladzad-Abbasabady, N.; Akbarian-Saravi, N. Ambulance routing in disaster response considering variable patient condition: NSGA-II and MOPSO algorithms. J. Ind. Manag. Optim. 2022, 18, 1035–1062. [Google Scholar] [CrossRef]
- Ray, T.; Liew, K. A swarm metaphor for multiobjective design optimization. Eng. Optim. 2002, 34, 141–153. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 2, pp. 1470–1477. [Google Scholar]
- Kaveh, M.; Mesgari, M.S.; Saeidian, B. Orchard Algorithm (OA): A new meta-heuristic algorithm for solving discrete and continuous optimization problems. Math. Comput. Simul. 2023, 208, 95–135. [Google Scholar] [CrossRef]
- Rada-Vilela, J.; Chica, M.; Cordón, Ó.; Damas, S. A comparative study of multi-objective ant colony optimization algorithms for the time and space assembly line balancing problem. Appl. Soft Comput. 2013, 13, 4370–4382. [Google Scholar] [CrossRef]
- Pu, X.; Song, X.; Tan, L.; Zhang, Y. Improved ant colony algorithm in path planning of a single robot and multi-robots with multi-objective. Evol. Intell. 2023. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, R.; Yin, Y.b.; Zou, S.l. Multi-objective path planning for mobile robot in nuclear accident environment based on improved ant colony optimization with modified A. Nucl. Eng. Technol. 2023, 55, 1838–1854. [Google Scholar] [CrossRef]
- Flor-Sánchez, C.O.; Reséndiz-Flores, E.O.; García-Calvillo, I.D. Kernel-based hybrid multi-objective optimization algorithm (KHMO). Inf. Sci. 2023, 624, 416–434. [Google Scholar] [CrossRef]
- Singh, P.; Muchahari, M.K. Solving multi-objective optimization problem of convolutional neural network using fast forward quantum optimization algorithm: Application in digital image classification. Adv. Eng. Softw. 2023, 176, 103370. [Google Scholar] [CrossRef]
- Chu, S.C.; Tsai, P.W. Computational intelligence based on the behavior of cats. Int. J. Innov. Comput. Inf. Control 2007, 3, 163–173. [Google Scholar]
- Pradhan, P.M.; Panda, G. Solving multiobjective problems using cat swarm optimization. Expert Syst.Appl. 2012, 39, 2956–2964. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.d.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Zouache, D.; Abdelaziz, F.B.; Lefkir, M.; Chalabi, N.E.H. Guided Moth–Flame optimiser for multi-objective optimization problems. Ann. Oper. Res. 2021, 296, 877–899. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Houssein, E.H.; Çelik, E.; Mahdy, M.A.; Ghoniem, R.M. Self-adaptive Equilibrium Optimizer for solving global, combinatorial, engineering, and Multi-Objective problems. Expert Syst. Appl. 2022, 195, 116552. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Laumanns, M.; Thiele, L.; Deb, K.; Zitzler, E. Combining convergence and diversity in evolutionary multiobjective optimization. Evol. Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef]
- Batista, L.S.; Campelo, F.; Guimaraes, F.G.; Ramírez, J.A. Pareto cone ε-dominance: Improving convergence and diversity in multiobjective evolutionary algorithms. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Ouro Preto, Brazil, 5–8 April 2011; pp. 76–90. [Google Scholar]
- Ikeda, K.; Kita, H.; Kobayashi, S. Failure of Pareto-based MOEAs: Does non-dominated really mean near to optimal? In Proceedings of the Congress on Evolutionary Computation (Cat. No. 01TH8546), Seoul, Republic of Korea, 27–30 May 2001; Volume 2, pp. 957–962. [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the Congress on Evolutionary Computation (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 825–830. [Google Scholar]
- Schott, J.R. Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization. Ph.D Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective optimization using evolutionary algorithms—A comparative case study. In Proceedings of the International Conference on Parallel Problem Solving From Nature, Amsterdam, The Netherlands, 27–30 September 1998; pp. 292–301. [Google Scholar]
- Van Veldhuizen, D.A.; Lamont, G.B. Multiobjective evolutionary algorithms: Analyzing the state-of-the-art. Evol. Comput. 2000, 8, 125–147. [Google Scholar] [CrossRef] [PubMed]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]













| Bi-objective test functions | |
| Test function | Characteristics |
| ZDT1 | with a convex front |
| ZDT2 | with a non-convex front |
| ZDT3 | with a discontinuous front |
| ZDT4 | with local Pareto-optimal fronts and therefore is highly multi-modal |
| ZDT6 | with a non-uniform search space |
| Three-objective test functions | |
| Test function | Characteristics |
| DTLZ1 | with a linear Pareto-optimal front |
| DTLZ2 | with a spherical Pareto-optimal front |
| DTLZ3 | with a many Pareto-optimal fronts |
| DTLZ4 | with Pareto-optimal front has dense set of solutions to exist near the |
| DTLZ5 | this problem will verify the ability of MOEA to converge to a degenerated curve |
| DTLZ6 | this problem has disconnected Pareto-optimal front |
| DTLZ7 | this problem has Pareto-optimal front which is a combination of a straight line and a hyper-plane |
| Algorithm | Best | Worst | Average | Median | Std |
|---|---|---|---|---|---|
| ZDT1 | |||||
| -GMOEO | 1.457.e-04 | 1.537.e-04 | 1.484.e-04 | 1.481.e-04 | 2.67.e-06 |
| cone-- GMOEO | 1.938.e-04 | 1.149.e-03 | 3.718.e-04 | 2.424.e-04 | 2.989.e-04 |
| MOPSO | 4.02.e-04 | 5.885.e-04 | 4.741.e-04 | 4.468.e-04 | 6.61.e-05 |
| MOGWO | 3.9.e-04 | 5.827.e-04 | 4.702.e-04 | 4.586.e-04 | 7.112.e-05 |
| ZDT2 | |||||
| -GMOEO | 1.4812.e-04 | 1.557.e-04 | 1.507.e-04 | 1.491.e-04 | 3.048.e-06 |
| cone-- GMOEO | 2.311.e-02 | 2.312.e-02 | 2.311.e-02 | 2.311.e-02 | 3.468.e-06 |
| MOPSO | 5.117.e-04 | 3.268.e-02 | 2.947.e-02 | 3.268.e-02 | 1.017.e-02 |
| MOGWO | 5.034.e-04 | 3.268.e-02 | 2.625.e-02 | 3.268 e-02 | 1.356.e-02 |
| ZDT3 | |||||
| -GMOEO | 9.031.e-03 | 9.093.e-03 | 9.07.e-03 | 9.078.e-03 | 2.263.e-05 |
| cone-- GMOEO | 1.716.e-03 | 2.321.e-02 | 6.072.e-03 | 4.186.e-03 | 6.442.e-03 |
| MOPSO | 1.103.e-02 | 2.041.e-02 | 1.484.e-02 | 1.123.e-02 | 4.784.e-03 |
| MOGWO | 4.550.e-04 | 6.723.e-04 | 5.549.e-04 | 5.380.e-04 | 6.8.e-05 |
| ZDT4 | |||||
| -GMOEO | 1.458.e-04 | 3.501.e-02 | 6.506.e-03 | 1.479.e-04 | 1.348.e-02 |
| cone-- GMOEO | 2.724.e-01 | 2.011 | 0.931 | 0.853 | 0.47 |
| MOPSO | 7.661.e-02 | 7.387.e-01 | 3.314.e-01 | 2.797.e-01 | 2.277.e-01 |
| MOGWO | 5.076.e-04 | 1.727.e-01 | 6.208.e-02 | 4.083.e-02 | 5.689.e-02 |
| ZDT6 | |||||
| -GMOEO | 1.177.e-04 | 1.205.e-04 | 1.188.e-04 | 1.186.e-04 | 8.225.e-07 |
| cone-- GMOEO | 1.552.e-03 | 3.238.e-02 | 1.048.e-02 | 9.128.e-03 | 8.442.e-03 |
| MOPSO | 2.918.e-04 | 6.732.e-04 | 3.978.e-04 | 3.711.e-04 | 1.040.e-04 |
| MOGWO | 3.401.e-04 | 5.679.e-04 | 4.691.e-04 | 4.621.e-04 | 6.797.e-05 |
| Algorithm | Best | Worst | Average | Median | Std |
|---|---|---|---|---|---|
| ZDT1 | |||||
| -GMOEO | 3.561.e-03 | 4.489.e-03 | 3.995.e-03 | 3.980.e-03 | 2.427.e-04 |
| cone-- GMOEO | 5.536.e-03 | 9.948.e-03 | 6.945.e-03 | 6.597.e-03 | 1.319.e-03 |
| MOPSO | 5.939.e-03 | 8.457.e-03 | 7.748.e-03 | 8.014.e-03 | 7.512.e-04 |
| MOGWO | 5.910.e-03 | 8.818.e-03 | 7.925.e-03 | 8.041.e-03 | 8.252.e-04 |
| ZDT2 | |||||
| -GMOEO | 3.136.e-03 | 4.343.e-03 | 3.717.e-03 | 3.686.e-03 | 3.741.e-04 |
| cone-- GMOEO | 5.595.e-01 | 5.6173.e-01 | NaN | NaN | NaN |
| MOPSO | 0 | 5.743.e-03 | 5.743.e-04 | 0 | 1.816.e-03 |
| MOGWO | 0 | 9.298.e-03 | 1.725.e-03 | 0 | 3.650.e-03 |
| ZDT3 | |||||
| -GMOEO | 2.875.e-03 | 4.324.e-03 | 3.562.e-03 | 3.783.e-03 | 5.303.e-04 |
| cone-- GMOEO | 1.117.e-02 | 8.719.e-02 | 3.704.e-02 | 2.484.e-02 | 2.564.e-02 |
| MOPSO | 4.023.e-03 | 6.853.e-03 | 5.317.e-03 | 5.302.e-03 | 8.792.e-04 |
| MOGWO | 9.662.e-03 | 1.776.e-02 | 1.327.e-02 | 1.333.e-02 | 2.539.e-03 |
| ZDT4 | |||||
| -GMOEO | 1.778.e-03 | 4.053.e-03 | 3.429.e-03 | 3.468.e-03 | 6.892.e-04 |
| cone-- GMOEO | 7.574.e-03 | 2.509.e-02 | 1.558.e-02 | 1.653.e-02 | 5.0318.e-03 |
| MOPSO | 3.809.e-03 | 1.093.e-02 | 6.698.e-03 | 6.344.e-03 | 1.885.e-03 |
| MOGWO | 0 | 7.6716.e-03 | NaN | NaN | NaN |
| ZDT6 | |||||
| -GMOEO | 2.941.e-03 | 3.188.e-02 | 5.993.e-03 | 3.125.e-03 | 9.096.e-03 |
| cone-- GMOEO | 3.476.e-03 | 5.731.e-02 | 1.244.e-02 | 6.353.e-03 | 1.639.e-02 |
| MOPSO | 3.793.e-03 | 6.614.e-03 | 5.404.e-03 | 5.449.e-03 | 8.192.e-04 |
| MOGWO | 5.935.e-03 | 8.491.e-03 | 7.346.e-03 | 7.336.e-03 | 9.165.e-04 |
| Algorithm | Best | Worst | Average | Median | Std |
|---|---|---|---|---|---|
| ZDT1 | |||||
| -GMOEO | 1 | 1 | 1 | 1 | 9.617.e-08 |
| cone-- GMOEO | 9.321.e-01 | 9.807.e-01 | 9.670.e-01 | 9.697.e-01 | 1.366.e-02 |
| MOPSO | 9.832.e-01 | 9.978.e-01 | 9.890.e-01 | 9.876.e-01 | 5.273.e-03 |
| MOGWO | 9.969.e-01 | 1 | 9.996.e-01 | 1 | 9.677.e-04 |
| ZDT2 | |||||
| -GMOEO | 1 | 1 | 1 | 1 | 2.384.e-07 |
| cone-- GMOEO | 7.070.e-01 | 7.071.e-01 | NaN | NaN | NaN |
| MOPSO | 9.842.e-01 | 9.842.e-01 | NaN | NaN | NaN |
| MOGWO | 1 | 1 | NaN | NaN | NaN |
| ZDT3 | |||||
| -GMOEO | 1 | 1 | 1 | 1 | 7.105.e-07 |
| cone-- GMOEO | 7.428.e-01 | 9.942.e-01 | 9.622.e-01 | 9.86.e-01 | 7.732.e-02 |
| MOPSO | 8.855.e-01 | 1 | 9.538.e-01 | 9.981.e-01 | 5.851.e-02 |
| MOGWO | 1 | 1 | 1 | 1 | 3.285.e-06 |
| ZDT4 | |||||
| -GMOEO | 7.071.e-01 | 1 | 9.428.e-01 | 1 | 1.206.e-01 |
| cone-- GMOEO | 7.23.e-01 | 8.625.e-01 | 7.812.e-01 | 7.728.e-01 | 5.347.e-02 |
| MOPSO | 7.297.e-01 | 8.791.e-01 | 8.112.e-01 | 8.158.e-01 | 5.253.e-02 |
| MOGWO | 1 | 1 | NaN | NaN | NaN |
| ZDT6 | |||||
| -GMOEO | 6.609.e-01 | 8.71.e-01 | 8.499.e-01 | 8.71.e-01 | 6.643.e-02 |
| cone-- GMOEO | 4.995.e-01 | 7.228.e-01 | 5.790.e-01 | 5.551.e-01 | 7.941.e-02 |
| MOPSO | 5.203.e-01 | 8.709.e-01 | 8.356.e-01 | 8.708.e-01 | 1.108.e-01 |
| MOGWO | 8.685.e-01 | 8.709.e-01 | 8.702.e-01 | 8.709.e-01 | 1.015.e-03 |
| Algorithm | Best | Worst | Average | Median | Std |
|---|---|---|---|---|---|
| DTLZ1 | |||||
| -GMOEO | 1.273.e-01 | 1.41.e-01 | 1.295.e-01 | 1.282.e-01 | 4.338.e-03 |
| cone-- GMOEO | 2.575.e-01 | 5.078.e-01 | 3.999.e-01 | 4.173.e-01 | 8.470.e-02 |
| MOPSO | 1.711.e-02 | 7.506.e-02 | 4.281.e-02 | 3.886.e-02 | 2.176.e-02 |
| MOGWO | 1.095.e-01 | 2.167.e-01 | 1.512.e-01 | 1.359.e-01 | 3.637.e-02 |
| DTLZ2 | |||||
| -GMOEO | 1.164.e-03 | 1.535.e-03 | 1.313.e-03 | 1.295.e-03 | 1.045.e-04 |
| cone-- GMOEO | 2.192.e-003 | 3.459.e-03 | 2.627.e-03 | 2.451.e-03 | 4.072.e-04 |
| MOPSO | 3.908.e-03 | 4.957.e-03 | 4.280.e-03 | 4.243.e-03 | 3.680.e-04 |
| MOGWO | 1.838.e-03 | 1.964.e-03 | 1.884.e-03 | 1.879.e-03 | 4.275.e-05 |
| DTLZ3 | |||||
| -GMOEO | 1.884 | 2.167 | 2.058 | 2.161 | 1.366.e-01 |
| cone-- GMOEO | 2.611 | 3.7 | 3.129 | 3.102 | 3.188.e-01 |
| MOPSO | 3.036.e-01 | 1.323 | 7.705.e-01 | 7.449.e-01 | 3.355.e-01 |
| MOGWO | 1.680 | 3.184 | 2.403 | 2.427 | 4.183.e-01 |
| DTLZ4 | |||||
| -GMOEO | 9.969.e-04 | 1.249.e-03 | 1.065.e-03 | 1.038.e-03 | 7.641.E.-5 |
| cone-- GMOEO | 6.365.e-03 | 1.275.e-02 | 8.881.e-03 | 8.155.e-03 | 2.018.e-03 |
| MOPSO | 1.384.e-03 | 1.388.e-02 | 1.085.e-02 | 1.388.e-02 | 4.972.e-03 |
| MOGWO | 2.534.e-03 | 9.658.e-03 | 4.148.e-03 | 2.922.e-03 | 2.747.e-03 |
| DTLZ5 | |||||
| -GMOEO | 7.543.e-05 | 7.973.e-05 | 7.757.e-05 | 7.694.e-05 | 1.651.e-06 |
| cone-- GMOEO | 2.333.e-03 | 3.163.e-03 | 2.679.e-03 | 2.662.e-03 | 2.522.e-04 |
| MOPSO | 1.318.e-04 | 8.166.e-04 | 3.342.e-04 | 2.498.e-04 | 2.222.e-04 |
| MOGWO | 4.979.e-04 | 7.256.e-04 | 6.089.e-04 | 6.028.e-04 | 7.248.e-05 |
| DTLZ6 | |||||
| -GMOEO | 7.456.e-05 | 7.876.e-05 | 7.654.e-05 | 7.651.e-05 | 1.250.e-06 |
| cone-- GMOEO | 8.665.e-05 | 9.938.e-04 | 6.114.e-04 | 6.515.e-04 | 3.044.e-04 |
| MOPSO | 1.338.e-02 | 7.989.e-02 | 5.544.e-02 | 5.785.e-02 | 1.957.e-02 |
| MOGWO | 1.303.e-04 | 1.861.e-04 | 1.601.e-04 | 1.588.e-04 | 1.798.e-05 |
| DTLZ7 | |||||
| -GMOEO | 1.37.e-03 | 1.968.e-03 | 1.554.e-03 | 1.510.e-03 | 1.928.e-04 |
| cone-- GMOEO | 7.949.e-03 | 1.812.e-02 | 1.498.e-02 | 1.624.e-02 | 4.033.e-03 |
| MOPSO | 1.086.e-02 | 1.148.e-02 | 1.117.e-02 | 1.109.e-02 | 2.115.e-04 |
| MOGWO | 8.084.e-04 | 1.812.e-02 | 9.516.e-03 | 7.817.e-03 | 6.555.e-03 |
| Algorithm | Best | Worst | Average | Median | Std |
|---|---|---|---|---|---|
| DTLZ1 | |||||
| -GMOEO | 2.1e-02 | 3.904.e-02 | 2.943.e-02 | 2.814.e-02 | 4.925.e-03 |
| cone-- GMOEO | 3.517.e-02 | 5.169.e-02 | 4.496.e-02 | 4.485.e-02 | 5.094.e-03 |
| MOPSO | 3.191.e-02 | 5.082.e-01 | 1.106.e-01 | 5.092.e-02 | 1.486.e-01 |
| MOGWO | 4.803.e-02 | 9.696.e-02 | 7.15.e-02 | 6.814.e-02 | 1.908.e-02 |
| DTLZ2 | |||||
| -GMOEO | 3.345.e-02 | 4.124.e-02 | 3.697.e-02 | 3.683.e-02 | 2.927.e-03 |
| cone-- GMOEO | 3.190.e-02 | 4.45.e-02 | 3.934.e-02 | 4.067.e-02 | 4.206.e-03 |
| MOPSO | 2.320.e-02 | 3.605.e-02 | 2.968.e-02 | 2.979.e-02 | 3.421.e-03 |
| MOGWO | 3.263.e-02 | 4.967.e-02 | 3.879.e-02 | 3.698.e-02 | 5.177.e-03 |
| DTLZ3 | |||||
| -GMOEO | 3.277.e-02 | 6.229.e-02 | 4.451.e-02 | 4.211.e-02 | 9.273.e-03 |
| cone-- GMOEO | 3.615.e-02 | 1.058.e-01 | 7.914.e-02 | 8.618.e-02 | 2.154.e-02 |
| MOPSO | 3.843.e-02 | 2.195.e-01 | 7.152.e-02 | 5.334.e-02 | 5.492.e-02 |
| MOGWO | 4.094.e-02 | 1.153.e-01 | 6.445.e-02 | 6.222.e-02 | 2.359.e-02 |
| DTLZ4 | |||||
| -GMOEO | 3.018.e-02 | 4.376.e-02 | 3.828.e-02 | 3.911.e-02 | 4.558.e-03 |
| cone-- GMOEO | 2.456.e-02 | 2.776.e-01 | 1.295.e-01 | 1.083.e-01 | 8.270.e-02 |
| MOPSO | 0 | 5.164.e-01 | 1.089.e-01 | 9.529.e-03 | 2.018.e-01 |
| MOGWO | 4.672.e-02 | 1.879.e-01 | 7.417.e-02 | 5.154.e-02 | 5.087.e-02 |
| DTLZ5 | |||||
| -GMOEO | 4.929.e-03 | 6.434.e-03 | 5.559.e-03 | 5.556.e-03 | 5.e-04 |
| cone-- GMOEO | 1.421.e-02 | 4.624.e-02 | 2.753.e-02 | 2.626.e-02 | 1.021.e-02 |
| MOPSO | 8.8222.e-03 | 1.826.e-02 | 1.232.e-02 | 1.161.e-02 | 3.170.e-03 |
| MOGWO | 1.431.e-02 | 2.18.e-02 | 1.726.e-02 | 1.627.e-02 | 3.060.e-03 |
| DTLZ6 | |||||
| -GMOEO | 4.55.e-03 | 5.833.e-03 | 5.19.e-03 | 5.249.e-03 | 3.658.e-04 |
| cone-- GMOEO | 6.183.e-03 | 5.302.e-02 | 3.313.e-02 | 3.773.e-02 | 1.965.e-02 |
| MOPSO | 2.3831.e-02 | 5.012.e-02 | 3.387.e-02 | 3.204.e-02 | 8.467.e-03 |
| MOGWO | 8.136.e-03 | 1.317.e-02 | 1.12.e-02 | 1.120.e-02 | 1.579.e-03 |
| DTLZ7 | |||||
| -GMOEO | 1.285.e-02 | 2.761.e-02 | 1.789.e-02 | 1.789.e-02 | 4.169.e-03 |
| cone-- GMOEO | 0 | 3.188.e-01 | NaN | NaN | NaN |
| MOPSO | 2.666.e-02 | 4.111.e-02 | 3.225.e-02 | 3.065.e-02 | 4.536.e-03 |
| MOGWO | 0 | 2.814.e-02 | 5.187.e-03 | 0 | 1.098.e-02 |
| Algorithm | Best | Worst | Average | Median | Std |
|---|---|---|---|---|---|
| DTLZ1 | |||||
| -GMOEO | 3.796.e-02 | 6.549.e-02 | 6.08.e-02 | 6.251.e-02 | 8.11.e-03 |
| cone-- GMOEO | 1.089.e-02 | 1.629.e-02 | 1.387.e-02 | 1.412.e-02 | 1.849.e-03 |
| MOPSO | 3.376.e-02 | 6.336.e-01 | 2.424.e-01 | 1.123.e-01 | 2.578.e-01 |
| MOGWO | 2.511.e-02 | 3.718.e-02 | 3.220.e-02 | 3.271.e-02 | 3.357.e-03 |
| DTLZ2 | |||||
| -GMOEO | 9.997.e-01 | 9.999.e-01 | 9.998.e-01 | 9.998.e-01 | 7.512.e-05 |
| cone-- GMOEO | 5.461.e-01 | 7.966.e-01 | 6.866.e-01 | 6.948.e-01 | 8.273.e-02 |
| MOPSO | 6.487.e-01 | 7.579.e-01 | 7.175.e-01 | 7.349.e-01 | 3.992.e-02 |
| MOGWO | 7.725.e-01 | 9.143.e-01 | 8.572.e-01 | 8.614.e-01 | 4.087.e-02 |
| DTLZ3 | |||||
| -GMOEO | 5.889.e-03 | 6.453.e-03 | 6.339.e-03 | 6.430.e-03 | 1.790.e-04 |
| cone-- GMOEO | 2.333.e-03 | 3.919.e-03 | 2.984.e-03 | 2.878.e-03 | 4.766.e-04 |
| MOPSO | 1.734.e-03 | 4.815.e-02 | 9.163.E.-3 | 3.639.e-03 | 1.452.e-02 |
| MOGWO | 4.371.e-03 | 5.321.e-03 | 4.777.e-03 | 4.673.e-03 | 3.066.e-04 |
| DTLZ4 | |||||
| -GMOEO | 9.997.e-01 | 9.999.e-01 | 9.998.e-01 | 9.999.e-01 | 7.13.e.-5 |
| cone-- GMOEO | 7.082.e-01 | 8.945.e-01 | 8.079.e-01 | 7.974.e-01 | 5.326.e-02 |
| MOPSO | 7.071.e-01 | 9.335.e-01 | NaN | NaN | NaN |
| MOGWO | 8.753.e-01 | 9.806.e-01 | 9.123.e-01 | 9.042.e-01 | 3.550. e-02 |
| DTLZ5 | |||||
| -GMOEO | 1 | 1 | 1 | 1 | 0 |
| cone-- GMOEO | 9.216.e-01 | 1 | 9.88.e-01 | 1 | 2.568.e-02 |
| MOPSO | 7.570.e-01 | 1 | 9.66.e-01 | 1 | 7.636.e-02 |
| MOGWO | 1 | 1 | 1 | 1 | 0 |
| DTLZ6 | |||||
| -GMOEO | 1 | 1 | 1 | 1 | 0 |
| cone-- GMOEO | 1 | 1 | 1 | 1 | 0 |
| MOPSO | 6.528.e-02 | 7.962.e-01 | 1.974.e-01 | 1.282.e-01 | 2.164.e-01 |
| MOGWO | 1 | 1 | 1 | 1 | 0 |
| DTLZ7 | |||||
| -GMOEO | 1 | 1 | 1 | 1 | 0 |
| cone-- GMOEO | 9.998.e-01 | 1 | NaN | NaN | NaN |
| MOPSO | 1 | 1 | 1 | 1 | 0 |
| MOGWO | 1 | 1 | NaN | NaN | NaN |
| cone--GMOEO | MOPSO | MOGWO | |
|---|---|---|---|
| ZDT1 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| ZDT2 | 1.7167.e-4 | 8.74498.e-5 | 1.1067.e-4 |
| ZDT3 | 2.8272.e-3 | 1.8267.e-4 | 1.8267.e-4 |
| ZDT4 | 1.8267.e-4 | 1.8267.e-4 | 2.4375.e-4 |
| ZDT6 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| DTLZ1 | 1.8267.e-4 | 1.8267.e-4 | 0.2413 |
| DTLZ2 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| DTLZ3 | 1.8267.e-4 | 1.8267.e-4 | 1.1329.e-2 |
| DTLZ4 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| DTLZ5 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| DTLZ6 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| DTLZ7 | 1.8165.e-4 | 1.8267.e-4 | 2.5525.e-2 |
| cone--GMOEO | MOPSO | MOGWO | |
|---|---|---|---|
| ZDT1 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| ZDT2 | 3.0303.e-2 | 1.7451.e-3 | 2.1226.e-2 |
| ZDT3 | 1.8267.e-4 | 2.4612.e-4 | 1.8267.e-4 |
| ZDT4 | 1.8267.e-4 | 5.8283.e-4 | 4.3420.e-3 |
| ZDT6 | 2.2022.e-3 | 2.8272.e-3 | 2.8272.e-3 |
| DTLZ1 | 2.4612.e-4 | 7.6853.e-4 | 1.8267.e-4 |
| DTLZ2 | 0.1619 | 7.6853.e-4 | 0.5205 |
| DTLZ3 | 2.8272.e-3 | 0.1404 | 3.7635.e-2 |
| DTLZ4 | 4.5863.e-3 | 0.4693 | 1.8267.e-4 |
| DTLZ5 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| DTLZ6 | 1.8267.e-4 | 1.8267.e-4 | 1.8267.e-4 |
| DTLZ7 | 0.2997 | 3.2983.e-4 | 1.7217.e-2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalabi, N.E.; Attia, A.; Bouziane, A.; Hassaballah, M.; Alanazi, A.; Binbusayyis, A. An Archive-Guided Equilibrium Optimizer Based on Epsilon Dominance for Multi-Objective Optimization Problems. Mathematics 2023, 11, 2680. https://doi.org/10.3390/math11122680
Chalabi NE, Attia A, Bouziane A, Hassaballah M, Alanazi A, Binbusayyis A. An Archive-Guided Equilibrium Optimizer Based on Epsilon Dominance for Multi-Objective Optimization Problems. Mathematics. 2023; 11(12):2680. https://doi.org/10.3390/math11122680
Chicago/Turabian StyleChalabi, Nour Elhouda, Abdelouahab Attia, Abderraouf Bouziane, Mahmoud Hassaballah, Abed Alanazi, and Adel Binbusayyis. 2023. "An Archive-Guided Equilibrium Optimizer Based on Epsilon Dominance for Multi-Objective Optimization Problems" Mathematics 11, no. 12: 2680. https://doi.org/10.3390/math11122680
APA StyleChalabi, N. E., Attia, A., Bouziane, A., Hassaballah, M., Alanazi, A., & Binbusayyis, A. (2023). An Archive-Guided Equilibrium Optimizer Based on Epsilon Dominance for Multi-Objective Optimization Problems. Mathematics, 11(12), 2680. https://doi.org/10.3390/math11122680








