Abstract
In the practical Continuous Variable Quantum Key Distribution (CVQKD) system, there is a large gap between the ideal theoretical model and the actual physical system. There are still some inevitable flaws, which give quantum hackers the opportunity to manipulate the channel in complex communication environments and launch Denial of Service attacks on the quantum channel. Therefore, a DoS attack-aware defense scheme for the CVQKD system based on convolutional neural networks (CNN) is proposed. The simulation results show that the proposed model can effectively detect DoS attacks launched by quantum hackers in CVQKD system in a complex communication environment, and the model has strong robustness due to the addition of the attention mechanism module. In addition, multiple sets of comparative experiments show that compared with the existing artificial neural network model, the CNN-based model has higher accuracy and stability.
Keywords:
continuous variable quantum key distribution; denial-of-service attacks; deep learning model; attention mechanism MSC:
81P94; 81P45
1. Introduction
In recent years, it has been observed that quantum key distribution (QKD) exhibits excellent information-theoretical security, and is employed for the secure transmission of cryptographic keys between authorized sender (Alice) and receiver (Bob). QKD is not derived from mathematical principles but is based on fundamental laws of quantum physics [1]. The theoretical unconditional security of QKD is guaranteed by the Heisenberg uncertainty principle [2] and the no-cloning principle of quantum states [3], which also ensures the detectability of Eve. Currently, discrete-variable (DV)QKD [4] and continuous-variable (CV)QKD [5,6,7] are the two main models of QKD systems. Compared to the DVQKD system, the CVQKD system has many advantages, such as its ease of implementation, compatibility with existing optical communication systems, and better application prospects.
The Gaussian Modulated Coherent State (GMCS) protocol is currently one of the most mature Continuous Variable Quantum Key Distribution (CVQKD) protocols. The system based on the GMCS protocol has the characteristics of classical light field, convenient preparation, and long-distance secure transmission, which can better meet the application requirements [8,9]. In addition, theoretically, continuous variable quantum key distribution has been proven to be secure against arbitrary collective attacks [10,11,12]. However, due to the difference between the idealized theoretical model and the actual physical system, Eve exploits the existing practical security loopholes to launch attacks on the CVQKD system or protocol, such as wavelength attack [13], calibration attack [14], local oscillator intensity (ILO) attack [15], and saturation attack [16]. Fortunately, a large number of researchers have proposed corresponding defense measures against possible attack strategies [17,18,19,20]. Moreover, in recent years, researchers have found that machine learning technology has significant advantages as a detection method in practical CVQKD systems. D. Huang and S. Liu summarized the work of using machine learning as an attack and defense detection method in CVQKD systems in recent years [21]. It is also mentioned that researchers now use machine learning to reduce the complexity of CVQKD systems to a certain extent while improving performance and ensuring system security. Furthermore, it is believed that neural network-based solutions require very few additional devices and can be easily implemented in practical CVQKD systems.
In fiber-based CVQKD systems, the transmittance is usually considered a constant and plays an important role in the subsequent parameter estimation process. In practical communication, the channel transmittance is highly likely to be controlled by Eve. By slightly changing the channel transmittance, Eve can cause significant parameter estimation errors in the subsequent process. As a result, the secure key rate is underestimated, then the estimated secure transmission distance could be reduced significantly, and the secure channel is insecure. Ultimately, communication interruption will be caused. This attack is similar in performance to denial-of-service attacks in classical channel communication. Y.Li et al. proposed a denial-of-service (DoS) attack strategy targeting the parameter estimation method in the communication process [22]. Dai et al. proposed a detection method based on the spectral estimation method, which effectively detected the low-rate denial-of-service (LDoS) attacks in CVQKD systems [23]. However, in practical implementations, the transmission of legitimate optical signals and the presence of real detectors and electronic components introduce inherent fluctuations, which pose challenges for accurate estimation. To address these challenges, Alice and Bob have to engage in multiple iterative computations to achieve precise estimation. Moreover, the estimation process usually occurs after the completion of the key transmission. In the unfortunate event of detecting an attack, the entire key data must be discarded, leading to substantial time and resource wastage. Hence, an efficient quantum denial-of-service (DoS) attack defense solution is needed to effectively resist such attacks.
This paper proposes an efficient detection scheme based on deep learning to detect DoS attacks targeting the parameter estimation method in CVQKD. The typical characteristics of two kinds of DoS attacks are studied, and the changes in these characteristics under attack are analyzed by referring to the normal state of not being attacked. A set of feature vectors labeled by different DoS attack types are constructed to train the neural network, and the data are preprocessed and input into the proposed neural network model. The trained neural network model can automatically detect abnormal feature vectors and classify them. Thus, a DoS attack detection model has been established, capable of recognizing DoS attacks launched by Eve, solely by employing a single forward propagation computation process. Bob can input the received keys into the model sequentially, and in the event of detecting any anomalous data, the transmission process will be immediately terminated. Consequently, Bob is alleviated from the need to wait for the completion of the key transmission process before assessing the system’s vulnerability to attacks, which will greatly improve the efficiency of the system. Using the proposed detection model, the corresponding experiments and simulations are carried out on the CVQKD system based on Gaussian modulation.
2. Principle
2.1. GMCS CVQKD System Description
In the ideal condition of GMCS-CVQKD modulation protocol, the sender Alice sends the eigenstate of the complementary observation quantities and following zero-center Gaussian distribution with a variance of to the receiver node Bob, and Bob adaptively performs one of the regular measurements with the null difference detection system. After several rounds of exchange, Alice and Bob will share a series of relative Gaussian variables and gain the key with further post-processing approaches which include parameter estimation, reserve correction, and amplification. In the parameter estimation of CVQKD systems, the traditional statistical method is commonly used to estimate the channel parameters. In a theoretical CVQKD system, Alice and Bob can share a set of interrelated data and , where x represents the canonical component modulated by Alice ( or ),y represents the canonical component value measured by Bob ( or ), and n represents the total amount of shared data. In the parameter estimation method, T and are used to indicate channel transmittance and channel excess noise, respectively. Therefore, the data transmission of Alice and Bob is usually assumed to be a normal linear transmission model, which can be expressed as
where and z follows zero-centered Gaussian distribution with variance .
However, in the CVQKD systems working situations, extra noise will be introduced into the system via complicated channel conditions and additional instruments [24]. To evaluate the security performance of the communication channel, a detailed channel and equipment parameters should be introduced to acquire calculations and evaluations with more precision. In general situations, characteristics such as the shot noise , the technical excess noise , the electrical noise , and the efficiency of zero-difference detector should be extra considered. Moreover, in the evaluation of the system’s theoretical security key rate, all these parameters related to key extraction are calculated in the unit of . For example, the detector’s electronic noise is expressed as and the technical excess noise of the system is expressed as . Therefore, the aforementioned Formula (1) can be rewritten into a normal linear transmission model under complex channels in actual communication
where, , and follows a Gaussian distribution with a mean of 0 and a variance of .
In the subsequent parameter estimation, Alice and Bob randomly extract m sets of data from the total amount of shared data n to evaluate the parameters T and of the quantum communication channel. According to Formula (2), the maximum likelihood estimation method can be used to calculate
where and are two separated estimators who obey normal distribution and chi-square distribution, respectively.
where and are and , respectively.
Therefore, we can use Formula (3) to fully estimate the transmittance T of the channel and the channel excess noise without considering the finite-size effect [25]. Meanwhile, when the total amount of data extracted is large enough, the chi-square distribution in Formula (4) can converge to an expressible normal distribution and the corresponding central interval can be calculated, which has been proved.
The confidence intervals for and can be expressed as follows
where and is a coefficient which obeys . Additionally, represents the confidence level. Moreover, erf(·) denotes the error function:
Since considering the finite-size effect [25] will only misguide the analysis process without changing the final result, the finite-size effect can be ignored. Next, the impact of Eve’s perturbation of quantum channel parameters on subsequent channel parameter estimates will be discussed.
2.2. Estimation of Quantum Channel Parameters in Complex Communication
In the communication process, the modulated data of Alice terminal are , and the measured data of Bob terminal are . Both and are Gaussian variables. Next, and are used to evaluate the parameters of the quantum channel, and then to investigate the estimation deviation of the channel transmittance T and channel excess noise under the attack. Their expression in the case of complex communication can be assumed as:
In the Formula (7), represents the amplitude of the coherent state for AM modulation, while represents the phase of the coherent state for PM modulation. In the Formula (8), T represents the channel transmittance and represents the efficiency of the homodyne detector. Notably, represents the phase drift of these quantum states during transmission, and it should be noted that these parameters are completely independent of each other. Additionally, represents the increase in noise due to channel excess noise , while represents the increase in noise due to scattered noise and detector electronic noise . Moreover, as the existing phase compensation technology can effectively suppress phase noise, it is reasonable to set the parameter A to 0 in the above formula. It is also important to consider that noise causes the mean of the amplitude to be 0. Additionally, the mean value is also equal to the modulation variance . Therefore, based on Formulas (7) and (8), the new formula can be easily obtained as:
Next, by utilizing X and Y and neglecting the finite-size effect of the parameter estimation block size m, the formulas below can be estimated by combining , , and Formula (3):
At the same time, the quantum channel transmittance T and channel over-noise can be obtained by transforming the aforementioned estimators and the parameters in the normal linear transmission model in the case of complex channels in actual communication.
Combining Formulas (7)–(12), the estimated value of quantum channel parameters in the complex communication environment can be obtained as:
Through the analysis of the Formula (13), it is clear that if the channel transmittance remains unchanged, the parameters of the channel excess noise can be estimated accurately. However, if Eve attacks the quantum communication channel and changes the transmittance of the channel, it will lead to inaccurate excess noise estimation of the channel which could cause a large deviation in the estimation of the channel security key rate. Then, the parameter change of the channel under Eve attack is analyzed, and the attack detection module will be proposed.
3. DoS Attack Launched by Eve in Complex Channel Environment
The purpose of this chapter is to study the security impact caused by Eve’s denial of service attacks on CVQKD system. Then provide a detection method in Bob to detect DoS attacks on the system. Finally, adjust the parameter estimation in the subsequent stages according to the detected attack types. Additionally, this chapter is only focusing on the detection scheme that can detect DoS attacks launched by Eve, not the subsequent parameter estimation adjustment scheme.
In the absence of an attack, the CVQKD system operates in a familiar pattern. Alice was a string of coherent state , coherent state of regular and variance component values for bivariate Gaussian distribution, and the key information encoded in the above. Alice sends it to the receiver node Bob, where is scatter shot noise, represents the modulation variance , and the intersection uncertainty variance . The quantum channel has the full characteristics of quantum channel transmission T, modulation variance Va, detector electronic noise , and technical excess noise introduced by the actual channel. All of these key extraction-related parameters are in units of granular noise . When the transmission is completed, the mean value and variance of the output of the two-mode state measured by Bob can be expressed as
where is the efficiency of the heterodyne detection or homodyne detector, .
From the above section, once the channel is attacked by Eve, the channel transmittance T will be changed, which will result in the deviation of the system channel parameter estimation. Finally, this lead to the deviation of the channel security key rate estimation, and the communication parties are forced to close the channel. Importantly, Eve can actively control the channel to interfere with the communication environment [26], but it is difficult to know the specific law of transmittance change of the quantum communication channel. According to [22], Eve can easily manipulate the channel so that the channel transmittance follows a two-point distribution or a uniform distribution. Therefore, under the assumption that the quantum channel is attacked by Eve, the channel transmittance T obeys a certain distribution. In the following sections, this paper will discuss the changes in quantum channel parameters when the transmittance T of the quantum channel follows the distribution of two points, respectively, in a complex communication environment, and then the case of uniform distribution will be derived.
3.1. Two-Point Distribution of Channel Transmittance T
In this section, it is assumed that the transmittance of the channel follows a two-point distribution. Under this condition, transmittance can be varied between 0 and , which is the channel transmittance in the case of complex quantum channels. Because Eva can manipulates this channel easily. Hence, the serious biases on channel estimation could be difficult to correct.
The assumptions previously stated can be precisely articulated using the mathematical expression , where denotes a binomial distribution with a single trial and success probability p. Subsequently, it can be deduced that and are equivalent to and , respectively. In particular, it is assumed in this context that the evaluation of the quantum channel parameter is ideal and regarded as its true value, based on which the following formula can be calculated using Formula (13).
where the parameter P represents the probability of channel transmission rate T being equal to , where P equals 1 in the absence of Eve attacks on the quantum communication channel. The parameter represents the actual excess noise in the channel. The “” represents the situation that the transmittance T of the quantum channel in a complex communication environment obeys the distribution of two points.
3.2. Uniform Distribution of Channel Transmittance T
In this scenario, the channel transmittance T is a uniformly distributed random variable between and , where is a constant such that . That is, T follows a uniform distribution with probability density function for . Hence, the expected values of T and are given by
Furthermore, by combining Formula (13), the following result can be obtained:
where the “” represents the situation that the transmittance T of the quantum channel in a complex communication environment obeys a uniform distribution. Using it in Formula (14), the Formula (17) can be derived:
Here, the technical noise is represented as .
3.3. CVQKD System Scheme in Complex Channel with Attack Detection Module
Figure 1 illustrates a remote CVQKD system, which incorporated a monitoring device in the experiment. Coherent light at 1550 nm was generated by Alice through an external telecommunication diode at a repetition rate of 1 MHz, with the pulse train split into a weak signal path and a strong local oscillator (LO) path by an unbalanced coupler. Before passing through a set of variable attenuators, the signal pulse underwent amplitude and phase modulation to enable control of the variance within a specified range. The signal and LO pulses were then delayed through the use of delay lines and Faraday mirrors, and polarization multiplexing was achieved by employing a polarization beam splitter (PBS) along two related optical paths. Both polarization and time-multiplexed paths were transmitted from Alice to Bob through a standard single-mode fiber quantum channel, whereupon the signal was received passively and uninterrupted by Bob. Eve may exist in the quantum channel during transmission.
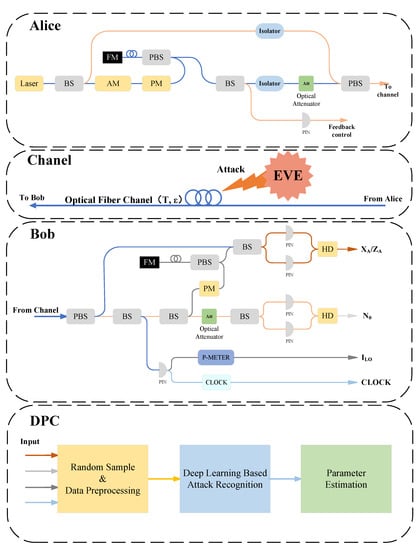
Figure 1.
Schematic diagram and experimental setup for acquiring training data. Laser: laser produce model; BS: beam splitter; AM: amplitude modulator; PM: phase modulator; PBS: polarizing beam splitter; Optical attenuator: makes the signal conform to the quantum signal level; HD: homodyne detection; FM: Faraday mirror; PIN: PIN photodiode. The data [/, , , ] collected by the QKD system will be transmitted to the DPC. DPC: data processing center used to sample analog signal, attack detection, and parameter estimation.
When receiving a signal, Bob passively mitigates interference between the signal and the LO by using an active polarization controller. Subsequently, the signal and LO pulse timing were superimposed through another delay line, and measurements were generated by using a scattered-noise limited zero-difference detector. Random real-time quadrature selection was made by Bob via the control of the measured phase using a phase modulator in the LO path. Additionally, a small proportion of the pulse within the LO optical path was extracted for real-time measurement of particle noise and LO power. This monitoring method was employed to avoid any interference with the actual key rate and standard communication of the system. Additionally, the utilization of three isolation modulators within the system served to prevent potential Trojan attacks [27,28]. Post-processing entailed the transmission of relevant parameters to the processing module (DPC) for security analysis.
It is noteworthy that the original processing module was augmented by additional data preprocessing programs and attack detection programs during the post-processing phase. Subsequent to detector analysis, the results were imported into further processes through a small interface program. In our past high repetition-rate CVQKD system experiment, real-time data collection and computation were facilitated by a computer equipped with 64 GB of memory, an Intel Core 5.0 GHz CPU, and a GeForce RTX 3090 GPU. This experimental process was considered to be optimally suited for systems operating within the 1–100 Mbps range.
4. Signal Detection Model
There are limited attack perception methods currently available for detecting DoS attacks on CVQKD systems, and the performance of the proposed traditional detection methods is not ideal. In this section, a neural network detection model with a neural network structure is introduced as a defense detection program for the CVQKD system. The network model is used to detect the scenario where Eve controls the channel and launches a DoS attack. This network enables existing CVQKD quantum communication systems to achieve a higher level of security without changing the original protocol. Different from traditional detection methods, this deep learning classifier considers classification and detection based on multiple coupling parameter details, rather than applying fixed thresholds to individual measurement parameters. It can extract potential abnormal data features from the actual system data without any prior assumptions.
4.1. Deep Learning Method
Deep learning has emerged as one of the most rapidly advancing and widely adopted subfields of machine learning [29], offering unprecedented computational capabilities for processing large volumes of data. Deep learning has become increasingly popular due to its ability to learn from large, complex datasets, and achieve state-of-the-art performance on a wide range of tasks, including image classification, object detection, and natural language processing. One of the key advantages of deep learning over traditional machine learning approaches is its ability to learn hierarchical representations of data through the use of multiple layers of artificial neural networks. Convolutional Neural Networks (CNNs) are a prominent neural network model that has found wide-ranging applications in tasks such as image processing [30,31,32], pattern recognition [33,34], natural language processing [35,36,37], and quantum communication [38].
CNN typically consists of several layers, including an input layer, one or more convolutional layers, a pooling layer, and one or more fully connected layers. [d=W.Y.]BeforePrior to being convolved in the convolutional layer, input data are typically normalized through the input layer, which can help to improve the convergence speed and overall performance of the CNN during training.
In the convolutional layer, a kernel is convolved with the output from the previous layer, followed by the activation function that applies a non-linear transformation to the resulting feature map. The output of each convolutional layer is the convolution of multiple input feature maps, which can be mathematically described as a dot product between the input and a set of learnable filters, which is mathematically described as [39]:
In the Formula (20), represents the pixel value of the input data, represents the weight of the convolution kernel, b represents the bias term, K and L represent the size of the convolution kernel, represents an element of the output feature vector, and represents the non-linear activation function.
After convolution, the activation function performs a non-linear operation on the output data of each convolution kernel. Non-linear activation functions can improve the non-linearity of neural network models and enhance the robustness of neural networks, thereby establishing complex non-linear mapping relationships between input and output data. is a classical activation function. When the input data are greater than 0, the derivative of the activation function remains 1, which is beneficial for overcoming the gradient dispersion problem during the backpropagation process. It can be expressed as
where is the output of convolution kernel; is the non-linear activation value of .
The activation function has been widely used in many deep learning models due to its simplicity and effectiveness in preventing the vanishing gradient problem.
The pooling operation is another key operation in CNN, which can reduce the dimensionality of the output feature vectors, lower the computational cost, and improve the robustness of the model. Max pooling, average pooling, and overlapping pooling are three common pooling operations. In average pooling, the average value of the feature vectors in each pooling window is taken as the output feature vector. This process can be described by the following equation
where is the output feature vector of the convolutional layer, K and L are the size of the pooling window, and is the output of the pooling layer.
The Attention Mechanism Module (AMM) is presented to enhance the robustness of CNN (AMM-CNN). The proposed approach utilizes a “Squeeze-and-Excitation” attention mechanism module to improve CNN performance by emphasizing relevant features and suppressing irrelevant ones [40]. Specifically, during the squeeze phase, AMM performs global pooling on the feature map of each channel to obtain a global statistic (e.g., mean or variance). In the excitation phase, AMM calculates a gating vector using the obtained global statistic to weight each channel’s feature map, thereby amplifying useful features and diminishing useless ones. The introduction of AMM results in CNN learning more representative and distinctive features, thereby improving the model’s accuracy and generalization ability. Additionally, AMM enhances CNN’s resistance to noise and perturbations, improving the model’s robustness.
The AMM comprises three primary operations, global pooling, squeezing, and exciting. The global pooling operation generates channel descriptors, as given by the following formula:
where represents the global descriptor of the c-th channel, and represents the feature value of the c-th channel at the i-th row and j-th column. Subsequently, the squeezing operation compresses the dimensionality of the channel descriptors to a lower dimension via a fully connected layer, as given by the following formula
where is an activation function, such as ReLU or Swish. Finally, the exciting operation transforms the squeezed descriptor into attention weights via another fully connected layer, as given by the following formula
where is the sigmoid function, and represents the attention weight of the c-th channel. The output feature map of the AMM is obtained by multiplying each channel’s feature value in the input feature map by its corresponding attention weight, as given by the following formula
where represents the output feature value of the c-th channel at the i-th row and j-th column.
The last layer of the convolutional neural network consists of a flattening layer, which transforms the output feature maps of the previous layer into a one-dimensional vector. This vector is then fed into a fully connected layer, which aggregates local information extracted by the convolutional and pooling layers to produce the final prediction. The output of the fully connected layer can be expressed as
where X is the input feature vector, W is the weight matrix, b is the bias term, Y is the predicted value, and is the activation function.
4.2. DoS Attack Detection Implementation Details
In the previous section, it is assumed that the transmittance T of the quantum channel under DoS attacks follows either a uniform distribution or a two-point distribution. This section will conduct simulation experiments in the CVQKD system shown in (Figure 1) to collect communication data without any attack, and we will launch attacks on the system and collect experimental data under DoS attacks.
In this experiment, the Python 3.8 and the Pytorch framework based on CUDA 11.3 were used for data preparation, model training, calculation, and verification of algorithm iterations. The program ran on a computer with 64 GB of memory, an Intel Core 5.0 GHz CPU, and a GeForce RTX 3090 GPU. Moreover, the trained model was tested under two possible DoS attacks in this experiment. Typically, in a safety CVQKD system, the system parameters are kept in dynamic stability. The experiment reasonably estimated the attack capability of the third party Eve, and added some possible noise. According to the standard realistic assumption for CVQKD [14], a long-distance CVQKD system was built with the following parameters. In experiment setup, = 0.7, = 0.01, = 0.1, = 0.4, = 10, , P = 0.9, U = 0.8, where the transmission distance L was 30 km, and the loss coefficient of the optical fiber was 0.2 dB/km. The local oscillator ILO at Bob’s side is set as photons per pulse with percent fluctuation. The data collected from Bob’s end consists of four dimensions. To train the classifier for detecting network attacks, three datasets were generated as training sets . The datasets represent normal data that have not been attacked. represents the datasets that have been attacked by Eve’s DoS attack, and the quantum channel transmittance rate T follows a two-point distribution. The datasets illustrate data that have been attacked by Eve’s DoS attack and the quantum channel transmittance rate T follows a uniform distribution. The one-hot encoding was performed on the collected data, and the label mapping relationship of each dataset was . were preprocessed by segmentation and feature vector extraction, and their categories were labeled. The length of each dataset in was , which is divided into groups, each containing data blocks. Therefore, the data vector of each data group can be transformed into a feature vector. Next, these feature vectors were substituted into the AMM-CNN for training to learn the features of different attack strategies. To speed up the optimal solution search of the gradient descent algorithm and eliminate the influence of different attributes with different scales, the data were min–max processed. In addition, three other datasets, which were , were also prepared as test sets and processed them in the same way. It should be noted that the data in the test set are completely independent of the data in the training set. Finally, these unlabeled feature vectors were imported into the trained AMM-CNN classifier to verify the performance of the attack classification. The activation function of the model was unified as the ReLU function, the loss function used the cross-entropy loss function, the batch-size was set to 128, and the learning rate was set to 0.01. The brief step can be sighted in Figure 2.
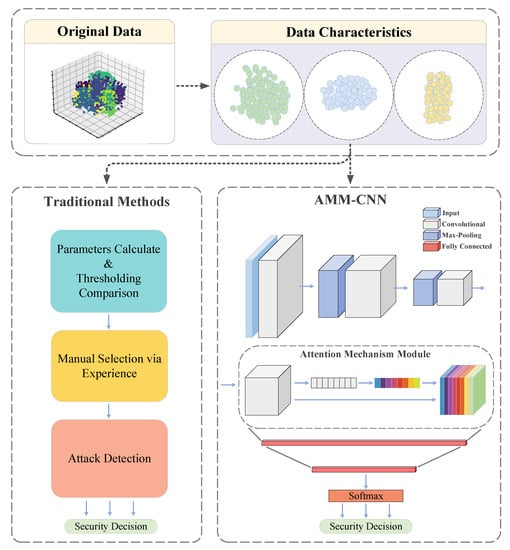
Figure 2.
Traditional attack detection (left) and deep learning attack detection based on AMM-CNN (right); The data collected by Bob will be transmitted to the detection model in real time. The original data shows the distribution of the parameters under the interference condition. Data characteristics represent the characteristics of three different types of data.
5. Performance
To evaluate the detection capability of Eve launched DoS attacks, we compared our proposed AMM-CNN and the Artificial Neural Network (ANN) model that was reproduced from the ANN paper [19]. The ANN model consists of three layers, the input layer, hidden layer, and softmax layer. Specifically, the parameter for the hidden layer is set to 15, which was chosen based on the recommendation in the ANN paper [19]. Furthermore, the training process and loss function of the ANN model are the same as those of the AMM-CNN model. The experiment results show that both the AMM-CNN and ANN models effectively detect DoS attacks in CVQKD systems. Considering the large amount of data processed and the complex feature mapping of the data, the AMM-CNN model has an advantage in detecting DoS attacks in a massive data feature perception. Therefore, it outperforms the ANN model in attack perception accuracy, with an accuracy rate of 98.7%. Although the ANN model has stronger interpretability, its accuracy rate of 91.6% is slightly inferior to the AMM-CNN model. The classification accuracy during the training process is shown in Figure 3a. In addition, the training loss curve of the AMM-CNN model in this experiment is shown in Figure 3b. Furthermore, the confusion matrix results of the AMM-CNN model are presented in Figure 4.
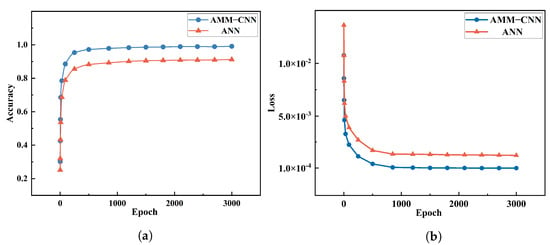
Figure 3.
(a) Accuracy function of two models with sufficient training data. (b) Loss function of two models with sufficient training data.
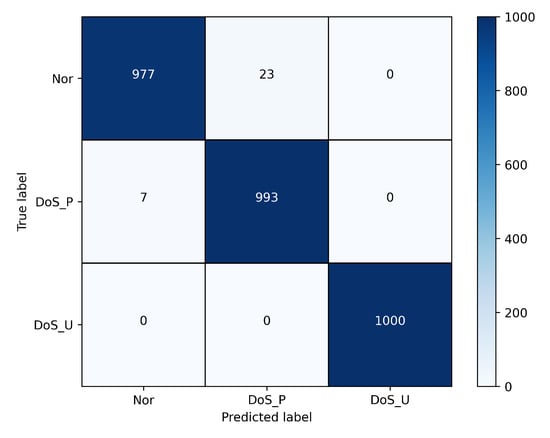
Figure 4.
The confusion matrix table for the AMM-CNN model. Nor: The “Nor” represents normal data that is not under DoS attack; DoS_P: The “DoS_P” represents the data whose quantum channel transmission rate T follows a two-point distribution after Eve’s DoS attack; DoS_U: The “DoS_U” represents the data whose quantum channel transmission rate T obeys uniform distribution after Eve DoS attack.
The performance difference between the two models can be attributed to several factors. Firstly, the ANN model requires a large number of parameters to process high-dimensional CVQKD data, which may cause overfitting. In contrast, the AMM-CNN model can reduce the dimension of the training dataset and reduce the number of parameters through convolution and pooling operations, making it more suitable for large-scale data processing. Secondly, the ANN model may not have considered the spatial information in the data, only treating it as a flattened vector input to the network. Meanwhile, the AMM-CNN model retains spatial structural information during the training process through convolution and pooling operations. Finally, compared with the ANN model, the AMM-CNN model requires less input data preprocessing. This is because the AMM-CNN model can extract features from the data through convolution, pooling operations, and the introduction of an attention mechanism module, while the ANN model requires more preprocessing to achieve better results.
To recap, the research results show that the AMM-CNN model has better detection performance for DoS attack data in the experiment’s CVQKD dataset, while the ANN model is slightly inferior but has better interpretability. The choice of model depends on specific application needs and available resources. Future research can explore more neural network models, combine the advantages of multiple models, and develop hybrid models to achieve better performance in detecting DoS attacks in CVQKD systems.
Moreover, the impact of different transmission distances on the evaluation metrics of the proposed attack detection model was investigated using the optimal parameters obtained from previous experiments. The same ANN model was used as a comparative experiment. As shown in Figure 5a, when the transmission distance L is 20 km to 55 km, it can be seen that the detection accuracy of the AMM-CNN model and the ANN model show a negative correlation with the transmission distance. That is, the model accuracy gradually decreased with an increase in the transmission distance. When L was less than 35 km, the proposed AMM-CNN model demonstrated a good detection performance for Eve’s DoS attacks, with the model accuracy hovering around 98.0%. However, when L equaled 40 km and greater, the model accuracy began to decrease slightly. This may be due to the influence of system noise and channel noise, which cause a deterioration in data quality as the transmission distance increases. As a result, the attack detection model gradually becomes less effective at extracting relevant features, thereby reducing its performance. Finally, when L equaled 55 km, the AMM-CNN accuracy was 71.3%, while the ANN accuracy was 61.7%. Overall, the results obtained from the AMM-CNN model were satisfactory.
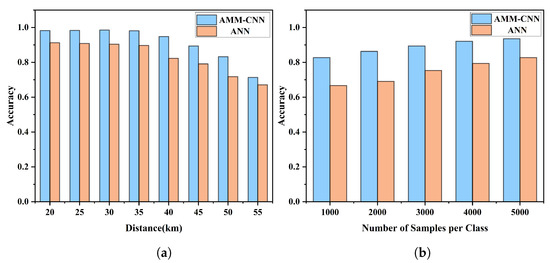
Figure 5.
(a) The detection accuracy corresponding to each distance. (b) The detection accuracy corresponding to each number of samples in the small sample case.
Additionally, experiments were conducted to test the performance of the attack detection model under small sample conditions, considering the limitation of the training data volume. The experiment gradually increased the size of the training dataset from 1000 to 5000, using the same dataset for testing. It can be easily observed from Figure 5b that the accuracy of the model gradually improved with the increase in sample size. Even under small dataset conditions, the proposed AMM-CNN model demonstrated excellent performance, whereas the performance of the ANN model was far inferior under small sample experiments. This also indicates that the AMM-CNN model has good feature extraction ability and robustness under small sample conditions. The introduction of the attention mechanism module in the AMM-CNN model enhances the model’s ability to focus on important features. By learning key information and context from the data, the attention mechanism guides the model to better distinguish between attacks and normal behavior, thereby improving accuracy. Furthermore, the weight allocation of attention allows the model to assign weights to features from different regions, reducing sensitivity to noise and attacks, thereby enhancing the robustness of the AMM-CNN model. This robustness enhancement enables the model to better handle variations and perturbations in the data, leading to improved system stability and reliability.
In summary, the AMM-CNN model can not only effectively learn the detailed distribution of DoS attack samples but also abstract potential time-dependent features and attribute-dependent features to detect potential threats robustly. In particular, the AMM-CNN model can achieve higher detection accuracy than other methods. Moreover, the AMM-CNN model has good robustness under conditions where only a few samples are available for learning.
6. Conclusions
In conclusion, the article presents a novel and unique defense strategy against quantum attacks on CVQKD systems in complex communication scenarios. Our proposed methodology stands out from existing approaches due to its incorporation of CNN deep learning algorithms and its comprehensive consideration of the impact of potential DoS attacks in realistic CVQKD systems. By harnessing the capabilities of deep learning algorithms, we trained an attack-aware model that exhibits an impressive detection accuracy of 98.7% against DoS attacks. This high accuracy in detecting DoS attacks demonstrates the effectiveness and reliability of our approach in addressing these specific threats. Moreover, our research includes comprehensive experiments conducted under various scenarios, such as long-distance and small-sample situations. By exploring previously uncharted territories, we have demonstrated the robustness and applicability of our method across diverse communication environments. Additionally, our work provides a fresh perspective within the realm of CVQKD systems. The seamless integration of deep learning and quantum cryptography not only enhances the security of CVQKD systems against quantum DoS attacks but also opens up unprecedented avenues for further advancements in quantum communication. This amalgamation paves the way for the development of more robust and efficient quantum communication protocols, with potential implications across a wide array of industries reliant on secure information exchange. To summarize, our research presents a distinctive and pioneering defense strategy against DoS attacks on CVQKD systems.
Author Contributions
Conceptualization, W.Y.; methodology, W.Y.; resources, D.H.; data curation, W.Y.; writing—original draft preparation, W.Y. and Y.Z.; software, W.Y. and Y.Z.; writing—review and editing, D.H.; supervision, D.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef]
- Gong, L.H.; Song, H.C.; He, C.S.; Liu, Y.; Zhou, N.R. A continuous variable quantum deterministic key distribution based on two-mode squeezed states. Phys. Scr. 2014, 89, 035101. [Google Scholar] [CrossRef]
- Lance, A.M.; Symul, T.; Sharma, V.; Weedbrook, C.; Ralph, T.C.; Lam, P.K. No-switching quantum key distribution using broadband modulated coherent light. Phys. Rev. Lett. 2005, 95, 180503. [Google Scholar] [CrossRef]
- Grosshans, F.; Van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238–241. [Google Scholar] [CrossRef]
- Navascués, M.; Grosshans, F.; Acin, A. Optimality of Gaussian attacks in continuous-variable quantum cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar] [CrossRef]
- Furrer, F.; Franz, T.; Berta, M.; Leverrier, A.; Scholz, V.B.; Tomamichel, M.; Werner, R.F. Continuous variable quantum key distribution: Finite-key analysis of composable security against coherent attacks. Phys. Rev. Lett. 2012, 109, 100502. [Google Scholar] [CrossRef]
- García-Patrón, R.; Cerf, N.J. Unconditional optimality of Gaussian attacks against continuous-variable quantum key distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A. Composable security proof for continuous-variable quantum key distribution with coherent states. Phys. Rev. Lett. 2015, 114, 070501. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.Z.; Kunz-Jacques, S.; Jouguet, P.; Weedbrook, C.; Yin, Z.Q.; Wang, S.; Chen, W.; Guo, G.C.; Han, Z.F. Quantum hacking on quantum key distribution using homodyne detection. Phys. Rev. A 2014, 89, 032304. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E. Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 2013, 87, 062313. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Liang, L.M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef]
- Qin, H.; Kumar, R.; Alléaume, R. Quantum hacking: Saturation attack on practical continuous-variable quantum key distribution. Phys. Rev. A 2016, 94, 012325. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, L.; Qin, H.; Sun, S.; Huang, P.; Wang, Y.; Wu, Z.; Guo, Y.; Huang, D. Beyond universal attack detection for continuous-variable quantum key distribution via deep learning. Phys. Rev. A 2022, 105, 042411. [Google Scholar] [CrossRef]
- Du, H.; Huang, D. Multi-Attack Detection: General Defense Strategy Based on Neural Networks for CV-QKD. Photonics 2022, 9, 177. [Google Scholar] [CrossRef]
- Mao, Y.; Huang, W.; Zhong, H.; Wang, Y.; Qin, H.; Guo, Y.; Huang, D. Detecting quantum attacks: A machine learning based defense strategy for practical continuous-variable quantum key distribution. New J. Phys. 2020, 22, 083073. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; Zhang, L.; Mao, Y.; Luo, H.; Guo, Y.; Huang, D. Sifting scheme for continuous-variable quantum key distribution with short samples. JOSA B 2022, 39, 694–704. [Google Scholar] [CrossRef]
- Huang, D.; Liu, S.; Zhang, L. Secure Continuous-Variable Quantum Key Distribution with Machine Learning. Photonics 2021, 8, 511. [Google Scholar] [CrossRef]
- Li, Y.; Huang, P.; Wang, S.; Wang, T.; Li, D.; Zeng, G. A denial-of-service attack on fiber-based continuous-variable quantum key distribution. Phys. Lett. A 2018, 382, 3253–3261. [Google Scholar] [CrossRef]
- Dai, E.; Huang, D.; Zhang, L. Low-rate denial-of-service attack detection: Defense strategy based on spectral estimation for CV-QKD. Photonics 2022, 9, 365. [Google Scholar] [CrossRef]
- Leverrier, A.; García-Patrón, R.; Renner, R.; Cerf, N.J. Security of continuous-variable quantum key distribution against general attacks. Phys. Rev. Lett. 2013, 110, 030502. [Google Scholar] [CrossRef] [PubMed]
- Leverrier, A.; Grosshans, F.; Grangier, P. Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 2010, 81, 062343. [Google Scholar] [CrossRef]
- Grosshans, F.; Cerf, N.J. Continuous-variable quantum cryptography is secure against non-Gaussian attacks. Phys. Rev. Lett. 2004, 92, 047905. [Google Scholar] [CrossRef]
- Gisin, N.; Fasel, S.; Kraus, B.; Zbinden, H.; Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 2006, 73, 022320. [Google Scholar] [CrossRef]
- Jain, N.; Anisimova, E.; Khan, I.; Makarov, V.; Marquardt, C.; Leuchs, G. Trojan-horse attacks threaten the security of practical quantum cryptography. New J. Phys. 2014, 16, 123030. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Liu, F.; Lin, G.; Shen, C. CRF learning with CNN features for image segmentation. Pattern Recognit. 2015, 48, 2983–2992. [Google Scholar] [CrossRef]
- Han, F.; Yao, J.; Zhu, H.; Wang, C. Underwater image processing and object detection based on deep CNN method. J. Sensors 2020, 2020, 6707328. [Google Scholar] [CrossRef]
- Huang, L.; He, M.; Tan, C.; Jiang, D.; Li, G.; Yu, H. Retracted: Jointly network image processing: Multi-task image semantic segmentation of indoor scene based on CNN. IET Image Process. 2020, 14, 3689–3697. [Google Scholar] [CrossRef]
- Wu, H.; Huang, Q.; Wang, D.; Gao, L. A CNN-SVM combined model for pattern recognition of knee motion using mechanomyography signals. J. Electromyogr. Kinesiol. 2018, 42, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Kwon, M.C.; Park, G.; Choi, S. Smartwatch user interface implementation using CNN-based gesture pattern recognition. Sensors 2018, 18, 2997. [Google Scholar] [CrossRef] [PubMed]
- Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative study of CNN and RNN for natural language processing. arXiv 2017, arXiv:1702.01923. [Google Scholar]
- Li, H. Deep learning for natural language processing: Advantages and challenges. Natl. Sci. Rev. 2018, 5, 24–26. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Xing, Z.; Li, X.; Ruan, X.; Luo, Y.; Zhang, H. Phase Compensation for Continuous Variable Quantum Key Distribution Based on Convolutional Neural Network. Photonics 2022, 9, 463. [Google Scholar] [CrossRef]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; Salt Lake City, UT, USA, 18–22 June 2018, pp. 7132–7141.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).