Correlations in Quantum Network Topologies Created with Cloning

Abstract

With progress in quantum technologies, the field of quantum networks has emerged as an important area of research. In the last few years, there has been substantial progress in understanding the correlations present in quantum networks. In this article, we study cloning as a prospective method to generate three party quantum networks which will help us to create larger networks. We analyze various quantum network topologies that can be created using cloning transformations. This would be useful in situations wherever the availability of entangled pairs is limited. In addition to that, we focus on the problem of distinguishing networks created by cloning from those that are created by distributing independently generated entangled pairs. We find that there are several states that cannot be distinguished using the Finner inequalities in the standard way. For such states, we propose an extension to the existing Finner inequality for triangle networks by further increasing the number of observers from three to four or six depending on the network topology. This takes into account the additional correlations that exist in the case of cloned networks. In the last part of the article, we use tripartite mutual information to distinguish cloned networks from networks created by independent sources and further use squashed entanglement as a measure to quantify the amount of dependence in the cloned networks.

1. Introduction

Quantum correlations have never failed to amaze researchers and have remained an important aspect of quantum information theory [1,2,3,4]. In recent years, several studies were conducted to further enhance our understanding about the nature of quantum correlations and other quantum resources. In particular, a resource theoretic framework was constructed to understand the role of these resources [5,6,7,8,9] in different information processing tasks. In addition, efforts have been made to extend the idea of quantum correlations and other quantum resources to three or more parties [10,11]. The idea is not only about quantum correlations in a multi-party scenario, but the reach also extends to quantum networks and internet [12,13,14,15,16,17,18,19,20]. These networks are in principle created by the distribution of entanglement to distant parties by one or multiple independent sources and the application of local unitaries to establish strong correlations in the entire network. In such scenarios, distant parties can establish direct correlation through intermediate nodes by repeater technology [21,22,23]. Whenever we talk about multi-party entanglement, monogamy plays a central role. In the case of quantum networks, since they can be created by distributing independently created entangled pairs, monogamy is not as applicable. Bell inequalities for such networks have also been studied in detail [24,25,26,27] and even enhanced in the way that they can be input-independent [25,28]. These ideas have further pushed our understanding towards real world quantum networks [18,19]. However, the study of correlations in quantum networks is still not complete, and in recent years, we have seen tremendous theoretical and experimental progress in terms of the establishment of quantum networks [20]. Most of these studies are restricted to simple network topologies like bi-local and triangle networks, which are created using an independent source that prepares and distributes entangled qubits to distant observers [15].

Quantum resources [1,6,7,9] on one hand give us a significant advantage in accomplishing various information processing tasks [5,21,23,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] over their classical counterparts, while on the other hand, they impose strict restrictions on certain kind of operations [46,47,48,49,50,51]. Among these restrictions, the No-cloning theorem prohibits us from perfectly cloning an arbitrary unknown quantum state [46]. However, it does not rule out the possibility of cloning states approximately (i.e., with fidelity of less than unity) [46,52,53,54,55,56,57,58] or with a certain probability of success. Approximate quantum cloning machines (QCMs) can further be classified into two types, namely (a) state-dependent [46,52,55,59,60] and (b) state-independent [52,54] cloners. Another kind of classification that can be made in the context of these cloning machines is based on the kind of output they produce. If all the cloning outputs are the same, then the cloning machine is called symmetric; otherwise, it is referred to as an asymmetric cloning machine [61,62].

For a quantum network to be functional, it is not necessary to have a network with a maximally entangled state, at least in the context of information processing tasks such as the sending of data qubits (teleportation) and cbits (super dense coding). As an example, we can take the context of teleportation, where if the fully entangled fraction f of the resource state $\rho$ is greater than $1/2$ (teleportation fidelity $F_{max}$ is greater than $2/3$), then we can always have quantum advantage. Similarly, in the case of super dense coding, if the quantum conditional entropy of the resource state is negative $S_{(A|B)}(\rho )<0$, the state is useful for super dense coding. In addition, it is not necessary that the channel has to be pure state. There are many mixed states for which such an advantage will be possible. In this article, we talk about the tripartite network that is obtained as an output of the cloning process.

To start with, we make another assumption that the source has a single maximally entangled state and wants to create a tripartite quantum network. We also study the process of establishing a network without the need for an independent source. We have considered the set of symmetric cloners that produce outputs with equal fidelity [55]. We use such cloners to create various types of quantum networks and made an effort to understand the limits of networks that are created by the process of cloning. One significant difference between networks created by cloning and by distributing independently created entangled states is the condition of statistical independence of resources, which relaxes the monogamy constraint and also makes the relevant Bell inequalities become non-linear in the latter case [20]. We show that by choosing specific initial states and cloning machine parameters, we can create networks that cannot be distinguished from those networks that are created by distributing independent entangled pairs. We thoroughly analyze such tripartite networks along with various topologies that are created and study how these networks can be distinguished from the ones that are created by distributing independent entangled pairs. We find several instances where these cannot be distinguished. We also try to quantify the amount of dependence on the initial source in networks with the help of an entanglement quantifier.

In Section 2, we first introduce and discuss various types of cloning techniques that have been used to create different three party quantum networks. These include local and non-local cloning operations, with the option of creating either two copies or three copies. In Section 3, we briefly describe all types of tripartite networks and also the Finner inequality to understand the limit it poses on network topology. We also introduce our extension to the Finner inequality to understand these limits more. In Section 4, we try to create tripartite network topologies with cloning by taking inspiration from [63]. Specifically, we create three kinds of network topologies for three distant observers, namely tripartite networks, bi-local, and genuine triangle networks. We study the problem of distinguishing these networks from traditional networks. We also study the constraints on such networks arising due to the quantum Finner inequalities [63]. In Section 5, we use a network witness created using tripartite mutual information to distinguish cloned networks from others since cloned networks are created using a single source. We also propose a method to quantify the statistical dependence on the initial single source present in the entire network. The objective of the study is to identify alternate ways of creating quantum networks so that in practice, whenever there is a limitation on the number of entangled states created, we can take the alternative approach of cloning and create large networks.

2. Approximate Quantum Cloning Machines

From the breakthrough paper from Wooters and Zurek, we know that perfect cloning is not possible according to the No-cloning theorem [46]. However, it does not rule out the possibility of cloning a quantum state approximately with a fidelity F less than unity [52]. The fidelity F can be expressed as

$$F=〈\mathsf{\Psi }|{\rho }^{out}|\mathsf{\Psi }〉,$$

(1)

where $\left|\mathsf{\Psi }\right.〉$ refers to the state to be cloned at the input port of the cloner and ${\rho }^{out}$ is the state obtained at its output port after applying the cloning transformation. In our study of networks, we use similar symmetric approximate cloning machines. The base version of all the cloning machines used in this work is the Buzek–Hillery cloning machine.

Here, we have used four variants of the Buzek–Hillery cloning machine to create three kinds of networks. The first cloning transformation is local $1\to 2$ cloning ($QC{L}_{1\to 2}$), where we apply two unitary transformations at the two ends of a spatially separated entangled pair to produce another copy of the local states. It is given by the following transformation [54]:

$$\begin{array}{c}{U}_{bh}{\left|{\mathsf{\Psi }}_i\right.〉}_{a_0}{\left|\Sigma \right.〉}_{a_1}{\left|X\right.〉}_x\to c{\left|{\mathsf{\Psi }}_i\right.〉}_a{\left|{\mathsf{\Psi }}_i\right.〉}_b{\left|X_{ii}\right.〉}_x\hfill \\ {\displaystyle +d\sum _{j\ne i}^M\left({\left|{\mathsf{\Psi }}_i\right.〉}_a{\left|{\mathsf{\Psi }}_j\right.〉}_b+{\left|{\mathsf{\Psi }}_j\right.〉}_a{\left|{\mathsf{\Psi }}_i\right.〉}_b\right){\left|Y_{ij}\right.〉}_x.}\hfill \end{array}$$

(2)

It is an M-dimensional quantum copying transformation acting on a state ${\left|{\mathsf{\Psi }}_i\right.〉}_{a_0}$ (where i ∈ {1, …, M}). This state is to be copied on a blank state ${\left|\Sigma \right.〉}_{a_1}$. Initially, the cloning machine was prepared in state ${\left|X\right.〉}_x$. After the cloning transformation, this is transformed into another set of state vectors ${\left|X_{ii}\right.〉}_x$ and ${\left|Y_{ij}\right.〉}_x$ (where $i,j$ ∈ {1, …, M}). Here, $\left|\mathsf{\Psi }\right.〉={\sum }_{i=1}^M{\alpha }_i\left|{\mathsf{\Psi }}_i\right.〉$, where $\left|{\mathsf{\Psi }}_i\right.〉$ are the basis vectors of the m qubit system with dimensions $M=2^m$, and ${\alpha }_i$ represents the probability amplitude, hence ${\sum }_{i=0}^M{\alpha }_i^2=1$. The modes $a_0$, $a_1$, and x represent the input, blank, and machine qubits, respectively. In this case, these transformed machine state vectors $\left(\left|X_{ii}\right.〉,\left|Y_{ij}\right.〉\right)$ are elements of the orthonormal basis set in the M-dimensional space. Here, $i,j$ are two indices that run from 1 to M. The coefficients c and d are the probability amplitudes which take real values. The relation between c and d can easily be obtained from the unitarity condition of cloning transformation—this relation is given by $c^2=1-2(m-1)d^2$. When we want to make use of state-independent versions of the cloner, we can calculate the specific value of the machine parameter d for which the coning outcome is not dependent on input states.

The second cloning transformation is $1\to 3$ ($QC{L}_{1\to 3}$) cloning on a single qubit. Here, we create three copies of a single qubit and distribute it to three parties to create a three-party network. This $1\to 3$ cloning transformation applied on a single qubit is given by

$$\begin{array}{c}\hfill U_{bh}{\left|{\mathsf{\Psi }}_i\right.〉}_{a_0}{\left|\Sigma \right.〉}_{a_1}{\left|\Sigma \right.〉}_{a_2}{\left|X\right.〉}_x\to c{\left|{\mathsf{\Psi }}_i\right.〉}_a{\left|{\mathsf{\Psi }}_i\right.〉}_b{\left|{\mathsf{\Psi }}_i\right.〉}_c{\left|X_{i}i\right.〉}_x\\ \hfill +d\sum _{j,k\ne i}^M({\left|{\mathsf{\Psi }}_i\right.〉}_a{\left|{\mathsf{\Psi }}_j\right.〉}_b{\left|{\mathsf{\Psi }}_k\right.〉}_c+{\left|{\mathsf{\Psi }}_i\right.〉}_a{\left|{\mathsf{\Psi }}_k\right.〉}_b{\left|{\mathsf{\Psi }}_j\right.〉}_c\\ \hfill +{\left|{\mathsf{\Psi }}_j\right.〉}_a{\left|{\mathsf{\Psi }}_i\right.〉}_b{\left|{\mathsf{\Psi }}_k\right.〉}_c+{\left|{\mathsf{\Psi }}_j\right.〉}_a{\left|{\mathsf{\Psi }}_k\right.〉}_b{\left|{\mathsf{\Psi }}_i\right.〉}_c\\ \hfill +{\left|{\mathsf{\Psi }}_k\right.〉}_a{\left|{\mathsf{\Psi }}_i\right.〉}_b{\left|{\mathsf{\Psi }}_j\right.〉}_c+{\left|{\mathsf{\Psi }}_k\right.〉}_a{\left|{\mathsf{\Psi }}_j\right.〉}_b{\left|{\mathsf{\Psi }}_i\right.〉}_c){\left|Y_{i}jk\right.〉}_x.\end{array}$$

(3)

The third transformation is non-local $1\to 2$ cloning transformation ($QCN{L}_{1\to 2}$), applied together on an entangled pair to create another copy of it. We follow this mechanism of cloning when we want to create bi-local networks [63], which is explained in the following sections. The cloning transformation is same as given in Equation (2) where $M=4$. To create a triangle network, we use the $1\to 3$ non-local cloning transformation ($QCN{L}_{1\to 3}$). We use this kind of cloning transformation to create genuine triangle networks [63]. In this case, the cloning transformation is the same as given in Equation (3), with $M=64$.

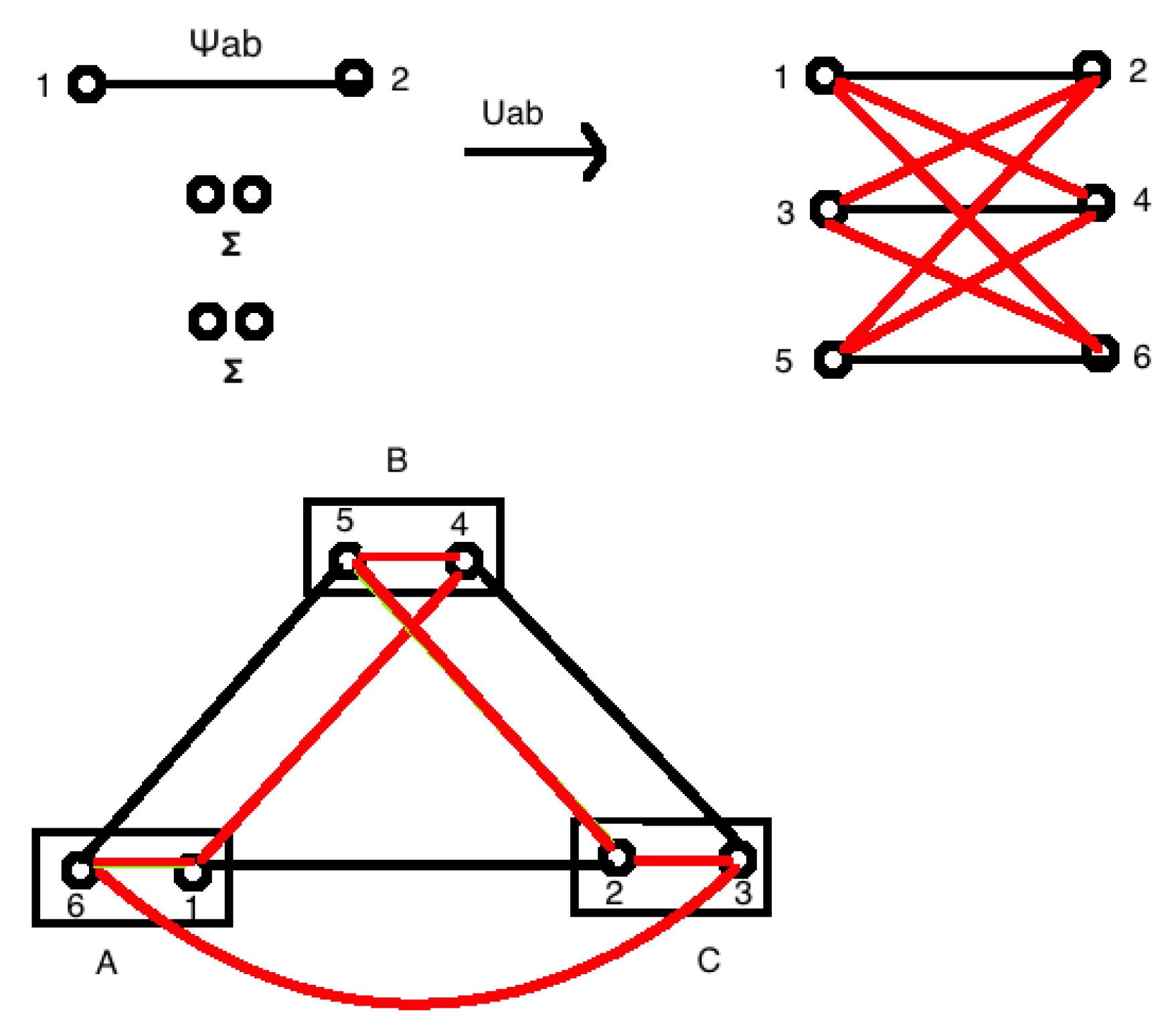
3. Three-Party Quantum Networks and Bounds and the Quantum Finner Inequalities

In this section, we give a brief overview of three-party networks. We begin by considering a quantum network with three observers A, B, and C. The network is created by one or more sources by sending quantum states to the different observers. Each of these parties carries out a measurement on the obtained quantum systems, with measurements outputs as a, b, and c. For the purpose of simplicity, we are free to choose $a,b,c$ from the binary values 0 and 1.

Three Inequivalent Networks:

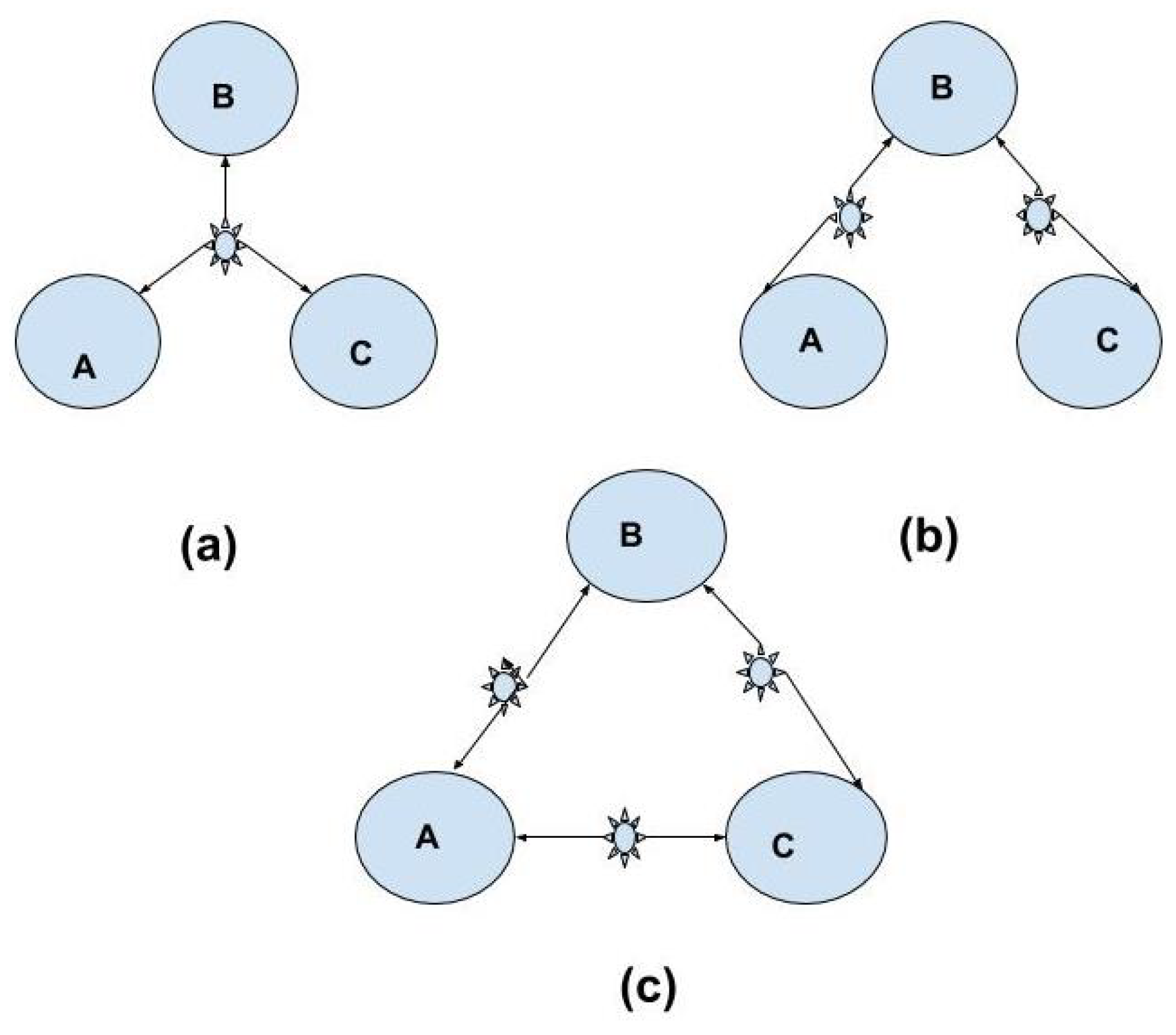
• For three observers, we can have three inequivalent networks. The first of the kind, shown in Figure 1a, is of a single common source communicating a quantum state to each of these three observers. We can see that any possible distribution $P\left(abc\right)$ can be obtained in this case. In fact, it is enough to restrict ourselves to classical sources here. The set of possible attainable distributions $P\left(abc\right)$ is nothing but the whole probability simplex with the normalization condition ${\sum }_{abc}P\left(abc\right)=1$.
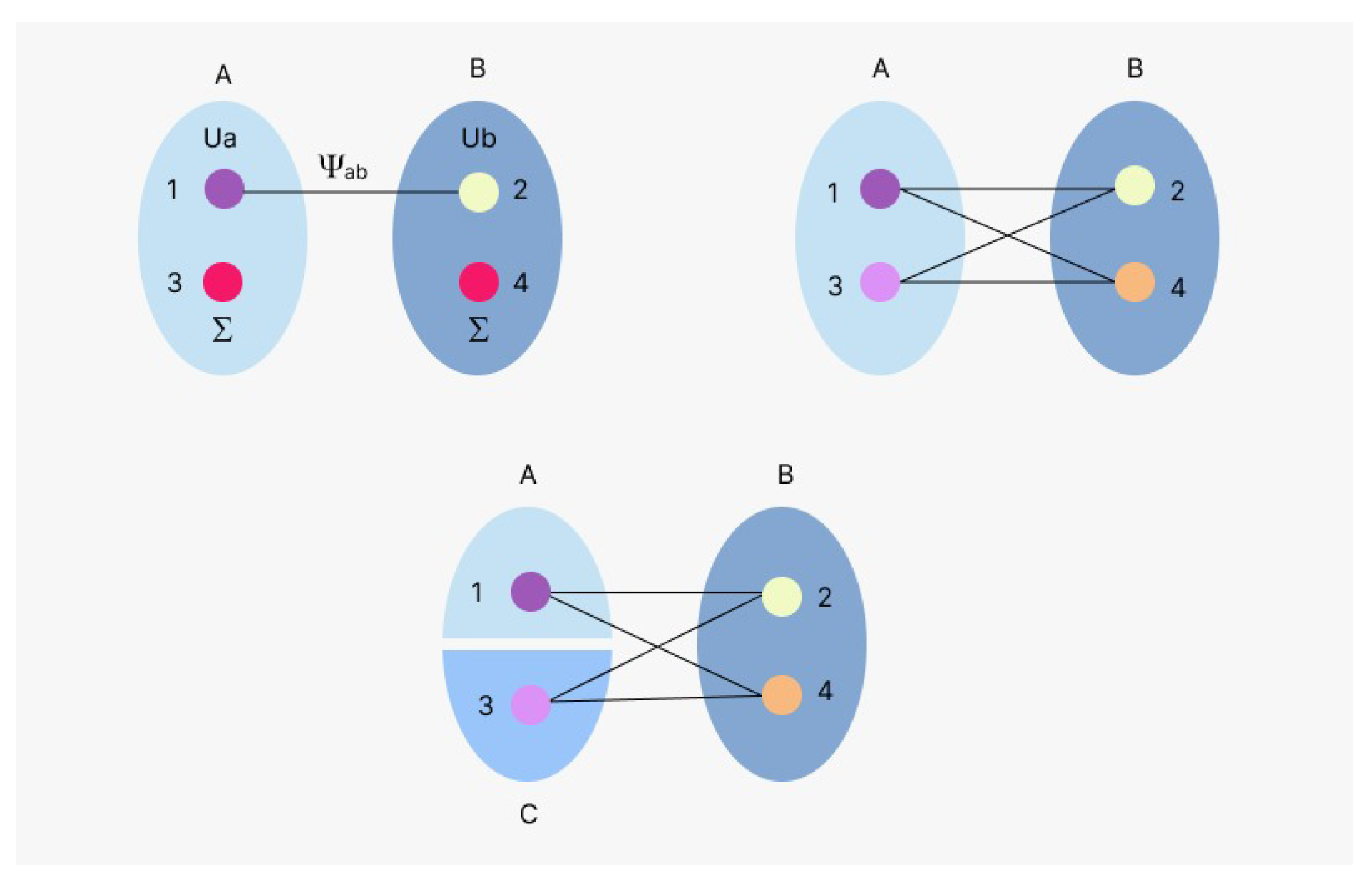
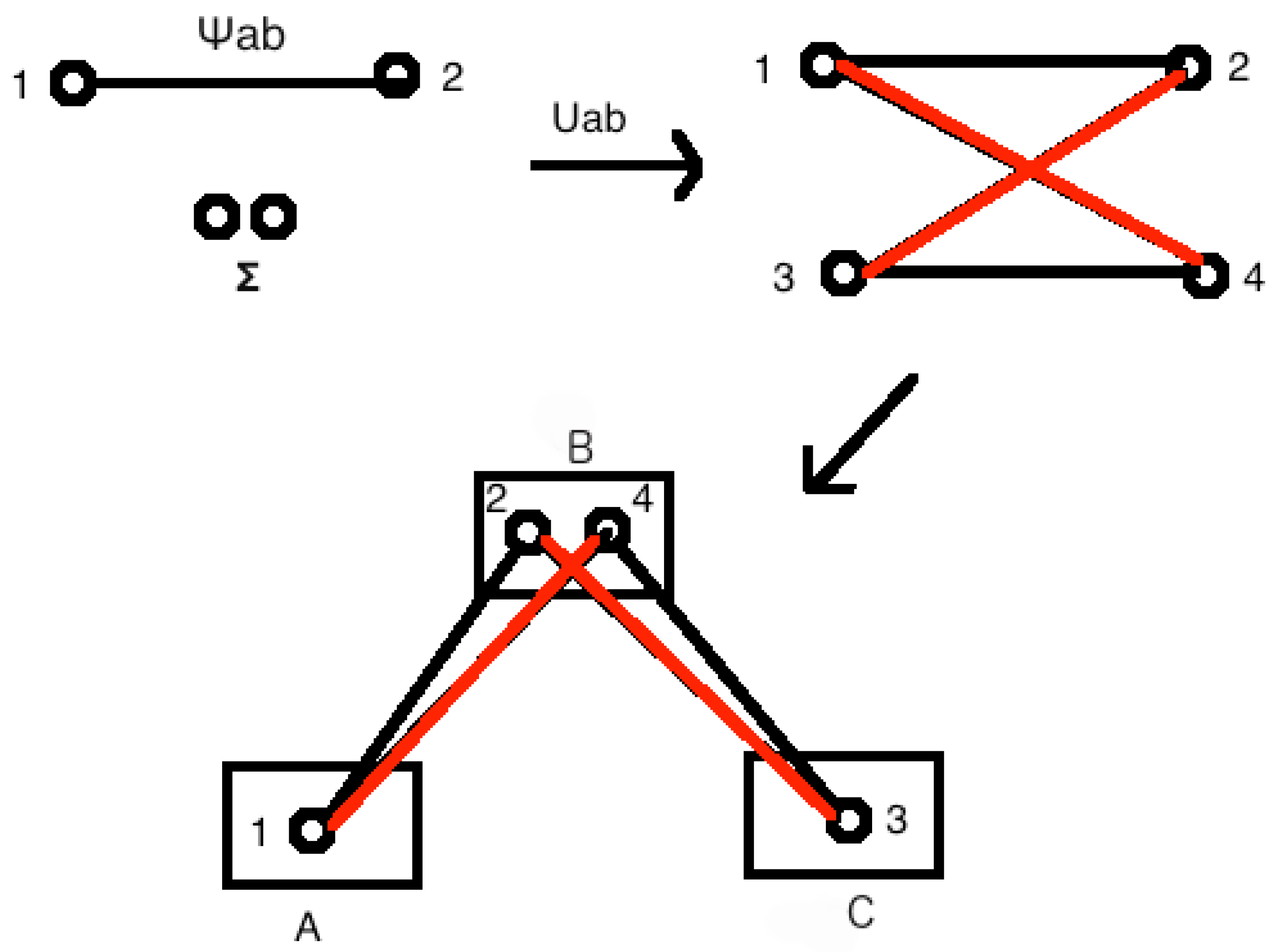
• Next, we consider the case when the triangle network is created by two independent sources, as in Figure 1b. One of the sources distributes a common state to the parties A and B while the other gives it to B and C. This is called a bi-local network. The interesting part of this network is that observers A and C are initially independent; however, they can be made to be correlated to each other through B. If we remove the node B from the network, these two become completely independent. To test the independence, we have the following condition [63]:

  $$\sum _{b}P\left(abc\right)=P\left(a\right)P\left(c\right).$$

  (4)
• Lastly, we have the most interesting and challenging three party network which is the triangle network [see Figure 1c]. This can be obtained from bilocal network by adding a source connecting A and C. Because of this additional source, there is no need for the independence condition as it no longer holds.

Quantum Finner Inequality: Quantum versions of the Finner inequalities as proposed by Renou et al. [63] put fundamental limits on network topologies that can be generated using independent sources of entangled pairs. This inequality is mathematically expressed as

$$P\left(abc\right)\le \sqrt{P\left(a\right)P\left(b\right)P\left(c\right)},$$

(5)

where $P\left(abc\right)$ is the probability of observing $abc$ on combined system, and $P\left(a\right)$ stands for the probability of getting a (the same for b and c) as a measurement outcome in the subsystem A, similarly for subsystems B and C, respectively.

If in a network topology we observe the violation of the quantum Finner inequality, we can surely say that the network is created using a single dependent source. However, in the case where there is no violation, we cannot say that these network topologies are created by using independent sources [63]. The network topologies we have in this article are all generated using the process of quantum cloning. We see several instances of such networks that cannot be distinguished (that it was the network created by independent source distributing entangled pairs or was it created by cloning a single source) by the quantum Finner inequalities. Since quantum cloning is a unitary transformation acting on the state to be cloned along with auxiliary blank states, any state that we derive as an outcome of cloning is physical. If the state obtained exhibits entanglement, we can use them to create a quantum network. All these networks are created by the physical process of quantum cloning, that is, by the application of unitary transformations on initial entangled or non-entangled states, so there is no such physical restriction in the terms of achieving these topologies, which was the case when the networks were created using independent sources. However, in this case, the restrictions arise in terms of the resource fullness of the networks created by cloning.

Modified Finner Inequality: We slightly modify the conditions given by the quantum Finner inequalities for bi-local networks, and we observe that they become more efficient in distinguishing the cloned networks. The modification is to make observer B perform two measurements, one on qubit 2 and another on qubit 4, instead of combined measurement on 24. The corresponding Finner inequalities become [63]

$$P\left(ab{b}^{\prime }c\right)\le \sqrt{P\left(a\right)P\left(b\right)P\left(b^{\prime }\right)P\left(c\right)},$$

(6)

where b is the observed outcome for qubit 2, and $b^{\prime }$ is the observation outcome of qubit 4. The main reason why the extension performs better than the original inequality is that in the cloned bi-local network, we have additional correlations as in ${\rho }_{14}$ and ${\rho }_{23}$. It is more like a four-party network, but one of the observers holds two shares.

4. Three Party Networks by Cloning

A typical quantum network consists of independent sources distributing entangled states to spatially separated nodes, which can then perform some operations on their part of the network. In this work, we partially relax the condition of having an independent source that distributes entangled pairs. We rather start with a single source and use cloning to create similar network topologies. Several tripartite network topologies are possible to create using quantum cloning. In the following subsections, we elaborate techniques to generate various quantum networks for three parties.

4.1. Three Copies of Single Qubit

The first and the most basic method used to generate a three-party network is by creating three copies of a single qubit and distributing it to three parties. We add the restrictions that the two-qubit states ${\rho }_{ab}={\rho }_{bc}={\rho }_{ca}$ (equality holds only in the case of symmetric cloning) must be entangled. In such a scenario, the Finner inequalities do not impose any restrictions, and the entire probability simplex $P\left(abc\right)$ is possible.

In Figure 2, we have shown the process of creating this type of network using cloning transformation, as given in Equation (3) for $M=2$. ${\mathsf{\Psi }}_{ab}$ is the initial single-qubit state, $\Sigma$ is the blank state, and U represents the cloning unitary. This is not actually a network, rather a multipartite correlation in triangle topology.

4.2. Local Cloning of Entangled Pair: Bi-Local Network

The first method we use here to create a bi-local network is by two local cloning operations. We start initially with two spatially separated parties A and B, which share an entangled pair ${\mathsf{\Psi }}_{ab}={\alpha }^2|00\rangle +\sqrt{1-{\alpha }^2}|11\rangle$. Parties A and B apply a local cloning transformation of the form given in Equation (2) on their share of the entangled pair. The transformation on the entangled pair can be given by $U_a\otimes U_b$. After the cloning and tracing of the machine states, the complete output state is given by ${\rho }_{1234}$, where qubits 1 and 3 are with observer A and qubits 2 and 4 are with observer B. It is important to note that the sub-states represented by qubits ${\rho }_{12}$, ${\rho }_{14}$, ${\rho }_{23}$, and ${\rho }_{34}$ are the same in case of symmetric cloning transformation which we have selected. In addition, the sub-states ${\rho }_{13}$ and ${\rho }_{24}$ are the same. We have shown this process in Figure 3.

We observe that under certain conditions on the initial entangled state, we can simultaneously make ${\rho }_{12}$ (also ${\rho }_{14}$, ${\rho }_{34}$, ${\rho }_{23}$) entangled and ${\rho }_{13}$ (also $\rho 24$) separable. To generate a bi-local network from such a configuration, A can send one of the qubits, say 3 to C; hence, we obtain a network in which A and C are not directly entangled but are entangled through B. It is interesting to note that whenever the qubit represented by ${\rho }_{13}$ is separable, the inequality given in Equation (4) is obeyed.

Another important aspect of the problem is distinguishability by the Finner inequalities—we see that there are several states that are created by local cloning and can be distinguished as being created by a single source using the Finner inequalities. This is represented in Figure 4. Here, the overlapping region of all three colors (brown, light, and dark green) represents those output states created by local cloning, which are entangled. Since we are using symmetric cloning, this means that all the outputs, namely ${\rho }_{12}$, ${\rho }_{14}$, ${\rho }_{23}$, ${\rho }_{14}$, are entangled; also, ${\rho }_{13}$ and ${\rho }_{24}$ are simultaneously separable. The dark green region in Figure 4 represents those bi-local cloned networks that can be distinguished by the application of the Finner Inequalities. The lighter green region shows additional bi-local cloned network states that can be distinguished as created by a single source using the modified Finner inequalities as given in Equation (6).

4.3. Bi-Local Network: Non Local Cloning

Similar to the case of local cloning, we can also prepare a bi-local network using non-local cloning. The difference here is that a single common source prepares the individual sources by the application of non-local cloning (unitary) transformation and then distributes qubits to the three parties involved to create a network. In this case, an independent third party has an entangled pair of particles; it applies a global unitary transformation $U_{ab}$ and creates a copy of the entangled pair. In this case as well, we find that ${\rho }_{12}$, ${\rho }_{14}$, ${\rho }_{23}$, and ${\rho }_{34}$ are equal and ${\rho }_{13}$ is equal to ${\rho }_{24}$. It is important to note here that the correlations are better copied in the case of non-local cloning, so we might actually be able to create a bi-local network with a wider range of input states (Figure 5).

The source after performing the cloning transformation sends the qubit 1 to observer A, qubit 3 to C, and qubits 2 and 4 to B. It is important to note that under certain selected input state parameters and machine state parameters, we can obtain the condition where qubits 1 and 3 are separable; also, qubits 2 and 4 are separable. In some overlapping range of input state parameters and machine states, we can also have entanglement between $1,2$ and $1,4$ and also among $2,3$ and $3,4$. Hence, we establish the condition of bi-locality.

Now, we focus on the distinguishability of these networks using the Finner inequalities. We see that there are networks that cannot be distinguished as created by single-source using cloning or an independent source distributing entangled pairs. These networks are represented in Figure 6. The complete shaded region shows all states where the cloning outputs are entangled and can be used for creating a network, and the dark green region represents those bi-local cloned networks that can be distinguished by application of the Finner Inequalities. The lighter green region shows additional bi-local cloned network states that can be distinguished as created by single source using the modified Finner inequalities as given in Equation (6).

4.4. Triangle Network: Non Local Cloning

The last network topology we consider is the extended triangle network. The extension is in terms of additional internal correlations that exist among the qubits held by the observers A, B, and C. Here, we start with an independent entangled pair with a third party and apply a cloning transformation of the type given in Equation (3) with $M=4$ to obtain three copies of the entangled pairs. In this case, other than the intended entanglement between ${\rho }_{12}$, ${\rho }_{34}$ and ${\rho }_{56}$, we also have ${\rho }_{14}$ = ${\rho }_{23}$ = ${\rho }_{16}$ = ${\rho }_{25}$ = ${\rho }_{36}$ = ${\rho }_{45}$, which are entangled for some specific machine state parameter and input states. On the other hand, ${\rho }_{13}$ = ${\rho }_{15}$ = ${\rho }_{35}$ = ${\rho }_{24}$ = ${\rho }_{26}$ = ${\rho }_{46}$ remain largely separable.

The network created by following this strategy is not a genuine triangle network, because it has other entangled states as well. The method of preparing such a network is shown in Figure 7. The solid lines represent entangled states, and the red color and the black color are used to demarcate two different types of states. It would be interesting to see if we can obtain the genuine triangle networks by finding a condition on the machine state parameter and the input states that can make ${\rho }_{14}$ (also ${\rho }_{23}$, ${\rho }_{16}$, ${\rho }_{25}$, ${\rho }_{36}$, and ${\rho }_{45}$) separable and keep ${\rho }_{12}$ (${\rho }_{34}$ and ${\rho }_{56}$) entangled.

Now, we focus on the distinguishability of these networks using the Finner inequalities. We see that there are networks that cannot be distinguished as created by a single source using cloning from independent sources distributing entangled pairs. These networks are represented in Figure 8. The parameter ${\alpha }^2$ on the x-axis represents the input state parameter and d on the y-axis represents the machine state parameter. The complete shaded region shows the states that are entangled in a triangle cloned network, the darker green region represents the states that can be distinguished by the original Finner inequalities, and the light green region represents the additional states that can be distinguished by the modified Finner inequality.

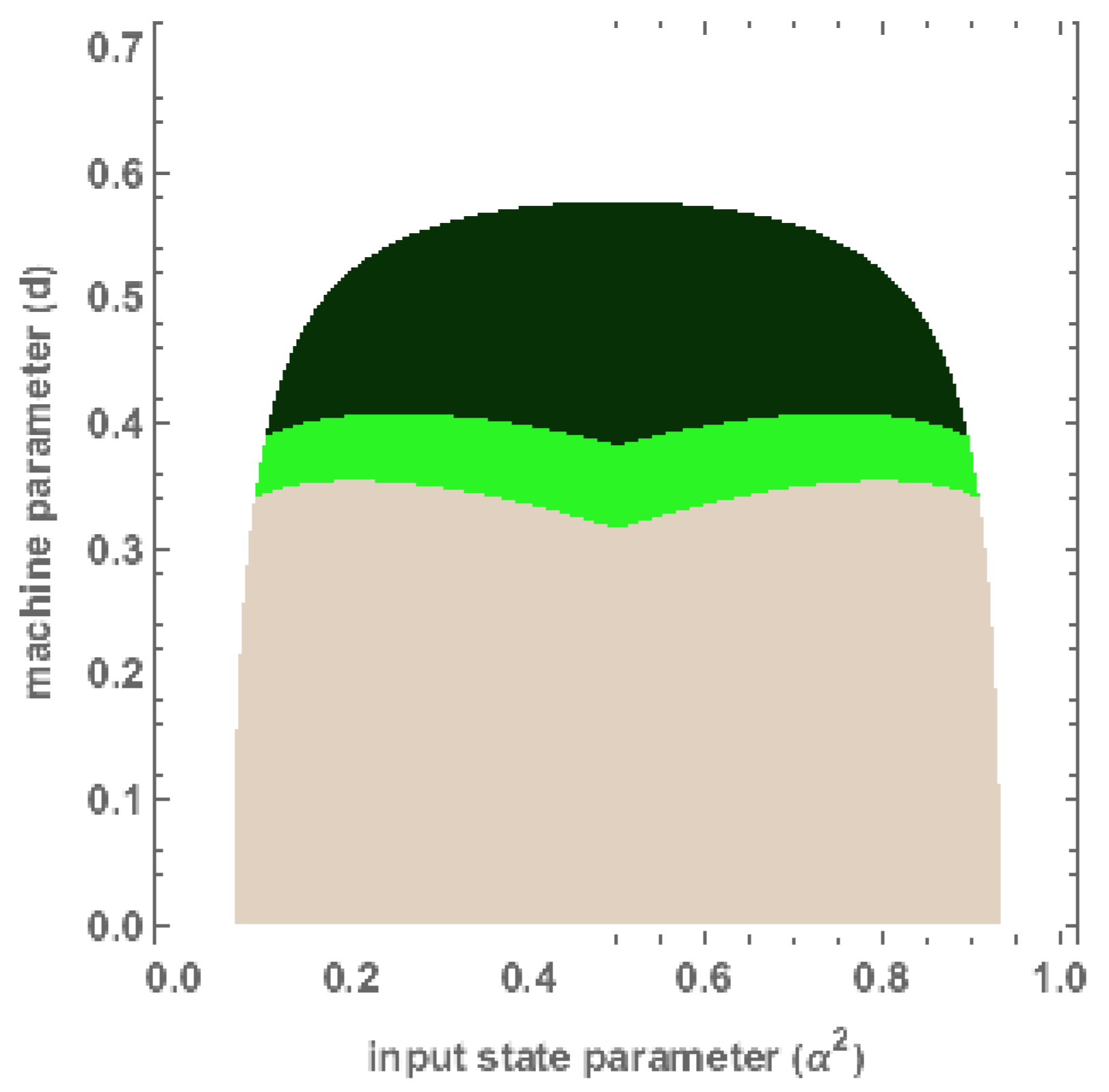
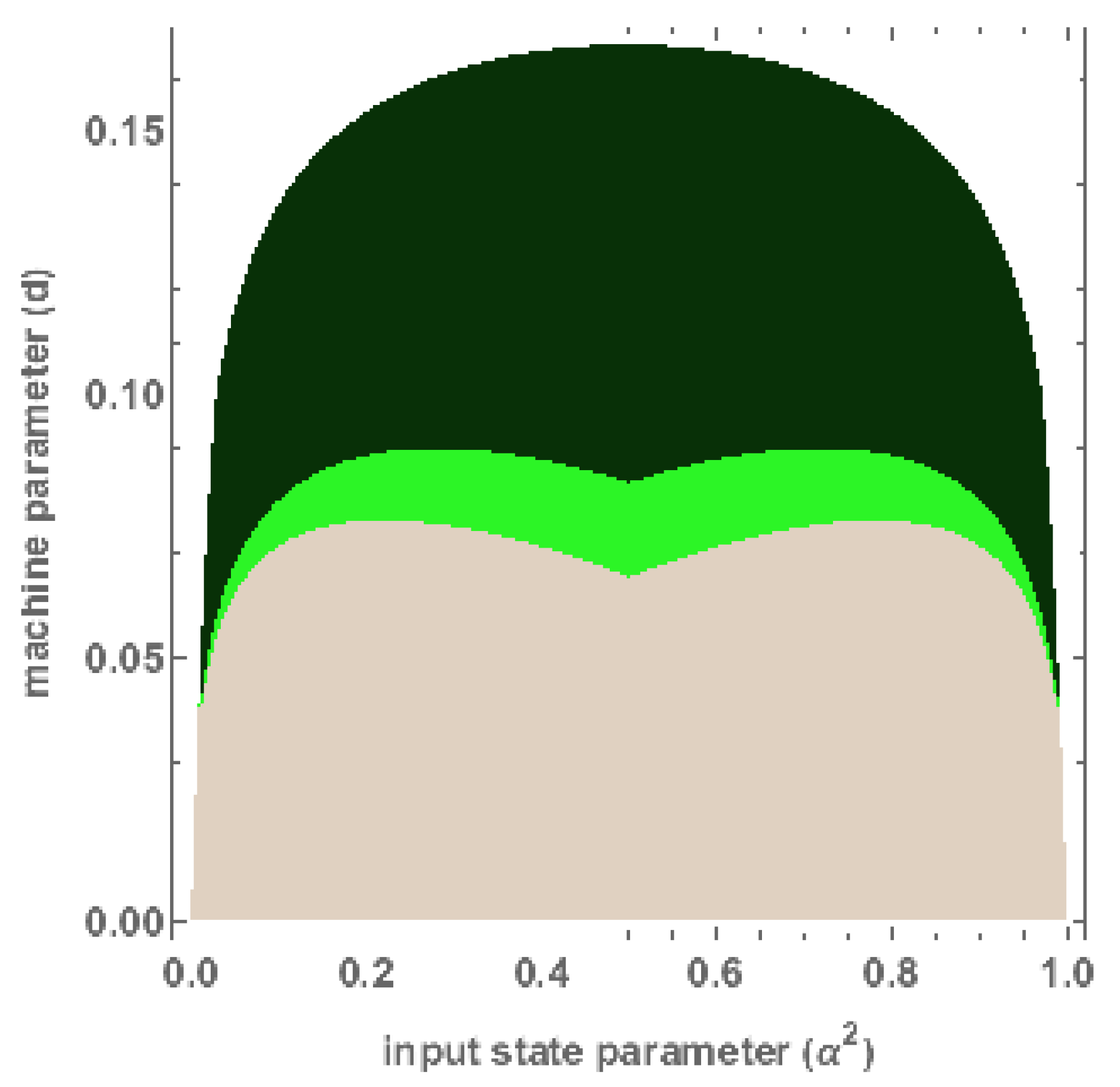
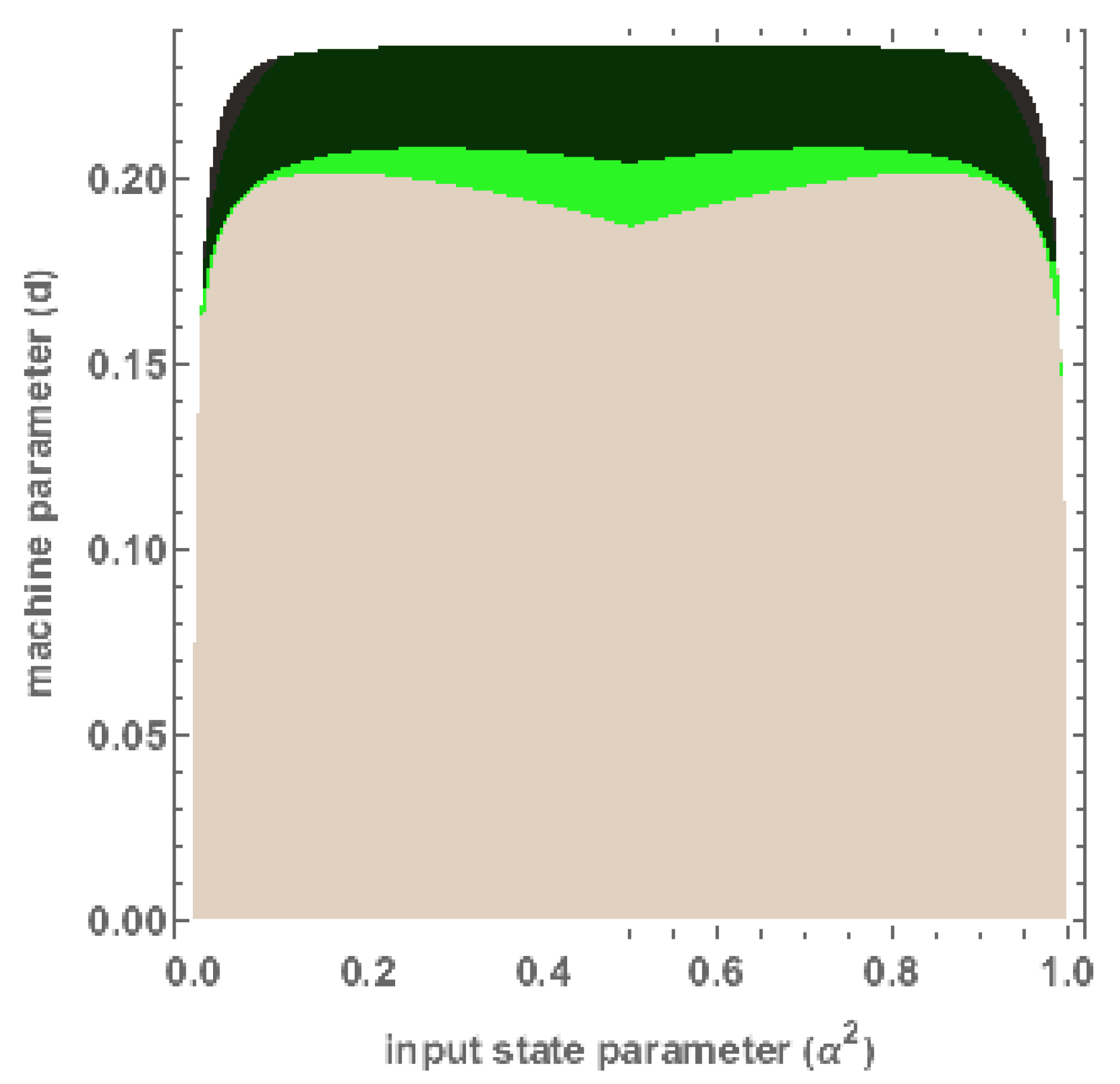
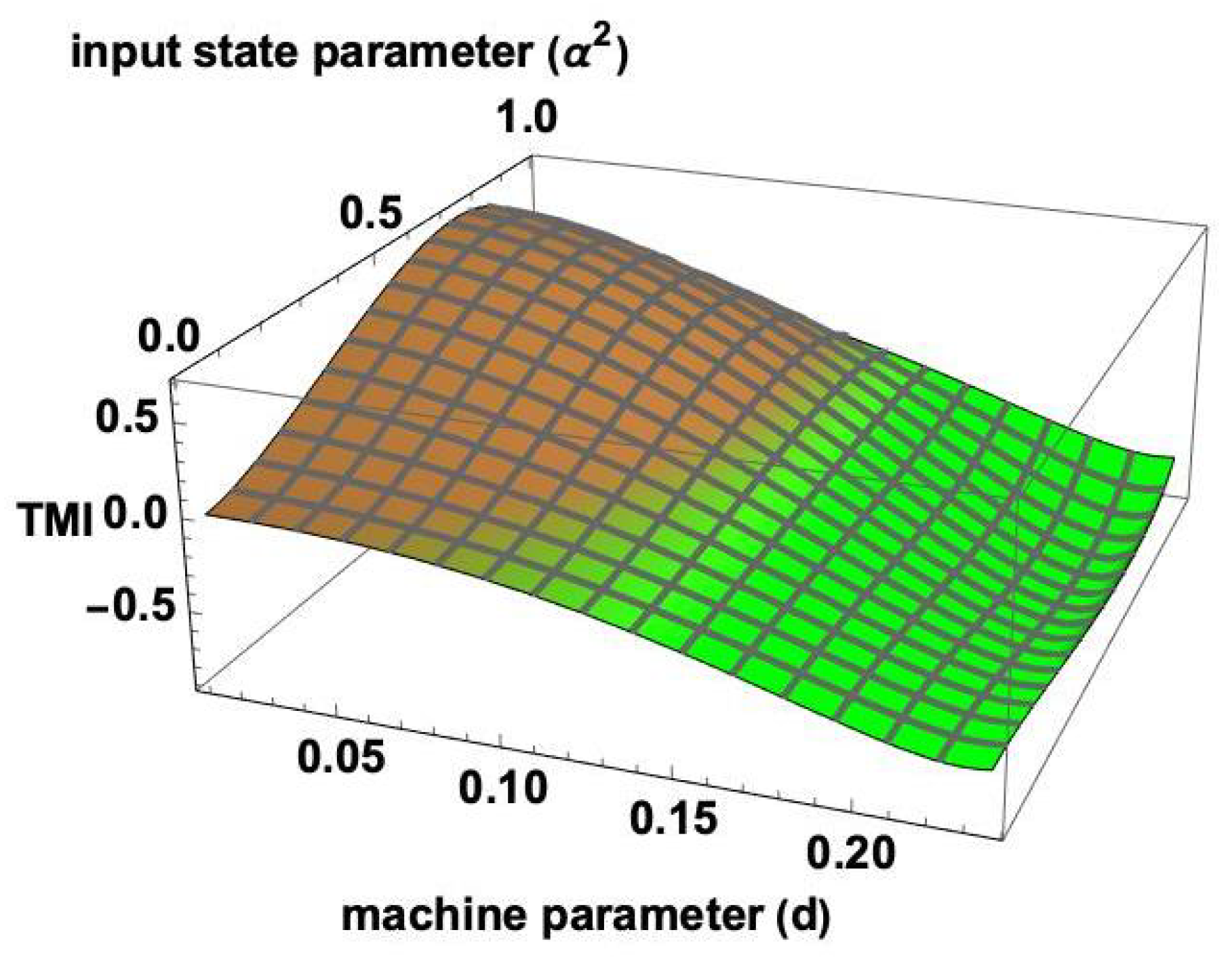
5. Witnessing Entanglement in Triangle Networks

In this section, we investigate quantum correlations in networks from the point of view of tripartite mutual information. We also use the notion of the network-based entanglement witness as defined in [64] to check if the networks created by cloning belong to ${\Delta }_i$, where ${\Delta }_i$ represents the quantum networks created by distributing entangled pairs created by independent sources. We use this witness to quantify the amount of violation and hence quantify the amount of dependence a source has in the case of networks generated with cloning. For this study, we restrict ourselves to only a genuine triangle network topology—the extension to other typologies that we have considered above is straightforward.

In the study by Kraft et al. [64], several observations are shared that can be used to detect if a state $\rho$ belongs to ${\Delta }_i$, which are as follows:

• $I_3(A:B:C)$ = 0 for any $\rho \in {\Delta }_i$. Here, I represents tripartite mutual information given by

  $$\begin{array}{c}{I}_3(A:B:C)=S\left(ABC\right)+S\left(A\right)+S\left(B\right)+S\left(C\right)\hfill \\ -S\left(AB\right)-S\left(AC\right)-S\left(BC\right).\hfill \end{array}$$

  (7)
  Intuitively, this means that there is no shared classical mutual information within the subsets of the quantum states owned by the parties A, B, and C, respectively.
• Let $E\left[\rho \right]$ be an entanglement measure that is additive on tensor products and monogamous. For any $\rho \in {\Delta }_i$, we have that $E_{X|YZ}\left[\rho \right]=E_{X|Y}\left[t{r}_Z\rho \right]+E_{X|Z}\left[t{r}_Y\rho \right]$ holds for all the bi-partitions $A|BC$, $B|AC$, and $C|AB$. The intuition here is that the entanglement on the bi-partition $A|BC$ should be equal to the sum of the entanglement in the reduced states, i.e., $A|B$ and $A|C$.

We have used squashed entanglement E [65] as a measure to quantify entanglement. Squashed entanglement guarantees additivity and monogamy properties. It is defined as

$$E_{sq}\left({\rho }^{AB}\right):=inf\{\frac{1}{2}I(A;B|E):{\rho }^{ABE} extension of {\rho }^{AB}\}.$$

(8)

Here, the minimum is taken over all extensions of ${\rho }^{AB}$ given by ${\rho }^{ABE}$, such that ${\rho }^{AB}=T{r}_E\left[{\rho }^{ABE}\right]$. $I(A;B|E)=$ $S\left(AE\right)$ + $S\left(BE\right)$−$S\left(ABE\right)$−$S\left(E\right)$ is the quantum conditional mutual information of ${\rho }^{ABE}$ [66].

We have considered cloned triangle networks for the analysis of observations 1 and 2. We first consider the observation 1 and test if the cloned triangle network ${\rho }^{ABC}$ falls into ${\Delta }_i$, i.e., the set of triangle networks created by independent sources, and then we use observation 2 for the cases where ${\rho }^{ABC}\notin {\Delta }_i$ to quantify the amount of dependence that each entangle pair has in such a network.

In Figure 9, we have shown the values for tripartite mutual information for various states ${\rho }_{ABC}$ obtained after cloning (creating two copies) a non-maximally entangled state, $\left|\psi \right.〉=\alpha \left|00\right.〉+\sqrt{1-{\alpha }^2}\left|11\right.〉$. Here, d represents the machine state parameter for the cloning machine. We see that both positive and negative values for the $TMI$ are obtained. If $TMI<0$, mutual information is monogamous, like entanglement measures. We see that there are no such states where $TMI$ is exactly zero; hence, all cloned triangle networks can be verified as not being part of ${\Delta }_i$.

We define the amount of dependence in cloned triangle networks as

$$D\left[{\rho }^{ABC}\right]=|E_{A|BC}\left[{\rho }^{ABC}\right]-E_{A|B}\left[t{r}_C{\rho }^{ABC}\right]-E_{A|C}\left[t{r}_B{\rho }^{ABC}\right]|.$$

(9)

Using this, we now have a quantitative measure of how much dependency on the initial variable ${\alpha }^2$, which was used by the source to create the non-maximally state, is left in the cloned triangle networks. In Figure 10, we have shown the dependence values present in non maximally entangled states as a function of state parameter $\alpha$. Here, for simplicity, the machine state parameter is set to 0.1. To generate this, we have calculated squashed entanglement in state ${\rho }_{123456}$ which represents the cloned triangle network given in Figure 7; this reduces to the calculation of

$$D\left[{\rho }^{123456}\right]=|E_{A|BC}\left[{\rho }^{123456}\right]-E_{A|B}\left[{\rho }^{1456}\right]-E_{A|C}\left[{\rho }^{1236}\right]|.$$

(10)

6. Conclusions

In this work, we identify quantum cloning as an alternate approach to create quantum networks that can be used whenever there is a limitation on the available number of maximally entangled states. We also study how to identify if a quantum network has been created by cloning or by using independently generated entangled states. Identification can further help us to estimate the capabilities and limitations of the network, which is part of the future extension of the study. We have created various tripartite network topologies with the help of cloning a bipartite two-qubit state. We have used several cloning techniques such as local and non-local with two copies and three copies to create various types of cloned networks. The creation of quantum networks is of importance because in all those situations where the entanglement cannot be generated, we can use the cloning process to obtain a larger network of correlated qubits. We explore the Finner inequalities to check if the obtained cloned networks can be distinguished from networks created by independent sources distributing entangled pairs. We note that some cloned networks cannot be distinguished. We further explore the tripartite mutual information and squashed entanglement to quantify this dependence for triangle networks.