An Outer Approximation Method for Scheduling Elective Surgeries with Sequence Dependent Setup Times to Multiple Operating Rooms

Abstract

In this paper, operating room planning and scheduling problems have been studied. In operating room planning, the allocation of patients to operating rooms and their sequencing are critical in determining the performance of operating rooms. In this paper, three surgery scheduling decisions are considered, including the number of operating rooms to open, the allocation of surgeries to operating rooms, and the sequencing of surgeries in allocated operating rooms. All the surgeries under consideration are elective, and surgery durations are considered deterministic. Further, it is considered that the surgeries have different specialties, and each operating room can accommodate a particular specialty of surgeries, i.e., heterogeneous operating rooms are considered in the current study. Before performing a surgery, setup time is required for operating room turnover and sterilization, and it is considered sequence dependent. A mixed integer nonlinear programming (MINLP) model is developed to minimize the overtime costs of operating rooms for allocation and surgery sequencing with sequence dependent setup times. An outer approximation (OA) method is proposed to solve the problem near optimally. Experiments are conducted to compare the performance of the proposed OA method with the standard mixed integer nonlinear programming model. Computational results show the efficiency of the proposed OA method. Later, a case data from a case hospital is collected and a case study is solved.

1. Introduction

The healthcare industry is one of the largest industries in the service sector [1]. Hospitals are the main units of the healthcare system. Operating rooms are considered to be one of the most critical resources of hospitals. More than 40% of the total revenue of a hospital is generated by operating rooms, and a large proportion of expenses is also associated with operating rooms [2]. In most situations, the operating rooms do not reach target utilization and hence the optimal allocation of surgeries to operating rooms is required to improve operating room utilization and cost saving. Thus, operating room planning and scheduling has attracted the attention of many researchers [3,4,5,6,7].

In literature, operating room planning and scheduling is divided into three hierarchical decision levels: strategic (long term), tactical (medium term), and operational levels (short term) [8,9]. At the strategic level, the hospital case mix is decided, hence it is also called case mix planning. Case mix planning aims to choose the ideal composition and volume of patients in a hospital [10]. At the tactical level, operating room time is divided among surgical specialties. Three scheduling policies are normally used at tactical level. In block scheduling, the operating room is fully reserved for surgeons. In modified block scheduling, some of the capacity is reserved for surgeons and the remaining capacity is shared by other surgeons. In open scheduling, surgeons share operating rooms and can move among them within a day [11,12,13]. Due to the flexibility of open scheduling, a greater number of patients can be accommodated, and hence it has been used by many researchers recently [13,14,15,16,17]. In the open scheduling policy, requests are made by the surgeons for the operating room time. These requests are made prior to the day of surgery and hence the list of elective patients is known in advance [1]. Due to its flexibility and greater patient admissions, an open scheduling policy to schedule elective patients in the operating rooms is used in the current study.

At the operational level, two major scheduling decisions are made. Firstly, a surgical case is assigned to a day and an operating room in the planning horizon, which is also known as advanced scheduling. Secondly, the sequence of surgeries in an operating room is planned, which is referred to as allocation scheduling [18]. In literature, operational level problems are the most studied problems [3,19,20,21,22,23]. However, the literature focuses more on advanced scheduling [2,9,24,25]. Some studies considered advanced and allocation scheduling simultaneously [3,13,22,23]. The present study investigates simultaneously the advanced scheduling and allocation scheduling of surgeries in operating rooms at operational level.

In operating rooms, surgeries of different types are performed that require different equipment during operations. Each operating room is equipped with different types of equipment and resources, which limits the ability of operating rooms to accommodate all surgery types [1]. In the current study, operating rooms are considered heterogeneous, and each operating room can only perform certain types of surgeries.

One surgery scheduling problem that occurs when operating rooms are shared among patients from different specialties in an open scheduling policy is that some setup work is required for preparing and sterilizing the operating room before the start of surgery. This is referred to as operating room turnover time. This setup work is dependent on the preceding surgery and is hence referred to as sequence dependent setup time. In literature, mostly the turnover time is incorporated into the surgery duration [26,27,28]. The reason for this is convenience or compliance with the practice of the hospital under study. Some researchers linked the cleaning or turnover time with the duration of surgeries; for example, smaller cleaning times for smaller surgeries and vice versa [4,29]. However, it is not realistic to incorporate operating room turnover time in surgery duration because it is dependent on the preceding surgery. Moreover, it is not practical to assume turnover or sterilization time based on the length of the surgery. Thus, it needs to be considered separately, and the current study explicitly considers the sequence dependent setup times for advanced and allocation scheduling of surgeries in heterogeneous operating rooms, which is limited in literature [1,30,31].

In the literature, various mathematical programming methods are used to formulate operating room planning and scheduling problems, including linear programming [32,33,34,35], goal programming [36,37,38], integer programming [39,40,41], mixed integer programming [15,19,42,43,44], quadratic programming [45,46,47,48], and constraint programming [1].

Within mixed integer programming, mixed integer linear programming is most widely used. Moosavi and Ebrahimnejad [4] developed a mixed integer linear programming model to solve tactical and operational problems integrated with upstream and downstream wards. In another study, Moosavi and Ebrahimnejad [3] solved combined advanced and allocation scheduling problems. They developed a mixed integer linear programming model for the solution of the problem. Oliveira et al. [20] developed an integer linear programming model to incorporate patient prioritization with the patient scheduling problem.

In some articles, mixed integer nonlinear programming is used to solve patient scheduling problems. Heydari and Soudi [49] developed a mixed integer nonlinear programming model (MINLP) for advanced and allocation scheduling problems. They proposed two stage stochastic programming methods to solve the problem. Batun et al. [12] determined the allocation and start time of surgeries in operating rooms using stochastic programming. Zhao and Li [1] developed a mixed integer nonlinear programming model to solve the elective surgery scheduling problem. They also developed a constraint programming model and compared the performance of a constraint programming model with a MINLP model.

In the literature, various solution methods, such as the exact method, heuristics, and metaheuristics, have been used to solve operating room planning and scheduling problems. Exact solution methods optimally solve operating room planning and scheduling problems. The advantage of exact solution methods is that they provide a single optimal solution. The exact methods used in literature include column generation [24,50,51,52,53], dynamic programming [54,55,56,57,58], branch and bound [42,59,60,61,62], branch and price [54,55,63,64,65], and branch and cut methods [66,67]. In addition, researchers have considered heuristics [68,69,70], hybrid methods [71,72], and metaheuristics [44,62,73] for operating room planning and scheduling problems. The operating room planning and scheduling is NP-hard [74], and therefore, different metaheuristics have also been applied to solve this problem in reasonable computation to get near-optimal results [75,76]. Most researchers have studied operating room planning and scheduling problems using simulated annealing [77], genetic algorithm [44], constructive heuristics [4], hybrid simulated annealing [72], Tabu search [23,78], hill climbing algorithms [79], artificial bee colony algorithm [31], and ant colony algorithm [80,81], etc. The metaheuristics are the most common in operating room planning and scheduling literature [44,62,72,82]. Due to the complexity of mixed integer nonlinear programming models, difficulties can arise in solving the problems. For large sized problems, using exact methods takes a lot of time, and in many situations a feasible solution is not obtained within a reasonable computational time [1]. Hence the present study is focused on developing a solution method of MINLP to obtain a near-optimal solution within a reasonable computational time without affecting the quality of the solution.

In the current study, a mixed integer nonlinear programming model like that of Zhao and Li [1] is developed and solved using the outer approximation method. Our study is different from that of Zhao and Li [1] in that the method we have used to solve the developed model has not been reported as being used for operating room planning and scheduling so far. Hence, the current study solved the advanced and allocation scheduling of elective patients with sequence dependent set up times and considering heterogenous operating rooms. Further, it proposes a method to approximately solve the developed MINLP model and investigates the quality of the solution obtained by the proposed method.

The primary contribution of the study is to consider the sequence dependent setup times between the successive surgeries in multiple heterogeneous operating rooms. In addition, a solution method based on the outer approximation method has been proposed to solve the operating room planning and scheduling problem. The rest of the paper is organized as follows: the problem description and mathematical formulation is presented in Section 2, Section 3 presents the proposed outer approximation method, Section 4 shows computational experiments and results, and Section 5 concludes the paper and gives some future research directions.

2. Problem Description and Mathematical Formulation

The problem considered in the current study is to determine the number of open operating rooms, the allocation of patients to operating rooms, and the sequencing of patients within the allocated operating rooms. The operating rooms are heterogeneous, i.e., only specific types of surgeries can be performed in the operating rooms. Elective patients are considered, and their surgery durations are taken as deterministic. On a tactical level, an open scheduling policy is used, i.e., operating rooms are shared among specialties. When operating rooms are shared by surgeons from different specialties, sequence dependent setup times occur, which are given special consideration in the current study. Further, it is assumed that surgeons, anesthesiologists, and other supporting staff are available and do not become the bottleneck. This section presents the mixed integer nonlinear program (MINLP) built for the elective surgery scheduling problem. Before formulating the model, the following notations are defined in

Table 1. Notations.

Parameters
$I$	The set of ORs
$i$	$\mathrm{The} \mathrm{index} \mathrm{of} \mathrm{ORs}, i=1,\dots , I$
$F_i$	The regular costs of OR per day
$O_i$	The unit overtime costs of OR
$T_i$	$\mathrm{The} \mathrm{regular} \mathrm{working} \mathrm{time} \mathrm{of} \mathrm{the} \mathrm{OR} i$
$M_i$	$\mathrm{The} \mathrm{maximum} \mathrm{available} \mathrm{time} \mathrm{of} \mathrm{OR} i$, including overtime
$J$	The set of surgeries under consideration
$j$	$\mathrm{The} \mathrm{index} \mathrm{to} \mathrm{represent} \mathrm{surgeries}, j=1,\dots , J$
$D_j$	The operation time
$N$	The set of specialities
$n$	The index of specialities
${\alpha }_{jn}$	$=1 \mathrm{if} \mathrm{surgery} j$$\mathrm{is} \mathrm{of} \mathrm{type} n$
$T_{{jj}^{\prime }}$	$\mathrm{Setup} \mathrm{time} \mathrm{of} \mathrm{surgery} j^{\prime }$$\mathrm{when} \mathrm{it} \mathrm{is} \mathrm{performed} \mathrm{after} \mathrm{surgery} j$
${\beta }_{in}$	$=1 \mathrm{if} \mathrm{surgery} \mathrm{of} \mathrm{type} n$$\mathrm{can} \mathrm{be} \mathrm{performed} \mathrm{in} \mathrm{OR} i$
$k$	$\mathrm{The} \mathrm{sequence} \mathrm{of} \mathrm{surgery} \mathrm{in} \mathrm{the} \mathrm{OR} k=1,\dots , J$
Decision variables
$y_i$	$=1 \mathrm{if} \mathrm{the} \mathrm{operating} \mathrm{room} i$ is used, 0 otherwise
$x_{ijk}$	$=1 \mathrm{if} \mathrm{surgery} j$$\mathrm{is} \mathrm{scheduled} \mathrm{at} \mathrm{the} \mathrm{position} k$$\mathrm{in} \mathrm{OR} i$, 0 otherwise
$z_i$	$\mathrm{Overtime} \mathrm{in} \mathrm{OR} i$

:

The mixed integer nonlinear programing model of the problem is developed as:

$$\min C={\displaystyle \sum _{i=1}^I{y}_i\left(F_i+O_i{z}_i\right)}$$

(1)

$${\displaystyle \sum _{k=1}^J{x}_{ijk}}\le {\displaystyle \sum _{n=1}^N{\beta }_{in}{\alpha }_{jn } \forall i,j}$$

(2)

$${\displaystyle \sum _{i=1}^I{\displaystyle \sum _{k=1}^J{x}_{ijk}=1 \forall j}}$$

(3)

$${\displaystyle \sum _{j=1}^J{x}_{ij(k+1)}}\le {\displaystyle \sum _{j=1}^J{x}_{ijk} k=1, . . . , J-1 \forall i}$$

(4)

$${\displaystyle \sum _{j=1}^J{x}_{ij1}}\le y_i \forall i$$

(5)

$${\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^J{x}_{ijk}}}{D}_j+{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J{x}_{ijk}{x}_{{ij}^{\prime }(k+1)}}}}{T}_{{jj}^{\prime }}-T_i\le z_i \forall i$$

(6)

$$z_i\ge 0 \forall i$$

(7)

$$z_i+T_i\le M_i \forall i$$

(8)

$$y_i\in \left\{0,1\right\} \forall i$$

(9)

$$x_{ijk}\in \left\{0,1\right\} \forall i,j,k$$

(10)

The objective function (1) consists of two terms. The first term represents fixed costs, and the second term represents the overtime costs of operating rooms. In the objective function, the decision variable $y_i$ is used, which is binary variable. This decision variable is 1 if the operating room is open and its value is 0 if the operating room is closed, which is first decision, i.e., the number of open operating rooms. The decision variable $z_i$ is used in the objective function, which is the overtime, and is calculated in Equation (6), which is based on the allocation and sequence of patients in the operating room and uses the value of $x_{ijk}$. The binary decision variable $x_{ijk}$ is used for the allocation of a surgery and its position in the sequence in the operating room.

Constraint (2) specifies that the surgery type must meet the requirements of an operating room. It gives the condition that a surgery can only be performed in a compatible operating room with the required equipment. Constraint (3) guarantees that each surgery should be scheduled once and avoids the scheduling of the same surgery in multiple operating rooms at the same time. Constraint (4) represents the precedence of surgeries in the operating room. This constraint maintains the sequence of surgeries and ensures that all positions in a sequence are occupied in a numerical order. Constraint (5) states that surgeries can only be scheduled in open operating rooms and that if an operating room is closed, no surgeries can be assigned to that operating room. Constraints (6) and (7) define the length of overtime of the operating room. Note that constraint (6) is quadratic, as set-up times are sequence dependent. Equation (6) consists of three terms: the first term calculates the total surgery duration of all the patients assigned to an operating room, the second term calculates the sequence-dependent setup times, and the third indicates the standard operating time in an operating room. This equation provides information on whether there will be overtime in the considered operating room based on the sequence provided by a particular solution. It is important to note that even if the overtime is 0 in a particular instance, the quadratic Equation (6) cannot be eliminated as this provides information about the overtime’s value. The model will remain nonlinear even if the overtime value is 0 in a particular set of instances. Constraint (8) states that the operating room’s maximum allowable time limit must be followed. Constraints (9) and (10) define the binary domain of decision variables.

3. Solution Method

This section explains the solution method adopted to solve the developed mixed integer nonlinear problem. The proposed outer approximation method is based on the cutting plane method [83,84,85]. Consider the following MINLP problem:

$$\min f\left(a,b\right)$$

(11)

$$S.t.g_j\left(a,b\right)\le 0 \forall j=1\dots m$$

(12)

$$a\in A,b\in B \mathrm{integer}$$

(13)

The decision variables are represented by vectors a and b and $f:{ℝ}^n\times {ℝ}^p\to ℝ$,$g:{ℝ}^n\times {ℝ}^p\to {ℝ}^m$ are two continuously differentiable functions. If we fix the vector of integer variables $b=b^l,b^l\in \mathbb{Z}$ for any iteration, $l$ we get a sub-problem in the following form:

$$\min f\left(a,b^l\right)$$

(14)

$$S.t.g_j\left(a,b^l\right)\le 0 \forall j=1\dots m$$

(15)

$$a\in A$$

(16)

If this problem is feasible, it is solved to get an optimal solution, and if the problem is infeasible, infeasibility is minimized by solving the problem. We get gradients of functions $f\left(a,b\right)$ and $g_j\left(a,b\right)$ at $\left(a^l,b^l\right)$, then a mixed integer problem that is equivalent to a mixed integer nonlinear problem (11)–(13) can be obtained:

$$\min \eta$$

(17)

$$S.t.\eta \ge f\left(a^l,b^l\right)+\nabla f\left(a^l,b^l\right)\left(\begin{array}{c}a-a^l\\ b-b^l\end{array}\right) \forall l=1\dots L$$

(18)

$$0 \ge g\left(a^l,b^l\right)+\nabla g\left(a^l,b^l\right)\left(\begin{array}{c}a-a^l\\ b-b^l\end{array}\right) \forall l=1\dots L$$

(19)

$$a\in A,b\in B \mathrm{integer}$$

(20)

where $L$ represents the number of trials for which the problem is solved. Problems (17)–(20) are the master problem. In this problem. Constraints (18)–(20) are used to outer approximate the objective function and constraints, respectively.

The sub-problem for the mixed integer nonlinear problem in this study is defined as:

$$\min C=f^l\left({\stackrel{⌢}{y}}_i^l,z_i^l\right)={\displaystyle \sum _{i=1}^I{\stackrel{⌢}{y}}_i\left(F_i+O_i{z}_i\right)}$$

(21)

subject to:

$${\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^J{\stackrel{⌢}{x}}_{ijk}}}{D}_j+{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J{\stackrel{⌢}{x}}_{ijk}{\stackrel{⌢}{x}}_{i{j}^{\prime }(k+1)}}}}{T}_{jj}-T_i\le z_i \forall i$$

(22)

$$z_i\ge 0 \forall i$$

(23)

$$z_i+T_i\le M_i \forall i$$

(24)

The hat indicates that the integer variables are fixed. The infeasibility can be minimized by solving the following problem:

$$\min u$$

(25)

$$S.t.g_j\left(a,b^l\right) \le u$$

(26)

$$a\in A,u\in ℝ$$

(27)

The feasibility problem of the proposed model is formulated as:

$$\min u = {\displaystyle \sum _i{u}_1\left(i\right)}+{\displaystyle \sum _i{u}_2}\left(i\right)$$

(28)

$$\begin{array}{l}{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^J{\stackrel{⌢}{x}}_{ijk}}}{D}_j+{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J{\stackrel{⌢}{x}}_{ijk}{\stackrel{⌢}{x}}_{{ij}^{\prime }(k+1)}}}}{T}_{jj}-T_i-z_i\\ \le u_1\left(i\right) \forall i\end{array}$$

(29)

$$z_i+T_i-M_i\le u_2\left(i\right) \forall i$$

(30)

$$z_i\ge 0, u_i\in ℝ$$

(31)

The outer approximation master problem is defined as:

$$\min \eta$$

(32)

subject to:

$$\eta \le UBD-\epsilon$$

(33)

$$\eta =f\left(x,y\right)\ge {\displaystyle \sum _{i=1}^I{y}_i\left(F_i+O_i{z}_i\right)}$$

$${\displaystyle \sum _{k=1}^J{x}_{ijk}}\le {\displaystyle \sum _{n=1}^N{\beta }_{in}{\alpha }_{jn } \forall i,j}$$

(34)

$${\displaystyle \sum _{i=1}^I{\displaystyle \sum _{k=1}^J{x}_{ijk}=1 \forall j}}$$

(35)

$${\displaystyle \sum _{j=1}^J{x}_{ij(k+1)}}\le {\displaystyle \sum _{j=1}^J{x}_{ijk} k=1, . . . , J-1 \forall i}$$

(36)

$${\displaystyle \sum _{j=1}^J{x}_{ijk}}\le y_i \forall i$$

(37)

$$\begin{array}{l}{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^J{x}_{ijk}}}{D}_j+{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J{x}_{ijk}{x}_{{ij}^{\prime }(k+1)}}}}{T}_{jj}-T{-}_i{z}_i+\\ {\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^J\left(x_{ijk}-x_{jk}^f\right)}}{D}_j+{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J\left(x_{ijk}-x_{ijk}^f\right)x_{{ij}^{\prime }(k+1)}}}}\\ +{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J{x}_{ijk}\left(x_{{ij}^{\prime }(k+1)}-x_{{ij}^{\prime }(k+1)}^f\right)}}}+T_{jj}-T{-}_i\left(z_i-z_i^f\right) \\ \le 0 \forall i f\in F^l\end{array}$$

(38)

$$\begin{array}{l}{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^J{x}_{ijk}}}{D}_j+{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J{x}_{ijk}{x}_{{ij}^{\prime }(k+1)}}}}{T}_{jj}-T{-}_i{z}_i+\\ {\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^J\left(x_{ijk}-x_{jk}^e\right)}}{D}_j+{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J\left(x_{ijk}-x_{ijk}^e\right)x_{{ij}^{\prime }(k+1)}}}}\\ +{\displaystyle \sum _{j=1}^J{\displaystyle \sum _{k=1}^{J-1}{\displaystyle \sum _{j^{\prime }=1}^J{x}_{ijk}\left(x_{{ij}^{\prime }(k+1)}-x_{{ij}^{\prime }(k+1)}^e\right)}}}+T_{jj}-T{-}_i\left(z_i-z_i^e\right) \\ \le 0 \forall i e\in E^l\end{array}$$

(39)

$$z_i\ge 0 \forall i$$

(40)

$$z_i+T_i\le M_i \forall i$$

(41)

$$y_i\in \left\{0,1\right\} \forall i$$

(42)

$$x_{ijk}\in \left\{0,1\right\} \forall i,j,k$$

(43)

where $F^l$ and $E^l$ represent the solution trials when the solution was feasible and infeasible, respectively. The accuracy of the algorithm is determined by $\epsilon$. For example, if the sub-problem gives an optimal solution, the proposed OA method will obtain an $\epsilon$-optimal solution. Further, it is unnecessary to get an optimal solution by solving the master problem; a feasible solution is sufficient. However, the number of iterations may increase if we get sub-optimal solutions. The proposed outer approximation method is explained in Figure 1 below. In Figure 1, $F^{-1}$ and $E^{-1}$ are the sets of iterations when the sub-problem (21)–(24) is feasible or infeasible respectively. Their values are initially represented as empty sets $\varphi$ because both sets of iterations are empty at the start of the method. As the iterations of the proposed OA method proceed, the sets are populated with respective feasible or infeasible iterations, as given in step (2) of the pseudocode in Figure 1.

4. Computational Experiments and Results

In this section, several operating room problems are solved to investigate the performance of the proposed OA method and compare it with the standard model. Further, a case study from a hospital is solved, and the results are discussed. The experiments are performed using CPLEX and are run on a laptop with an Intel Core i3 processor of 2.00 GHz and 4.00 GB of RAM.

The data used for comparison of the performance of the proposed OA method is generated randomly. For the arrival of elective surgery patients, it is assumed that the elective patients follow a discrete uniform distribution derived from historical data. Patients’ length of stay in an operating room is generated using lognormal distribution [9,86]. Sequence dependent setup times are generated randomly for different specialties. For the case study, data from a case hospital are collected and the case study is solved for a period of two weeks.

Various instances of different sizes are solved to compare the performance of the proposed method. For each instance, CPU time, objective function values, and data sample specifications are recorded and presented in

Table 2. CPU time and objective function values along with data samples specifications.

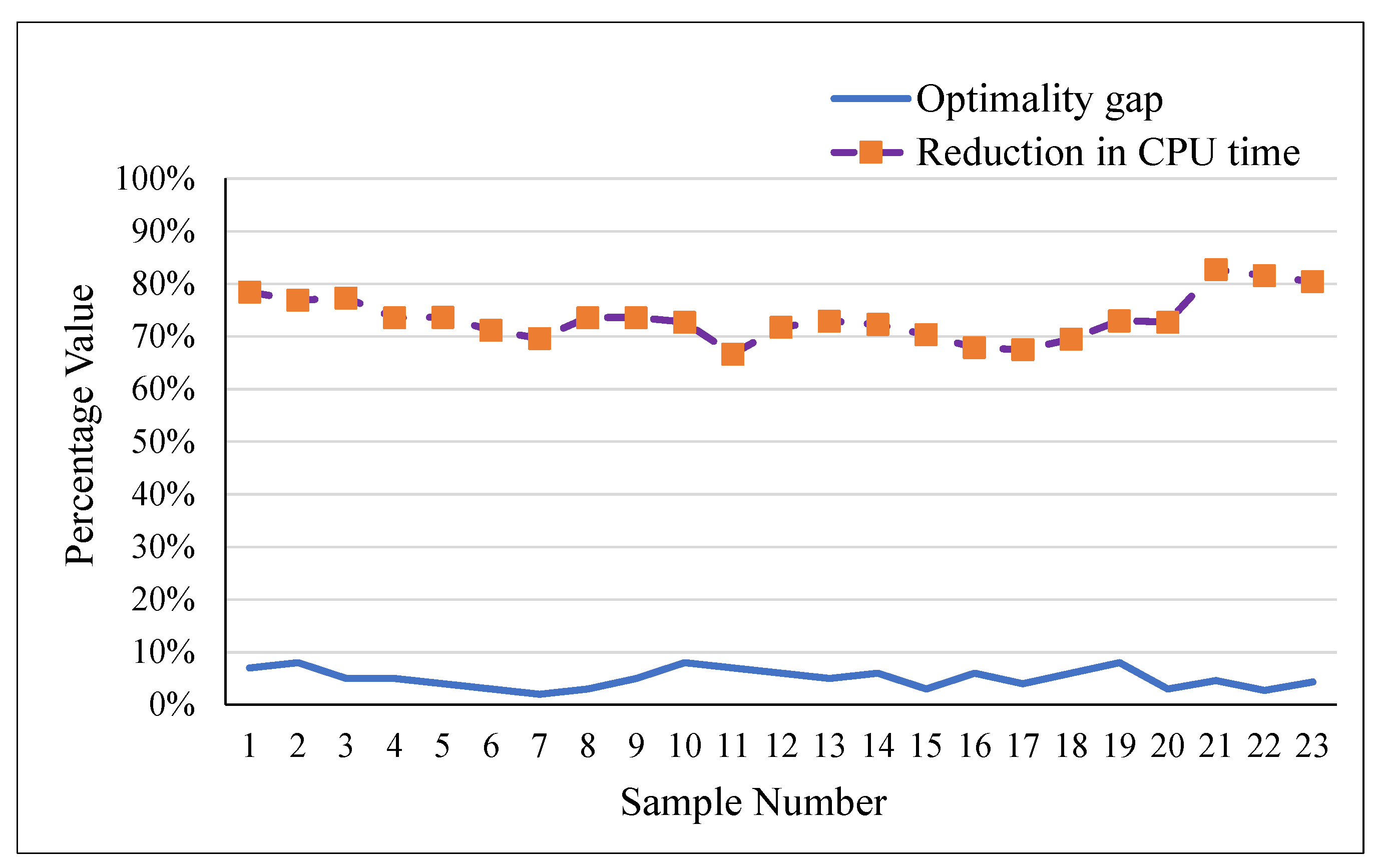
Sample	No. of Patients	Specialties	ORs	Standard Model		Outer Approximation
				CPU (s)	Objective	CPU (s)	Objective	Optimality Gap	Reduction in CPU Time
1	15	3	2	51	11,960	11	12,795	7%	78%
2	20	3	2	52	11,120	12	12,053	8%	77%
3	25	3	3	53	16,040	12	16,867	5%	77%
4	30	4	3	53	21,240	14	22,342	5%	74%
5	35	4	4	57	25,320	15	26,315	4%	74%
6	40	4	4	59	28,940	17	29,691	3%	71%
7	45	4	4	56	29,100	17	29,791	2%	70%
8	50	4	5	72	35,720	19	36,644	3%	74%
9	55	5	5	72	36,020	19	37,800	5%	74%
10	60	5	6	77	38,440	21	41,600	8%	73%
11	70	5	6	75	42,700	25	45,500	7%	67%
12	75	5	6	78	43,840	22	46,600	6%	72%
13	80	5	7	85	49,480	23	51,960	5%	73%
14	85	5	7	83	48,300	23	51,120	6%	72%
15	90	5	7	81	51,140	24	52,728	3%	70%
16	95	5	8	81	56,800	26	60,060	6%	68%
17	100	6	8	80	58,100	26	60,332	4%	68%
18	105	6	8	82	57,460	25	60,810	6%	70%
19	110	6	9	100	64,920	27	70,240	8%	73%
20	115	6	9	99	66,340	27	68,164	3%	73%
21	200	6	10	272	71,210	47	74,650	5%	83%
22	250	6	11	315	75,250	58	77,380	3%	82%
23	300	6	12	358	77,440	70	80,960	4%	80%

.

In Table 2, ORs represents the number of open operating rooms. Objective function values and CPU time for both the standard model and the proposed OA method are compared. It can be observed that the OA model provides better results with lesser CPU time as compared to the standard model. The OA model gives the value of the objective function with a minimum optimality gap of 2%. The optimality gap used in the current study is calculated using (44):

$$Optimality Gap \%=\frac{x_{\min }-x_i}{x_{\min }}\times 100$$

(44)

where, $x_{\min }$ is the minimum value of the objective function and is obtained through the standard model, and $x_i$ is the value of the objective function obtained using the OA method at each iteration. It is observed that OA obtained better results in a shorter time. This indicates the efficiency of the OA method.

Further, a comparison of the optimality gap with the percentage reduction in CPU time is drawn in Figure 2. It can be seen from Figure 2 that for all of the considered problem instances, the proposed method provided near-optimal results with lesser optimality gaps and a significant reduction in the computational time. For example, for problem 1, the optimality gap with the proposed OA method is 7%, and the percentage reduction in CPU time is 78%. Similarly, for problem 9, the optimality gap is 5%, with a 74% reduction in computational time.

Equation (45) represents the formula for calculating the percentage reduction in CPU time, where $t_{MINLP}$ is the CPU time using the standard model and $t_{OA}$ is the CPU time for the proposed OA method. It is observed from Figure 2 that the OA method provides better results in lesser CPU time.

$$Reduction in CPU Time \%=\frac{t_{MINLP}-t_{OA}}{t_{MINLP}}\times 100$$

(45)

Hence, it can be concluded that the proposed OA method provides good quality near-optimal results in shorter CPU times as compared to the exact method.

The convergence graph of the proposed method is presented in Figure 3 for 23 test problems. It is observed that OA converges after two iterations in the majority of instances. Equation (46) represents the formula used to find the percentage convergence value in the current study:

$$Percentage convergence \%=\frac{x_i-x_{\min }}{x_{\min }}\times 100$$

(46)

where, $x_{\min }$ is the minimum value of the objective function out of all the iterations of the OA method, and $x_i$ is the value of the objective function obtained using the OA method at each iteration.

Case Study

To further investigate the performance of the proposed OA method, surgery data from a case hospital is collected and a case study is solved for a period of two weeks. The results of the case study are summarized in

Table 3. Summary of case study results.

Day	Patients	Operating Rooms	CPU (s)	Objective	Average OR Overutilization	Average OR Overtime
1	40	4	16	27,800	5%	98
2	43	5	16	26,100	0%	11
3	40	5	16	33,620	4%	86
4	40	5	15	35,380	4%	104
5	48	5	17	36,100	5%	111
6	40	5	16	33,100	3%	81
7	49	4	15	25,700	4%	71
8	41	5	15	33,500	4%	85
9	50	5	17	33,780	4%	88
10	47	5	20	33,200	3%	82
11	50	5	17	36,440	5%	114
12	43	4	15	28,960	6%	112
13	41	4	15	26,480	4%	81
14	45	4	20	28,680	6%	109
15	43	5	18	34,880	4%	99

. The hospital under study has eight operating rooms with two operating rooms reserved for emergency patients. There are patients of six different specialties and the aim is to minimize the operating room costs of both regular and overtime costs.

Regular time costs can be minimized by deciding how many operating rooms to leave open for a given day. Similarly, overtime costs can be reduced by minimizing the average overtime in operating rooms. The results in Table 3 show that the proposed method results in less overtime values with the average overutilization of operating rooms up to 6%.

5. Conclusions and Suggestions for Future Research

In this paper, a method based on outer approximation is proposed to solve patient scheduling problems considering sequence dependent setup times in multiple heterogeneous operating rooms. Initially, a mixed integer nonlinear model is developed and solved using CPLEX solver. Moreover, an efficient outer approximation method is proposed to solve the problem near-optimally. The results obtained using the OA method are compared with the standard model. The performance metrics considered are the quality of the solution and the efficiency of the method. The computational results indicate the efficiency of the proposed OA method. Specifically, the proposed method outperforms the original MINLP model in terms of CPU time. It obtains near optimal results in comparatively less CPU time. This study extends the current operating room planning and scheduling literature in that it proposes a method to efficiently solve nonlinear problems. However, the current study has some limitations. In the current study, only the operating rooms are considered; it can be further extended to include upstream and downstream wards as well as other personnel, such as anesthesiologists, and material resources along with the scheduling of operating rooms.

Moreover, as the proposed OA method relies on the feasibility of the obtained solution and infeasible solutions can increase the number of iterations. The feasibility of the obtained solution is greatly affected by the value of the Boolean variables provided for each iteration. Thus, a good quality initial set of Boolean decision variables can result in better solutions with lesser number of iterations. Hence, it is proposed that this method may be used as a hybrid with some efficient heuristics to find good quality feasible solutions to avoid the unnecessary greater number of iterations that can further reduce the computational time.